Abstract
Federated learning, with its unique privacy protection mechanisms and distributed model training capabilities, provides an effective solution for data security by addressing the challenges associated with the inability to directly share private data due to privacy concerns. It exhibits broad application potential across various fields, particularly in scenarios such as autonomous vehicular networks, where collaborative learning is required from data sources distributed across different clients, thus optimizing and enhancing model performance. Nevertheless, in complex real-world environments, challenges such as data poisoning and labeling errors may cause some clients to introduce label noise that significantly exceeds ordinary levels, severely impacting model performance. The following conclusions are drawn from research on extreme label noise: highly polluted data severely affect the generalization capability of the global model and the stability of the training process, while the reweighting strategy can improve model performance. Based on these research conclusions, we propose a method named Enhanced Knowledge Distillation and Particle Swarm Optimization for Federated Learning (FedDPSO) to deal with extreme label noise. In FedDPSO, the server dynamically identifies extremely noisy clients based on uncertainty. It then uses the particle swarm optimization algorithm to determine client model weights for global model aggregation. In subsequent rounds, the identified extremely noisy clients construct an interpolation loss combining pseudo-label loss and knowledge distillation loss, effectively mitigating the negative impact of label noise overfitting on the local model. We carried out experiments on the CIFAR10/100 datasets to validate the effectiveness of FedDPSO. At the highest noise ratio under Beta = (0.1, 0.1), experiments show that FedDPSO improves the average accuracy on CIFAR10 by 15% compared to FedAvg and by 11% compared to the more powerful FOCUS. On CIFAR100, it outperforms FedAvg by 8% and FOCUS by 5%.
1. Introduction
Federated learning (FL), a novel distributed machine learning framework, has been widely applied in real-world scenarios such as autonomous vehicular networks. The core idea is to achieve collaborative training between servers and clients, addressing data privacy issues while circumventing various restrictions on data collection [1,2]. Compared to traditional centralized machine learning, federated learning offers stronger privacy protection, as the original data of the clients remains local, thereby reducing the risk of data leakage [3,4]. However, federated learning faces a key challenge of label noise in practical applications. Generally, the performance of a model depends on the quantity and quality of the training data, and the data in the actual application scenario of federated learning are usually distributed and heterogeneous [5]. For example, in autonomous vehicular networks, each vehicle shares information during operation and collects and annotates raw data. Due to privacy protection constraints, these raw data cannot be directly uploaded to the server for centralized training. The diversity of data sources and the complexity of annotation during the data collection process render incorrect labeling inevitable, resulting in varying degrees of inaccuracies in the data labels of each vehicle. According to statistics, labeled datasets generated in real-world environments typically have label noise ranging from 8.0% to 40.0% [6,7]. Training without noise handling results in the model overfitting to label noise, reducing its accuracy and generalization capability [8]. Extracting high-quality labeled data from large datasets incurs significant resource consumption, and achieving a completely clean dataset is virtually impossible in practice. Furthermore, in some extreme cases, federated learning faces even more severe challenges. This research considers an extreme case: the training of the model inevitably requires the participation of many clients. Due to unintentional mislabeling, deliberate data poisoning, or other factors, some clients may have extreme label noise (up to 90%), referred to as extremely noisy clients. These clients not only significantly interfere with the training of the global model but may also impede its effective convergence. Implementing label correction for these clients is also costly and technically complex. Therefore, developing robust federated learning models in the presence of interference from extremely noisy clients is a task of practical significance [9].
In recent years, it has been discovered that noisy data in the real world significantly degrade the quality of model training. Effectively handling noisy data has become a critical challenge in the field of machine learning [10,11]. To alleviate the impact of noisy data in model training, many novel and advanced methods [10,12,13,14] have been proposed and effectively applied to federated learning with label noise. The core idea behind these methods is that each client model has the opportunity to contribute to the global model through aggregation. This relies on the key assumption that each client has a relatively low noise ratio. However, in real-world scenarios, the client may contain extreme label noise due to uncertainties such as model poisoning, data loss, and incorrect labeling. Training models on extremely noisy clients leads to significant performance degradation and makes the training process highly unstable. Although directly discarding extremely noisy clients during model aggregation is preferable to reweighting clients, this approach contradicts the original intent of federated learning [15]. Therefore, it is necessary to design robust denoising methods to mitigate the adverse effects of extremely noisy clients on the global model and to use an adaptive global model aggregation algorithm to improve the performance of the global model.
Based on the above analysis, we propose FedDPSO to mitigate the negative impact of highly contaminated data from extremely noisy clients. The interpolation loss based on pseudo-label loss and knowledge distillation loss is devised to mitigate the risk posed by incorrect information in noisy data, and an improved reweighting strategy based on particle swarm optimization is used to tune the global model aggregation. Pseudo-labeling enables the model to learn more realistic data features. Knowledge distillation facilitates local models to learn the outputs of the global model on local data [16], optimizing the training of extremely noisy clients. The particle swarm optimization algorithm evaluates the performance of the provisional global model to determine the optimal weight allocation [17]. First, the server leverages the local models uploaded by clients to dynamically identify extremely noisy clients based on uncertainty [18]. The server then employs the particle swarm optimization algorithm to compute client model weights for global model aggregation. This weighted averaging strategy effectively enhances the performance of the global model. In subsequent rounds, the identified extremely noisy clients construct the interpolation loss combining pseudo-label loss and knowledge distillation loss for specialized local training, effectively mitigating the negative impact of label noise overfitting on the local model. The main contributions of this work are as follows:
- The application of the particle swarm optimization algorithm to weight adjustment is investigated. The particle swarm optimization algorithm employs a population-based approach to perform a global search for the optimal weights. It uses the prediction results of a provisional aggregation model on an auxiliary dataset as a criterion, updating the positions and velocities of particles through continuous iterations to search for the optimal solution in the weight space.
- The FedDPSO approach is proposed. The server dynamically identifies extremely noisy clients by predicting uncertainty with local models and then uses the particle swarm optimization algorithm to adjust the aggregation weights for global model aggregation. Extremely noisy clients construct the interpolation loss of the pseudo-label loss and knowledge distillation loss to train the local model.
- Experimental results on various datasets demonstrate that this method mitigates the impact of highly polluted data from extremely noisy clients on the global model and effectively enhances the robustness of model training.
This paper is divided into six sections. Section 1 introduces the significant damage to the global model caused by extremely noisy clients and the FedDPSO method to deal with this problem. Section 2 reviews existing noise processing methods and their application in federated learning. Section 3 provides a detailed description of the FedDPSO method. Section 4 presents experiments to demonstrate the effectiveness of FedDPSO. Section 5 discusses the efficiency and effectiveness of the proposed method. Section 6 concludes this paper.
2. Related Works
2.1. Federated Learning with Label Noise
Label noise has become one of the critical obstacles to the practical application of federated learning. Methods for addressing data heterogeneity have encountered certain difficulties in dealing with label noise, and traditional label noise processing is also not necessarily applicable in distributed learning [19]. Numerous label noise handling methods are primarily divided into the following categories: sample selection [20], loss function adjustment [21], regularization [22], and robust model architecture [23]. There are many studies about how federated learning can cope with label noise. A more straightforward approach is to utilize clean data on the server for evaluating the noise level of the models involved in aggregation, and the server can redistribute the aggregation weights depending on the noise level [24]. In addition, FOCUS [12] uses clean data stored in the server to estimate the trustworthiness of participating client models, normalizing the mutual cross entropy loss to adaptively adjust the aggregation weights. Although the additional auxiliary data are limited by privacy, they offer advantages in aspects such as deployment simplicity, communication overhead, and others. FedCorr [13] identifies clean and noisy clients by utilizing the dimensionality of the models’ prediction subspaces, then it uses the estimated noise rate as a regularization factor to fine-tune the global model on clean clients and correct data labels of noisy clients. RoFL [14] selects confidence samples with small losses to train and create local centroids and transfer the aligned centroids between the client and the server. An interesting observation is that model is initially able to memorize only simple instances and adapts to more complex instances as the training period progresses. For this analysis, Fed-NCL [10] estimates data quality and model differences to identify noisy clients, and it uses robust hierarchical aggregation to adaptively aggregate client models. However, these methods are built on the basis that all clients can make a useful contribution to model aggregation. This may be difficult to satisfy in scenarios with extremely noisy clients due to the intense interference of highly noisy data [15].
2.2. Knowledge Distillation
Knowledge distillation is a technique used for model compression and transfer learning, which is now one of the crucial model optimization and application techniques in deep learning [16]. It is a teacher–student training structure in such a way that a trained teacher model usually provides the knowledge and supervises the student model to acquire the knowledge through knowledge distillation [25,26]. One of its advantages is that it can effectively boost the prediction and generalization capability of the model. By learning the knowledge from the teacher model, we can transport the knowledge from the complex teacher model to the simple student model at the cost of a slight performance loss, and the student model can obtain richer feature representations and improve its generalization capability to unknown data. In addition, the knowledge transmission mechanism of knowledge distillation can be applied to several domains [27], e.g., data augmentation, privacy and security preservation, etc. Hinton et al., in their pioneering work on knowledge distillation [28], proposed using the output probability distribution of the teacher model to guide the student model, an approach that helps to provide richer training signals and mitigates the overfitting problem. Recently, some progress has been made in research around the application of knowledge distillation to federated learning. Li et al. proposed the FedMD algorithm [16], where the client estimates the predicted scores using the shared public dataset and the server performs the average aggregation operation. With the help of knowledge distillation, the client model fits the average prediction scores of the public dataset to achieve global knowledge migration. Zhu et al. proposed FedGen [29], a data-independent federated knowledge distillation algorithm, which does not require the distilled data and provides distilled samples via a training generator. Jeong et al. proposed a federated knowledge migration approach without the aid of distilled data, FedDistill [30], in which each client computes an average prediction score for each category to send to the server for average aggregation, and the client downloads the global category prediction scores, which are used as regular terms to migrate the global knowledge into the local model during local training in later rounds. In summary, knowledge distillation has a rich potential for application in federal learning, which can provide effective solutions for federated learning through model compression, data imbalance handling, privacy protection, transfer learning, and enhanced model robustness [31].
2.3. Particle Swarm Optimization Algorithm
Meta-heuristic algorithms are a class of algorithms that have been widely researched and show great potential in engineering applications, machine learning, etc. Some advanced algorithms such as HMO [32], FDB [33], and MGL-MRFO [34] have been proposed and applied in practice. Among the meta-heuristic algorithms, the Particle Swarm Optimization algorithm (PSO) is a well-known stochastic swarm intelligent optimization algorithm inspired by the behavior of bird flocks searching for food in nature, which is an efficient way to search for the optimal solution in the solution space [35,36]. Currently, PSO has been successfully applied to optimization problems in many domains including engineering, economics, computer science, etc., and has gradually proved to be reliable and productive in real-life scenarios. For example, Zhu et al. [37] proposed a multi-strategy particle swarm algorithm based on exponential noise for solving the low-altitude penetration problem in a safe space. In addition, guiding the application of PSO to federated learning is an active research topic. In a federated learning setting where participants do not need to share personal data and only locally train local models for uploading servers to collaboratively train machine learning models, this process requires an optimization algorithm that balances server and client training objectives. Here, PSO is applicable, as it combines the characteristics of global optimization and local tuning [38]. Next, the advantages of PSO in terms of easy implementation, fast convergence, high computational speed, and low memory requirements make it a practical choice for federated learning with limited computational resources and time [39]. Devarajan et al. [40] proposed the aPSO-FLSADL model with a modified particle swarm optimization algorithm based on a mutation operator for parameter optimization in federated learning. Houssein et al. [38] used the particle swarm optimization algorithm of an improved version of FedImpPSO to update the global model by collecting scores from a local model mainly used for federated learning, improving the robustness of the algorithm under unstable network conditions. Zhao et al. [41] investigated a particle swarm optimization algorithm based on statistical instantaneous state information to optimize wireless federated learning networks with communication delay constraints by maximizing the number of active clients. Papers such as these on the application of PSO in federated learning have shown that PSO presents excellent performance in multiple directions in federated learning. It has the capability of global search and local optimization, which can effectively optimize model parameters and better coordinate the training of the global model, providing a new way to achieve efficient training on large-scale datasets [42]. In the future, the application of PSO in federated learning will be further expanded and improved with increases in privacy and security requirements [43].
3. Methods
In this section, we describe in detail the effective method FedDPSO proposed for federated learning in the presence of extremely noisy clients, starting from the problem definition.
3.1. Problem Definition
Federated learning is widely applied in scenarios that require the protection of data privacy and security, helping us to achieve a balance between information sharing and model training in fields such as autonomous vehicular networks and healthcare. In a typical federated learning setting, to safeguard the data security of the clients, the server or other participants are not allowed to access the local data of the clients. Instead, clients train local models and upload them to the server to collaboratively generate a global model [44]. In practical applications, due to uncertainties such as mislabeling or data poisoning, the local data collected by clients may contain extreme label noise. The local model can overfit extreme label noise, resulting in more severe performance degradation than that caused by ordinary noise [45]. Regarding the noise ratio, the range can vary from 0% to 100%. Assuming that a client’s label noise level is around 90%, it is classified as an extremely noisy client. We place particular emphasis on these clients, classified as extremely noisy, which is of significant importance in research on federated learning.
3.2. Framework Overview
The FedDPSO’s basic architecture is shown in Figure 1. In each round, the server first dynamically identifies clean and extremely noisy clients. The server then uses the particle swarm optimization algorithm to adjust the aggregation weights and evaluate the performance of the provisional global model to obtain the best weights for the global model aggregation. In subsequent rounds, the extremely noisy clients train the local model with the interpolation loss based on pseudo-label loss and knowledge distillation loss, while the clean clients train with conventional cross-entropy loss. The auxiliary dataset is used on the server side to identify extremely noisy clients and evaluate the provisional global model. It does not combine with clients’ personal training data. This method of data isolation reduces privacy risks.
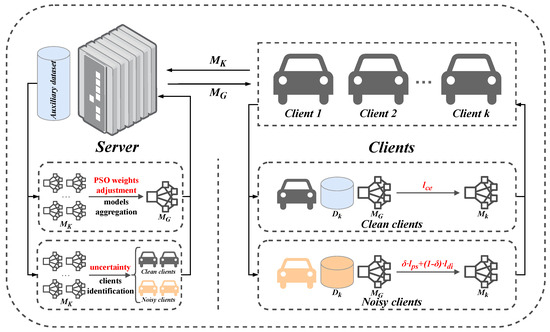
Figure 1.
FedDPSO basic architecture.
3.3. Identification of Extremely Noisy Clients
In each round of communication, the server randomly selects a subset of clients that need to upload model parameters to the server. After this, the first task of the server is to identify extremely noisy clients. Clients in will be classified into two categories, clean clients with less label noise and extremely noisy clients with more label noise. Based on previous work, we use model uncertainty [18] to identify extremely noisy clients, an approach that aims to infer the reliability of a client’s model through model uncertainty, thus effectively distinguishing clean clients from extremely noisy ones. The data used in the identification process can be data of with labels removed. The probability of label classes C in the model is given as follows:
where label , is the sampled with label c, represents the distribution of the dropout operation performed by the local model during the inference process, and the local model is trained on the local dataset . T is the number of rounds of inference performed for each sample, and denotes the parameters sampled from . The uncertainty based on is calculated as follows:
Uncertainty is commonly employed to evaluate the reliability of the model. When exceeds the uncertainty threshold , we refer to client k as an extremely noisy client. This means that client k has a significant volume of anomalous data that may negatively affect the performance of the model. As demonstrated in the research conducted by Yang et al. [15], setting within the range of [0.12, 0.14] enables accurate identification of extremely noisy clients.
3.4. Model Training for Extremely Noisy Clients
After the server identifies the in round t, special treatment will be applied to the training of models starting from the next round. This treatment is designed to discourage overfitting of label noise and provide a way for to contribute meaningfully to the global model. Given that most of the data in consist of noisy data, for the training of models, we first adopt semi-supervised learning, which discards noisy labels and generates pseudo-labels. The pseudo label generation formula is as follows:
where denotes the probability distribution of the pseudo-labels. denotes the class index with the highest probability. is the largest probability value in the pseudo-label probability distribution. represents the logits output of the local model . is the distillation temperature, which is used to regulate the smoothness of the softmax function. After obtaining the pseudo-labels, the pseudo-label loss is calculated based on the cross-entropy loss:
where i represents the i-th sample. are the selected samples with high confidence of client k. is the cross-entropy loss function that calculates the loss between the model output and the pseudo-label . is the indicator function that returns 1 if the condition is true and 0 otherwise. is the decision threshold for this indicator function.
The essence of knowledge distillation is to transfer knowledge from the teacher model to the student model in order to improve the performance of the student model. It is a model compression technique, but in practical applications, it is also used as a strategy to transfer knowledge or aid in training. It is not only limited to knowledge transfer between complex models and simple models; it can also be used for knowledge transfer of the same-dimensional models. Inspired by the work of [46,47,48], in local training, the global model as the teacher model corrects the training of the local model by providing its probability distribution for the local data. This approach helps to prevent the local model from deviating too much from the global while reducing its risk of overfitting due to label noise. Specifically, the client k pre-stores the global model received in this round and then trains using to obtain the new local model . Since the local data of are highly contaminated and the quality of the pseudo-labels is unstable, needs to learn logits output of for the local data to prevent the local model from deviating too much from the global model caused by overfitting of label noise. The knowledge distillation loss function is given as follows:
where represents the logits output of the global model , and denotes the KL divergence loss for and . Finally, the client k obtains the pseudo-label loss and knowledge distillation loss. On the basis of these two losses, the interpolation loss for model training is calculated as follows:
Here, is a balancing factor that dynamically adjusts the contributions of the two losses. It is defined as follows:
where is calculated from the relative magnitude of the pseudo-label loss and the knowledge distillation loss. The dynamic balance of the loss allows the local model to rely more on pseudo-label loss when the pseudo-labels are relatively reliable. When significant model divergence occurs, it corrects the bias by learning the probability distribution of the global model, thereby reducing the risk of overfitting and enhancing the stability and accuracy of learning.
3.5. Global Model Aggregation
After the client completes local training and uploads the local model to the server, in addition to identifying the extremely noisy clients, the server also uses PSO to adjust the aggregate weights of the global model for generating the best-performing global model. Figure 2 illustrates the PSO principle of operation. Each particle adjusts the weight list according to the velocity and updates the pbest of the particle based on the prediction result of the provisional global model on , and the replacement gbest of the better-performing pbest is the optimal weight list.
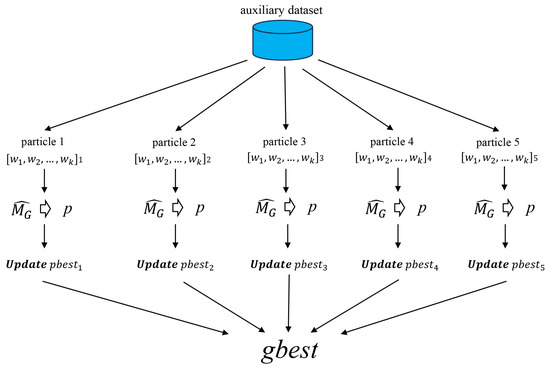
Figure 2.
PSO principle of operation.
PSO searches for the optimal solution by simulating the movement and cooperation of particles in the solution space. Each particle is considered a potential answer to a mathematical optimization problem in a D dimensional space. Each particle has a given position and velocity, and there is also a local memory called pbest that is used to record the best position experienced by the particle so far. In addition, the global best position is also recorded in a global shared memory called gbest for the best position found by the particle swarm so far. Each particle adjusts its speed and position according to pbest and gbest, gradually approaching the global optimal solution. The velocity is calculated for each particle using the following formula:
To optimize the effect of weight calculation, we define as the weight of particle i with respect to client k. The PSO speed update formula is improved as follows:
where t is the current iteration round. refers to the weight of the previous round particle i with respect to client k. and are the inertia weight that controls the effect of . and are the acceleration coefficients. and are random numbers between 0 and 1. pbest and gbest are the local optimal weight list of the particles and the global optimal weight list of the particle swarm, respectively, including the following:
Referring to the work of Li et al. [49], Equation (10), known as the chaotic mapping function, is introduced to increase randomness. is the initial random number in the range [0, 1], and r generates oscillations during the iteration process, which promotes more diverse particle motions. T is the maximum number of iteration rounds. To reduce communication overhead, we set a smaller number of T and particles, and this configuration is effective. The reason is that the optimal weight list is derived by comparing the performance of the temporary global model, which is initially obtained through FedAvg aggregation. Therefore, after adjusting the weights using PSO, the performance of the global model is always better than or at least equal to that of FedAvg (as proven in Section 4.5). and denote the maximum and minimum values of the inertia weights, respectively, controlling the linear rise of the inertia weights and the nonlinear drop in . As the number of iteration rounds increases, gradually increases and the effect of gbest on the velocity update gradually increases [50]. This means that the gradually increasing role of gbest enables the algorithm to converge faster to the neighborhood of the global optimal solution. is closely related to the nonlinear drop in . As increases, the overall decline of goes from large to small, resulting in a stable convergence to the optimal solution. This nonlinear inertial weight drop helps the algorithm to balance the global and local search capabilities of the particles. The weight update of particle i is given as follows:
The weight must be between [0, 1], otherwise it is initialized to 0. Then, normalization is performed. After the weight calculation, the global model aggregation is as follows:
If the prediction accuracy for the provisional global model in , then it updates the pbest of the particle.
where the number of correctly predicted samples is , and the total number of samples in is . The algorithm compares the prediction accuracy of the weight lists pbest and gbest at the end of each iteration, replaces gbest with pbest if , and finally outputs gbest as the optimal weight list. Algorithm 1 shows the training process of FedDPSO.
| Algorithm 1 Enhanced Knowledge Distillation and Particle Swarm Optimization for Federated Learning (FedDPSO) |
| Input: the global round T, the uncertainty threshold for Identify , the distillation temperature , the total number of clients . is the inertial weight, and are the maximum and minimum values of the inertia weights, and are the acceleration coefficients. |
| Output: the global model |
| 1: Initialize global model send to each client |
| 2: for to T do |
| 3: // Server executes: |
| 4: Randomly select a set of clients |
| 5: for do |
| 6: ← LocalUpdate(k, ) |
| 7: end for |
| 8: Dynamically identify and with Equations (1) and (2) |
| 9: Calculate global model aggregate weights with Equations (9) and (13) |
| 10: Generate global model with Equation (14) |
| 11: |
| 12: // Client executes: |
| 13: function LocalUpdate(k, ) |
| 14: if then |
| 15: Update local model with Equation (6) |
| 16: else |
| 17: Update local model with |
| 18: end if |
| 19: return |
| 20: end function |
| 21: end for |
4. Experiments
4.1. Experimental Setup
Datasets and models: Both CIFAR10 and CIFAR100 [51] contain 50,000 training images and 10,000 test images. We conduct experiments based on the CIFAR10 and CIFAR100 datasets. CIFAR10 and CIFAR100 both cut 95% of the training set as client data and 5% as an auxiliary dataset. In the experiments, we evaluate the performance of FedDPSO using the resnet-18 model.
Baseline: FedDPSO demonstrates the effect by comparing five methods. FedAvg [52] performs average aggregation of client-side upload models at the server. FedProx [53] introduces a regularization term of = 0.01 during client training for constraining the local model update to cope with the unbalanced data distribution problem. Mixup [54] sets = 0.1 to generate a mixing coefficient to control the mixing ratio of data augmentation for obtaining richer data samples. Mixing can effectively reduce the memory of noisy data and suppress the overfitting phenomenon. RoFL [14] exchanges feature centroids between clients and the server. FOCUS [12] calculates the mutual cross entropy of local and baseline data to quantify client trustworthiness in order to adjust the weights assigned to clients in the model aggregation.
Noise distribution: In our experiments, we evaluate the performance of FedDPSO under three Beta distributions. Specifically, we use the Beta distributions to generate different noise ratios assigned to each client, and we inject symmetric label noise according to the noise ratios. The principle of symmetric label noise injection is to remove the real labels from a given label list, then randomly select a label among the remaining labels as a replacement to simulate the real labels being mislabeled.
4.2. Implementation Detail
In this study, a uniform setup was used for all experiments in order to ensure a fair comparison. The experiments were carried out using Python 3.10, Intel Xeon Gold 6430 and NVIDIA GeForce RTX 4090. The development framework is PyTorch 2.1.0. Specifically, the experiments on CIFAR10 were set up with N = 50 clients involved in training, and the experiments on CIFAR100 were set up with N = 20 clients involved in training, randomly selecting clients number K = 10 in each round, with 100 global rounds. Meanwhile, SGD was used as the optimizer in all the experiments, with a learning rate of 0.05. The local training round was 10, and the batch size was 32. The PSO iteration was 5, and the number of particles was 5, = 1.0, = 1.0, = 0.6, = = 1.5. The distillation temperature = 2.0, the uncertainty threshold = 0.12, the decision threshold = 0.6. We used a Dirichlet distribution with = 0.7, controlling the degree of data heterogeneity to distribute the training data in a non-IID manner to each client. Dirichlet distributions have important applications in a variety of probabilistic modeling and statistical inference problems.
4.3. Noise Ratio Effect
In this section, we evaluate the effect of noise ratio on model training. Figure 3 shows the distribution of noise ratios for 100 clients under three Beta distributions. Overall, Beta = (0.1, 0.1) has the overall maximum noise ratio, and heavy-noise clients are the most numerous. Beta = (0.1, 0.3) has the overall minimum noise ratio, and light-noise clients are the most numerous. Beta = (0.3, 0.5) has the overall medium noise ratio, and the client noise ratios show a diverse distribution between 0 and 1. As shown in Figure 4, we performed FedAvg experiments to compare the effects of no noise and three Beta distributions. From the experiments, it is evident that the model was best trained with higher stability in the no noise condition. Under the no noise condition, the test accuracy of CIFAR10 and CIFAR100 converged steadily to 82% and 61%, respectively. With the gradual increase in the noise level, the model training processes generated oscillations which were manifested as convergence difficulties and were most significant at Beta = (0.1, 0.1). Therefore, it can be concluded that highly contaminated data have a serious impact on the stability and performance of the global model.
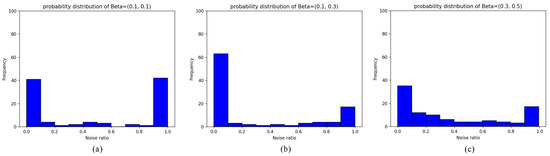
Figure 3.
Comparison of client noise ratios distribution. (a) Obeying Beta = (0.1, 0.1). (b) Obeying Beta = (0.1, 0.3). (c) Obeying Beta = (0.3, 0.5).
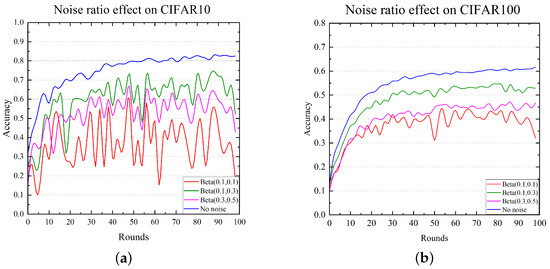
Figure 4.
Comparison of FedAvg performance following no noise and three Beta distributions. (a) Noise ratio effect on CIFAR10. (b) Noise ratio effect on CIFAR100.
4.4. Method Comparison Analysis
In this section, we evaluate FedDPSO against other methods across two datasets and three Beta distributions to highlight its strengths and limitations. Table 1 presents the test accuracy of different FL methods, calculated as the average of the top 10 highest accuracies. The CIFAR10 experiments show that the overall performance of FedAvg is normal; FedProx performs slightly lower than FedAvg and does not play a obvious role; Mixup plays a role in the Beta = (0.1, 0.1) distribution, which contains the most extremely noisy clients, improving around 1.3%, but it does not perform well in the other two noise distributions; RoFL performs well at high overall noise ratio, with approximately 2% improvement over FedAvg; FOCUS improves about 2–3.5% compared to FedAvg and is second only to FedDPSO in overall performance; FedDPSO performs the best, improving most significantly under the Beta = (0.1, 0.1) distribution, with a 15% improvement compared to FedAvg, an 11% improvement compared to FOCUS, and excellent performance in the other two noise distributions. The more complex CIFAR100 experiments show that Mixup outperforms FedAvg in all noise distributions; RoFL has not performed as well as expected; FOCUS’s overall performance is still second only to FedDPSO, but it is the best in the Beta = (0.1, 0.3) distribution; FedDPSO continued to perform best overall. Compared with FedAvg, the improvement is 8% in the Beta = (0.1, 0.1) distribution, but the improvements are not obvious in the other two noise distributions. Experiments on both datasets show that FedDPSO performs well in federated learning with extremely noisy clients and effectively improves model performance.

Table 1.
Test accuracy of different FL methods across three beta distributions.
We maintain the overall characteristics of the test accuracy to draw the renderings for visually comparing various methods of handling label noise. Figure 5 presents the training processes of different methods on the CIFAR10 and CIFAR100 datasets. Analyzing Figure 5, it can be obviously observed that there are different degrees of oscillations in the model training of these methods due to the interference of extremely noisy clients. As the number of extremely noisy clients increases, such oscillations become more obvious, especially the stronger interference under the Beta = (0.1, 0.1) distribution, which leads to abnormally difficult convergence. Different from other methods, FedDPSO oscillates weaker on CIFAR10, and its global model performance outperforms the other methods on both datasets. This is mainly because we attenuated the effects of label noise during local model training and utilized the particle swarm optimization algorithm to adjust the aggregate weights. Comparative experiments under different noise distributions indicate that FedDPSO has a stronger noise treatment capability than the other FL methods in federated learning for extremely noisy clients.
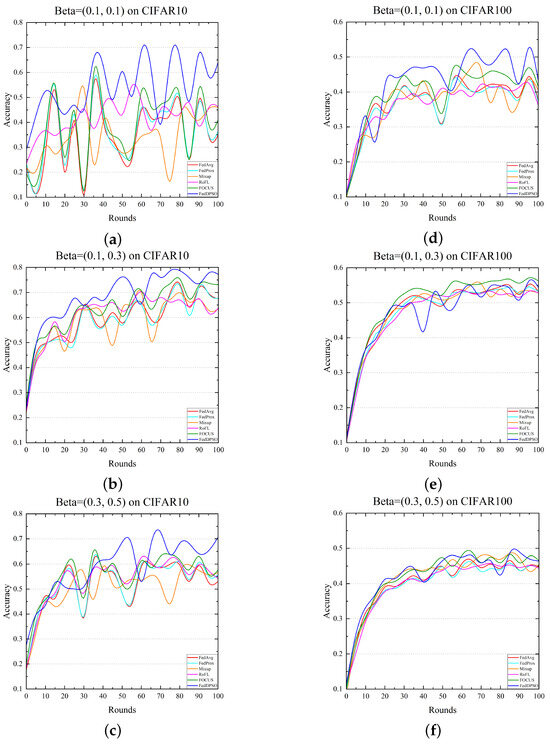
Figure 5.
Comparison of training processes of different methods on the CIFAR10 and CIFAR100 datasets when client noise ratios following three Beta distributions. (a) Obeying Beta = (0.1, 0.1) on CIFAR10. (b) Obeying Beta = (0.1, 0.3) on CIFAR10. (c) Obeying Beta = (0.3, 0.5) on CIFAR10. (d) Obeying Beta = (0.1, 0.1) on CIFAR100. (e) Obeying Beta = (0.1, 0.3) on CIFAR100. (f) Obeying Beta = (0.3, 0.5) on CIFAR100.
4.5. Ablation Study
Hyperparameter analysis: The decision threshold tuning experiment aims to investigate the impact of different values on the proposed method and select the most representative value. As shown in Table 2, the experiments evaluated the test accuracy under the settings of = {0.5, 0.6, 0.7, 0.8}. Multiple experiments were conducted across three Beta distributions and two datasets to compare the influence of different thresholds on the performance of the proposed method. Analysis of the experimental results revealed that when = 0.6, FedDPSO demonstrated better generalization capability.

Table 2.
Test accuracy of decision threshold tuning under different values.
Module analysis: To further validate the proposed method, we conducted a module comparison experiment to evaluate the two main components of FedDPSO, which are particle swarm optimization and interpolation loss parts. For ease of memorization, we refer to them simply as FedPSO and FedD. The FedPSO experiments do not use the interpolation loss component, and all clients are trained normally. The FedD experiments do not employ the particle swarm optimization component and only perform federated averaging operations. The module comparison experiment was conducted under the Beta = (0.1, 0.1) distribution, which clearly demonstrates the advantages and disadvantages of the methods in this high-noise environment. Table 3 shows the test accuracies of the different modules.

Table 3.
Test accuracy of module comparison under Beta = (0.1, 0.1).
The variation in the test accuracy of the module comparison experiment is reflected in Figure 6. We analyzed the experimental phenomena of FedAvg, FedPSO, FedD, and FedDPSO. Overall, high noise levels had a serious impact on model training. Compared with the case with no noise, all of the methods had different degrees of vibration. In Figure 6, we can clearly observe that FedPSO and FedD both improved the performance of the model. This shows that PSO contributes to a better global model through weight adjustment, while interpolation loss effectively deals with label noise overfitting. These components work together to validate the effectiveness of FedDPSO in dealing with extreme noise problems.
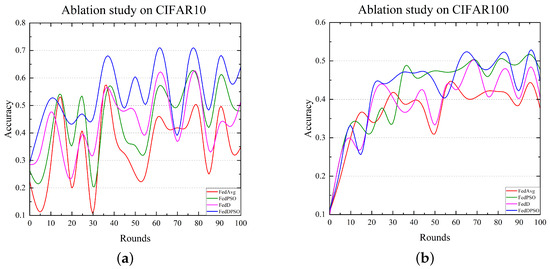
Figure 6.
Accuracy change of module comparison experiment when Beta = (0.1, 0.1). (a) Test accuracy on CIFAR10. (b) Test accuracy on CIFAR100.
5. Discussion
5.1. Communication and Computation Costs
In this research, FedDPSO integrates particle swarm optimization, interpolation loss, and an essential noise detection mechanism. Compared to the traditional FedAvg, the computational costs increased by approximately 40%, while the communication costs remained unchanged. While this additional computation overhead imposes higher computational demands on both clients and the server, the associated cost is justified by significant performance gains. The experimental results show that FedDPSO exhibits remarkable accuracy gains in training the global model, especially when addressing extreme label noise. Therefore, despite the rise in computation costs, the performance enhancement demonstrates its strong potential for practical applications.
5.2. Stability and Robustness
Extreme label noise is more difficult to handle than normal noise, and its impact on federated learning applications is particularly significant. Although FedDPSO alleviated overfitting caused by label noise to some extent, the oscillations during training still expose its lack of robustness. The experimental analysis shows that this instability mainly arises from the highly noisy and complex data environment, which makes it difficult for the global model to effectively capture the true data distribution, thus reducing the credibility of the pseudo-label loss. While introducing more powerful models may improve performance, it also significantly increases communication and computational costs. Therefore, based on the analysis of extremely noisy clients in this paper, future work can focus on optimizing the pseudo-label generation strategy and designing more robust optimization methods to further enhance the stability and robustness of FedDPSO in extreme noise environments.
5.3. Limitation and Scalability
Although FedDPSO has shown good performance, it still has some limitations, particularly regarding the auxiliary dataset, which is a topic worth discussing. First, the auxiliary dataset can be obtained through data sharing protocols, public data, and artificial testing, but these methods may also lead to additional resource consumption and potential leakage risks. In certain special circumstances, we can slightly relax data privacy restrictions, but for some sensitive data, it remains difficult to apply. Secondly, we have not yet considered the issue of label noise or missing labels in the auxiliary dataset. In our research, particle swarm optimization relies on labels for weight adjustment, so noise can lead to inaccuracies in weight adjustment. It is necessary to design an evaluation function that does not rely on labels to enhance the robustness of weight adjustment.
6. Conclusions
Federated learning in practical applications may be impacted by various uncertainties, such as model poisoning, data loss, and incorrect labeling, leading to highly contaminated data and extreme label noise, which can severely affect the training of the global model. To tackle this critical issue, we propose an enhanced method called FedDPSO, which combines the techniques of the particle swarm optimization algorithm and knowledge distillation. This method aims to improve model performance in a federated learning environment with extremely noisy clients. The core idea of FedDPSO is to optimize model training on extremely noisy clients by using the interpolation loss based on pseudo-label loss and knowledge distillation loss. Then, the server uses the particle swarm optimization algorithm to adjust the aggregate weights of the client models, thereby improving the performance of the global model. We used resnet-18 to validate the effectiveness of FedDPSO on the CIFAR10 and CIFAR100 datasets, and the experimental results show that in the presence of extremely noisy clients, FedDPSO is able to effectively improve the model performance. This suggests that FedDPSO can be applied to federated learning with extremely noisy clients. Further experiments showed that the robustness of this method needs improvement. Additionally, auxiliary datasets containing noise are also worth considering. Therefore, future work will focus on developing general robust frameworks against extreme label noise, which has practical implications for federated learning applications.
Author Contributions
Conceptualization, C.O. and Y.L.; methodology, C.O. and Y.L.; software, Y.L. and J.M.; validation, C.O. and J.M.; formal analysis, C.O. and J.M.; investigation, C.Z. and Z.X.; resources, C.Z. and Z.X.; data curation, C.Z. and Z.X.; writing—original draft preparation, C.O. and J.M.; writing—review and editing, T.L. and D.Z.; supervision, T.L. and D.Z.; project administration, D.Z.; funding acquisition, T.L. and C.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education of Humanities and Social Science Project, China (grant no. 19YJAZH047).
Data Availability Statement
The research data can be obtained from the corresponding authors upon reasonable request. The datasets are available online.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Posner, J.; Tseng, L.; Aloqaily, M.; Jararweh, Y. Federated learning in vehicular networks: Opportunities and solutions. IEEE Netw. 2021, 35, 152–159. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Z.; Tian, S.; Huang, F.; Li, J.; Li, X.; Igorevich, K.K.; Ma, J. TFL-DT: A trust evaluation scheme for federated learning in digital twin for mobile networks. IEEE J. Sel. Areas Commun. 2023, 41, 3548–3560. [Google Scholar] [CrossRef]
- Qi, P.; Chiaro, D.; Piccialli, F. Small models, big impact: A review on the power of lightweight Federated Learning. Future Gener. Comput. Syst. 2025, 162, 107484. [Google Scholar] [CrossRef]
- Wang, X.; Han, Y.; Wang, C.; Zhao, Q.; Chen, X.; Chen, M. In-edge ai: Intelligentizing mobile edge computing, caching and communication by federated learning. IEEE Netw. 2019, 33, 156–165. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Z.; Fu, H.; Zhu, P.; Chen, L.; Hu, Q. Hybrid noise-oriented multilabel learning. IEEE Trans. Cybern. 2019, 50, 2837–2850. [Google Scholar] [CrossRef] [PubMed]
- Xiao, T.; Xia, T.; Yang, Y.; Huang, C.; Wang, X. Learning from massive noisy labeled data for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2691–2699. [Google Scholar]
- Wei, J.; Zhu, Z.; Cheng, H.; Liu, T.; Niu, G.; Liu, Y. Learning with noisy labels revisited: A study using real-world human annotations. arXiv 2021, arXiv:2110.12088. [Google Scholar]
- Arpit, D.; Jastrzebski, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M.S.; Maharaj, T.; Fischer, A.; Courville, A.; Bengio, Y.; et al. A closer look at memorization in deep networks. In Proceedings of the International Conference on Machine Learning, ICML, Sydney, NSW, Australia, 6–11 August 2017; pp. 233–242. [Google Scholar]
- Miao, Y.; Xie, R.; Li, X.; Liu, Z.; Choo, K.K.R.; Deng, R.H. Efficient and secure federated learning against backdoor attacks. IEEE Trans. Dependable Secur. Comput. 2024, 21, 4619–4636. [Google Scholar] [CrossRef]
- Tam, K.; Li, L.; Han, B.; Xu, C.; Fu, H. Federated noisy client learning. IEEE Trans. Neural Netw. Learn. Syst. 2023, 36, 1799–1812. [Google Scholar] [CrossRef]
- Zhao, Z.; Chu, L.; Tao, D.; Pei, J. Classification with label noise: A Markov chain sampling framework. Data Min. Knowl. Discov. 2019, 33, 1468–1504. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Qin, X.; Yu, H.; Chan, P.; Shen, Z. Dealing with label quality disparity in federated learning. In Federated Learning: Privacy and Incentive; Springer: Cham, Switzerland, 2020; pp. 108–121. [Google Scholar]
- Xu, J.; Chen, Z.; Quek, T.Q.; Chong, K.F.E. Fedcorr: Multi-stage federated learning for label noise correction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10184–10193. [Google Scholar]
- Yang, S.; Park, H.; Byun, J.; Kim, C. Robust federated learning with noisy labels. IEEE Intell. Syst. 2022, 37, 35–43. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, L.; Zhang, Y.; Zhang, Y.; Han, B.; Cheung, Y.m.; Wang, H. Federated learning with extremely noisy clients via negative distillation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 14184–14192. [Google Scholar]
- Li, D.; Wang, J. Fedmd: Heterogenous federated learning via model distillation. arXiv 2019, arXiv:1910.03581. [Google Scholar]
- Chen, K.; Zhou, F.; Liu, A. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl.-Based Syst. 2018, 139, 23–40. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, ICML, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Mendieta, M.; Yang, T.; Wang, P.; Lee, M.; Ding, Z.; Chen, C. Local learning matters: Rethinking data heterogeneity in federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8397–8406. [Google Scholar]
- Yao, Y.; Sun, Z.; Zhang, C.; Shen, F.; Wu, Q.; Zhang, J.; Tang, Z. Jo-src: A contrastive approach for combating noisy labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 5192–5201. [Google Scholar]
- Ghosh, A.; Kumar, H.; Sastry, P.S. Robust loss functions under label noise for deep neural networks. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Xia, X.; Liu, T.; Han, B.; Gong, C.; Wang, N.; Ge, Z.; Chang, Y. Robust early-learning: Hindering the memorization of noisy labels. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Volume 31. [Google Scholar]
- Tuor, T.; Wang, S.; Ko, B.J.; Liu, C.; Leung, K.K. Overcoming noisy and irrelevant data in federated learning. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5020–5027. [Google Scholar]
- Ba, J.; Caruana, R. Do deep nets really need to be deep? In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Urban, G.; Geras, K.J.; Kahou, S.E.; Aslan, O.; Wang, S.; Caruana, R.; Mohamed, A.; Philipose, M.; Richardson, M. Do deep convolutional nets really need to be deep and convolutional? arXiv 2016, arXiv:1603.05691. [Google Scholar]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge distillation: A survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Zhu, Y.; Yu, X.; Chandraker, M.; Wang, Y.X. Private-kNN: Practical differential privacy for computer vision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11854–11862. [Google Scholar]
- Jeong, E.; Oh, S.; Kim, H.; Park, J.; Bennis, M.; Kim, S.L. Communication-efficient on-device machine learning: Federated distillation and augmentation under non-iid private data. arXiv 2018, arXiv:1811.11479. [Google Scholar]
- Yao, D.; Pan, W.; Dai, Y.; Wan, Y.; Ding, X.; Yu, C.; Jin, H.; Xu, Z.; Sun, L. FedGKD: Towards Heterogeneous Federated Learning via Global Knowledge Distillation. IEEE Trans. Comput. 2024, 73, 3–17. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Zhou, C.; Yan, S.; Xue, J. Human memory optimization algorithm: A memory-inspired optimizer for global optimization problems. Expert Syst. Appl. 2024, 237, 121597. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Aras, S.; Gedikli, E. Fitness-distance balance (FDB): A new selection method for meta-heuristic search algorithms. Knowl.-Based Syst. 2020, 190, 105169. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Zhou, C.; Yan, S. Manta ray foraging optimization based on mechanics game and progressive learning for multiple optimization problems. Appl. Soft Comput. 2023, 145, 110561. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Shen, J.; Zhou, C.; Li, T.; Yan, S. A multi-strategy particle swarm algorithm with exponential noise and fitness-distance balance method for low-altitude penetration in secure space. J. Comput. Sci. 2023, 74, 102149. [Google Scholar] [CrossRef]
- Houssein, E.H.; Sayed, A. Boosted federated learning based on improved Particle Swarm Optimization for healthcare IoT devices. Comput. Biol. Med. 2023, 163, 107195. [Google Scholar] [CrossRef]
- Park, S.; Suh, Y.; Lee, J. FedPSO: Federated learning using particle swarm optimization to reduce communication costs. Sensors 2021, 21, 600. [Google Scholar] [CrossRef] [PubMed]
- Devarajan, G.G.; Nagarajan, S.M.; Daniel, A.; Vignesh, T.; Kaluri, R. Consumer product recommendation system using adapted PSO with federated learning method. IEEE Trans. Consum. Electron. 2023, 70, 2708–2715. [Google Scholar] [CrossRef]
- Zhao, Z.; Xia, J.; Fan, L.; Lei, X.; Karagiannidis, G.K.; Nallanathan, A. System optimization of federated learning networks with a constrained latency. IEEE Trans. Veh. Technol. 2021, 71, 1095–1100. [Google Scholar] [CrossRef]
- Supriya, Y.; Gadekallu, T.R. Particle swarm-based federated learning approach for early detection of forest fires. Sustainability 2023, 15, 964. [Google Scholar] [CrossRef]
- Kandati, D.R.; Gadekallu, T.R. Federated learning approach for early detection of chest lesion caused by COVID-19 infection using particle swarm optimization. Electronics 2023, 12, 710. [Google Scholar] [CrossRef]
- Liu, J.; Xu, H.; Wang, L.; Xu, Y.; Qian, C.; Huang, J.; Huang, H. Adaptive asynchronous federated learning in resource-constrained edge computing. IEEE Trans. Mob. Comput. 2021, 22, 674–690. [Google Scholar] [CrossRef]
- Burgert, T.; Ravanbakhsh, M.; Demir, B. On the effects of different types of label noise in multi-label remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5413713. [Google Scholar] [CrossRef]
- Jiang, X.; Sun, S.; Wang, Y.; Liu, M. Towards federated learning against noisy labels via local self-regularization. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 862–873. [Google Scholar]
- Lin, T.; Kong, L.; Stich, S.U.; Jaggi, M. Ensemble distillation for robust model fusion in federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2351–2363. [Google Scholar]
- Yuan, L.; Tay, F.E.; Li, G.; Wang, T.; Feng, J. Revisiting knowledge distillation via label smoothing regularization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3903–3911. [Google Scholar]
- Li, W.; Liang, P.; Sun, B.; Sun, Y.; Huang, Y. Reinforcement learning-based particle swarm optimization with neighborhood differential mutation strategy. Swarm Evol. Comput. 2023, 78, 101274. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, X. A particle swarm optimization algorithm with empirical balance strategy. Chaos Solitons Fractals X 2023, 10, 100089. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, AISTATS, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond empirical risk minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).