Abstract
Unmanned aerial vehicles (UAVs) are highly versatile and cost-effective, making them an attractive option for various applications. In UAV networks, it is essential to implement a digital signature scheme to ensure the integrity and authentication of commands sent to UAVs. Moreover, this digital signature scheme not only maintains the real-time performance of UAVs while executing commands but also protects the identity privacy of the signer. To meet these needs, we propose an efficient threshold attribute-based proxy signature (t-ABPS) scheme that integrates a threshold predicate specifically designed for UAV networks. The formal security proof for the t-ABPS scheme demonstrates its existential unforgeability under selective-attribute and chosen-message attacks (EUF-sA-CMA) in the random oracle model. This scheme also ensures the identity privacy of the signer. Furthermore, we evaluate the computational costs and communication costs associated with the proposed scheme. Our analysis indicates that the t-ABPS scheme is more computationally efficient than other existing attribute-based proxy signature schemes, but it has higher communication costs.
1. Introduction
In the field of aviation technology, an unmanned aerial vehicle (UAV) is generally defined as an aircraft without a human pilot on board. When equipped with specialized equipment, such a vehicle can perform a wide range of tasks. The successful execution of these functions often relies on collaboration with additional computational devices and communication infrastructure. These components, along with the UAVs, can form a UAV network, which typically centers around the UAVs. As shown in Figure 1, a UAV network may include various components, such as UAVs, a command center, ground control stations (GCSs), satellites, mobile command vehicles, airships, etc. UAV networks exhibit several characteristics, including high mobility, dynamic topological structure, intermittent connectivity, and varying link quality [1,2].
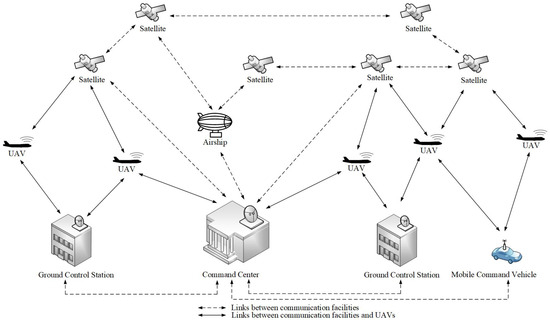
Figure 1.
UAV network.
With the rapid development of artificial intelligence (AI) and UAV technology, many UAVs now have autonomous capabilities that allow them to operate without real-time human control. These UAVs can independently plan routes and execute missions without any human intervention. Consequently, it is essential to protect the commands sent to these UAVs. Digital signature schemes are typically employed to ensure the integrity and authenticity of these commands.
1.1. Problem Statement
In a UAV network, it is crucial for every UAV to be connected to a command center, which holds the highest authority over the UAV. The command center sends commands to UAVs to instruct them to perform various tasks. Since UAVs have limited computation and communication resources and are often in airspace where conditions are unknown, links between UAVs and the command center or other communication facilities are usually considered insecure. The command center and other communication facilities have sufficient computation and communication resources, so links between them are usually considered secure. In order to protect the integrity and authentication of the commands sent from the command center to UAVs, it is necessary to implement a digital signature scheme.
The command center generates a digital signature for each command and sends both the command and its signature to the UAV. The UAV then conducts a signature verification process. If the signature is valid, the UAV will carry out the command; otherwise, it will consider the command counterfeit and will refuse to execute it.
There is a delay in transmitting commands from a command center to a UAV. Minimizing this delay is crucial, as it significantly impacts the UAV’s real-time operational effectiveness. One effective method to reduce this delay is to shorten the distance between the command center and the UAV. Therefore, the command center should be located as close to the UAV as possible.
However, a UAV is often deployed to a remote location far from the command center. In these situations, intermittent connections and varying link quality within UAV networks can hinder the timely reception of commands and signatures. To address this challenge, the command center may temporarily delegate command authority to a local agent near the UAV, such as a ground control station. This local agent is responsible for issuing commands and computing signatures on behalf of the command center. Once the commands and corresponding signatures are generated, the agent transmits them to the UAV. The UAV then verifies the signatures to determine whether to execute the commands. This requirement can be efficiently addressed through the implementation of a proxy signature scheme.
Some users want to issue commands to a UAV anonymously. A traditional digital signature scheme typically requires a user’s digital certificate or identification, which significantly increases the risk of revealing the user’s identity. A feasible solution is to allow command issuance based on attributes rather than identity. Each user possesses a set of attributes, and only those users whose attributes meet the specified requirements can issue commands to the UAV. In this case, the UAV only needs to confirm that the command was issued by a user with the required attributes without needing to identify the user, thus protecting the user’s identity privacy. This can be achieved through the implementation of an attribute-based signature (ABS) scheme.
In conclusion, we find that an attribute-based proxy signature (ABPS) scheme is more suitable for UAV networks. An ABPS scheme not only improves the real-time reception of commands by UAVs but also protects the privacy of the signer’s identity. However, many ABPS schemes tend to have high computational costs. It is necessary to reduce the computational costs in an ABPS scheme. To address this issue, we propose an efficient threshold ABPS (t-ABPS) scheme for UAV networks.
1.2. Our Contributions
In addressing the challenge of high computational overheads associated with attribute-based signature schemes, we present an efficient threshold attribute-based proxy signature (t-ABPS) scheme. The motivation behind this work stems from the growing need to enhance the performance and practicality of attribute-based cryptographic systems, especially in resource-constrained environments, such as UAV networks. By introducing a proxy signature scheme, we aim to make it possible for the original signer to send messages and signatures to the verifier in a timely manner.
To demonstrate the security of the proposed scheme, we prove its existential unforgeability. This property ensures that the scheme is resistant to potential attacks.
Furthermore, we perform a comprehensive analysis of the scheme’s efficiency, evaluating both the computation and communication costs. The results show that the proposed scheme significantly reduces the computational costs, making it more suitable for practical deployment in scenarios where computational resources are limited. The communication costs of the proposed scheme are larger than those of existing schemes.
The primary contribution of this paper lies in providing an efficient solution to the computational inefficiencies inherent in attribute-based signature schemes. By streamlining the attributes of the signers and verifier, we achieve a balance between security and efficiency, offering a promising signature scheme for applications in the UAV networks.
1.3. Organization of the Remainder of the Paper
The structure of this paper is organized as follows. Section 2 presents a comprehensive review of related work. Section 3 introduces the necessary preliminaries essential for understanding the subsequent discussion. In Section 4, we formally define the model and security framework of the proposed t-ABPS scheme. A detailed description of our t-ABPS scheme is provided in Section 5, with a thorough analysis of its properties and performance discussed in Section 6. Finally, Section 7 concludes the paper.
2. Related Work
2.1. Security Solutions for UAV Networks
Zhi et al. analyzed threats in a UAV system and considered that unsafe links between UAV and ground control stations are susceptible to attacks [3]. Samanth et al. considered it necessary to propose more suitable digital signature schemes for UAV networks [4]. Khan et al. proposed an identity-based generalized signcryption scheme for flying ad hoc networks [5]. Din et al. analyzed this scheme [5] and showed that it is not secure. They proposed an improved signcryption scheme [6]. Wang et al. proposed a data aggregate authentication scheme based on the ID-based encryption for UAV cluster networks [7]. Jan and Khan proposed two security frameworks for UAV networks [8]. One is based on identity and the other is an authentication scheme based on an aggregate signature scheme. He et al. proposed a certificateless designated verifier proxy signature (CLDVPS) scheme [9] for UAV networks. Xu et al. considered that a CLDVPS scheme [9] cannot resist user impersonation attacks and proposed an efficient CLDVPS scheme [10]. Abdel-Malek et al. proposed a lightweight authentication mechanism based on proxy signature for a swarm of UAVs [11]. Qu and Zeng proposed a certificateless proxy signcryption scheme for a UAV network [12]. Liu et al. proposed a lightweight trustworthy message exchange scheme for UAV networks by aggregating the cryptography and trust management technologies [13]. We compare some security solutions in Table 1. The symbol “√” indicates that the scheme meets the corresponding security, while the symbol “×” indicates that the scheme does not meet the corresponding security.

Table 1.
Comparison of security solutions.
2.2. Attribute-Based Signature Schemes
In 2008, Maji et al. formally defined the security requirements of an ABS scheme and proposed a concrete ABS scheme [14]. They proved the security of this scheme in the generic group model. Furthermore, they discussed the possible applications of the ABS scheme. Su et al. proposed a revocable attribute-based signature scheme [15]. Zhang et al. proposed a reusable ABS scheme where the signer generated the signature associated with its attributes [16]. They defined this scheme and its security model and proposed a concrete construction. Blazy et al. proposed an anonymous attribute-based designated verifier signature scheme [17]. In this scheme, only users obtaining the attributes that satisfy the predicate can verify the signature. Liu et al. proposed a revocable and comparable ABS scheme from lattices [18]. This scheme implements user revocation and resists quantum attacks.
ABS schemes with a single attribute authority have some disadvantages. For example, a single attribute authority is a single point of failure and is not conducive to attribute segmentation. Therefore, Li et al. proposed an ABS with multiple attribute authorities [19]. There is a central attribute authority and some distributed attribute authorities in this ABS scheme. However, more ABS schemes with multiple attribute authorities do not need a central attribute authority, which are distributed ABS schemes. Li et al. proposed a flexible and distributed ABS scheme that supports various access structures [20]. Su et al. proposed a distributed ABS scheme for electricity trading in the smart grid [21].
One of the disadvantages of ABS schemes is higher computational costs for the user in computing and verifying the signature. In order to reduce the computational costs of the signer, Chen et al. proposed two outsourced ABS schemes [22]. In these schemes, the computational costs of the signer is outsourced to a signing cloud service provider. Tao et al. [23] proposed an outsourced distributed ABS scheme with multiple attribute authorities. Xiong et al. [24] proposed a server-aided ABS scheme. This scheme reduces the computational costs of the signer and verifier. Huang and Lin analyzed this scheme and considered that it cannot provide anonymity and is forgeable. Therefore, Huang and Lin proposed an improved scheme [25]. Li et al. proposed a distributed server-aided ABS scheme with multiple attribute authorities [26].
Liu et al. defined an ABPS scheme and constructed a concrete ABPS scheme [27]. He et al. proposed an ABPS scheme for UAV networks and proved its security [28]. He et al. also proposed an ABPS scheme that supports a flexible threshold predicate for UAV networks [29].
3. Preliminaries
3.1. Complexity Assumption
Definition 1 (Computational Diffie–Hellman (CDH) Problem).
The variables are unknown. Given , compute .
3.2. Lagrange Interpolation
Let be a -degree polynomial over and S be a d-element set over . The polynomial can be constructed as where .
4. Formal Model and Security Model of a t-ABPS Scheme
In this section, we use the following notations in Table 2.

Table 2.
Notations and descriptions.
4.1. Formal Model of a t-ABPS Scheme
A t-ABPS scheme typically involves four principal entities, an attribute authority (AA), an original signer (OS), a proxy signer (PS), and a verifier (Ver). The AA is responsible for initializing the system and generating private keys required by the OS and PS. The OS generates a warrant and computes a delegation for the PS, who then computes a signature based on the received delegation and its private key. The verifier verifies the signature. The ABPS scheme is fundamentally structured around the algorithms Setup, Extract, DelG, DelV, Sign, and Verify. The inputs and outputs of these algorithms are similar to those of ABPS-HL1 [28] scheme and ABPS-HL2 [29] scheme.
4.2. Security Model of a t-ABPS Scheme
Unforgeability
According to the security models in [30], we also divide adversaries into three categories, , , and . We mainly consider and in the security model. We introduce the concept of existential unforgeability under selective-attribute and chosen-message attacks (EUF-sA-CMA).
1. EUF-sA-CMA against
The EUF-sA-CMA against is formally defined through the following game.
(1) Initialization: selects the challenge attribute set and the challenge message .
(2) Setup: The challenger selects a security parameter and executes the Setup algorithm to generate and . Subsequently, executes the Extract algorithm to generate and for an OS. Similarly, generates and for a PS. retains the and confidentially while transmitting along with the tuple to the adversary .
(3) Queries: is permitted to issue a polynomially bounded number of queries to three distinct oracles: the private key extraction oracle (), the delegation generation oracle (), and the signing oracle (). The inputs and outputs of these oracles are listed in the Table 3.

Table 3.
Inputs and outputs of different oracles.
(4) Forgery: outputs a signature on , , and .
wins the game if the forgery meets the following conditions:
- has not previously submitted any to such that .
- has not previously submitted the pair (, ) to .
- has not previously submitted the tuple (, , ) to .
- The signature is valid.
Definition 2 (EUF-sA-CMA against ).
A t-ABPS scheme possesses EUF-sA-CMA against if the success probability of any polynomially bounded adversary in the aforementioned game is negligible. It is expressed as , where ε represents a negligible value.
2. EUF-sA-CMA against
The EUF-sA-CMA against is defined through a similar game. Its Initialization and Setup phases are similar to these phases in the game of EUF-sA-CMA against . The difference is that retains confidentially and transmits to . In the Queries phase, is permitted to issue a polynomially bounded number of queries to and . Finally, outputs a signature on , , and .
wins the game if the forgery meets the following conditions:
- has not previously submitted any to such that .
- has not previously submitted the triplet (, , ) to .
- The signature is valid.
Definition 3 (EUF-sA-CMA against ).
A t-ABPS scheme possesses EUF-sA-CMA against if the success probability of any polynomially bounded adversary in the aforementioned game is negligible. It is expressed as , where ε represents a negligible value.
Definition 4 (EUF-sA-CMA).
A t-ABPS scheme has EUF-sA-CMA if it has EUF-sA-CMA against and .
5. t-ABPS Scheme for UAV Networks
5.1. Overview of a t-ABPS Scheme
In the t-ABPS scheme, there are four primary participants: an AA, an OS, a PS, and a Ver. In the context of a UAV network, we assume the presence of an AA, a command center, a ground control station, and a UAV. The command center serves as the OS and possesses the attribute set and private key . The ground control station acts as the PS, holding the attribute set and private key , while the UAV functions as the verifier and has the attribute set . For the sake of clarity and simplicity in both research and presentation, we assume that both the OS and the PS share the same threshold within the proposed t-ABPS scheme. Our t-ABPS scheme mainly includes the following steps, which are illustrated in Figure 2.
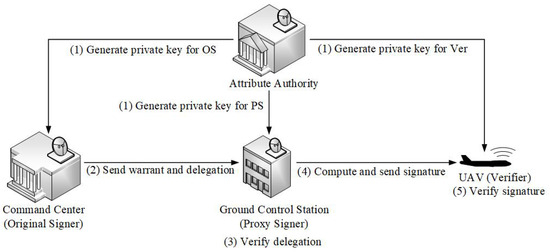
Figure 2.
t-ABPS scheme.
(1) An AA generates private key for a command center, a ground control station, and a UAV, respectively.
(2) The command center plays the role of the trusted original signer. It generates a warrant, computes a delegation, and sends them to the ground control station over a secure link.
(3) The ground control station plays the role of the trusted proxy signer. It verifies the delegation.
(4) The ground control station computes the signature of a command. It sends them to the UAV over an insecure link.
(5) The UAV plays the role of the verifier. It verifies the signature.
5.2. t-ABPS Scheme
The proposed t-ABPS scheme is composed of the following key algorithms.
5.2.1. Setup
We use and to denote two cyclic multiplicative groups with prime order q. Let be a bilinear map. We define three hash functions and the attributes as elements in . The AA initializes the system as follows.
- (i)
- It randomly selects the generator , , and .
- (ii)
- It computes and .
- (iii)
- It outputs the public parameters and sets as the master key.
5.2.2. Extract
The AA generates private keys for the command center (OS), ground control station (PS), and UAV (Ver). It is supposed that , , and are the attribute sets of the command center, ground control station, and UAV, respectively, and . The AA selects a degree polynomial such that . It generates private keys for the command center as follows.
- (i)
- It randomly selects .
- (ii)
- It computes the private key for command center as for every .
The AA generates private keys for the ground control station as follows.
- (i)
- It randomly selects .
- (ii)
- It computes the private key for the ground control station as for every .
The AA generates private keys for the UAV as follows.
- (i)
- It randomly selects .
- (ii)
- It computes the private key for UAV as for every .
5.2.3. Delegation Generate
The command center generates delegation for the ground control station as follows.
- (i)
- It randomly generates for .
- (ii)
- It generates the warrant w for the proxy signer.
- (iii)
- It computes the delegation as , , , where .
- (iv)
- It sends to the ground control station.
5.2.4. Delegation Verify
The ground control station verifies the delegation as follows.
- (i)
- It chooses a set , where and .
- (ii)
- It verifies the delegation by checking if the equation holds.
5.2.5. Sign
The ground control station computes the signature as follows.
- (i)
- It randomly generates for .
- (ii)
- It computes the signature as , , , where .
- (iii)
- It sends to the UAV.
5.2.6. Verify
The UAV verifies the proxy signature as follows.
- (i)
- It chooses a set , where and .
- (ii)
- It verifies the signature by checking if the equation holds.
- (iii)
- It outputs a boolean value if the equation holds. Otherwise, it outputs a boolean value .
6. t-ABPS Scheme Analysis
6.1. Correctness
Firstly, we prove the correctness of the algorithms DelGen and DelVer.
Secondly, we prove the correctness of the algorithms Sign and Verify.
Therefore, the t-ABPS scheme is correct.
6.2. Security Analysis
In this subsection, we prove that our t-ABPS scheme possesses unforgeability.
Theorem 1.
The proposed ABPS scheme achieves EUF-sA-CMA against in the random oracle model, provided that the CDH assumption holds in group .
Proof.
implements an attack on our t-ABPS scheme with a success probability of . It issues , , , , , and queries to the oracle (), oracle (), oracle (), , , and , respectively. We will construct an algorithm that uses to solve the CDH problem with a probability . This algorithm is provided with a random instance of the CDH problem, represented as , where x and y are randomly selected from . Our goal is to construct such that it can compute , therefore solving the CDH problem.
outputs the challenge attribute set . randomly selects , and sets , . will query these oracles above as follows, where the random numbers , , are selected from .
: submits a query to with an input i. If , will output . Otherwise, will output . It adds the output to the -List.
: submits a query to with an input . If , will output . Otherwise, will output . It adds the output to the -List.
: submits a query to with an input . If , will output . Otherwise, will output . It adds the output to the -List.
: submits a query to with an input and . defines three sets , and , . For , simulates the key as . For , sets , , and . It simulates the key as , .
: submits a query to with an input (w, ). If , can obtain the simulated private key by querying the , and then it can generate the delegation based on the key. If and , it is aborted. If and , selects random number and sets , where . It also selects a degree polynomial such that . It simulates the delegation as , , .
: submits a query to with an input . If and , it is aborted. Otherwise, outputs the signature.
After these queries, outputs a forged signature on (, , ). We can obtain the following equation.
Therefore, can compute
According to the security model, we compute , where n is the number of attributes in the . Therefore, this scheme has EUF-sA-CMA against . □
Theorem 2.
The proposed ABPS scheme achieves EUF-sA-CMA against in the random oracle model, provided that the CDH assumption holds in the group .
Proof.
The proof is similar to the proof Theorem 1. We compute . Therefore, this scheme has EUF-sA-CMA against . □
In conclusion, this ABPS scheme has EUF-sA-CMA.
In the t-ABPS scheme, the original signer uses its own attributes rather than identity to compute the delegation. The proxy signer also uses its own attributes rather than identity to compute the signature. An adversary cannot obtain the identities of the signers. The original signer and the proxy signer do not obtain each other’s identity information. Therefore, the t-ABPS scheme protects the signer’s identity privacy.
6.3. Efficiency Analysis
In this subsection, we compare the efficiency of our t-ABPS scheme to some other schemes, which include the ABPS-HL1 [28] scheme and the ABPS-HL2 [29] scheme. Firstly, we compare their computational costs based on the computational time of different algorithms. Secondly, we compare their communication costs according to the length of the signature.
6.3.1. Computational Costs
Each of these ABPS schemes uses some basic operations, such as exponential operations, hash operations, and pairing operations. We theoretically analyze these schemes and obtain the amount of these operations in the algorithm Sign and algorithm Verify, respectively. The results are listed in Table 4 and Table 5, where n represents the number of attributes, and k represents the threshold value.

Table 4.
Amount of some operations in Sign.

Table 5.
Amount of some operations in Verify.
We obtain the computational time of these basic operations by using the Java pairing-based cryptography (jPBC) library [31]. The experimental environment is a PC with Intel i5-13400 CPU and 16 GB RAM. We use a pairing. In this pairing, the variable is equal to 160, which refers to the bit length of the order of the group’s generator and the variable is equal to 512, which refers to the bit length of the finite field. The experiment results show that the exponential operation, hash operation, and pairing operation take ms, ms, and ms respectively.
According to the analysis and experiment results, we are able to estimate the computational time of algorithm Sign and algorithm Verify in these ABPS schemes. For the convenience of research and presentation, it is assumed the variables . The results are illustrated in Figure 3 and Figure 4.
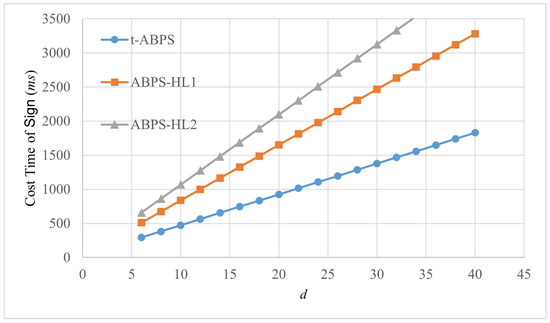
Figure 3.
Comparison of computational time (ms) of Sign algorithms in different schemes.
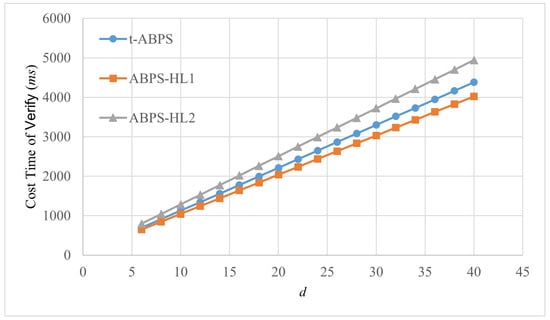
Figure 4.
Comparison of computational time (ms) of Verify algorithms in different schemes.
Figure 3 presents a comparative analysis of the computational time in milliseconds (ms) for computing signatures as a function of the variable d, which extends from 6 to 40. This metric is important for evaluating the efficiency of algorithm Sign in the t-ABPS scheme, the ABPS-HL1 scheme, and the ABPS-HL2 scheme.
The t-ABPS scheme shows a gradual increase in the computational time of algorithm Sign. It suggests that this scheme maintains a relatively stable performance increase. The ABPS-HL1 scheme shows a more pronounced increase in the computational time of algorithm Sign. The ABPS-HL2 scheme shows the most significant increase in the computational time of algorithm Sign. These steeper slopes may imply less efficient handling of a larger number of attributes. In summary, the t-ABPS scheme is the most efficient in terms of cost time of algorithm Sign, followed by ABPS-HL1, with ABPS-HL2 being the least efficient. Therefore, the ground control station, as the proxy signer, takes the least time to compute the proxy signature.
Figure 4 it shows the computational time of the algorithm Verify in different schemes. The computational time grows linearly with the value of the variable d. When the variable , the computational times of the algorithm Verify are very close in the three schemes. However, as the value of the variable d increases, the differences in computational time among the three schemes become more obvious. The computational time of the t-ABPS scheme is longer than that of the ABPS-HL1 scheme and shorter than that of the ABPS-HL2 scheme. Therefore, the UAV, as the verifier, also takes less time to verify the proxy signature.
In order to better reflect the computational time by the different schemes as a whole, we calculated the sums of the computational times by the algorithm Sign and the algorithm Verify in different schemes. The results are illustrated as Figure 5. The sum also grows linearly with the value of the variable d. When the variable , the sums are very close in the three schemes. However, as the value of the variable d increases, the differences become more obvious. Overall, the t-ABPS scheme needs less computational time. That is, the ground control station and verifier need less time to compute and verify the signature.
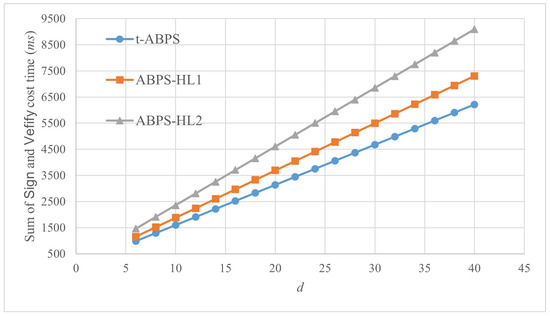
Figure 5.
Comparison of the sums of the computational time of the algorithms Sign and Verify (ms).
6.3.2. Communication Costs
A signer needs to send a digital signature to a verifier. Therefore, we consider the length of the signature to be the communication cost. We theoretically analyze the length of these signature schemes in Table 6. The communication cost of t-ABPS is at the same level as that of the ABPS-HL1 and ABPS-HL2 schemes.

Table 6.
Signature length of different ABPS schemes.
For more accurate analyses, it is assumed the variables , and bits. The results are illustrated in Figure 6.
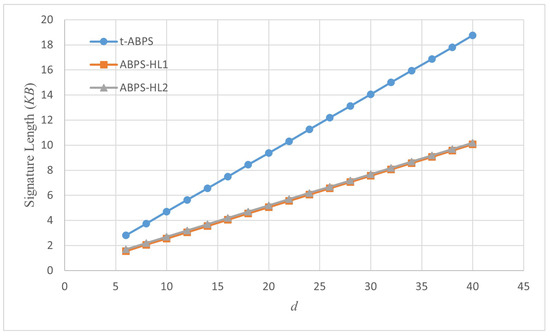
Figure 6.
Comparison of the signature length of the schemes (KB).
This graph offers a detailed examination of the signature length in kilobytes (KB) for three distinct algorithms, t-ABPS, ABPS-HL1, and ABPS-HL2, across a variable d that spans from 6 to 40. Regardless of the value of the variable d taken between 6 and 40, the signature length of the t-ABPS scheme is longer than that of the other two schemes. The t-ABPS scheme shows an obvious upward trajectory, indicating an increase in signature length. This trend suggests that t-ABPS prioritizes lower computational costs, albeit at the expense of larger signature sizes. The ABPS-HL1 and ABPS-HL2 schemes demonstrate a more gradual ascent in signature length. It implies a more balanced approach to computational costs and signature length. Therefore, the t-ABPS scheme has larger communication costs than the other schemes.
6.3.3. Discussion
In this section, we analyzed the security and efficiency of the t-ABPS scheme and other ABPS schemes.
1. Security
We proved the t-ABPS scheme has EUF-sA-CMA in the random oracle model (ROM). It protects the original signer’s privacy and the proxy signer’s privacy because it uses attributes instead of identities to compute and verify the signature. No one can obtain the identities of the signers from the signatures.
The ABPS-HL1 scheme has been proven to have EUF-sA-CMA in the random oracle model. The ABPS-HL2 scheme has been proven to have existential unforgeability under selective-predicate and chosen-message attacks (EUF-sP-CMA). Both of the two schemes use attributes instead of identities to compute and verify the signatures, which protects the identity privacy of signers.We compare the security of the three ABPS schemes as shown in Table 7. The symbol “√” indicates that the scheme meets the corresponding security.

Table 7.
Security comparisons of t-ABPS, ABPS-HL1, and ABPS-HL2.
2. Efficiency
We compared the t-ABPS scheme, ABPS-HL1 scheme, and ABPS-HL2 scheme in terms of computational costs and communication costs.
For the Sign algorithms in the different schemes, the t-ABPS scheme, the ABPS-HL1 scheme, and the ABPS-HL2 scheme have lower computational costs, medium computational costs, and higher computational costs, respectively. For the Verify algorithms in the different schemes, they have medium computational costs, lower computational costs, and higher computational costs respectively. We have summed the computational costs of the algorithms Sign and Verify to obtain the overall computational costs. The results show the t-ABPS scheme, ABPS-HL1 scheme, and ABPS-HL2 scheme have lower computational costs, medium computational costs, and higher computational costs respectively. The t-ABPS scheme has lower computational costs because it does not use the default attribute set, which simplifies this scheme.
The communication costs of the three schemes are at the same level. For more accurate analyses, the ABPS-HL1 scheme and ABPS-HL2 scheme have lower communication costs, while the t-ABPS scheme has higher communication costs. We compare the efficiency of the three ABPS schemes in Table 8.

Table 8.
Efficiency comparisons of t-ABPS, ABPS-HL1, and ABPS-HL2.
7. Conclusions
With the rapid development of AI technology, more and more UAVs are capable of flying autonomously without requiring real-time control from an operator. In this case, it is crucial to ensure the security of the commands sent to the UAVs.
To address this problem, we propose an efficient t-ABPS scheme. This scheme protects the integrity and authentication of commands, reduces the propagation delay, and protects the privacy of the user’s identity. We prove that t-ABPS has EUF-sA-CMA. Furthermore, we analyze the efficiency of t-ABPS in terms of computational costs and communication costs. The results indicate that the t-ABPS scheme has lower computational costs and higher communication costs.
In the t-ABPS scheme, it does not use a default attribute set, which reduces the flexibility of the scheme. Moreover, the UAV as the verifier still has higher computational costs. Next, we will further research how to reduce the computational costs of the UAV.
Author Contributions
Conceptualization, L.H., Y.G. and Y.Y.; software, L.H.; validation, Y.G. and Y.Y.; formal analysis, L.H.; writing—original draft preparation, L.H.; writing—review and editing, L.H., Y.G. and Y.Y.; supervision, Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Henan grant number 242300420296 and the Doctor Research Fund of Zhengzhou University of Light Industry grant number 2022BSJJZK15.
Data Availability Statement
Data available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gupta, L.; Jain, R.; Vaszkun, G. Survey of important issues in UAV communication networks. IEEE Commun. Surv. Tutor. 2016, 18, 1123–1152. [Google Scholar] [CrossRef]
- Guo, J.; Gao, H.; Liu, Z.; Huang, F.; Zhang, J.; Li, X.; Ma, J. ICRA: An intelligent clustering routing approach for UAV ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2447–2460. [Google Scholar] [CrossRef]
- Zhi, Y.; Fu, Z.; Sun, X.; Yu, J. Security and privacy issues of UAV: A survey. Mob. Netw. Appl. 2020, 25, 95–101. [Google Scholar] [CrossRef]
- Samanth, S.; Prema, K.V.; Balachandra, M. Security in Internet of drones: A comprehensive review. Cogent Eng. 2022, 9, 2029080. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, I.; Nisar, S.; Noor, F.; Qureshi, I.M.; Khanzada, F.; Khattak, H.; Aziz, M.A. Multiaccess edge computing empowered flying ad hoc networks with secure deployment using identity-based generalized signcryption. Mob. Inf. Syst. 2020, 2020, 8861947. [Google Scholar] [CrossRef]
- Din, N.; Waheed, A.; Zareei, M.; Alanazi, F. An improved identity-based generalized signcryption scheme for secure multi-access edge computing empowered flying ad hoc networks. IEEE Access 2021, 9, 120704–120714. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Lai, C.; Wang, Z. A provably secure aggregate authentication scheme for unmanned aerial vehicle cluster networks. Peer-Peer Netw. Appl. 2020, 13, 53–63. [Google Scholar]
- Jan, S.U.; Khan, H.U. Identity and aggregate signature-based authentication protocol for IoD deployment military drone. IEEE Access 2021, 9, 130247–130263. [Google Scholar] [CrossRef]
- He, L.; Ma, J.; Shen, L.; Wei, D. Certificateless designated verifier proxy signature scheme for unmanned aerial vehicle networks. Sci. China Inf. Sci. 2021, 64, 1–15. [Google Scholar] [CrossRef]
- Xu, Z.; Luo, M.; Vijayakumar, P.; Peng, C.; Wang, L. Efficient certificateless designated verifier proxy signature scheme using UAV network for sustainable smart city. Sustain. Cities Soc. 2022, 80, 103771. [Google Scholar] [CrossRef]
- Abdel-Malek, M.A.; Akkaya, K.; Bhuyan, A.; Ibrahim, A.S. A proxy signature-based swarm drone authentication with leader selection in 5G networks. IEEE Access 2022, 10, 57485–57498. [Google Scholar] [CrossRef]
- Qu, Y.; Zeng, J. Certificateless proxy signcryption in the standard model for a UAV network. IEEE Internet Things J. 2022, 9, 15116–15127. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, J.; Huang, F.; Cai, D.; Wu, Y.; Chen, X.; Igorevich, K.K. Lightweight trustworthy message exchange in unmanned aerial vehicle networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2144–2157. [Google Scholar] [CrossRef]
- Maji, H.K.; Prabhakaran, M.; Rosulek, M. Attribute-based signatures. In Proceedings of the Cryptographers’ Track at the RSA Conference 2011, San Francisco, CA, USA, 14–18 February 2011. [Google Scholar]
- Su, Q.; Zhang, R.; Xue, R.; Li, P. Revocable attribute-based signature for blockchain-based healthcare system. IEEE Access 2020, 8, 127884–127896. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.; Cai, S.; Yang, L.; Liao, Y.; Zhou, S. An efficient reusable attribute-based signature scheme for mobile services with multi access policies in fog computing. Comput. Commun. 2022, 196, 9–22. [Google Scholar] [CrossRef]
- Blazy, O.; Brouilhet, L.; Conchon, E.; Klingler, M. Anonymous attribute-based designated verifier signature. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 1–11. [Google Scholar] [CrossRef]
- Liu, L.; Hsu, C.; Au, M.H.; Harn, L.; Cui, J.; Zhao, Z. A revocable and comparable attribute-based signature scheme from lattices for IoMT. J. Syst. Archit. 2024, 154, 103222. [Google Scholar] [CrossRef]
- Li, J.; Au, M.H.; Susilo, W.; Xie, D.; Ren, K. Attribute-based signature and its applications. In Proceedings of the 5th ACM Symposium on Information, Computer and Communications Security, Beijing, China, 13–16 April 2010. [Google Scholar]
- Li, Y.; Chen, X.; Yin, Y.; Wan, J.; Zhang, J.; Kuang, L.; Dong, Z. SDABS: A flexible and efficient multi-authority hybrid attribute-based signature scheme in edge environment. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1892–1906. [Google Scholar] [CrossRef]
- Su, Q.; Zhang, R.; Xue, R.; Sun, Y.; Gao, S. Distributed attribute-based signature with attribute dynamic update for smart grid. IEEE Trans. Ind. Inform. 2022, 19, 9424–9435. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Huang, X.; Li, J.; Xiang, Y.; Wong, D.S. Secure outsourced attribute-based signatures. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3285–3294. [Google Scholar] [CrossRef]
- Tao, Q.; Cui, X.; Iftekhar, A. A novel lightweight decentralized attribute-based signature scheme for social co-governance. Inf. Sci. 2024, 654, 119839. [Google Scholar] [CrossRef]
- Xiong, H.; Bao, Y.; Nie, X.; Asoor, Y.I. Server-aided attribute-based signature supporting expressive access structures for industrial Internet of things. IEEE Trans. Ind. Inform. 2020, 16, 1013–1023. [Google Scholar] [CrossRef]
- Huang, Z.; Lin, Z. Secure server-aided attribute-based signature with perfect anonymity for cloud-assisted systems. J. Inf. Secur. Appl. 2022, 65, 103066. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Han, J.; Liu, C.; Zhang, Y.; Wang, H. Decentralized attribute-based server-aid signature in the internet of things. IEEE Internet Things J. 2021, 9, 4573–4583. [Google Scholar] [CrossRef]
- Liu, X.; Ma, J.; Xiong, J.; Zhang, T.; Li, Q. Personal health records integrity verification using attribute based proxy signature in cloud computing. In Proceedings of the 6th International Conference on Internet and Distributed Computing Systems, Hangzhou, China, 28–30 October 2013. [Google Scholar]
- He, L.; Ma, J.; Wei, D. Attribute-based proxy signature scheme for unmanned aerial vehicle networks. J. Commun. 2021, 42, 87–96. [Google Scholar]
- He, L.; Gan, Y.; Zhang, Y. Attribute-based proxy signature scheme supporting flexible threshold predicate for UAV networks. Electronics 2023, 12, 4854. [Google Scholar] [CrossRef]
- Huang, X.; Susilo, W.; Mu, Y.; Wu, W. Proxy signature without random oracles. In Proceedings of the Second International Conference on Mobile Ad-hoc and Sensor Networks, Hong Kong, China, 13–15 December 2006. [Google Scholar]
- Caro, A.D.; Iovino, V. jPBC: Java pairing based cryptography. In Proceedings of the 2011 IEEE Symposium on Computers and Communications, Kerkyra, Greece, 28 June–1 July 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).