Research on Formation Recovery Strategy for UAV Swarms Based on IVYA-Nash Algorithm

Abstract

Contemporary multi-UAV formations face dual challenges of obstacle avoidance and rapid formation recovery. To enable UAV swarms to efficiently restore their predefined configurations post-obstacle navigation, a formation recovery strategy grounded in Nash equilibrium game theory is proposed in this paper. By integrating the IVY optimization algorithm, a collaborative control model that systematically balances individual UAV interests with swarm-level objectives through carefully designed optimization criteria is established. Comparative experimental results demonstrate that, compared to traditional formation obstacle-avoidance algorithms, Improved Particle Swarm Optimization (IPSO), Ant Colony Optimization (ACO), and Genetic Algorithm (GA), our method exhibits superior performance across multiple key metrics, including average path length, formation accuracy rate, recovery time, and total time consumption. Real-flight tests on a multi-UAV platform confirm IVYA-Nash surpasses improved APF in formation accuracy and aerodynamic disturbance resistance, proving robustness in dynamic multi-agent scenarios. The work provides an efficient and reliable solution for coordinated control of UAV formations in complex environments.

1. Introduction

The formation control of multi-UAV systems has remained a research hotspot for decades. With expanding applications in military reconnaissance, logistics transportation, and disaster rescue [1,2,3,4,5], UAV formations face escalating challenges in obstacle-rich environments. These systems must not only execute efficient path planning but also maintain formation stability and mission coordination during obstacle avoidance requirements that impose extreme demands on cooperative control.

With the rapid development of UAV swarm applications, their use cases extend far beyond military reconnaissance and logistics. UAV swarms are increasingly employed in industrial inspections, agricultural monitoring, environmental sensing, disaster response, and UAV light shows, demonstrating the need for reliable formation control in diverse scenarios [6]. However, state-of-the-art (SOTA) swarm intelligence approaches such as PSO, ACO, GA, and reinforcement learning-based methods suffer from notable drawbacks when operating in highly dynamic and high-dimensional environments. For instance, PSO and GA typically face slow convergence and premature local optima, while APF-based methods often trap UAVs in local minima. These gaps directly motivate the development of our proposed IVYA-Nash framework [7,8,9].

Existing research on UAV formations has mainly focused on path planning, obstacle avoidance, and cooperative control using approaches such as game theory [6] and swarm intelligence algorithms [10,11,12,13,14]. For instance, Zhang et al. [13] demonstrated that an improved PSO (IPSO) can effectively handle 3D obstacle avoidance in multi-UAV formations. However, traditional PSO frameworks face inherent limitations in formation recovery: static inertia weights restrict adaptability to dynamic environments, which undermines both avoidance efficiency and the stability of formation restoration. Moreover, they often fail to converge to globally optimal solutions in real time.

Beyond PSO, other strategies attempt to enhance specific capabilities or adapt to specialized environments. Yu’s evolutionary RL improves exploration efficiency [14], Li’s hybrid SAQPSO-SA enhances target tracking [15], Wu’s DSCA-IRRT addresses urban path planning efficiency [16], and Kabore introduces onboard perception for GPS-denied control [17]. Zhu’s integration of APF with consensus control [18] directly tackles obstacle avoidance during recovery, while Wu’s HPIO [19] and Sun’s compensation look-ahead algorithm [20] improve cooperative avoidance and heading optimization in complex scenarios. Despite these advances, three critical gaps remain: (i) Nash-based methods often assume complete information, making them less effective under communication constraints [21]; (ii) path planning and formation control are frequently treated as separate problems, ignoring their dynamic coupling in obstacle-rich environments, which leads to issues such as GA’s slow convergence [22] or APF’s susceptibility to local minima [13,23]; and (iii) while some methods improve global search (e.g., IVY [10]), they do not systematically integrate dynamic obstacle avoidance, reducing robustness in multi-conflict scenarios [24].

Classic swarm intelligence algorithms such as GA, HS, ABC, and GWO have also been applied to UAV path planning. Yet, in high-dimensional, dynamic, cooperative game problems, they suffer from high computational overhead, parameter sensitivity, and a tendency to fall into local optima. For example, GA converges too slowly for real-time decision-making, and GWO struggles with complex constraints. These limitations underscore the need for an algorithm that can balance global exploration with local exploitation, while maintaining computational efficiency for real-time multi-UAV recovery.

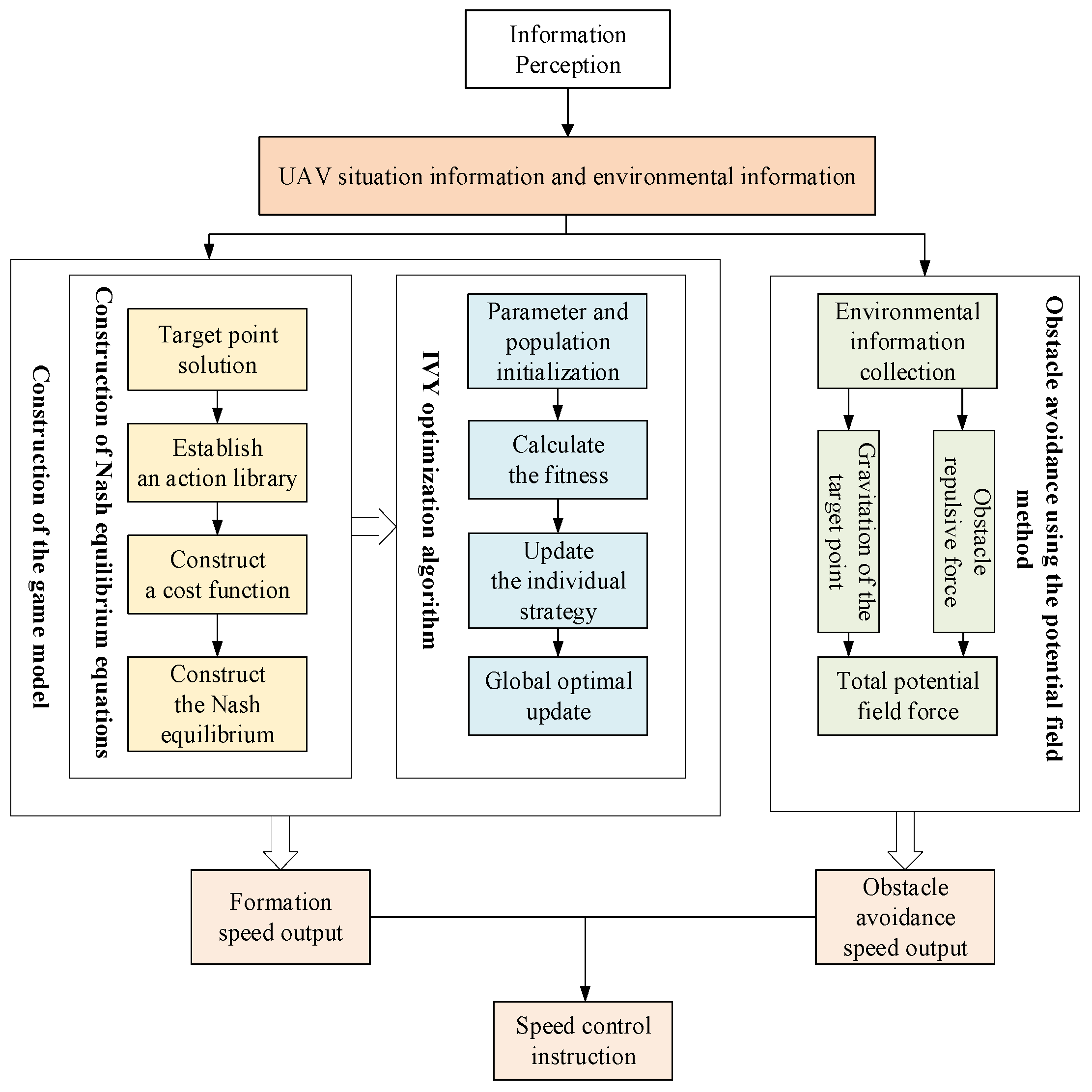
To address these challenges, the paper proposes an IVYA-Nash cooperative optimization framework for UAV formation recovery, featuring three key innovations: First, the Ivy Algorithm (IVYA) solves non-cooperative game Nash equilibria through biomimetic growth mechanisms, balancing global exploration and local exploitation to overcome convergence bottlenecks in dynamic optimization [25]. Second, a multi-objective cost function fusion mechanism is developed that transforms the virtual structure method’s rigid constraints into elastic potential fields, enabling dynamic trade-offs between formation stability and obstacle avoidance flexibility. Third, a hierarchical decision architecture enhances swarm coordination through IVYA’s adaptive perturbation strategies.

Recent advances further highlight emerging directions in UAV swarm coordination. Bu et al. [26] reviewed formation control methods and outlined key challenges. Chen et al. [27] demonstrated that DRL can enhance swarm coverage and tracking through prior experience, while Zhao et al. [28] developed a distributed formation planning method emphasizing scalability. These works confirm the importance of reinforcement learning and distributed optimization. Building on this trend, our IVYA-Nash framework integrates game-theoretic decision-making with a metaheuristic optimizer to achieve robust and efficient formation recovery in dynamic environments.

The Ivy algorithm mimics Hedera helix’s phototropism and climbing growth patterns. Its stochastic perturbation vectors help escape local optima, while nonlinear convergence mechanisms excel in solving high-dimensional non-convex Nash equilibrium problems. Compared to PSO’s inertia updates and ACO’s genetic operations, IVYA demonstrates higher search efficiency in obstacle environments (as shown in Section 3), providing novel theoretical tools for real-time decision-making in complex game scenarios.

The key innovations of this work are threefold, each directly addressing limitations in existing methods, as illustrated in Figure 1.

(i)

IVYA introduces biomimetic growth mechanisms that balance global exploration with local exploitation, overcoming convergence bottlenecks in PSO and ACO.

(ii)

By integrating Nash equilibrium into formation recovery, the proposed framework systematically couples obstacle avoidance with formation maintenance, addressing the limitations of decoupled designs in prior works.

(iii)

An elastic potential field mechanism is developed to enhance adaptability during obstacle negotiation, ensuring both recovery speed and formation stability in complex environments.

Overall, existing UAV swarm formation recovery methods can be classified into four categories. Classical control approaches are simple and efficient but often lack robustness. Swarm intelligence algorithms (PSO, ACO, GA, HS, GWO) offer global search but suffer from slow convergence. Game-theoretic methods enable distributed decision-making but usually assume perfect communication. Reinforcement learning approaches provide adaptability in dynamic settings but require heavy training and face generalization challenges. In contrast, our proposed IVYA-Nash framework combines the distributed optimization of game theory with the convergence efficiency of the Ivy Algorithm, achieving faster recovery and stronger robustness while remaining computationally feasible for real-time swarm operations.

2. Problem Formulation and Model Architecture

2.1. Problem Formulation

The Multi-UAV formation game problem studied in this paper can be described as: UAVs evaluate their expected costs based on environmental information, individual status and overall formation requirements in a UAV formation mission. And then determine the optimal action plans for all participants through game-theoretic interactions, aiming to rapidly reform the formation and reaching the designated destination.

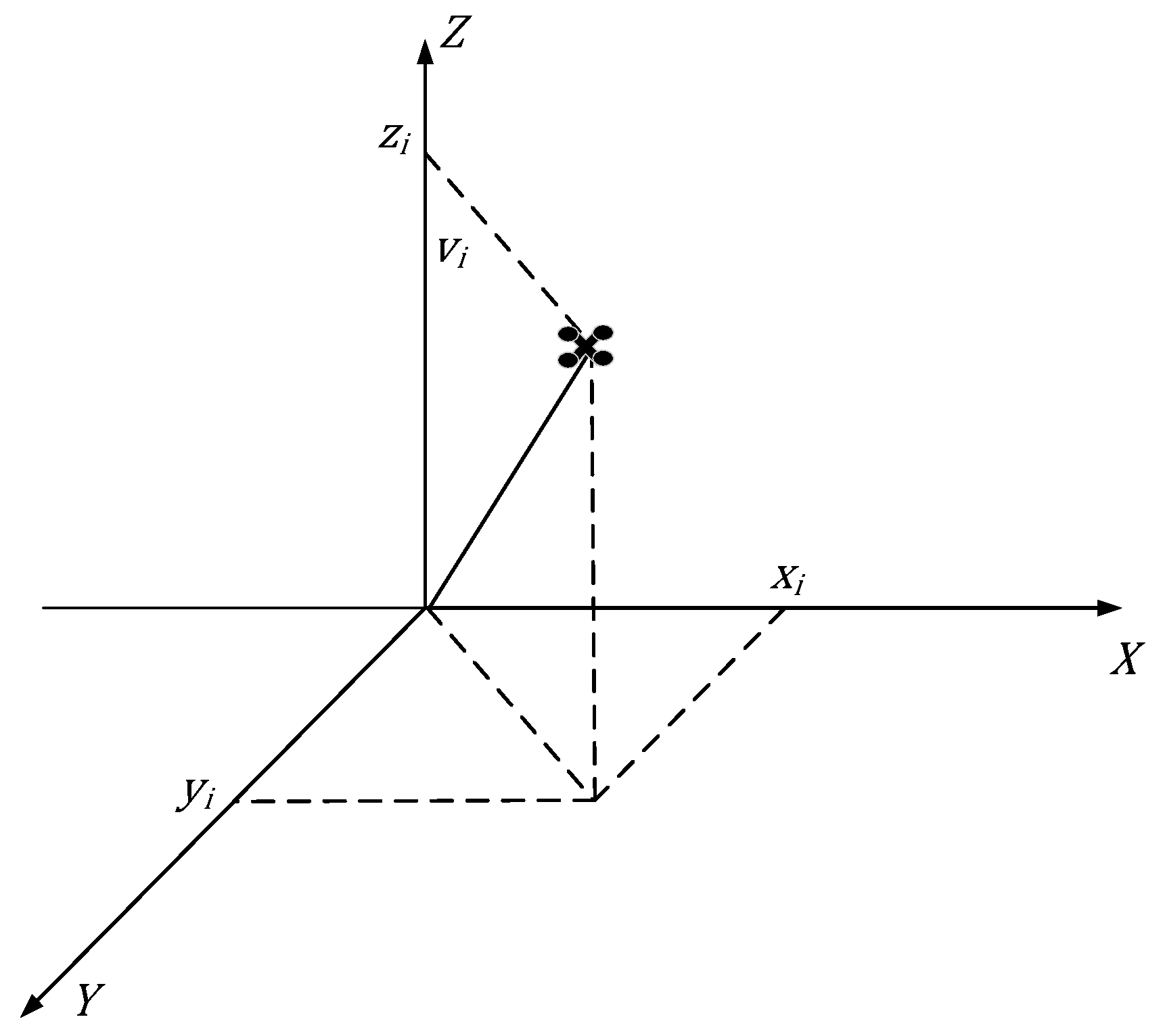
For each UAV in the formation, its state can be represented as:

$$X_i=\left[\begin{array}{lll}{x}_i\hfill & y_i\hfill & z_i\hfill \\ v_{xi}\hfill & v_{yi}\hfill & v_{zi}\hfill \end{array}\right],$$

(1)

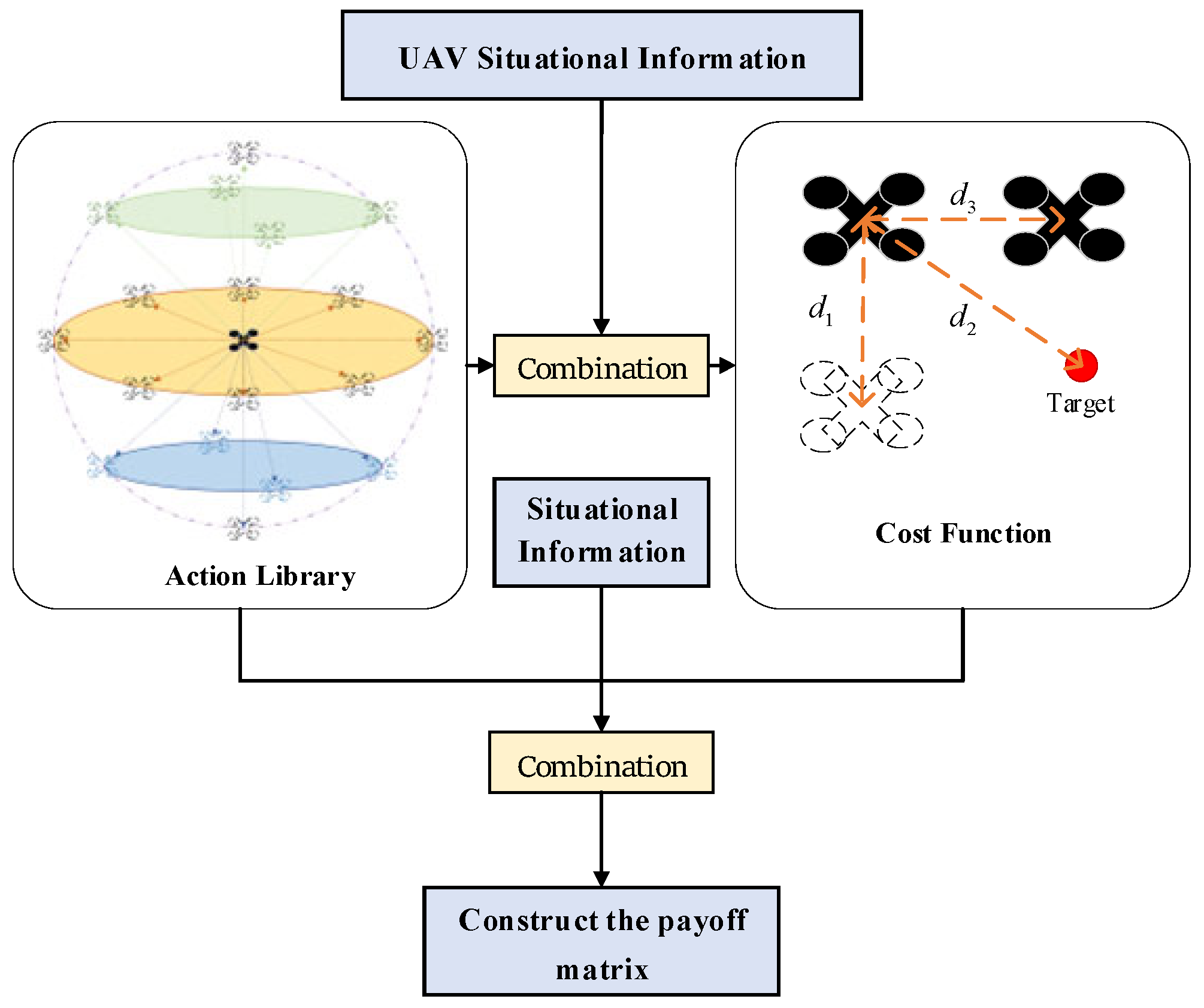
where $x,y,z$ denote the 3D coordinates of the $\mathrm{i}\text{-}\mathrm{th}$ UAV, and $v_x,v_y,v_z$ represent its velocity components along three axes. Let $N$ denote the UAV swarm set. The action library for the next moment is constructed as:

$${\Omega }_i=\left[\begin{array}{lll}{x}_i^{\ast }\hfill & y_i^{\ast }\hfill & z_i^{\ast }\hfill \\ v_{xi}^{\ast }\hfill & v_{yi}^{\ast }\hfill & v_{zi}^{\ast }\hfill \end{array}\right]$$

(2)

where $x_i^{\ast },y_i^{\ast },z_i^{\ast }$ represent the 3D coordinates of the $\mathrm{i}\text{-}\mathrm{th}$ UAV at the next moment, and $v_{xi}^{\ast },v_{yi}^{\ast },v_{zi}^{\ast }$ denote its velocity values at the next moment. The drone’s action is as shown in Figure 2.

2.2. Construction of Formation Game Model

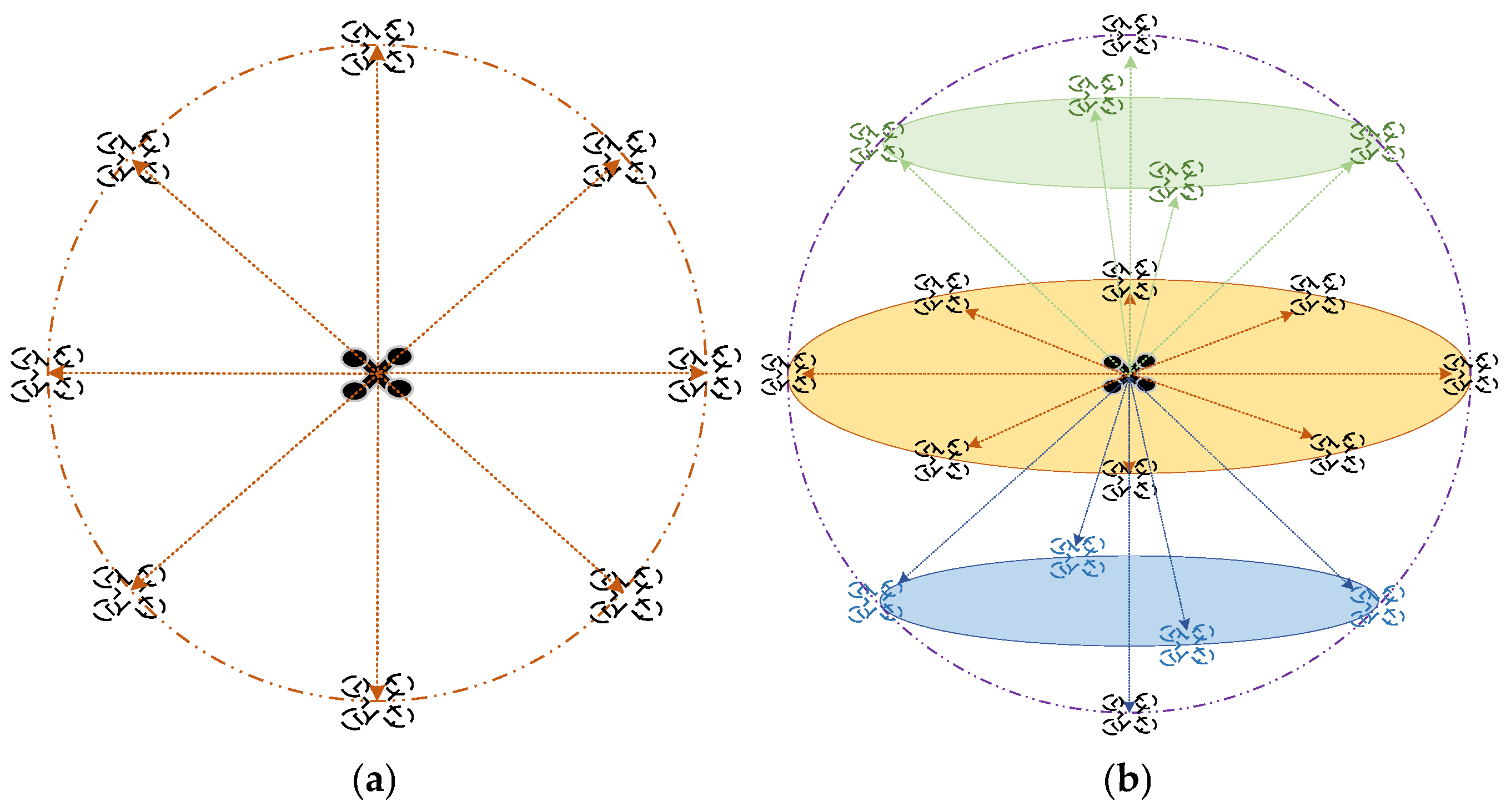
To establish the UAV formation recovery game model, we first construct the UAV action library, as illustrated in Figure 3. This study designs a three-dimensional UAV action library based on attitude and velocity control methods. The action library design is formulated as follows:

$$\left\{\begin{array}{c}{v}_x=v\cos \theta \cos \phi \\ v_y=v\cos \phi \sin \theta \\ \begin{array}{l}{v}_z=v\sin \phi \end{array}\end{array}\right.$$

(3)

where $\theta$ is the angle between the $xy\text{-}plane$ and the projection of the UAV on the $xy$-plane, $\phi$ is the angle between the $z\text{-}axis$ and the velocity of the UAV, and $v$ is the velocity of the UAV. To prevent sudden changes in velocity caused by strategy selection issues, the following smoothing function is defined:

$$v_{\mathrm{s}}(t)=\alpha v_s(t)+(1-\alpha )\cdot v_{\mathrm{s}}(t-\Delta t)$$

(4)

where $v_{\mathrm{s}}(t)$ denotes the magnitude of velocity vector at time $t$, $v_{\mathrm{s}}(t-\Delta t)$ is the velocity value at the previous moment, and $\alpha \in \left[0,1\right]$ is the parameter value. The schematic diagram of the UAV action library is illustrated as follows.

2.3. Construction of Formation Game Model

The UAV formation restoration requires restoring the UAVs to their initial formation, as illustrated in Figure 4. The target points of UAVs after the overall movement of the formation are calculated using the virtual structure method, with the formula as follows:

$$P_i=P_a+offset\cdot r_i$$

(5)

where $P_i=(x_i,y_i,z_i)$ is the target position of the $\mathrm{i}\text{-}\mathrm{th}$ UAV, $P_a$ is the position of the virtual UAV after the change in the formation position, and $r_i$ is the distance between the $\mathrm{i}\text{-}\mathrm{th}$ UAV and the virtual UAV.

Constructing the UAV situation cost function is a crucial step in realizing the UAV formation game. The objective of the game problem proposed in this paper is to make the cost function converge to the Nash equilibrium point through a heuristic optimization algorithm. For each UAV participating in the game, the target cost function is as follows:

$$J_i={\displaystyle \frac{{\eta }_1}{N}}\cdot ‖{\Omega }_i-{\omega }_i\cdot X_i‖+{\displaystyle \frac{{\eta }_2}{N}}\cdot ‖P_i-{\omega }_i\cdot {\mathcal{\partial }}_i‖$$

(6)

where $P_i$ denotes the target (desired) position UAV $i$, ${\mathcal{\partial }}_i$ is the current position of the UAV $i$, ${\Omega }_i$ is the action plan of the UAV $i$ at the next time step, $X_i$ is the action of the UAV i at the current moment, and ${\eta }_1$ and ${\eta }_2$ are both weight coefficients. ${\eta }_1$ adjusts the weight of the action difference term, and ${\eta }_2$ adjusts the weight of the position deviation term. ${\omega }_i$ is the weight coefficient of the UAV $i$, which adjusts the influence of the current action and position.

For each player participating in the game, the goal is to minimize the above-mentioned cost function. However, in this process, it is inevitable that the cost functions of other players will increase. To optimize the overall formation efficiency, it is necessary to construct the Nash equilibrium condition as the optimization objective. The Nash equilibrium in the UAV formation restoration problem proposed in this paper is defined as follows:

For the cost function $J_i$ of each UAV, it depends not only on its own behavior but also on the behaviors of other UAVs. The main meaning is that no player can unilaterally change its behavior under the Nash equilibrium to reduce its cost. It is defined as: ${\eta }^{\prime }=\mathrm{col}\left\{{\eta }_1^{\ast },\dots ,{\eta }_k^{\ast }\right\}\in \Omega$ is a Nash equilibrium solution if for any $i\in {\Omega }_i$, the following condition is satisfied:

$$J_i\left({\eta }_i^{*},{\eta }_{-i}^{*}\right)⩽J_i\left({\eta }_i,{\eta }_{-i}^{*}\right),\hspace{0.33em}\hspace{0.33em}\forall {\eta }_i\in {\Omega }_i$$

(7)

where ${\Omega }_i$ is the set of admissible strategies for the $\mathrm{i}\text{-}\mathrm{th}$ UAV. From the definition of the Nash equilibrium, it can be seen that once the strategies of UAVs form a Nash equilibrium, no UAV will unilaterally deviate from the Nash equilibrium, and the UAV formation will maintain flight in the achieved equilibrium state.

From the above, the formation game problem can be transformed into a non-cooperative game Nash equilibrium solving problem. The formation game can be described by a triple $\Lambda =\{\mathcal{T},J(\eta ),\Omega \}$, where $\mathcal{T}$ is the set of players, $\Omega =\forall {\Omega }_i$ is the strategy space of the players participating in the game ($\eta \in {\Omega }_i\subseteq R^n$ is the strategy space of the $\mathrm{i}\text{-}\mathrm{th}$ player), $\eta \in {\Omega }_i\subseteq R^n$ is the current strategy of the UAVs, and $J(\eta )$ is the overall pay-off matrix, as shown below:

$$J(\eta )=\left[\begin{array}{ccc}{j}_1({\eta }_1)& \cdots & j_1({\eta }_k)\\ \cdots & j_i({\eta }_j)& \cdots \\ j_n({\eta }_1)& \cdots & j_n({\eta }_k)\end{array}\right]$$

(8)

where $j_i({\eta }_j)$ is the cost function of the $\mathrm{i}\text{-}\mathrm{th}$ player participating in the formation game.

Based on the above model construction, the Nash equilibrium is further solved. The next-step solutions of all UAVs participating in the game are the next-step actions of the UAVs. The construction process of the game model is shown in the following figure:

In Figure 5, d1, d2, and d3 represent the position differences of the drone from its position at the next moment, the position difference between the drone and the target point, and the distance between drones, respectively.

2.4. Nash Equilibrium Solution and Problem Transformation

The Ivy Algorithm was selected due to its superior ability to escape local optima and handle non-convex optimization problems. Inspired by Hedera helix’s phototropism and climbing behavior, IVYA achieves nonlinear convergence and high-dimensional optimization efficiency. In this study, we conducted comparative evaluations with GA, PSO, and ACO, which confirm the advantages of IVYA in terms of convergence speed, robustness, and recovery accuracy.

To solve this non-linear function, this paper introduces the chaos-enhanced IVY algorithm (Chaotic Ivy Optimizer, IVYA-C) to find the Nash equilibrium solution of the game problem. The algorithm mimics the growth process of ivy plants with chaotic dynamics. By combining chaotic perturbation, random exploration, and global-optimal guidance, it achieves an improved balance between local exploitation and global optimization. The state of each UAV is described by an optimization function incorporating chaotic factors. The IVYA-C algorithm dynamically adjusts the positions of UAVs using chaotic mapping, enabling individual actions to meet local requirements while effectively optimizing the overall objective. Its fitness function $f\left(l_i\right)$ is:

$$\min f\left(l_i\right)\leftarrow \min {\displaystyle \sum }_{j\ne i}{\left[J(\eta )-\mathbb{E}\left(J(\eta )\right)\right]}^2$$

(9)

where $J(\eta )$ is the pay-off matrix, $\mathbb{E}\left(•\right)$ is the expected payoff of the payoff matrix. The steps of the Ivy optimization algorithm are as follows (Algorithm 1):

Algorithm 1 IVYA-C

1 Begin

2  Initialize the parameters of the Ivy algorithm: $I_{\min },I_{\max },Ite{r}_{\max },N_{pop},$ and set the initial iteration number: $Iter=1$

3  Initialize chaotic parameters: $\mu =4.0,p_{chaos}=0.3$

4  Initialize the population $\overrightarrow{I}=\left(I_1,I_2,\dots ,I_i,\dots ,I_{\mathrm{Npop}}\right)$ using chaotic initialization:

for each individual $i$

$x=\mathrm{rand}\left(\right)$

for each dimension:

$x=\mu \cdot x\cdot (1-x)$

$I_{i,d}=I_{\min }+\mathrm{rand}\cdot \left(I_{\max }-I_{\min }\right)$

Store chaotic state $C_i=x$

5  Calculate fitness values $f\left(l_i\right)$ for all individuals. Sort by fitness (high to low. Set optimal individual ($I_{best}=I_1$)

6  while $Iter\le Ite{r}_{\max }$ do

7    for $i=1$ to $N_{pop}$ do:

8     Chaotic perturbation with probability $p_{chaos}$

if $\mathrm{rand}\left(\right)\text{<}{p}_{chaos}$:

$C_i=\mu \cdot C_i\cdot \left(1-C_i\right)$

$I_i=I_i+0.1\cdot \left(I_{\max }-I_{\min }\right)\cdot \left(C_i-0.5\right)$

$I_i=\min \left(\max \left(I_i,I_{\min }\right),I_{\max }\right)$

end if

9       Calculate growth vector: $\Delta g_{v_i}=\left|N(1,D)\right|\times \left(I_i-I_{\mathrm{best}}\right)$

10        Calculate: $\Delta g_{v_i}^{\prime }=rand\times \Delta g_{v_i}$

11        Select random neighbor $I_{ii}$ from population

12        if ($f\left(I_{ii}\right)<f\left(I_i\right)$) then

13         $\beta =\left(2+C_i\right)/2[\mathrm{Originally}\text{:}(2+\mathrm{rand})/2]$

14         $I_i^{\mathrm{new}}=I_i+\beta \times \Delta g_{v_i}^{\prime }\times \left(I_{ii}-I_i\right)$

15        else

16         $I_i^{\mathrm{new}}=I_i+\Delta g_{v_i}^{\prime }\times \left(C_i-0.5\right)\times \left(I_{\max }-I_{\min }\right)$

17        end if

18        Evaluate new fitness $f\left(I_i^{new}\right)$

19        Calculate $\Delta g_{v_i}^{\prime \prime }=|N(1,D)|\times \left(I_i^{\mathrm{new}}-I_i\right)$

20        Add $I_i^{new}$ to merged population: ${\overrightarrow{I}}_{\mathrm{merged}}=\left\{\overrightarrow{I},{\overrightarrow{I}}^{\mathrm{new}}\right\}$

21    end for

22    Merge populations: ${\overrightarrow{I}}_{total}=\overrightarrow{I}\cup {\overrightarrow{I}}^{\mathrm{new}}$

23    Sort ${\overrightarrow{I}}_{total}$ by fitness.

24    Select top $N_{pop}$ individuals.

25    Update $I_{best}=I_1$ (current best individual)

26    $Iter=Iter+1$

27    end while

28   Output global optimal solution (drone optimal strategy)

29 End

In the described algorithm, $I_i$ denotes the position of the $\mathrm{i}\text{-}\mathrm{th}$ individual, where $\mathrm{rand}$ represents a uniformly distributed random number within the interval $[0,1]$. The search space boundaries are defined by $[I_{\min },I_{\max }]$. The term $\Delta g_{v_i}$ corresponds to the growth vector of the $\mathrm{i}\text{-}\mathrm{th}$ individual, which guides its directional evolution during optimization. The operator $\mathcal{N}(1,D)$ generates normally distributed random numbers with mean 1 and dimension D, while $\odot$ signifies element-wise multiplication between vectors. Through iterative optimization, this algorithm converges to the Nash equilibrium solution, which determines the optimal velocity strategy for each UAV. The resultant velocity control vector is formulated as:

$$v_{formation,i}(t)={\delta }_i^{\ast }$$

(10)

where ${\delta }_i^{\ast }$ represents the optimized velocity strategy derived from the Ivy algorithm, directing UAVs toward their target positions while maintaining swarm coordination.

2.5. Obstacle Avoidance Controller Implementation

During UAV formation flight, sudden obstacles may emerge. Without timely obstacle avoidance and trajectory replanning, the mission may fail. The artificial potential field method is a common local path planning approach with advantages including low control requirements, high computational efficiency, good robustness, and smooth trajectory generation. However, it tends to trap UAVs in local optima. To address this limitation, this paper adopts an improved potential field method that combines the strengths of artificial potential fields and non-potential vector field methods. The key innovation lies in making the overall repulsive field orthogonal to the gravitational field under specific conditions, thereby resolving obstacle avoidance challenges and preventing UAV stagnation in local potential field minima.

The conventional APF method defines two fundamental forces, as shown in Figure 6a. Attractive Force towards the target:

$${\mathsf{\Phi }}_{a,i}=-k_a\left(q_i-q_{\mathrm{goal}}\right)$$

(11)

where $k_a>0$ tunes attraction strength, and $q_{\mathrm{goal}}$ denotes the target position. Repulsive Force from obstacles:

$${\Phi }_{r,i}=\left\{\begin{array}{ll}{k}_r\left({\displaystyle \frac{1}{d_{\mathrm{obs}}}}-{\displaystyle \frac{1}{d_{\mathrm{safe}}}}\right){\displaystyle \frac{q_i-q_{\mathrm{obs}}}{{‖q_i-q_{\mathrm{obs}}‖}^3}}\hfill & \mathrm{if} d_{\mathrm{obs}}\le d_{\mathrm{safe}}\hfill \\ 0\hfill & \mathrm{otherwise} \hfill \end{array}\right.$$

(12)

where $q_i$ and $q_{\mathrm{obs}}$ denote the 3D position vectors of the UAV and obstacle, respectively. The term $d_{obs}=‖q_i-q_{\mathrm{obs}}‖$ calculates their Euclidean separation distance. The repulsive force comprises three key components:

The non-potential orthogonal vector field method modifies the conventional potential field approach by retaining only the orthogonal components between repulsive and attractive forces when their angle exceeds 90 degrees, as shown in Figure 6a. For the $\mathrm{i}\text{-}\mathrm{th}$ UAV, the angle ${\chi }_i\in [0,\mathsf{\pi }]$ between attractive force ${\Phi }_{a,i}$ and repulsive force ${\Phi }_{r,i}$ is defined as:

$$\cos {\chi }_i={\displaystyle \frac{{\Phi }_{a,i}^T{\Phi }_{r,i}}{‖{\Phi }_{a,i}‖‖{\Phi }_{r,i}‖}}$$

(13)

According to the above, based on the angle function and the conventional potential field method function, the following potential field force function ${\Phi }_{\mathrm{ovf},i}$ can be obtained and is defined as:

$${\Phi }_{\mathrm{ovf},i}=\left\{\begin{array}{l}-\mathrm{sat}\left({\Phi }_{\mathrm{a},i}+P_{\mathrm{a},i}\right.\left.\times \mathrm{sat}\left({\Phi }_{\mathrm{r},i},v_{\mathrm{m},i}^{\prime }\right),v_{\mathrm{m},i}\right)\cos {\chi }_i\in \left[{\mu }_i,0\right]\\ -\mathrm{sat}\left({\Phi }_{\mathrm{a},i}\right.\left.+\mathrm{sat}\left({\Phi }_{\mathrm{r},i},v_{\mathrm{m},i}^{\prime }\right),v_{\mathrm{m},i}\right)\cos {\chi }_i\in \left[-1,{\mu }_i\right)\cup (0,1]\end{array}\right.$$

(14)

$$P_{\mathrm{a},i}=I_n-{\displaystyle \frac{{\Phi }_{\mathrm{a},i}{\Phi }_{\mathrm{a},i}^{\mathrm{T}}}{{‖{\Phi }_{\mathrm{a},i}‖}^2}}$$

(15)

where $v_{\mathrm{m},i}$ is the maximum speed of the UAV; $\mathrm{sat}$ is a limiting function to prevent the speed output value from exceeding $v_{\mathrm{m},i}$. It can be seen from the above formula that the field-free orthogonal vector field has a defect, that is, it is discontinuous at $\cos {\chi }_i=\mu$, which will lead to the non-existence of ${\Phi }_{\mathrm{ovf} ,\mathrm{i}}$. For UAVs, it will cause a sudden change in the desired speed command. Therefore, a smooth function is proposed and defined as

$$\tau \left(x,d_1,d_2\right)=\left\{\begin{array}{cc}0& x\le d_1\\ A{x}^3+B{x}^2+Cx+D& d_1\le x\le d_2\\ 1& d_2\le x\end{array}\right.$$

(16)

where $A=2/{\left(d_1-d_2\right)}^3$, $B=-3\left(d_1+d_2\right)/{\left(d_1-d_2\right)}^3$, $C=6d_1{d}_2/{\left(d_1-d_2\right)}^3$, $D=\left(d_1^3-3d_1^2{d}_2\right)/{\left(d_1-d_2\right)}^3$ are parameters. Thus, an improved field-free orthogonal vector field method with a continuous transition process is proposed as

$${\Phi }_{\mathrm{movf},i}=\left\{\begin{array}{cc}-\mathrm{sat}\left({\Phi }_{\mathrm{a},i}+P_{\mathrm{a},i}\right.\left.\times \mathrm{sat}\left({\Phi }_{\mathrm{r},i},v_{\mathrm{m},i}^{\prime }\right),v_{\mathrm{m},i}\right)& \cos {\chi }_i\in [-1,0]\\ -\mathrm{sat}\left({\Phi }_{\mathrm{a},i}+\mathrm{sat}\left({\Phi }_{\mathrm{r},i},v_{\mathrm{m},i}^{\prime }\right),v_{\mathrm{m},i}\right)& \cos {\chi }_i\in (0,1]\end{array}\right.$$

(17)

where $P_{\mathrm{ma},i}=I_n-{\gamma }_i{\displaystyle \frac{{\Phi }_{\mathrm{a},i}{\Phi }_{\mathrm{a},i}^{\mathrm{T}}}{{‖{\Phi }_{\mathrm{a},i}‖}^2}}$, ${\gamma }_i=\tau \left(\cos {\chi }_i,{\mu }_i,-{\displaystyle \frac{2\sqrt{5}{\mu }_i}{5{\alpha }_i}}\right)$.

By using this orthogonal vector field method, obstacles in the formation path can be effectively avoided. Combined with the UAV formation methods proposed in the previous sections, the formation restoration and formation transformation of UAVs can be efficiently completed. Thus, the speed control input for obstacle avoidance can be obtained as:

$$v_{\mathrm{obs},i}=k_v\cdot {\Phi }_{\mathrm{movf},i}$$

(18)

where $v_{\mathrm{obs},i}$ is the obstacle-avoidance speed input, ${\Phi }_{\mathrm{movf},i}$ is the output of the potential field force function, and $k_v$ is the speed adjustment gain, which adjusts the mapping intensity of the potential field force on the speed.

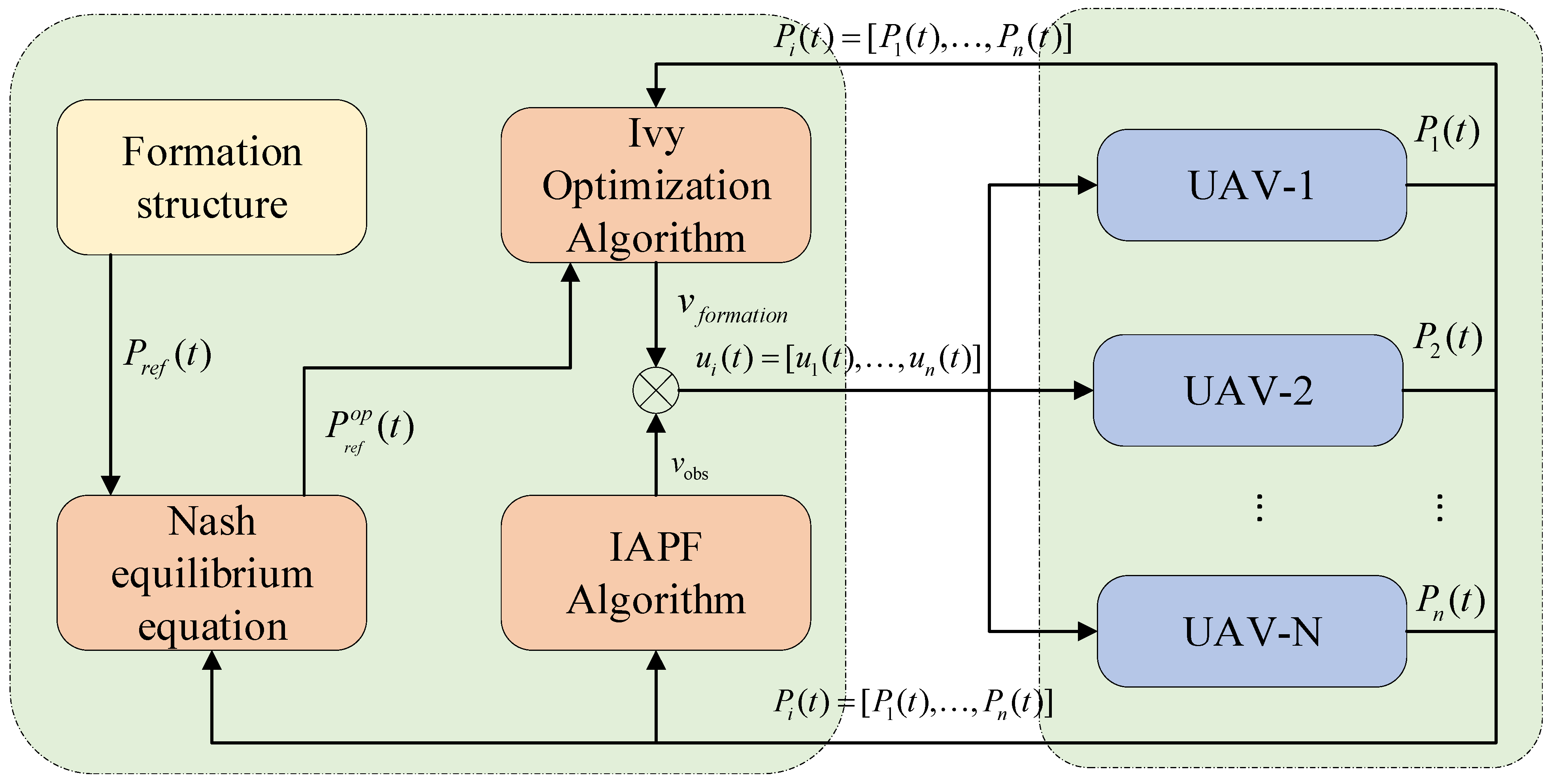
2.6. Implementation of the Total Controller

To achieve the efficient execution of UAV formation restoration and obstacle-avoidance tasks, this paper designs a comprehensive total controller that integrates formation restoration control and obstacle-avoidance control. By using an optimization algorithm to solve the Nash equilibrium of the multi-UAV system, the optimal control strategy for each UAV is generated. The core objective of the total controller is to calculate the optimal control input for each UAV, enabling them to move coordinately towards the target position in a dynamic environment and quickly avoid obstacles when encountered, thereby maintaining the stability and safety of the formation.

The control input of the total controller for each UAV is:

$$u_i(t)=\alpha v_{formation,i}+(1-\alpha )v_{\mathrm{obs},i}$$

(19)

where $v_{\mathrm{formation},i}$ is the control input for formation restoration; $v_{\mathrm{obstacle},i}$ is the control input for obstacle avoidance; and $\alpha \in [0,1]$ is an adjustment factor that controls the priority of the formation restoration and obstacle-avoidance tasks. The proof of the controller’s stability is detailed in Appendix A. The algorithm flow is shown in Figure 7.

3. Experimental Comparison

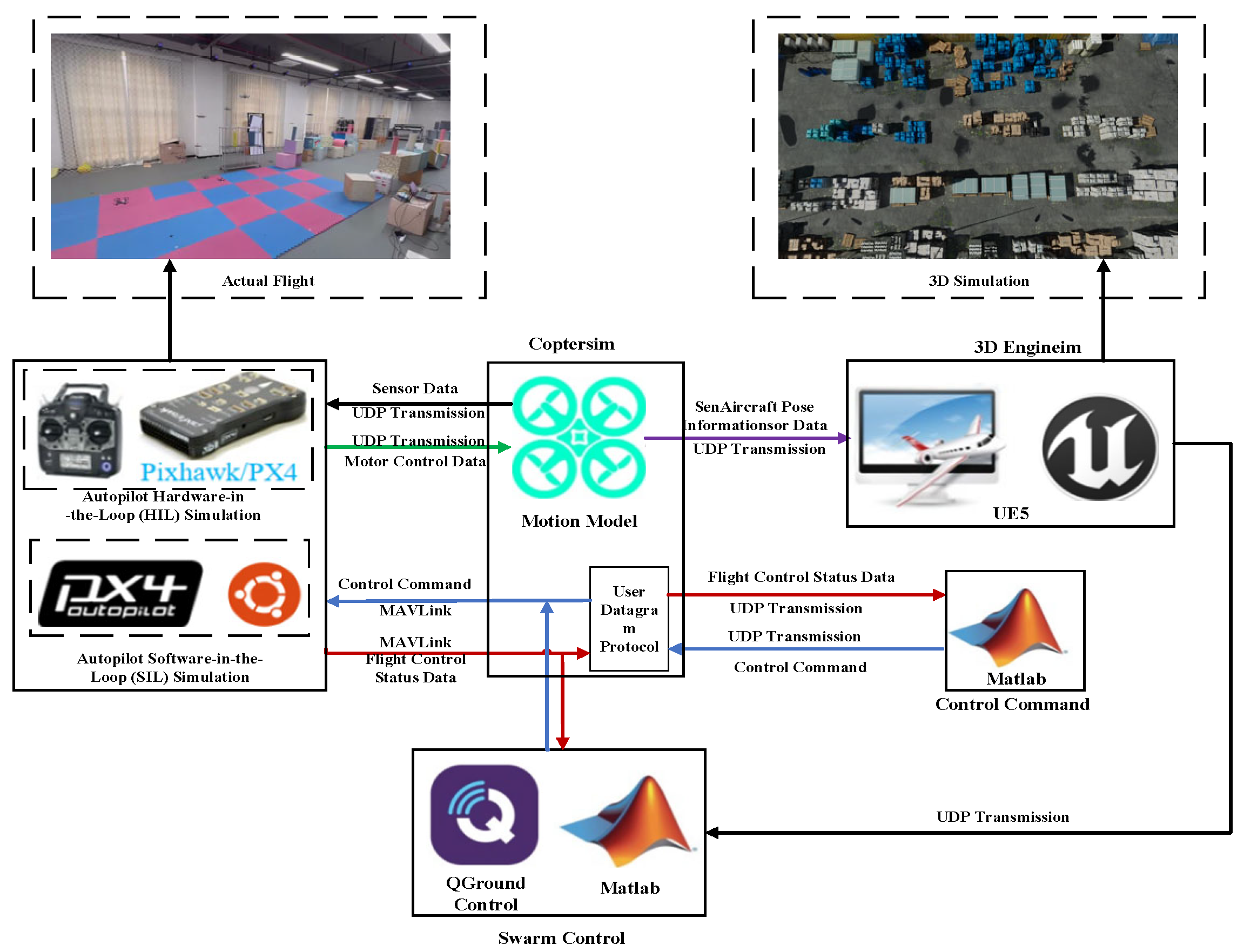
The method proposed in this paper is verified by digital simulation platforms and real-flight tests. The first step is the digital simulation verification. Multiple programming languages such as Python3.11, MATLAB R2024a, and C++ on the Windows platform are used to conduct digital simulation verification of the designed algorithm. In combination with the RflySim3D simulation platform, the verification results are fully demonstrated.

The Rflysim simulation platform consists of flight control modules, Coptersim modules, 3D display modules, swarm control modules, and vision control modules. This platform can provide UAV flight simulations based on the UE engine, and can simulate the flight control controller environment and control command transmission in real time. The architecture of the Rflysim platform and its 3D simulation are shown in the following Figure 8.

In the process of solving the Nash equilibrium, the parameter settings of the solution algorithm in this paper are as follows (

Table 1. Experimental Parameters.

Algorithm	Value
IVYA-C	$N=20,MaxIter=100,I_{\min }=0,I_{\max }=3,\Delta g_{v_i}=0.5,\mu =4.0,p_{chaos}=0.3$
IVYA	$N=20,MaxIter=100,I_{\min }=0,I_{\max }=3,\Delta g_{v_i}=0.5,\mu =4.0$
IPSO [11]	$N=20,MaxIter=100,{\eta }_1=1.5,{\eta }_2=1.5,w\_\max =0.9,w\_\min =0.4$
GA	$N=20,MaxIter=100,p_c=0.8,p_m=0.1$.
ACO	$N=20,\alpha =1.0,\beta =2.0,\rho =0.5,Q=100$

):

The key parameters of the IVYA-C algorithm, including the population size, maximum iterations, and chaos probability, were determined through a series of preliminary experiments to balance solution quality and computational cost. For instance, the chaos probability was set to a small value (e.g., 0.03) to introduce sufficient randomness for escaping local optima without disrupting the convergence process. The number of iterations was set to ensure convergence across all benchmark algorithms, providing a fair basis for comparison. A detailed sensitivity analysis of these parameters is a valuable direction for future work to fully characterize their impact on performance.

This paper conducts multiple types of formation method comparison experiments, mainly comparing the formation recovery ability and formation transformation ability of UAVs. The algorithm comparisons include the leader–follower method and the virtual structure method. The experiments include comparisons of path length, time, and convergence speed.

The formation accuracy rate $\gamma$ in this paper is defined by the following formula:

$$\gamma =\left(1-{\displaystyle \frac{1}{N}}{\displaystyle \sum }_{i=1}^N\left({\displaystyle \frac{\parallel P_i-P_i^{\ast }\parallel }{P_i^{\ast }}}\right)\right)\times 100\%$$

(20)

where $P_i$ is the position of the $\mathrm{i}\text{-}\mathrm{th}$ UAV, and $P_i^{\ast }$ is its target position.

3.1. Simulation Comparison Experiment of Formation Restoration

To comprehensively verify the effectiveness of the UAV formation restoration strategy proposed in this paper, digital simulation experiments were carried out using MATLAB. The experiments involved multiple comparative tests, benchmarking our proposed method against the traditional improved APF method and three other widely used swarm intelligence algorithms: the Genetic Algorithm (GA), Improved Particle Swarm Optimization (IPSO), and Ant Colony Optimization (ACO). In addition, 3D simulation experiments and real-flight verifications were conducted to evaluate the adaptability and robustness of the algorithm.

The experimental parameter settings and experimental results are as follows (

Table 2. Experimental Comparisons.

Evaluation Index	Method of This Paper	Improved APF	IPSO	ACO	GA
Average Path Length/m	27.05	25.70	25.91	29.21	26.10
Formation Accuracy Rate	95.63%	96.51%	92.91%	94.51%	92.42%
Recovery Time/s	6.4	7.6	7.2	7.8	7.1
Total Time Consumption/s	15.42	17.89	17.51	16.80	17.22

):

The experimental results indicate that the algorithm proposed in this paper outperforms other algorithms in terms of formation recovery speed. Not only is its convergence speed slightly faster than other algorithms, but it can also fully meet the computing power requirements of conventional UAV equipment. Overall, compared with other algorithms, the IVYA-Nash algorithm better aligns with the operational needs of current UAV formations. Comparisons of fitness values and experimental simulation results are presented in Figure 9 and Figure 10.

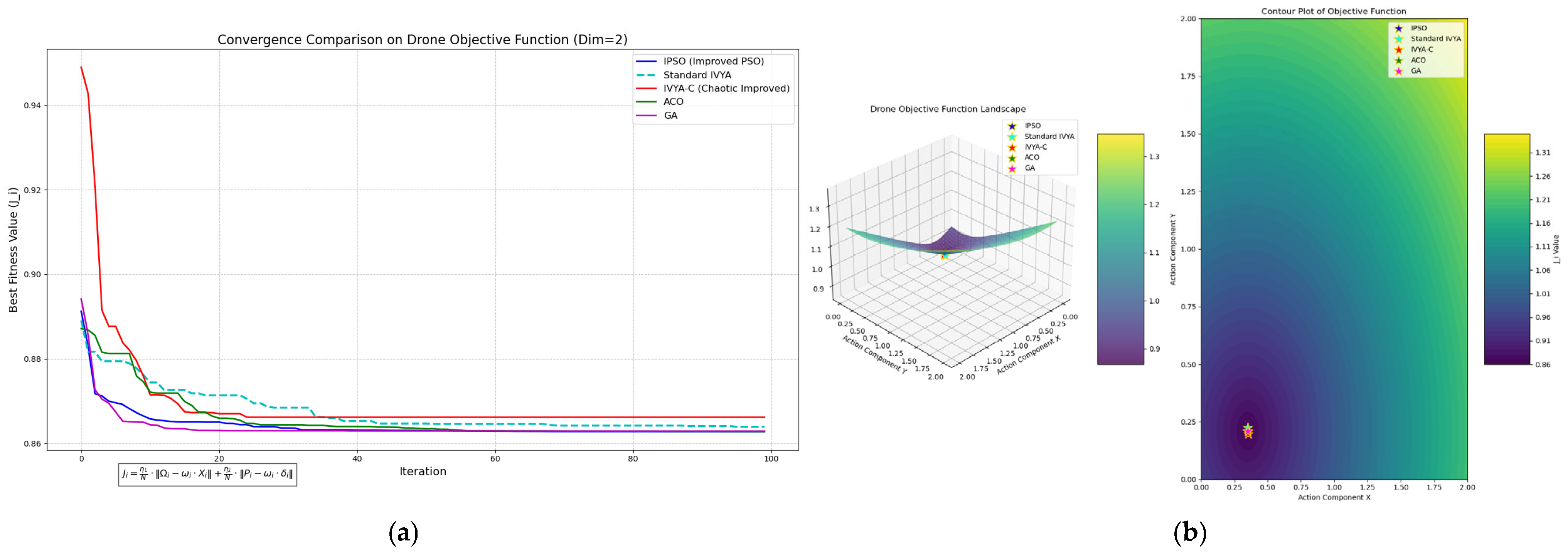
As illustrated in the convergence comparison (Figure 9), the proposed IVYA-Nash algorithm achieves the fastest convergence speed and the lowest steady-state error among all tested methods. While PSO, ACO, and GA converge slowly and often stagnate near local optima, IVYA-Nash rapidly reduces the objective function value within the first 10 iterations and maintains superior stability thereafter. This demonstrates its strong global search capability and efficiency in avoiding local minima.

Figure 9b presents the objective function landscape. The results show that IVYA-Nash converges closest to the global optimum with concentrated solutions, while the other algorithms exhibit more scattered distributions around suboptimal regions. This highlights the robustness and precision of IVYA-Nash in complex optimization spaces.

As can be seen from Table 2 and Figure 10, to verify the performance of the method proposed in this paper in UAV formation obstacle-avoidance tasks, the experimental results were compared against the improved APF method, the Genetic Algorithm (GA), Particle Swarm Optimization (IPSO), and Ant Colony Optimization (ACO). A comprehensive evaluation was carried out based on four indicators: average path length, formation accuracy rate, recovery time, and total time consumption.

The proposed algorithm demonstrates strong overall advantages across several key performance metrics. In terms of Recovery Time, the proposed method is the fastest at 6.4 s, significantly outperforming GA (7.1 s), IPSO (7.2 s), Improved APF (7.6 s), and ACO (7.8 s), reflecting its highly efficient real-time decision-making capability. Similarly, its Total Time Consumption of 15.42 s is considerably lower than all other algorithms, proving its excellent computational efficiency.

Regarding Formation Accuracy Rate, the proposed method achieves 95.63%, second only to the Improved APF (96.51%) but markedly better than ACO (94.51%) and significantly higher than IPSO (92.91%) and GA (92.42%), indicating its superior ability to maintain formation integrity during dynamic recovery.

As for the Average Path Length, the 27.05 m of the proposed method is slightly longer than that of Improved APF (25.70 m), GA (26.10 m), and IPSO (25.91 m). This can be seen as a reasonable trade-off: the algorithm sacrifices the shortest possible path in exchange for much faster decision-making and recovery speed, while also ensuring a higher degree of formation accuracy. As can also be observed from the trajectories in Figure 10, the path of the proposed method is smoother, avoiding sharp turns and formation disturbances that might result from an excessive focus on the shortest path.

Overall, the experimental data demonstrates that, compared to other benchmark algorithms including GA, the proposed IVYA-Nash method strikes the best balance between recovery speed, computational efficiency, and formation robustness, resulting in superior overall performance.

On the basis of completing the simulation experiments, this study further conducted 3D simulation and real-flight experiments to verify the feasibility and effectiveness of the proposed formation cooperative control strategy based on non-cooperative games in actual scenarios. The experiments were carried out in an indoor flight laboratory. The experimental environment was similar to that of the simulation experiments, with multiple static and dynamic obstacles set up to simulate UAV formation tasks in complex environments.

This paper first simulated an industrial warehousing environment where the passage width was narrow, and UAVs needed to maintain a relatively close distance to complete the obstacle-avoidance task. The design intention of this scenario was to verify the inter-UAV obstacle-avoidance ability of UAVs in high-density environments and the stability of the formation during group flight.

The UAVs needed to maintain a column formation to pass through the narrow passage while avoiding mutual interference. During this process, individual UAVs might need to make minor altitude or speed adjustments to ensure the overall passage of the formation. In a narrow space, a minor deviation of an individual UAV might lead to the instability of the overall formation structure. Therefore, strict path control and dynamic obstacle-avoidance strategies were required. The simulation diagram is shown as follows in Figure 11.

3.2. Verified by Real Flight Experiments

The experiment was conducted with 20 small quad-rotor UAVs. Each UAV was equipped with a high-precision positioning system and a communication module to ensure real-time acquisition of position and status information in an indoor environment. The scene was set up according to the MATLAB simulation experiment, with obstacles added in the middle. During the real-flight tests, the multi-UAV system executed the designated formation obstacle-avoidance task. In this process, more than ten UAVs successfully avoided obstacles and subsequently re-established the formation. The real-flight experiment was carried out with the following parameters and initial conditions: the radius of each UAV was 0.15 m, the row-to-row distance of the UAV formation was 1.2 m, the distance between adjacent UAVs in each row was 1 m, and the moving speed was 0.3 m/s. At the beginning of the real-flight, all UAVs took off in place and entered the target positions after the formation started.

In the real-flight experiments, the communication delay among UAVs was maintained within 15 ms, which ensured reliable real-time interaction for formation recovery. All experiments were conducted in an indoor environment without electromagnetic interference, thereby providing stable communication links. Under these conditions, the proposed IVYA-Nash framework demonstrated effective obstacle avoidance and rapid formation recovery.

During the real-flight process, the UAVs were initially set to take off at different positions and automatically form a square formation. As can be seen from the following group of figures, the UAV formation could perform adaptive obstacle-avoidance when encountering obstacles and could adaptively restore the original formation and continue to move after obstacle-avoidance. This shows that the method proposed in this paper can be applied to actual UAV flights.

This study constructed a narrow channel experimental environment based on the Rflysim3D simulation platform, with field flight tests validating the formation compression capability of the proposed algorithm. As demonstrated in Figure 12c, the algorithm successfully achieved a dual-layer formation flight mode.

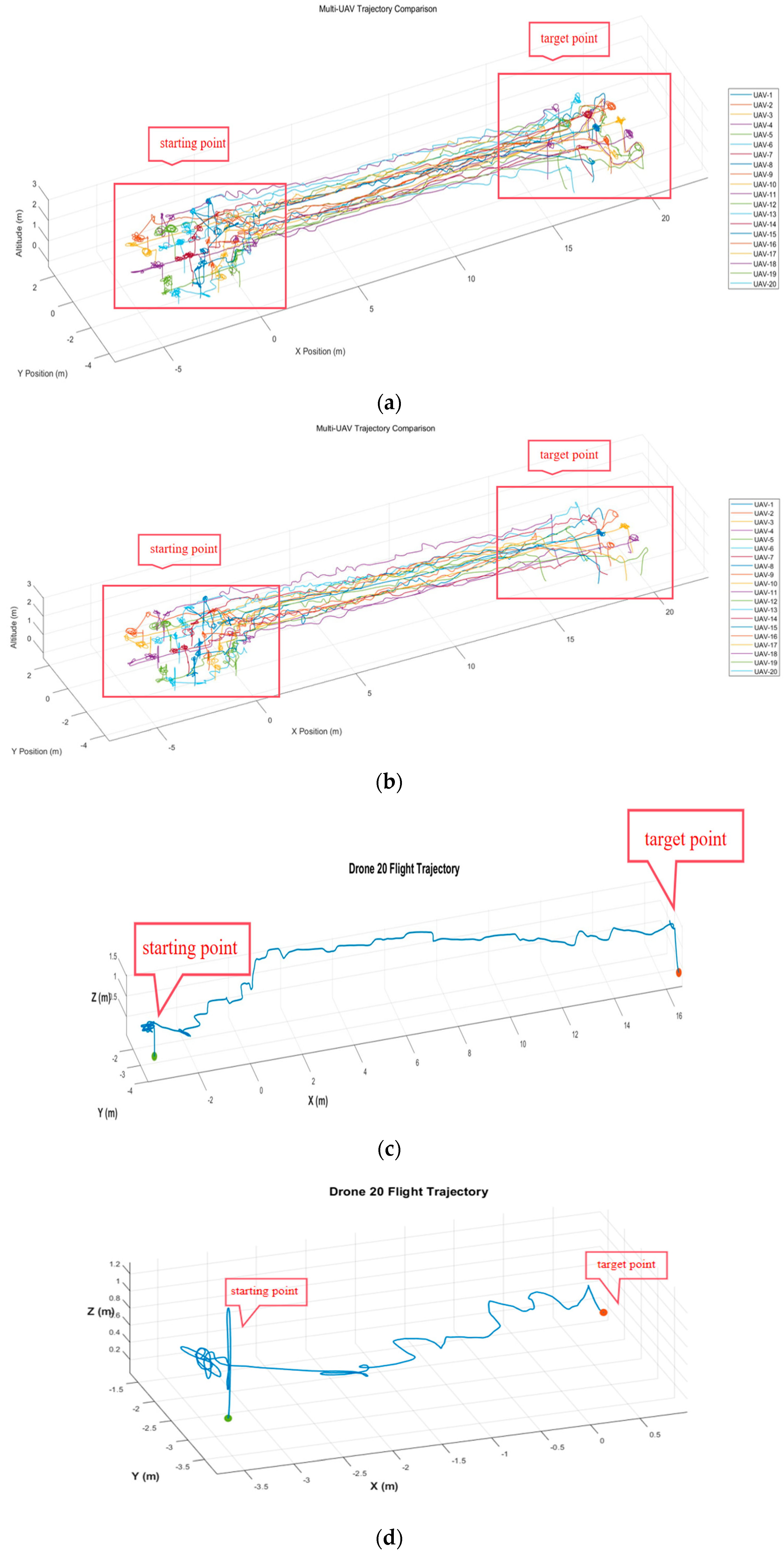
Figure 13 provides a detailed comparison between the proposed IVYA-Nash method and the conventional Artificial Potential Field (APF) approach. Subplots (a) and (b) illustrate the 3D flight trajectories of 20 UAVs under both methods. With APF (subplot a), multiple UAVs exhibit unstable flight and collision tendencies, leading to eventual crashes due to aerodynamic interference, especially among vertically stacked drones. In contrast, our method (subplot b) ensures smoother trajectories and stable convergence toward the target points, maintaining the swarm formation without collisions. Subplots (c) and (d) further present the individual flight paths of UAV #20 under APF and our method, respectively. The APF-based trajectory (subplot c) shows significant oscillations and instability, while the IVYA-Nash trajectory (subplot d) remains smooth and successfully reaches the target. These results highlight the superior robustness, safety, and autonomous formation recovery capability of the proposed approach in cooperative multi-UAV control.

Figure 14 quantitatively characterizes the terminal positioning accuracy during formation assembly through box plots, where the box spans reveal error distribution characteristics. Experimental results demonstrate that our method achieves an average total-distance positioning error of 5.39 cm, representing a 94.5% accuracy improvement over the conventional potential field method’s 99.1 cm. Error distribution analysis shows our method maintains a stable median error of 5.12 cm, while the baseline exhibits significant outliers. This validates the proposed method’s millimeter-level precision and robust anti-interference capability in terminal positioning phases.

During practical flight operations, environmental uncertainties-including intermittent communication delays, stochastic aerodynamic disturbances, and illumination-dependent visual positioning artifacts-introduce systematic errors in formation control. To rigorously evaluate performance, we define the formation accuracy rate η as the percentage of UAVs satisfying positioning error threshold $\gamma$:

$$\gamma =\left({\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^N\mathbb{I}\left(d_i\le T\right)}{N}}\right)\times 100\%$$

(21)

where $d$ denotes the minimum approach distance (in meters) for the $i\text{-}th$ UAV, $T$ represents the allowable maximum error threshold (in meters), and $N$ is the total number of UAVs. $\mathbb{I}\left(•\right)$ represents the indicator function, which equals 1 if the specified condition is satisfied and 0 otherwise.

As evidenced by

Table 3. Formation Accuracy at Different Thresholds.

Threshold Method	Method of This Paper	Improved APF
T = 0.1	85%	45%
T = 0.15	95%	60%
T = 0.3	100%	75%

, the proposed algorithm demonstrates superior performance over the APF method across three distinct error threshold scenarios (0.3 m/0.15 m/0.1 m). Remarkably, it achieves 100% formation accuracy rate when the positioning error threshold is set at 0.3 m. Field experiments further confirm the methodology’s practical efficacy, showing greater performance advantages compared with other simulation-tested approaches, thereby substantiating its engineering applicability.

4. Discussion

While the experimental results validate the effectiveness of the IVYA-Nash algorithm for a 20-UAV swarm, it is important to discuss the computational complexity and scalability for larger formations. The time complexity of the proposed algorithm is primarily determined by the IVYA-C optimization process, which is on the order of O($T\times M\times D$), where T is the number of iterations, $M$ is the population size, and $D$ is the problem dimension ($D = 3N$ for a swarm of $N$ UAVs).

For larger swarms (e.g., $N>50$), the linear increase in dimension $D$ will lead to a corresponding increase in computation time. However, the distributed nature of the game-theoretic model allows for potential parallelization, where subsets of UAVs could compute their strategies concurrently, mitigating the scalability challenge. The current implementation on standard hardware demonstrates real-time feasibility for the tested swarm size, but deployment on larger swarms would likely require more powerful onboard processors or edge computing resources to maintain the same rapid decision-making performance.

5. Conclusions

This paper proposes a UAV formation restoration strategy based on the Nash equilibrium game theory and constructs a UAV collaborative control model by combining with the IVY optimization algorithm. By constructing a reasonable game model to balance the interests of individual UAVs and the overall formation, this method can ensure that the UAV formation can quickly restore its formation and efficiently complete obstacle avoidance tasks in complex environments. The Ivy algorithm avoids the problem of local optimal solutions through global search during the optimization process, enabling the UAV formation to better adapt to changes in obstacles and target adjustments in dynamic environments.

The experimental results verify the superiority of this method in multiple performance indicators. Especially in terms of path planning, formation restoration accuracy, restoration speed, and obstacle avoidance efficiency, it performs significantly better than improved APF, the Particle Swarm Optimization (PSO) algorithm, and the Ant Colony Optimization (ACO). In particular, the combination of the game model based on the Nash equilibrium and the Ivy algorithm enables UAVs to effectively improve task execution efficiency and robustness while ensuring the stability of the formation.

In the real flight experiment, real-flight comparative tests conducted on a multi-UAV collaborative platform demonstrated that the proposed LVYA-Nash algorithm significantly outperforms the conventional Artificial Potential Field (APF) method in core performance metrics, including formation accuracy maintenance and resistance to aerodynamic disturbances from neighboring aircraft. These results validate its robustness advantages in highly dynamic multi-agent interaction scenarios.

Future work will focus on further optimizing the computational efficiency of the Ivy algorithm and exploring its applications in larger-scale and multi-task complex environments. To further enhance the external validity of our findings, future experiments should include outdoor trials in more challenging, unstructured environments, particularly under GPS-denied or windy conditions. In addition, the real-time performance and adaptability of the algorithm will also be the key points for further improvement, aiming to provide a more efficient solution for multi-UAV collaborative operations.

Limitations and Future Work: While the proposed IVYA-Nash algorithm demonstrates strong performance in both simulations and real-flight experiments, several limitations remain. First, the current tests were conducted in controlled indoor environments, and large-scale outdoor experiments have not yet been implemented. Second, potential collisions with dynamic external entities such as other UAVs or birds were not modeled.

Future work will therefore focus on (i) optimizing the computational efficiency of IVYA, (ii) conducting large-scale outdoor swarm experiments, (iii) incorporating dynamic obstacle modeling, and (iv) integrating reinforcement learning methods to enhance adaptability.