Abstract
This paper presents a comprehensive methodology for the multiobjective tuning of MIMO proportional integral derivative (PID) controllers using advanced metaheuristic strategies. The proposed approach formulates a cost function based on two conflicting performance criteria—the integral of absolute error (IAE) and the integral of absolute derivative of control (IADU)—to explore the trade-off between tracking performance and control effort systematically. Three metaheuristic techniques are employed: stochastic hill climbing, a Voronoi-based heuristic, and the Nondominated Sorting Genetic Algorithm (NSGA-II). A novel Multiobjective Optimization Design (MOOD)-based classification framework is incorporated to facilitate decision making across the Pareto front. The methodology is validated on three benchmark MIMO plants, demonstrating its robustness and generalizability. The results highlight that the NSGA-II controller achieves the lowest IADU value of 0.3694 in the mass damper system while maintaining acceptable performance metrics. The inclusion of a PID-split strategy further enhances system flexibility. This study emphasizes the value of metaheuristics in navigating complex design spaces and delivering tailored control solutions for multiobjective scenarios.
Keywords:
multiobjective; PID; tuning; MIMO; metaheuristics; NSGA-II; Voronoi; optimization; control; heuristics; MOOD; utopia; evolutionary; trade-off; classification; performance; effort; Pareto; splitting; robustness 1. Introduction
The optimal tuning of PID controllers in multivariable systems presents persistent challenges due to conflicting design objectives such as high-precision tracking and minimized actuation effort [1,2,3,4]. This research introduces a structured methodology that employs multiobjective optimization to balance these trade-offs through the simultaneous minimization of the integral of absolute error (IAE) and the integral of absolute derivative of the control signal (IADU). While the IAE measures the tracking accuracy by penalizing sustained deviations between the reference and output, the IADU quantifies the smoothness of the control action by integrating the magnitude of its rate of change. Minimizing the IADU therefore discourages abrupt variations in the control signal, which improves noise resilience and reduces actuator stress, complementing the pursuit of fast and accurate regulation [5,6].
Rather than relying on classical analytical tuning, the method leverages metaheuristic search techniques to explore the complex parameter landscape [7,8,9]. Three algorithms—stochastic search, Voronoi-based evolution, and NSGA-II—serve as the backbone of this search process, yielding Pareto fronts populated with nondominated controller candidates [10,11]. The MOOD classification framework is then used to guide post-optimization selection by segmenting the solutions into preference zones for performance, control effort, and compromise [12,13].
The main contribution of this work lies in integrating classical performance indices (IAE and IADU) into a unified multiobjective framework for MIMO PID design and combining metaheuristic search with MOOD-based classification to achieve both systematic exploration and the interpretable selection of controller solutions—an approach not jointly addressed in prior studies.
This study investigates two central hypotheses: (1) that metaheuristic search strategies significantly enhance the ability to extract balanced PID parameters in MIMO systems and (2) that the zone-based classification of Pareto solutions improves decision making in practical control design.
This paper is structured to provide a comprehensive overview of the proposed multiobjective PID tuning methodology and its performance across real-world MIMO systems. Section 2 reviews the state of the art in multiobjective control and recent advances in the heuristic tuning of PID controllers. Section 3 introduces the proposed methodology, detailing the design of a multiobjective cost function based on the IAE and IADU and the integration of three distinct metaheuristic optimization strategies. Section 4 presents the implementation of this methodology, including the MOOD framework for decision support, and evaluates the method through simulation on benchmark plants such as a two-tank system, a two-zone HVAC model, and a mass damper mechanical system. The work includes a comparative analysis of Pareto fronts, time-domain responses, and control effort metrics. Finally, Section 5 draws key conclusions, emphasizing the effectiveness of heuristic strategies in navigating trade-offs and validating the applicability of the approach to practical multivariable control systems.
2. State of the Art
The application of multiobjective optimization techniques to controller tuning has garnered increasing attention across diverse engineering systems. Recent studies demonstrate the adaptability of these approaches in managing complex trade-offs between control performance criteria. For instance, optimization-based strategies have been applied to biped robots [14], quadrotors [15], DC-DC converters [16,17], robotic manipulators [18], tank controllers [19], and wind turbines [20], each showing the potential of metaheuristics in achieving balanced controller performance. Similarly, in MIMO systems, advanced techniques have been explored to address multivariable challenges in feedforward and feedback structures [10,21]. This paper builds upon the foundational work of Prof. Gilberto Reynoso-Meza, who has made significant contributions to evolutionary multiobjective optimization in control engineering [22,23,24,25,26]. His holistic design procedures and benchmark proposals have laid the groundwork for formalizing the tuning of PID and PI controllers using evolutionary algorithms in both SISO and MIMO frameworks.
Among the most influential contributions to the field of multiobjective optimization, Chen et al. [27] stand out with 126 citations, proposing a dynamic two-archive evolutionary algorithm that handles problems with a changing number of objectives—an aspect rarely addressed in the previous literature. Sahib and Ahmed [28] follow with a highly cited paper introducing a novel performance criterion for PID controller tuning based on Pareto front solutions. Thai Doan Chuong [29] offers a rigorous theoretical approach to robust Pareto optimality through limiting subdifferentials and duality, while Povalej [30] contributes a quasi-Newton method leveraging BFGS approximations for faster convergence. These and other top-cited papers are summarized in Table 1, which outlines each study’s methodology and research focus [31,32,33,34,35,36].

Table 1.
Top 10 papers with methodologies.
Recent contributions have advanced the understanding of PID robustness by providing analytical characterizations and trade-offs. For instance, delay margins in second-order systems were rigorously studied, showing pseudoconcavity properties and performance implications [37]. Complementary results addressed first-order unstable plants, where multiplicity-induced dominancy strategies enabled robust pole placement under delay uncertainty [38]. Robustness against gain and phase variations has been examined in filtered PID implementations, clarifying achievable margins under performance constraints [39]. Data-driven approaches have also emerged, combining virtual reference feedback tuning with set membership identification to enforce robust stability guarantees [40]. Broader nonlinear contexts, such as stochastic drum boiler systems, further highlight robustness-oriented control strategies [41]. In parallel, adaptive control strategies have been explored for nonlinear soft robotic systems, where dynamic pole motion and error-based adaptive controllers enhance stability without overshoot [42], differing from optimization-focused PID tuning.
Recent advances in multiobjective optimization highlight its versatility across complex engineering domains. Priority-based strategies have been proposed to balance steady-state performance and economic benefits in predictive control frameworks [43]. In energy systems, hybrid agricultural powertrains have benefited from crowding-adaptive evolutionary algorithms, achieving significant reductions in fuel consumption and emissions [44]. Benchmarking studies have further expanded constrained multiobjective optimization to large-scale scenarios, introducing realistic features and scalable testing environments [45]. Complementing these developments, comprehensive surveys have synthesized methodologies spanning evolutionary and machine learning approaches, offering insights into practical applications and emerging research challenges [46].
The coauthorship map generated using VOSviewer (Figure 1) provides a visual representation of international research collaboration in the field of multiobjective PID control. The layout highlights key countries contributing to the literature, with the United States and the People’s Republic of China emerging as dominant nodes—indicative of both high publication volumes and strong global collaboration. Surrounding these hubs are nations such as Iran, Brazil, Italy, Canada, and Japan, which also show significant involvement in joint research initiatives. European countries, including France, Belgium, Spain, and Sweden, appear clustered, reflecting established regional cooperation networks. The proximity and font sizes of the country names are proportional to the frequency and strength of coauthorship links, allowing for the quick identification of leading contributors and potential partners. This visualization underscores the global nature of research in multiobjective control systems and suggests a balanced blend of mature and emerging research economies involved in advancing the field.
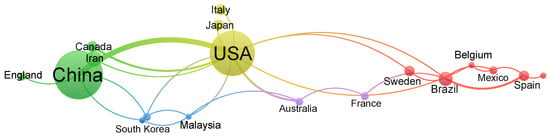
Figure 1.
Country coauthorship network visualized using VOSviewer version 1.6.20.
3. Methodology
The proposed methodology aims to develop a flexible and interpretable multiobjective framework for the automatic tuning of MIMO PID controllers. By leveraging performance and effort-based criteria, the method formulates the tuning problem as a multiobjective optimization task with competing objectives: tracking precision and control effort minimization. The core of the approach is grounded in the definition of a generalized continuous-time state-space plant model, allowing compatibility with a broad class of real-world multi-input multi-output systems. A diagonal PID controller is applied, and its parameters are optimized using multiple metaheuristic strategies. Three distinct optimization techniques are considered: stochastic mutation (similar to scatter search), a Voronoi-based geometric approach, and the evolutionary NSGA-II algorithm. These are executed independently to produce diverse Pareto-optimal sets.
To support interpretability and decision making, a zone-based Multiobjective Optimization Outcome Distribution (MOOD) framework is employed to classify the Pareto front into interpretable solution spaces. The methodology also integrates a comparative evaluation phase based on time-domain performance, control energy, and disturbance rejection. In order to demonstrate real-world applicability, the proposed framework is tested on three benchmark MIMO systems: a two-tank liquid level system, a two-zone thermal HVAC system, and a coupled mass damper mechanical system. Each subsystem validates the methodology’s robustness, flexibility, and scalability across industrially relevant dynamic environments.
3.1. State-Space Plant Modeling and MIMO PID Control
In the multiobjective control of real-world processes, a state-space modeling framework offers a structured and scalable approach, particularly for multivariable systems. A continuous-time linear time-invariant (LTI) model is used to describe the plant, where the system dynamics are represented in terms of internal state evolution and output behavior. The general form of the plant model is given by
Here, denotes the state vector, the control input, and the output. The matrices A, B, C, and D define the structure and response of the system. For the purposes of this study, square MIMO configurations are considered, where the number of control inputs matches the number of outputs (). Each control channel is assumed to be independently actuated, allowing decentralized controller design with minimal cross-channel interference. This modeling approach is advantageous in evaluating the interaction between multiple controller gains and system outputs in a multiobjective optimization setting.
To regulate each input–output pair, a decentralized proportional–integral–derivative (PID) control strategy is implemented in a parallel structure. Unlike traditional SISO PID control, the MIMO architecture in this work employs a diagonal PID matrix, where each control signal is computed independently using local error dynamics. For the i-th control channel, the control law is defined as
where is the tracking error between the reference signal and the output . The gains , , and represent the proportional, integral, and derivative terms, respectively, for the i-th loop. Each control law operates independently, assuming minimal dynamic coupling, which is a valid approximation for many industrial systems. This decentralized control structure simplifies the controller tuning process while maintaining the ability to handle multivariable dynamics.
For digital implementation and optimization, the plant model is discretized using a zero-order hold method with a fixed sampling period . The continuous-time control law in Equation (2) is then numerically integrated using first-order methods, and the derivative term is approximated through backward differencing. Figure 2 presents the complete MIMO control structure, where each control loop independently regulates a plant input using a dedicated PID controller. This modular arrangement allows flexible tuning via metaheuristic search algorithms and provides a robust foundation for multiobjective optimization based on the trade-offs between control performance and effort.
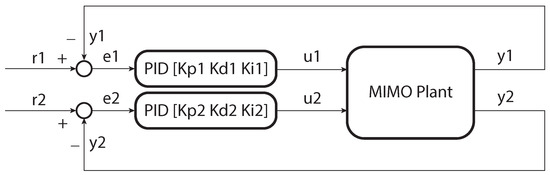
Figure 2.
Block diagram of a square MIMO system regulated by decentralized PID controllers.
3.2. PI-D Split Controller Variant
As an alternative to the conventional PID structure, this study evaluates a PI-D split controller for each channel in the MIMO configuration. The PI-D formulation separates the integral and proportional actions from the derivative term by applying the latter directly to the system output rather than the error signal. This decoupling improves the robustness to measurement noise and enhances the stability, particularly in systems where derivative action on the full error may amplify high-frequency disturbances. The decentralized PI-D controller maintains a diagonal architecture, independently regulating each input–output pair of the system. The control law for the i-th loop is expressed as
where , and the derivative term is computed solely on the system output. This structure avoids derivative action responding to setpoint changes, thereby reducing spikes in control signals and enhancing actuator longevity. The PI-D strategy is simulated within the same multiobjective optimization framework as the conventional PID, ensuring the consistent benchmarking of performance, robustness, and actuation effort across all MIMO test scenarios presented.
3.3. Multiobjective Cost Function Design
The design of PID controllers within a multiobjective optimization framework requires the formalization of performance indices that reflect both system tracking capabilities and control signal quality. In this work, two classical yet effective time-domain criteria are employed as competing objective functions. The first, the integral of absolute error (IAE), measures the total accumulated deviation between the system output and the reference trajectory over the simulation horizon. The second, the integral of absolute derivative of the control signal (IADU), penalizes sharp or oscillatory control actions by quantifying the total variation in the input signal. Together, these objectives define a trade-off surface in the objective space, promoting solutions that are not only accurate but also smooth and energy-efficient in actuation.
Let denote the reference signal and the system output for the i-th channel. The multiobjective cost function is thus expressed as the vector
Each component is formally defined as
The first term favors fast and accurate output regulation, while the second discourages large variations in control effort, which are often undesirable in physical systems due to actuator limitations or mechanical stress. By optimizing both simultaneously, a balanced set of PID parameters can be obtained that respects both tracking performance and control smoothness.
In the discrete-time simulation environment, numerical approximations of the above integrals are implemented using the trapezoidal rule. This allows compatibility with algorithmic optimization routines that require simulation-based evaluations of performance. The resulting Pareto front captures the inherent trade-offs between the two criteria and serves as the decision-making foundation for controller selection.
To guarantee well-posed optimization and avoid unbounded control actions, each PID gain is restricted to lie within predefined intervals. These constraints ensure that the search space remains physically meaningful while preventing instability in the closed-loop response. For the i-th control loop, the parameters are subject to the following box conditions. As expressed in (7), each gain is bounded independently, ensuring that all controller variables remain finite throughout the optimization process.
3.4. Validation on Real Plants
To validate the generality, scalability, and applicability of the proposed PID tuning framework, the full optimization and evaluation procedure is implemented on three benchmark MIMO processes commonly referenced in the control systems literature. All selected plants are inherently multivariable, coupling multiple input–output channels, and present diverse dynamic behaviors including nonlinearity, interaction, and variable time constants. These characteristics pose challenges to controller design and tuning, especially when multiple objectives are simultaneously considered. By applying the methodology to physically grounded models, the robustness and adaptability of each metaheuristic strategy can be thoroughly assessed. Furthermore, the results offer meaningful insights into how optimization trade-offs manifest under real-world operating conditions.
The first case study involves a two-tank liquid level system, a hydraulically coupled process used frequently in laboratory-scale control experiments. The model describes the fluid dynamics in two interconnected tanks, where each input corresponds to an inflow rate controlled by a valve and each output reflects the measured liquid height in each tank. The state variables typically represent liquid levels and flow rates, while the inputs affect the inlet flow and the outputs measure the tank levels. This system is representative of many industrial processes, such as chemical mixing, water treatment, and fuel distribution, making it an ideal validation platform for advanced multiobjective PID design.
3.5. Metaheuristic Optimization Strategies
To efficiently explore the high-dimensional, nonconvex search space defined by the PID controller parameters, this work adopts three metaheuristic optimization strategies. Heuristic methods are well suited to multiobjective controller tuning problems due to their flexibility, global search capabilities, and minimal reliance on gradient information. The adopted approaches include a stochastic random mutation algorithm (symbolized by a die icon), a Voronoi-based adaptive sampling method (represented with a tessellated mesh), and the established Nondominated Sorting Genetic Algorithm II (NSGA-II, shown with a DNA strand). Each method is designed to balance exploration and exploitation in the search space, aiming to produce a well-distributed Pareto front. Figure 3 illustrates the schematic framework, where the flow proceeds from the MIMO state-space plant and PID controller configuration into the multiobjective optimization engine. The three heuristic paths feed into the generation of the Pareto front, from which solutions are filtered via MOOD classification zones and the utopia point selector before being validated on real physical systems.
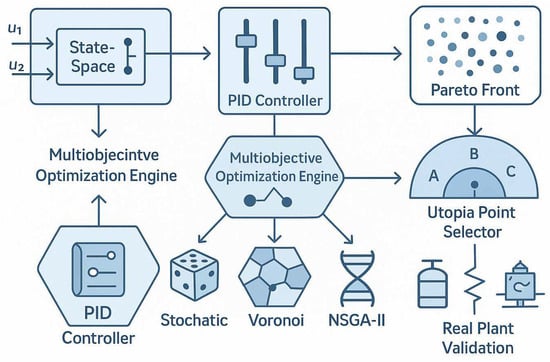
Figure 3.
Conceptual schematic of the multiobjective PID tuning framework for MIMO systems. The diagram visualizes the integration of stochastic, Voronoi, and NSGA-II heuristics within a symbolic optimization pipeline, leading to Pareto-optimal solutions and final plant validation.
3.6. Stochastic Method Using Random Mutation
The simple yet effective heuristic strategy implemented in this study is based on stochastic random mutation. Inspired by scatter search and evolutionary population models, this method iteratively perturbs candidate solutions by adding small Gaussian noise to each parameter. The approach does not require gradient information or predefined models of the objective function, making it suitable for complex, nonlinear control surfaces. It begins by initializing a population of candidate solutions uniformly across the defined parameter space. At each generation, the entire population is mutated and evaluated with respect to the multiobjective cost function. The mutation step encourages exploration, while the bounding operation ensures that solutions remain within feasible physical and operational limits. Despite its simplicity, the method can approximate nondominated fronts efficiently and offers baseline performance for comparison with more structured heuristics. The full algorithmic structure is outlined in Algorithm 1.
| Algorithm 1 Stochastic Multiobjective PID Tuning via Random Mutation |
|
3.7. Voronoi-Based Heuristic Search
The second heuristic strategy employs a Voronoi-based sampling mechanism to enhance the diversity and adaptive exploration across the decision space. This approach leverages the geometric partitioning properties of Voronoi diagrams to guide offspring generation. After evaluating the initial population, each solution is treated as the generator of a Voronoi cell. New candidate solutions are sampled from regions within or near high-performing Voronoi cells, promoting local refinement while preserving diversity across the objective front. Unlike purely stochastic mutation, this method introduces spatial awareness, encouraging sampling in less crowded or unexplored areas. The goal is to dynamically allocate search effort toward promising zones, reducing redundancy and improving convergence to well-distributed Pareto fronts. This structure naturally aligns with multiobjective optimization, as each cell implicitly encodes the performance context through its fitness values. The overall algorithmic flow is summarized in Algorithm 2.
| Algorithm 2 Voronoi-Based Multiobjective PID Tuning |
|
3.8. NSGA-II: A Well-Established Evolutionary Multiobjective Algorithm
Among the available multiobjective optimization methods, NSGA-II has become a foundational algorithm due to its effectiveness in balancing convergence and diversity across the Pareto front. NSGA-II employs evolutionary operators such as crossover and mutation, combined with nondominated sorting and crowding distance mechanisms, to guide the search. Its elitist selection strategy ensures that the best trade-off solutions are retained across generations while encouraging diversity through distance-based metrics. In this implementation, the population is initialized randomly, and binary tournament selection is used to generate parents. Simulated binary crossover (SBX) and polynomial mutation operators produce offspring, which are then combined with the parent population. A nondominated sorting process partitions the combined set into Pareto fronts, and individuals are selected based on both the dominance rank and crowding distance until the population size is restored. This balance of dominance and diversity makes NSGA-II particularly well suited for tuning controllers in systems with conflicting objectives. The complete algorithmic structure is outlined in Algorithm 3.
| Algorithm 3 NSGA-II for Multiobjective PID Controller Tuning |
|
3.8.1. MOOD Framework Integration
In multiobjective optimization problems, even after obtaining a well-distributed Pareto front, the decision maker is often faced with the challenge of selecting a solution that aligns with specific performance or implementation preferences. To aid this selection process, the MOOD framework is integrated to classify solutions into interpretable decision zones. Each solution is labeled according to its dominant characteristic: Zone A prioritizes high performance (low IAE), Zone B minimizes control effort (low IADU), and Zone C represents a compromise between the two. Solutions that do not excel in either metric are grouped into Zone D. This classification enhances decision interpretability by segmenting the trade-off surface into actionable regions, allowing engineers to focus on solutions that align with system requirements. The zone assignment is based on statistical quantile thresholds and is visualized to support interactive design decisions. The classification logic is detailed in Algorithm 4.
| Algorithm 4 MOOD-Based Pareto Front Classification |
|
3.8.2. Comparative Evaluation
After optimization, a comparative analysis is conducted to assess the quality of the solutions produced by each metaheuristic strategy. Three key criteria are used to evaluate controller performance: step response accuracy, control effort, and disturbance rejection. These metrics reflect classical and practical control design goals. The step response test measures how closely and quickly the output follows a reference signal. Control effort is evaluated by the magnitude and smoothness of the actuation signal, with excessive variations penalized. Disturbance rejection examines how well the controller maintains output regulation in the presence of step-like perturbations in system dynamics. These criteria are measured consistently across all Pareto-optimal solutions. To ensure a fair comparison, only the stochastic, Voronoi-based, and NSGA-II approaches are included in the visual Pareto front overlays; the weighted-sum approach is excluded due to its known distortion of front curvature. Algorithm 5 summarizes the evaluation steps applied to each method.
| Algorithm 5 Comparative Evaluation of Optimization Strategies |
|
4. Analysis and Discussion
Figure 4 presents a comparative visualization of the Pareto fronts obtained from three distinct metaheuristic approaches applied to the MIMO PID tuning problem: stochastic mutation, Voronoi-based sampling, and NSGA-II. Each curve represents a set of nondominated solutions in the trade-off space between tracking performance (IAE) and control effort (IADU). The NSGA-II method exhibits superior coverage and front diversity, while the Voronoi strategy concentrates solutions near the low-effort region. Stochastic search yields a wider, less structured spread. The best-performing solutions for each method are also highlighted, providing clear reference points for multicriteria selection and further analysis.
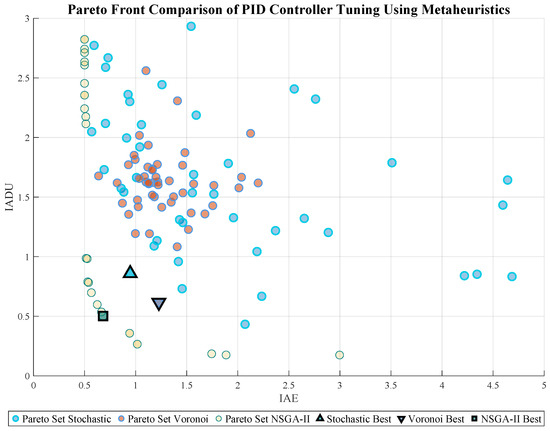
Figure 4.
Comparison of Pareto fronts obtained from three different metaheuristic methods for MIMO PID tuning: stochastic search, Voronoi-based heuristic, and NSGA-II.
Figure 5 illustrates the time-domain step responses of the two output channels, and , of a MIMO system controlled by PID parameters optimized through three distinct metaheuristics: stochastic search, a Voronoi-based heuristic, and NSGA-II. All methods achieve setpoint tracking with varying transient characteristics. The NSGA-II-based controller demonstrates the fastest rise and lowest steady-state error across both outputs. The Voronoi approach yields smoother transitions with slightly delayed settling. The stochastic method exhibits higher overshoot and slower convergence. These results highlight the influence of the optimization strategy on system dynamics and underscore the importance of multiobjective tuning in MIMO PID control design.
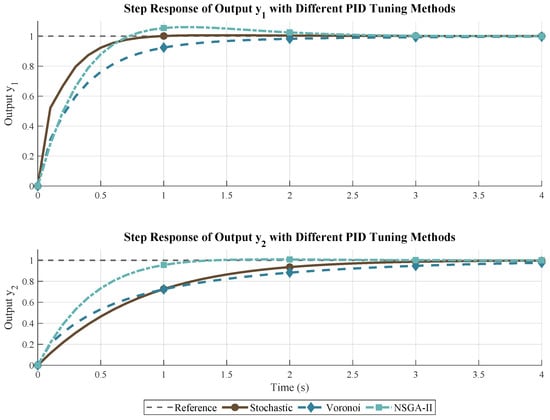
Figure 5.
Step responses of a MIMO system’s outputs and under PID controllers tuned by three different metaheuristic techniques.
Figure 6 shows the control inputs and generated by the PID controllers optimized using the three metaheuristic techniques. The control signals reveal notable distinctions in actuation behavior. The NSGA-II controller produces moderately aggressive inputs but with smooth transitions, ensuring balanced performance and effort. In contrast, the Voronoi-based approach achieves smoother control profiles with a visibly lower amplitude, reflecting its optimization bias toward minimal control action. The stochastic method results in higher and more oscillatory actuation, particularly in the initial transient. These differences corroborate the step response findings and further demonstrate the impact of the optimization strategy on the control quality.
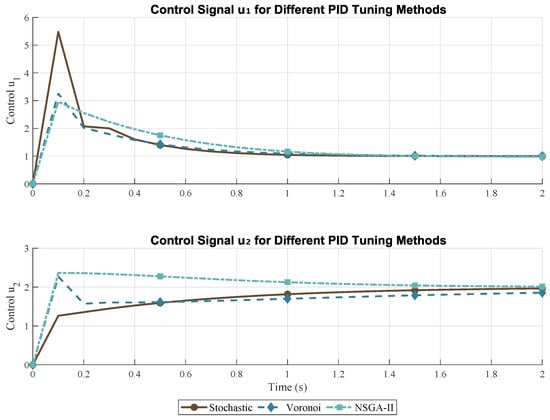
Figure 6.
Control signals and generated by PID controllers tuned using three different metaheuristic techniques.
Figure 7 compares the Pareto fronts derived from metaheuristic optimization strategies with the solution set produced using a classical weighted-criteria approach. The highlighted points denote the best-performing controllers selected via three distinct criteria: weighted minimum, utopia reference, and Voronoi-based geometric reasoning. The weighted approach, while straightforward, confines the solution space to a narrow region, potentially overlooking high-quality trade-offs. In contrast, the metaheuristic techniques—particularly Voronoi—yield broader, more balanced Pareto distributions. These differences illustrate the advantage of nonscalarized optimization when exploring conflicting objectives such as performance and control effort, providing richer and more interpretable options for controller deployment decisions.
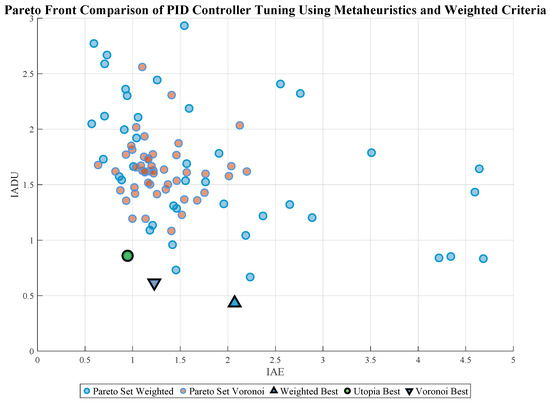
Figure 7.
Comparison of Pareto fronts obtained from PID controller tuning using metaheuristic strategies and a weighted criteria approach. The best-performing controllers under weighted, utopia, and Voronoi criteria are represented with the three last markers.
Figure 8 illustrates the classification of Pareto-optimal PID controllers obtained from the Voronoi-based metaheuristic using the MOOD framework. The solution space is partitioned into four decision-making zones: A (high tracking performance), B (minimal control effort), C (compromise), and D (nondominant). This visual demarcation enables structured selection according to design priorities. Notably, Zone C contains a dense cluster of well-balanced solutions, while Zones A and B host more specialized configurations. The geometric clarity offered by Voronoi-based optimization complements the interpretability of MOOD zoning, providing actionable insights for the selection of a controller that best satisfies application-specific trade-offs between precision and energy expenditure.
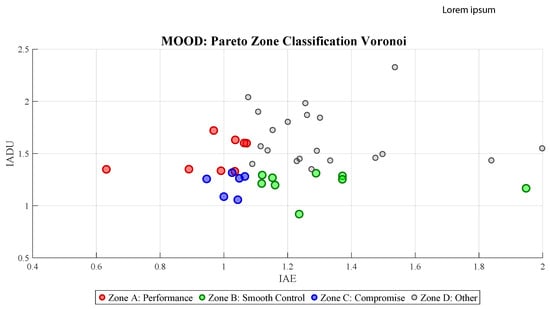
Figure 8.
MOOD diagram showing the classification of Pareto-optimal PID controller solutions obtained via the Voronoi-based metaheuristic.
Figure 9 illustrates the generational evolution of the Pareto fronts resulting from the Voronoi-based metaheuristic during the PID tuning process. Each iteration incrementally refines the solution space, reducing dominated regions and guiding the population toward optimal trade-offs between performance (IAE) and control effort (IADU). The densification observed near the lower-left corner of the front reveals the algorithm’s convergence towards high-quality, compromise-driven solutions. This evolution underscores the efficacy of geometric sampling in steering the population efficiently, particularly in high-dimensional MIMO contexts. Tracking such progression offers valuable insights into the convergence properties and stability of the optimization procedure.
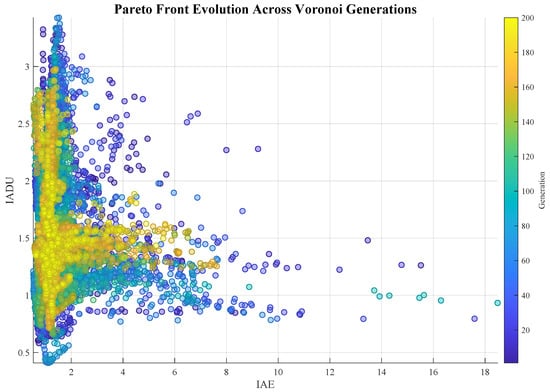
Figure 9.
Evolution of Pareto fronts across generations using the Voronoi-based metaheuristic for PID controller tuning, highlighting the algorithm’s convergence behavior in a MIMO control context.
The comparison highlights the impact of incorporating a PID-split strategy within the NSGA-II framework is in Figure 10. Both solution sets are plotted in the IAE-IADU objective space, demonstrating their distribution and coverage. The PID-split configuration shows a shifted and often superior Pareto front, particularly in the compromise region, where reductions in both error and control effort are critical. The highlighted best-performing controllers reinforce the advantages of decoupling integral and derivative actions in enhancing adaptability. These results suggest that the split structure allows finer tuning flexibility, especially for MIMO systems where cross-channel dynamics introduce challenges in maintaining an optimal control balance.
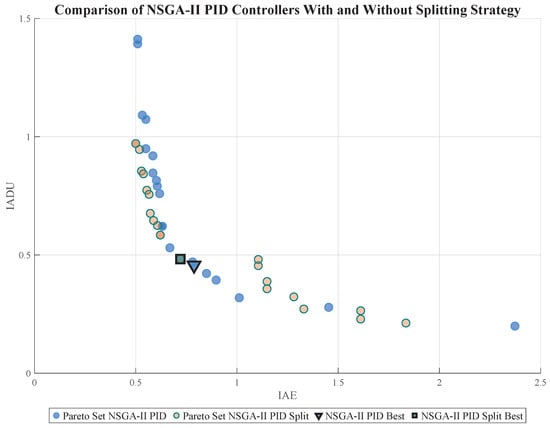
Figure 10.
Comparison of Pareto-optimal solutions obtained from NSGA-II-based PID controller tuning with and without applying a splitting strategy.
The plotted step responses for the MIMO system outputs and , in Figure 11, demonstrate the dynamic performance achieved using PID controllers tuned through NSGA-II, with and without the split-based configuration. The figure reveals that the PID-split variant exhibits faster settling times and more symmetric transient behavior across both channels. This improved responsiveness underscores the utility of decoupling integral and derivative effects in MIMO loops, allowing for the more targeted shaping of dynamic behavior. The standard configuration shows slightly slower convergence and more pronounced overshoot, suggesting that the split structure contributes positively to closed-loop stability and transient response quality.
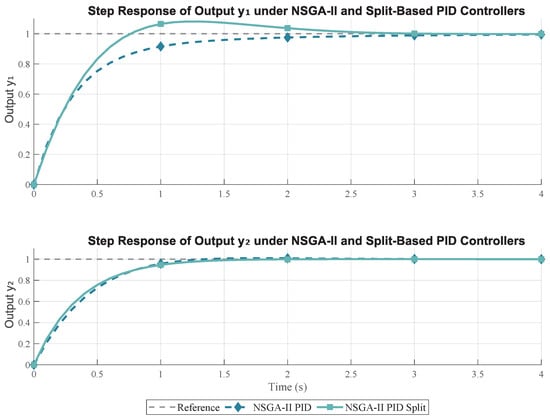
Figure 11.
Step responses of the MIMO system outputs and under PID controllers tuned with the NSGA-II algorithm, comparing the standard configuration with the split-based approach.
The control signals and , in Figure 12, generated by the PID controllers tuned with NSGA-II exhibit distinguishable profiles between the standard and split-based implementations. As illustrated, the split-based PID configuration demands significantly lower actuation magnitudes while preserving control authority, particularly during transient phases. This reduction in control effort implies improved energy efficiency and reduced actuator stress, which is critical for practical deployment in multiloop systems. The smoother and more bounded trajectories from the split controller confirm its ability to balance responsiveness and actuation costs, highlighting its relevance when dealing with real-time control constraints or hardware limitations in MIMO environments.
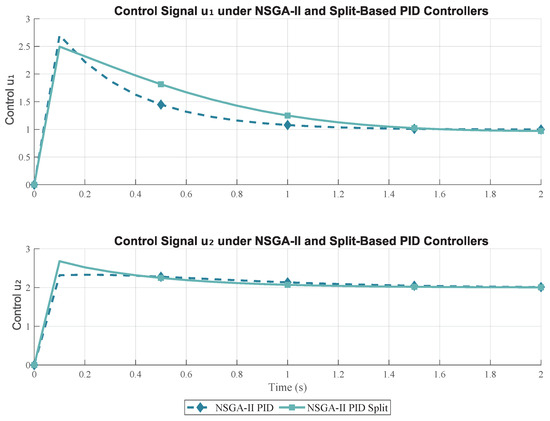
Figure 12.
Control signals and applied to the MIMO system using PID controllers tuned via NSGA-II, comparing the classic and split-based configurations. The plots show the actuation effort required under each strategy.
Table 2 and Figure 13 provide a comprehensive performance evaluation of the three implemented metaheuristic strategies—stochastic hill climbing, Voronoi-based search, and NSGA-II—when applied to the two-tank MIMO system. The Pareto front in the figure reveals a clear trade-off structure between the two objectives, the IAE and IADU, with each method generating a distinct solution frontier. Notably, the NSGA-II approach yields the lowest IADU and the smallest overshoot (Mp), indicating superior control smoothness and transient responses. Conversely, the stochastic method achieves the fastest settling time (Ts) and the lowest IAE, reflecting high tracking accuracy but with increased control effort. Voronoi heuristics, while slightly less optimal in extremities, offer a balanced compromise between performance and actuation costs. These outcomes, tabulated in Table 2, emphasize that each heuristic may outperform the others in specific aspects, highlighting the relevance of multiobjective approaches. The figure also marks the best solutions for each method, facilitating a visual comparison and reinforcing the necessity of decision-making frameworks like MOOD in selecting the most suitable controller per application scenario.

Table 2.
Performance comparison of PID controllers tuned using three metaheuristics for the two-tank MIMO system. Bold values indicate the best performance per metric.
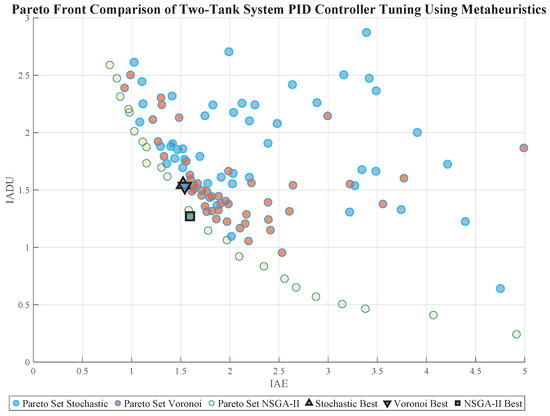
Figure 13.
Pareto front comparison of PID controller tuning methods for the two-tank MIMO system. The best-performing solution for each method is in the three last markers.
The results presented in Table 3 and Figure 14 offer a comparative assessment of three metaheuristic strategies applied to the two-tank MIMO system for PID tuning. Table 3 quantitatively demonstrates controller performance using four key metrics: IAE, IADU, maximum overshoot (), and settling time (). Each heuristic demonstrates strengths in different criteria, with the NSGA-II method achieving the best compromise in control effort and overshoot, while the stochastic approach excels in minimizing the IAE and settling time.

Table 3.
Performance comparison of PID controllers tuned using three metaheuristics for the two-zone HVAC system. Bold information values indicate the best performance per metric.
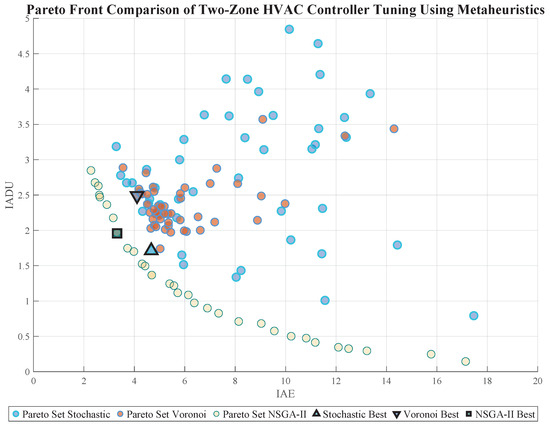
Figure 14.
Pareto front comparison of PID controller tuning for the two-zone HVAC system. The best solution from each method is marked on the graph.
The Figure 14 highlights the solution diversity and spread of trade-offs obtained via each metaheuristic. The best-performing individuals—selected based on utopian or heuristic-specific criteria—are marked to illustrate each method’s ability to converge toward distinct regions of the objective space. This multicriteria view reveals that the NSGA-II technique consistently produces well-distributed fronts, while the Voronoi approach shows superior mid-range balance, and the stochastic variant tends to favor faster dynamics. Collectively, these plots demonstrate the relevance of each method depending on specific design preferences and contribute to informed decision making in MIMO PID controller synthesis.
The Table 4 and Figure 15 assess the PID tuning strategies on the mass damper MIMO system underscores the practical impact of the optimization methodology on the control trade-offs. Table 4 highlights the distinct performance characteristics offered by each metaheuristic. Voronoi heuristics deliver the lowest integral of absolute error (IAE) and near-zero overshoot, reflecting highly accurate and stable regulation. In contrast, NSGA-II achieves the most energy-efficient control profile, as evidenced by the lowest IADU value. Stochastic search demonstrates a moderate balance across metrics.

Table 4.
Performance comparison of PID controllers tuned using three metaheuristics for the mass damper MIMO system. Bold information values indicate the best performance per metric.
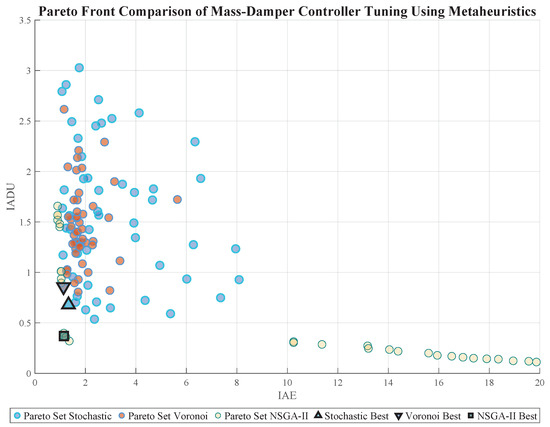
Figure 15.
Pareto front comparison of PID controller tuning strategies applied to the mass damper MIMO system. The best-performing solution from each method is marked on the plot.
Figure 15 complements the quantitative analysis by illustrating the spread and convergence of the Pareto-optimal fronts. Voronoi-generated solutions exhibit a favorable compromise curve, offering diverse tuning options that minimize both the tracking error and actuation demand. This reinforces the methodology’s adaptability to different performance needs and emphasizes its robustness for mechanical applications where precision and damping are critical. The figure also confirms the capacity of each algorithm to explore the solution space with distinct optimization behavior.
An important aspect revealed by the study is the robustness of the proposed framework. By balancing the IAE, which penalizes persistent tracking errors, with the IADU, which discourages abrupt control actions, the resulting controllers are naturally resilient to both external disturbances and measurement noise. This dual perspective allows the tuned PIDs to recover quickly from perturbations while avoiding excessive sensitivity to sensor fluctuations or actuator limits. The consistent performance observed across three different benchmark plants further underscores this robustness, showing that the methodology adapts well to diverse dynamics without relying on case-specific adjustments or fragile parameter settings.
The presented study demonstrates the effectiveness of a multiobjective PID tuning framework for MIMO systems, incorporating three distinct metaheuristic strategies—stochastic search, Voronoi-based sampling, and NSGA-II—and extending them with the MOOD selection layer for interpretability. The results across three representative real-world plants validate the generality and robustness of the approach. The Voronoi heuristic emerges as a strong candidate, offering competitive control accuracy with smooth effort trade-offs. The MOOD classification proves essential in distinguishing solutions based on decision-maker preferences.
Furthermore, the PID-split variant enhances the flexibility of the tuning process by enabling finer response shaping, particularly in systems with interaction dynamics. The comparative evaluation shows that the framework enables the systematic exploration of the Pareto surface, avoiding the distortions introduced by scalarization methods. Ultimately, the integration of metaheuristics, performance–effort metrics, and structured visualization contributes to more informed and adaptable control design in complex MIMO environments, ensuring alignment with practical engineering priorities.
5. Conclusions and Future Works
This study addressed the complex task of PID controller tuning for MIMO systems using a structured multiobjective optimization methodology. By integrating the tuning process with performance and control effort objectives, the approach supported a flexible trade-off analysis via Pareto fronts. The inclusion of the MOOD framework further enriched decision making, aligning the tuning outcomes with system-specific priorities. Tested on three benchmark MIMO plants, the framework provided a coherent pipeline from plant modeling to final implementation. The ability to navigate optimality under multiple criteria marks a significant step toward controller designs that are both technically sound and practically grounded.
The use of metaheuristic algorithms—stochastic search, Voronoi-based optimization, and NSGA-II—proved essential in efficiently exploring the design space and extracting nondominated controller solutions. Each algorithm contributed unique sampling behavior, aiding in diversity and convergence across the Pareto surface. Specifically, Voronoi-based heuristics offered smooth, well-distributed fronts, and NSGA-II reliably delivered convergence to optimal trade-off boundaries. These findings underscore the value of heuristic-driven approaches in multiobjective control design, especially for nonlinear or high-dimensional problems where analytical tuning becomes intractable.
Comparative evaluations revealed that, for the two-tank MIMO system, the NSGA-II algorithm achieved a minimum control effort (IADU) of 1.2713 while maintaining high performance. This result highlights the ability of the method to minimize actuator stress without compromising tracking behavior. Similarly, the Voronoi-based method provided highly competitive solutions across all tested systems. These results validate the approach as a viable and effective means of obtaining balanced controller designs, demonstrating performance that often exceeds that of traditional tuning methods by a measurable margin.
For the mass damper system, the Voronoi heuristic delivered the best IAE score of 1.1340, outperforming the alternatives in minimizing the tracking error. This result affirms the strength of spatially guided sampling in targeting optimal zones of the decision space. Furthermore, the implementation of the MOOD framework allowed for the explicit categorization of these solutions, enabling the intuitive selection of controller parameters based on operational emphasis. Such a blend of heuristic optimization and interpretability enhances the method’s applicability in real engineering scenarios, where nuanced trade-offs between performance and effort are necessary.
While the present study validates the methodology across three representative benchmark plants, its scope remains limited to the simulation-based analysis of linearized models. Future research should extend this framework to explicitly address nonlinear dynamics, enabling a comparison with approaches such as dynamic pole motion for enhanced adaptability. Likewise, incorporating experimental verification on laboratory-scale platforms will provide empirical grounding of the observed trade-offs. Additional directions include extending the methodology to constrained control scenarios and integrating robustness margins directly into the optimization layer. These developments will further consolidate the applicability of the proposed framework in complex and uncertain engineering environments.
Funding
This research was funded by Universidad UTE, grant number 4000. The funding covered the costs associated with publishing in Electronics.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This paper presents results from a research project conducted at Universidad UTE. Universidad UTE has provided financial support for the article processing charges (APC) under funding number 4000, and fosters an encouraging environment for academic research and innovation. All figures and images in this article have been designed and verified to be accessible for readers with color vision deficiencies.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Lucio, Y.L.S.; Mariani, V.C.; Coelho, L.S. Multi-Objective Grouped Grey Wolf Optimization of PID Controllers Applied to a Water Treatment Plant Model. In Proceedings of the 2023 IEEE Congress on Evolutionary Computation (CEC 2023), Chicago, IL, USA, 1–5 July 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Abdellatif, O.; Issa, M.; Ziedan, I.; El, B. Optimization of PID Controller Parameter Using the Geometric Mean Optimizer. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2024, 15, 1098–1103. [Google Scholar] [CrossRef]
- Saab, S.S. A Stochastic PID Controller for a Class of MIMO Systems. Int. J. Control 2017, 90, 463–478. [Google Scholar] [CrossRef]
- Olmez, Y.; Ozmen Koca, G.; Akpolat, Z.H. Recent Metaheuristics on Control Parameter Determination. Int. J. Optim. Control Theor. Appl. (IJOCTA) 2025, 15, 166–182. [Google Scholar] [CrossRef]
- Hanuma Naik, R.; Ashok Kumar, D.V.; Sujatha, P. Independent Controller Design for MIMO Processes Based on Extended Simplified Decoupler and Equivalent Transfer Function. Ain Shams Eng. J. 2020, 11, 343–350. [Google Scholar] [CrossRef]
- Rayguru, M.M.; Roy, S.; Kar, I.N. Time-Scale Redesign-Based Saturated Controller Synthesis for a Class of MIMO Nonlinear Systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4681–4692. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Oliva, D. Fractional Order PID Controller Design for an AVR System Using Chaotic Yellow Saddle Goatfish Algorithm. Mathematics 2020, 8, 1182. [Google Scholar] [CrossRef]
- Pongfai, J.; Angeli, C.; Shi, P.; Su, X.; Assawinchaichote, W. Optimal PID Controller Autotuning Design for MIMO Nonlinear Systems Based on the Adaptive SLP Algorithm. Int. J. Control Autom. Syst. 2021, 19, 392–403. [Google Scholar] [CrossRef]
- Pinzón, S.; Pavón, W. Diseño de Sistemas de Control Basados en el Análisis del Dominio en Frecuencia. Rev. Téc. Energ. 2019, 15, 76–82. [Google Scholar] [CrossRef]
- Javadian, A.; Nariman-zadeh, N.; Jamali, A. Evolutionary Design of Marginally Robust Multivariable PID Controller. Eng. Appl. Artif. Intell. 2023, 121, 105938. [Google Scholar] [CrossRef]
- Somefun, O.A.; Akingbade, K.; Dahunsi, F. The Dilemma of PID Tuning. Annu. Rev. Control 2021, 52, 65–74. [Google Scholar] [CrossRef]
- Zatarain Salazar, J.; Kwakkel, J.H.; Witvliet, M. Evaluating the Choice of Radial Basis Functions in Multiobjective Optimal Control Applications. Environ. Model. Softw. 2024, 171, 105889. [Google Scholar] [CrossRef]
- Liu, C.; Duan, Q.W.; Zhang, C.; Luo, Y.; Qiu, X.X.; Xia, W.Q.; Li, H.; Mao, Y. Extending the LQR to the Design of PID Type-II and Type-III Control Loops. IET Control Theory Appl. 2023, 17, 713–743. [Google Scholar] [CrossRef]
- Abedzadeh Maafi, R.; Etemadi Haghighi, S.; Mahmoodabadi, M.J. Pareto Optimal Design of a Fuzzy Adaptive Sliding Mode Controller for a Three-Link Model of a Biped Robot via the Multi-Objective Improved Team Game Algorithm. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 428. [Google Scholar] [CrossRef]
- Kouritem, S.A.; Mahmoud, M.; Nahas, N.; Abouheaf, M.I.; Saleh, A.M. A Self-Adjusting Multi-Objective Control Approach for Quadrotors. Alex. Eng. J. 2023, 76, 543–556. [Google Scholar] [CrossRef]
- Aguila-Leon, J.; Chiñas-Palacios, C.; Vargas-Salgado, C.; Hurtado-Perez, E.; Garcia, E.X.M. Particle Swarm Optimization, Genetic Algorithm and Grey Wolf Optimizer Algorithms Performance Comparative for a DC-DC Boost Converter PID Controller. Adv. Sci. Technol. Eng. Syst. 2021, 6, 619–625. [Google Scholar] [CrossRef]
- Águila-León, J.; Chiñas-Palacios, C.D.; Vargas-Salgado, C.; Hurtado-Perez, E.; García, E.X.M. Optimal PID Parameters Tuning for a DC-DC Boost Converter: A Performance Comparative Using Grey Wolf Optimizer, Particle Swarm Optimization and Genetic Algorithms. In Proceedings of the 2020 IEEE Conference on Technologies for Sustainability (SusTech), Santa Ana, CA, USA, 23–25 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ziamanesh, S.; Salimi, H.S.; Tavana, A.; Ghavifekr, A.A. Parameter Tuning of Discontinuous Lyapunov-Based Controller Based on the Grey Wolf Optimization Algorithm Applied to a Robotic Manipulator. In Proceedings of the 8th International Iranian Conference on Signal Processing and Intelligent Systems (ICSPIS 2022), Shahrood, Iran, 28–29 December 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Pazmiño, R.; Pavon, W.; Armstrong, M.; Simani, S. Performance Evaluation of Fractional Proportional–Integral–Derivative Controllers Tuned by Heuristic Algorithms for Nonlinear Interconnected Tanks. Algorithms 2024, 17, 306. [Google Scholar] [CrossRef]
- Maroufi, O.; Choucha, A.; Chaib, L. Hybrid Fractional Fuzzy PID Design for MPPT-Pitch Control of Wind Turbine-Based Bat Algorithm. Electr. Eng. 2020, 102, 2149–2160. [Google Scholar] [CrossRef]
- Mae, M.; Ohnishi, W.; Fujimoto, H. MIMO Multirate Feedforward Controller Design with Selection of Input Multiplicities and Intersample Behavior Analysis. Mechatronics 2020, 71, 102442. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Sanchis, J.; Blasco, X.; Herrero, J.M. Multiobjective Evolutionary Algorithms for Multivariable PI Controller Design. Expert Syst. Appl. 2012, 39, 7895–7907. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Kagami, R.M. Controller Tuning with Multi-Objective Optimization: Benchmark Definitions for SISO Linear Systems—A PI Controller Case. IFAC-PapersOnLine 2024, 58, 126–131. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Sanchis, J.; Blasco, X.; Martinez, M. Algoritmos Evolutivos y su Empleo en el Ajuste de Controladores del Tipo PID: Estado Actual y Perspectivas. RIAI—Rev. Iberoam. Autom. Inform. Ind. 2013, 10, 251–268. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Carrillo-Ahumada, J.; Marques, T. Multi-Objective Machine Learning for Control Performance Assessment in PID Control Loops. IFAC-PapersOnLine 2024, 58, 168–173. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Blasco-Ferragud, X.; Sanchis-Saez, J.; Herrero-Durá, J.M. Controller Tuning with Evolutionary Multiobjective Optimization: A Holistic Multiobjective Optimization Design Procedure. In Controller Tuning with Evolutionary Multiobjective Optimization; Intelligent Systems, Control and Automation: Science and Engineering; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Chen, R.; Li, K.; Yao, X. Dynamic Multiobjectives Optimization with a Changing Number of Objectives. IEEE Trans. Evol. Comput. 2018, 22, 157–171. [Google Scholar] [CrossRef]
- Sahib, M.A.; Ahmed, B.S. A new multiobjective performance criterion used in PID tuning optimization algorithms. J. Adv. Res. 2016, 7, 125–134. [Google Scholar] [CrossRef]
- Chuong, T.D. Optimality and Duality for Robust Multiobjective Optimization Problems. Nonlinear Anal. Theory Methods Appl. 2016, 134, 127–143. [Google Scholar] [CrossRef]
- Povalej, Ž. Quasi-Newton’s Method for Multiobjective Optimization. J. Comput. Appl. Math. 2014, 255, 765–777. [Google Scholar] [CrossRef]
- Mercader, P.; Åström, K.J.; Baños, A.; Hägglund, T. Robust PID Design Based on QFT and Convex-Concave Optimization. IEEE Trans. Control Syst. Technol. 2017, 25, 441–452. [Google Scholar] [CrossRef]
- López, V.G.; Lewis, F.L. Dynamic Multiobjective Control for Continuous-Time Systems Using Reinforcement Learning. IEEE Trans. Autom. Control 2019, 64, 2869–2874. [Google Scholar] [CrossRef]
- Parisi, S.; Pirotta, M.; Restelli, M. Multi-objective Reinforcement Learning through Continuous Pareto Manifold Approximation. J. Artif. Intell. Res. 2016, 57, 187–227. [Google Scholar] [CrossRef]
- Eichfelder, G.; Krüger, C.; Schöbel, A. Decision Uncertainty in Multiobjective Optimization. J. Glob. Optim. 2017, 69, 485–510. [Google Scholar] [CrossRef]
- Zamani, M.; Soleimani-Damaneh, M.; Kabgani, A. Robustness in Nonsmooth Nonlinear Multi-objective Programming. Eur. J. Oper. Res. 2015, 247, 370–378. [Google Scholar] [CrossRef]
- de Oliveira, V.A. Optimality Conditions and Duality for a Class of Continuous-Time Linear Optimization Problems. Comput. Appl. Math. 2024, 43, 278. [Google Scholar] [CrossRef]
- Chen, J.; Ma, D.; Xu, Y.; Chen, J. Delay Robustness of PID Control of Second-Order Systems: Pseudoconcavity, Exact Delay Margin, and Performance Tradeoff. IEEE Trans. Autom. Control 2022, 67, 1194–1209. [Google Scholar] [CrossRef]
- Ma, D.; Boussaada, I.; Chen, J.; Bonnet, C.; Niculescu, S.I.; Chen, J. PID Control Design for First-Order Delay Systems via MID Pole Placement: Performance vs. Robustness. Automatica 2022, 137, 110102. [Google Scholar] [CrossRef]
- Mao, Q.; Xu, Y.; Chen, J.; Georgiou, T.T. Implementation-Oriented Filtered PID Control: Optimization of Robustness Margins. Automatica 2023, 152, 110974. [Google Scholar] [CrossRef]
- D’Amico, W.; Farina, M. Virtual Reference Feedback Tuning for Linear Discrete-Time Systems with Robust Stability Guarantees Based on Set Membership. Automatica 2023, 157, 111228. [Google Scholar] [CrossRef]
- Ku, C.-C. Robust Controller Design for Nonlinear Uncertain Stochastic Drum-Boiler System. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2378–2383. [Google Scholar] [CrossRef]
- Song, K.Y.; Behzadfar, M.; Zhang, W.J. A Dynamic Pole Motion Approach for Control of Nonlinear Hybrid Soft Legs: A Preliminary Study. Machines 2022, 10, 875. [Google Scholar] [CrossRef]
- Sun, H.; Zou, T.; Wang, J.; Yang, Z.; Zheng, H. Priority-Based Strategy for Multi-Objective Steady-State Optimization in Double-Layer Model Predictive Control. In Proceedings of the 2022 13th Asian Control Conference (ASCC), Jeju, Republic of Korea, 4–7 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 720–725. [Google Scholar] [CrossRef]
- Yang, Q.; Wei, M.; Su, J.; Duan, Y.; Zhu, J. Multi-Objective Optimization of Hybrid Agricultural Powertrain via Crowding-Adaptive NSGA-II with Dynamic Population Control. Energy 2025, 335, 138124. [Google Scholar] [CrossRef]
- Qiao, K.; Liang, J.; Yu, K.; Guo, W.; Yue, C.; Qu, B.; Suganthan, P.N. Benchmark Problems for Large-Scale Constrained Multi-Objective Optimization with Baseline Results. Swarm Evol. Comput. 2024, 86, 101504. [Google Scholar] [CrossRef]
- Hao, Y.; Zhao, C.; Zhang, Y.; Cao, Y.; Li, Z. Constrained Multi-Objective Optimization Problems: Methodologies, Algorithms and Applications. Knowl.-Based Syst. 2024, 299, 111998. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).