Smooth and Robust Path-Tracking Control for Automated Vehicles: From Theory to Real-World Applications

Abstract

Path tracking is a fundamental challenge in the development of automated driving systems, requiring precise control of vehicle motion while ensuring smooth and stable actuation signals. Advancements in this field often lead to increasingly complex control solutions that demand significant computational effort and are difficult to parameterize. A novel variable structure path-tracking control approach that is based on the geometrically optimal solution of a Dubins car offers a promising solution to this challenge. The controller generates an n-smooth and differentially bounded steering angle, and with n + 1 parameters, it can be tuned towards performance, robustness, or low magnitude of the steering angle derivatives. In prior work, this controller demonstrated its performance, robustness, and tunablity in various simulations. In this contribution, we address the challenges of implementing this controller in a real vehicle, including system dead time, low sampling rates, and discontinuous paths. Key adaptations are proposed to ensure robust performance under these conditions. The controller is integrated into a comprehensive automated driving system, incorporating planning and velocity control, and evaluated during an overtaking maneuver (double-lane change) in a real-world setting. Experimental results show that the implemented controller successfully handles system dead time and path discontinuities, achieving consistent tracking errors of less than $0.3$ m.

1. Introduction

One of the most pressing challenges in modern robotics is the navigation of autonomous vehicles, which requires the seamless integration of perception, planning, and control systems. A key task in this context is path tracking, which involves accurately following a predetermined trajectory while accounting for vehicle dynamics, environmental disturbances, and system limitations.

The effectiveness of path tracking depends strongly on the chosen control strategy. Model-free approaches, such as PID [1], are attractive due to their simplicity and low computational burden, but they rely heavily on expert tuning and degrade under nonlinear dynamics, particularly at high speeds or on sharp curves [2,3,4,5]. To address these limitations, model-based geometric controllers such as Pure Pursuit [6] and Stanley [7] have been widely applied. These methods leverage geometric relations between vehicle poses and reference paths, enabling efficient real-time operation. However, their reliance on simplified kinematic assumptions limits performance at higher speeds and under significant dynamic effects. More advanced methods—such as sliding mode control (SMC) [8,9], linear quadratic regulation (LQR) [10], and model predictive control (MPC) [11,12,13]—explicitly incorporate vehicle models and constraints, offering improved robustness and optimality at the expense of increased computational cost and implementation complexity.

While these approaches have been extensively studied in simulations, the transition from theoretical control design to real-world deployment presents additional obstacles that are often underrepresented in the literature. Controllers implemented on real vehicles must contend with actuation delays, sensor noise, trajectory discontinuities, and computational limits. The literature review [14] synthesizes recent advances in path tracking control, with particular attention to methods that have demonstrated real-world applicability or strong potential for implementation. Publications that demonstrate validated real-world implementations of path tracking are [15,16,17,18]. In particular the novel controller we previously introduced [19] has never been validated on a real vehicle. This leaves open the critical question of whether its theoretical guarantees—smoothness, tunability, and convergence—can withstand the challenges of physical implementation. To address this gap, the present paper makes the following contributions:

1.

First real-world implementation of the proposed path-tracking controller, bridging the gap between its theoretical foundation and deployment on a test vehicle.

2.

Compensation of system dead time using a recently developed method that has not yet been demonstrated in real-world path-tracking applications.

3.

Robustness to discontinuous reference trajectories, achieved by extending the controller with a lookahead mechanism. While lookahead concepts are well-established in geometric controllers, this is their first application to the proposed controller framework.

4.

Demonstration of intuitive parameter tuning, showcasing how the controller’s inherent multi-objective design translates into practical tuning strategies for balancing stability, responsiveness, and comfort.

Through experiments with a Ford Mondeo hybrid, we show that these innovations enable the controller to operate robustly under localization errors, actuator dynamics, and computational limits. The results validate its potential as a practical, real-world path-tracking solution that preserves the original mathematical guarantees.

The remainder of this work is structured as follows: Section 2 summarizes the novel controller, detailing its characteristics and benchmarking its performance. Section 3 describes the real-world test conditions and the vehicle-embedded system. The necessary controller adaptations for these conditions are introduced in Section 4. Section 5 presents the tuning process and final vehicle tests. Finally, the work is concluded in Section 6.

2. Smooth and Robust Steering Controller: Theory and Characteristics

In [19] we presented a multi-objective path-tracking control for car-like vehicles with differentially bounded n-smooth outputs. This approach is shortly summarized in this section. The control law and its parameters are presented; the characteristics are described, and the controller is bench-marked against state-of-the-art controllers.

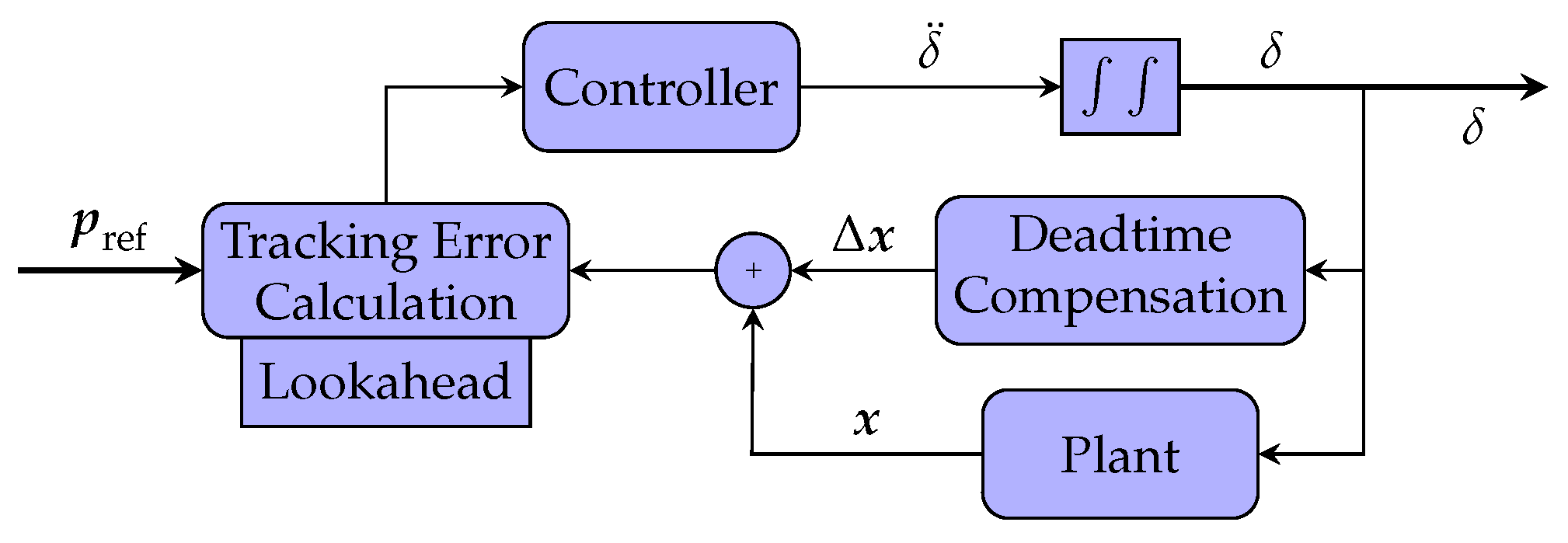
2.1. Controller Overview

The controller is based on a sliding mode controller, which steers the vehicles axis along the Dubins-optimal curve.

$$\begin{array}{cc}\hfill \kappa & =\overline{\kappa }·\mathrm{sign}\left(\sigma \left(\mathit{x}\right)\right)\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill \sigma & =-e-{\displaystyle \frac{1-cos\psi }{(1-k_{\mathrm{rob}})\overline{\kappa }}}·\mathrm{sign}(sin\psi )\hfill \end{array}$$

(1b)

where $\kappa$ is the path curvature and $\sigma$ is the sliding surface, creating the Dubins-optimal path for reaching a straight reference path. e and $\psi$ are the control errors as visualized in Figure 1. The lateral error e is measured orthogonal to the reference path at ${\mathit{p}}_{\mathrm{ref}}$ and is the shortest distance between the rear wheel and the reference path. While $\overline{\kappa }$ is the maximum curvature the vehicle can reach, the sliding surface is designed to approach the reference path on a larger radius of curvature $(1-k_{\mathrm{rob}})\overline{\kappa }$ to introduce a control reserve and consequently obtain robustness to disturbances.

With kinematic relations, we could compute the steering angle $\delta$ such that the rear wheels of the vehicle follow the curvature $\kappa$. However, this steering angle would be discontinuous, as is $\kappa$. To obtain smoothness, we do not force the rear wheel to follow the Dubins curve, but rather the front wheel. The rear wheel is trailoring the front wheel asymptotically with a smooth curvature, and thus the vehicle has a smooth steering angle. This is illustrated in Figure 2.

To push this further, we introduce a fictive lead wheel that follows the Dubins curve. The front wheel follows the smooth curvature, while the rear wheel follows with smooth change in curvature ${\kappa }^{\prime }$. We describe the vehicle, extended with the lead wheel, with the state vector containing the control error of the rear wheel and the steering angles:

$$\mathit{x}={\left[\begin{array}{cccc}e& \psi & \delta & {\delta }_{\mathrm{l}}\end{array}\right]}^T$$

(2)

where ${\delta }_{\mathrm{l}}$ is the fictive steering angle of the lead wheel. From kinematic trailor equations, we obtain the relation between ${\delta }_{\mathrm{l}}$ and the steering rate ${\delta }^{\prime }$:

$${\delta }_{\mathrm{l}}=arctan\left(\left({\displaystyle \frac{tan\delta }{\lambda }}+{\delta }^{\prime }\right)·{\lambda }_{\mathrm{l}}·cos\delta \right)$$

(3)

According to [19], the control law extended for the lead wheel is

$$\begin{array}{cc}\hfill {\kappa }_{\mathrm{l}}& ={\overline{\kappa }}_{\mathrm{l}}·\mathrm{sign}\left(\sigma \left(\mathit{x}\right)\right)\hfill \end{array}$$

(4a)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sigma \left(\mathit{x}\right)& =-(e+sin\psi ·\lambda +sin(\psi +\delta )·{\lambda }_{\mathrm{l}})\hfill \\ & -{\displaystyle \frac{1-cos(\psi +\delta +{\delta }_{\mathrm{l}})}{(1-k_{\mathrm{rob}})·{\overline{\kappa }}_{\mathrm{l}}}}\mathrm{sign}(sin(\psi +\delta +{\delta }_{\mathrm{l}}))\hfill \end{array}\end{array}$$

(4b)

where ${\kappa }_{\mathrm{l}}$ is the curvature of the lead wheel and $k_{\mathrm{rob}}\in [0,1)$ is the parameter for robustness.

The control signal ${\kappa }_{\mathrm{l}}$ is a fictive value, representing the curvature of the path that the vehicle is following (tracking with its fictive lead wheel). It directly relates to the steering rate of the fictive lead wheel and consequently (as can be seen in Relation (3)) to the steering acceleration. The steering acceleration is

$$\begin{array}{cc}\hfill {\delta }_{\mathrm{l}}^{\prime }& ={\displaystyle \frac{{\kappa }_{\mathrm{l}}}{cos\delta ·cos{\delta }_{\mathrm{l}}}}-{\displaystyle \frac{tan\delta }{\lambda }}-{\delta }^{\prime }\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill {\delta }^{\prime \prime }& ={\displaystyle \frac{{\delta }_{\mathrm{l}}^{\prime }}{{cos}^2{\delta }_{\mathrm{l}}·cos\delta ·{\lambda }_{\mathrm{l}}}}-{\delta }^{\prime }/\lambda +{\delta }^{\prime 2}tan\delta \hfill \end{array}$$

(5b)

In summary, to implement the control law, the following steps are necessary:

1.

Define parameters ${\overline{\kappa }}_{\mathrm{l}}$, ${\lambda }_{\mathrm{l}}$, and $k_{\mathrm{rob}}$, as will be described in the next subsection.

2.

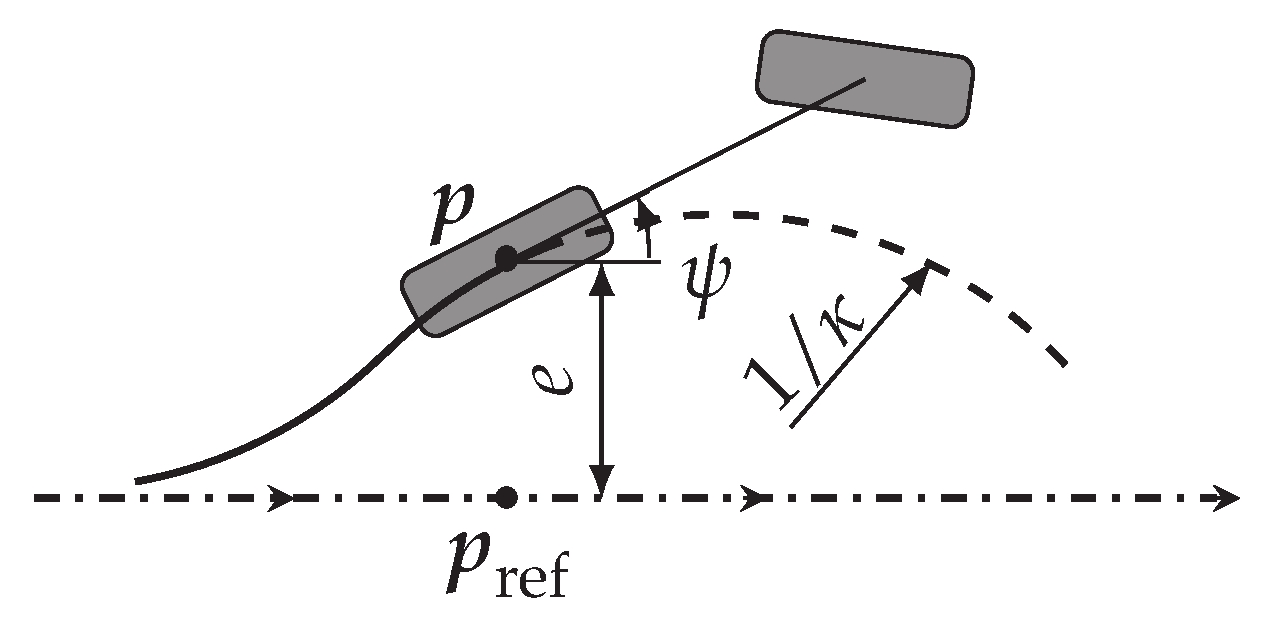
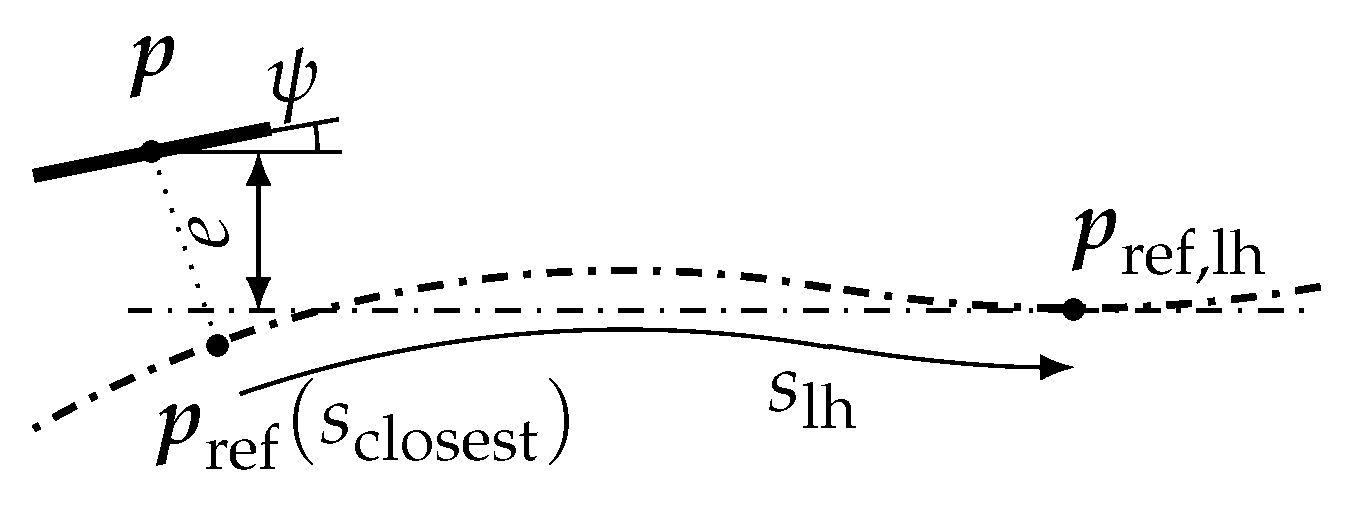
Measure the tracking error e and orientation error $psi$ as depicted in Figure 2.

3.

Compute the control signal ${\kappa }_{\mathrm{l}}$ from (4).

4.

Compute the steering acceleration ${\delta }^{″}$ from (5). This is the output of the controller.

2.2. Steering Constraints and Parameterization

Applying the steering acceleration (Equation (5)) to the steering system, the steering angle, steering rate, and steering acceleration are bounded. We define the maximum curvature ${\overline{\kappa }}_{\mathrm{l}}$ such that $\delta \le \overline{\delta }$, where

$$\begin{array}{cc}\hfill {\overline{\kappa }}_{\mathrm{l}}& :={\displaystyle \frac{\overline{\kappa }}{\sqrt{1+(\overline{\kappa }·{\lambda }_{\mathrm{l}}}{)}^2}}\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill \overline{\kappa }& ={\displaystyle \frac{sin\overline{\delta }}{{\lambda }_0}}.\hfill \end{array}$$

(6b)

The bounds of the steering rate and steering acceleration are

$$\begin{array}{cc}\hfill |{\delta }^{\prime }|& \le \left({\kappa }_{\mathrm{f}}-{\displaystyle \frac{sin\delta }{\lambda }}\right)/cos\delta \hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill |{\delta }_0^{″}|& <{\displaystyle \frac{2}{{\underline{r}}^2}}·\left({\displaystyle \frac{{\underline{r_2}}^2}{\underline{r_1}·{\lambda }_1}}+{\displaystyle \frac{{\underline{r_1}}^2}{\underline{r}·{\lambda }_0}}+{\displaystyle \frac{{\lambda }_0}{\underline{r}}}+2{\displaystyle \frac{{\lambda }_0}{\underline{r_1}}}\right),\hfill \end{array}$$

(7b)

with $\underline{r}={\displaystyle \frac{{\lambda }_0}{tan{\overline{\delta }}_0}}$, $\underline{r_1}={\displaystyle \frac{{\lambda }_1}{tan{\overline{\delta }}_1}}$ and $\underline{r_1}=1/{\overline{\kappa }}_1$.

In [19] a parameterization scheme is described. By specifying limits for the steering angle and rate (derivative in time) $\dot{\delta }$, the control parameters ${\lambda }_0,{\lambda }_1$ and $\overline{\delta }$ are dynamically tuned.

2.3. Inherent Characteristics and Robustness

The proposed controller exhibits several key properties that make it suitable for real-world automotive applications:

1.

Inherent Robustness: Founded on a sliding mode control principle, the controller provides inherent robustness against matched disturbances. This ensures stability is maintained even in the presence of model uncertainties, such as errors in the vehicle’s understeer gradient or other parametric variations that act within the control channel.

2.

Minimal Model Dependency: The control law is derived from the kinematic bicycle model. Consequently, its only required vehicle parameter is the wheelbase. It is independent of dynamic parameters (e.g., mass, tire cornering stiffness, and inertia), making it broadly applicable across different vehicle platforms without the need for extensive re-parameterization.

3.

Rule-Based Parameterization: The control parameters $k_{\mathrm{rob}}$, ${\lambda }_0$, ${\lambda }_1$, and $\overline{\delta }$ directly relate to specific properties: robustness, the steering rate, steering smoothness, and the maximum steering angle. Thus, the controller tuning process is decoupled from environment-dependent parameters (e.g., tire–road friction and weather conditions), simplifying deployment and ensuring consistent performance across diverse operating conditions.

4.

Performance at the Actuation Limits: A primary strength of the controller is its well-defined and predictable behavior when operating close to the steering constraints. This makes it particularly effective for demanding maneuvers such as navigation on narrow, winding roads or aggressive obstacle avoidance, as discussed and demonstrated in [19,20].

The basic control performance, including tracking accuracy and steering behavior, is quantitatively evaluated in the subsequent section through a comparative benchmark with other state-of-the-art controllers during a double-lane-change maneuver.

2.4. Comparison to State-of-the-Art Controllers

The performance of the proposed controller is evaluated through a double-lane-change maneuver and benchmarked against two state-of-the-art controllers selected for specific, complementary reasons:

• A higher-order sliding mode (HOSM) controller [21] is chosen because it shares a key characteristic with our method: the explicit enforcement of hard constraints on the steering angle and its rate of change. Its application to vehicle path tracking is described in [19].
• The Pure Pursuit controller [6] is selected. It is a widely adopted baseline in vehicle path tracking due to its simplicity and low computational footprint.

Both benchmarks represent low-computational-effort approaches, ensuring a fair comparison focused on control performance rather than algorithmic complexity.

The HOSM controller was tuned to minimize tracking error within its strict constraints. The Pure Pursuit controller, which lacks inherent constraint handling, was parameterized to yield a steering effort comparable to the proposed controller. The resulting trajectories are shown in Figure 3.

The HOSM controller exhibits a larger tracking error and more aggressive steering activity. The Pure Pursuit controller generates a significant tracking error for both the front and rear axles. In contrast, the proposed controller achieves near-ideal tracking of the front axle, a design objective that inherently results in a larger rear axle error. Furthermore, the Pure Pursuit controller violates the steering constraints, a limitation that would be exacerbated on paths with higher curvatures. Figure 3 also reveals that the Pure Pursuit controller exhibits overshoot and a slower convergence rate compared to the proposed method.

3. Real Test Conditions

We apply the controller on a passenger vehicle: the fourth-generation Ford Mondeo hybrid. It is equipped with a Dataspeed by-wire kit [22], providing a CAN interface to the throttle, the brakes, and a steering controller. The proposed controller is embedded in an automated driving stack that is shortly described in the next section. The section is followed by sections describing the steering system and vehicle localization.

The test is conducted on a two-lane testing ground comprising a straight road segment of approximately 170 m, as shown in Figure 4. During the tests, the asphalt was dry, with clear weather conditions.

3.1. AD System and Driving Maneuver

The AD system is designed for fully automated driving in urban environments. For testing the path-tracking controller, we manually trigger a double-lane-change maneuver with constant velocity. The active components of the AD system are shown in Figure 5 and consist of a trajectory planner, a path-tracking controller, and a velocity-tracking controller. It receives sensor data from a global positioning system described in Section 3.3 and outputs steering and throttle signals to the actuation system described in Section 3.2.

The trajectory planner creates a smooth path (a Catmull–Rom spline [23]) from one lane to the left lane and then back to the original lane. The path is shown in Figure 6. The path is $G^1$ continuous, meaning that the tangents change continuously along the path, while the curvature is discontinuous. The curvature reaches maximal values of $0.28$ m⁻¹.

The presented path-tracking controller outputs the steering angle $\delta$ into the steering system. The actual control signal, the steering acceleration ${\delta }^{″}$, acts as the internal state to guarantee smoothness and bounded derivatives of $\delta$.

The velocity controller is a PID controller that outputs pedal positions of the throttle and brake to the actuation system.

3.2. Steering System

The steering system consists of a controller that sets the steering torque such that the steering rod follows the target angle. The step response of the steering system is shown in Figure 7. After a dead time of 80 ms, the steering angle is reached at a rate of maximum $0.472$ rad/s. The response to a sine steering input is shown in Figure 8. The target steering angle is sampled at 50 Hz.

3.3. Positioning System

Localization is performed using an inertial navigation system (INS). This consists of the Novatel ProPak 6 GNSS receiver (Hexagon AB, T2E 8Z9 Calgary, AB, Canada, 2017), coupled with two antennas and an inertial measurement unit (IMU). Using the RTK (real-time kinematic positioning) method with IMU coupling, the GNSS receiver can achieve centimetre-level positioning accuracy and estimate the heading (the angle from true north). The inertial navigation system (INS) is mounted near the rear axle. A calibration measurement revealed a constant orientation bias of $0.054$ rad between the INS-reported heading and the vehicle’s actual direction of travel. While this bias does not directly impair the controller’s stability, it introduces a significant error in the estimated front axle position. This estimation is computed by translating the rear axle position by the wheelbase length along the biased heading. Consequently, a systematic front axle position error of approximately $0.15$ m arises. This error manifests as a constant lateral offset in the tracked path but does not otherwise degrade the control performance.

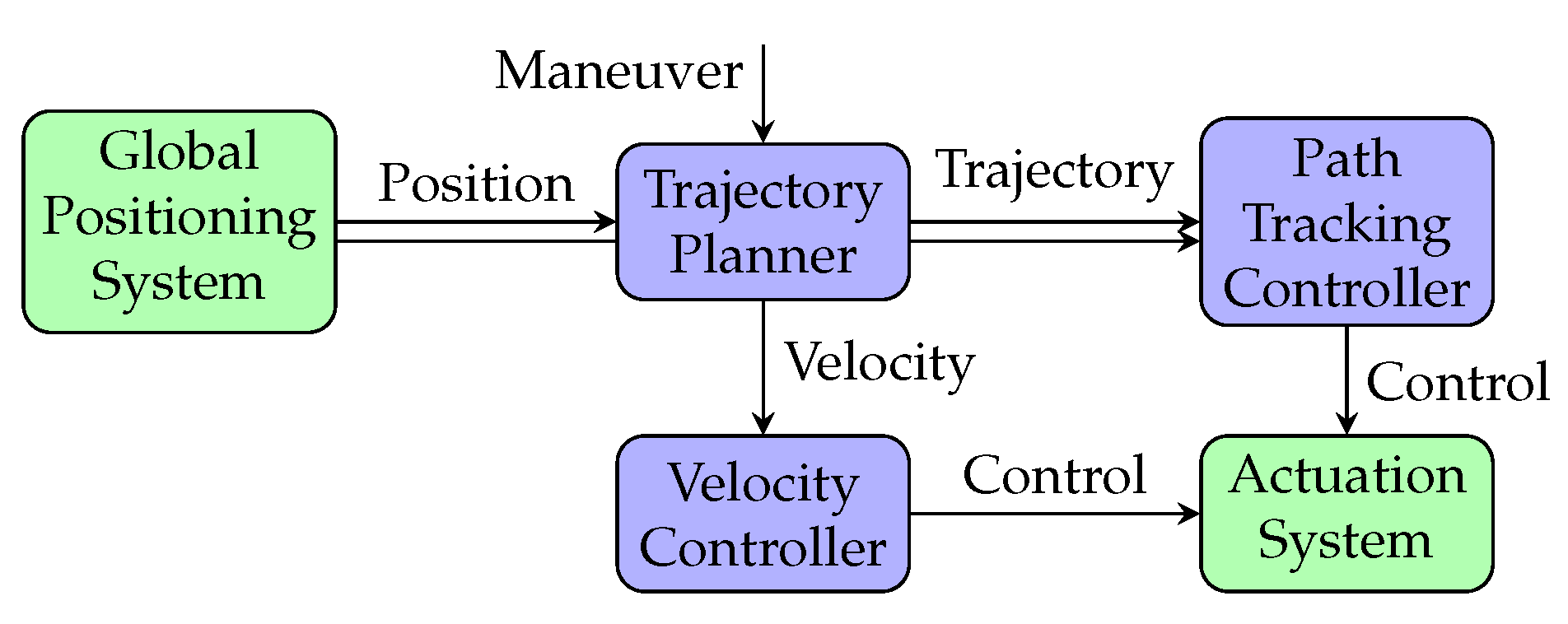
3.4. System Integration

To connect the AD system with the steering system and the positioning system in the vehicle, we use the asynchronous high-performance platform RTMaps [24]. The sensor and actuator interfaces as well as the path-tracking controller are implemented in C++ to minimize the processing time, achieving a result below 20 ms. The INS outputs measurements at 100 Hz, while the path-tracking controller and the actuation system operate at 50 Hz. The processing time of the controller is 20 ms, and the sub-sampling of the actuation system produces delays of up to 45 ms. The steering controller adds an additional delay of 150 ms (the steering response in Figure 7 is simplified to an average delay). The delay of the INS is unknown. We will approximate the total delay by tuning the dead-time compensation for the optimal delay.

4. Controller Adpations

To make the controller applicable in the real test conditions, some adaptions are necessary, which are presented in this section.

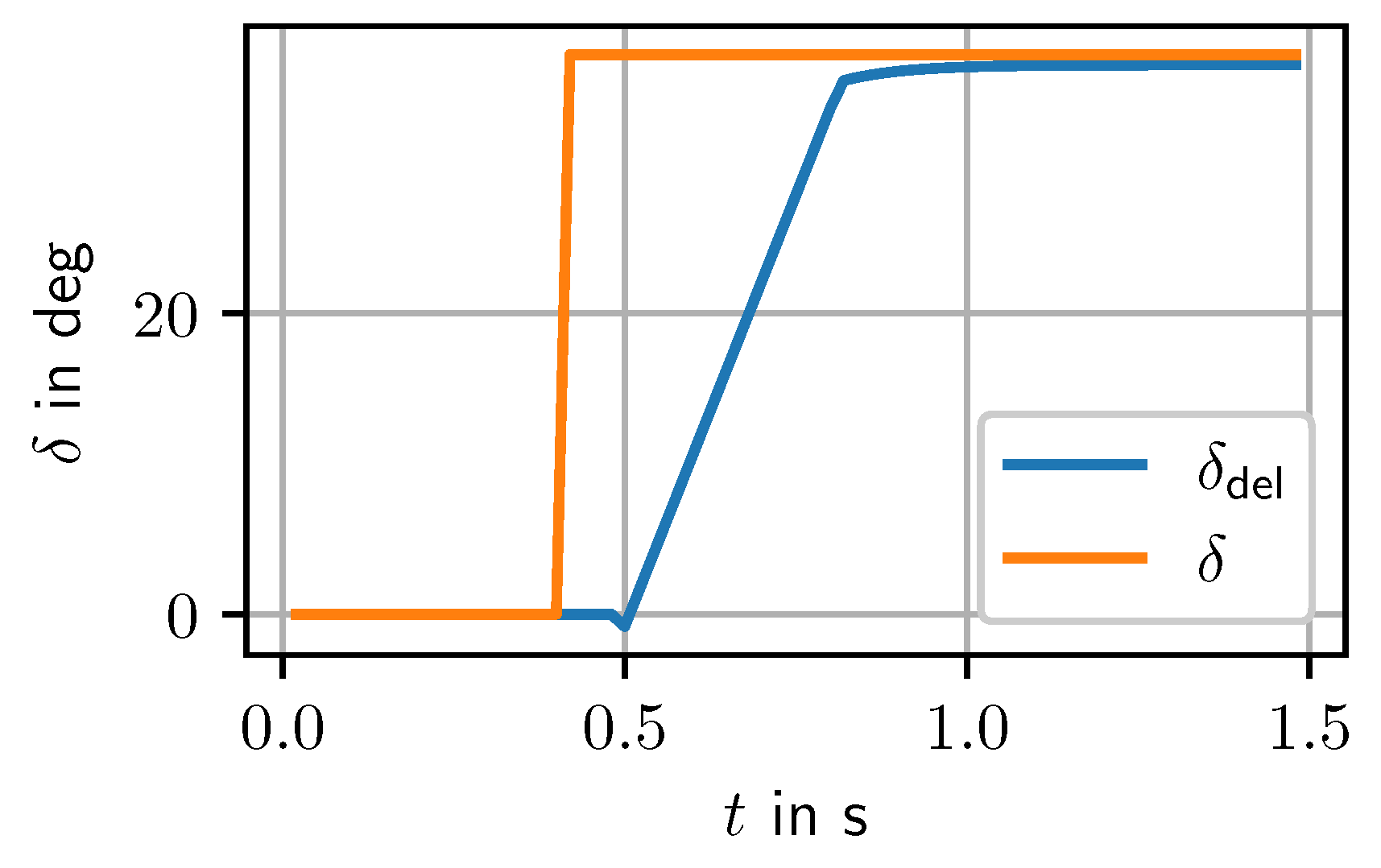
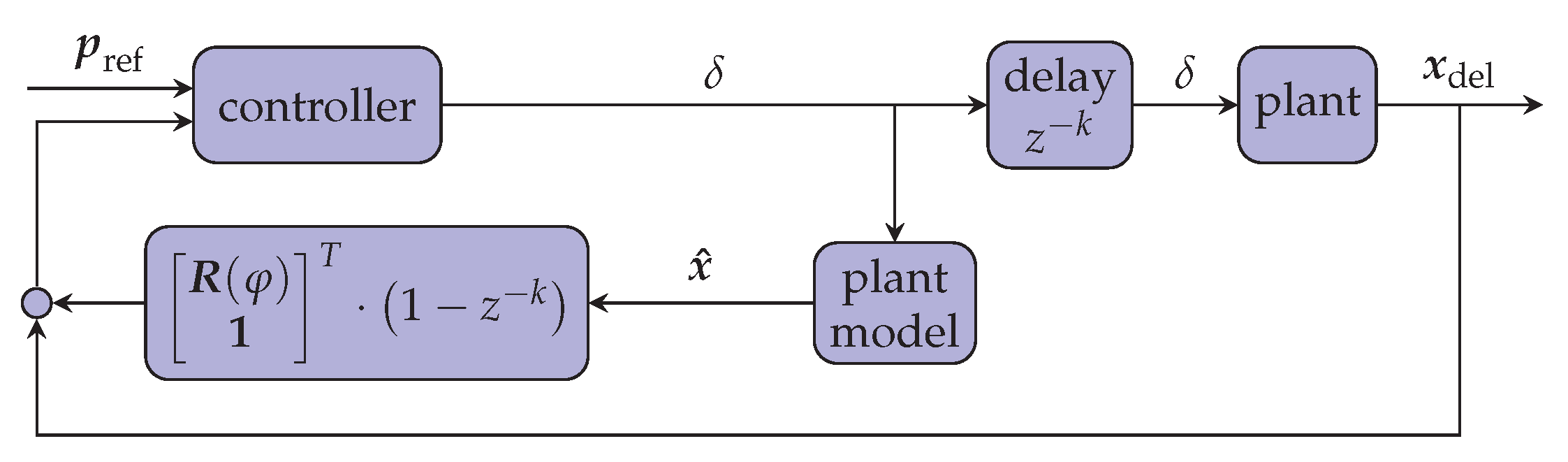
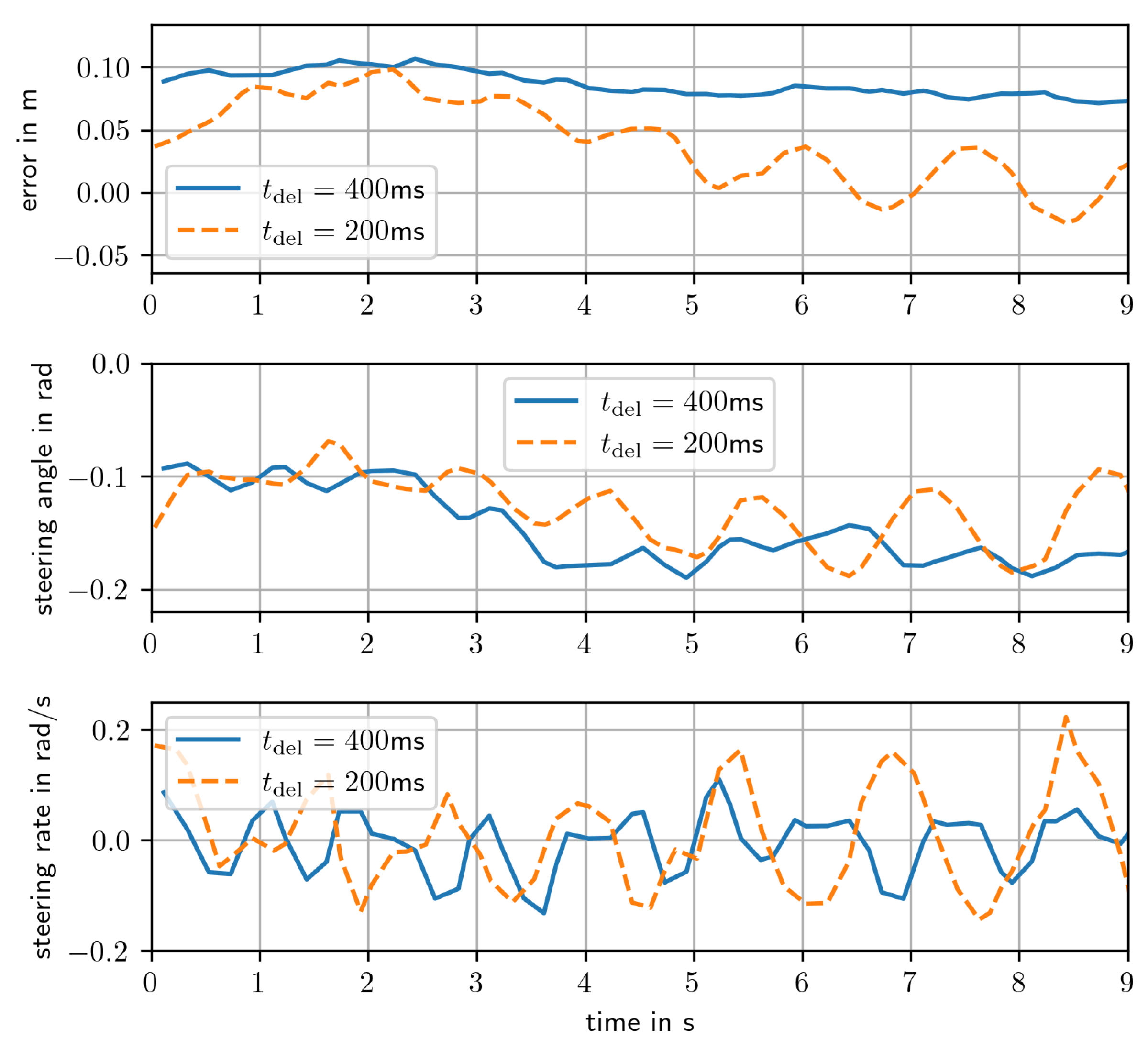
4.1. Dead-Time Compensation

Due to delays in the actuation system, interfaces, and components, there is a total dead time $t_{\mathrm{del}}$ of more than 150 ms in the closed loop system. To compensate this, we apply the kinematic-based prediction method presented in [25]. The structure is similar to the Smith predictor [26], but the estimated prediction vector is transformed by the measured orientation of the vehicle to compensate for divergence of the plant model and the real plant. The structure is shown in Figure 9. The state estimate $\widehat{\mathit{x}}=\left[\begin{array}{cc}\widehat{\mathit{p}}& \widehat{\psi }\end{array}\right]$ follows the plant model:

$$\begin{array}{cc}\hfill {\widehat{\mathit{p}}}_{i+1}& ={\widehat{\mathit{p}}}_i+{\displaystyle \frac{\mathit{R}\left({\widehat{\psi }}_i\right)}{{\dot{\psi }}_i}}·\left[\begin{array}{c}sin({\dot{\psi }}_i·\Delta t)\\ 1-cos({\dot{\psi }}_i·\Delta t)\end{array}\right]·v_i\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill {\widehat{\psi }}_{i+1}& ={\widehat{\psi }}_i+{\displaystyle \frac{tan{\widehat{\delta }}_i}{\lambda }}·v_i·\Delta t\hfill \end{array}$$

(8b)

where $\mathit{R}(·)$ is the rotation matrix, $\Delta t$ is the discrete time step, v is the longitudinal velocity, and i is the index progressing in time $i=\lfloor t/\Delta t\rfloor$.

According to [25] and as illustrated in Figure 9, the dead-time-compensated vehicle state (the output of the dead-time compensator) $\mathit{y}$ is the delayed (measured) vehicle state ${\mathit{x}}_{\mathrm{del}}$ plus the state prediction based on the estimated state $\widehat{\mathit{x}}$:

$${\mathit{y}}_i={\mathit{x}}_{\mathrm{del},\mathit{i}}+{\left[\begin{array}{c}\mathit{R}({\widehat{\psi }}_i-{\psi }_i)\\ 1\end{array}\right]}^T·({\widehat{\mathit{x}}}_{\mathrm{del},i+k}-{\widehat{\mathit{x}}}_{\mathrm{del},i})$$

(9)

where k relates to the dead time $k=\lfloor t_{\mathrm{del}}/\Delta t\rfloor$. This predicted state is used to compute e and $\psi$ for the control law in Equation (4). The dead-time compensation achieved the best results with a compensation of $t_{\mathrm{del}}=400$ ms.

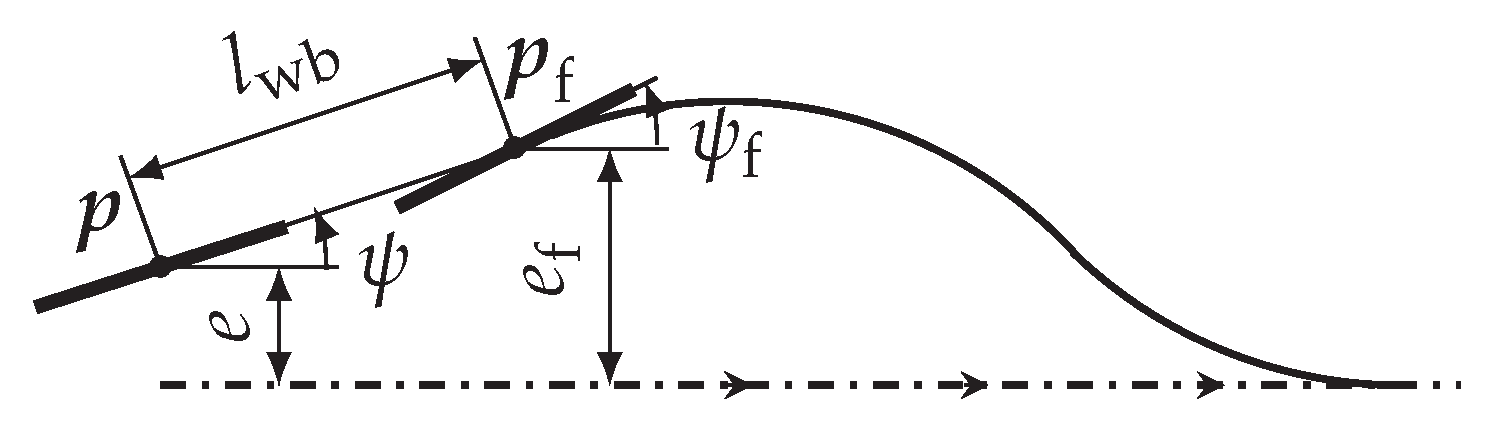
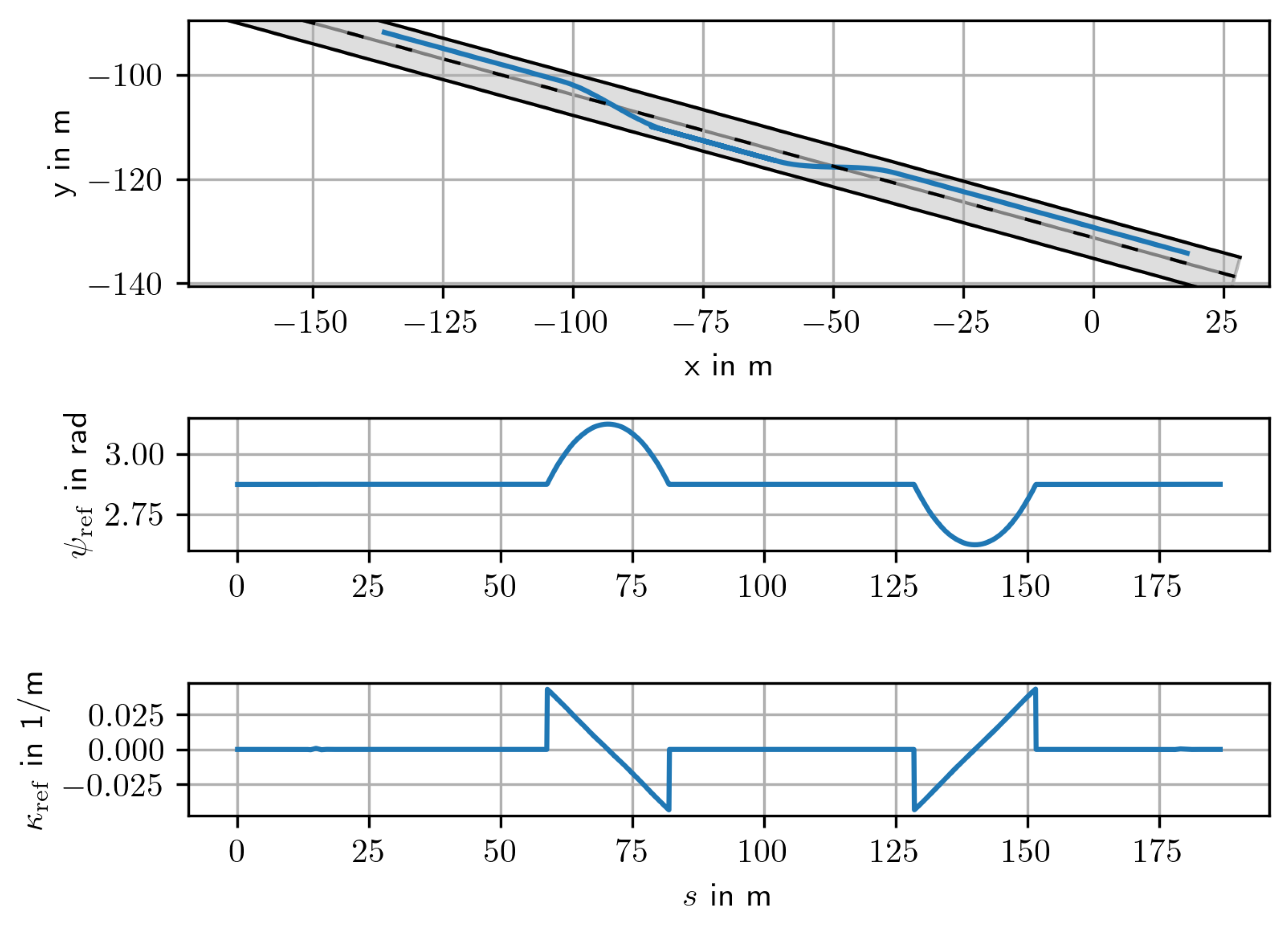
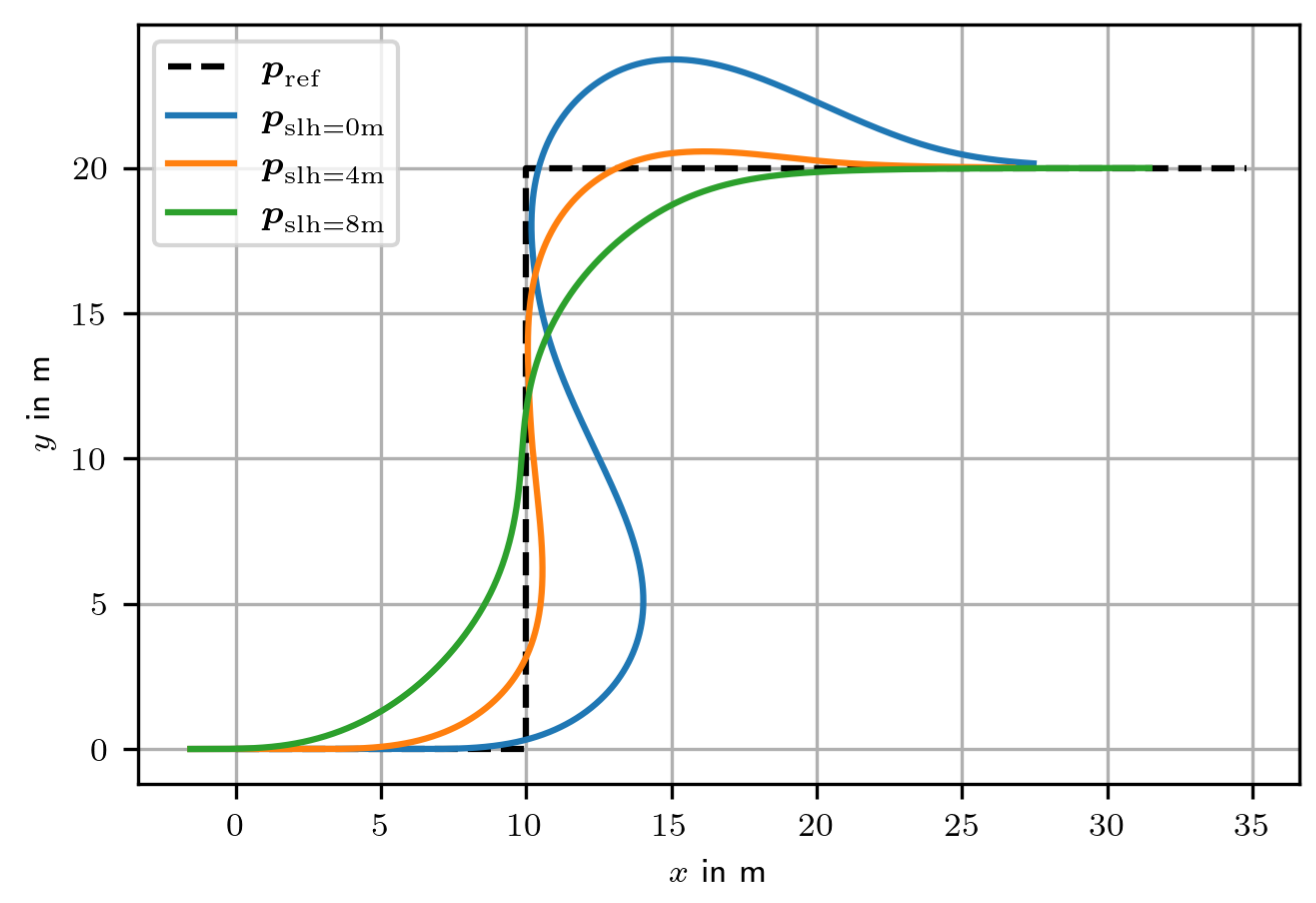
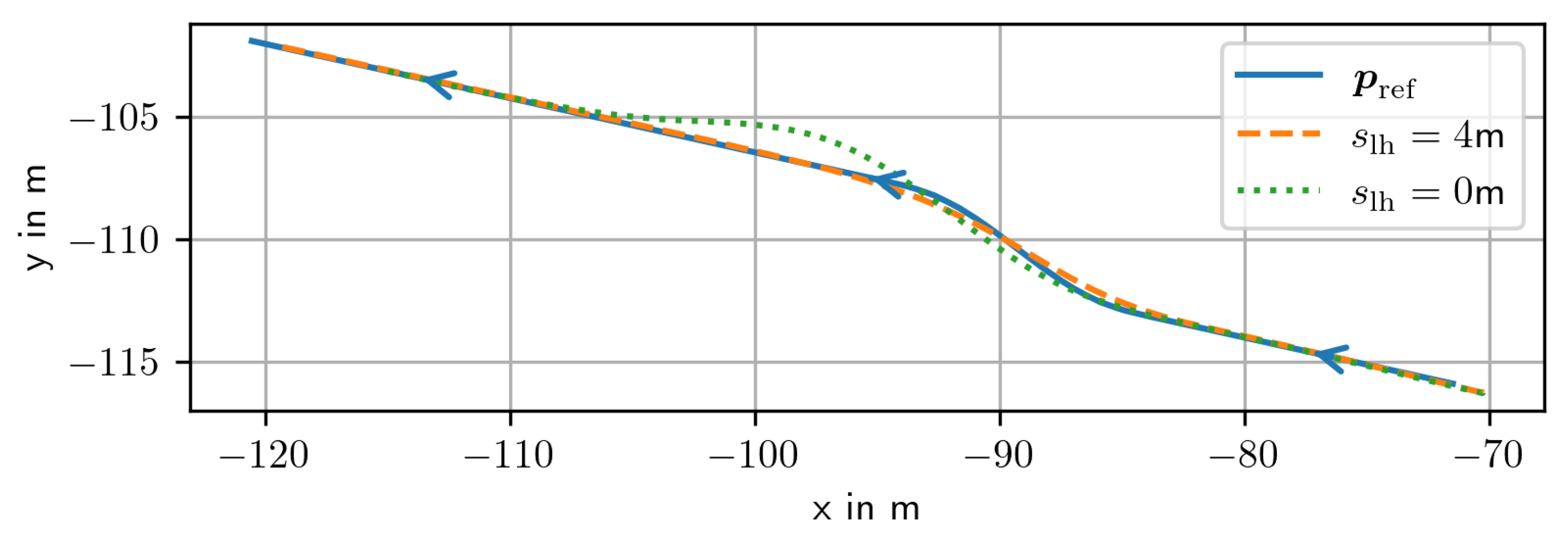
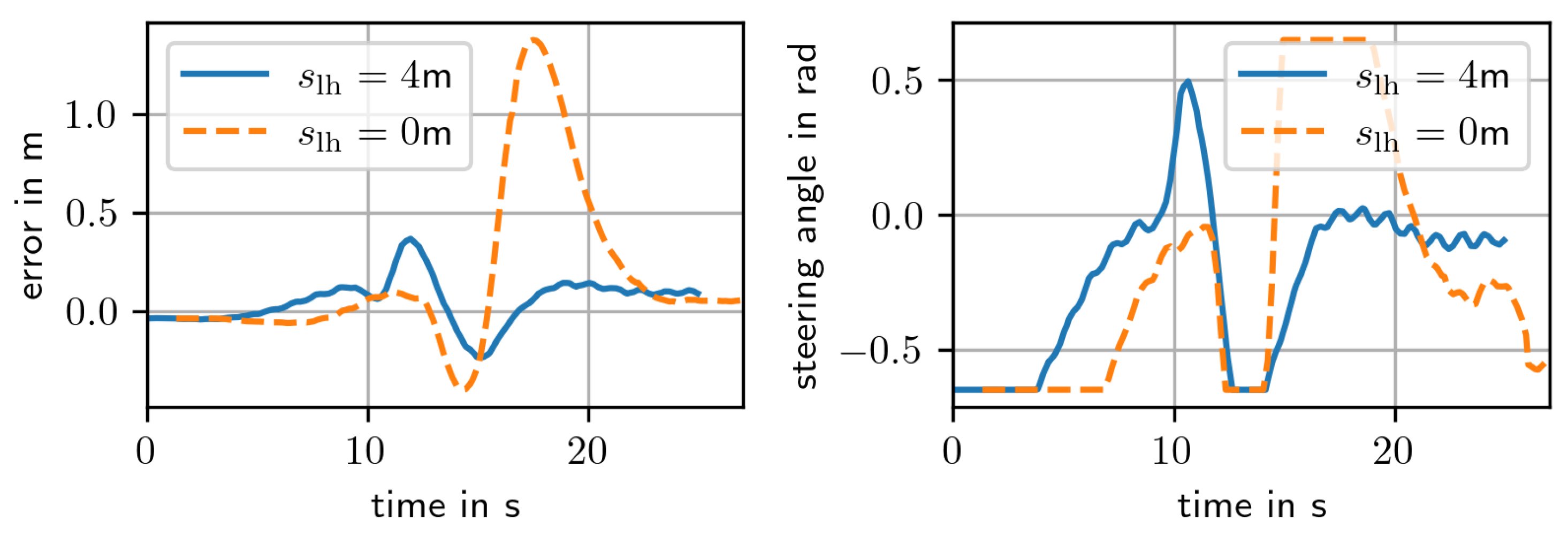
4.2. Look-Ahead Distance

With dead-time compensation, the controller can react to disturbances and changes in path geometry in time. However, if the path geometry does not satisfy the continuity constraints resulting from the steering constraints (i.e., if the path does not have continuous, bounded curvatures or changes in curvature), the vehicle will still be unable to follow the path. To improve tracking behavior for discontinuities in paths, we introduce a look-ahead system. The effect of this is shown in Figure 10, providing an example of a path with a discontinuous orientation. Without a look-ahead distance, the controller only responds to changes in path orientation once the vehicle has reached the edge of the path. With a look-ahead distance, however, the controller reacts earlier, creating a path with low or no overshoot.

The look-ahead distance $s_{\mathrm{lh}}$ is a constant value measured along the reference path. From the new reference position $p_{\mathrm{ref}}$ the control errors e and $\psi$ are computed as before. This is illustrated in Figure 11. A look-ahead distance of 4 m was determined empirically for the present application.

4.3. Summary of Adaptions

The controller presented in Section 2 is adapted to compensate dead time and to handle discontinuities in the reference path. The final structure of the controller with adaptions is shown in Figure 12. As described in Section 3.1, the output of the controller, i.e., the input into the steering system, is the steering angle $\delta$. Therefore, the control signal $\ddot{\delta }$ is integrated in time. The dead-time compensation module predicts the movement of the vehicle to compensate the dead time in the plant (the actuation and measurement system). From the resulting state estimate $\mathit{x}+\Delta \mathit{x}$, the tracking error ${\left[\begin{array}{cc}e& \psi \end{array}\right]}^T$ is calculated, incorporating the look-ahead distance.

5. Parameter Tuning and Test Results

Test drives are conducted in the real vehicle to determine the appropriate values for the tuning parameters. After that, the final tests in the double-lane-change maneuver are conducted. The three tuning parameters are as follows:

1.

The dead time to be compensated $t_{\mathrm{del}}$: Rather than determining the actual dead time in system tests, we conduct tests to directly determine the optimal time estimate for compensating for dead time.

2.

The look-ahead distance $s_{\mathrm{lh}}$: The optimal distance depends on the geometry of the reference path and is therefore determined in a representative maneuver.

3.

The maximum steering acceleration $\ddot{\delta }$: To increase smoothness, steering acceleration can be limited at the cost of control performance. While a theoretical optimum has been discussed in [19], robustness to model parameters proves to be more relevant in reality.

5.1. Compensated Dead Time

The controller is evaluated on a straight reference path, with the steering signal only compensating for disturbances. When the dead time is not estimated correctly, constant oscillations will occur. In Figure 13 the result of two test drives is shown. While the steering rate oscillates in both cases, with a correct estimate of the dead time ($t_{\mathrm{del}}=400$ ms), the oscillations in the steering angle and tracking error are significantly reduced. Note that the tracking error is unequal to zero because of the error in orientation measurement, as discussed in Section 3.3.

5.2. Look-Ahead Distance

The lane-change maneuver involves a jump in the curvature of the reference path. To react to this in time, a look-ahead distance is required. When the value chosen is too large, the controller is cutting corners, while a value too small leads to overshooting and can even destabilize the controller. In Figure 14, a test drive of a lane-change maneuver with and without look-ahead distances is shown. Without a look-ahead distance, the controller only reacts to the lane change when the reference path has already changed. The first change in curvature leads to a control error such that the second change in curvature (back to straight on the new lane) creates a saturation of the steering angle and an even larger overshooting of the vehicle, as shown in Figure 15. With a look-ahead distance, the controller reacts 3 s ahead in time, resulting in a small cutting corner effect of $0.36$ m and an overshoot below $0.05$ m.

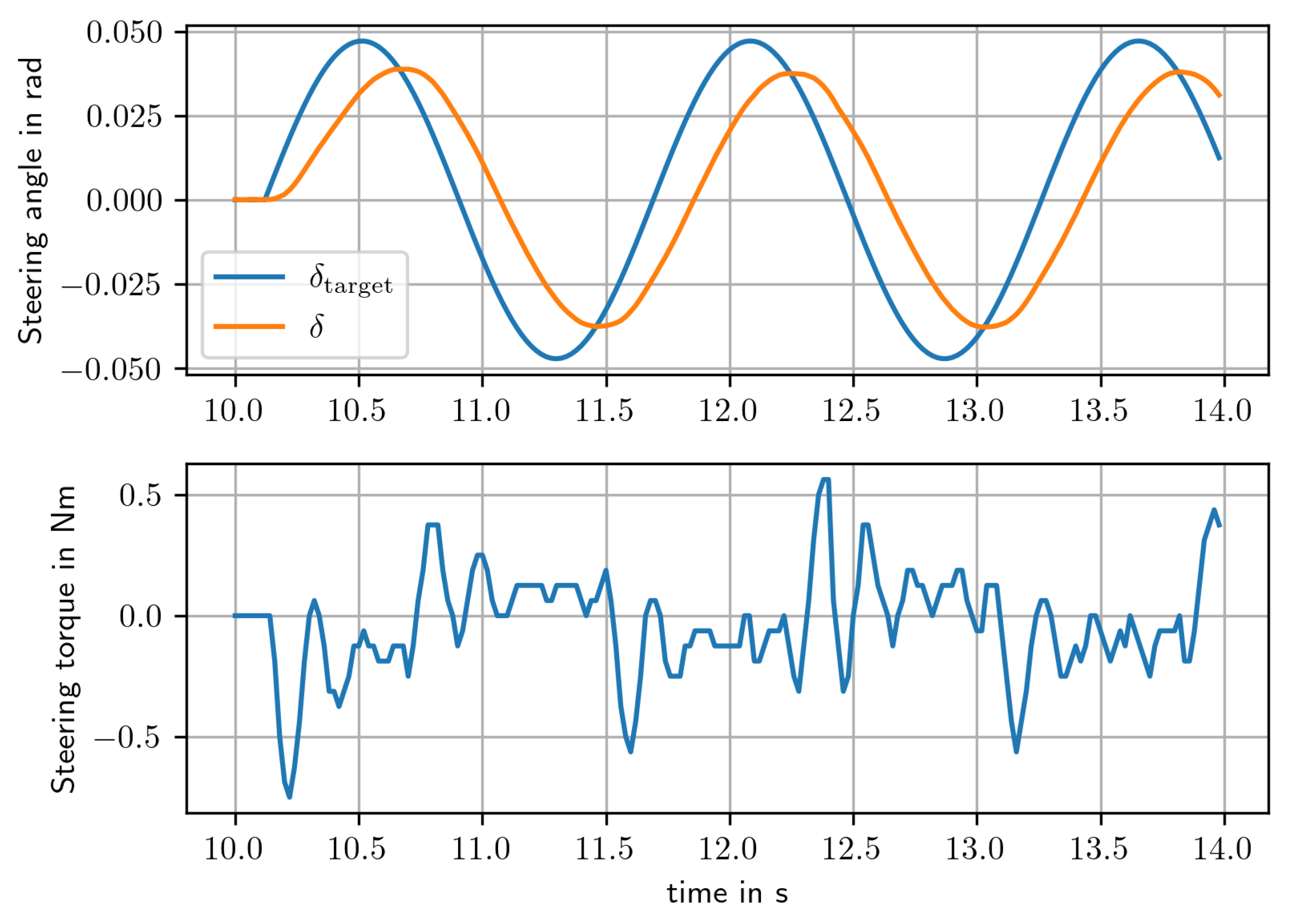
5.3. Maximum Steering Acceleration

As is visible in Figure 13 and Figure 15, even though the dead time is optimally compensated, there are still oscillations in the steering angle. While this does not impair the tracking error, the comfort and driver acceptance are significantly reduced. To solve this problem, we significantly increase the maximum steering acceleration.

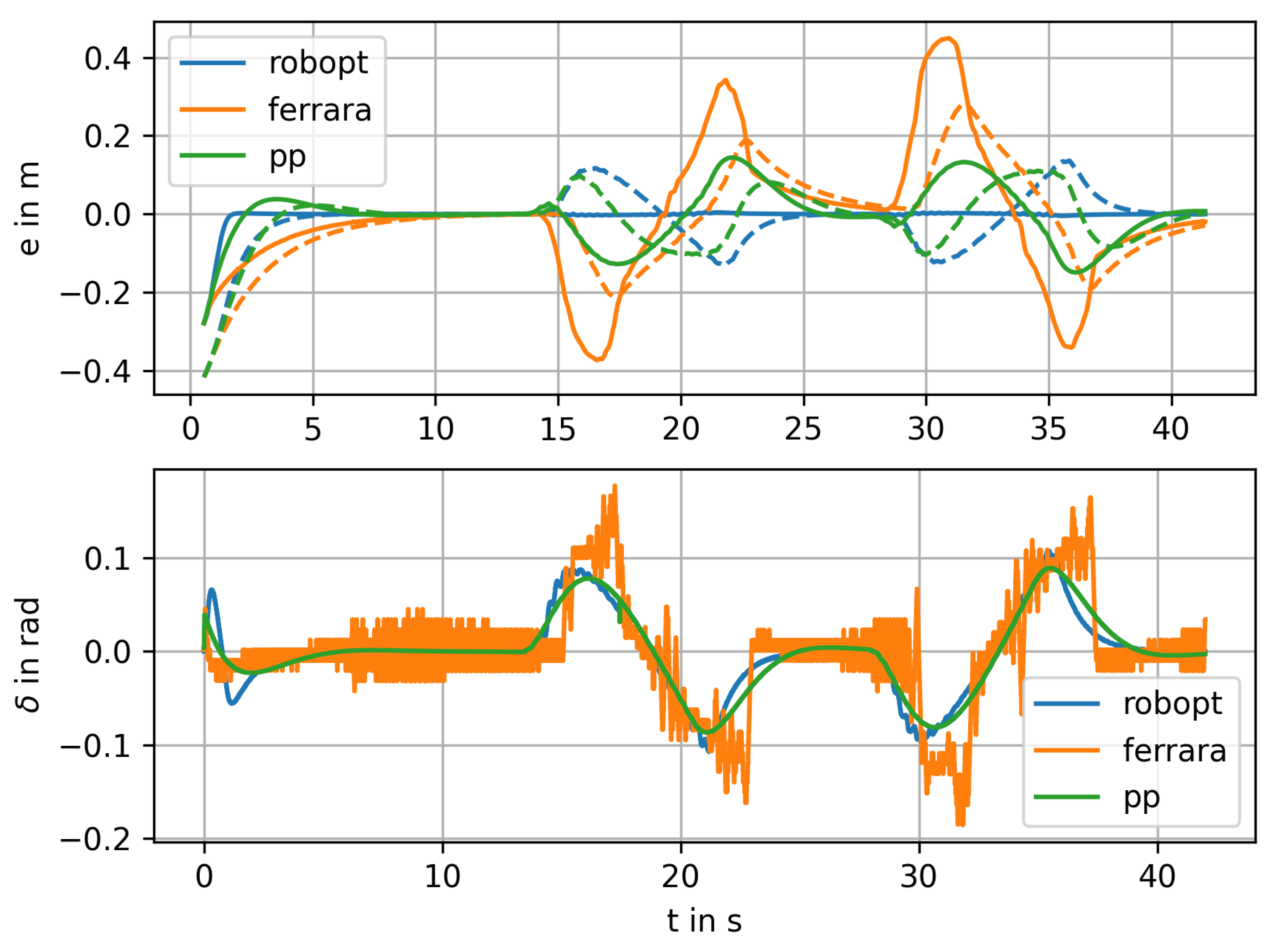
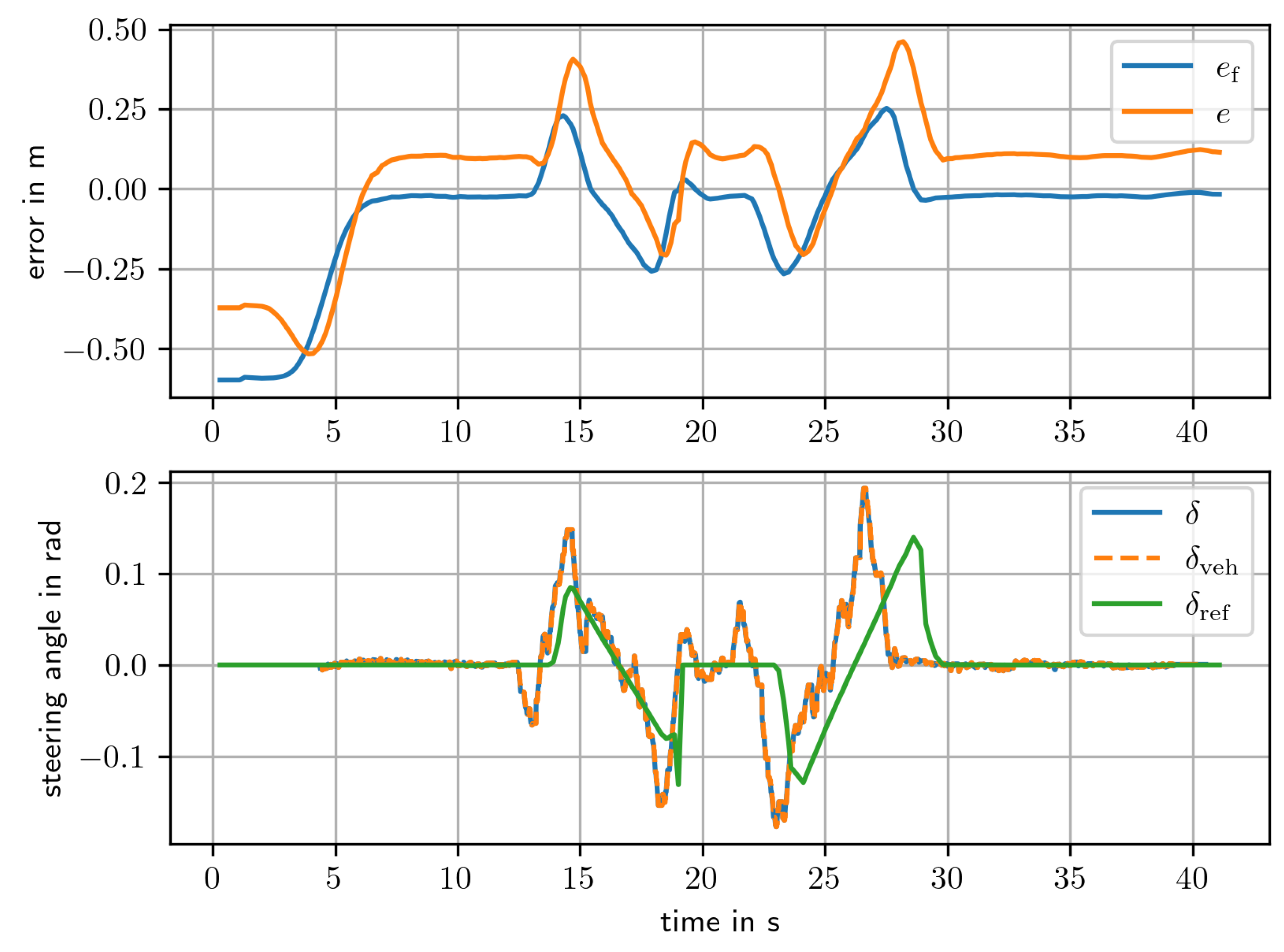
5.4. Final Tests

For the final test, the vehicle is manually positioned close to the reference path. Then, the AD system is activated, and the double-lane-change maneuver is manually triggered. The results of the double-lane-change maneuver are shown in Figure 16. The vehicle starts with an initial offset of approximately $0.5$ m from the path, approaching it with the front wheel within $3.4$ s (approximately $10.2$ m) without overshooting. During the lane change, the front wheel reaches a maximum error of $0.27$ m. Throughout the test, the steering angle remains well below its maximum, while the steering rate reaches its maximum of $27.0$ deg/s multiple times.

Due to the dead-time compensation and the look-ahead distance, the steering angle $\delta$ leads the reference paths’ curvature and the corresponding reference steering angle, with ${\delta }_{\mathrm{ref}}=arctan\left({\kappa }_{\mathrm{ref}}·\lambda \right)$. It is also interesting to note that the profile of the reference steering angle differs from the reference curvature shown in Figure 16 due to the linear approximation of the polynomial curve. The steering rate ${\delta }^{\prime }$ remains within the specified range except for the initial value. The actual initial steering angle is not known to the controller, so it is set to the desired value. This occurs immediately and at one other point in time, which may be the result of numeric errors due to discrete-time differentiation.

6. Discussion and Conclusions

In this section, the presented work is summarized, the novel contributions are highlighted, and an outlook of future work is given.

6.1. Summary

In [20] the concept of a robust controller based on the Dubins-optimal path has been theoretically analyzed. In [19], this controller has been extended to fit real-world applications in a car-like vehicle. By introducing continuity and constraints of the steering signal, the controller not only becomes applicable, but also tunable regarding comfort, tracking behavior, and robustness at different velocities.

In this present work, real-world validation is conducted by integrating the controller into an AD system. However, important aspects have still not been handled. Real vehicle tests show that dead time in the control loop leads to significant oscillations in the steering signal and thus the vehicle path. The vehicle reacts to discontinuous changes in the reference path too late, causing unnecessary overshoot.

By adding dead-time compensation and a look-ahead distance, these problems can be overcome. Each feature comes with one parameter that is tuned once, is based on simple driving tests, and seems to fit well for all subsequent driving tests. While the $C^1$ smooth steering angle is necessary to overcome the chattering effect in the steering signal, tests showed that limiting the steering acceleration leads to low-frequency oscillations in the steering signal that indeed do not impair the tracking behavior but decrease the driver acceptance. By setting the steering acceleration limit to large values, the steering behavior looks more normal.

Finally, after tuning three intuitive parameters (dead time, look-ahead distance, and steering acceleration), the controller with the $C^1$ smooth steering angle and dead-time compensation successfully performs the double-lane-change maneuver despite disturbances such as steering delays and pose measurement errors.

6.2. Contributions

This work bridges theory and practice by demonstrating how a theoretically sound controller can be adapted to meet real-world demands. Building upon the robust, Dubins-based optimal controller introduced in [20] and its subsequent extension for real-world applicability in [19], this paper’s primary contribution is the development and validation of a practical implementation framework that overcomes critical real-world challenges.

Our novel contributions are threefold:

1.

We introduced and validated a dead-time compensation method that directly mitigates system latency, a primary source of steering oscillation and instability in automated vehicles.

2.

We implemented a look-ahead mechanism that enables the controller to proactively handle disturbances such as discontinuous reference paths, preventing excessive overshoot and improving safety.

3.

We established an intuitive, three-parameter tuning procedure (for dead time $t_{\mathrm{del}}$, look-ahead distance $s_{\mathrm{lh}}$, and maximum steering acceleration $\ddot{\delta }$) that transitions the controller from a theoretical model to a robust system optimized for real-world performance and passenger comfort.

6.3. Outlook

Despite the successful results presented, this study has limitations that outline pathways for future work. The validation was conducted using a single maneuver (the double-lane-change maneuver) at a fixed speed. Future work must include more diverse scenarios, such as winding roads, longer-duration drives, and a wider range of speeds, to fully characterize the controller’s performance and parameter sensitivity. Furthermore, while the system showed robustness to existing measurement errors, a more extensive evaluation of disturbance effects is needed.