Modeling of Malware Propagation in Wireless Mobile Networks with Hotspots Considering the Movement of Mobile Clients Based on Cosine Similarity
Abstract
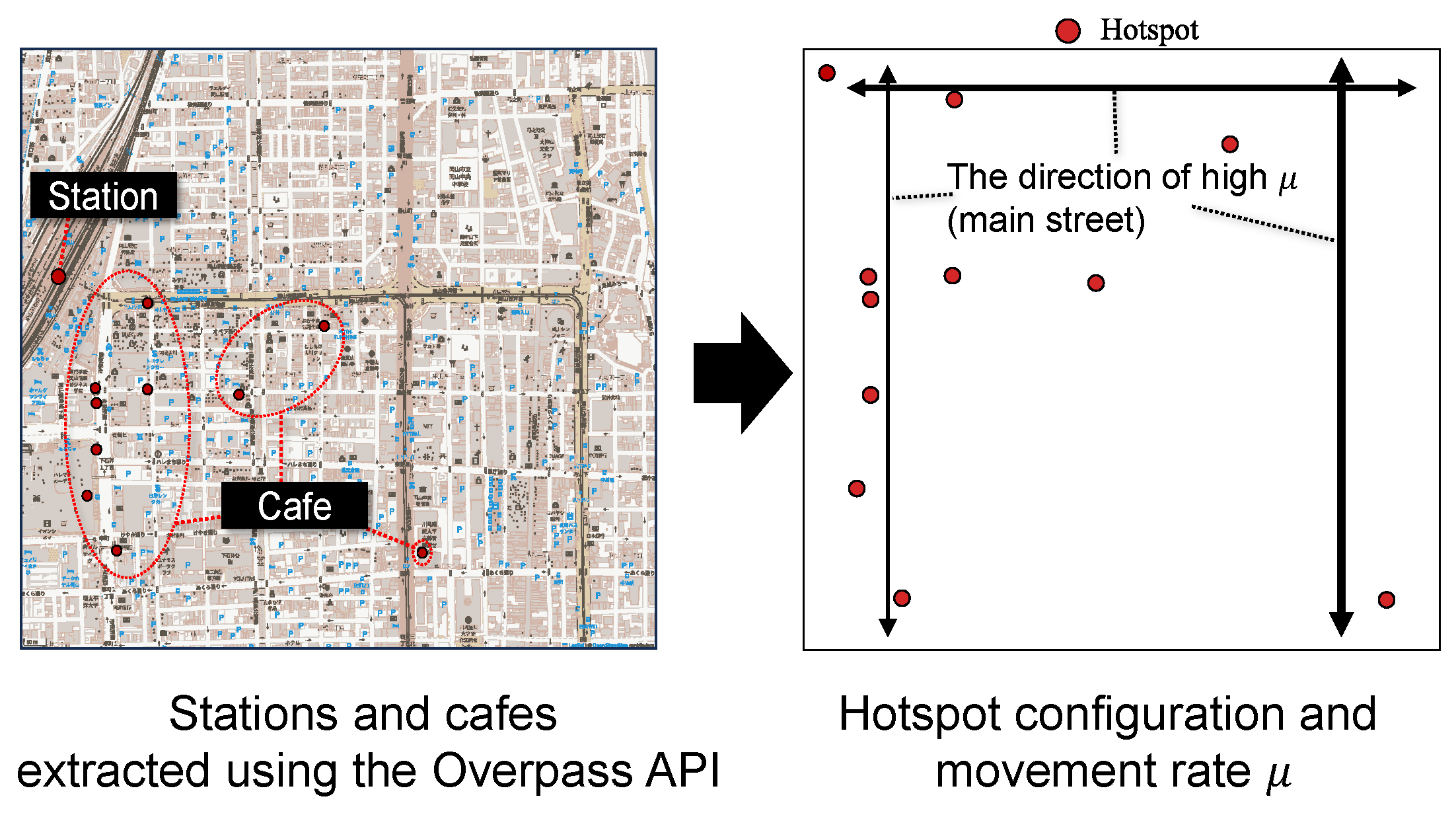
1. Introduction
- We propose a novel deterministic epidemic model that incorporates non-uniform mobility influenced by the presence of hotspots, addressing the limitations of existing models based on uniform movement assumptions.
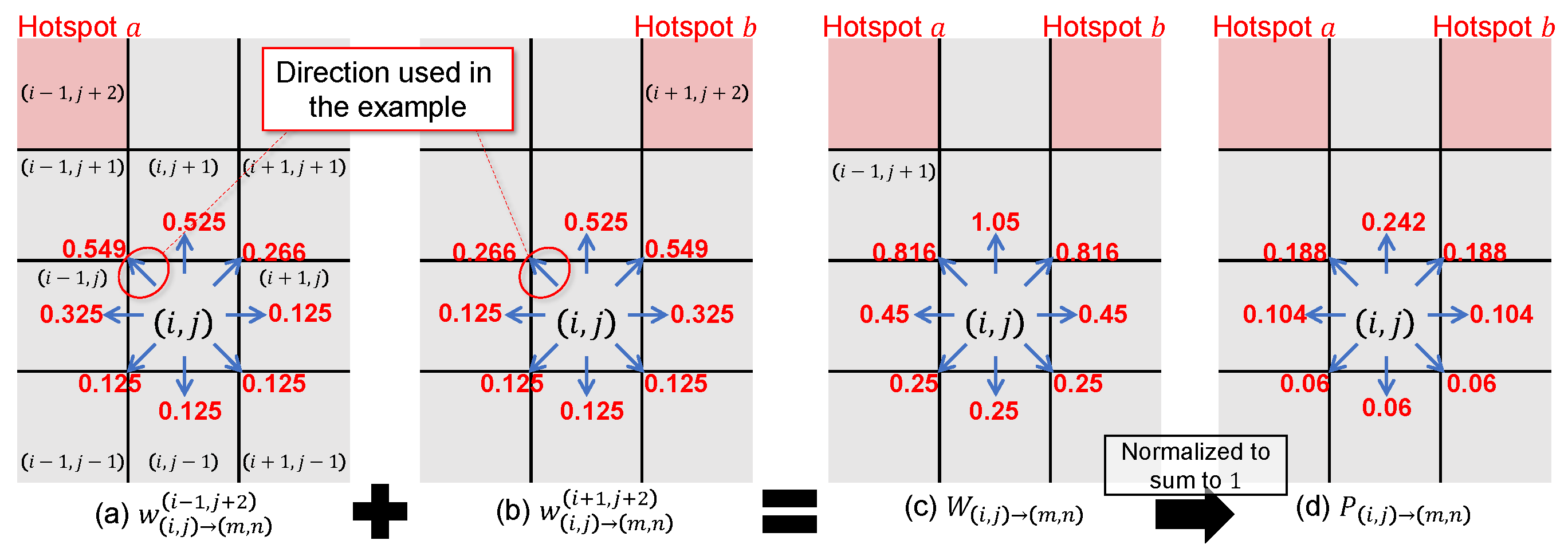
- We introduce a location-dependent mobility mechanism using cosine similarity to model the directional tendency of mobile hosts toward nearby hotspots in a mathematically tractable manner.
- We formulate a system of ODEs that integrates the proposed mobility model to analyze the dynamics of malware propagation in hotspot-influenced environments.
- Through numerical experiments, we demonstrate that the proposed model captures malware spreading behavior in mobile scenarios with hotspots.
2. Related Work
2.1. Evolution of Cyber Attacks
2.2. Epidemic Model
2.3. Mobility Modeling and Cosine Similarity
3. System Model
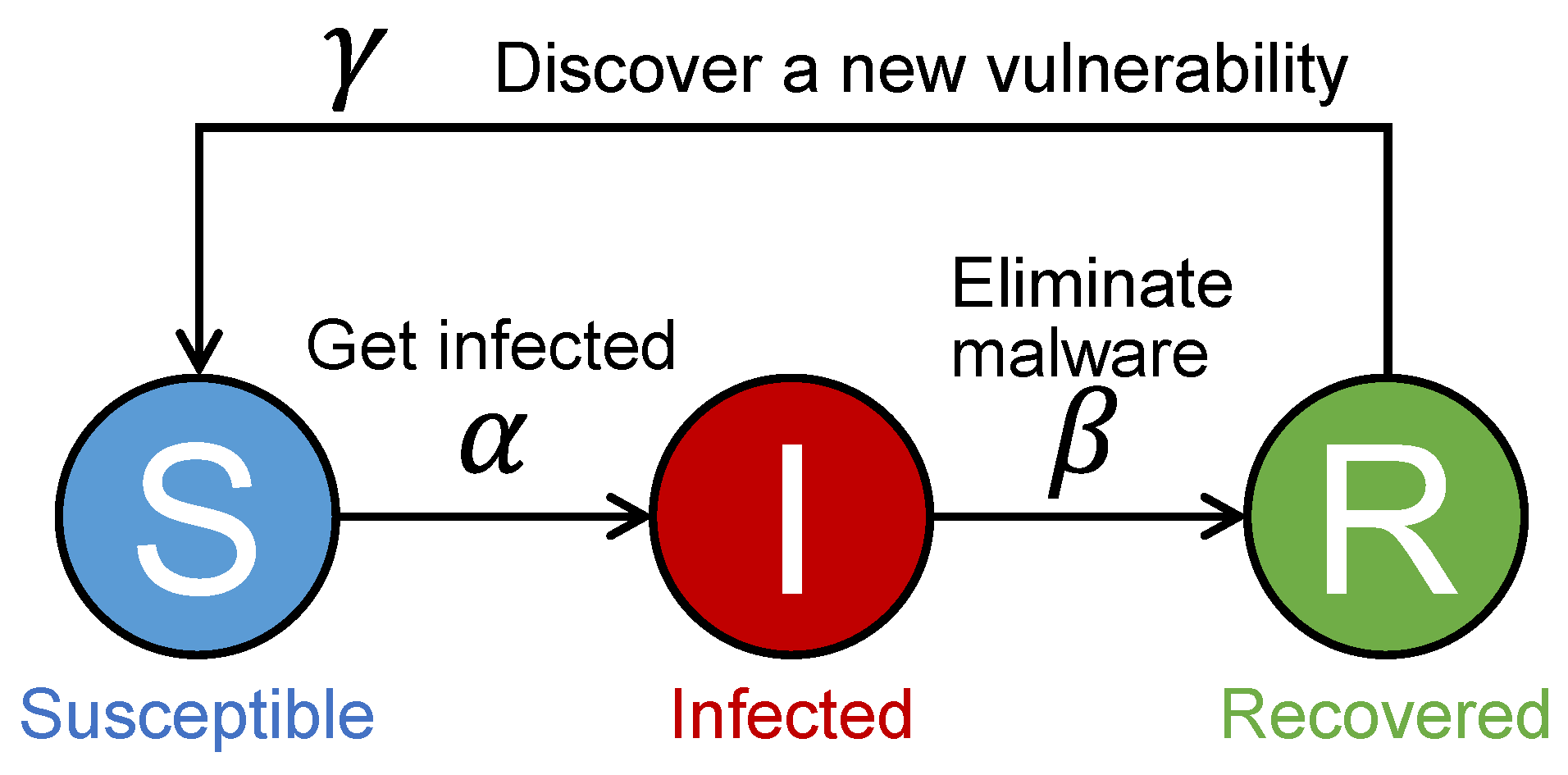
3.1. Standard SIRS Model
- Susceptible hosts become infected with the malware through contact with infected hosts and transition to state I.
- Infected hosts eliminate the malware from themselves and then transition to state R.
- Recovered hosts become susceptible again due to the discovery of a new vulnerability and transition to state S.
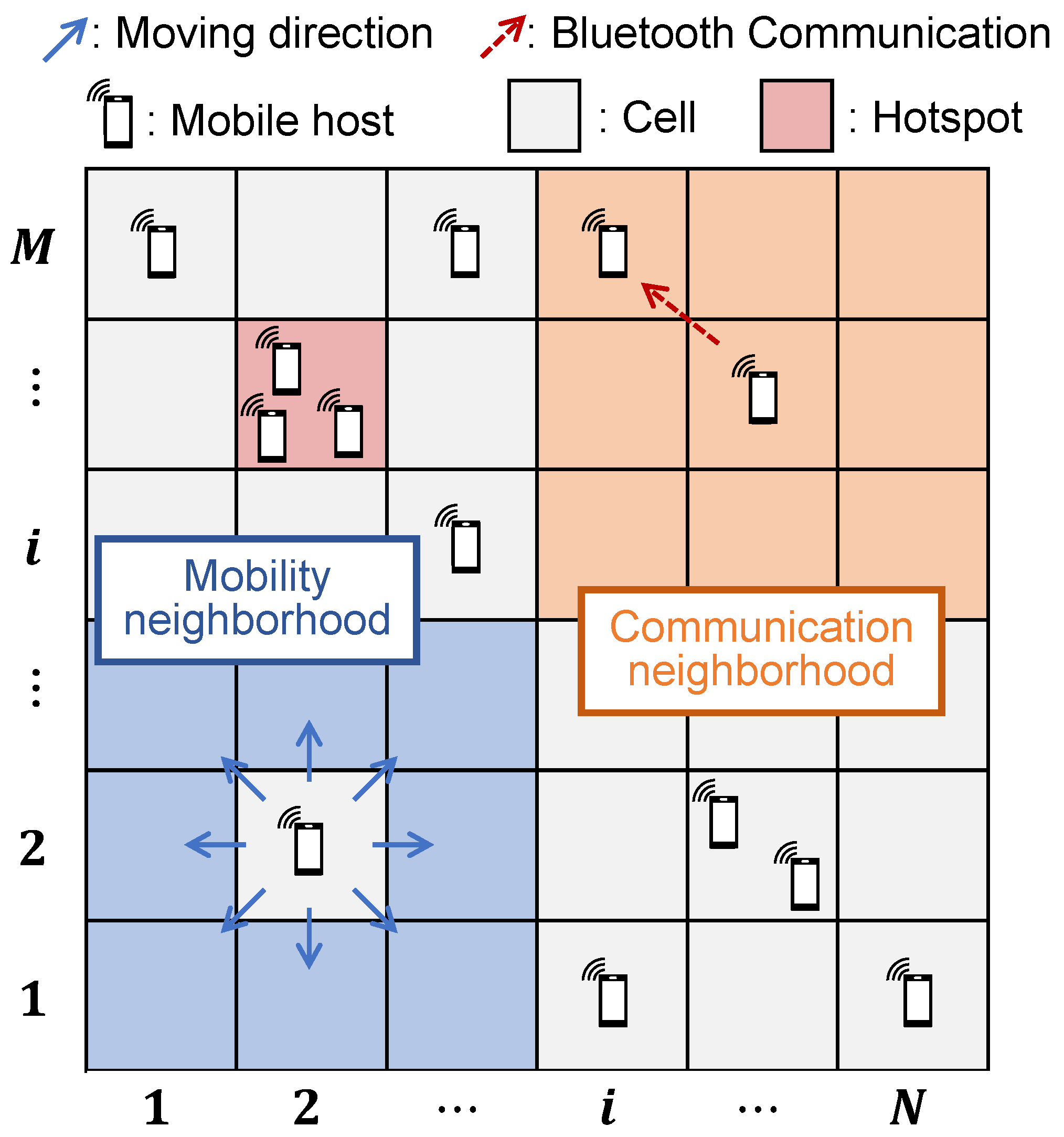
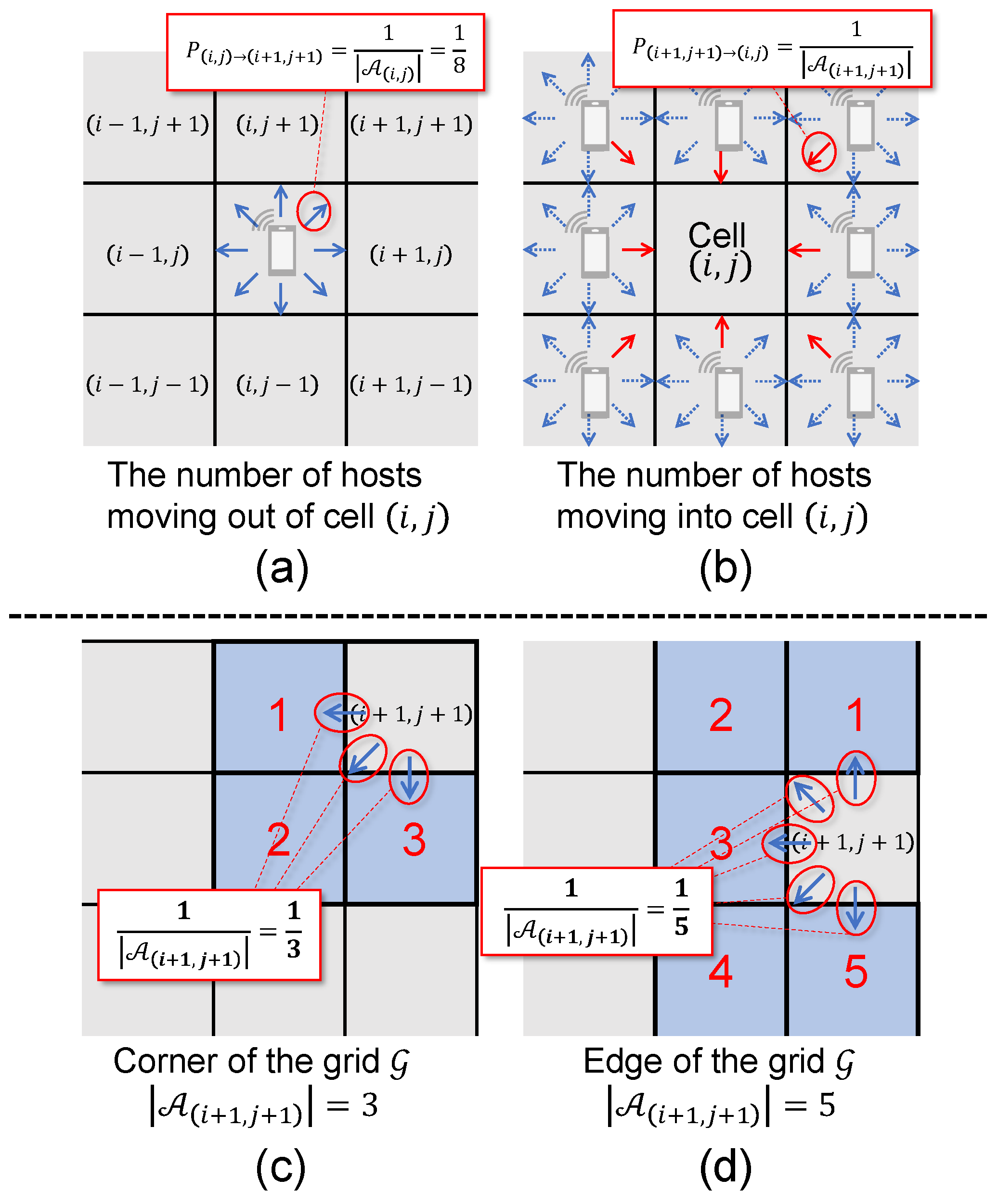
3.2. Mobility and State Transition Model
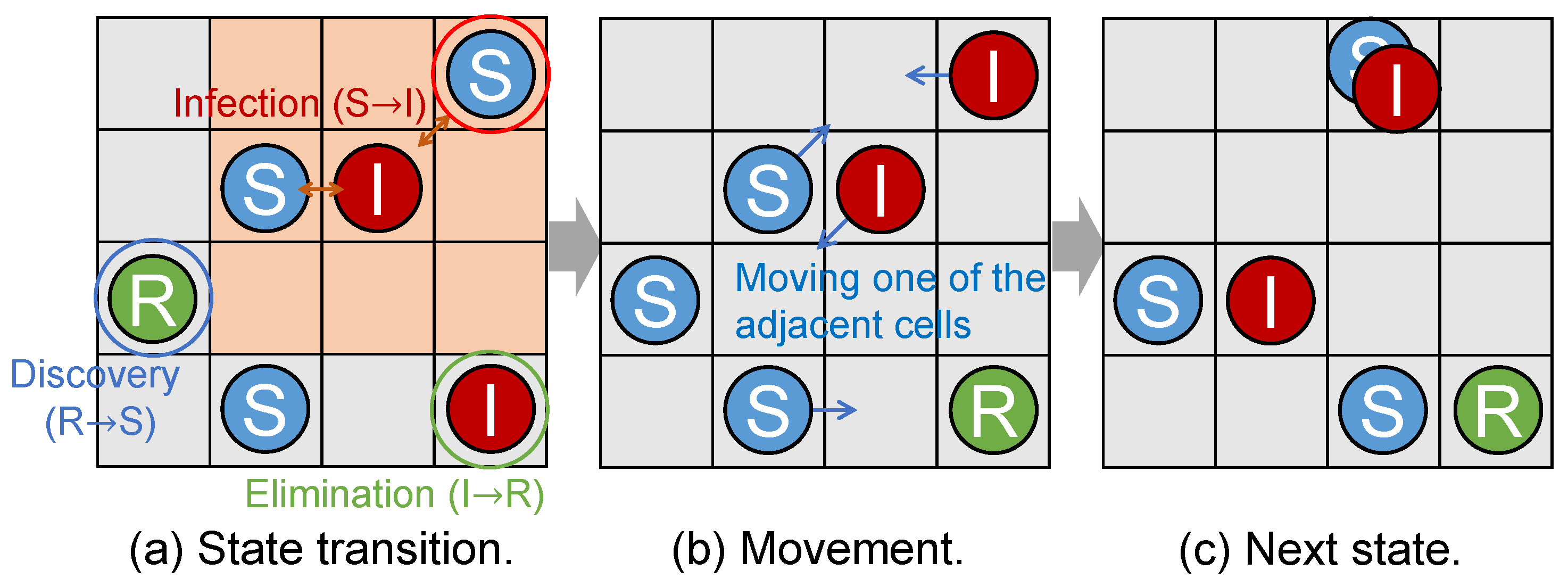
- (1)
- An infected host located at cell infects a susceptible host located in its neighborhood according to a Poisson process with the infection rate . The susceptible host transitions to the infected state.
- (2)
- An infected host eliminates the malware according to a Poisson process with the elimination rate . The infected host transitions to the recovered state.
- (3)
- A recovered host becomes susceptible again due to the discovery of a new vulnerability according to a Poisson process with the elimination rate . The recovered host transitions to the susceptible state.
- (4)
- A host located at cell moves to one of adjacent cells according to a Poisson process with the moving rate . The destination cell is selected based on movement strategies discussed later.
4. Proposed Epidemic Model
4.1. Epidemic Model of Malware Propagation on Mobile Hosts
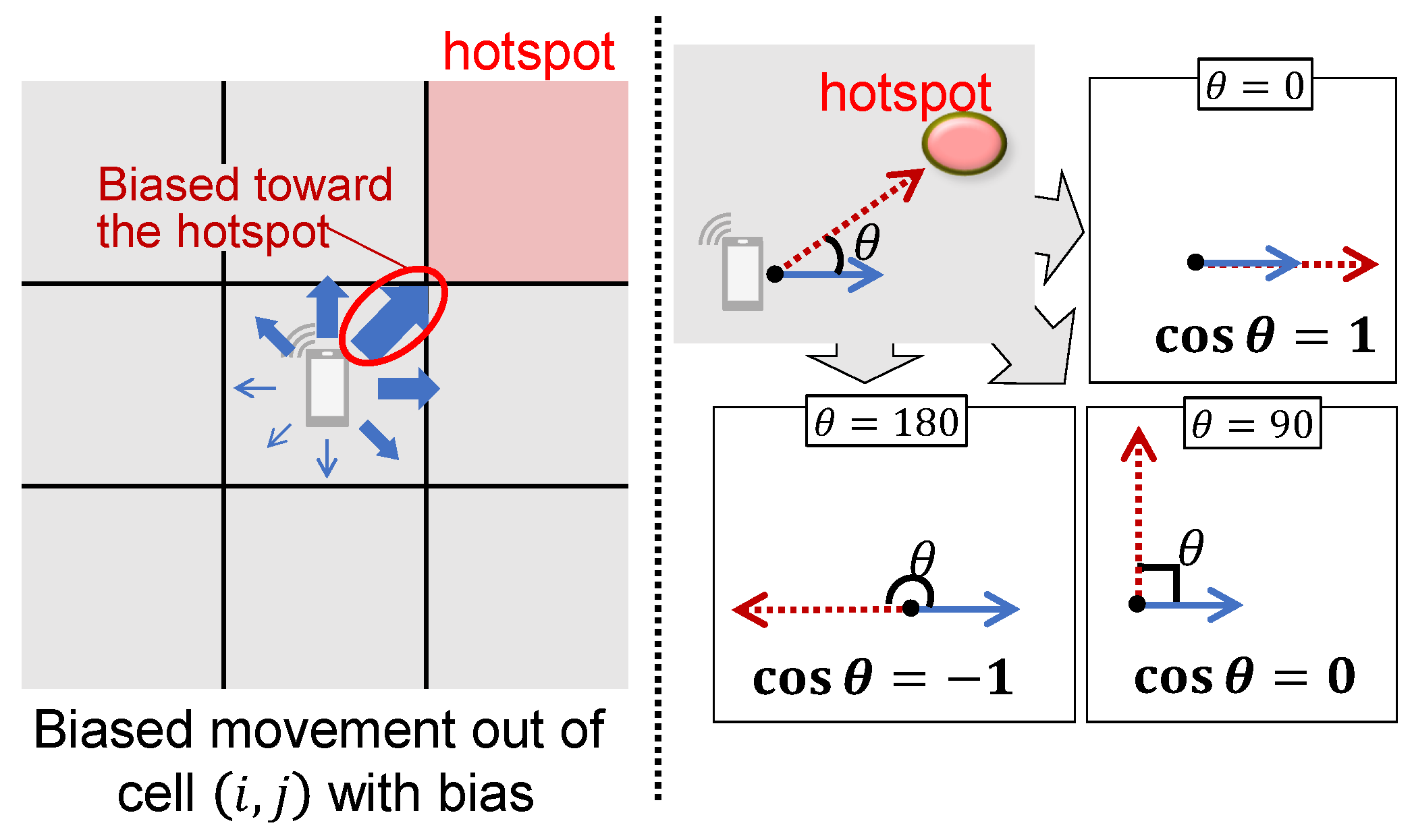
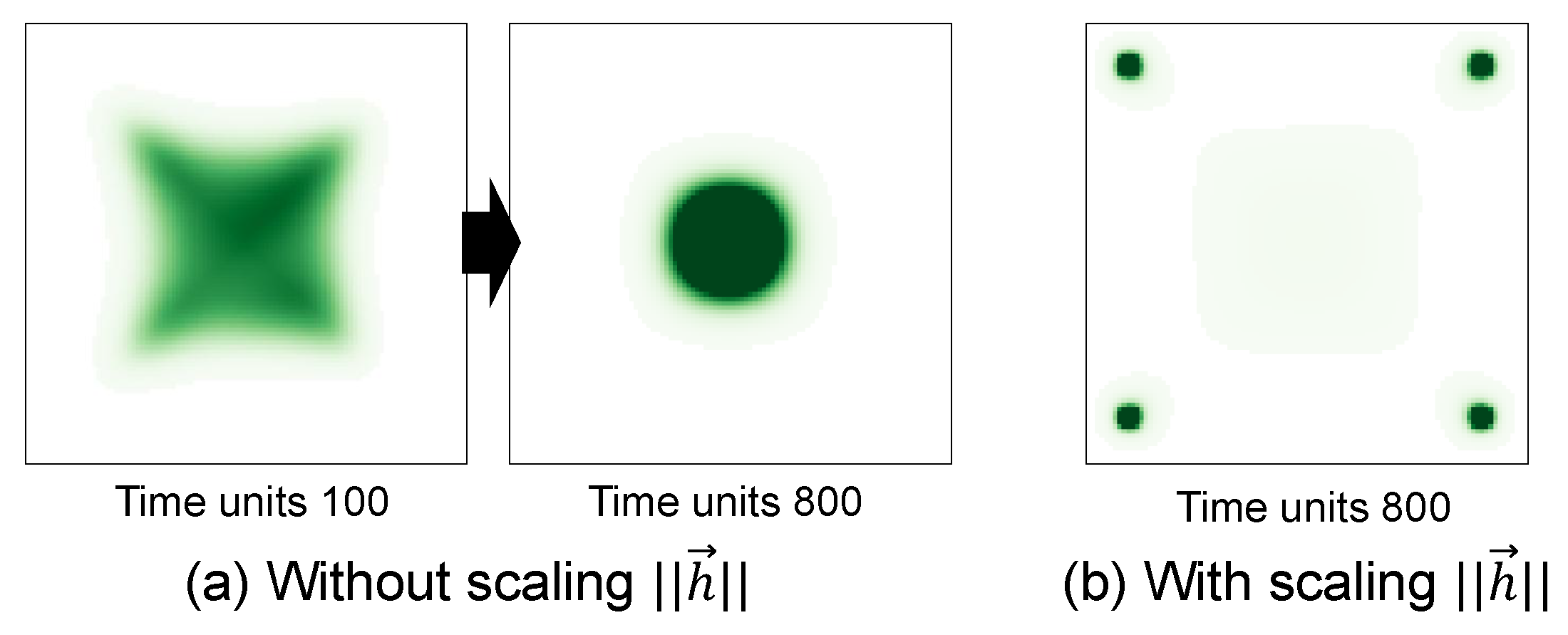
4.2. Movement Strategy
4.2.1. Random Movement Strategy
4.2.2. Hotspot-Aware Movement Strategy
5. Numerical Evaluations
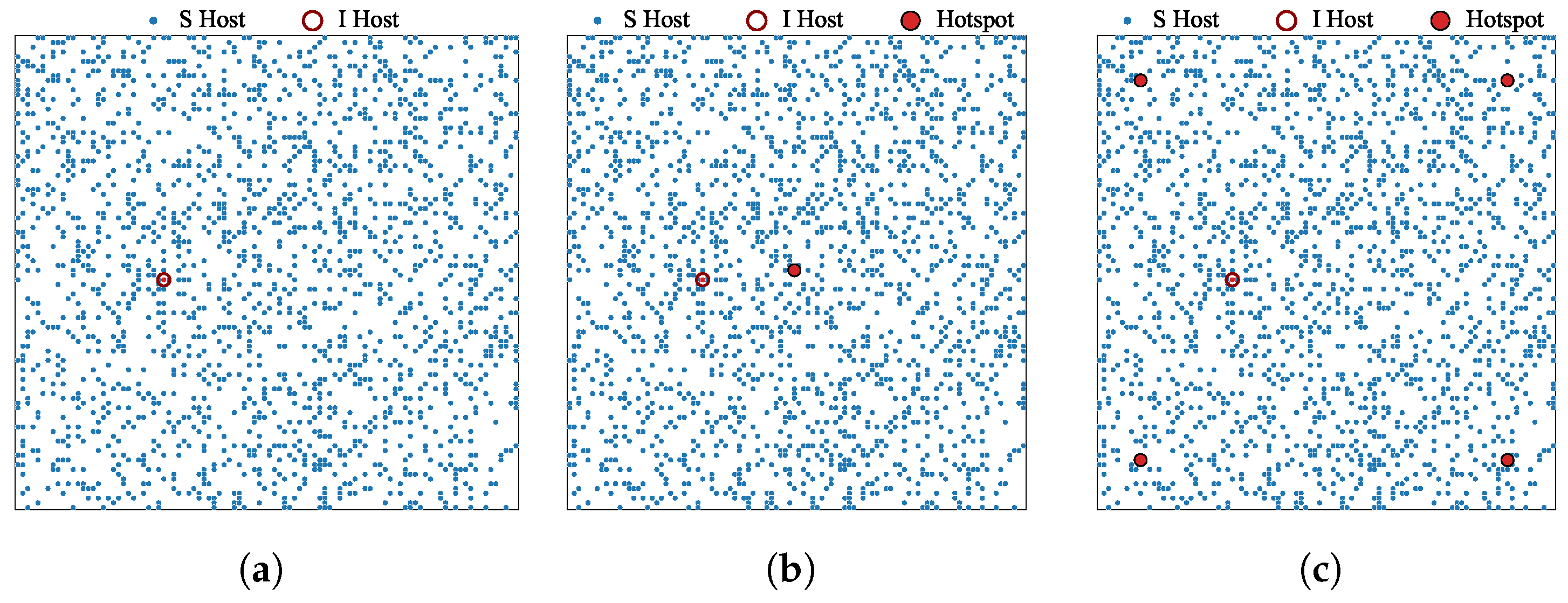
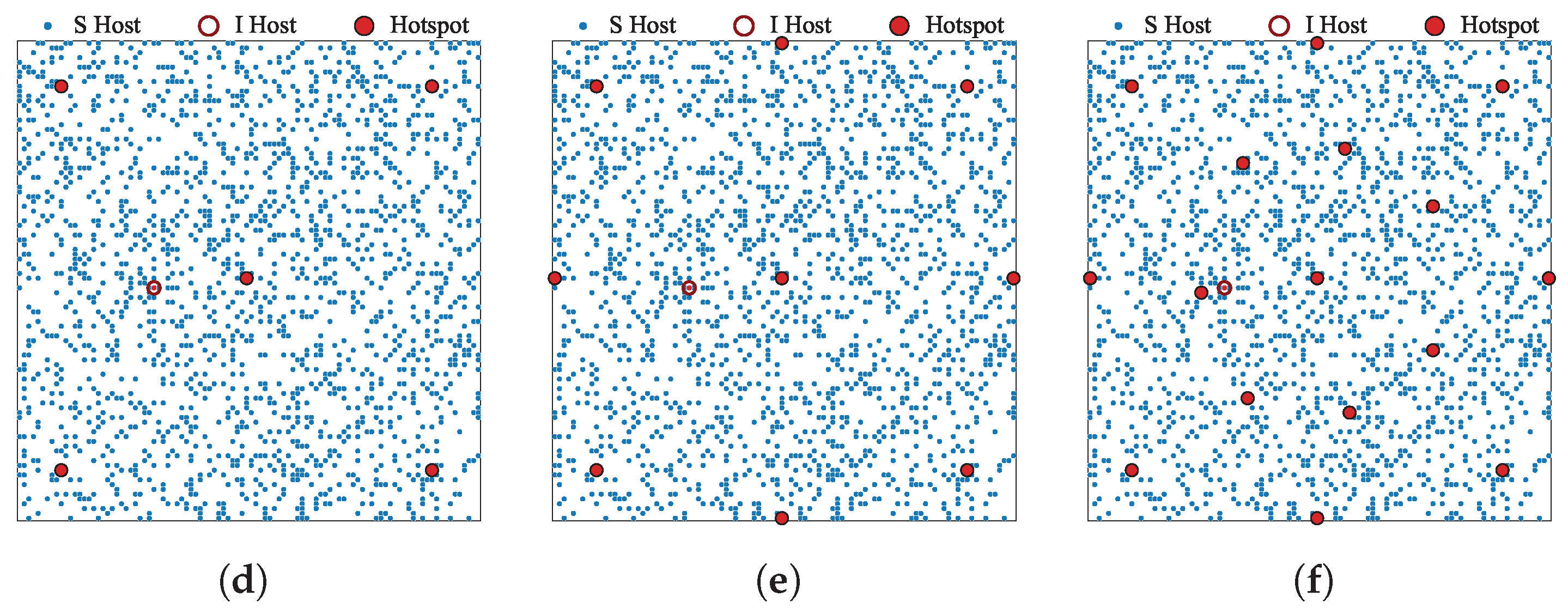
5.1. Model
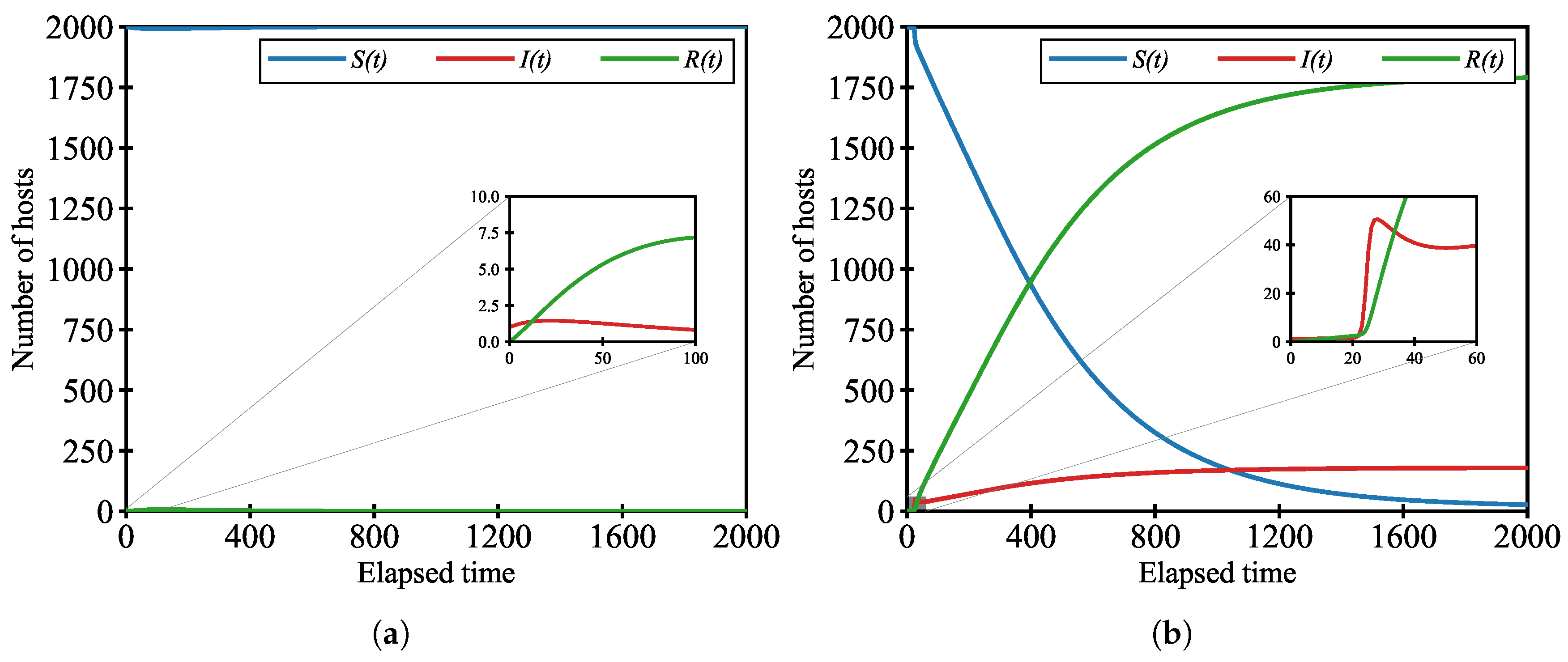
5.2. Result
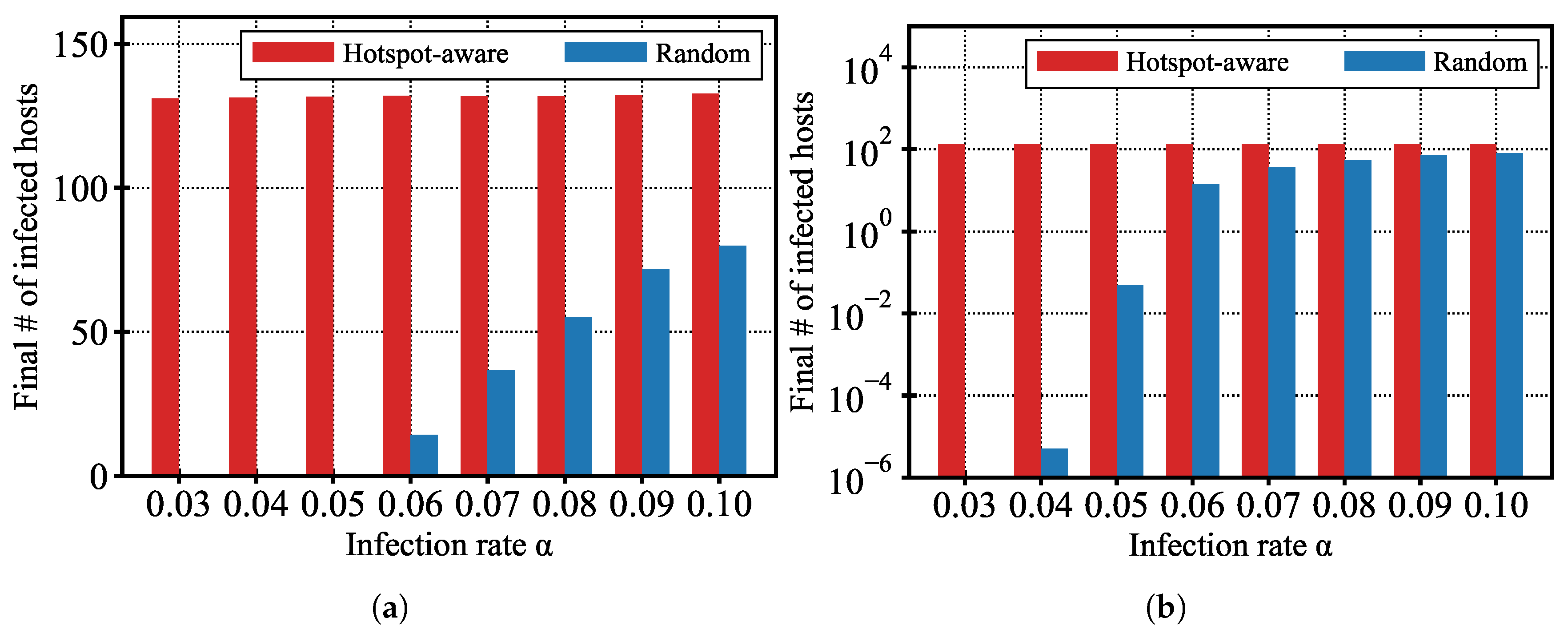
5.2.1. Impact of Malware Infection Rate
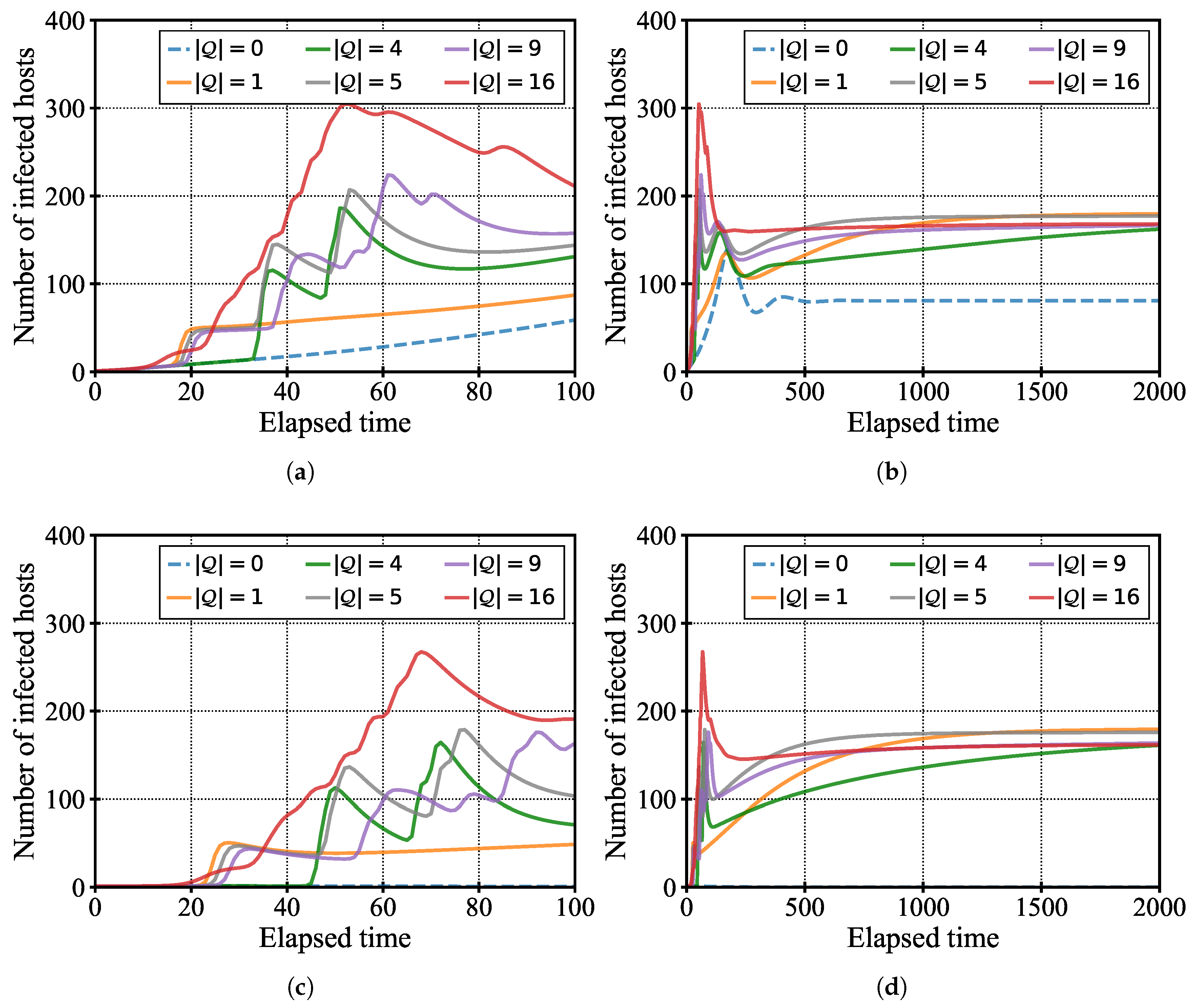
5.2.2. Impact of the Number of Hotspots
6. Discussion
6.1. Modeling Fidelity
6.2. Empirical Data Integration
6.3. Computational Scalability
6.4. Practical Applicability and Policy Insights
7. Conclusions and Future Work
7.1. Conclusions
7.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cisco. Cisco Annual Internet Report (2018–2023) White Paper. Technical Report. 2018. Available online: https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html (accessed on 1 August 2025).
- Lonzetta, A.M.; Cope, P.; Campbell, J.; Mohd, B.J.; Hayajneh, T. Security Vulnerabilities in Bluetooth Technology as Used in IoT. J. Sens. Actuator Netw. 2018, 7, 28. [Google Scholar] [CrossRef]
- Ronen, E.; Shamir, A.; Weingarten, A.O.; O’Flynn, C. IoT Goes Nuclear: Creating a ZigBee Chain Reaction. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 195–212. [Google Scholar] [CrossRef]
- Milanovic, A.F.; Melikov, N.; Legezo, D. Skygofree: Following in the Footsteps of HackingTeam. 2018. Available online: https://securelist.com/skygofree-following-in-the-footsteps-of-hackingteam/83603/ (accessed on 28 June 2025).
- Zeng, W.; Zhang, C.; Liang, X.; Xia, J.; Lin, Y.; Lin, Y. Intrusion detection-embedded chaotic encryption via hybrid modulation for data center interconnects. Opt. Lett. 2025, 50, 4450–4453. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. 1927, 115, 700–721. [Google Scholar]
- Gonzalez, G.; Larraga, M.E.; Alvarez-Icaza, L.; Gomez, J. Bluetooth Worm Propagation in Smartphones: Modeling and Analyzing Spatio-Temporal Dynamics. IEEE Access 2021, 9, 75265–75282. [Google Scholar] [CrossRef]
- Miura, H.; Abukawa, S.; Kimura, T.; Hirata, K. Modeling of malware diffusion with mobile devices in intermittently connected networks. In Proceedings of the 2022 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Chiang Mai, Thailand, 7–10 November 2022; pp. 1756–1759. [Google Scholar] [CrossRef]
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.L. Limits of Predictability in Human Mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef]
- Toole, J.L.; Lin, Y.R.; Muehlegger, E.; Shoag, D.; González, M.C. Coupling human mobility and social ties. J. R. Soc. Interface 2015, 12, 20141128. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Dong, Y.; Xu, J.; Chawla, N.V. Correlation between social proximity and mobility similarity. Sci. Rep. 2017, 7, 11975. [Google Scholar] [CrossRef] [PubMed]
- Memon, M.W.; Singh, A.V.; Raj, R.G. Analysis and Implementation of Human Mobility Behavior Using Similarity Analysis Based on Co-Occurrence Matrix. Sensors 2022, 22, 9898. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Truong, T.C.; Zelinka, I. A Survey on Artificial Intelligence in Malware as Next-Generation Threats. Mendel 2019, 25, 27–34. [Google Scholar]
- Truong, T.C.; Diep, Q.B.; Zelinka, I. Artificial Intelligence in the Cyber Domain: Offense and Defense. Symmetry 2020, 12, 410. [Google Scholar] [CrossRef]
- Kudo, T.; Kimura, T.; Inoue, Y.; Aman, H.; Hirata, K. Stochastic modeling of self-evolving botnets with vulnerability discovery. Comput. Commun. 2018, 124, 101–110. [Google Scholar] [CrossRef]
- Shi, Y.; Davaslioglu, K.; Sagduyu, Y.E. Generative Adversarial Network in the Air: Deep Adversarial Learning for Wireless Signal Spoofing. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 294–303. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Wang, Y.; Ke, L.; Tan, Y. A feature-vector generative adversarial network for evading PDF malware classifiers. Inf. Sci. 2020, 523, 38–48. [Google Scholar] [CrossRef]
- Li, H.; Zhou, S.; Yuan, W.; Li, J.; Leung, H. Adversarial-Example Attacks Toward Android Malware Detection System. IEEE Syst. J. 2020, 14, 653–656. [Google Scholar] [CrossRef]
- Armis. BlueBorne Cyber Threat Impacts Amazon Echo and Google Home. 2017. Available online: https://www.armis.com/blog/blueborne-cyber-threat-impacts-amazon-echo-and-google-home/ (accessed on 28 June 2025).
- Armis. The Attack Vector “BlueBorne” Exposes Almost Every Connected Device. 2017. Available online: https://media.armis.com/PDFs/wp-blueborne-bluetooth-vulnerabilities-en.pdf (accessed on 28 June 2025).
- Ruge, J.; Pohlmann, J.K.; Holtz, T.; Hollick, M. Frankenstein: Advanced Wireless Fuzzing to Exploit New Bluetooth Escalation Targets. In Proceedings of the 29th USENIX Security Symposium (USENIX Security 20), Boston, MA, USA, 12–14 August 2020; USENIX Association: Berkeley, CA, USA, 2020; pp. 19–36. [Google Scholar]
- Xiao, X.; Fu, P.; Dou, C.; Li, Q.; Hu, G.; Xia, S. Design and analysis of SEIQR worm propagation model in mobile internet. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 341–350. [Google Scholar] [CrossRef]
- Shen, S.; Zhou, H.; Feng, S.; Liu, J.; Zhang, H.; Cao, Q. An Epidemiology-Based Model for Disclosing Dynamics of Malware Propagation in Heterogeneous and Mobile WSNs. IEEE Access 2020, 8, 43876–43887. [Google Scholar] [CrossRef]
- Okamura, H.; Kobayashi, H.; Dohi, T. Markovian modeling and analysis of Internet worm propagation. In Proceedings of the 16th IEEE International Symposium on Software Reliability Engineering (ISSRE’05), Chicago, IL, USA, 8–11 November 2005. [Google Scholar]
- Peng, S.; Wu, M.; Wang, G.; Yu, S. Propagation model of smartphone worms based on semi-Markov process and social relationship graph. Comput. Secur. 2014, 44, 92–103. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, Z.; Kong, X.; Liu, Z.; Liu, X. A movement-aware measure for trajectory similarity and its application for ride-sharing path extraction in a road network. Int. J. Geogr. Inf. Sci. 2024, 38, 1703–1727. [Google Scholar] [CrossRef]
- MATLAB. Available online: https://jp.mathworks.com/products/matlab.html (accessed on 15 June 2021).
- Olbricht, R. Overpass API. 2024. Available online: https://overpass-api.de/ (accessed on 22 August 2025).
- Kotz, D.; Henderson, T.; Abyzov, I. CRAWDAD: A Community Resource for Archiving Wireless Data at Dartmouth. 2004. Available online: https://crawdad.org (accessed on 24 August 2025).
- Miura, H.; Kimura, T.; Hirata, K. Deterministic epidemic modeling of future botnet malware with a contact process. IEICE Commun. Express 2021, 10, 295–300. [Google Scholar] [CrossRef]
- Miura, H.; Abukawa, S.; Kimura, T.; Hirata, K. Approximate modeling of malware diffusion on wireless mobile devices. In Proceedings of the 2023 Asia Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Taipei, Taiwan, 31 October–3 November 2023; pp. 2144–2148. [Google Scholar] [CrossRef]

| Parameters | Description | Value |
|---|---|---|
| H | Total number of hosts | 2000 |
| Total number of cells | ||
| Number of hotspots | 0, 1, 4, 5, 9, 16 | |
| Malware infection rate | ||
| Malware elimination rate | ||
| Vulnerability discovery rate | ||
| Movement rate | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miura, H.; Kimura, T.; Hirata, K. Modeling of Malware Propagation in Wireless Mobile Networks with Hotspots Considering the Movement of Mobile Clients Based on Cosine Similarity. Electronics 2025, 14, 3528. https://doi.org/10.3390/electronics14173528
Miura H, Kimura T, Hirata K. Modeling of Malware Propagation in Wireless Mobile Networks with Hotspots Considering the Movement of Mobile Clients Based on Cosine Similarity. Electronics. 2025; 14(17):3528. https://doi.org/10.3390/electronics14173528
Chicago/Turabian StyleMiura, Hideyoshi, Tomotaka Kimura, and Kouji Hirata. 2025. "Modeling of Malware Propagation in Wireless Mobile Networks with Hotspots Considering the Movement of Mobile Clients Based on Cosine Similarity" Electronics 14, no. 17: 3528. https://doi.org/10.3390/electronics14173528
APA StyleMiura, H., Kimura, T., & Hirata, K. (2025). Modeling of Malware Propagation in Wireless Mobile Networks with Hotspots Considering the Movement of Mobile Clients Based on Cosine Similarity. Electronics, 14(17), 3528. https://doi.org/10.3390/electronics14173528






