Abstract
The proliferation of mobile devices has generated exponential data growth, driving efforts to extract value. However, mobile data often presents non-independent and identically distributed (non-IID) challenges owing to varying device, environmental, and user factors. While data sharing can mitigate non-IID issues, direct raw data transmission poses significant security risks like privacy breaches and man-in-the-middle attacks. This paper proposes a secure data-sharing mechanism using principal component analysis (PCA). Each node independently builds a local PCA model to reduce data dimensionality before sharing. Receiving nodes then recover data using a similarly constructed local PCA model. Sharing only dimensionally reduced data instead of raw data enhances transmission privacy. The method’s effectiveness was evaluated from both legitimate user and attacker perspectives. Experimental results demonstrated stable accuracy for legitimate users post-sharing, while attacker accuracy significantly dropped. The optimal number of principal components was also experimentally determined. Under optimal configuration, the proposed method achieves up to 42 times greater memory efficiency and superior privacy metrics compared with conventional approaches, demonstrating its advantages.
1. Introduction
With the convergence of artificial intelligence and ICBM technologies (IoT, cloud, big data, and mobile), an intelligent information society has emerged, where the human capacity for high-level information processing is implemented through information and communications technology [1]. In line with this transformation, there is a rapidly growing demand to integrate various types of sensitive data, such as medical records, location information, and transaction histories, with AI technologies [2,3,4]. Furthermore, efforts are actively underway to create new value by collecting and analyzing data in real time using various types of terminal devices [5].
However, data collected from personal devices exhibit diverse distributions and characteristics depending on the device environment and user attributes, which leads to a violation of the independent and identically distributed (IID) assumption and gives rise to the non-IID problem [6]. Non-IID data typically follow imbalanced distributions, which result in degraded model performance compared with models designed based on IID data [7]. A representative approach for addressing the non-IID issue is data sharing across devices [6], through which individual devices exchange their local data to balance the overall distribution and improve training efficiency. Nevertheless, shared data may include sensitive personal information such as user activity patterns, health records, and location data, thereby introducing serious privacy concerns and security threats such as man-in-the-middle attacks [8,9]. Therefore, incorporating privacy protection and secure transmission is crucial when designing data-sharing mechanisms [10,11].
To address these concerns, various techniques have been developed to protect datasets, with differential privacy and homomorphic encryption representing prominent approaches [12,13]. Differential privacy protects individual privacy by introducing random noise into the dataset, thereby reducing the likelihood of inferring the original data, albeit at the cost of reduced utility or accuracy [14]. By contrast, homomorphic encryption enables computations such as addition and multiplication to be performed directly on encrypted data, thereby preserving privacy while supporting data processing; however, its practical deployment is constrained by computational overhead and high latency in such schemes [15,16].
Principal component analysis (PCA) is an unsupervised learning method that reduces data dimensionality while preserving as much variance as possible. It is commonly used for data compression and noise reduction [17]. By applying PCA, high-dimensional data can be transformed into a lower-dimensional space for a more concise representation. This not only reduces memory and computational costs during data transmission but also mitigates the risk of information exposure during the process. PCA is designed to preserve the statistical properties of the original data, even after dimensionality reduction, making it possible to recover the original data based on a reduced representation. However, this recovery process inevitably involves some degree of information loss, which is referred to as reconstruction error. Although the reduced data may not exactly match the original data, they can still retain essential features.
This work proposes a PCA-based secure data-sharing mechanism to address the non-IID problem and protect privacy during data exchange. In the proposed method, each node independently trains a PCA model on its local data and generates dimensionally reduced data for sharing. The receiving side then uses its own PCA model, trained similarly, to recover the shared data. This process helps prevent the exposure of sensitive information contained in the original data. In particular, because only compressed values are shared in the proposed mechanism, even in the event of a man-in-the-middle attack during transmission, it is difficult to recover data that closely resemble the original data, thereby enhancing privacy protection. Furthermore, a novel metric for quantitatively evaluating privacy preservation performance is introduced, and the effectiveness and practicality of the proposed method are demonstrated through experiments.
The main contributions of this paper are as follows:
- A privacy-preserving data-sharing mechanism is proposed to mitigate the non-IID problem.
- The proposed mechanism was comprehensively evaluated in terms of accuracy, memory usage, and privacy protection performance, demonstrating superior performance compared with conventional methods.
- The performance was analyzed from both attacker and legitimate user perspectives through experiments simulating data leakage scenarios, verifying that the proposed method effectively prevents privacy exposure.
The remainder of this paper is organized as follows. Section 2 reviews related work. Section 3 describes the structure and operational principles of the proposed data-sharing mechanism. Section 4 presents the experimental setup and provides a quantitative performance evaluation based on experimental results. Finally, Section 5 concludes the paper.
2. Related Work
This section reviews conventional studies conducted to ensure data sharing among nodes.
Ref. [18] proposed a dual-encryption and proxy-based system that integrates AES-based symmetric key encryption with ciphertext-policy attribute-based encryption (CP-ABE) to enable secure data sharing in a mobile cloud environment. In this method, the user encrypts data using a symmetric key and CP-ABE, whereas the proxy server performs the signing and decryption functions. Although this approach offers strong security, it suffers from complex key management issues, particularly when user attributes change.
Ref. [19] introduced a data-sharing mechanism that integrates deep learning with blockchain technologies to securely share distributed medical image data. The framework restricts access to authorized hospitals via smart contracts and constructs a global model by sharing only the trained weights through the InterPlanetary File System (IPFS), avoiding direct transmission of the dataset. Although the model improves classification performance, it encounters challenges, such as the complexity of smart contract-based authentication procedures and the high computational and operational costs associated with blockchain.
Ref. [20] presented a secure data-transmission method for cloud environments by integrating a blockchain-based distributed system with IPFS. The data owner encrypts the file, uploads it to the IPFS, divides it into N secret fragments, and controls access via a dual-key management system. Although this approach mitigates single-point-of-failure issues and reduces transmission overhead, it lacks quantitative evaluation in terms of security, performance, and privacy.
Ref. [21] outlined a permissioned blockchain and deep learning (PBDL) framework that integrates blockchain, smart contracts, and deep learning techniques to securely share data in industrial healthcare systems. Although the framework improves security compared with conventional technologies, it is inefficient in terms of memory and computational resources owing to its structural complexity.
Ref. [22] proposed an identity-based encryption (IBE) scheme based on the learning with errors (LWE) problem to protect the privacy of sensitive data shared in Internet of Nano-Things (IoNT) environments. This scheme performs encryption and decryption using the unique identity of the user, thereby enabling a lightweight security protocol suitable for resource-constrained IoNT devices without requiring a complex key management infrastructure. However, this scheme does not sufficiently address the initial key distribution mechanism, and its effectiveness has not been experimentally verified.
Ref. [23] proposed a blockchain-based, privacy-preserving framework for vehicle data sharing to mitigate risks associated with identity exposure and malicious attacks during wireless transmission of sensitive data such as GPS coordinates, sensor readings, and brake information. This framework employs zero-knowledge proof to ensure both anonymity and auditability and incorporates an efficient multi-sharding protocol to reduce blockchain communication costs while maintaining security in fast-moving vehicular environments. Although the study evaluated the effectiveness of reducing communication costs, it lacked sufficient experimental analysis of the security of the proposed method.
Ref. [24] conducted a comparative analysis of use cases across domains such as healthcare, supply chains, and transportation to identify the privacy–performance–cost trade-off and proposed blockchain-empowered data sharing (BlockDaSh), a permissioned blockchain reference architecture. BlockDaSh aims for high trust, low cost, and strong usability by recording only metadata on-chain, encrypting the original data, and storing it off-chain to minimize communication and storage overhead. The architecture leverages the blockchain consensus mechanism to ensure data integrity and traceability. However, its evaluation is primarily based on literature reviews and case studies and therefore does not provide quantitative performance metrics.
Ref. [25] proposed an AES-ECDH-secret-sharing-based encryption framework for secure sharing of medical data over a public cloud infrastructure. The file content was fully encrypted using AES, the session key was exchanged via ECDH, and the key was split using a two-out-of-three secret-sharing scheme to enable patient-centric access control and maintain confidentiality. Theoretical and simulation-based analyses indicated that the framework prevents data exposure even in scenarios involving server compromises or insider attacks, although it introduces latency during the encryption-based upload process.
Ref. [26] presented SmartCrypt, an encryption framework designed for securely storing and sharing large-scale time-series data generated and accumulated in smart manufacturing (IIoT) environments while simultaneously supporting real-time analytics. In this approach, data are encrypted in chunks, enabling servers to compute statistical aggregates such as sums and averages directly over ciphertext. Upon sharing, the data owner distributes a token derived from internal nodes of a GGM key derivation tree, allowing the recipient to decrypt only the specified intervals and resolutions. SmartCrypt combines lightweight homomorphic encryption scheme optimized for stream data with hierarchical key derivation tokens, offering both privacy and real-time accessibility, albeit limited by the complexity of key life-cycle management.
Table 1 presents a comparison of conventional studies in terms of privacy protection, costs, and usability. The comparison reveals that most conventional approaches fail to effectively resolve the trade-offs among security, cost, and usability. To address these limitations, this paper proposes a data-sharing mechanism that balances privacy protection, memory efficiency, and performance, thereby complementing the shortcomings of conventional methods.

Table 1.
Privacy, cost, and usability evaluation of conventional studies.
3. Privacy-Preserving Data Sharing via PCA-Based Dimensionality Reduction
This section proposes a PCA-based secure data-sharing mechanism to address the trade-offs among privacy protection, cost, and usability. The proposed mechanism leverages PCA, a dimensionality-reduction technique, to transform high-dimensional raw data into lower-dimensional representations before sharing. Therefore, even if data are intercepted during transmission, it becomes difficult to recover the original information, thereby effectively reducing the risk of privacy breaches.
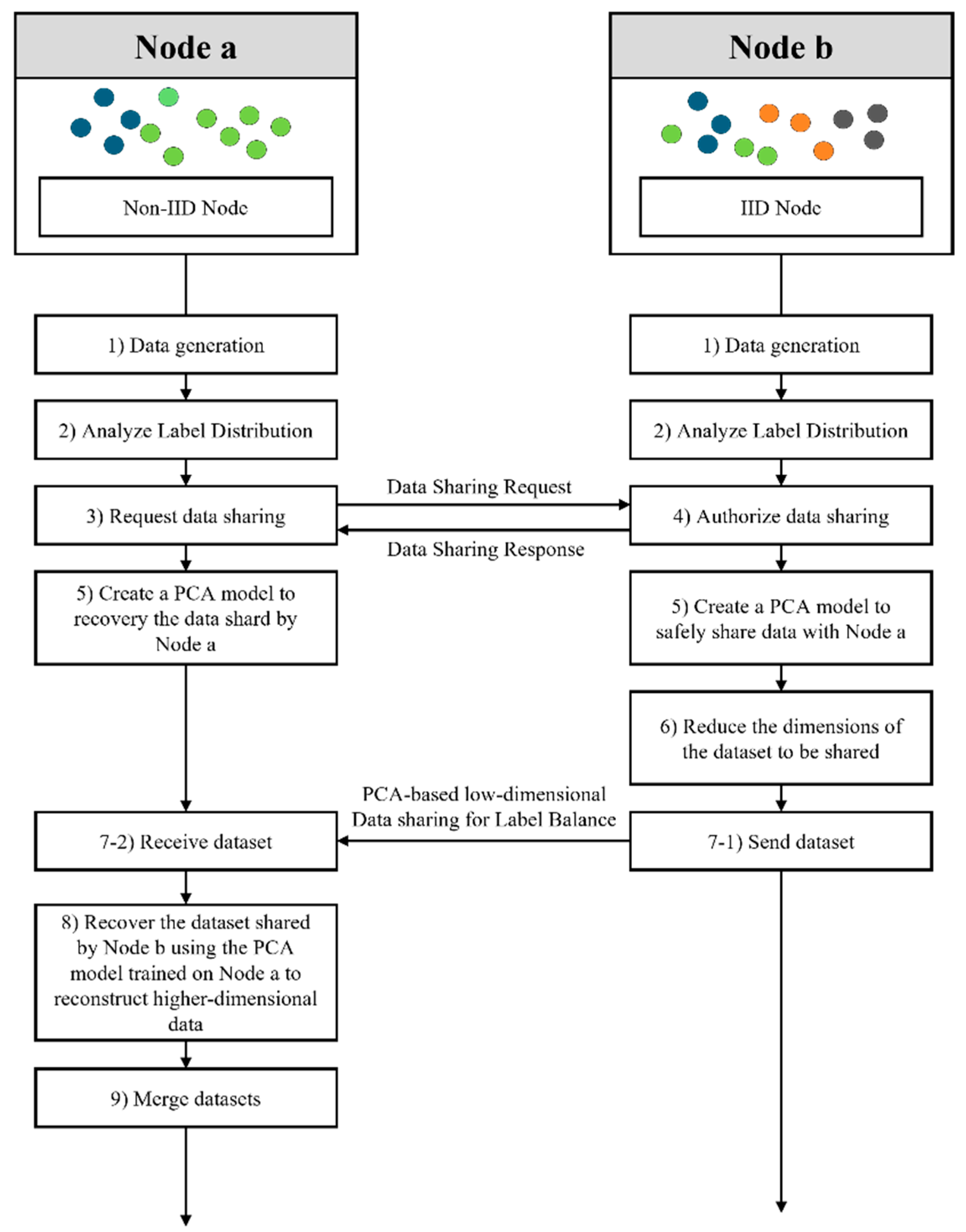
Figure 1 illustrates the overall architecture of the proposed mechanism. Node a is configured as a non-IID node with class imbalance, while Node b is set up as a relatively balanced IID node. Each node independently collects and analyzes data to determine whether it suffers from distributional imbalance. Once Node a identifies a non-IID issue, it requests data sharing from Node b, which possesses sufficiently IID characteristics. Upon approval, Node b trains a PCA model on its dataset and uses it to reduce the dimensionality of the data before transmitting the transformed data to Node a. Simultaneously, Node a trains its own PCA model using its local data and utilizes this model to recover the high-dimensional data from the low-dimensional input received from Node b. The recovered data are then merged with Node a’s existing dataset and used for further training.
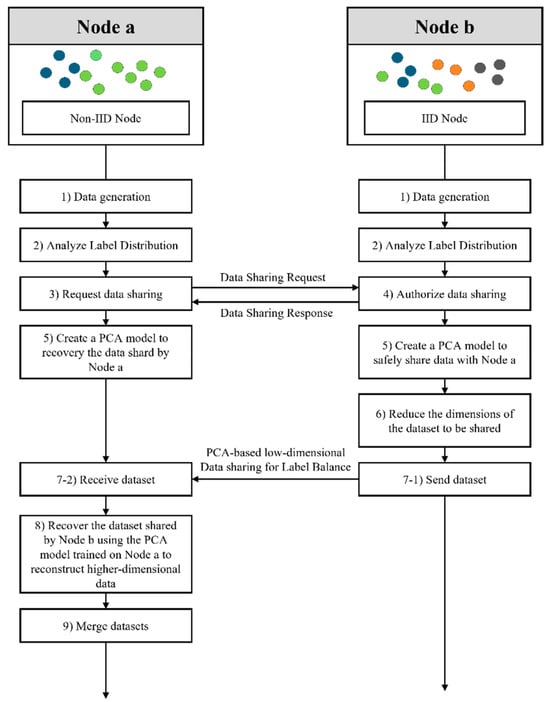
Figure 1.
Flowchart of secure data-sharing mechanism based on principal component analysis.
The core strength of this mechanism lies in its ability to protect sensitive information through dimensionality reduction using PCA. The PCA model compresses the data by selecting only the top principal components and discarding the less significant ones. Consequently, it becomes difficult to reconstruct low-dimensional data in their original form. This property ensures that even if a man-in-the-middle attack occurs, the attacker cannot easily recover the original data, thereby minimizing the risk of privacy leakage. Additionally, by reducing the number of features in the transmitted data, the proposed approach reduces communication costs and memory consumption.
To ensure the effective operation of the proposed mechanism, three technical validations must be performed in advance. First, it must be demonstrated that when an attacker intercepts and attempts to recover the reduced data using PCA, the reconstructed data are not similar to the original data. Secondly, it should be verified that when the receiver recovers data using its own PCA model, the original learning performance is maintained. Finally, a clear criterion must be established to determine the optimal number of principal components that minimize information loss during dimensionality reduction while maintaining efficiency.
4. Evaluation
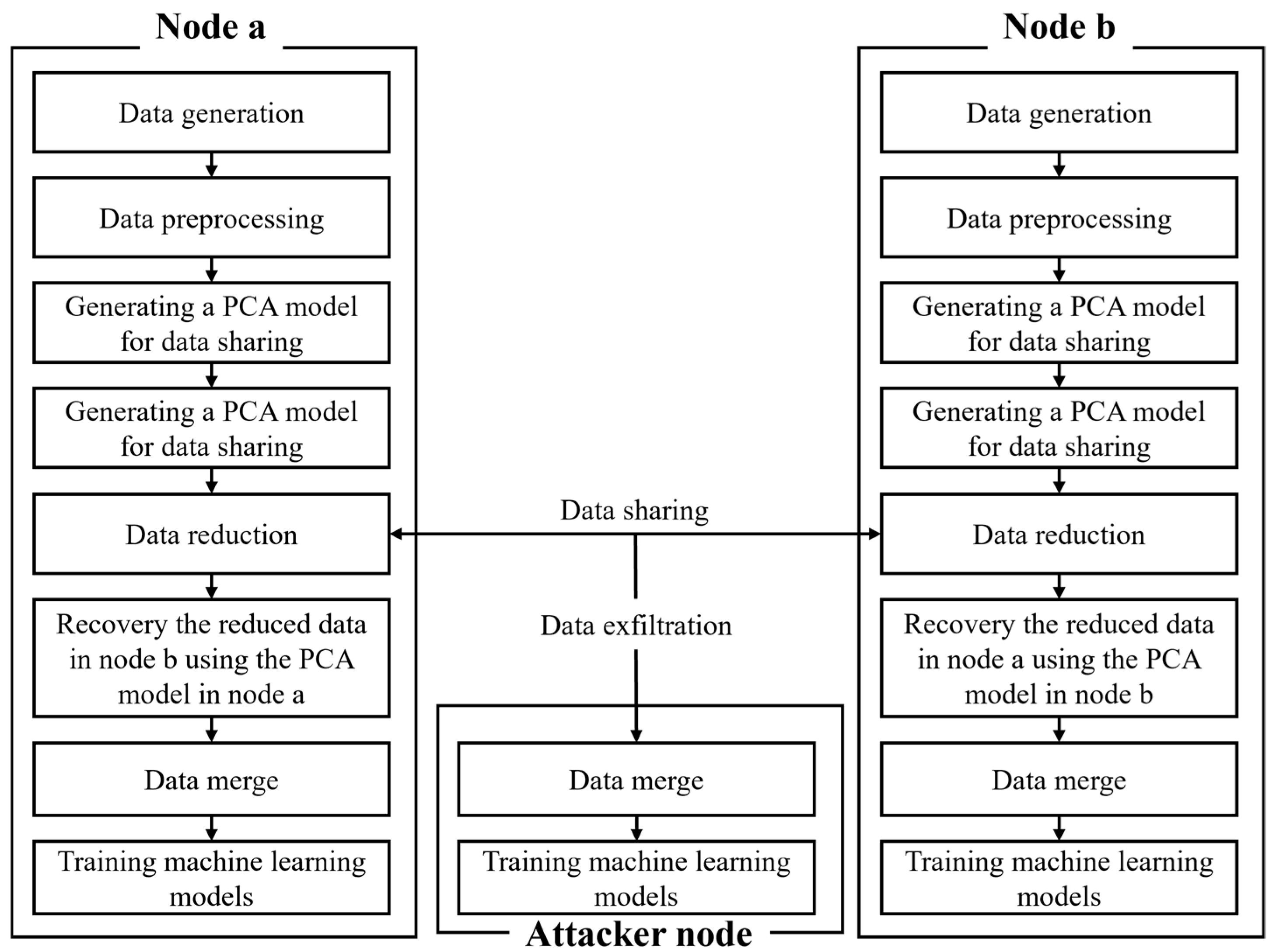
This section implements the proposed data-sharing mechanism and quantitatively evaluates its effectiveness by comparing model performance before and after data sharing. The experiment was conducted under a man-in-the-middle (MITM) scenario in which an attacker intercepts the data shared between Node a and Node b to empirically analyze the possibility of information leakage. To verify the attacker’s ability to recover data, the ability of each node to maintain its performance and the optimal number of principal components, the experimental environment was configured as illustrated in Figure 2.
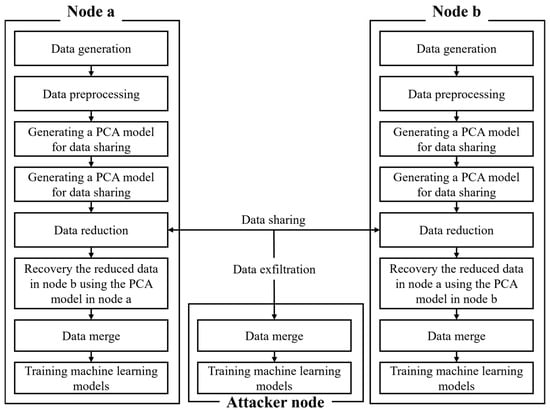
Figure 2.
Experimental structure diagram.
First, each node preprocessed its own data and independently built a PCA model to reduce the dimensionality of its data. Subsequently, the dimensionally reduced data were shared between the nodes, and the attacker intercepted the shared data and used them for training. The attacker trained a model based on the shared low-dimensional data using its PCA model. Each node recovered the received data using its own PCA model, merged the received data with its original data, and performed a performance evaluation based on machine learning. Using this setup, the experiment verifies whether the attacker’s ability to recover information is minimized while each node maintains its learning performance.
In this context, it is crucial to assess the extent to which an adversary can reconstruct the original data from the low-dimensional representations they obtain. To address this, a preliminary evaluation is conducted wherein an attacker attempts to recover the data using a PCA model trained on random data. This preliminary step facilitates in assessing the feasibility of such reconstruction attacks prior to the main experiment.
4.1. Experimental Environment and Dataset
The experiment was conducted based on the following assumptions. First, all the nodes were assumed to collect data with the same set of features. Second, each node independently applied its own PCA model for dimensionality reduction and reconstruction—these PCA models were not shared externally. Third, during the PCA-based dimensionality reduction process, both the sending and receiving nodes used the same number of principal components. These assumptions reflect a collaborative learning setting within the same domain, where such conditions are typically valid. However, if the sender and the receiver employ PCA models trained on different bases, accurate reconstruction of the original data becomes either infeasible or yields significantly low performance. Within this framework, the present experiment aimed to quantitatively evaluate the extent to which an attacker can reconstruct the original data.
This study used the publicly available dataset UNSW-NB15, which is designed for network intrusion detection [27,28,29,30,31]. The dataset includes network traffic information and consists of a total of nine attack types and 45 features. The preprocessing steps included the removal of unnecessary features, label encoding, and data normalization. In the feature-removal step, ID information, which does not contribute to determining traffic types, was deleted. Because attack_cat was used as the label, the feature indicating the presence of an attack was also removed. Label encoding was performed using the LabelEncoder module from scikit-learn, which encodes string features such as proto, service, and state. In addition, the attack_cat labels were encoded by replacing “normal” with 0, “generic” with 1, and “exploit” with 2. Finally, the data values were normalized using scikit-learn StandardScaler to adjust the scale across the features.
Next, the data were collected according to the purpose of this study. Among the nine attack types, this study selected two attack types—exploit and generic—and included three labels, including normal. To evaluate performance differences based on data imbalance, the data ratio for each node, from Node 1 to Node 8, was varied. Specifically, the imbalance ratios for Nodes 1 and 2 were set to 1:20, those for Nodes 3 and 4 to 1:10, those for Nodes 5 and 6 to 1:5, and those for Nodes 7 and 8 to 1:2. Odd-numbered nodes used the generic label as the minority class, whereas even-numbered nodes used the exploit label as the minority class. The data composition and ratios for each node are listed in Table 2. For the training data, the majority class was fixed at 5000 samples, while the minority class was adjusted according to the specified ratios. The test dataset contained 1500 samples per label, ensuring that each node underwent testing with the same number of data points.

Table 2.
Configuring datasets for each node.
4.2. Experiment and Analysis of Results
The core objective of the proposed method was to demonstrate that even if an attacker intercepts dimensionally reduced data, it is infeasible to recover the original data. Consequently, an experiment was conducted to verify the recoverability of the original data from PCA-based dimensionally reduced data. In other words, this study aimed to experimentally evaluate the difficulty an attacker would encounter when attempting to reconstruct the original data from low-dimensional projections obtained via a man-in-the-middle attack. For data recovery, it was assumed that the attacker generates an arbitrary PCA model using a dataset with the same number of features as the legitimate user data. Accordingly, the attacker is assumed to have trained the model on a random dataset with the same number of features.
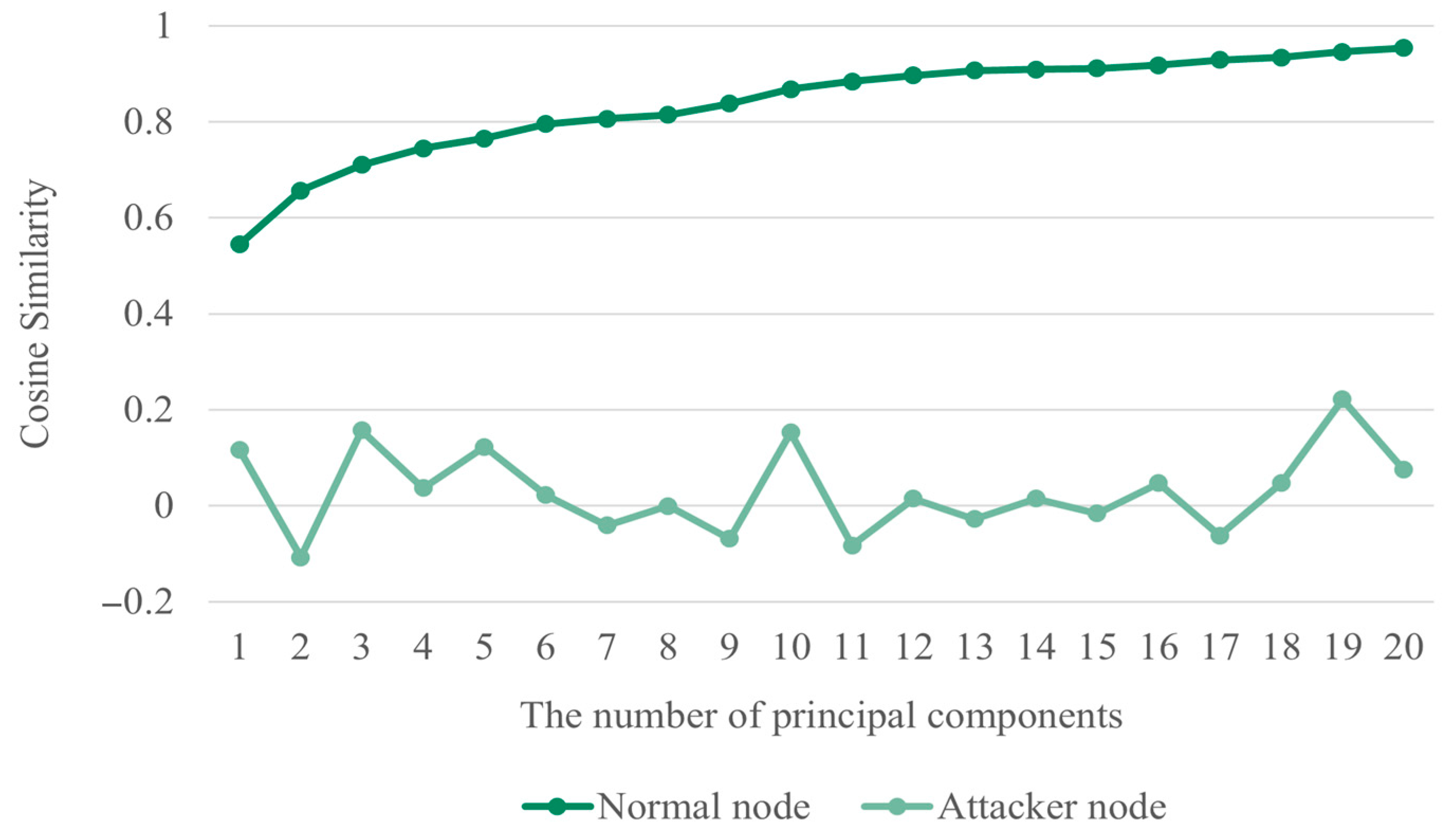
To evaluate the similarity between the attacker’s recovered dataset and the original dataset, cosine similarity was measured. Cosine similarity ranges from −1 to 1, where a value closer to 1 indicates higher similarity. The experimental results are presented in Figure 3. For a legitimate node, the similarity to the original data increases as the number of principal components increases; however, they are not identical. By contrast, the attacker’s similarity remains low regardless of the number of principal components. These results confirm that data compressed through PCA are difficult to recover in their original form.
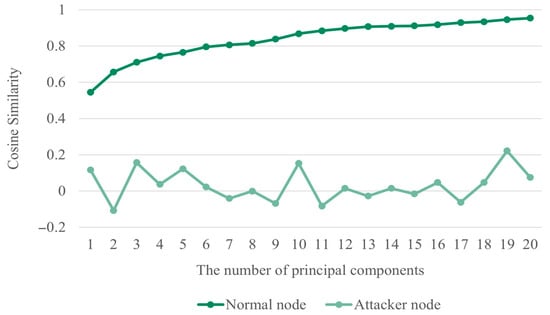
Figure 3.
Cosine similarity by principal component value.
Second, it was necessary to preliminarily demonstrate whether learning performance can be maintained after data sharing when the PCA models used for data compression and recovery are generated in different environments. To perform dimensionality reduction and recovery using different PCA models, the models must be trained on datasets with the same number of features, feature orders, and labels, and the principal component settings must be consistent. The number of principal components in a PCA model can be set either as a ratio or a fixed value. When set as a ratio, the number of selected principal components may vary depending on the data distribution, which can cause inconsistencies during recovery. By contrast, fixing the number of principal components as an integer smaller than the total number of features allows the dimensionality to remain consistent during both compression and recovery, enabling stable data sharing and recovery.
This section verifies whether model performance is maintained in an environment where the proposed data-sharing mechanism is applied. Consequently, learning was conducted using non-IID data before sharing and the data collected by each node after dimensionality reduction, mutual sharing, and recovery. The results were compared and analyzed.
Table 3 shows the results of the multiclass classification before and after data sharing. The evaluation results confirm that performance remains stable even after data sharing, suggesting that meaningful data recovery is possible even when the models used for dimensionality reduction and recovery differ, provided that certain conditions are met. Additionally, the accuracy improved marginally, as data sharing partially alleviated data imbalance. This indicates that the proposed method can simultaneously achieve information sharing and improve learning performance without degrading data quality.

Table 3.
Results of pilot testing of data-sharing mechanism.
Table 4 presents classification accuracy before and after data sharing according to the number of principal components and data imbalance ratios. The experimental results showed that performance remained stable up to 20 principal components. For readability and analysis efficiency, Table 4 evaluates performance with principal components set to 20, 15, 10, 5, 3, 2, and 1, respectively. Furthermore, since overall performance was best at a bias ratio of 1:10, subsequent experiments fixed the data bias ratio at 1:10 and were conducted on Node 3 and Node 4.

Table 4.
Accuracy per node based on principal component value.
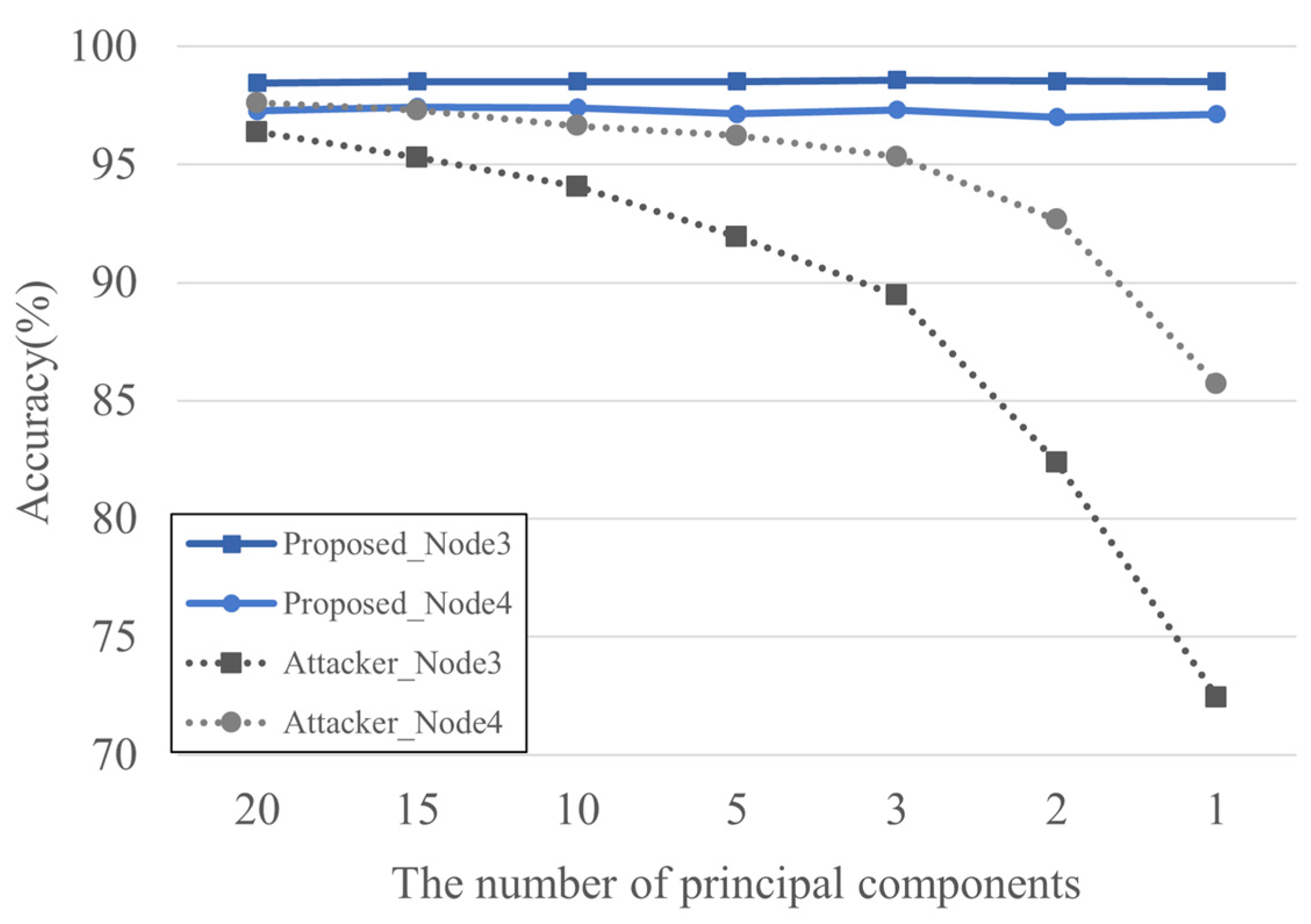
Figure 4 shows the classification accuracy according to changes in the number of principal components when the data bias ratio was 1:10. The experimental results indicate that the legitimate node maintained consistent performance regardless of the number of principal components, whereas the attacker node’s accuracy dropped by more than 24% as the number of principal components decreased. In other words, although the attacker’s data recovery performance deteriorated significantly, the legitimate node maintained stable performance. Based on this performance difference, it can be concluded that when the number of principal components is set to one, the legitimate node achieves high accuracy while the attacker’s performance is at its lowest, which is the optimal condition for secure data sharing.
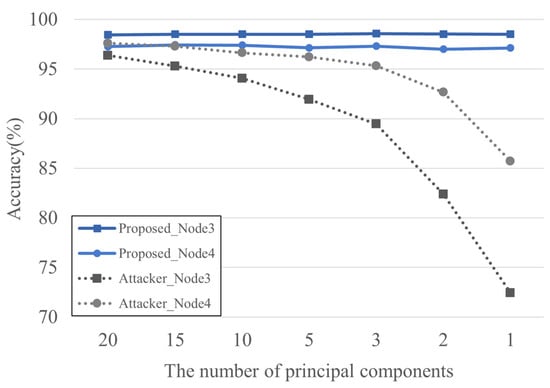
Figure 4.
Node-by-node accuracy based on principal component values at a 1:10 ratio.
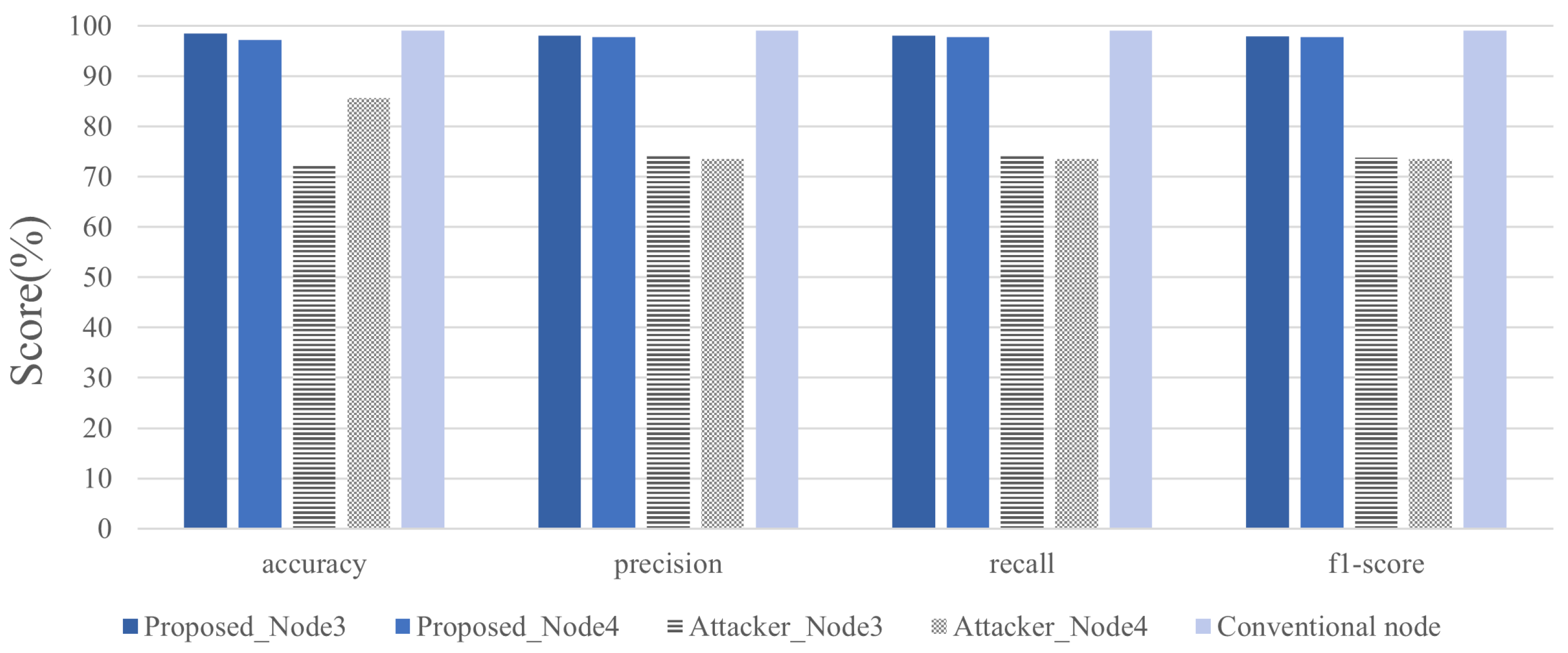
Figure 5 compares the accuracy, precision, recall, and F1 scores of the attacker node, legitimate node, and conventional model when the data bias ratio was 1:10 and the number of principal components was set to 1. The conventional model shared the entire dataset without preprocessing and achieved the highest performance. In contrast, the proposed model showed approximately 1% lower performance than the conventional model, but demonstrated superior accuracy, precision, and F1 score compared with the attacker model, thereby proving that it simultaneously ensures data privacy protection and practical performance.
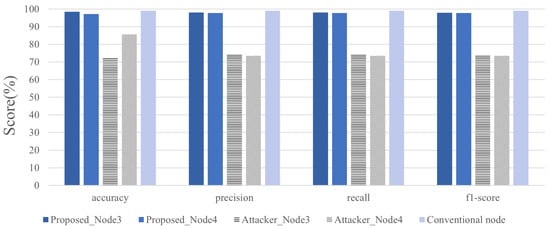
Figure 5.
Accuracy, precision, recall, and F1 scores of normal and attacker nodes when the principal component value is 1 at a 1:10 ratio.
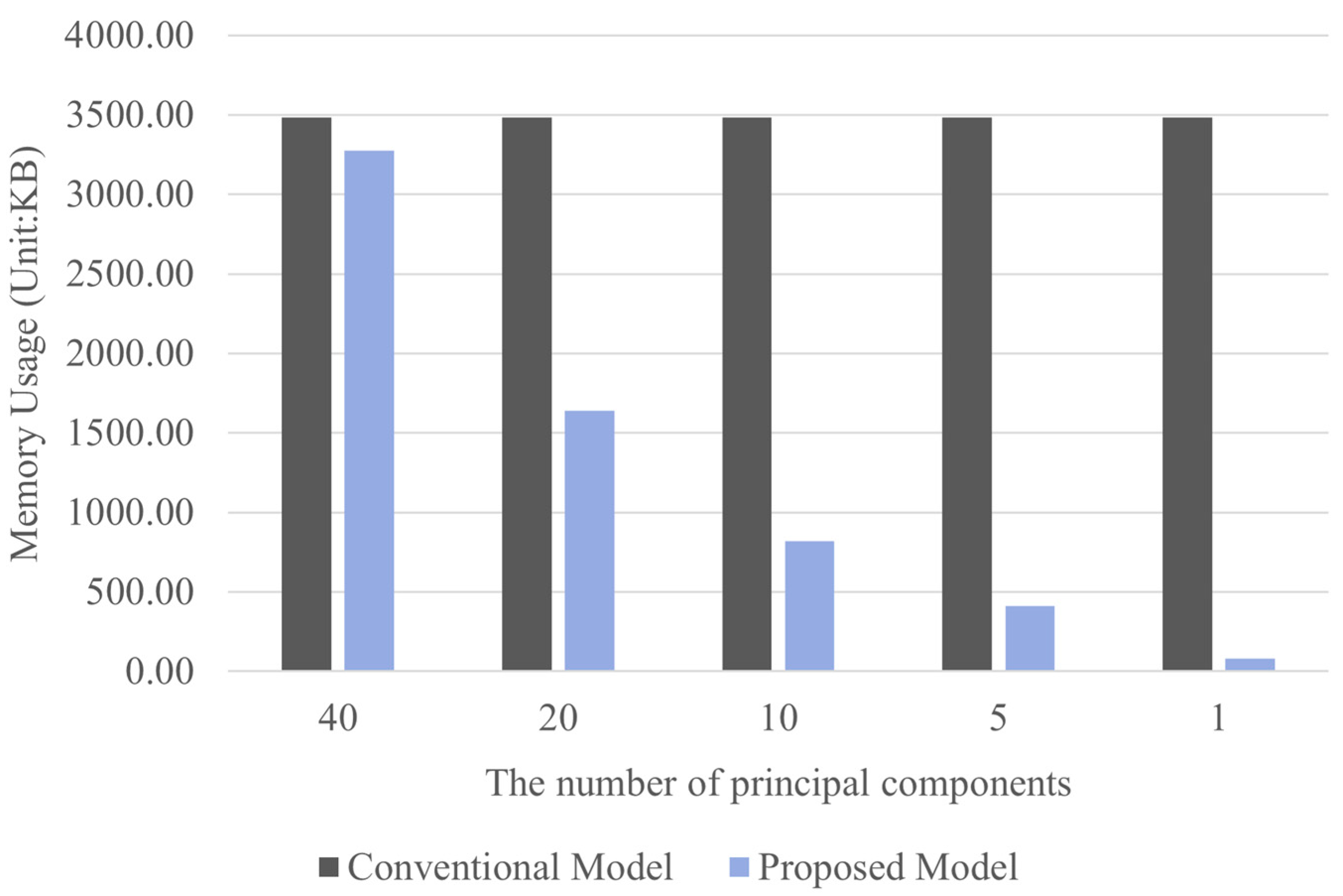
Figure 6 compares the memory usage between the conventional and proposed models based on the number of principal components when the data bias ratio was 1:10. The conventional approach is inefficient in terms of memory usage because it transmits the entire original dataset, whereas the proposed model significantly reduces memory used for data transmission and reception by compressing the data into a single principal component. Based on the optimal number of principal components identified earlier, the proposed model is approximately 42 times more memory-efficient than the conventional model. This result demonstrates that the proposed method not only effectively reduces resource usage and protects data privacy but also has high practical value in terms of system efficiency.
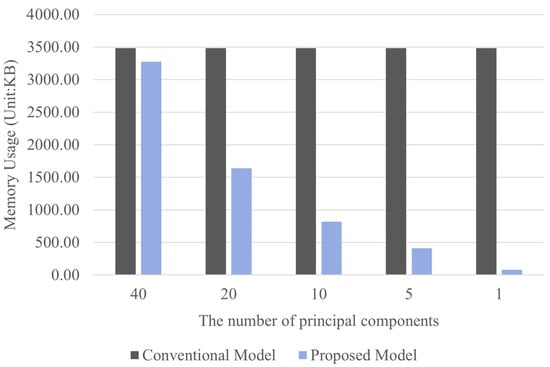
Figure 6.
Memory usage based on principal component values at 1:10 ratio.
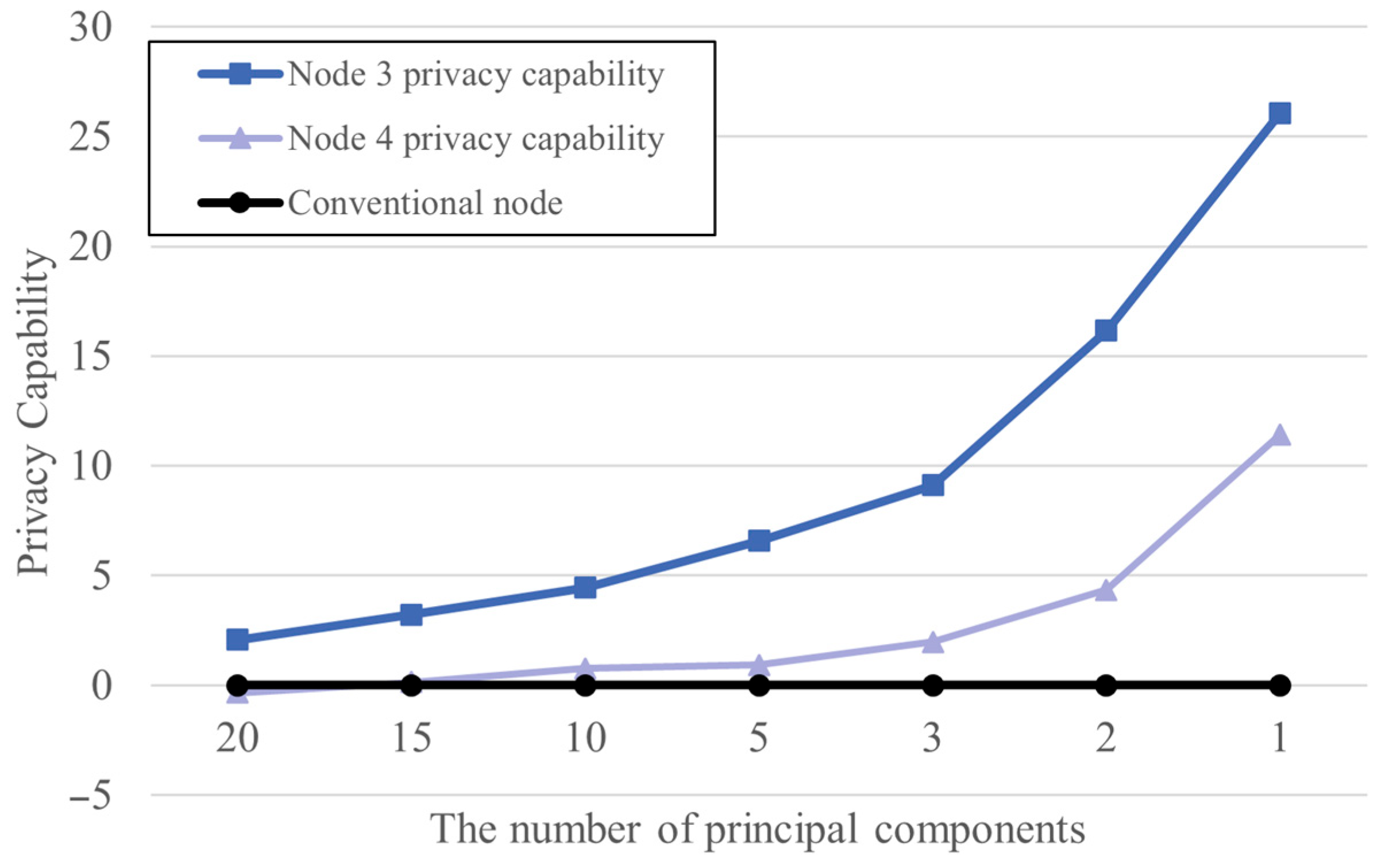
Privacy Capability = (Normal Accuracy − Attacker Accuracy)
To evaluate whether the proposed method effectively protects data privacy, a privacy metric was defined and used. The privacy metric, defined in Equation (1), represents the difference between the accuracy of the legitimate node and that of the attacker node [32]. Higher accuracy of the legitimate node is maintained while the attacker’s accuracy decreases, thereby enhancing data protection. Therefore, a larger privacy metric indicates a safer data-sharing environment.
Figure 7 shows the changes in privacy metrics according to the number of principal components. The experimental results demonstrate that as the number of principal components decreases, the privacy metric improves, suggesting that dimensionality reduction effectively enhances privacy protection performance.
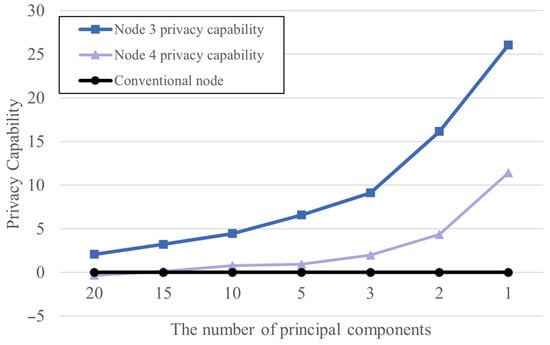
Figure 7.
Privacy capability by principal component values at a 1:10 ratio.
Furthermore, the proposed data-sharing mechanism was confirmed to be practical in that it was able to stably maintain the legitimate node’s accuracy while effectively lowering the attacker node’s accuracy, regardless of the number of principal components. In particular, when the number of principal components was set to a minimum value of 1, the privacy metric was highest, while memory usage for data transmission and reception was significantly reduced, demonstrating excellent cost efficiency.
5. Conclusions
Recent studies on data sampling and secure data sharing in class-imbalanced environments exhibit several limitations, highlighting the need to establish secure data-sharing environments. This requirement is particularly critical for AI-enabled devices operating under resource constraints, where memory and energy efficiency during data transmission and reception must be considered key evaluation metrics. To address these challenges, this study proposes a novel data-sharing mechanism that utilizes PCA-based dimensionality reduction. Experimental results demonstrated that legitimate nodes maintained their original performance even after dimensionality reduction, whereas attacker nodes experienced a performance decline of up to 24% as the number of principal components decreased, confirming the difficulty of data recovery. Notably, when the number of principal components was set to 1, the proposed method achieved approximately 42 times the memory savings compared with conventional full data-sharing methods, in conjunction with the highest privacy metric, demonstrating superior performance in both data security and resource efficiency. In conclusion, the data-sharing mechanism proposed in this study enables the maintenance of learning performance while simultaneously achieving privacy protection and efficiency.
However, this study has certain limitations, as it lacks a comparative analysis of computational efficiency, reconstruction accuracy, and privacy robustness against a range of existing privacy-preserving methods. Moreover, it relies on specific assumptions for data recovery, making it unsuitable for heterogeneous environments with varying data schemas. Therefore, in future work, we aim to conduct a more comprehensive analysis that incorporates diverse heterogeneous environments and state-of-the-art privacy-preserving techniques. In addition, we plan to investigate the generalizability of the proposed approach across a broader range of datasets and settings, including both linear and nonlinear data structures, as well as alternative data compression strategies.
Author Contributions
Conceptualization, Y.-J.L., N.-Y.S. and I.-G.L.; methodology, Y.-J.L., N.-Y.S. and I.-G.L.; software, Y.-J.L.; validation, Y.-J.L.; formal analysis, N.-Y.S.; investigation, N.-Y.S. and Y.-J.L.; resources, Y.-J.L. and N.-Y.S.; data curation, Y.-J.L. and N.-Y.S.; writing—original draft preparation, N.-Y.S. and Y.-J.L.; writing—review and editing, I.-G.L. and Y.-J.L.; visualization, I.-G.L.; supervision, I.-G.L.; project administration, funding acquisition, I.-G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Trade, Industry and Energy (MOTIE) under a Training Industrial Security Specialist for High-Tech Industry grant (RS-2024-00415520) supervised by the Korea Institute for Advancement of Technology (KIAT), the Ministry of Science and ICT (MSIT) under the ICAN (ICT Challenge and Advanced Network of HRD) program (grant IITP-2022-RS-2022-00156310), the National Research Foundation of Korea (NRF) (grant RS-2025-00518150), and the Information Security Core Technology Development program (grant RS-2024-00437252) supervised by the Institute of Information & Communication Technology Planning & Evaluation (IITP).
Data Availability Statement
The dataset used in this study was the UNSW-NB15 dataset, which is available at https://research.unsw.edu.au/projects/unsw-nb15-dataset (last accessed on 2 July 2025).
Conflicts of Interest
Author Na-Yeon Shin was employed by the company T & D SOFT. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript: Table of Abbreviations
| IBE | identity-based encryption |
| ICBM | IoT, cloud, big data, and mobile |
| IID | independent and identically distributed |
| IoNT | Internet of Nano-Things |
| IoT | Internet of Things |
| IPFS | InterPlanetary File System |
| LWE | learning with errors |
| MITM | man-in-the-middle |
| PBDL | permissioned blockchain and deep learning |
| PCA | principal component analysis |
References
- Kankanhalli, A.; Charalabidis, Y.; Mellouli, S. IoT and AI for smart government: A research agenda. Gov. Inf. Q. 2019, 36, 304–309. [Google Scholar] [CrossRef]
- Allam, Z.; Dhunny, Z.A. On big data, artificial intelligence and smart cities. Cities 2019, 89, 80–91. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, D.; Huang, C.; Zhang, H.; Dai, N.; Song, Y.; Chen, H. Artificial intelligence in sustainable energy industry: Status quo, challenges and opportunities. J. Clean. Prod. 2021, 289, 125834. [Google Scholar] [CrossRef]
- Dlamini, Z.; Francies, F.Z.; Hull, R.; Marima, R. Artificial intelligence (AI) and big data in cancer and precision oncology. Comp. Struct. Biotechnol. J. 2020, 18, 2300–2311. [Google Scholar] [CrossRef]
- Betty, J.J.; Ganesh, E.N. Big data and internet of things for smart data analytics using machine learning techniques. In Proceedings of the International Conference on Computer Networks Big Data and IoT (ICCBI-2019), Madurai, India, 19–20 December 2019; Pandian, A., Palanisamy, R., Ntalianis, K., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Ma, X.; Zhu, J.; Lin, Z.; Chen, S.; Qin, Y. A state-of-the-art survey on solving non-IID data in Federated Learning. Future Gener. Comput. Syst. 2022, 135, 244–258. [Google Scholar] [CrossRef]
- Criado, M.F.; Casado, F.E.; Iglesias, R.; Regueiro, C.V.; Barro, S. Non-IID data and Continual Learning processes in Federated Learning: A long road ahead. Inf. Fusion 2022, 88, 263–280. [Google Scholar] [CrossRef]
- Al-Turjman, F.; Zahmatkesh, H.; Shahroze, R. An overview of security and privacy in smart cities’ IoT communications. Trans. Emerg. Telecommun. Technol. 2022, 33, e3677. [Google Scholar] [CrossRef]
- Ioannidou, I.; Sklavos, N. On general data protection regulation vulnerabilities and privacy issues, for wearable devices and fitness tracking applications. Cryptography 2021, 5, 29. [Google Scholar] [CrossRef]
- Zheng, X.; Cai, Z. Privacy-preserved data sharing towards multiple parties in industrial IoTs. IEEE J. Sel. Areas Commun. 2020, 38, 968–979. [Google Scholar] [CrossRef]
- Holla, H.; Sasikumar, A.A.; Gutti, C.; Thumula, K. Advanced privacy and security techniques in federated learning against sophisticated attacks. In Proceedings of the 13th International Symposium on Digital Forensics and Security (ISDFS), Boston, MA, USA, 24–25 April 2025; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Xie, Q.; Jiang, S.; Jiang, L.; Huang, Y.; Zhao, Z.; Khan, S.; Dai, W.; Liu, Z.; Wu, K. Efficiency optimization techniques in privacy-preserving federated learning with homomorphic encryption: A brief survey. IEEE Internet Things J. 2024, 11, 24569–24580. [Google Scholar] [CrossRef]
- Thantharate, P.; Bhojwani, S.; Thantharate, A. DPShield: Optimizing differential privacy for high-utility data analysis in sensitive domains. Electronics 2024, 13, 1233. [Google Scholar] [CrossRef]
- Ahmed, E.O.; Ahmed, A. Differential privacy for deep and federated learning: A survey. IEEE Access 2022, 10, 22359–22380. [Google Scholar] [CrossRef]
- Frimpong, E.; Nguyen, K.; Budzys, M.; Khan, T.; Michalas, A. GuardML: Efficient privacy-preserving machine learning services through hybrid homomorphic encryption. In Proceedings of the 39th ACM/SIGAPP Symposium on Applied Computing (SAC ‘24), Avila, Spain, 8–12 April 2024; Association for Computing Machinery: New York, NY, USA, 2024; pp. 953–962. [Google Scholar] [CrossRef]
- Ishiyama, T.; Suzuki, T.; Yamana, H. Latency-aware inference on convolutional neural network over homomorphic encryption. In Proceedings of the International Conference on Information Integration and Web Intelligence (iiWAS 2022), Virtual Event, 28–30 November 2022; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; Volume 13635, pp. 324–337. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Fugkeaw, S. A secure and efficient data sharing scheme with outsourced signcryption and decryption in mobile cloud computing. In Proceedings of the IEEE International Conference on Joint Cloud Computing (JCC), Oxford, UK, 23–26 August 2021. [Google Scholar]
- Singh, A.K.; Saxena, D. A cryptography and machine learning based authentication for secure data-sharing in federated cloud services environment. J. Appl. Sec. Res. 2022, 17, 385–412. [Google Scholar] [CrossRef]
- Athanere, S.; Thakur, R. Blockchain based hierarchical semi-decentralized approach using IPFS for secure and efficient data sharing. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 1523–1534. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, P.; Tripathi, R.; Gupta, G.P.; Islam, A.K.M.N.; Shorfuzzaman, M. Permissioned blockchain and deep learning for secure and efficient data sharing in industrial healthcare systems. IEEE Trans. Ind. Inform. 2022, 18, 8065–8073. [Google Scholar] [CrossRef]
- Prajapat, S.; Rana, A.; Kumar, P.; Das, A.K. Quantum safe lightweight encryption scheme for secure data sharing in Internet of Nano Things. Comput. Electr. Eng. 2024, 117, 109253. [Google Scholar] [CrossRef]
- Junqin, H.; Linghe, K.; Jingwei, W.; Guihai, C.; Jianhua, G.; Gang, H.; Muhammad, K.K. Secure data sharing over vehicular networks based on multi-sharding blockchain. ACM Trans. Sens. Netw. 2024, 20, 1–23. [Google Scholar] [CrossRef]
- Thanh, L.N.; Nguyen, L.; Hoang, T.; Bandara, D.; Wang, Q.; Lu, Q.; Xu, X.; Zhu, L.; Chen, S. Blockchain-empowered trustworthy data sharing: Fundamentals, applications, and challenges. ACM Comput. Surv. 2025, 57, 1–36. [Google Scholar] [CrossRef]
- Kumar, K.P.; Prathap, B.R.; Thiruthuvanathan, M.M.; Murthy, H.; Pillai, V.J. Secure approach to sharing digitized medical data in a cloud environment. Data Sci. Manag. 2024, 7, 108–118. [Google Scholar] [CrossRef]
- Halder, S.; Newe, T. Enabling secure time-series data sharing via homomorphic encryption in cloud-assisted IIoT. Future Gener. Comput. Syst. 2022, 133, 351–363. [Google Scholar] [CrossRef]
- Nour, M.; Jill, S. UNSW-NB15: A comprehensive data set for network intrusion detection systems (UNSW-NB15 network data set). In Proceedings of the 2015 Military Communications and Information Systems Conference (MilCIS), Canberra, Australia, 10–12 November 2015; IEEE: New York, NY, USA, 2015. [Google Scholar]
- Nour, M.; Jill, S. The evaluation of Network Anomaly Detection Systems: Statistical analysis of the UNSW-NB15 dataset and the comparison with the KDD99 dataset. Inf. Sec. J. Glob. Perspect. 2016, 25, 18–31. [Google Scholar] [CrossRef]
- Nour, M.; Jill, S.; Gideon, C. Novel geometric area analysis technique for anomaly detection using trapezoidal area estimation on large-scale networks. IEEE Trans. Big Data 2017, 5, 481–494. [Google Scholar] [CrossRef]
- Nour, M.; Gideon, C.; Jill, S. Big Data Analytics for Intrusion Detection System: Statistical Decision-Making Using Finite Dirichlet Mixture Models. In Data Analytics and Decision Support for Cybersecurity; Springer: Cham, Switzerland, 2017; pp. 127–156. [Google Scholar]
- Mohanad, S.; Siamak, L.; Nour, M.; Marius, P. NetFlow datasets for machine learning-based network intrusion detection systems. In Big Data Technologies and Applications, Proceedings of the BDTA WiCON 2020 2020, Virtual Event, 11 December 2020; Deze, Z., Huang, H., Hou, R., Rho, S., Chilamkurti, N., Eds.; Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Kil, Y.S.; Lee, Y.J.; Jeon, S.E.; Oh, Y.S.; Lee, I.G. Optimization of privacy-utility trade-off for efficient feature selection of secure Internet of things. IEEE Access 2024, 12, 142582–142591. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).