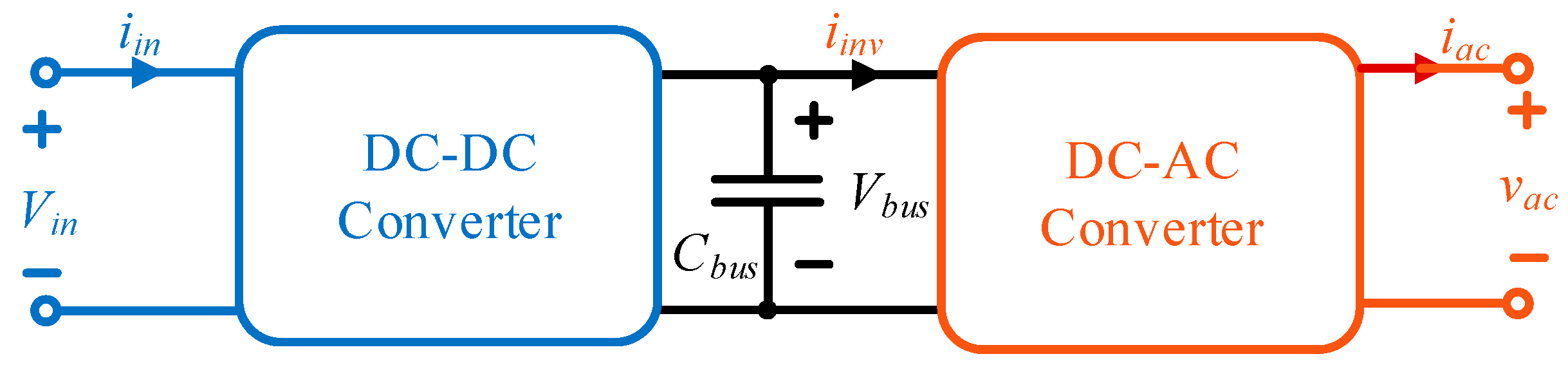A Hybrid Second Harmonic Current Mitigation Strategy for Two-Stage Single-Phase DC–AC Converters

Abstract

The instantaneous AC-side output power of a two-stage single-phase inverter pulsates at twice the output voltage frequency, inducing second harmonic current (SHC) in the front-end DC–DC converter. While conventional SHC mitigation methods mainly focus on controller optimization for PWM-controlled DC–DC converters, LLC resonant converters, which have been widely adopted in two-stage single-phase inverters for high efficiency and soft-switching characteristics, lack tailored solutions due to frequency modulation complexities. To address this gap, this paper first analyzes the propagation mechanism of the SHC in terms of converter output impedance. Then, by simultaneously lowering the open-loop gain and increasing the output impedance of the DC–DC converter at 2f_N, this paper proposes a hybrid SHC mitigation strategy that achieves low SHC and fast dynamic performance for frequency-modulated LLC converters. Finally, a 28 V DC to 220 V/50 Hz AC inverter was developed, and the experimental results verified the effectiveness of the proposed control strategy.

1. Introduction

As the aviation industry evolves toward More-Electric Aircraft (MEA) and All-Electric Aircraft (AEA), onboard power systems are increasingly adopting more efficient architectures such as variable-frequency AC (e.g., 230 VAC, 360–800 Hz) [1,2,3]. However, despite the high efficiency and power density this advanced system offers, specialized power sources tailored for avionics remain incompatible with standard ground equipment. Therefore, a critical need persists for efficiently and reliably converting conventional onboard 28 V DC power to standard 220 V/50 Hz AC to operate crucial medical devices, passenger electronics, and specialized instruments.

Addressing this challenge, two-stage single-phase inverter systems [4], which comprise a front-end DC–DC converter cascaded with a downstream DC–AC inverter, have emerged as prevalent solutions for integrating onboard 28 V DC with ground equipment. This configuration offers advantages in applications requiring wide-range DC input voltage regulation and scenarios involving a high voltage ratio between input sources and output requirements [5]. The front-end DC–DC converter regulates the variable DC input voltage into a stable intermediate DC bus voltage while providing galvanic isolation between input and output. The downstream DC–AC inverter then transforms this regulated DC voltage into the AC output, either to power electrical loads or synchronize with the utility by injecting controlled AC current.

The topology of the two-stage single-phase inverter is shown in Figure 1. The inherent double-frequency power fluctuation in single-phase AC systems creates an instantaneous power imbalance between the AC and DC sides [4,5]. This imbalance induces a double-frequency harmonic current in the front-end DC–DC converter, resulting in elevated switching device current stress, reduced conversion efficiency, and increased intermediate DC bus voltage ripple. Therefore, suppression of this second harmonic current (SHC) is critical to ensure system reliability and performance.

Previous research has explored numerous methods to mitigate SHC in front-end DC–DC converters. The most straightforward approach involves enlarging the intermediate DC bus capacitance [6]. However, this method necessitates the use of bulky electrolytic capacitors, significantly compromising the converter power density. Moreover, an LC resonant circuit tuned at twice the fundamental frequency (2f_N) can be paralleled with the DC bus [6], creating a low-impedance path to absorb SHC. However, the resonant circuit is sensitive to frequency or parameter deviations and reduces the system power density.

To achieve SHC attenuation while preserving power density, researchers have proposed active filtering methods without the utilization of bulky passive components. In [7,8,9,10], an active harmonic compensation circuit is shunt-connected to the intermediate DC bus to inject a phase-inverted SHC, matching the amplitude and frequency of the inherent ripple caused by the downstream DC–AC inverter, thereby canceling the ripple current and stabilizing the bus voltage. However, these approaches introduce trade-offs including increased system complexity, higher implementation costs, and additional switching losses that degrade overall efficiency.

Aiming for SHC suppression without ancillary hardware components, recent advancements have focused on advanced control methodologies for front-end DC–DC converters. These strategies employ dynamic impedance reshaping and adaptive feedforward compensation to attenuate harmonic propagation, while avoiding the need for additional filtering circuits through advanced modulation techniques and multi-loop control architectures. In [11], a high bandwidth inner current loop is inserted after the DC voltage loop of the front-end DC–DC converter to suppress the SHC. Although the SHC can be mitigated, the cutoff frequency of the DC voltage loop is reduced substantially to ensure proper decoupling between the voltage and current control loops. This bandwidth limitation, in turn, degrades the converter’s transient response. An inductor current feedforward strategy, which introduces a virtual resistor in series with the output inductor of the front-end DC–DC converter, is proposed in [12]. However, the virtual resistor elevates the converter output impedance across the whole frequency band, leading to dynamic performance degradation. By implementing a notch filter and PR controller in the voltage control loop [13], the converter output impedance can be reduced significantly at a selected frequency twice the fundamental frequency. However, its control performance is sensitive to the grid frequency, deteriorating rapidly once the frequency deviates. Reference [14] employs a notch filter integrated into the voltage control loop to attenuate the loop gain at twice the fundamental frequency. While effective in harmonic suppression, this approach introduces a significant phase lag, critically constraining the achievable voltage loop crossover frequency and thereby limiting system dynamic performance. Considering that high impedance is preferred only at two times the fundamental frequency, a series bandpass filter-based inductor current feedback control strategy is proposed in [15] to achieve SHC mitigation with enhanced system dynamic performance. In [16], by simultaneously introducing the intermediate bus voltage and inductor current feedback, two virtual impedances are introduced at the output of the DC–DC converter for increasing the converter’s double frequency impedance while decreasing impedance of other frequency bands, further improving the dynamic characteristics of the system. An active disturbance rejection controller based on a notch filter is proposed in [17] for boost converter front-ended two-stage inverters with the voltage loop bandwidth higher than 2f_N. A similar impedance shaping-based SHC mitigation method is proposed for boost PFC converter front-ended PMSM drives [18].

However, existing SHC mitigation strategies predominantly target pulse-width modulation (PWM)-controlled front-end DC–DC converters. In contrast, frequency-modulated LLC resonant converters—favored for high voltage gain, high efficiency, high power density, and inherent soft-switching capabilities—have emerged as a prevalent front-end solution. Current active power decoupling methods primarily utilize PWM duty cycle adjustments to inject virtual impedance, enabling second-order power pulsation suppression. However, limited research addresses SHC mitigation in frequency-modulated LLC resonant converters, where variable switching frequency operation complicates impedance shaping and necessitates novel control paradigms to harmonize harmonic suppression with resonant tank dynamics. In [19], different SHC transfer characteristics of the LLC converter are analyzed, and a parameter design guideline to prevent SHC amplification during fixed-frequency operation is proposed. A voltage-oriented state plane feedforward-based second harmonic voltage ripple suppression method is proposed in [20] for an LLC converter front-ended two-stage rectifier. While this approach eliminates the need for state variable sensing, its efficacy critically depends on precise system modeling. A nonlinear feedforward-based strategy is proposed in [21] for SHC suppression in LLC converter front-ended two-stage rectifiers. While demonstrating effective harmonic attenuation, this method requires accurate system modeling and significant switching frequency variations to adapt to dynamic output current conditions, inducing system efficiency degradation.

To address these challenges, this work proposes a composite SHC mitigation strategy integrating notch filtering and virtual impedance synthesis for LLC converter front-ended single-phase inverters. Unlike existing PWM and PFM-based SHC suppression methods requiring multi-sensor implementations or suffering from wide frequency deviations, the proposed approach achieves comparable harmonic attenuation using only one additional current sensor while maintaining low switching frequency variations. In addition, considering that the converter’s fundamental frequency only relies on the inverter control strategy, the performance of the proposed virtual impedance and the notch filter-based SHC strategy is robust against system parameter variations. By utilizing the downstream inverters’ inherent voltage stabilization capability, the frequency modulation range of the front-end DC–DC converter can be further constrained, enhancing the system efficiency. Section 2 initially elaborates on SHC propagation characteristics under open-loop and closed-loop control of the LLC converter. Section 3 investigates the proposed hybrid SHC mitigation strategy, while Section 4 shows the controller design method and impedance analysis. Experimental results are analyzed and discussed in Section 5. Finally, conclusions are presented in Section 6.

2. SHC Propagation Characteristic Analysis Based on SLLC Converters

Conventional LLC resonant converters are widely adopted for high-efficiency applications due to their inherent soft-switching capabilities, enabling zero-voltage switching (ZVS) of primary-side transistors and zero-current switching (ZCS) of secondary rectifiers across full-load conditions [22]. However, in applications such as the 28 V DC to 220 V/50 Hz AC single-phase inverter investigated in this work, which requires an 8:1 voltage boost ratio and high input currents, the conventional LLC topology faces a significant limitation due to large resonant tank losses. To address this, a secondary-side resonant LLC topology (SLLC) [23] is implemented as the front-end DC–DC stage. By relocating the resonant network to the transformer’s secondary side, circulating currents in the resonant tank are minimized, reducing conduction losses compared to primary-resonant LLC configurations. As illustrated in Figure 2, the two-stage architecture comprises the SLLC converter and a downstream inverter. Note that a single-phase full-bridge topology is adopted for the DC–AC converter, which is regulated by a dual-loop voltage/current controller and bipolar SPWM modulation strategy. For the purpose of SHC analysis, this paper models the inverter as a parallel connection of an ideal DC current source and an SHC source. This approach is justified since this paper mainly focuses on the suppression of the second harmonic current.

Due to the double-frequency (2f_N) pulsating power of the inverter, the SHC from the DC–AC stage is inherently shared between the front-end DC–DC converter and the intermediate DC bus capacitor in two-stage single-phase inverters, as depicted in Figure 2. This SHC propagation originates from the impedance characteristics of the current flow path, where the converter output impedance Z_o(s) and bus capacitor admittance Y_Cbus(s) jointly govern harmonic current distribution at 2f_N.

The SLLC resonant converter regulates output voltage by modulating its switching frequency to adjust the voltage gain of the resonant tank. Unlike pulse-width modulation (PWM)-based counterparts, its small-signal modeling is inherently complex due to the nonlinear dynamics of resonant operation. To address this, the extended describing function (EDF) method [24] is applied under the fundamental harmonic approximation (FHA) framework, enabling the derivation of frequency-domain transfer characteristics. When operating in below resonant or resonant frequency modes (f_sw ≤ f_r), the SLLC converter achieves high conversion efficiency by realizing ZVS across primary devices, and the corresponding equivalent small-signal circuit is illustrated in Figure 3. In the figure, i_inv denotes the current of the downstream DC–AC inverter stage, C_bus denotes the capacitor of the intermediate DC bus, ${\widehat{v}}_g$, ${\widehat{\omega }}_s$, ${\widehat{v}}_{bus}$ are the disturbance of the input voltage, switching frequency, and output voltage, respectively. Z_o(s) and Z_o1(s) are the open-loop output impedance of the SLLC converter with and without C_bus, respectively. K_v and K_d are the coefficients of the controlled voltage source, and can be expressed as follows:

$$K_v=\left\{\begin{array}{c}{\displaystyle \frac{4}{{\pi }^2}}{\displaystyle \frac{kn{V}_g\mathrm{\Omega }(1+k-\frac{1}{{\mathrm{\Omega }}^2})}{R_{ac}\sqrt{(1+k-\frac{1}{{\mathrm{\Omega }}^2}{)}^2+(\frac{1}{\mathrm{\Omega }}-\mathrm{\Omega }{)}^2(\frac{{\pi }^2}{8}kQ{)}^2}}}, \mathsf{\Omega }={\displaystyle \frac{{\mathrm{\Omega }}_s}{{\mathrm{\Omega }}_r}}\ge 1\\ {\displaystyle \frac{2k}{\pi \mathit{sin}(\mathrm{\Omega }\pi /2)}}{\displaystyle \frac{1}{\sqrt{(1+k-\frac{1}{{\mathrm{\Omega }}^2}{)}^2+(\frac{1}{\mathrm{\Omega }}-\mathrm{\Omega }{)}^2(\frac{{\pi }^2}{8}kQ\frac{1}{\mathit{sin}(\mathrm{\Omega }\pi /2)}{)}^2}}},\mathsf{\Omega }<1\end{array}\right.$$

(1)

$$K_d=\left\{\begin{array}{c}-{\displaystyle \frac{4n{V}_g}{\pi }}{\displaystyle \frac{1}{k{\mathrm{\Omega }}_r}}, \mathrm{\Omega }\ge 1\\ \begin{array}{c}{\displaystyle \frac{4nk{V}_g}{\pi \cdot {\mathrm{\Omega }}_r}}[{\displaystyle \frac{-\frac{\pi }{2}\frac{\mathit{cos}(\pi \mathrm{\Omega }/2)}{{\mathit{sin}}^2(\pi \mathrm{\Omega }/2)}}{\sqrt{(1+k-\frac{1}{{\mathrm{\Omega }}^2}{)}^2+(\frac{1}{\mathrm{\Omega }}-\mathrm{\Omega }{)}^2(\frac{{\pi }^2}{8}kQ{)}^2}}}+\\ {\displaystyle \frac{\left(\right(\frac{1}{{\mathrm{\Omega }}^2}-{\mathrm{\Omega }}^2\left)\right(\frac{{\pi }^2}{8}kQ{)}^2-(1+k-\frac{1}{{\mathrm{\Omega }}^2})\frac{2}{{\mathrm{\Omega }}^2})\frac{1}{\mathrm{\Omega }\mathit{sin}(\pi \mathrm{\Omega }/2)}}{(\sqrt{(1+k-\frac{1}{{\mathrm{\Omega }}^2}{)}^2+(\frac{1}{\mathrm{\Omega }}-\mathrm{\Omega }{)}^2(\frac{{\pi }^2}{8}kQ{)}^2}{)}^3}}], \Omega <1\end{array}\end{array}\right.$$

(2)

$$L_e=\left\{\begin{array}{c}(1+{\displaystyle \frac{1}{{\mathsf{\Omega }}^2}})L_r,\hspace{1em}\mathsf{\Omega }\ge 1\\ (1+{\displaystyle \frac{1}{{\mathsf{\Omega }}^2}})L_r+(1-\mathsf{\Omega })L_s,\omega <1\end{array}\right.$$

(3)

Based on the derived small signal model, the system control block diagram can be obtained to facilitate stability analysis and controller design for robust voltage regulation under wide input variations. Considering that the system input voltage is stable, ${\widehat{v}}_g\left(s\right)$ is approximately 0. Then, the open-loop and closed-loop control block diagrams of the system can be obtained and are depicted in Figure 4 and Figure 5, respectively.

Consequently, the system transfer function from output voltage to switching frequency can be derived as (3). Note that the derivation with a switching frequency smaller than the resonance frequency is illustrated for the sake of simplicity. As can be seen from Figure 6, the derived model aligns well with that in the simulation, validating the small-signal approximation accuracy. Consequently, the voltage loop PI controller can be designed by setting the bandwidth and phase margin to 450 Hz and 45°, respectively. Note that the parameters of the converter are listed in

Table 1. Parameters of the converter.

Converter Name	Parameter	Value
Front-end SLLC converter	Transformer turn ratio Tr	1:14
	Resonant inductance Lr	159.2 µH
	Auxiliary inductor Ls	955.2 µH
	Resonant capacitor Cr	15.91 nF
	Intermediate bus capacitor Cbus	470 µF
	Intermediate bus voltage Vbus	380 V
	Resonant frequency fr	100 kHz
	Virtual impedance	400 Ω
Down-stream full-bridge inverter	Output inductance Lf	10 mH
	Output capacitor Cf	700 nF
	Switching frequency fs	20 kHz
	Output power Po	400 VA
	Voltage loop controller kpv kr	0.015 20
	Current loop controller kpi kii	2, 400

.

$$G_{vs}(s)={\displaystyle \frac{{\widehat{v}}_{bus}}{{\widehat{f}}_s}}={\displaystyle \frac{2\pi {\widehat{v}}_{bus}}{{\widehat{\omega }}_s}}={\displaystyle \frac{4{\pi }^2{K}_d{R}_o}{s^2{L}_e{C}_{out}{R}_o{\pi }^2+s{L}_e{\pi }^2+8R_o}}$$

(4)

After designing the converter parameters, this paper employs an impedance-based analytical framework to quantify SHC propagation dynamics in the two-stage inverter. The methodology focuses on frequency-dependent interactions through admittance ratio analysis. According to Figure 4, the open-loop output impedance of the SLLC converter can be derived as follows:

$$Z_o(s)=-{\displaystyle \frac{{\widehat{v}}_o}{{\widehat{i}}_{inv}}}={\displaystyle \frac{s{L}_e{\pi }^2}{8+C_{bus}{L}_e{\pi }^2{s}^2}}$$

(5)

where ω_s denotes the switching frequency, ω_r denotes the resonance frequency, and L_e denotes the equivalent inductance. Assuming C_bus is small enough and all the SHC is provided by the SLLC converter, then the SLLC converter open-loop output impedance without the output capacitor can be derived as follows:

$$Z_{o1}(s)\approx {\displaystyle \frac{s{L}_e{\pi }^2}{8}}$$

(6)

In order to analyze the SHC flow path under open-loop state, the corresponding equivalent circuit of the SLLC converter is drawn in Figure 7. As can be seen, the SHC from the downstream DC–AC converter is supplied by both the converter and the intermediate bus capacitor, and the SHC division ratio is governed by the frequency-dependent impedance magnitudes at 2f_N.

Then, the SHC of the SLLC converter output current under open-loop control can be derived as follows:

$$i_{R\_op}={\displaystyle \frac{8}{8+C_{bus}{L}_e{\pi }^2{s}^2}}{i}_{2nd}$$

(7)

where i_2nd is the SHC required by the load, and i_Cbus is the capacitor current. Note that L_e remains constant, since the open-loop SLLC converter operates at a fixed switching frequency. Under these conditions, (7) reveals that the amplitude of the SHC provided by the SLLC converter is inversely proportional to the intermediate bus capacitance.

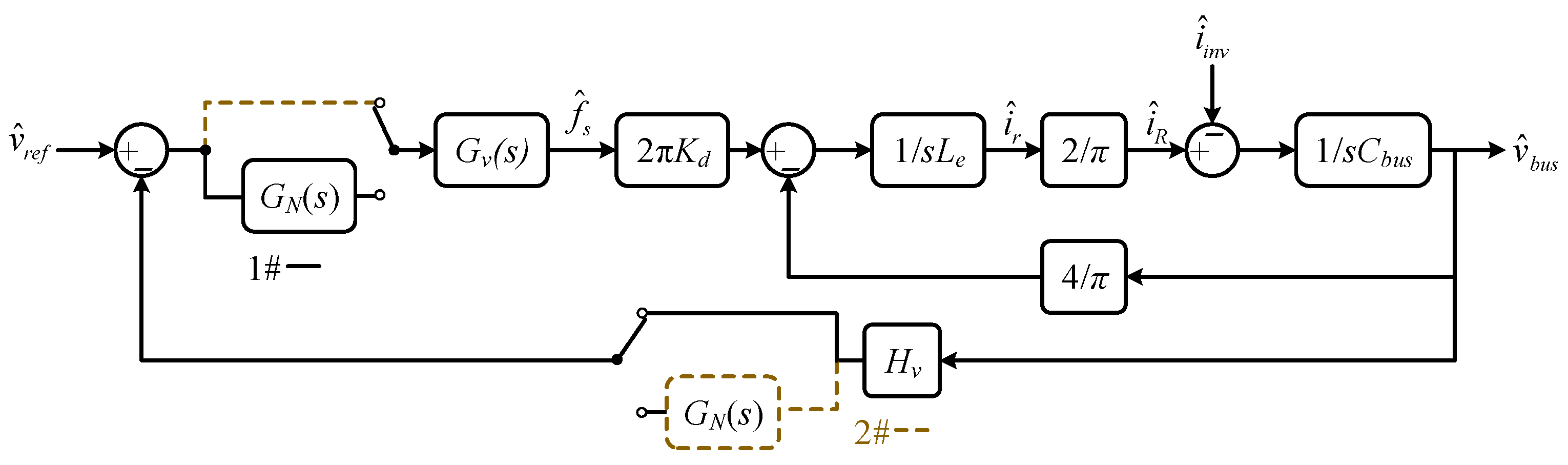
By shifting the comparison point in the closed-loop control block diagram shown in Figure 5, the equivalent control block diagram is obtained as depicted in Figure 8. Based on the figure, the SHC flow path of the SLLC converter under feedback control can be modeled, and the corresponding equivalent circuit is depicted in Figure 9. As can be seen, the controller introduces a virtual impedance Z_vs(s) in parallel with the open-loop output impedance Z_o1(s). Note Z_vs(s) can be derived as follows:

$${\displaystyle \frac{1}{Z_{vs}(s)}}=H_v{G}_v(s)2\pi K_d{\displaystyle \frac{1}{s{L}_e}}{\displaystyle \frac{2}{\pi }}={\displaystyle \frac{4H_v{K}_d{G}_v\left(s\right)}{s{L}_e}}$$

(8)

Meanwhile, the SHC of the SLLC converter output current under closed-loop control can be derived as follows:

$$i_{R\_cl}={\displaystyle \frac{8+4G_v\left(s\right)H_v{K}_d{\pi }^2}{8+4G_v\left(s\right)H_v{K}_d{\pi }^2+C_{bus}{L}_e{\pi }^2{s}^2}}{i}_{2nd}$$

(9)

where i_{R_cl} is the SHC provided by the converter under closed-loop state.

Assuming a proportional–integral (PI) controller is utilized in the voltage control loop, then Z_vs(s) can be further derived as follows:

$${\displaystyle \frac{1}{Z_{vs}\left(s\right)}}={\displaystyle \frac{1}{Z_{vs1}\left(s\right)}}+{\displaystyle \frac{1}{Z_{vs2}\left(s\right)}}={\displaystyle \frac{1}{s^2\frac{L_e}{4H_v{K}_d{k}_{iv}}}}+{\displaystyle \frac{1}{s\frac{L_e}{4H_v{K}_d{k}_{pv}}}}$$

(10)

where k_pv and k_iv are the proportional and integral coefficients of the voltage controller, respectively. From (10), it can be seen that Z_vs(s) is the parallel connection of Z_vs1(s) and Z_vs2(s). Note that Z_vs1(s) can be seen as a negative resistor due to its constant −180° phase angle, while Z_vs2(s) behaves like an inductor at 2f_N. The existence of both impedances contributes to lowering the SLLC converter output impedance, and as k_pv/k_iv increases, the output impedance can be further decreased. Consequently, increased SHC conductance through the front-end SLLC converter via the resonant tank, H-bridge, and DC input capacitor, as illustrated in Figure 10. This unintended redistribution introduces higher switching and passive component losses, revealing a compromise in intermediate bus voltage regulation: the voltage regulation capability of the controller inherently conflicts with the SHC mitigation performance.

3. Proposed SHC Mitigation Strategy

3.1. Principle of the SHC Mitigation Strategy

According to Figure 5, the transfer function from the converter switching frequency to the output voltage, and the corresponding voltage loop gain T(s) are derived as follows:

$$G_{v\_fs}(s)={\displaystyle \frac{4K_d{\pi }^2}{s^2{\pi }^2{L}_e{C}_{bus}+8}}$$

(11)

$$T_v\left(s\right)=H_v{G}_v\left(s\right)G_{v\_fs}\left(s\right)$$

(12)

Then, the closed-loop output impedance of the SLLC converter can be derived as follows:

$$Z_{o\_CL}(s)={\displaystyle \frac{Z_o\left(s\right)}{1+T_v\left(s\right)}}$$

(13)

By substituting (5), (11), and (12) into (13), and assuming C_bus is sufficiently small to be neglected, most of the SHC flows into the front-end converter. Under these circumstances, the closed-loop output impedance of the SLLC converter without C_bus can be derived as follows:

$$Z_{o1\_CL}(s)={\displaystyle \frac{Z_{o1}\left(s\right)}{1+0.5H_v{G}_v\left(s\right)K_d{\pi }^2}}$$

(14)

Effective suppression of the SHC within the front-end SLLC converter necessitates enlarging the amplitude of Z_{o1_CL}(s) at twice the fundamental frequency. As derived in (14), two distinct strategies enable this increase:

(1) Lowering the amplitude of the system open-loop gain at 2f_N.

(2) Increasing the amplitude of the open-loop output impedance Z_{o1_CL}(s) at 2f_N.

It is important to note that increasing Z_{o1_CL}(s) through the first method has a limit: the maximum value of Z_{o1_CL}(s) that can be reached is Z_o1(s), which occurs when the amplitude of G_v(s) at 2f_N becomes zero. Moreover, to effectively absorb SHC and limit voltage ripple at the intermediate DC bus, C_bus must be sized based on the double-frequency power pulsation, and the minimum capacitance can be derived as follows:

$$C_{bus}={\displaystyle \frac{P_o}{2\pi \cdot V_{bus}\cdot \Delta V_{bus}}}{\displaystyle \frac{1}{f_{ac}}}$$

(15)

where P_o is the output power, V_bus is the intermediate bus voltage, and ΔV_bus is the maximum allowable voltage ripple.

3.2. Hybrid SHC Mitigation Strategy

Based on the two suppression principles established in the previous section, this paper proposes a hybrid SHC mitigation strategy for two-stage single-phase inverters. This approach can simultaneously attenuate the voltage loop gain at 2f_N through notch filter integration and amplify open-loop output impedance at 2f_N via virtual impedance synthesis. This coordinated action achieves SHC reduction while maintaining voltage loop bandwidth to overcome the compromise between harmonic suppression and dynamic performance degradation observed in conventional methods.

3.2.1. Notch Filter-Based SHC Mitigation Strategy

To attenuate the open-loop gain at 2f_N, a notch filter-based SHC mitigation strategy (NFS), where the filter G_N(s) centered at 2f_N is cascaded within the voltage loop regulator G_v(s), is proposed. The control block diagram is shown in Figure 11, and the expression of G_N(s) is given as follows:

$$G_N(s)={\displaystyle \frac{(s/{\omega }_N{)}^2+1}{(s/{\omega }_N{)}^2+s/(Q\cdot {\omega }_N)+1}}$$

(16)

The frequency-selective attenuation mechanism elevates the output impedance characteristic of the SLLC converter at 2f_N, thereby redirecting SHC circulation to the DC bus capacitor rather than through power semiconductor components. Significantly, the control architecture maintains the converter loop gain across non-targeted frequencies, ensuring enhanced harmonic impedance shaping for SHC mitigation and preservation of transient response dynamics. The proposed notch filter-based strategy demonstrates placement flexibility, achieving equivalent SHC suppression when implemented in the voltage feedback loop configuration, as shown in Figure 11. Note that to ensure system stability when implementing the NFS strategy, the output of the notch filter is cascaded with a unity-gain low-pass filter.

After inserting a filter into the voltage control loop, the closed-loop output impedance of the SLLC converter can be derived as follows:

$$Z_{o1\_CL\_NF}(s)={\displaystyle \frac{Z_{o1}\left(s\right)}{1+0.5H_v{G}_v\left(s\right)G_N\left(s\right)K_d{\pi }^2}}$$

(17)

3.2.2. Virtual Impedance-Based SHC Mitigation Strategy

As can be seen from (17), the NFS control strategy has a limited influence on the SLLC converter’s closed-loop output impedance. Accordingly, following the SHC suppression principle listed in the previous section, a series of virtual impedance Z_s(s) is introduced at the output of the diode rectifier bridge, thereby significantly increasing the closed-loop output impedance of the SLLC converter, as shown in Figure 12.

The virtual impedance Z_s(s) must exhibit frequency-selective characteristics to balance impedance enhancement and dynamic performance preservation. Specifically, Z_s(s) should be designed to present high impedance exclusively at 2f_N for harmonic suppression, while maintaining near-zero impedance across all other frequencies. This targeted impedance profile prevents broad-spectrum output impedance amplification that would otherwise degrade the converter’s transient response and voltage regulation bandwidth. The required amplitude–frequency response of Z_s(s), featuring a sharp resonance peak at 2f_N, is rigorously defined in Figure 13.

According to Figure 13, the basic form of the virtual impedance Z_s(s) is as follows:

$$Z_s\left(s\right)=r_s{G}_{BPF}\left(s\right)$$

(18)

where r_s is the impedance amplitude of Z_s(s) at 2f_N, G_BPF(s) is the transfer function of the bandpass filter (BPF) centered at 2f_N with the following expression.

$$G_{BPF}(s)={\displaystyle \frac{{\omega }_{b}s}{s^2+{\omega }_{b}s+{{\omega }_0}^2}}$$

(19)

where ω_b = 2πf_b is the BPF bandwidth, ω₀ = 2πf₀ is the BPF center frequency. Note that the gain of the BPF is 1 at 2f_N. To ensure sufficient coverage of voltage frequency variations, f_b must maintain a minimum threshold. Conversely, excessive bandwidth expansion would introduce undesirable impedance amplification in out-of-band frequency ranges. Through systematic analysis of these competing requirements, an optimal bandwidth of f_b = 10 Hz has been determined in this paper, achieving effective frequency selectivity while maintaining satisfactory out-of-band rejection characteristics.

Based on the aforementioned analysis, virtual impedance can be achieved through feedback control of the SHC, which is extracted from the rectifier bridge output current using the BPF. This configuration leads to the modified SLLC converter control architecture, as shown in Figure 14. Then, the equivalent output impedance of the converter can be expressed as follows:

$$Z_R(s)={\displaystyle \frac{ {\pi }^2}{8}}(s{L}_e+r_s{G}_{BPF}(s))$$

(20)

where Z_R(s) is the output impedance with VI implemented.

As can be seen from (20), the output impedance of the SLLC converter at 2f_N can be adjusted by tuning r_s.

To implement a series virtual impedance within the control system, the feedback point for the rectifier bridge current shown in Figure 14 can be moved forward to either the output or input of the voltage controller. The former method effectively superimposes a double-frequency component onto the switching frequency via the feedback branch. The latter, however, superimposes a double-frequency voltage component onto the reference voltage through its feedback branch. While their working principles are identical, the design of the transfer function and control parameters on their respective feedback branches differs. Control block diagrams of the two methods are shown in Figure 15 and Figure 16, respectively. Note that transfer functions of the feedback are shown in Equations (21) and (22), respectively.

$$G_f(s)={\displaystyle \frac{1}{4K_d}}$$

(21)

$$G_f^{\prime }(s)={\displaystyle \frac{1}{4K_d{G}_v\left(s\right)}}$$

(22)

After adopting the control strategy of series virtual impedance of the rectifier bridge branch, the closed-loop output impedance of the SLLC converter that does not include C_bus is as follows:

The closed-loop output impedance of the SLLC converter, excluding C_bus, can be expressed as follows after implementing the series virtual impedance control strategy:

$$Z_{o1\_CL\_VI}(s)={\displaystyle \frac{{\pi }^2(s{L}_e+r_s{G}_{BPF}(s\left)\right)}{8+4G_v\left(s\right)H_v{K}_d{\pi }^2}}$$

(23)

3.2.3. The Proposed Hybrid SHC Mitigation Method

To achieve a superior SHC suppression effect, this paper proposes to simultaneously implement the NFS and VI-based SHC mitigation strategy. This hybrid method can increase the open-loop output impedance of the SLLC converter at 2f_N while reducing the voltage loop gain at the same frequency, and consequently, further amplifies the SLLC converter’s closed-loop output impedance at 2f_N. The control block diagram of the SLLC converter under this hybrid control scheme is shown in Figure 17, and its closed-loop output impedance is derived in (24).

$$Z_{o1\_CL\_NF+BPF}(s)={\displaystyle \frac{Z_R\left(s\right)}{1+0.5G_v\left(s\right)G_N\left(s\right)H_v{K}_d{\pi }^2}}$$

(24)

4. Parameters Design and Performance Analysis

4.1. Closed-Loop Parameter Design

According to Mason’s theorem, the open-loop gain of the system with virtual impedance shown in Figure 15 can be derived as follows:

$$T_{v\_BPF}(s)={\displaystyle \frac{4{\pi }^2{G}_v\left(s\right)H_v{K}_d}{8+{\pi }^{2}s{C}_{bus}(s{L}_e+r_s{G}_{BPF}(s\left)\right)}}$$

(25)

As Figure 18 illustrates, the system’s open-loop gain exhibits two resonant spikes and sharp phase jumps in its amplitude and frequency curve, due to the influence of G_BPF(s). These characteristics can potentially lead to system instability, and to suppress these resonant spikes, a damping resistor, r_d, can be added in series with the introduced VI r_sG_BPF(s). This modification smooths the phase-frequency curve of the loop gain, thereby increasing the system stability margin. Based on a trial-and-error approach, r_d is set to 0.1r_s to effectively suppress the resonant peak with minimal impact on SHC mitigation performance.

By replacing r_sG_BPF(s) with r_sG_BPF(s) + r_d in (25), the system loop gain with a damping resistor can be derived as follows:

$$T_{v\_BPF\_D}(s)={\displaystyle \frac{4{\pi }^2{G}_v\left(s\right)H_v{K}_d}{8+{\pi }^{2}s{C}_{bus}(s{L}_e+r_s{G}_{BPF}(s)+r_d)}}$$

(26)

The yellow line shown in Figure 18 is the loop gain Bode plot after damping. It can be seen that the resonant peak is effectively suppressed, and the severity of system phase changes is reduced, significantly enhancing stability margins.

Normally, a PI controller is utilized as the voltage regulator with the following expression:

$$G_v(s)=K_p+{\displaystyle \frac{K_i}{s}}$$

(27)

where the crossover frequency f_L is as follows:

$$f_L={\displaystyle \frac{K_i}{2\pi K_p}}$$

(28)

To enhance SHC mitigation performance, the system cutoff frequency is set below 2f_N. This prevents interaction with the filter introduced by the NFS strategy, which is centered at 2f_N. When f_L of the PI controller is significantly smaller than the system cutoff frequency, the voltage controller can be simplified to a proportional controller, K_p. Then, by the definition of cutoff frequency, the system loop gain is as follows:

$$\left|T_{v\_BPF\_D}\right(j2\pi f_c\left)\right|=1$$

(29)

Based on (28) and (29), K_p and K_i can be derived as follows:

$$K_p={\displaystyle \frac{\sqrt{{\left(8-4{\pi }^4{f_c}^2{L}_e{C}_{bus}\right)}^2+(0.2{\pi }^3{f}_c{C}_{bus}{r}_s{)}^2}}{4{\pi }^2{H}_v{K}_d}}$$

(30)

$$K_i=10\pi \cdot K_p$$

(31)

Note that f_L is 5 Hz in the paper.

Moreover, to analyze the SHC magnitude entering the front-end DC–DC converter following the implementation of the proposed controller, the transfer function relating the DC–AC converter input current to the DC–DC converter rectifier output current is derived as follows:

$$G_{i{i}_{BP{F}_D}}\left(s\right)={\displaystyle \frac{8+4G_v\left(s\right)H_v{K}_d{\pi }^2}{8+4{\pi }^2{G}_v\left(s\right)H_v{K}_d+{\pi }^{2}s{C}_{bus}\left(s{L}_e+r_s{G}_{BPF}\left(s\right)+r_d\right)}} (0-1)$$

Then, α_SHC, which stands for the percentage of the SHC contained in the rectifier bridge of the SLLC converter, can be obtained as follows:

$$\begin{array}{l}\left|G_{i{i}_{BP{F}_D}}\left(j2\pi \cdot 2f_{ac}\right)\right|= \\ {\displaystyle \frac{\sqrt{{\left(4{\pi }^2{H}_v{K}_d{K}_p+8\right)}^2}}{\sqrt{(4.4{\pi }^{3}Cbus{f}_{ac}rs{)}^2+{\left(4{\pi }^2{H}_v{K}_d{K}_p+8-16{\pi }^4{C}_{bus}{f_{ac}}^2{L}_e\right)}^2}}}\le {\alpha }_{SHC}\end{array}$$

(32)

With α_SHC = 0.05, and by incorporating the data from Table 1 into (32), the magnitude of the VI can be derived as follows:

$$r_s\ge 368.5$$

(33)

According to (33), if the SHC flowing into the SLLC converter is confined within 5%, the value of r_s should be larger than 368.5 Ω. However, since the actual BPF is non-ideal, increasing r_s will also elevate the output impedance of the SLLC converter in frequency bands other than 2f_N, thereby affecting the converter’s dynamic performance. Consequently, r_s cannot be too large and is set to 400 Ω in the paper. After designing the VI, parameters of the voltage loop controller can then be obtained utilizing (30) and (31), respectively.

4.2. SLLC Converter Output Impedance Comparison Under Different Control Strategies

The closed-loop output impedance of the SLLC converter under different control strategies is shown in Figure 19. Note that the solid black line indicates the impedance of the intermediate bus capacitor. The following can be observed from Figure 19:

• When the SLLC converter operates under closed-loop control without an SHC suppression strategy, its closed-loop output impedance, Z_{o1_CL}(s), is much smaller than the impedance of the intermediate bus capacitor at 2f_N. This leads to a significant amount of SHC flowing into the SLLC converter.
• When adopting the NFS control strategy, the integrated notch filter ensures that the closed-loop voltage control does not significantly reduce the output impedance at 2f_N. Consequently, the amplitude of the SLLC converter closed-loop output impedance, Z_{o1_CL_NF}(s), at 2f_N is notably increased, leading to a reduction in the second harmonic current content within the converter.
• Implementation of the VI-based SHC mitigation strategy introduces a series-connected virtual impedance within the rectifier bridge, selectively increasing the SLLC converter output impedance at 2f_N. Consequently, the magnitude of the output impedance Z_{o1_CL_BPF}(s) rises significantly, reducing SHC penetration into the SLLC converter.
• Implementation of both the NF- and VI-based control strategy—cascading a notch filter in the voltage loop and inserting virtual impedance in series with the rectifier bridge—maximizes the magnitude of the SLLC converter output impedance Z_{o1_CL_NF+BPF}(s) at 2f_N. This selective impedance peaking achieves optimal SHC suppression.

5. Experimental Verification

To validate the proposed control strategy, a two-stage DC–AC converter prototype was developed in this paper. Key parameters are detailed in Table 1, with the physical implementation shown in Figure 20. Note that the parameters design strategy of the DC–AC converter has been well-established in previous studies [25,26]; this paper presents only the designed parameter values. To analyze the SHC mitigation performance, this section presents experimental results for the proposed NF, VI, and NF+VI control strategies with a detailed comparison.

The open- and closed-loop converter input current, resonant inductor current, intermediate bus voltage, output voltage, and output current waveforms are shown in Figure 21 and Figure 22, respectively. As can be seen, the closed-loop implementation increases the SHC amplitude in the input current from 30% to 70% based on FFT analysis, attributed to a significant reduction in the SLLC converter output impedance under closed-loop control. While achieving bus voltage stabilization within required fluctuation ranges, this amplified SHC propagation reveals the limitation of solely relying on front-end converter closed-loop regulation, as the resultant harmonic deterioration compromises system efficiency and reliability, necessitating complementary harmonic suppression strategies for balanced voltage and power quality performance.

Figure 23 indicates that after implementing the NF-based SHC mitigation strategy, the SHC amplitude is significantly reduced, and the SHC content in i_dc is about 37%, slightly higher than that of the open-loop state, but substantially lower than the 70% SHC content measured under conventional closed-loop control. These results show the correctness of the theoretical analysis regarding system impedance characteristics. Notably, while the NFS strategy successfully mitigates the SHC induced by closed-loop feedback control, its inherent limitation prevents additional impedance injection at 2f_N. The SHC content increase compared to that of the open-loop system stems from this restricted impedance compensation capability, illustrating the practical constraints of the NFS strategy for SHC suppression.

Figure 24 presents the inverter steady-state waveforms under the VI-based control strategy, while Figure 25 illustrates the FFT analysis of the converter input current. As can be seen, the SHC content in i_dc reduces to about 5.2%, which demonstrates that connecting virtual impedance in series with the converter effectively increases the SLLC converter closed-loop output impedance amplitude at 2f_N, thereby suppressing the SHC of the input current. Although the SHC content is slightly higher than the designed α_SHC (5%), it can validate the effectiveness of the proposed impedance-based analysis. This mitigation mismatch is brought about by the digital delay of the controller and parasitic parameters of the SLLC converter.

To further enhance SHC mitigation performance, the NF and VI-based hybrid strategy is implemented simultaneously. Figure 26 and Figure 27 show the corresponding steady-state waveforms of the inverter. As can be seen from the figures, the converter input current pulsation is barely visible, and the SHC content in i_dc significantly reduces to approximately 1.75%. This enhanced performance demonstrates that the combination of reducing the voltage loop gain and increasing the SLLC converter output impedance maximizes the closed-loop output impedance magnitude at the selected frequency 2f_N, thereby achieving optimal SHC mitigation performance. These experimental results align closely with the impedance-based analysis presented in Figure 19. Then, α_SHC under different control strategies is listed in

Table 2. Comparison of the SHC content under different control strategies.

Control Policy	Second Harmonic Current Content
Open loop	30%
closed loop	70%
NF	37%
VI	5.2%
NF+VI	1.75%

to show the performance of the proposed SHC mitigation strategy.

To validate the controller performance against AC frequency variations, experiments were conducted by changing the inverter reference frequency to 49.5 Hz. As shown in Figure 28, a slight degradation in mitigation performance is observed, with the input current THD increasing from 2.18% to 2.52%. The slight performance degradation is attributed to the gain reduction in the NF and BPF at off-nominal frequencies. A trade-off exists where increasing the filter bandwidth improves frequency adaptation at the expense of peak mitigation performance. However, these results still validate the robustness of the controller against AC frequency deviations.

To verify the converter’s dynamic performance under the proposed hybrid control strategies, experiments were conducted during load transients. Figure 29 shows waveforms during load step changes, specifically from full load to half load and back from half load to full load. As shown, both the DC-link current (i_dc) and the intermediate bus voltage ripple (ΔV_bus) exhibit minimal overshoot and undershoot, settling rapidly to the new steady state. This confirms the excellent dynamic characteristics of the system under the proposed control strategy. Moreover, the input current THD at half load was calculated and is presented in Figure 30. The results show that the THD is comparable to that under full-load conditions, confirming the effectiveness of the proposed control strategy across various operational states.

6. Conclusions

This paper investigated a two-stage single-phase inverter with an SLLC resonant converter as its front-end stage. To address the prevalent SHC problem, the paper first analyzed its generation mechanism and propagation path. Building upon this, the paper proposes a hybrid SHC mitigation strategy for the DC side. The proposed strategy integrates a notch filter in the voltage loop along with a series virtual impedance implemented at the output of the SLLC converter. Experimental results demonstrate that the proposed control strategy mitigates the SHC content to 1.75% while simultaneously ensuring robust dynamic characteristics for the system.