A High-Efficiency GaN-on-Si Power Amplifier Using a Rapid Dual-Objective Optimization Method for 5G FR2 Applications
Abstract
1. Introduction
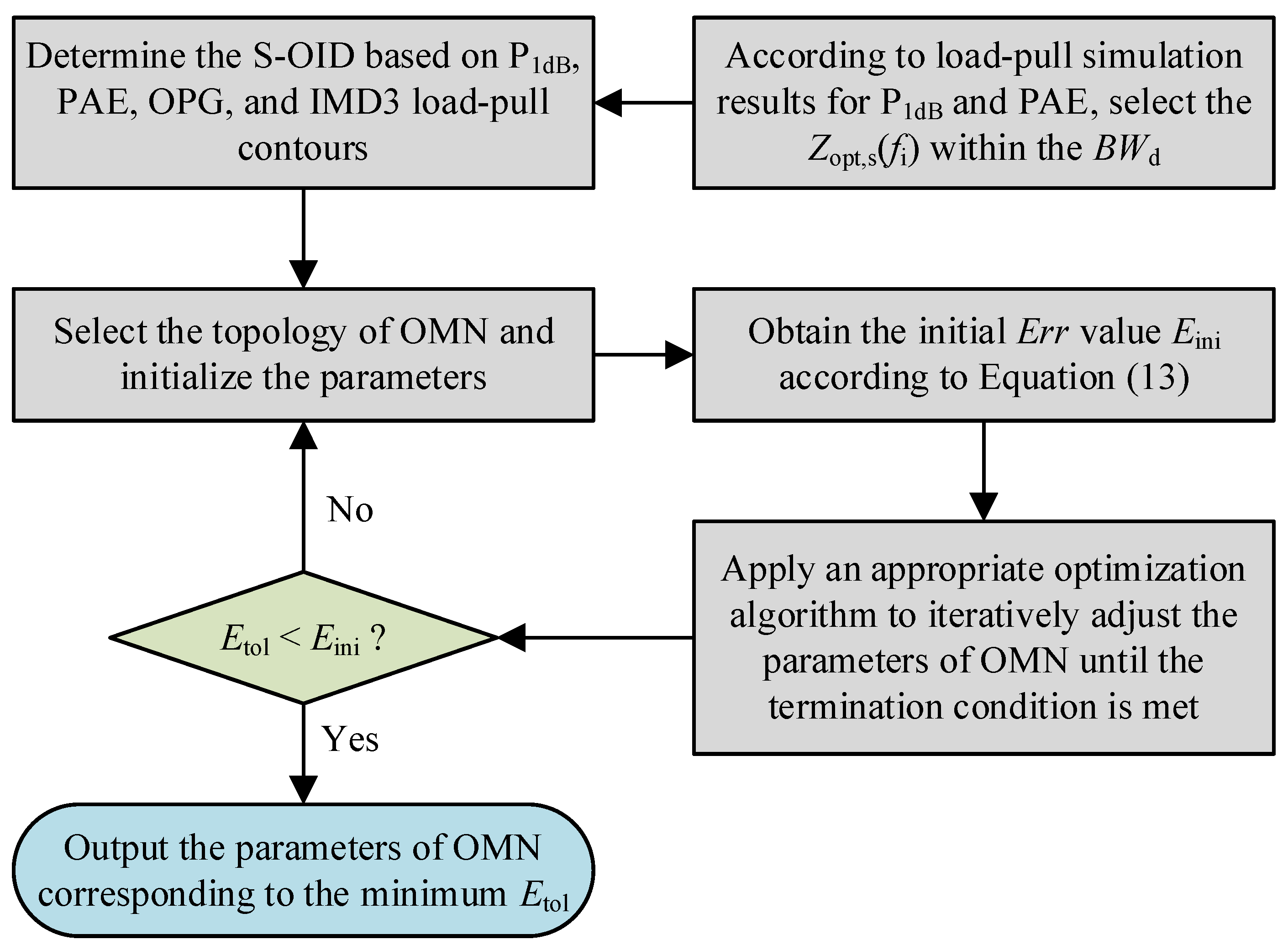
2. A Rapid Output Matching Optimization Method with Dual-Objective Orientation
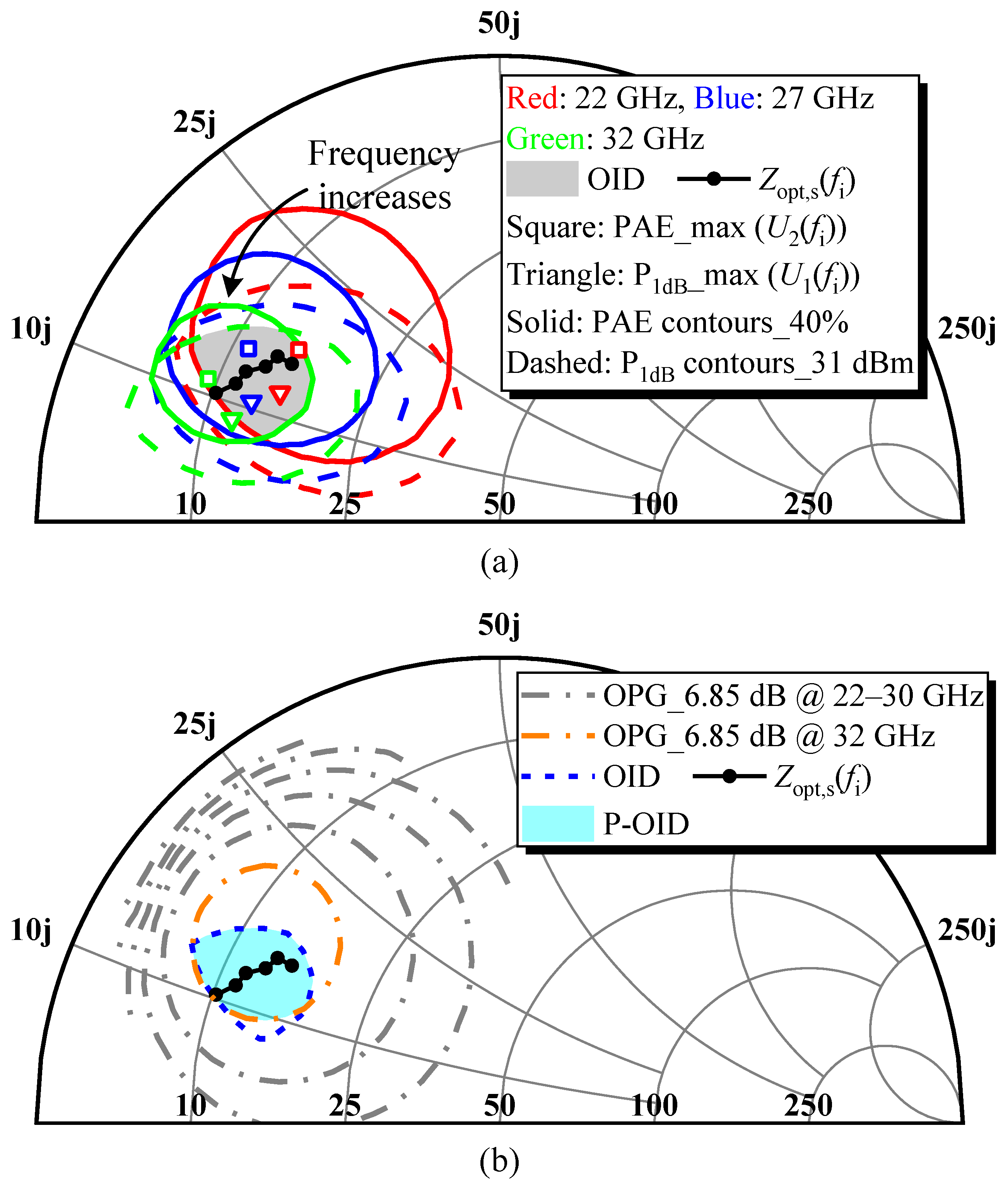
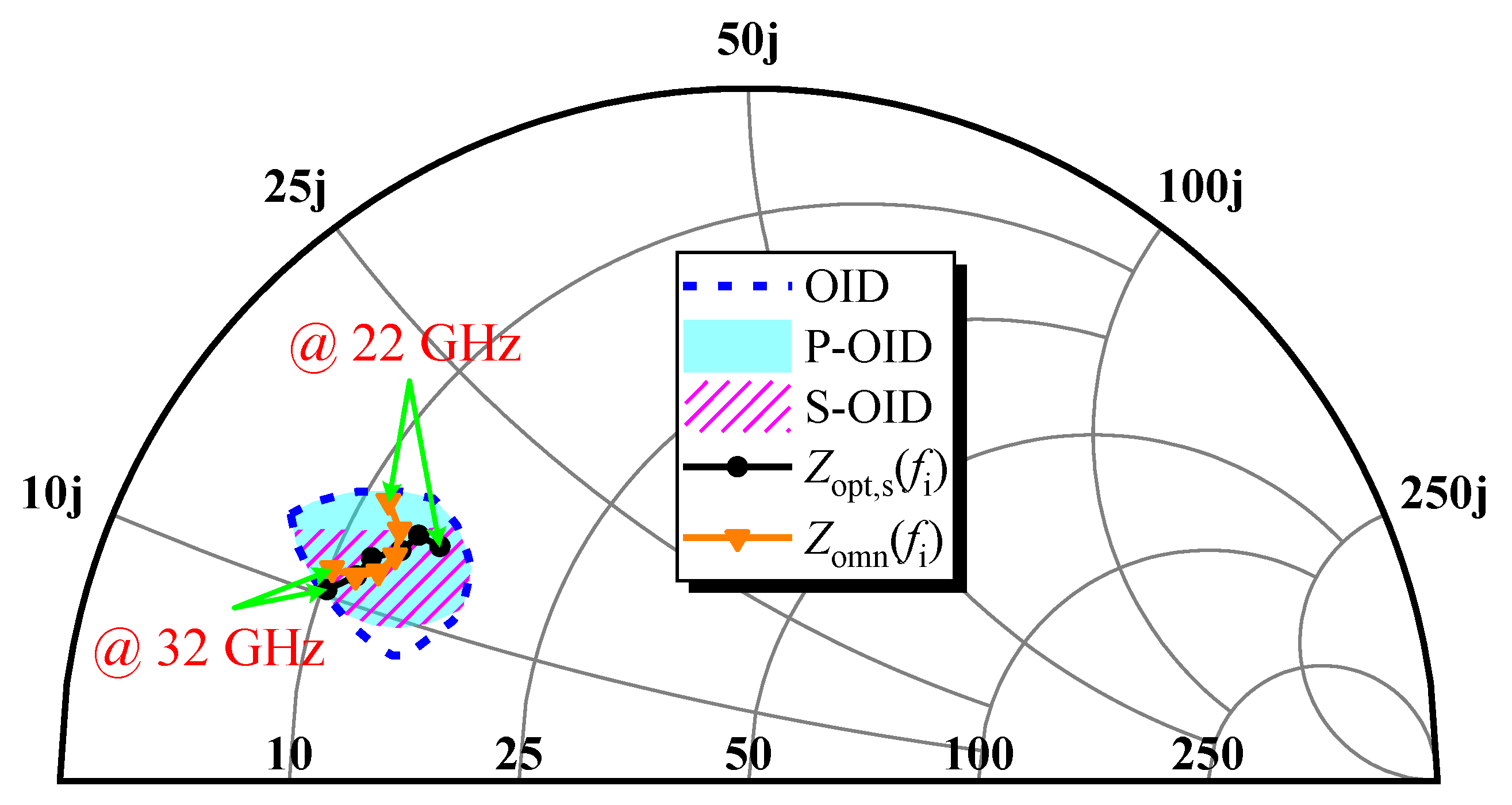
2.1. Selection of the Optimal Load Impedance
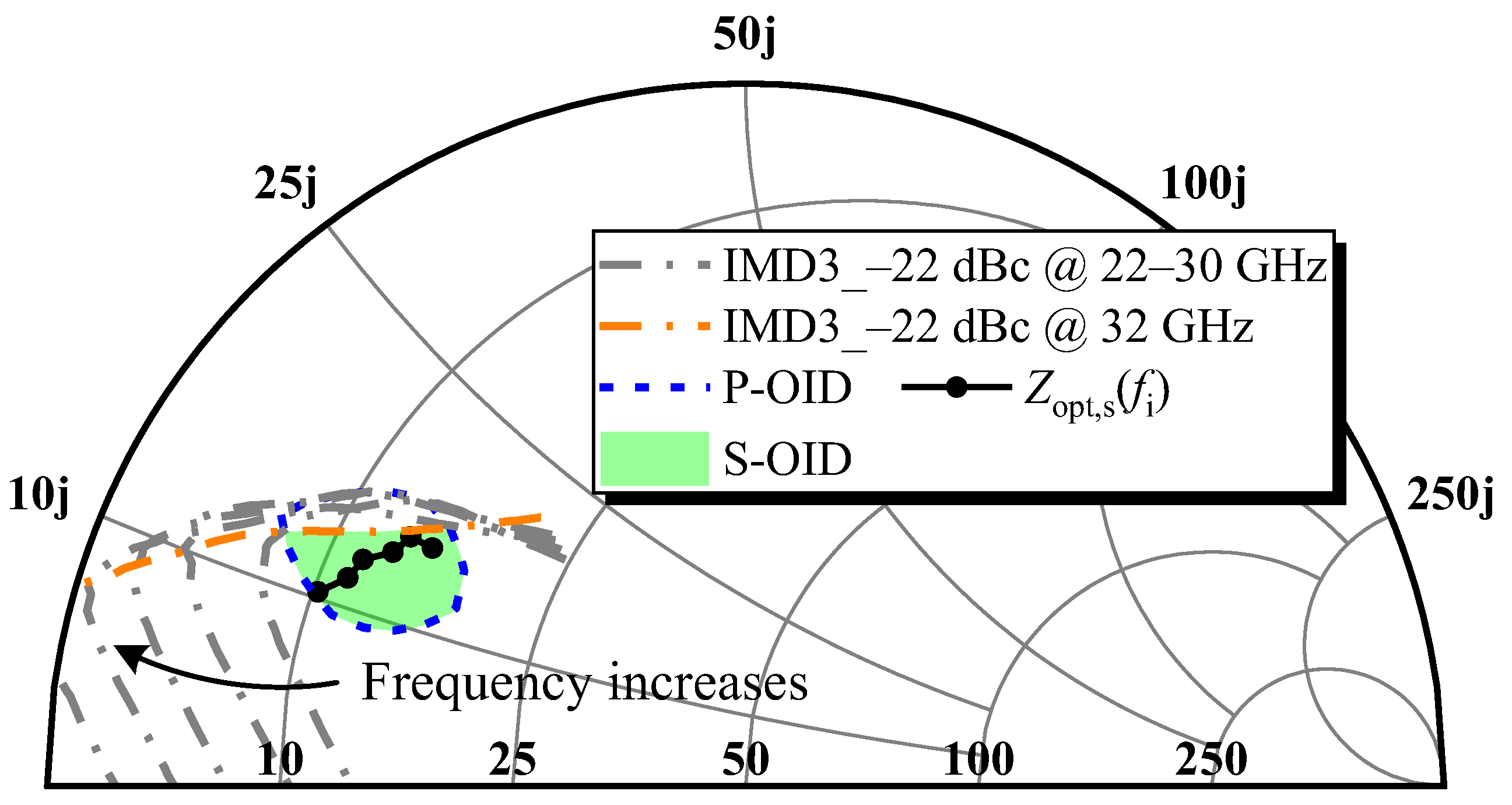
2.2. Determination of the Optimal Impedance Domain
2.3. Verification of the Impedance Point Within the OID
2.4. Error Function Formulation
- (1)
- The out-of-domain penalty
- (2)
- The matching error
- (3)
- Weight allocation
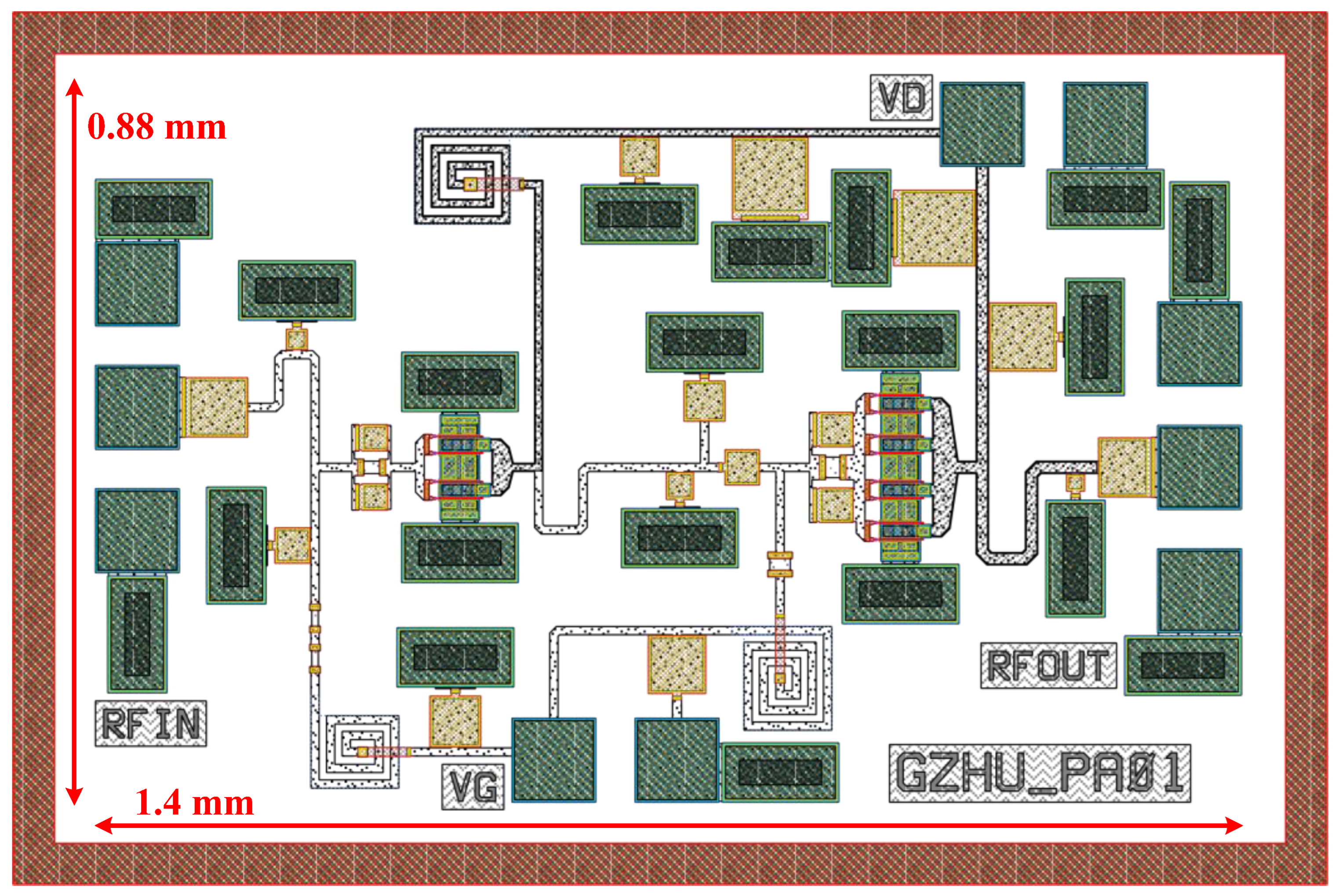
3. Broadband PA Implementation
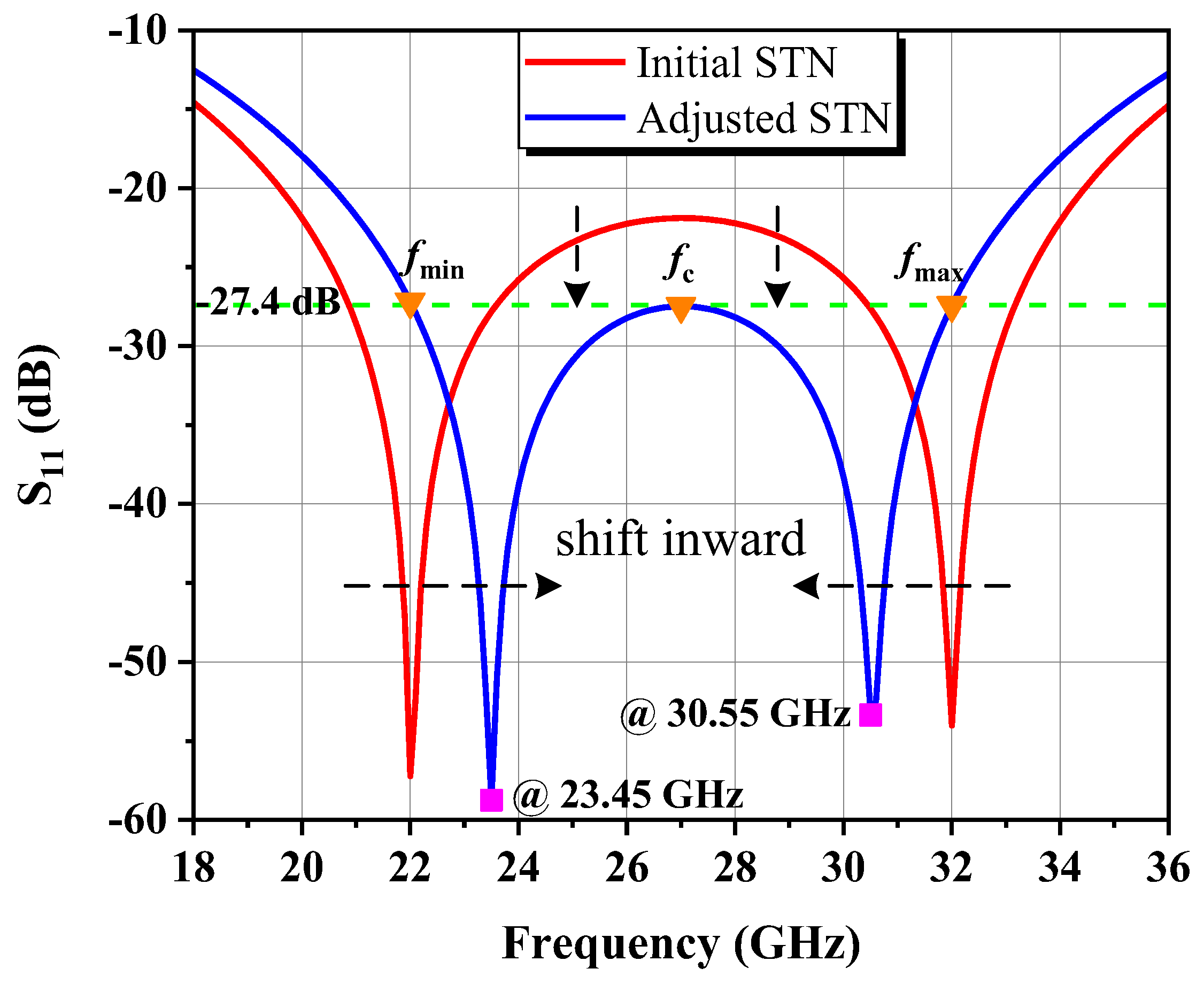
3.1. The Synthesized Transformer Output Matching Network
3.2. Interstage and Input Matching Network Design
4. Simulation Results
4.1. Small-Signal Characterization
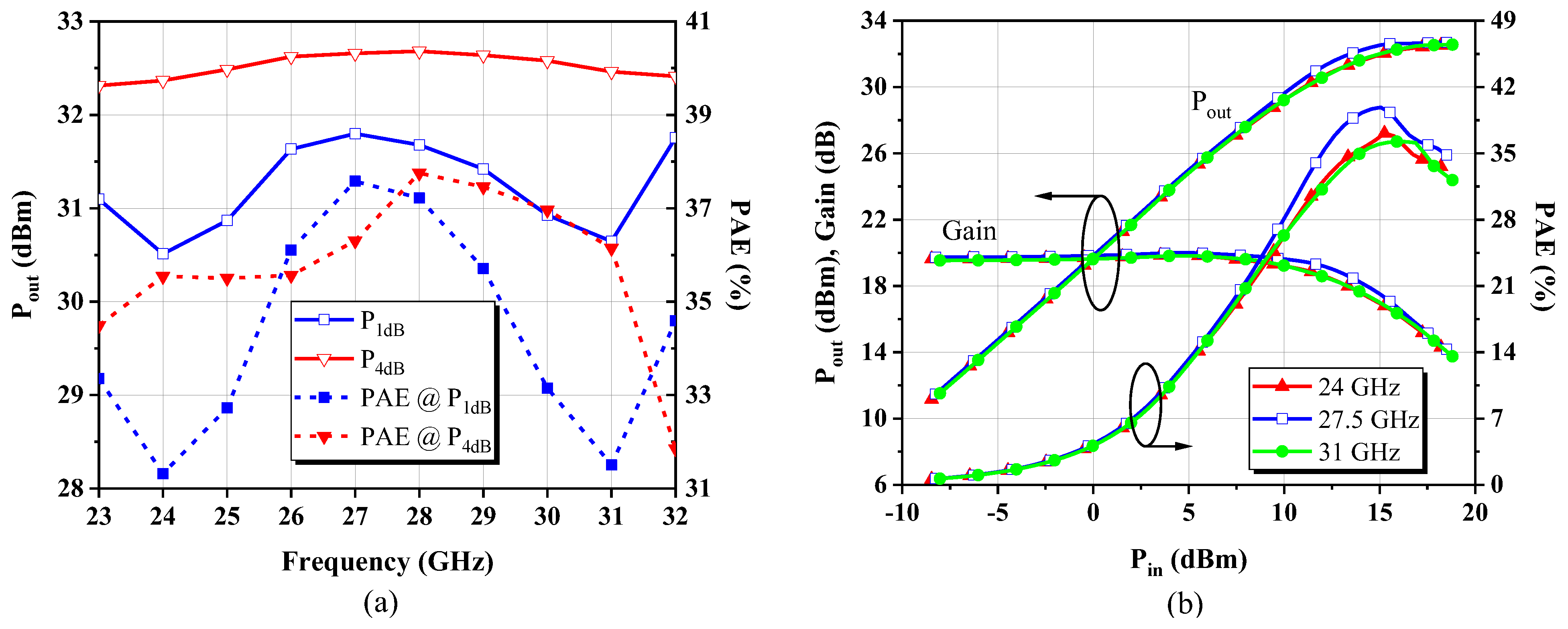
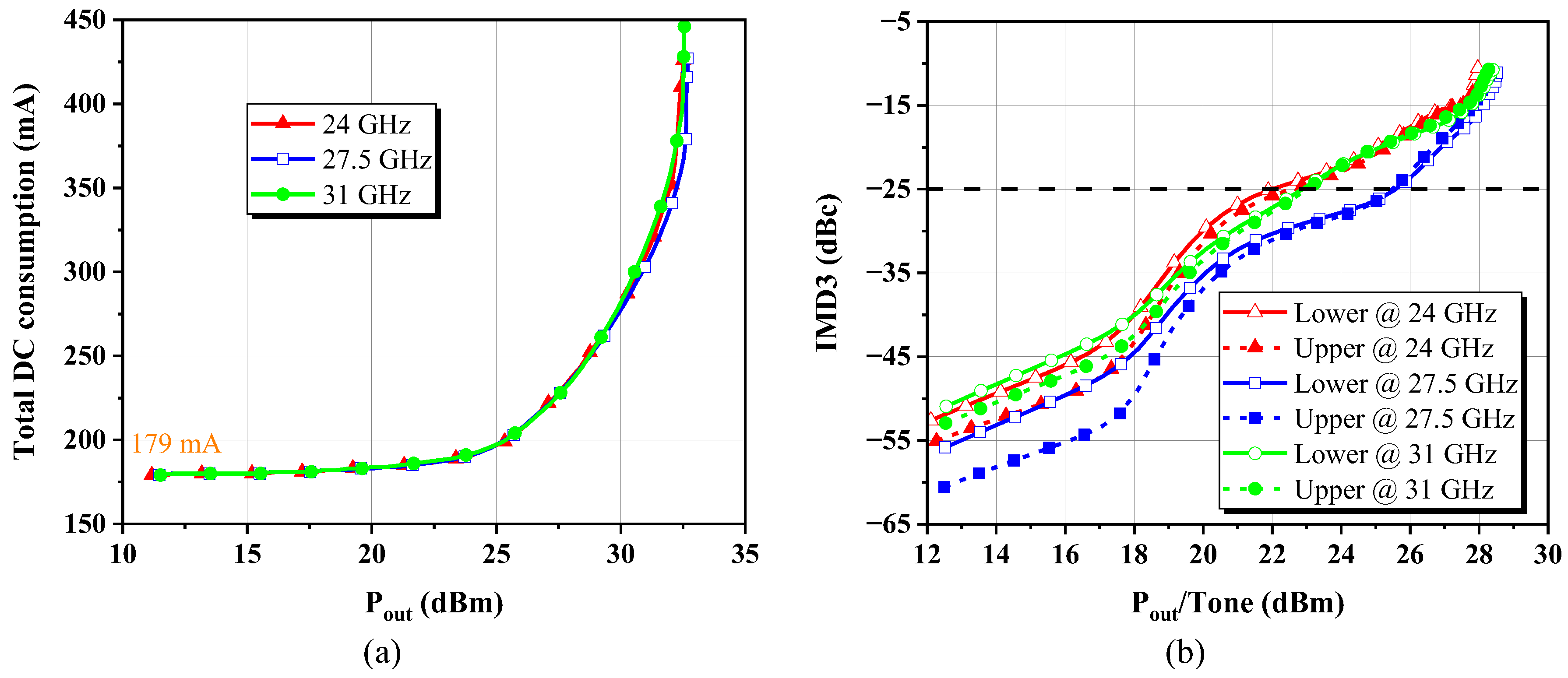
4.2. Large-Signal Characterization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3GPP | Third-generation partnership project |
| 5G | Fifth-generation mobile communication network |
| 5G-A | 5G-Advanced |
| ADS | Advanced design system |
| CAD | Computer-aided design |
| CMOS | Complementary metal oxide semiconductor |
| CW | Continuous-wave |
| EM | Electromagnetic |
| FBW | Fractional bandwidth |
| FoM | Figure of merit |
| FR | Frequency range |
| GaAs | Gallium arsenide |
| GaN | Gallium nitride |
| GaN-on-Si | Gallium nitride-on-silicon |
| HB | Harmonic balance |
| HEMT | High-electron-mobility transistor |
| IMD3 | Third-order intermodulation distortion |
| IMN | Input matching network |
| ISMN | Interstage matching network |
| ITR | Impedance transformation ratio |
| MMIC | Monolithic microwave integrated circuit |
| mmWave | Millimeter-wave |
| MN | Matching network |
| OID | Optimal impedance domain |
| OMN | Output matching network |
| OPG | Operating power gain |
| PA | Power amplifier |
| PAE | Power-added efficiency |
| P-OID | Preferred optimal impedance domain |
| PSO | Particle swarm optimization |
| SATCOM | Satellite communication |
| SOI | Silicon-on-insulator |
| S-OID | Strict optimal impedance domain |
| SRFT | Simplified real-frequency technique |
| STN | Synthesized transformer network |
| SWaP-C | Size, weight, power, and cost |
References
- Azari, M.M.; Solanki, S.; Chatzinotas, S.; Kodheli, O.; Sallouha, H.; Colpaert, A.; Mendoza Montoya, J.F.; Pollin, S.; Haqiqatnejad, A.; Mostaani, A.; et al. Evolution of Non-Terrestrial Networks from 5G to 6G: A Survey. IEEE Commun. Surv. Tutorials 2022, 24, 2633–2672. [Google Scholar] [CrossRef]
- Xiao, Y.; Ye, Z.; Wu, M.; Li, H.; Xiao, M.; Alouini, M.-S.; Al-Hourani, A.; Cioni, S. Space-Air-Ground Integrated Wireless Networks for 6G: Basics, Key Technologies, and Future Trends. IEEE J. Sel. Areas Commun. 2024, 42, 3327–3354. [Google Scholar] [CrossRef]
- He, S.; Zhang, Y.; Wang, J.; Zhang, J.; Ren, J.; Zhang, Y.; Zhuang, W.; Shen, X. A Survey of Millimeter-Wave Communication: Physical-Layer Technology Specifications and Enabling Transmission Technologies. Proc. IEEE 2021, 109, 1666–1705. [Google Scholar] [CrossRef]
- Longhi, P.E.; Pace, L.; Costanzo, F.; Ciccognani, W.; Colangeli, S.; Giofrè, R.; Leblanc, R.; Suriani, A.; Vitobello, F.; Limiti, E. 32–36-GHz Single-Chip Front-End MMIC Featuring 35-dBm Output Power and 3.2-dB Noise Figure with 60- and 100-Nm GaN/Si HEMTs. IEEE Trans. Microw. Theory Tech. 2024, 72, 160–172. [Google Scholar] [CrossRef]
- Sonnenberg, T.; Romano, A.; Miller, N.C.; Popović, Z. A W-Band GaN MMIC Single-Chip T/R Front End. IEEE Trans. Microw. Theory Tech. 2024, 72, 5830–5837. [Google Scholar] [CrossRef]
- Nikandish, R. GaN Integrated Circuit Power Amplifiers: Developments and Prospects. IEEE J. Microw. 2023, 3, 441–452. [Google Scholar] [CrossRef]
- Jeong, H.; Lee, H.D.; Park, B.; Jang, S.; Kong, S.; Park, C. Three-Stacked CMOS Power Amplifier to Increase Output Power with Stability Enhancement for Mm-Wave Beamforming Systems. IEEE Trans. Microw. Theory Tech. 2023, 71, 2450–2464. [Google Scholar] [CrossRef]
- Kim, K.; Choi, I.; Lee, K.; Choi, S.-U.; Kim, J.; Choi, C.-G.; Song, H.-J. Analysis and Design of Multi-Stacked FET Power Amplifier with Phase-Compensation Inductors in Millimeter-Wave Band. IEEE Trans. Microw. Theory Tech. 2023, 71, 1877–1889. [Google Scholar] [CrossRef]
- Fu, Z.-H.; Li, M.-X.; Ma, T.-G.; Wu, C.-S.; Lin, K.-Y. Millimeter-Wave GaAs Ultra-Wideband Medium Power Amplifier and Broadband High-Power Power Amplifier for 5G/6G Applications. IEEE J. Emerg. Sel. Top. Circuits Syst. 2024, 14, 111–121. [Google Scholar] [CrossRef]
- Meghdadi, M.; Medi, A. Design of 6–18-GHz High-Power Amplifier in GaAs pHEMT Technology. IEEE Trans. Microw. Theory Tech. 2017, 65, 2353–2360. [Google Scholar] [CrossRef]
- Shi, J.; Fang, X.; Yu, H.; Sui, J.; Cheng, K.-K.M. Novel Wideband Millimeter-Wave GaN Power Amplifier Design Using Transistors with Large Drain Capacitance and High Optimum Load Impedance. IEEE Trans. Circuits Syst. II 2023, 70, 4309–4313. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, X.; Xia, J.; Liu, R.; Dong, Q.; Chen, P.; Zhang, L.; Jiang, X.; Yu, C.; Hong, W. A 23–29.5 GHz Three-stage Mm-wave GaN Power Amplifier Using Arbitrary Two-port Complex-impedance Matching Method. Circuit Theory Appl. 2023, 51, 5103–5115. [Google Scholar] [CrossRef]
- Cai, Q.; Zhu, H.; Zeng, D.; Xue, Q.; Che, W. A Three-Stage Wideband GaN PA for 5G Mm-Wave Applications. IEEE Trans. Circuits Syst. II 2022, 69, 4724–4728. [Google Scholar] [CrossRef]
- Peng, L.; Yan, J.; Zhang, Z.; Zhang, G. An Efficient 24–30 GHz GaN-on-Si Driver Amplifier Using Synthesized Matching Networks. Micromachines 2023, 14, 175. [Google Scholar] [CrossRef]
- Wang, K.; Xu, J.-X.; Zhang, X.Y. A 24–31 GHz GaN-on-Si Power Amplifier MMIC. In Proceedings of the 2021 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition (iWEM), Guangzhou, China, 28–30 November 2021; pp. 1–3. [Google Scholar]
- Peng, L.; Chen, J.; Zhang, Z.; Zhang, G. Design of an Efficient 24–30 GHz GaN MMIC Power Amplifier Using Filter-Based Matching Networks. Electronics 2022, 11, 1934. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, J.; Lv, G.; Chen, W.; Guo, Y. Gain and Power Enhancement with Coupled Technique for a Distributed Power Amplifier in 0.25- Μm GaN HEMT Technology. IEEE Trans. VLSI Syst. 2024, 32, 1523–1534. [Google Scholar] [CrossRef]
- Chen, K.; Peroulis, D. Design of Highly Efficient Broadband Class-E Power Amplifier Using Synthesized Low-Pass Matching Networks. IEEE Trans. Microw. Theory Tech. 2011, 59, 3162–3173. [Google Scholar] [CrossRef]
- Yang, M.; Xia, J.; Guo, Y.; Zhu, A. Highly Efficient Broadband Continuous Inverse Class-F Power Amplifier Design Using Modified Elliptic Low-Pass Filtering Matching Network. IEEE Trans. Microw. Theory Tech. 2016, 64, 1515–1525. [Google Scholar] [CrossRef]
- Zhang, X.; Li, S.; Huang, D.; Chi, T. A Millimeter-Wave Three-Way Doherty Power Amplifier for 5G NR OFDM. IEEE J. Solid-State Circuits 2023, 58, 1256–1270. [Google Scholar] [CrossRef]
- Yarman, B.S.; Carlin, H.J. A Simplified “Real Frequency” Technique Applied to Broad-Band Multistage Microwave Amplifiers. IEEE Trans. Microw. Theory Tech. 1982, 30, 2216–2222. [Google Scholar] [CrossRef]
- Matthaei, G.L. Tables of Chebyshev Impedance–Transforming Networks of Low-Pass Filter Form. Proc. IEEE 1964, 52, 939–963. [Google Scholar] [CrossRef]
- Dawson, D.E. Closed-Form Solutions for the Design of Optimum Matching Networks. IEEE Trans. Microw. Theory Tech. 2009, 57, 121–129. [Google Scholar] [CrossRef]
- Meng, X.; Yu, C.; Liu, Y.; Wu, Y. Design Approach for Implementation of Class-J Broadband Power Amplifiers Using Synthesized Band-Pass and Low-Pass Matching Topology. IEEE Trans. Microw. Theory Tech. 2017, 65, 4984–4996. [Google Scholar] [CrossRef]
- Saad, P.; Fager, C.; Cao, H.; Zirath, H.; Andersson, K. Design of a Highly Efficient 2–4-GHz Octave Bandwidth GaN-HEMT Power Amplifier. IEEE Trans. Microw. Theory Tech. 2010, 58, 1677–1685. [Google Scholar] [CrossRef]
- Kuwata, E.; Alimohammadi, Y.; Liu, X.; Bell, J.; Tasker, P.; Shinjo, S.; Benedikt, J. Effects of Load Impedances at Third Order Intermodulation Tones. In Proceedings of the 2020 15th European Microwave Integrated Circuits Conference (EuMIC), Utrecht, The Netherlands, 10–15 January 2020; pp. 201–204. [Google Scholar]
- Ghanipour, P.; Stapleton, S.; Kim, J.-H. Load–Pull Characterization Using Different Digitally Modulated Stimuli. IEEE Microw. Wireless Compon. Lett. 2007, 17, 400–402. [Google Scholar] [CrossRef]
- Huang, P.-C.; Tsai, Z.-M.; Lin, K.-Y.; Wang, H. A 17–35 GHz Broadband, High Efficiency PHEMT Power Amplifier Using Synthesized Transformer Matching Technique. IEEE Trans. Microw. Theory Tech. 2012, 60, 112–119. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, Y.; Luo, L.; Wang, Q.; Zhang, Y.; Yan, B.; Xu, R.; Xu, Y. Design of 18–40 GHz GaN Reactive Matching Power Amplifiers Using One-order and Two-order Synthesised Transformer Networks. IET Microw. Antennas Propag. 2022, 16, 78–90. [Google Scholar] [CrossRef]



| fi (GHz) | U1(fi) (Ω) | U2(fi) (Ω) | Zopt,s(fi) (Ω) |
|---|---|---|---|
| 22 | 15.6 + j12.3 | 15.4 + j16.8 | 15.5 + j15.3 |
| 24 | 14.1 + j13.1 | 13.9 + j16.4 | 14.0 + j15.3 |
| 26 | 14.3 + j11.2 | 12.9 + j15.5 | 13.4 + j14.1 |
| 28 | 12.8 + j10.4 | 11.5 + j14.2 | 11.9 + j12.9 |
| 30 | 12.7 + j9.8 | 10.9 + j12.5 | 11.5 + j11.6 |
| 32 | 12.2 + j8.6 | 9.3 + j11.2 | 10.3 + j10.3 |
| fi (GHz) | Zopt,s(fi) (Ω) | PAE (%) | wi |
|---|---|---|---|
| 22 | 15.5 + j15.3 | 54.02 | 0.115 |
| 24 | 14.0 + j15.3 | 52.58 | 0.133 |
| 26 | 13.4 + j14.1 | 51.34 | 0.151 |
| 28 | 11.9 + j12.9 | 50.03 | 0.172 |
| 30 | 11.5 + j11.6 | 48.73 | 0.196 |
| 32 | 10.3 + j10.3 | 46.97 | 0.234 |
| Ropt | Cout | L2-M | M | L1-M | C1 | RL | |
|---|---|---|---|---|---|---|---|
| Initial | 26 Ω | 0.27 pF | 0.9 pH | 190.47 pH | 177.56 pH | 0.14 pF | 50 Ω |
| Adjusted | 26 Ω | 0.27 pF | 6.19 pH | 176.35 pH | 174.69 pH | 0.14 pF | 50 Ω |
| Ref. | [9] | [11] | [12] | [13] | [14] | [15] | This Work |
|---|---|---|---|---|---|---|---|
| Process | 0.15 μm GaAs | 0.15 μm GaN/SiC | 0.15 μm GaN/SiC | 0.1 μm GaN/Si | 0.1 μm GaN/Si | 0.1 μm GaN/Si | 0.1 μm GaN/Si |
| BW. (GHz) | 24–32 | 24.5–29 | 23–29.5 | 24–29 | 24–30 | 24–31 | 24–31 |
| FBW (%) | 28.6 | 16.8 | 24.8 | 18.9 | 22.2 | 25.5 | 25.5 |
| Supply (V) | 5 | 28 | 20 | 12 | 12 | 12 | 12 |
| Gain (dB) | 16.5 ± 0.5 | 11.5 ± 2.2 | 32.5 ± 2.5 | 20 ± 1.3 | 19.3 ± 1 | 25.5 ± 1.5 | 19.7 ± 0.5 |
| Pout (dBm) | 29 ± 0.6 | 29.8 ± 0.4 | 34.1 ± 0.8 | 30.7 ± 0.7 | 30.6 ± 0.5 | 34.3 ± 0.3 | 32.5 ± 0.2 |
| PAE (%) | 27–33 b | 28.3–42.8 c | 24.7–39.1 c | 27.6–38.9 b | 30.9–39.8 a | 35.8–37.4 b | 35.5–37.8 a |
| Size (mm2) | 2.4 × 1.1 | 2.1 × 1.3 | 3.4 × 1.9 | 2.2 × 1.3 | 1.65 × 0.78 | 3.25 × 1 | 1.4 × 0.88 |
| FoM | 41.8 | 4.4 | 10.8 | 15.8 | 45.7 | 61.3 | 104.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, L.; Ye, Z.; Zhang, Y.; Zhang, C.; Fu, Y.; Qin, J.; Liang, Y. A High-Efficiency GaN-on-Si Power Amplifier Using a Rapid Dual-Objective Optimization Method for 5G FR2 Applications. Electronics 2025, 14, 2996. https://doi.org/10.3390/electronics14152996
Peng L, Ye Z, Zhang Y, Zhang C, Fu Y, Qin J, Liang Y. A High-Efficiency GaN-on-Si Power Amplifier Using a Rapid Dual-Objective Optimization Method for 5G FR2 Applications. Electronics. 2025; 14(15):2996. https://doi.org/10.3390/electronics14152996
Chicago/Turabian StylePeng, Lin, Zuxin Ye, Yawen Zhang, Chenxuan Zhang, Yuda Fu, Jian Qin, and Yuan Liang. 2025. "A High-Efficiency GaN-on-Si Power Amplifier Using a Rapid Dual-Objective Optimization Method for 5G FR2 Applications" Electronics 14, no. 15: 2996. https://doi.org/10.3390/electronics14152996
APA StylePeng, L., Ye, Z., Zhang, Y., Zhang, C., Fu, Y., Qin, J., & Liang, Y. (2025). A High-Efficiency GaN-on-Si Power Amplifier Using a Rapid Dual-Objective Optimization Method for 5G FR2 Applications. Electronics, 14(15), 2996. https://doi.org/10.3390/electronics14152996






