High-Throughput Post-Quantum Cryptographic System: CRYSTALS-Kyber with Computational Scheduling and Architecture Optimization

Abstract

With the development of a quantum computer in the near future, classical public-key cryptography will face the challenge of being vulnerable to quantum algorithms, such as Shor’s algorithm. As communication technology advances rapidly, a great deal of personal information is being transmitted over the Internet. Based on our observation that the Kyber algorithm exhibits a significant number of idle cycles during execution when implemented following the conventional software procedure, this paper proposes a high-throughput scheduling for Kyber by parallelizing the SHA-3 function, the sampling algorithm, and the NTT computations to improve hardware utilization and reduce latency. We also introduce the 8-stage pipelined SHA-3 architecture and multi-mode polynomial arithmetic module to increase area efficiency. By also optimizing the hardware architecture of the various computational modules used by Kyber, according to the implementation result, an aggregate throughput of 877.192 kOPS in Kyber KEM can be achieved on TSMC 40 nm. In addition, our design not only achieves the highest throughput among existing studies but also improves the area and power efficiencies.

1. Introduction

With the development of quantum computing technology, traditional encryption algorithms are facing severe challenges, especially in the field of public-key cryptography. Historically, public-key cryptography has relied on complex mathematical operations, such as the integer factorization problem, for example, the Rivest–Shamir–Adleman (RSA) cryptosystem, and elliptic curve cryptography (ECC). However, suitable algorithms and large-scale quantum computers can easily address these problems. For example, Shor’s algorithm  [1] is a quantum algorithm that uses quantum computers to accelerate the process of integer factorization. Therefore, research institutions around the world have already begun to develop post-quantum cryptography (PQC) that can effectively resist the threats posed by quantum computers while remaining secure on classical computers. The National Institute of Standards and Technology (NIST) also started standardizing public-key encryption and key-encapsulation mechanism (PKE/KEM) algorithms as early as 2016. CRYSTALS-Kyber is a PKE/KEM standardized by NIST under the name ML-KEM in August 2023 [2,3]. Kyber is built upon the module-learning-with-errors (MLWE) problem over lattices, forming a robust foundation for its encryption and key exchange protocols [4,5].

The methods for implementing Kyber in hardware can be mainly divided into two categories. One is to support instruction set extension to increase hardware flexibility [6,7,8], the other is to accelerate specific computations of Kyber to enhance overall performance [9,10,11,12,13,14,15,16,17,18].

The work [6] entailed the design of 20 customized instruction codes to facilitate the control and operation of Kyber. It also proposed a parallel scheduling in polynomial sampling and SHA-3 computation [19] to decrease the required cycles. A vector-architecture processor based on RISC-V called VPQC was proposed in [8], which has a custom instruction set extended from RISC-V to improve the flexibility and efficiency in ASIC.

Since Kyber requires modular reductions after addition, subtraction and multiplication, ref. [18] proposed the K²-RED modular reduction algorithm to decrease the additional cost of memory utilization. Chauhan et al. [9] proposed a reconfigurable and hardware-efficient KECCAK architecture that integrates SHAKE functionality and supports dynamic input processing, enabling compatibility with a wide range of post-quantum cryptographic algorithms, including Kyber. In addition, Alrayes et al. [16] investigated pipeline optimization techniques for SHA-3 on FPGA, analyzing how different levels of pipelining impact performance, latency, and resource usage. The study [17] implemented a systolic array architecture for the number-theoretic transform (NTT) to enhance throughput during NTT operations. Furthermore, it also developed an out-of-order execution mechanism to reduce the overall latency. Shimada et al. [15] presented a high-throughput CRYSTALS-Kyber processor featuring pipelined NTT and SHA-3 units, achieving a good balance between performance and energy efficiency. Li et al. [12] proposed a secure and energy-efficient post-quantum crypto-processor based on modular design and separated secure/public memory architecture, achieving an energy consumption of $2.76 \mathsf{\mu }\mathrm{J}$ for the complete Kyber KEM operation. Subsequently, an ultra-low-power variant [11] further reduced the energy to $0.72 \mathsf{\mu }\mathrm{J}$ and chip area to $0.34 {\mathrm{mm}}^2$, making it well suited for resource-constrained edge devices.

Since the standardization of post-quantum cryptography has been finalized, Kyber—now established as the first NIST-approved KEM—has been integrated into various secure communication protocols. In server-side environments, the growing demand for large-scale and latency-sensitive cloud services requires systems to handle a high number of concurrent secure connections. Post-quantum key exchange using Kyber has already been adopted or proposed in TLS 1.3, QUIC (HTTP/3), VPN gateways, and edge cloud platforms. These scenarios demand frequent and efficient key encapsulation, making high-throughput Kyber implementations critical for maintaining performance at scale. We present a solution that can significantly reduce computational latency and enhance performance by optimizing computational scheduling and hardware architecture. For clarity, this work focuses on Kyber512.

The contributions of this work are briefly listed below:

• We propose a high-throughput scheduling for Kyber by parallelizing and pipelining the SHA-3 function, the sampling algorithm, and the NTT computations. The proposed scheduling reduces the time required to generate the necessary polynomial coefficients to just one-fourth of that required by the conventional software procedure.
• Due to the iterative and repetitive nature of hash operations in Kyber, pipeline bubbles are inevitable with both round-based and unrolled-pipeline architectures. Therefore, we propose an 8-stage pipelined architecture that effectively addresses feedback issues during the absorbing and squeezing phases of SHA-3 operations.
• We propose a multi-mode polynomial arithmetic module based on an unrolled-pipeline mixed-radix architecture, which can be configured into different modes for various polynomial computations in Kyber. Moreover, it employs resource-sharing techniques to maximize the utilization of each pipeline stage within a limited and reasonable hardware area.

The rest of this paper is organized as follows. In Section 2, we briefly describe the background of Kyber. In Section 3, our proposed efficient scheduling and high-speed architecture are presented. In Section 4, we discuss the experimental results. Finally, Section 5 draws the conclusions.

2. Preliminaries

Learning with Errors (LWE) is a cryptographic problem based on the hardness of the Closest Vector Problem in lattice theory. It is formulated as follows: given a public matrix $\mathit{A} \in {\mathbb{Z}}_q^{k\times k}$ and a noisy vector $\mathit{t}=\mathit{A}\mathit{s}+\mathit{e} \in {\mathbb{Z}}_q^k$, recover the secret vector $\mathit{s} \in {\mathbb{Z}}_q^k$. The error vector $\mathit{e} \in {\mathbb{Z}}_q^k$ consists of small random entries. The presence of $\mathit{e}$ makes the problem computationally intractable and forms the security foundation for many lattice-based schemes.

Kyber adopts a structured variant called Module Learning with Errors (MLWE) [20], which generalizes LWE to polynomial rings. In MLWE, the matrix $\mathit{A}$ and vectors $\mathit{s}$, $\mathit{e}$, and $\mathit{t}$ have the same dimensions as in LWE, but their entries are polynomials with coefficients in a finite field, rather than individual integers. The problem is defined as:

$$MLW{E}_{\mathit{A}}(\mathit{s},\mathit{e})=\mathit{t}=\mathit{A}·\mathit{s}+\mathit{e}.$$

(1)

To accelerate polynomial multiplication in MLWE-based schemes such as Kyber, the Number Theoretic Transform (NTT) is used. As a finite-field analog of the Discrete Fourier Transform, the NTT converts polynomials from the coefficient domain to a form that allows efficient element-wise (point-wise) multiplication. The result is then transformed back using the inverse NTT (INTT).

2.1. Symbol Definition

The integer polynomials ring modulo $X^n$ + 1 is defined as $R_q={\mathbb{Z}}_q\left[X\right]/\left(X^n+1\right)$ in which n = 256 is the dimension and q = 3329 is the prime modulus. Thus, the polynomial $F\in R_q$ can be defined as $F={\sum }_{i=0}^{n-1}{f}_i{X}^i$ where $f_i\in {\mathbb{Z}}_q$ for all i.

2.2. Auxiliary Functions in Kyber

To better understand the Kyber algorithm, we need to first illustrate various functions it uses, as follows:

• Hash function: The hash function used in Kyber is the SHA-3 algorithm. Four different SHA-3 modes are employed to increase randomness in Kyber: SHA3-256, SHA3-512, SHAKE128, and SHAKE256.
• Sampling function: The sampling functions in Kyber include SampleNTT and SamplePolyCBD. The former primarily samples coefficients from the NTT domain for the matrix $\widehat{\mathit{A}}$, while the latter provides property with a centered binomial distribution (CBD) on ${\mathbb{Z}}_q$. In this work, the hat on top, $\widehat{(·)}$, represents a term in the NTT domain.
• Compress function: The compress function primarily serves two purposes: reducing the size of the ciphertext and creating an error tolerance gap for MLWE during decryption. The function compresses the input x into the range $\{0,1,\dots ,2^d-1\}$, $d\in \{1,4,10\}$, and then the result is rounded to the nearest integer, as shown below:

  $$\begin{array}{c}\hfill {\mathrm{Compress}}_d\left(x\right)=⌈\left({\displaystyle \frac{2^d}{q}}\right)·x⌋mod{2}^d\end{array}$$

  (2)
  However, if the compression module is directly implemented with (2), it would require 256 dividers for fully parallel processing. Therefore, we propose a hardware-friendly implementation to reduce its complexity.

2.3. Kyber KEM Algorithms

Kyber is one of the post-quantum KEM algorithms standardized by NIST and consists of key-generation, encapsulation and decapsulation. These algorithms are introduced below.

• Key-Generation: The key-generation algorithm produces a public key pk and a secret key sk. The function is derived from the MLWE-based construction in (1), where the secret vector $\mathit{s}$ and error vector $\mathit{e}$ are sampled from the centered binomial distribution (CBD), and the matrix $\widehat{\mathit{A}}$ is sampled uniformly in the NTT domain. The resulting pk consists of ($\widehat{\mathit{t}}$, $\rho$), where $\rho$ is derived from SHA3-512 applied to a random seed d, and the secret key sk is the NTT form of $\mathit{s}$. A simplified version of the key-generation process is listed as follows in Algorithm 1:

Algorithm 1: K-PKE: Key Generation

Output: Public key pk, Secret key sk 1  $d\leftarrow \mathrm{RandomBytes}\left(\right)$; 2  $(\rho ,\sigma )\leftarrow \mathrm{SHA}3\_512\left(d\right)$; 3  $\widehat{\mathit{A}}\in R_q^{k\times k}\mathrm{in}\mathrm{NTT}\mathrm{domain}\leftarrow \mathrm{Gen}\_\mathrm{matrix}\left(\rho \right)$; 4  $(\mathit{s},\mathit{e})\in R_q^k\leftarrow \mathrm{CBD}\_{\mathrm{Sample}}_{{\eta }_1}\left(\sigma \right)$; 5  $(\widehat{\mathit{s}},\widehat{\mathit{e}})\leftarrow (\mathrm{NTT}\left(\mathit{s}\right),\mathrm{NTT}\left(\mathit{e}\right))$; 6  $\widehat{\mathit{t}}\leftarrow \widehat{\mathit{A}}\circ \widehat{\mathit{s}}+\widehat{\mathit{e}}$; 7  $(pk,sk)\leftarrow (\mathrm{Encode}(\widehat{\mathit{t}}\parallel \rho ),\mathrm{Encode}\left(\widehat{\mathit{s}}\right))$; 8  return  $(pk,sk)$

• Encapsulation: The encapsulation algorithm takes the public key pk and the message m as input to produce the ciphertext ct and a 32-byte shared secret key K. First, m is decompressed to generate an error tolerance gap, resulting in $\mu$, where bit “0” maps to 0 and bit “1” maps to 1665. Next, the ciphertext components are computed as $\mathit{u}=\mathrm{INTT}({\widehat{\mathit{A}}}^T\circ \widehat{\mathit{r}})+{\mathit{e}}_1$ and $\mathit{v}=\mathrm{INTT}({\widehat{\mathit{t}}}^T\circ \widehat{\mathit{r}})+{\mathit{e}}_2+\mu$. Finally, the shared key K is derived as the first 32 bytes of $\mathrm{SHA}3-512(\mathit{m},\mathrm{SHA}3-256(\mathit{pk}\left)\right)$, and the ciphertext ct consists of (Compress ($\widehat{\mathit{u}}$), Compress (v)). A simplified version of the encryption process is listed as follows in Algorithm 2:

Algorithm 2: K-PKE: Encryption

Input: Public key pk, Message m, Random coins r Output: Ciphertext c   1 $(\widehat{\mathit{t}},\rho )\leftarrow \mathrm{Decode}\left(\mathit{pk}\right)$   2 ${\widehat{\mathit{A}}}^T\in R_q^{k\times k}\mathrm{in}\mathrm{NTT}\mathrm{domain}\leftarrow \mathrm{Gen}\_\mathrm{matrix}\left(\rho \right)$   3 $\mathit{r}\in R_q^k\leftarrow \mathrm{CBD}\_{\mathrm{Sample}}_{{\eta }_1}\left(r\right)$   4 ${\mathit{e}}_1\in R_q^k\leftarrow \mathrm{CBD}\_{\mathrm{Sample}}_{{\eta }_2}\left(r\right)$   5 ${\mathit{e}}_2\in R_q\leftarrow \mathrm{CBD}\_{\mathrm{Sample}}_{{\eta }_2}\left(r\right)$   6 $\widehat{\mathit{r}}\leftarrow \mathrm{NTT}\left(\mathit{r}\right)$   7 $\mathit{u}\leftarrow \mathrm{INTT}({\widehat{\mathit{A}}}^T\circ \widehat{\mathit{r}})+{\mathit{e}}_1$   8 $\mathit{v}\leftarrow \mathrm{INTT}({\widehat{\mathit{t}}}^T\circ \widehat{\mathit{r}})+{\mathit{e}}_2+\mathrm{Decompress}\left(\mathit{m}\right)$   9 $(c_1,c_2)\leftarrow (\mathrm{Encode}\left(\mathit{u}\right),\mathrm{Encode}\left(\mathit{v}\right))$ 10  return  $(c_1\parallel c_2)$

• Decapsulation: The decapsulation algorithm takes dk and ct as input to produce the shared secret key K. Firstly, ${\mathit{m}}^{\prime }$ is computed as Compress($\mathit{v}-$INTT(${\widehat{\mathit{s}}}^T\circ \widehat{\mathit{u}}$)). Next, K is the first 32 bytes of SHA3-512(${\mathit{m}}^{\prime }$, h), where h is SHA3-256(ek). Finally, through re-encryption verification, the same K can be obtained. A simplified version of the decryption process is listed as follows in Algorithm 3:

Algorithm 3: K-PKE: Decryption

Input: Secret key sk, Ciphertext c Output: Message m 1  $(\mathit{u},v)\leftarrow \mathrm{Decode}\left(\mathit{c}\right)$ 2  $\widehat{\mathit{s}}\leftarrow \mathrm{Decode}\left(\mathit{sk}\right)$ 3  $\mathit{m}\leftarrow \mathrm{Compress}\left(v-\mathrm{INTT}\left(\widehat{\mathit{s}}\circ \mathrm{NTT}\left(\mathit{u}\right)\right)\right)$ 4  return $\mathit{m}$

2.4. Mathematical Foundations of the Kyber Mixed Radix-2/4 NTT

Although [21] presents a radix-4 NTT algorithm applicable to Kyber, it does not provide a derivation showing how the radix-4 butterfly arises from combining two radix-2 stages. In contrast, the mathematical derivation in [22] demonstrates that the Number Theoretic Transform (NTT) adopted in Kyber can be decomposed using a radix-2 structure. Based on this foundation, the derivation is further extended to show that two consecutive radix-2 stages can be consolidated into a single radix-4 stage. Consequently, the original 7-stage radix-2 NTT in Kyber can be equivalently realized using three radix-4 stages and one radix-2 stage.

A mathematical derivation is presented to establish the theoretical foundation for merging two consecutive radix-2 stages into a single radix-4 butterfly. This formulation serves as the basis for constructing an equivalent mixed-radix structure applicable to Kyber’s NTT.

The NTT are written as a summation of N items:

$$\begin{array}{c}\hfill {\widehat{f}}_i=\sum _{j=0}^{N-1}{f}_j·{\gamma }_{2N}^j·{\omega }_N^{ij},\mathrm{for}i=0,1,\dots ,N-1.\end{array}$$

(3)

• ${\omega }_N$ is the N-th primitive root of unity modulo q.
• ${\gamma }_N$ is a scaling factor introduced to simplify reduction, where ${\omega }_N={\gamma }_N^2$.

The initial radix-2 decomposition can be written as [22]:

$$\begin{array}{cc}\hfill {\widehat{f}}_i& =\underset{\mathrm{NTT\; of\; even-indexed\; inputs}}{\underbrace{{\displaystyle }\sum _{j=0}^{N/2-1}{f}_{2j}·{\gamma }_N^j·{\omega }_{N/2}^{ij}}}+\underset{\mathrm{Twiddle\; rotation\; term}}{\underbrace{{\gamma }_{2N}·{\omega }_N^i}}·\underset{\mathrm{NTT\; of\; odd-indexed\; inputs}}{\underbrace{{\displaystyle }\sum _{j=0}^{N/2-1}{f}_{2j+1}·{\gamma }_N^j·{\omega }_{N/2}^{ij}}}\hfill \\ \hfill & =\underset{\mathrm{Partial\; sum\; from\; even\; terms}}{\underbrace{{\widehat{f}}_i^{\left(0\right)}}}+\underset{\mathrm{Weighted\; partial\; sum\; from\; odd\; terms}}{\underbrace{{\gamma }_{2N}·{\omega }_N^i·{\widehat{f}}_i^{\left(1\right)}}}\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{2}}-1,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\widehat{f}}_{i+N/2}& =\underset{\mathrm{Partial\; sum\; from\; even\; terms}}{\underbrace{{\widehat{f}}_i^{\left(0\right)}}}-\underset{\mathrm{Weighted\; partial\; sum\; from\; odd\; terms}}{\underbrace{{\gamma }_{2N}·{\omega }_N^i·{\widehat{f}}_i^{\left(1\right)}}},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{2}}-1.\hfill \end{array}$$

(5)

We now expand both ${\widehat{f}}_i^{\left(0\right)}$ and ${\widehat{f}}_i^{\left(1\right)}$ from Equations (4) and (5) using another radix-2 decomposition. For $i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1$, the even-indexed partial NTT ${\widehat{f}}_i^{\left(0\right)}$ becomes:

$$\begin{array}{cc}\hfill {\widehat{f}}_i^{\left(0\right)}& =\sum _{j=0}^{N/4-1}{f}_{4j}·{\gamma }_N^j·{\omega }_{N/4}^{ij}+{\gamma }_N·{\omega }_{N/2}^i·\sum _{j=0}^{N/4-1}{f}_{4j+2}·{\gamma }_N^j·{\omega }_{N/4}^{ij},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\hfill \end{array}$$

(6)

Similarly, the odd-indexed partial NTT ${\widehat{f}}_i^{\left(1\right)}$ becomes:

$$\begin{array}{cc}\hfill {\widehat{f}}_i^{\left(1\right)}& =\sum _{j=0}^{N/4-1}{f}_{4j+1}·{\gamma }_N^j·{\omega }_{N/4}^{ij}+{\gamma }_N·{\omega }_{N/2}^i·\sum _{j=0}^{N/4-1}{f}_{4j+3}·{\gamma }_N^j·{\omega }_{N/4}^{ij},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\hfill \end{array}$$

(7)

By grouping terms according to their input index patterns—namely, even-of-even, odd-of-even, even-of-odd, and odd-of-odd—we define four partial sums ${\widehat{f}}_i^{(0,0)},{\widehat{f}}_i^{(0,1)},{\widehat{f}}_i^{(1,0)},{\widehat{f}}_i^{(1,1)}$ as follows:

$$\begin{array}{cc}\hfill {\widehat{f}}_i^{(0,0)}& =\sum _{j=0}^{N/4-1}{f}_{4j}·{\gamma }_N^j·{\omega }_{N/4}^{ij},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\widehat{f}}_i^{(0,1)}& =\sum _{j=0}^{N/4-1}{f}_{4j+2}·{\gamma }_N^j·{\omega }_{N/4}^{ij},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\widehat{f}}_i^{(1,0)}& =\sum _{j=0}^{N/4-1}{f}_{4j+1}·{\gamma }_N^j·{\omega }_{N/4}^{ij},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\widehat{f}}_i^{(1,1)}& =\sum _{j=0}^{N/4-1}{f}_{4j+3}·{\gamma }_N^j·{\omega }_{N/4}^{ij},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\hfill \end{array}$$

(11)

Substituting Equations (6) and (7) into Equation (4), we obtain:

$$\begin{array}{cc}\hfill {\widehat{f}}_i& =\left({\widehat{f}}_i^{(0,0)}+{\gamma }_N·{\omega }_{N/2}^i·{\widehat{f}}_i^{(0,1)}\right)+{\gamma }_{2N}·{\omega }_N^i·\left({\widehat{f}}_i^{(1,0)}+{\gamma }_N·{\omega }_{N/2}^i·{\widehat{f}}_i^{(1,1)}\right)\hfill \\ \hfill & ={\widehat{f}}_i^{(0,0)}+{\gamma }_N·{\omega }_{N/2}^i·{\widehat{f}}_i^{(0,1)}+{\gamma }_{2N}·{\omega }_N^i·{\widehat{f}}_i^{(1,0)}+{\gamma }_{2N}·{\gamma }_N·{\omega }_N^i·{\omega }_{N/2}^i·{\widehat{f}}_i^{(1,1)}\hfill \\ \hfill & ={\widehat{f}}_i^{(0,0)}+{\gamma }_{2N}·{\omega }_N^i·{\widehat{f}}_i^{(1,0)}+{\gamma }_{2N}^2·{\omega }_N^{2i}·{\widehat{f}}_i^{(0,1)}+{\gamma }_{2N}^3·{\omega }_N^{3i}·{\widehat{f}}_i^{(1,1)},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1.\hfill \end{array}$$

(12)

Similarly, from Equation (5), we derive:

$$\begin{array}{cc}\hfill {\widehat{f}}_{i+N/2}& ={\widehat{f}}_i^{(0,0)}+{\gamma }_N·{\omega }_{N/2}^i·{\widehat{f}}_i^{(0,1)}-{\gamma }_{2N}·{\omega }_N^i·{\widehat{f}}_i^{(1,0)}-{\gamma }_{2N}·{\gamma }_N·{\omega }_N^i·{\omega }_{N/2}^i·{\widehat{f}}_i^{(1,1)}\hfill \\ \hfill & ={\widehat{f}}_i^{(0,0)}-{\gamma }_{2N}·{\omega }_N^i·{\widehat{f}}_i^{(1,0)}+{\gamma }_{2N}^2·{\omega }_N^{2i}·{\widehat{f}}_i^{(0,1)}-{\gamma }_{2N}^3·{\omega }_N^{3i}·{\widehat{f}}_i^{(1,1)},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1.\hfill \end{array}$$

(13)

To derive the other outputs ${\widehat{f}}_{i+N/4}$ and ${\widehat{f}}_{i+3N/4}$, we apply phase rotation patterns in the radix-4 structure using the 4th root of unity ${\omega }_N^{N/4}$. The resulting expressions are:

$$\begin{array}{ll}{\widehat{f}}_{i+N/4}=& {\widehat{f}}_i^{(0,0)}+{\gamma }_{2N}·{\omega }_N^i·{\omega }_N^{N/4}·{\widehat{f}}_i^{(1,0)}\\ & -{\gamma }_{2N}^2·{\omega }_N^{2i}·{\widehat{f}}_i^{(0,1)}-{\gamma }_{2N}^3·{\omega }_N^{3i}·{\omega }_N^{N/4}·{\widehat{f}}_i^{(1,1)},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\end{array}$$

(14)

$$\begin{array}{ll}{\widehat{f}}_{i+3N/4}=& {\widehat{f}}_i^{(0,0)}+{\gamma }_{2N}·{\omega }_N^i·{\omega }_N^{3N/4}·{\widehat{f}}_i^{(1,0)}\\ & -{\gamma }_{2N}^2·{\omega }_N^{2i}·{\widehat{f}}_i^{(0,1)}-{\gamma }_{2N}^3·{\omega }_N^{3i}·{\omega }_N^{3N/4}·{\widehat{f}}_i^{(1,1)},\mathrm{for}i=0,1,\dots ,{\displaystyle \frac{N}{4}}-1\end{array}$$

(15)

This result corresponds exactly to a radix-4 butterfly where the four partial sums ${\widehat{f}}_i^{(0,0)},{\widehat{f}}_i^{(0,1)},{\widehat{f}}_i^{(1,0)},{\widehat{f}}_i^{(1,1)}$ are processed in a single stage, this derivation provides the mathematical foundation for implementing the Kyber NTT using a mixed-radix architecture.

3. Proposed Hardware Architecture

3.1. Proposed Computational Scheduling

Since Kyber is based on MLWE, it requires the generation of $\mathit{A}$, $\mathit{s}$, and $\mathit{e}$ during its computation process. We observed that, in the computational procedure of Kyber’s pseudocode [3], the matrix $\widehat{\mathit{A}}$ is generated first, followed by the sequential generation of vectors $\mathit{s}$ and $\mathit{e}$. However, the sampling time for $\mathit{s}$ and $\mathit{e}$ is shorter than that for $\widehat{\mathit{A}}$. Upon completion of the sampling of $\mathit{s}$ and $\mathit{e}$, they can perform NTT first to improve overall throughput. Therefore, there are opportunities for parallel processing between SHA-3, sampling, and NTT operations.

To that end, we propose an optimized scheduling framework, as shown in Figure 1, that overlaps SHA-3 hashing, sampling, and NTT computations. We first pipeline the SHA-3 core into 8 stages, where each stage executes three Keccak permutation rounds. This allows the hardware to output hash values at regular intervals without pipeline bubbles. These hash outputs are then alternately fed into two dedicated samplers: SamplePolyCBD (used for $\mathit{s}$ and $\mathit{e}$) and SampleNTT (used for $\mathit{A}$).

Figure 1. Proposed computational scheduling.

Moreover, as SamplePolyCBD only requires two hash blocks to generate a polynomial while SampleNTT requires four, we prioritize $\mathit{s}$ and $\mathit{e}$ generation. This design enables polynomials from SamplePolyCBD to be transformed by the NTT unit earlier. Meanwhile, SampleNTT continues sampling polynomials for $\mathit{A}$ in the background. This interleaved scheduling absorbs the latency of SHA-3, sampling, and NTT operations. As a result, it significantly improves throughput and area efficiency, without additional buffering or complex control logic.

3.2. Proposed High-Speed Architecture

Figure 2 presents the overall architecture of this work, including a multi-mode polynomial arithmetic, SHA-3, sampling, and compress and decompress modules, which can be configured for key generation, encapsulation, and decapsulation in Kyber. It also illustrates the data flow configuration for key generation, while the data flows for encapsulation and decapsulation are similar and omitted here.

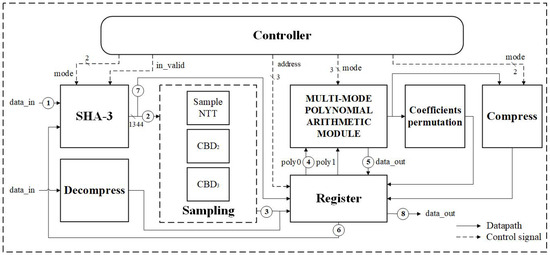
Figure 2. Proposed architecture for Kyber KEM. The data flow of key generation is also illustrated.

For the key generation described in (1), firstly, the input data are processed through the SHA-3 module to compute the seeds for $\mathit{A}$, $\mathit{s}$ and $\mathit{e}$. Next, these seeds are sampled to obtain the correct coefficients. The vectors $\mathit{s}$ and $\mathit{e}$ are then computed using the multi-mode polynomial arithmetic module for NTT, followed by pointwise multiplication and modular addition. Finally, the generated pk and sk are processed through SHA3-256 to produce the final ek and dk.

3.3. Multi-Mode Polynomial Arithmetic Module

Since Kyber is based on the MLWE problem, it involves several polynomial operations, including the NTT, INTT, pointwise multiplication, modular addition, and modular subtraction. The fundamental computation units for these operations are modular adders, modular subtractors, and modular multipliers, which can be combined into a common butterfly architecture. Therefore, we utilize resource-sharing techniques to balance high throughput with hardware efficiency in implementing these operations.

There exist various implementation approaches for the Number Theoretic Transform (NTT) used in the Kyber algorithm. One prominent method is the mixed-radix NTT architecture [23], which serves as a foundational concept for mixed-radix implementations. In [21], a mixed-radix method combining radix-2 and radix-4 butterfly operations was proposed to optimize the NTT architecture, particularly benefiting implementations with an odd number of stages.

However, these existing approaches typically utilize only a small number of butterfly units for computation, which leads to a performance bottleneck in high-throughput Kyber scenarios. To address this issue, we propose a mixed-radix architecture based on a fully unrolled-pipeline technique. By leveraging this technique, the performance bottleneck caused by the limited number of butterfly units is effectively addressed, thereby enabling high-throughput operation suitable for practical Kyber deployments. Moreover, the proposed design eliminates the need for an additional address generator, thereby enhancing throughput and achieving a more efficient and scalable implementation suitable for post-quantum cryptographic applications. These hardware architectures are introduced below.

• Proposed Mixed-Radix $2^1/4^3$ Butterfly Architecture: we propose a mixed-radix architecture based on unrolled-pipeline techniques. Under this architecture, additional computational resources such as address generators or delay registers are not required to determine the input address for the next stage. Moreover, by fully unrolling the computation, polynomial operations are no longer the bottleneck in Kyber.
  Due to the mathematical background in Kyber, where the 512th primitive root cannot be found, it is unfeasible to perform a 256-point transformation for NTT/INTT, limiting the operation to 128 points. As a result of this factor, the polynomial must be divided into odd and even terms and transforming them using the same roots of unity in Kyber. Based on this characteristic, we design an 128-point mixed-radix $2^1/4^3$ NTT/INTT architecture to compute the 256-term polynomial NTT and INTT; the incoming 256-term polynomial needs to be divided into odd and even groups, and then input into the mixed-radix architecture sequentially. However, when performing pointwise multiplication, modular addition, and modular subtraction, the 256-term polynomial can be directly input into the mixed-radix architecture for computation. Figure 3 is the block diagram of the proposed mixed-radix $2^1/4^3$ architecture. In the proposed mixed-radix architecture, the first stage consists of 64 sets radix-2 butterfly, while each of the second to fourth stages consist of 32 sets radix-4 butterfly; the individual radix-2 and radix-4 butterfly units are shown in Figure 4 and Figure 5, respectively. The reordering module, required due to the shared architecture between the NTT and INTT, is shown in Figure 6. Since all modules are pipelined, the input interface of this module receives 256 polynomial coefficients simultaneously, with each coefficient represented in 12 bits, resulting in a total input width of 3072 bits. The output follows the same format. A control signal, mode, determines the operational behavior of the module.
  

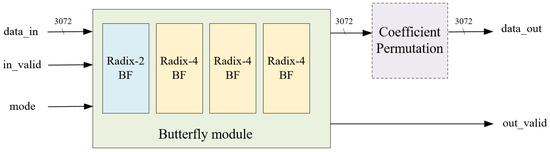  Figure 3. The block diagram of the proposed mixed-radix NTT architecture.
  

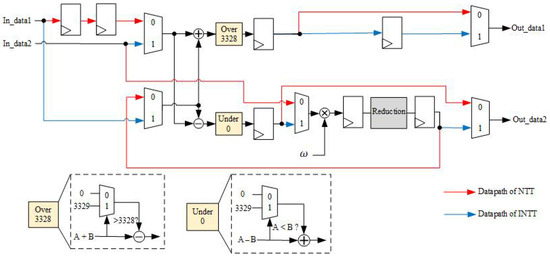  Figure 4. Hardware architecture of radix-2 butterfly.
  

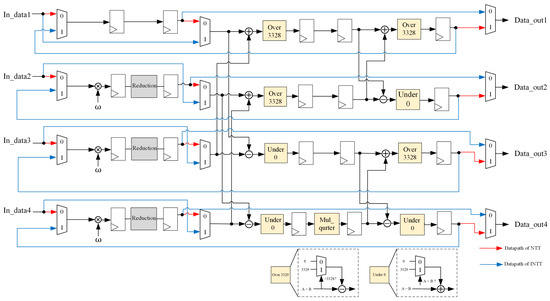  Figure 5. Hardware architecture of radix-4 butterfly.
  

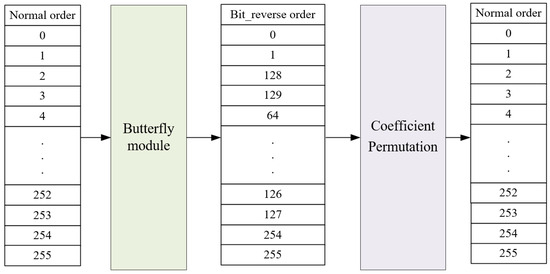  Figure 6. Order adjustment for the coefficient permutation.
  In the original algorithm, the output addresses of each stage in the NTT and INTT operations differ, resulting in distinct unfolded architectures. This design arises because, during NTT computation, the input is in normal order while the output is in bit-reversed order, whereas INTT operates in the opposite manner. To create a shared architecture capable of computing both NTT and INTT, adjustments are necessary. Thus, we designed a coefficient permutation module to ensure the correctness of the order after transformation. This module adjusts the output order from being bit-reversed to normal, as shown in Figure 6. Notably, due to the unroll-pipeline architecture, the permutation module only requires rewiring without needing any logic gates.
• Proposed Hardware Architecture of Radix-2 Butterfly: To achieve high throughput, we implement the radix-2 butterfly using a three-stage pipelined architecture, combined with modular adders, modular subtractors, and multipliers. Since the product may exceed q-1 after multiplication, we need to insert a modular reduction unit after the multipliers.
  The modular reduction unit in our design is based on [7], which proposes a hardware-friendly modular reduction algorithm tailored for Kyber’s mathematical background. The proposed reduction unit effectively simplifies the modular reduction operation for 24-bit products under ${\mathbb{Z}}_q$. The proposed algorithm decomposes the 24-bit product into its upper 12 bits and lower 12 bits, and utilizes mathematical manipulations to simplify values that exceed 12 bits, thereby simplifying the modular reduction operation. The detailed implementation of the radix-2 butterfly is shown in Figure 4. The red datapath represents the three-stage pipelined architecture of the single-stage radix-2 NTT butterfly, including modular addition, subtraction, and multiplication.
  To reduce resource usage, arithmetic units are shared between the single-stage radix-2 NTT and INTT butterflies. The blue datapath illustrates the INTT butterfly that reuses the same computational resources.
• Proposed Hardware Architecture of Radix-4 Butterfly: We implement the radix-4 butterfly in a five-stage pipelined architecture. The mul_quarter modules of NTT and INTT are constant multiplications designed for ${\omega }_4^1$ and ${\omega }_4^{-1}$, respectively. These modules adopt the same modular multiplication strategy as the radix-2 design, where the product is followed by a modular reduction to ensure correctness. The detailed implementation of the radix-4 butterfly is shown in Figure 5. The red datapath represents the five-stage pipelined architecture of a single-stage radix-4 NTT butterfly, which includes modular addition, subtraction, and multiplication. To minimize resource consumption, arithmetic units are shared between the radix-4 NTT and INTT butterflies. The blue datapath highlights the INTT computation, which reuses the same set of arithmetic units.
  When implementing the INTT, it is necessary to multiply all output coefficients by the modular inverse of the number of points used in the computation at the final stage. Our proposed approach preprocesses the roots of unity in the radix-4 butterfly at the final stage. Figure 7 represents the radix-4 INTT butterfly in the final stage. The blue multiplier denotes the additional multiplication for the modular inverse, while the black ones perform multiplication with the roots of unity after preprocessing in the original radix-4 INTT butterfly. Here, we preprocess the roots of unity and modular inverse offline; 3303 is the modular inverse of 128 in ${\mathbb{Z}}_q$. Through this method, the mixed-radix $2^1/4^3$ INTT architecture can eliminate 75% of the computational workload at the final stage.
  

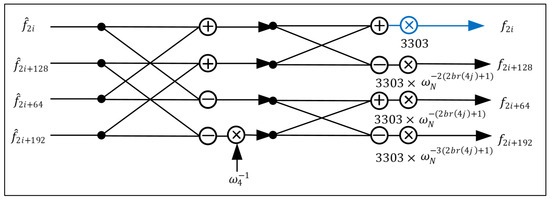  Figure 7. The final stage of the radix-4 INTT butterfly.

3.4. SHA-3 Module

SHA-3 consists mainly of 24 rounds of iteration functions, where each round implements five types of operations: $\theta ,\rho ,\pi ,\chi ,\iota$ [19]. Due to the iterative and repetitive nature of hash operations, implementing a 24-stage fully unrolled-pipeline architecture for Kyber would consume excessive resources and cause pipeline bubbles. This is because the SHA-3 requires feedback processing for more than one absorbing or squeezing operation, leading to inefficient performance in a fully unrolled-pipeline architecture. Therefore, according to the proposed scheduling, we propose a pipelined architecture with 8 stages, as shown in Figure 8. The Keccak state register pads the 1344-bit input data to 1600 bits, and then processes the computation of 24 rounds over an 8-stage pipeline. This design approach can effectively address feedback issues during the SHA-3 operations.

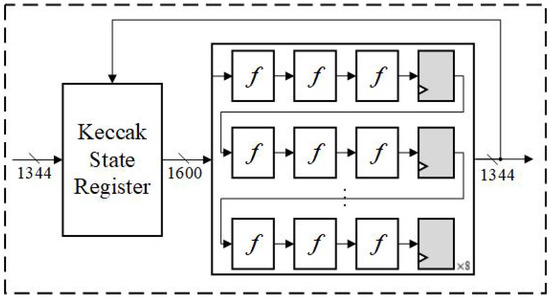
Figure 8. Proposed 8-stage pipelined SHA-3 architecture.

3.5. Sampling Module

In addition to optimizing the hardware architecture of the multi-mode polynomial arithmetic module and SHA-3 modules, the sampling module also affects the overall throughput of Kyber. According to the computation scheduling, the SampleNTT module must complete its operation within 2 clock cycles. Therefore, we have designed the SampleNTT module to sample 84 bytes per clock cycle. As for ${\mathrm{SamplepolyCBD}}_2$ and ${\mathrm{SamplepolyCBD}}_3$, they must be able to sample 64 and 66 bytes per clock cycle, respectively.

3.6. Compress Module

Due to different values of d in (2), the Compress function can be configured into three modes: ${\mathrm{Compress}}_1$, ${\mathrm{Compress}}_4$, and ${\mathrm{Compress}}_{10}$. For ${\mathrm{Compress}}_1$, the computation can be seen as compressing to 1 if input x is between 833 and 2496; otherwise, it is compressed to 0. Therefore, it only requires implementation using comparators and does not need additional optimization. Hence, our focus for optimization lies in ${\mathrm{Compress}}_4$ and ${\mathrm{Compress}}_{10}$. Firstly, taking ${\mathrm{Compress}}_{10}$ as an example, $2^{10}/3329$ is approximately 0.3076, represented in binary as ${0.0100111011}_2$. To ease the hardware implementation, it can be approximated as shown in (16):

$${\displaystyle \frac{2^{10}·x}{3329}}\approx {\displaystyle \frac{315·x}{1024}}.$$

(16)

According to (2), rounding operations are necessary. However, since (16) already approximates the computation, we can easily find the approximation number to be added for rounding. Finally, the formal simplifications of the ${\mathrm{Compress}}_4$ and ${\mathrm{Compress}}_{10}$ functions can be expressed as (17) and (18), respectively,

$${\mathrm{Compress}}_4\left(x\right)=\lceil {\displaystyle \frac{2^4·x+1664}{3329}}\rfloor =\lfloor {\displaystyle \frac{315·x+\mathrm{32,701}}{65536}}\rfloor$$

(17)

$${\mathrm{Compress}}_{10}\left(x\right)=\lceil {\displaystyle \frac{2^{10}·x+1664}{3329}}\rfloor \approx \lfloor {\displaystyle \frac{315·x+484}{1024}}\rfloor .$$

(18)

Even though ${\mathrm{Compress}}_{10}$ does not have an optimal approximation expression after simplification, the result of (18) is still very close to the correct result. Therefore, a simple comparator can be used for error correction purposes to filter out incorrect terms, as shown in Figure 9. For ${\mathrm{Compress}}_4$, the optimal rounding approximation was found to be 32,701. Therefore, no further error corrections are necessary, as the result of (17) equals (2) using fixed-point representations.

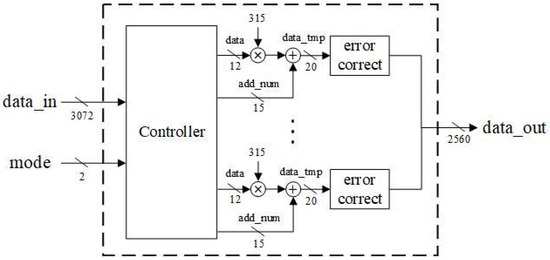
Figure 9. Proposed architecture of the Compress module.

4. Experimental Results

Firstly, as mentioned in Section 3, we found opportunities for parallel processing between SHA-3, sampling, and NTT operations. Therefore, we proposed a computational scheduling for reducing the computation time and improving the overall throughput. The speedup of the proposed computation scheduling compared to that of the original pseudocode is shown in Figure 10. Notably, the speedup in computation latency can only be observed when using the same hardware module. For the key generation phase, our proposed scheduling reduces the total computational latency to approximately 140 clock cycles. This speedup is achieved by parallelizing the sampling and SHA-3 operations. Specifically, the computational latency of the sampling is fully absorbed by the SHA-3 module. As a result, our proposed computational scheduling significantly reduces the computation time, achieving an average reduction of about 23% compared to the pseudocode scheduling.

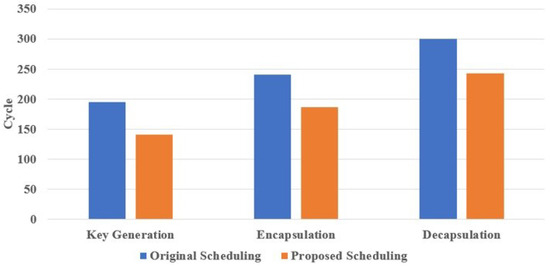
Figure 10. The speedup of proposed computational scheduling.

Next, to validate the hardware cost and performance of our proposed design, we use the Synopsys Design Compiler with the TSMC 40 nm standard cell library for logic synthesis. Additionally, the power consumption is estimated by gate-level simulations at 500 MHz. Table 1 shows the implementation results of the proposed design and state-of-the-art works. To further analyze the area usage within our design, we provide a detailed breakdown in Table 2. The polynomial arithmetic unit and SHA-3 engine together account for a significant portion of the area—40.1% and 26.5%, respectively—because both modules are fully unrolled and deeply pipelined to maximize throughput. This design decision trades area for speed and is the main contributor to our high throughput of 877.192k operations per second. The “Others” category, which accounts for 28.2% of the total area, includes controller logic and registers.

Table 1. Comparison of synthesis results with state-of-the-art.

Work	Tech. (nm)	Freq. (MHz)	Logic Gates (kGE) b	Memory (kB)	Cycles a (kCCs)	Total Time a ($\mathsf{\mu }$s)	Throughput a (kOPS)	Area Eff. a (kOPS/kGE)	Power Eff. a (kOPS/W)
[8]	28	300	979	12	144.5	482	2.074	0.002	78.13
[17]	28	540	697	24.75	72.2	134	7.462	0.011	900.01
[6]	65	200	95	80	21	105	9.523	0.091	–
[17] c	28	540	623	36.75	7.6	14	71.428	0.114	–
[17] d	28	540	623	36.75	6	11	90.909	0.146	–
[15]	65	336	1370	–	6.132	12.9	77.519	0.0566	–
[24]	180	93	160	7.37	7.7	82.8	12.077	0.075	156.25
[12]	40	115	532	14	12.245	106.49	9.391	0.018	362.32
[11]	40	270	253	7	21.143	78.31	12.270	0.051	1388.89
This Work	40	500	3183	–	0.57	1.14	877.192	0.276	2272.73

^a The cycles, total time, throughput, area efficiency, and power efficiency are the results of (Key-Generation + Encapsulation + Decapsulation). ^b The area is represented by the two-input NAND equivalent gate counts for fair comparison, where a two-input NAND gate is 0.68 $\mathsf{\mu }$m². ^c [17] with in-order instruction execution, without dynamic scheduling. ^d [17] with out-of-order instruction execution, with dynamic scheduling. Eff.: Efficiency.

Table 2. Area breakdown of major modules in the proposed design.

Module	Logic Gates (kGE)	Area (%)
SHA-3	843.495	26.5%
Multi-mode Polynomial Arithmetic Unit	1276.383	40.1%
CBD Sampler	6.366	0.2%
Compression/Decompression	159.15	5.0%
Others	897.606	28.2%

To provide a comprehensive evaluation, we compare our architecture with prior works that pursue both similar and differing design goals. Since ref. [8] adopts a RISC-V processor with an extended instruction set to enhance hardware computation flexibility, it focuses on general-purpose architectural enhancements. However, despite specific optimizations, this approach falls short in improving overall computational efficiency. On the other hand, refs. [11,12] are specifically designed for low-power scenarios, such as energy-constrained IoT and edge devices. Given the differing application contexts, direct comparison in terms of raw throughput and area may not fully reflect the effectiveness of each design. To provide a more comprehensive evaluation, we additionally consider the area efficiency and power efficiency as key metrics.

The works [6,17] optimize the computations and modules required for Kyber to achieve higher throughput and area efficiency. Notably, [17] ^c and [17] ^d can accelerate all operations required by Kyber, resulting in superior performance across various metrics. Compared to these designs, the implementation results in Table 1 show that the proposed design achieves the highest throughput of 877.192 kilo-operations per second (kOPS) for Kyber KEM, significantly outperforming all prior designs. Although the area of our design is significantly larger than that of lightweight implementations such as [11,12], which are specifically optimized for energy-constrained IoT and edge devices, our architecture achieves the highest area efficiency of 0.276 kOPS/kGE, demonstrating excellent hardware utilization. Furthermore, the proposed design also achieves the highest power efficiency of 2272.73 kOPS/W, indicating that our performance gains do not come at the cost of energy waste but rather optimize both speed and energy per operation.

In summary, while refs. [11,12] offer compact and ultra-low-power solutions tailored for edge applications, and ref. [8] demonstrates higher flexibility through a RISC-V based general-purpose design, these approaches sacrifice performance either because they are not optimized for Kyber, or because they are designed for low-resource environments. In contrast, our design targets performance-critical scenarios such as data centers or high-throughput systems, where maximizing throughput, area efficiency, and power efficiency is essential.

5. Conclusions

To meet the growing demand for secure high-throughput data transmission in cloud services, we propose an optimized CRYSTALS-Kyber hardware design that parallelizes NTT, SHA-3, and sampling operations for improved utilization and reduced latency. Synthesized under the TSMC 40 nm node, our design achieves a throughput of 877.192 kOPS and demonstrates the highest area efficiency among existing works at 0.276 kOPS/kGE. In addition, it achieves the highest power efficiency of 2272.73 kOPS/W, ensuring that performance gains are delivered without excessive energy consumption. These results highlight the suitability of our architecture for server-side applications, where maximizing both computational throughput and energy efficiency is essential for large-scale, performance-critical workloads.

While this work focuses on throughput-oriented architectural optimization, secure hardware deployment in real-world applications also requires consideration of side-channel resistance and fault tolerance. In future work, we plan to explore integrating basic countermeasures to enhance robustness against such attacks, depending on specific deployment scenarios.

Although our current implementation targets Kyber512, the proposed architecture is extensible to support Kyber768 and Kyber1024. These higher security levels would primarily require additional SHA-3 executions and sampling operations to generate more polynomials, as well as increased NTT computations due to the larger matrix dimensions. Modifications to the control logic and expanded on-chip memory would also be necessary to support the storage and processing of a larger number of polynomials. The Compress module can likewise be extended to support parameters such as $d=5$ and $d=11$, by applying the same fixed-point approximation and rounding techniques presented in this work. These extensions can be integrated without a fundamental redesign of the architecture, and we plan to investigate them further in future research.