Abstract
The rapid advancement of electronic technology demands circuit designs that minimize power consumption while maximizing performance. The power supply rejection ratio (PSRR) is a critical metric for quantifying an amplifier’s ability to suppress supply noise, yet accurately predicting PSRR in high-frequency domains and complex multi-stage architectures is increasingly challenging. In this work, we introduce a new framework for PSRR prediction that overcomes these limitations. Leveraging a simplified circuit abstraction based on Thevenin’s theorem, we reduced multi-stage operational amplifiers to “black-box” models—collapsing intricate small-signal networks into a tractable form without sacrificing accuracy. Building on this foundation, we proposed the Power-Supply Rejection Gain-Bandwidth (PGB) metric, which concisely captures the trade-off between an amplifier’s DC PSRR and the frequency range over which that rejection is effective. Using PGB, designers gain an intuitive figure-of-merit for early-stage optimization of PSRR. We validated the efficacy of the combined black-box modeling and PGB approach through detailed case studies, including a 180 nm CMOS two-stage op-amp design. These findings confirmed that the proposed black box plus PGB framework can reliably guide the design of analog circuits with stringent PSRR requirements.
1. Introduction
The rapid advancement of electronic technology has created an urgent need for low-power, high-performance circuit designs [1,2,3,4]. In this context, fundamental building blocks—such as operational amplifiers (op-amps), low-dropout regulators (LDOs), and bandgap references—have become increasingly vital. Ensuring circuit stability under diverse operating conditions is therefore paramount. The power supply rejection ratio (PSRR) is a key metric for quantifying a circuit’s ability to suppress perturbations from the power supply, directly influencing signal integrity and overall system stability. For example, in high-precision medical devices [5], improved PSRR enhances measurement accuracy and diagnostic reliability; in high-speed communication systems, strong PSRR attenuates supply noise during data transmission; and in portable devices, high PSRR extends battery life while bolstering immunity to interference.
Traditional PSRR calculation techniques predominantly rely on low-frequency equivalent circuit models and simplified pole-zero analyses [6,7,8]. However, at elevated frequencies and in complex multi-stage or high-speed communication circuits, the interaction between supply noise and parasitic elements becomes pronounced, often rendering these low-frequency approximations inaccurate or cumbersome. Moreover, existing methods lack a unified theoretical framework and a standardized calculation procedure, compelling designers to expend significant effort on custom analyses and verification for each new circuit topology. Such limitations impede design efficiency and can stifle innovation.
Researchers have developed numerous circuit-level techniques to enhance PSRR, but each approach is typically tailored to a specific application, underscoring the need for a generalized modeling framework. For example, Kim’s NMOS LDO regulator employs an intrinsic gain-tracking ripple-cancellation scheme to achieve exceptional PSRR in voltage regulators [1], while Zhang’s chopper stabilization technique maintains high PSRR across the audio band in a Class D amplifier [9]. Although these methods are effective within their intended domains, they remain application-specific and do not provide a universal theory for PSRR prediction.
Furthermore, many contemporary designs struggle to sustain high PSRR at higher frequencies. For instance, an output capacitor-less LDO optimized for ultra-low-voltage operation achieves only around 30 dB of PSRR at 10 kHz, highlighting the shortcomings of conventional techniques in high-frequency or low-headroom scenarios [10]. Collectively, these examples demonstrate the critical importance of PSRR optimization but also indicate that current methods lack the versatility to span diverse circuit topologies and operating conditions. Consequently, a more universal and systematic modeling approach is essential for reliably predicting and optimizing PSRR from DC up to mid-frequency ranges in a time-efficient manner.
To address these challenges, we propose a black-box modeling approach for PSRR prediction in multi-stage op-amps. The core idea is to condense a multi-stage amplifier into a simplified equivalent model using Thevenin’s theorem, treating the first amplification stage as an abstracted “black box.” By deriving the Thevenin equivalent output of the first stage and reintegrating it into the overall circuit, the PSRR calculation is significantly simplified without sacrificing accuracy. This approach provides an analytical yet intuitive understanding of how each stage contributes to the overall PSRR, inherently capturing important design parameters such as pole zero locations and gain bandwidth limits. Compared to brute force SPICE simulations or highly complex small-signal models, the black-box method drastically reduces the analytical effort required to evaluate PSRR, making early-stage design analysis more accessible and efficient.
Additionally, we introduce a novel metric termed the Power-Supply Rejection Gain-Bandwidth (PGB) product to characterize the mid-frequency behavior of PSRR. Analogous to an op-amp’s gain-bandwidth product, the PGB is defined as the product of an amplifier’s DC PSRR and the frequency of its dominant PSRR zero. This metric encapsulates the intrinsic trade-off between strong low-frequency supply noise rejection and the bandwidth over which that rejection is maintained. A higher PGB value signifies that an amplifier’s PSRR remains effective over a wider frequency range, whereas a lower PGB indicates that the PSRR begins to degrade at a lower frequency. By using the PGB metric, designers can more intuitively assess the balance between PSRR and other performance parameters (such as stability margins or overall bandwidth) within the target frequency range. An important advantage of the PGB-based evaluation is that it obviates the need for complicated high-frequency small-signal modeling (e.g., extensive S-parameter analyses). Instead, key characteristics like the DC PSRR and the first pole (or zero) frequency are extracted directly, providing an efficient first-order approximation of PSRR performance across the frequency spectrum. The proposed methodology is applicable from DC up to the amplifier’s unity-gain bandwidth (UGB).
Importantly, our framework offers a unified explanation for why different circuit architectures with identical low-frequency PSRR can exhibit divergent PSRR roll-off behaviors as they approach the UGB. For instance, consider an LDO regulator and a two-stage op-amp that are both optimized for a similar DC PSRR value. Despite comparable low-frequency performance, these two circuits may demonstrate distinct PSRR profiles at mid-to-high frequencies due to differences in their internal gain distribution and the placement of poles and zeros. Our PGB-centric analysis captures this phenomenon, allowing designers to anticipate and account for such architecture-dependent variations in PSRR behavior.
We validated the proposed approach by designing and simulating representative multi-stage amplifier circuits. In particular, a two-stage operational amplifier implemented in a 180 nm CMOS process was used as a case study to compare our analytical PSRR predictions against conventional AC simulation results. The results show that the black box + PGB method can predict the PSRR curve within approximately 2 dB of full SPICE simulation across the frequency band while requiring significantly less computational effort. We further verified that these predictions hold after post-layout extraction: even with layout parasitic effects, the PSRR performance closely matched the pre-layout analysis. This robustness against layout-induced degradation demonstrated the practical viability of our modeling framework for industrial analog design.
In summary, the key contributions of this work include the following:
- A black-box PSRR modeling framework—We developed a simplified equivalent modeling technique for multi-stage op-amps using Thevenin’s theorem, which drastically reduces analysis complexity and provides clear insight into stage-wise contributions to PSRR.
- Introduction of the PGB metric—We proposed the Power-Supply Rejection Gain-Bandwidth product as a new figure of merit that links an amplifier’s DC PSRR to its effective bandwidth, enabling intuitive evaluation of PSRR trade-offs without resorting to complex high-frequency modeling.
- Unified theoretical insight—The proposed framework offers a unified theoretical explanation for disparate PSRR behaviors in different circuit topologies, bridging the gap between low-frequency PSRR requirements and high-frequency performance outcomes.
Finally, the remainder of this paper is organized as follows: Section 2 presents the theoretical foundation of the black-box PSRR model and details the derivation procedure, including pole zero analysis for various amplifier topologies. Section 3 demonstrates the design example of this method in a complex circuit. Section 4 shows the simulation performance of the circuit in Section 3 and the differences between different PSRR calculation methods. Section 5 summarizes the methods of this paper.
2. Method
2.1. Related Work
We leveraged Allen’s interpretation of PSRR [7] and developed a “black box” model that simplifies the intricate circuitry. This model is particularly applicable to Thevenin Equivalent Circuit Analysis, where the Thevenin theorem simplifies linear resistor networks with independent sources into a single voltage source in series with a resistance. Specifically, for any single-port network N, the port can be represented equivalently by a voltage source—whose value corresponds to the open-circuit voltage ()—in series with a resistance , which is the equivalent resistance observed at the port when all independent sources are deactivated. As shown in Figure 1, the Thevenin theorem simplifies linear resistor networks with independent sources into a single voltage source in series with a resistance.
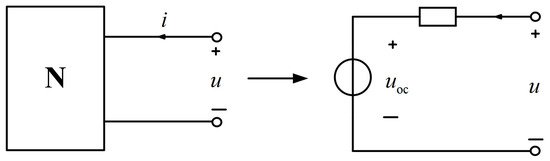
Figure 1.
Thevenin equivalent circuit.
2.2. Proposed Methodology
In this section, we employed the proposed black-box theory to analyze the PSRR of various operational amplifiers.
2.2.1. PSRR Calculation for P-Input Two-Stage Op-Amps
In this op-amp, the input stage typically includes two P-input MOSFETs ( and ) that receive the input signal and provide initial amplification. Transistors and serve as load devices and work in conjunction with and to enhance the gain of the input stage. Current mirrors consisting of and supply a stable bias current to the input stage while ensuring that the currents in and are balanced. In the output stage, transistor further amplifies the signal from the input stage and provides adequate drive capability for the load, as depicted in Figure 2.
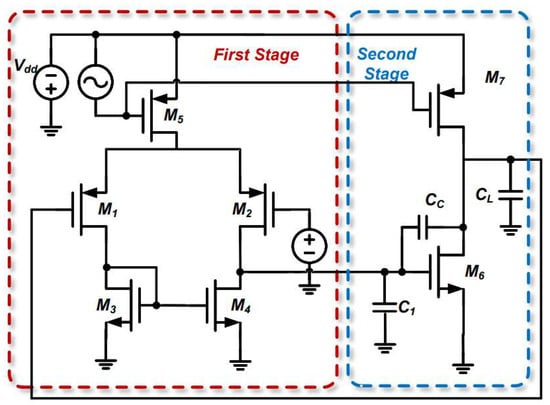
Figure 2.
Typical structure of a P-input two-stage op-amp.
To simplify the calculation, we treat the first stage of the op-amp as a “black box” with input terminals, denoted as , and an output terminal, denoted as . This is illustrated in Figure 3.
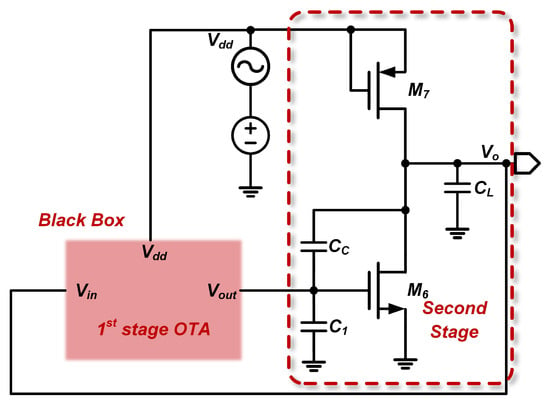
Figure 3.
Two-stage op-amp circuit after “black box” abstraction.
The processing of the first stage is performed in several steps:
- (a)
- Evaluating the impact of on the Thevenin equivalent output voltage of the first stage
The first stage is viewed as an independent module. Based on the Thevenin theorem, the equivalent voltage generated by it is given by .
- (b)
- Evaluating the impact of on the Thevenin equivalent output voltage of the first stage
For a differential input , as shown in Figure 4, the corresponding Thevenin equivalent output voltage is as follows:
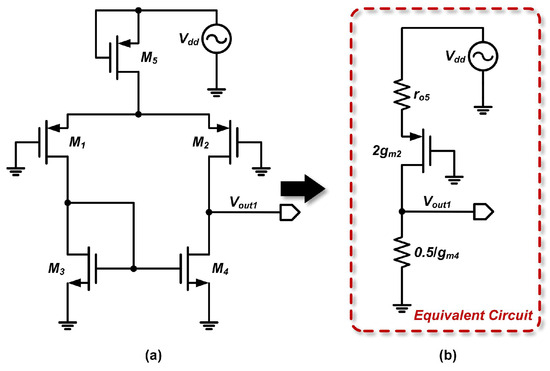
Figure 4.
Thevenin equivalent circuit for the first stage of the op-amp. (a) Original circuit of the first stage; (b) Thevenin equivalent circuit.
Likewise, for a common-mode input , the corresponding Thevenin equivalent output voltage is as follows:
The common-mode output voltage is relatively small and can be combined with the differential output voltage. Therefore, the common-mode contribution is typically neglected in subsequent calculations. The construction of the Thevenin equivalent circuit is illustrated in Figure 5.
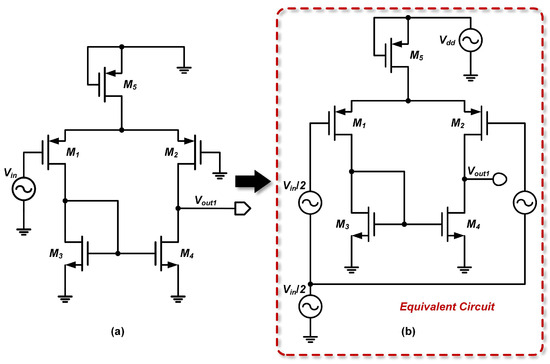
Figure 5.
Thevenin equivalent output voltage of the first stage. (a) Original circuit of the first stage; (b) Thevenin equivalent circuit.
- (c)
- Constructing the Thevenin equivalent circuit
Using the superposition theorem, the first stage is further simplified to a structure consisting of a voltage source and a resistor, as shown in the lower left area of Figure 6, where represents the output resistance of the first stage.
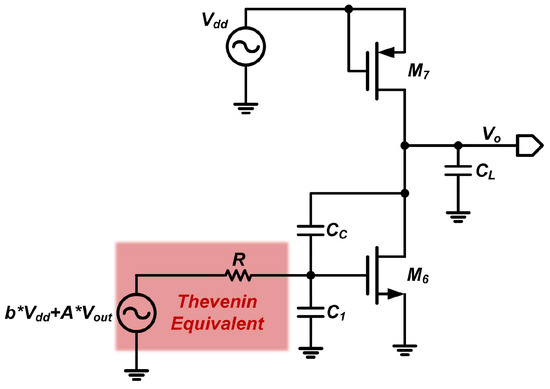
Figure 6.
Thevenin equivalent circuit of the op-amp.
- (d)
- Deriving the PSRR transfer function
Figure 7 illustrates the equivalent circuit for the two-stage op-amp. Taking into account the gate-drain capacitance of , we employ small-signal analysis to formulate the node current equations and thereby derive the PSRR transfer function.
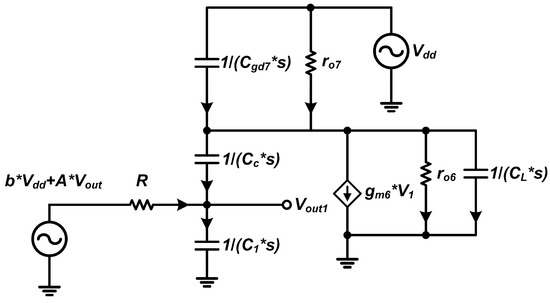
Figure 7.
Small-signal equivalent model.
Furthermore, in the PSRR transfer function derived from the black-box model, two primary zeros appear, referred to as and . The first zero, , corresponds to the frequency at which supply-induced noise contributions from the first and second amplifier stages cancel each other, resulting in a null (zero) in the PSRR response. The second zero, , occurs at a higher frequency and typically arises from a secondary coupling mechanism or parasitic feedback path within the op-amp. For clarity in analysis, we assume resides at a lower frequency than . This assumption isolates the low-frequency behavior dominated by and aligns with the typical frequency ordering in multi-stage analog circuits. Similarly, when examining the pole locations, we assume a dominant low-frequency pole ( < ) to maintain consistency in the frequency domain analysis. With these definitions and assumptions in place, we now proceed to derive the DC PSRR value and identify the corresponding zero and pole positions. It should be noted that in standard multi-stage amplifiers, the two zeros caused by the first-stage output and third-stage feedback equivalence typically satisfy < .
First, we write the node’s current equation at node .
Similarly, we write the node’s current equation at node .
By equating (5) and (7), we obtain the following:
In the derivation above, it is assumed that , due to matching requirements. If we set and , we obtain , , and
Next, we derive the DC PSRR value as well as the positions of the zero and pole.
Assuming , , , and for stability, we have .
Further assuming leads to the following:
The location of is the closest to the origin relative to the first pole. Whether the DC PSRR value is positive or negative depends on the specific values of N and M. When N is approximately twice that of M, the DC PSRR value becomes very high; however, the zero also shifts closer to the origin.
The PSRR is influenced by two signal paths within the op-amp. In the first path, the signal entering from reduces the output voltage at low frequencies; in the second path, the signal entering from has the opposite effect and increases the output voltage. For simplification, the drain of is grounded, thereby neglecting the signal contribution from and resulting in a positive DC PSRR gain. Under ideal bias current source conditions, if N is greater than twice that of M, the PSRR is negative; if N is less than twice that of M, the PSRR is positive. The location of the zero is also closely related to the ratio of these two parameters.
Although PSRR has always been a key performance indicator in circuit design research, previous studies have focused more on the analysis of low frequencies or specific topologies, and have not fully considered unified indicators to evaluate overall performance across frequency bands. Therefore, no indicators similar to PGB have been proposed in the previous literature. Traditional methods usually rely on low-frequency models or simulation analysis of specific frequency bands, making it difficult to provide designers with a unified and intuitive tool to quickly evaluate the impact of parameter changes on the overall frequency response.
To overcome this limitation, the PGB indicator proposed in this work directly links the DC PSRR performance with its effective frequency range, forming an intuitive and unified evaluation system. This allows researchers to quickly and intuitively evaluate the sensitivity of key circuit parameters to PSRR performance in the early stages of design, effectively guiding the fine adjustment of parameters to meet the frequency performance requirements in specific application scenarios. This advantage will be further demonstrated and verified in the detailed simulation analysis in Chapter 4.
By approximating the PSRR curve as having a single zero, and drawing an analogy with the gain-bandwidth product in op-amps, we define PGB as the product of the zero frequency and the DC PSRR value:
Figure 8 illustrates a simplified PSRR curve (dominated by a single zero) to explain the PGB concept. The baseline curve CDE represents the original PSRR response: point C marks the DC PSRR value, and point D is the dominant zero’s frequency, beyond which the PSRR magnitude declines at approximately −20 dB/decade (segment D–E). If a design parameter is increased toward 2M (with other parameters fixed), the PSRR shifts to curve ABE. In this modified response, point A indicates a significantly higher DC PSRR and point B is the new dominant zero at a lower frequency (closer to the origin). This adjustment boosts the PSRR at DC and low frequencies (enhancing the low-frequency portion around point C, i.e., the “” segment) but causes the −20 dB/dec roll-off to begin earlier (segment B–E), so the overall PGB remains essentially unchanged. In other words, raising the DC PSRR alone improves supply-noise rejection in the low-frequency region but does not extend the high-frequency response—an analog to the gain–bandwidth trade-off in amplifiers. Consequently, if the operating frequency lies in the original curve’s high-frequency region (segment D–E), this parameter change provides little improvement at that frequency.
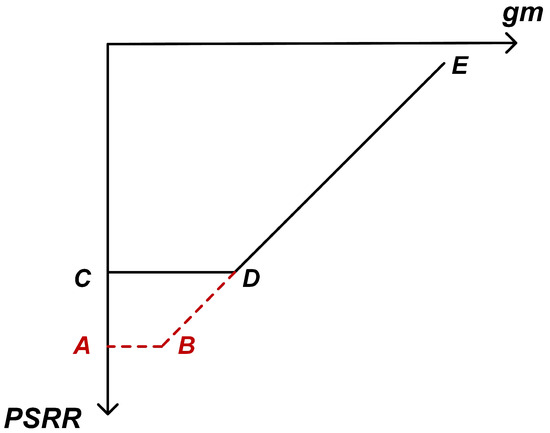
Figure 8.
Impact of varying on the frequency characteristics of PSRR.
This process bears some similarity to considerations of the loop bandwidth (GB) of the two-stage op-amp. Increasing a particular parameter directly enhances the DC PSRR value, which is beneficial for our analysis. Under stability constraints, reducing the parameter shifts outward, thereby improving the frequency response; similarly, increasing shifts the BE line outward; increasing and directly optimizes the DC PSRR value; while increasing and raises the DC PSRR value but also moves closer to the origin, benefiting only the low-frequency response—the PGB remains unchanged, and hence the improvement at high frequencies is limited. However, since the bandwidth that the industry is concerned about is usually low-frequency, PGB can play a vital role in the design of specific fields.
2.2.2. PSRR Calculation for N-Input Two-Stage Op-Amps
In this subsection, we employ a similar analytical approach to examine the PSRR of N-input two-stage op-amps, thus demonstrating the portability of the new PSRR calculation theory.
Based on the analysis in Section A for a typical P-input two-stage op-amp, we consolidate the simplified flowchart for a typical N-input two-stage op-amp into a single diagram, as shown in Figure 9.
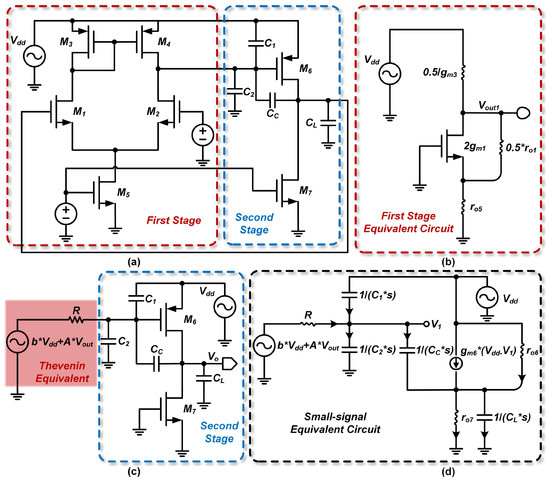
Figure 9.
Simplified flow chart of a standard N-input two-stage op amp. (a) Full circuit of the two-stage op-amp; (b) First stage equivalent circuit; (c) Second stage with Thevenin equivalent circuit of the first stage; (d) Small-signal equivalent circuit of the second stage.
The following quantities are computed: the Thevenin equivalent voltage due to from the first stage, the Thevenin equivalent voltage due to , the PSRR, the DC PSRR value, the zero, the pole, and the PGB.
From Figure 9b, the Thevenin equivalent voltage due to is given by , which is calculated as follows:
Similarly, the Thevenin equivalent voltage due to is , which is calculated as follows:
Using the node current equations, we obtain the following:
Equating (20) and (21) yields the following:
PSRR Calculation:
Under the assumptions that and , we approximate expressions for the DC PSRR value and the zero can be derived as follows:
Assuming that , , , , the pole of the PSRR is approximately given by the following:
Similarly, the calculation of PGB follows the same procedure as described previously.
From (29), it is apparent that the PGB of the N-input is relatively smaller. It is evident that by increasing the output resistance R of the first stage and the small-signal resistance of , the DC PSRR value improves. However, the point shifts closer to the origin, thereby enhancing only the low-frequency portion of the response, while the PGB remains unchanged. Under stability constraints, reducing shifts away from the origin and improves the frequency characteristics. Comparing the PGB values for the P-input and N-input two-stage op-amps (under ideal bias conditions), the frequency response of the P-input op-amp is superior by an order of magnitude.
2.2.3. P-Input Folded Cascade Op-Amps
The folded cascade configuration is an efficient design for the input stage of operational amplifiers, effectively enhancing both input impedance and gain while simultaneously improving power supply rejection. Building upon the methodology employed for P and N-input two-stage op-amps, we analyze the widely used P-input folded cascade op-amp structure and derive the corresponding analytical equations.
In Figure 10, the capacitor is a parasitic capacitor located between the s. Although its placement may initially seem counterintuitive for enhancing PSRR, actually plays a vital role in stabilizing the output voltage by providing a low-impedance path for high-frequency noise and supply-induced disturbances. This helps in filtering out unwanted noise, which is crucial for improving the PSRR. Among all the parasitic capacitances present in the circuit, is considered the most significant due to its larger capacitance value and strategic position in the feedback loop, which maximizes its positive impact on PSRR enhancement.
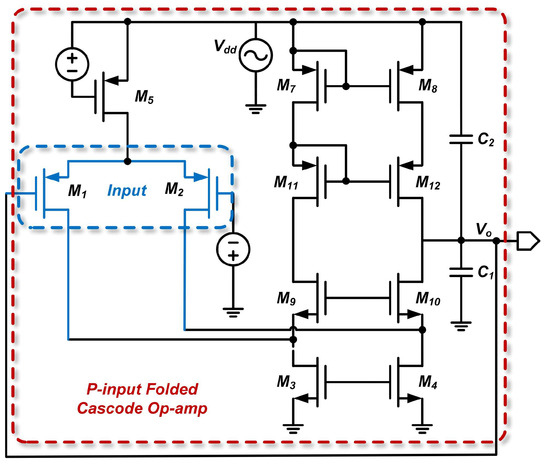
Figure 10.
P-input folded cascade op-amp.
Using the Thevenin theorem, we first derive the open-circuit output voltage of the first stage. This open-circuit voltage can be computed by applying the superposition principle. The analytical approach is similar to that for the P- and N-input two-stage op-amps. First, the effect of the drain input signal from on the output is calculated. The circuit is modeled using the small-signal equivalent and further simplified via Norton’s theorem, as shown in Figure 11, yielding a Thevenin equivalent voltage of .
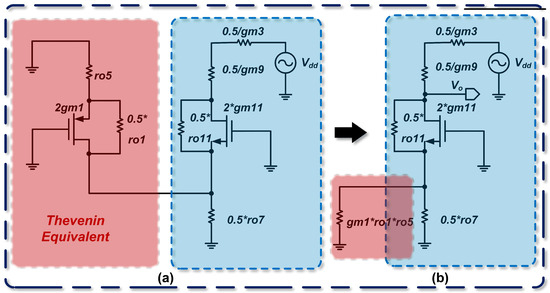
Figure 11.
Equivalent circuit for the folded cascade op-amp. (a) Thevenin equivalent circuit combined with the second stage elements; (b) Modified equivalent circuit after transformation, showing the adjusted components and connections.
Next, we calculate the effects of the drain input signals from and on the output. The resulting Thevenin equivalent voltage is .
where it is found that .
Subsequently, the effect of on the output is computed; as shown in Figure 12, the Thevenin equivalent voltage induced by is . Finally, by applying the superposition theorem, the circuit is reduced to its simplest form.
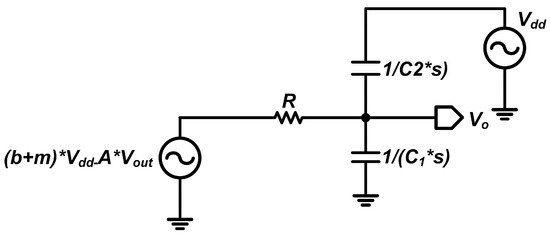
Figure 12.
Folded cascade op-amp simplified using the superposition theorem.
denotes the output resistance of the first stage. To calculate the PSRR, the values of and must be determined. Based on the circuit diagram, we write the node current equation at as follows:
Which simplifies to the following:
In this example, . The inverse of the DC PSRR value is equal to the op-amp gain. The PGB is then derived as follows:
Key design insights include:
- (a)
- Increasing directly raises the DC PSRR value.
- (b)
- Reducing the parasitic capacitance improves the frequency response.
- (c)
- The op-amp’s dominant pole is associated with its output node. Consequently, augmenting shifts this pole closer to the origin, which is advantageous for enhancing both the system stability and the PSRR’s frequency response. However, it is crucial to strike a balance with the required bandwidth; one cannot indiscriminately reduce the bandwidth without considering the overall system performance requirements.
2.2.4. N-Input Folded Cascade Op-Amps
Following the approach in Section 2.2.3, we analyze the N-input folded cascade op-amp. Figure 13 consolidates the simplified flowchart for a typical N-input two-stage op-amp.
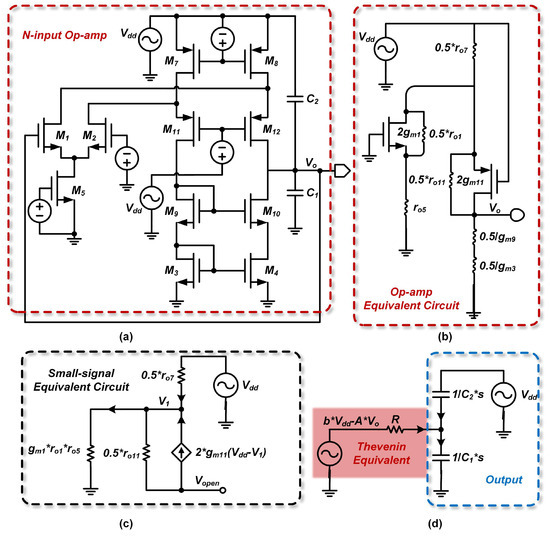
Figure 13.
Simplified flowchart for a typical N-input two-stage op-amp. (a) Full N-input op-amp circuit; (b) Simplified equivalent circuit of the op-amp; (c) Small-signal equivalent circuit; (d) Thevenin equivalent circuit with output stage.
From the Thevenin equivalent circuit, we obtain the following:
where the equivalent resistance is .
Using resistive voltage division, the Thevenin equivalent voltage is found to be , where:
The Thevenin equivalent voltage induced by is , where:
and denotes the output resistance of the first stage. By writing the node current equation at node , the relationship between and is obtained as follows:
Subsequently, the PSRR is calculated as follows:
where is the compensation capacitor and represents the parasitic capacitance. Since the op-amp’s input resistance R is very high, the zero is located near the origin, while the pole is far from the origin.
3. Case Study
High-speed, high-resolution analog-to-digital converters (ADCs) are both a central research focus and a critical building block in modern analog IC design. To validate the applicability of our black-box PSRR derivation methodology in industrial-scale, complex analog circuits, this section presents the design of a high-performance operational amplifier specifically optimized for ADC front-end applications. We begin by applying the proposed black-box PSRR derivation and then contrast its results with those obtained using two conventional PSRR calculation techniques. Next, we derive closed-form expressions for other key performance metrics, such as gain-bandwidth product, phase margin, and slew rate. At the end of this section, we specify the transistor dimensions determined by these multiple analytical constraints. In Section 4, we present a comprehensive suite of simulation results, including the following:
- (a)
- A comparative assessment of the three PSRR calculation methods in terms of accuracy.
- (b)
- Demonstration of PSRR improvement following targeted parameter adjustments guided by the PGB metric.
- (c)
- Pre-layout simulation of all key performance metrics.
- (d)
- Layout implementation followed by post-layout parasitic-extracted simulations.
3.1. Circuit Architecture
In high-speed, high-resolution ADC design, the demands on bandwidth, gain, and PSRR are exceptionally stringent. While traditional telescopic cascade amplifiers can achieve very high gain, they introduce extra poles and exhibit limited output swing.
As shown in Figure 14, Our proposed architecture includes a folded cascade input stage, a common-source output stage, a feedforward compensation network, a common-mode feedback (CMFB) loop, and a wide-swing biasing scheme—each component fine-tuned to optimize critical performance metrics. The folded cascade input stage provides high gain and an extended input common-mode range, while the common source output stage offers low output impedance and strong drive capability. The feedforward network enhances high-frequency responses by introducing a compensatory zero to counteract phase lag, and the CMFB loop maintains a stable output common-mode voltage.
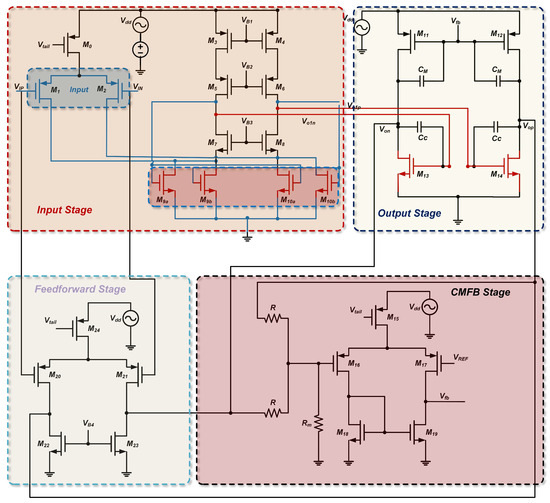
Figure 14.
Circuit architecture.
In the following section, we first present the design specifications crafted to meet the rigorous demands of high-speed, high-resolution ADC front-end applications. Section 3.2 subsequently provides a thorough derivation of the key PSRR metric. We present the design specifications as shown in Table 1.

Table 1.
The design specifications of this circuit.
3.2. PSRR Derivation
3.2.1. Black-Box Model
We calculate the PSRR using the method presented in Section 2. Referring to Figure 10, the first stage of op-amps can be represented as follows:
Referring to the calculation in Figure 9, replace the original “b” with “here” and substitute it with the PSRR transfer function that can be directly obtained.
Assuming , , , ,
If , :
In the next two sections, Section 3.2.2 and Section 3.2.3, we provide a brief summary of the ideas and final expressions of other PSRR calculation methods.
3.2.2. Small-Signal Model
To quantify the power-supply rejection of our two-stage op-amp, we replace the whole circuit with its small-signal equivalent. In this model, supply-noise can couple to the output via three dominant paths:
- Cascade-load path (through the cascade devices)
- Tail-source path (through the tail current source back into the differential pair)
- Feedforward path (through the dedicated feedforward transistor and CMFB/output network)
We derive each contribution in turn and then form the overall PSRR transfer function.
- (a)
- Tail-Source Path
Supply noise is coupled through the finite output resistance of the tail current-source transistor into the input differential pair. The small-signal voltage at the tail node is as follows:
- (b)
- Feedforward Path
A dedicated feedforward transistor detects the supply noise, transforms it into a small-signal voltage, and injects it through the CMFB/output network into the final output. Its coupling coefficient is as follows:
And this noise is further amplified by the feedforward gain.
- (c)
- Aggregate PSRR Expression
Let be the gain from the feedforward injection point to the output. Summing the three noise-coupling paths, the single-ended noise transfer from supply to production is as follows:
For a differential input signal, the amplifier gain is . Thus, the power-supply rejection ratio is expressed as follows:
3.2.3. Signal-Flow Graph and Mason’s Gain Formula
To obtain a closed-form PSRR expression that naturally extends to arbitrarily complex feedback networks, we construct the signal-flow graph (SFG) of our two-stage amplifier and apply Mason’s gain formula. Figure 15 illustrates the SFG nodes and directed branches marked with their small-signal gains.
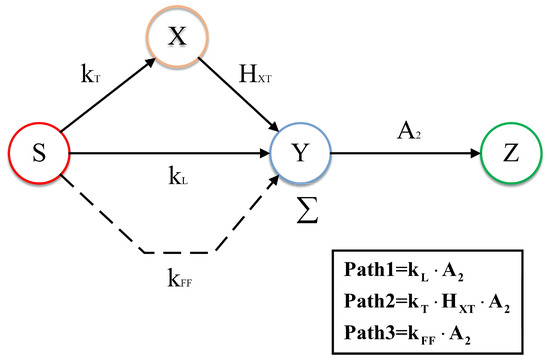
Figure 15.
The signal-flow graph (SFG) of our two-stage amplifier.
- (a)
- Node Definitions
Summing all three contributions, the single-ended noise transfer from the supply to the output is as shown in Table 2:

Table 2.
Node Descriptions and Small-Signal Voltages.
- (b)
- Directed Branch GainsWe assign a directed branch gain for each forward connection from node A to node B:
- S → Y (Cascade-load path):
- S → X (Tail-source path):
- X → Y (Tail-to-mid conversion):where is the first-stage open-loop gain.
- S → Y (Feedforward path):
- Y → Z (Second-stage gain):
- (c)
- Forward-Path EnumerationIn this SFG, there are three non-intersecting forward paths from the supply-noise node S to the output Z:
- Path 1 (Load):
- Path 2 (Tail):
- Path 3 (Feedforward):
Because there are no independent feedback loops external to these forward paths, Mason’s formula simplifies to the sum of all forward-path gains as follows:
- (d)
- PSRR Definition
The open-loop differential gain of the complete amplifier is as follows:
Accordingly, the low-frequency PSRR (ratio of signal-gain to supply-noise gain) in dB is as follows:
3.3. Other Key Performance Metrics
In this section, we quantitatively analyze the open-loop DC gain and the GBW, since these three metrics jointly determine the amplifier’s linearity, speed, and supply noise immunity.
- (a)
- Gain Expression
The transconductance of the input stage, Gm1, is given as follows:
The voltage gain is expressed as follows:
- (b)
- Transfer Function Optimization
As illustrated in Figure 16, the feedforward stage introduces a zero-pole pair in the transfer function, compensating for the dominant pole. This minimizes phase lag and extends the high-frequency bandwidth. The transfer function is given by the following equation:
where:
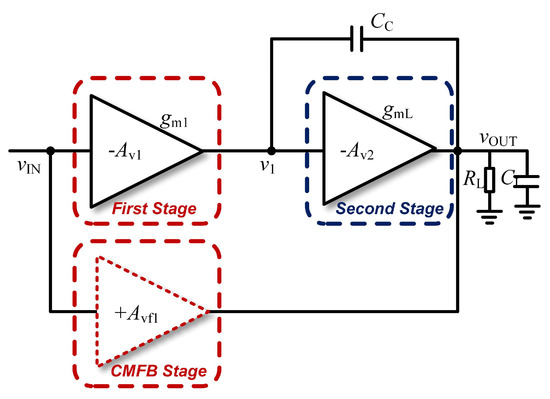
Figure 16.
Equivalent block diagram.
- (c)
- PGB
PGB encapsulates both low-frequency rejection (DC PSRR) and the frequency range of effective noise suppression.
From (68), we obtain:
The PSR is defined as the ratio of output voltage change to the power supply perturbation, representing how strongly supply disturbances couple directly into the output. In contrast, the PSRR is commonly defined as the inverse of this ratio or, equivalently, as the difference between the amplifier’s gain and PSR, namely:
Using this metric, designers can quantitatively evaluate low-frequency noise rejection and intuitively assess the high-frequency suppression bandwidth, thus allowing for a systematic optimization of power supply noise performance. We can intuitively express which factors are related to the performance of the circuit’s PSRR in the mid- and low-frequency bands. After the initial simulation, we can quickly modify certain parameters to further improve the PSRR performance of the target frequency band while ensuring that other performance metrics meet the design requirements in each frequency band. Therefore, the introduction of PGB helps researchers to further optimize the performance of certain parameters in the early stages of complex circuit design.
3.4. Transistor Sizing Under Multi-Constraints
Based on the target specifications below, device ratios are chosen by hand calculation and Cadence verification.
Table 3 displays the final dimensions of each transistor after readjustment according to the PGB method. The design requirements are met across all indicators, resulting in a favorable FOM value. The PSRR calculation method proposed in this article offers new insights for future circuit design, while the PGB optimization method can simplify the complex process of PSR calculation.

Table 3.
Sizes obtained from the multiple constraints.
Based on our calculations, the black-box model in the PSRR derivation inherently enforces the necessary conditions of the other two methods. For example, whereas Methods B and C require > 100.0, our black-box approach demands > 105—a stricter criterion that underpins the superior accuracy of our results. Consequently, the device dimensions we derive simultaneously satisfy the requirements of all three PSRR calculation methods.
In Section 4, we present comprehensive Cadence simulations alongside a detailed comparison of the three PSRR derivation techniques.
4. Simulation Results and Layout
4.1. PSRR Calculation Simulation Results
In this section, we apply the proposed method to design a fully differential op-amp with high PSRR. The circuit was designed using Cadence Virtuoso IC617 (Cadence Design Systems, Inc., San Jose, CA, USA) with a 180 nm CMOS process, and the supply voltage was set to 1.8 V at 27 °C. Based on the transistor W/L ratios derived in Section 3.4, the amplifier schematic is implemented in Cadence for simulation. The resulting performance metrics are then benchmarked against the analytical predictions to validate the accuracy of the proposed PSRR calculation method.
Table 4 summarizes the key parameters extracted by each of the three PSRR derivation techniques and the corresponding PSRR values they predict. Among the three approaches, the black-box model yields results that most closely match the simulation.

Table 4.
PSRR calculation simulation results of different methods.
The calculation time in the figure is the average time taken by all members of our team to design circuits using this method alone. It is for reference only. However, as illustrated in Figure 17, our method also outperforms the others in both computational efficiency and predictive precision.
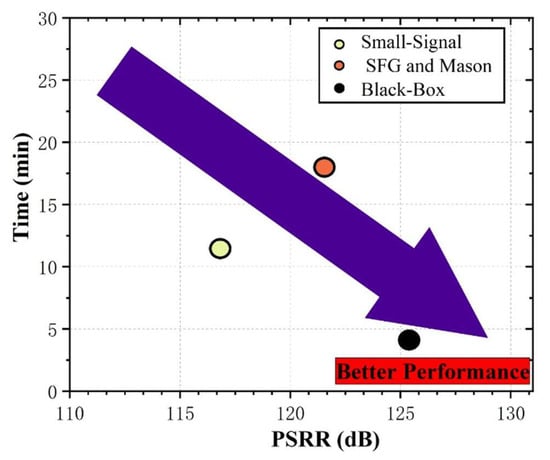
Figure 17.
Comparison of complexity and accuracy of different PSRR calculation methods.
4.2. PGB-Guided PSRR Optimization
According to the derived formula, the PGB metric enables rapid assessment of how increasing or reducing the PSRR bandwidth affects it, allowing the optimal compensation point to be pinpointed during early hand calculations or quick simulations.
As illustrated in Figure 18, Figure 19 and Figure 20, optimizing these parameters through the intuitive guidance provided by PGB enhances PSRR performance. Given the explicit mathematical relationship between PSRR and PSR, improvements in PSRR achieved through the PGB approach can indirectly yet effectively inform designers on how to optimize PSRR performance. This demonstrates the practical advantage of using the PGB metric as an intuitive design tool, bridging the gap between the complex PSR calculations commonly encountered in industrial practice and straightforward PSRR optimization.
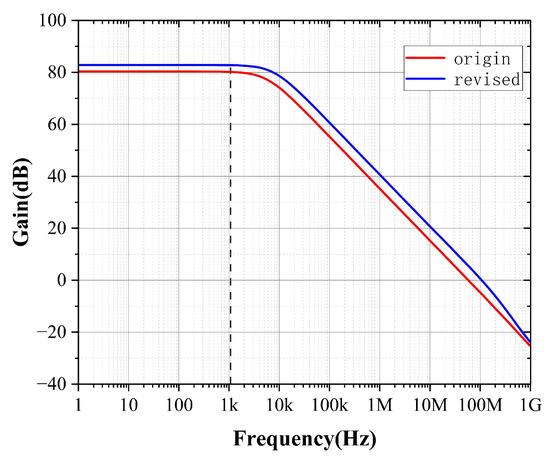
Figure 18.
Gain simulation experiment.
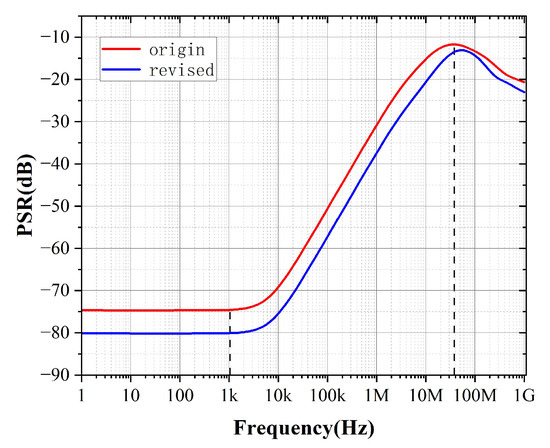
Figure 19.
PSR simulation experiment.
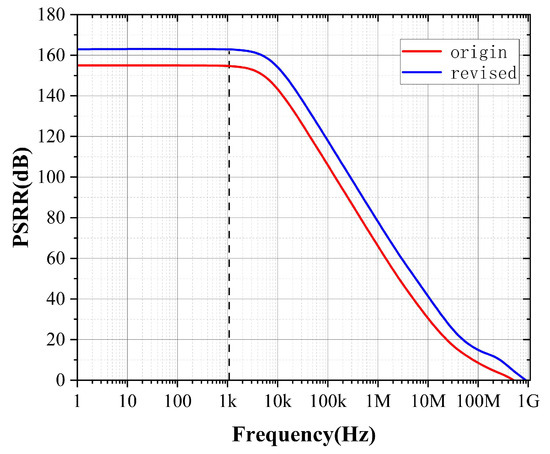
Figure 20.
PSRR simulation experiment.
If we use the black-box method to derive PSRR and calculate PGB for all common op amps, we can clearly compare the impact of different key parameters on different op-amps and evaluate the PSRR performance of different architectures in the target frequency band. The intuitive comparison of PGB of different op-amps can help researchers select architectures in industrial design and derive and optimize them in the early stages of design.
4.3. Comprehensive Robustness Assessment
In practical industry designs, PSR is typically a direct concern because it quantifies the amount of power-supply noise propagating into the signal path. However, analyzing and optimizing PSR directly is complicated due to intricate interactions among circuit parameters and the resulting mathematical complexity. Conversely, analyzing both PSR and PSRR—especially using our proposed PGB methodology—is significantly more straightforward and intuitive. By utilizing the PGB framework, we know that we can enhance the performance of PSRR by increasing gm or reducing according to (68). The simulation results before and after the modification are shown below.
We also performed additional simulations on the circuit. Figure 21 shows the circuit’s basic indicators at different process corners, and Figure 21d shows the circuit’s PSRR at each process corner after PGB operation adjustment.
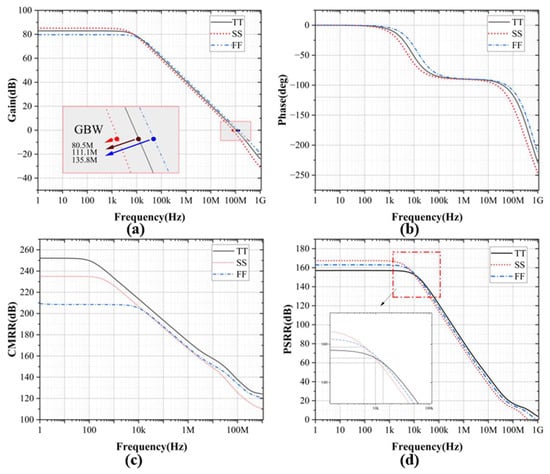
Figure 21.
Simulation results at different process corners of the proposed OTA. (a) The AC gain, (b) Phase, (c) CMRR, (d) PSRR.
The PSRR of this circuit is more than 157dB at 1 kHz for all process corners. It has an excellent PSRR at high frequencies as well. We also tested the PSRR and PSR performances of the circuit under different temperature conditions, as shown in Figure 22.
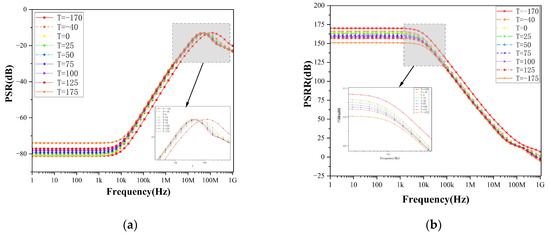
Figure 22.
PSRR and PSR performance of the circuit under different temperature conditions. (a) PSR, (b) PSRR.
We ran 200-point Monte Carlo simulations across three process corners (TT, SS, and FF), included device mismatch with a 3σ threshold based on the foundry PDK, and varied the temperature at 0 °C, 27 °C, and 85 °C. The results are shown in Figure 23.
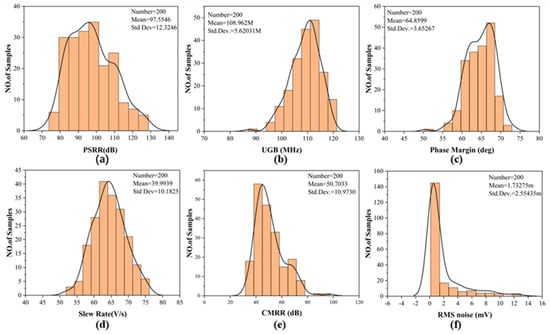
Figure 23.
Monte Carlo simulation of (a) PSRR, (b) Unity gain bandwidth, (c) Phase margin, (d) Slew rate, (e) CMRR, (f) RMS noise.
As summarized in Table 5, we benchmarked our design against recent works to highlight its superior performance. These metrics demonstrate that our amplifier not only meets but significantly exceeds industry benchmarks in gain, bandwidth, speed, noise rejection, and power efficiency.

Table 5.
Performance of the implemented OTA in comparison to the existing works.
4.4. Layout-Level Implementation and Multi-Constraint Sizing
To further validate our PSRR prediction methodology in industrial processes, we completed the full layout and performed post-layout simulations as shown in Figure 24. These results confirm that our black-box + PGB approach not only preserves schematic-level accuracy and design simplicity but also maintains robust performance despite layout-induced parasitics, demonstrating its readiness for industrial implementation.
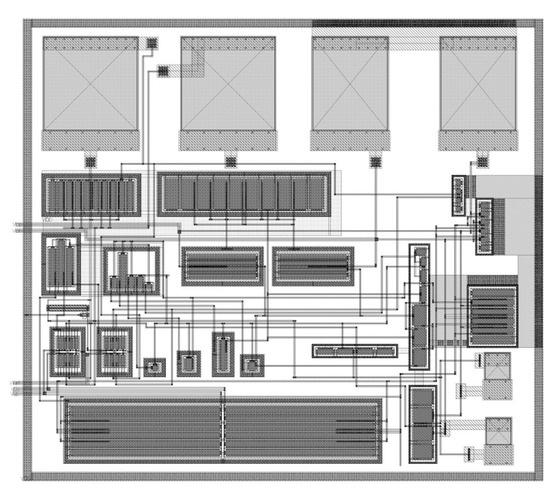
Figure 24.
Layout of the proposed OTA.
As shown in Figure 25, the post-simulation results show that the circuit can still maintain performance close to the pre-simulation when considering parasitic effects and matching, further confirming the feasibility of our design method in complex circuits.
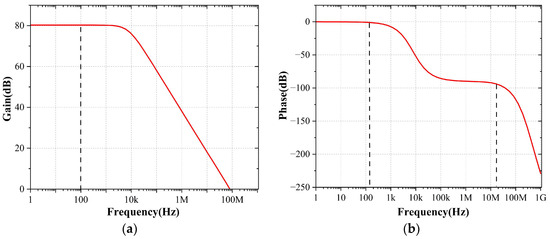
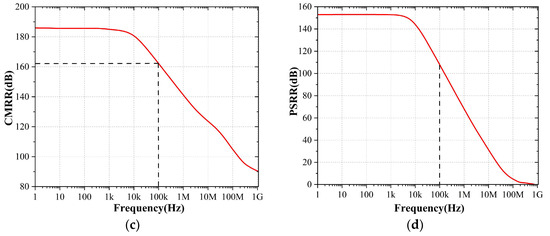
Figure 25.
Post-layout simulation results of the proposed OTA. (a) The AC gain, (b) Phase, (c) CMRR, (d) PSRR.
The designed OTA exhibits exceptional performance across all key metrics, making it an ideal candidate for high-speed, high-resolution ADC front-end stages. Post-layout simulations reveal a PSRR of 150 dB at 1 kHz and a mid-band roll-off consistent with schematic-level predictions, underscoring the robustness of our methodology against layout parasitics.
5. Conclusions
The simulation results in Section 4 demonstrated that by leveraging Thevenin’s equivalence principle, the proposed method transforms multi-stage op-amps into simplified black-box models, significantly reducing computational complexity while enhancing intuitive analysis. The introduced PGB metric, which correlates the DC PSRR value with the first dominant pole frequency, eliminates the reliance on exhaustive S-parameter modeling. This enables a computationally efficient evaluation of PSRR performance within the target frequency band. While the PGB framework assumes validity primarily below the GBW—a constraint inherent to its first-order approximation—it remains efficient for industrial design scenarios where critical PSRR specifications typically reside in low-to-mid frequency ranges. If we calculate the PGB for all op-amps, we can clearly compare the effects of key parameters on different op-amps and evaluate the PSRR performance of various architectures within the target frequency band. Having a PGB analysis for all op-amps makes it easier to select the op-amp architecture in some designs and provides guidance for initial design and optimization. The PGB metric provides actionable insights for optimizing PSRR through parameter adjustments and facilitates rapid comparative analysis of competing circuit topologies.
The proposed framework not only simplifies PSRR analysis for asymmetric and multi-stage circuits but also provides actionable insights for optimizing key parameters (e.g., transconductance, compensation capacitance) to meet stringent industrial requirements. The future work is to use black-box modeling to derive the PSRR of all common op-amps and compare their PGB metrics. This will provide design engineers with a comprehensive overview for selecting the most suitable architecture. Additionally, efforts will be made to extend this approach to LDOs. Since LDOs are typically located close to the load and are highly sensitive to power supply noise, their PSRR characteristics are critical for ensuring effective power supply rejection and output stability. In the context of LDOs, the calculation of PSRR must take into account not only the performance of the op-amp itself but also the combined effects of the feedback network and load capacitance. This ensures effective suppression of power supply noise across a wide frequency range. Therefore, applying the PGB metric to the modeling and optimization of LDO circuits is essential. By adjusting parameters such as output transistor dimensions and compensation networks, the PSRR performance of LDOs can be enhanced. The intuitive framework provided by PGB also accelerates the comparison of different topologies, offering reliable architectural selection criteria for industrial LDO designs with high PSRR requirements.
Author Contributions
Conceptualization, Y.Z.; methodology, Y.Z.; software, Y.Z.; validation, Y.Z.; formal analysis, Y.Z. and R.L.; investigation, X.Y. and R.L.; resources, T.L.; data curation, Y.Z.; writing—original draft preparation, X.Y.; writing—review and editing, T.L. and J.H.; visualization, Y.Z. and X.Y.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition: J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data for this article are available upon request.
Conflicts of Interest
Author Tailai Li was employed by the company Hangzhou Zhicun (Witmem) Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Kim, J.S.; Ha, S.; Jeong, H.; Roh, J. A High-PSRR NMOS LDO Regulator With Intrinsic Gain-Tracking Ripple Cancellation Technique. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 4951–4960. [Google Scholar] [CrossRef]
- Colli-Menchi, A.I.; Torres, J.; Sánchez-Sinencio, E. A Feed-Forward Power-Supply Noise Cancellation Technique for Single-Ended Class-D Audio Amplifiers. IEEE J. Solid-State Circuits 2014, 49, 718–728. [Google Scholar] [CrossRef]
- Chiu, C.-C.; Huang, P.-H.; Lin, M.; Chen, K.-H.; Lin, Y.-H.; Tsai, T.-Y.; Lee, C.C.-C. A 0.6 V Resistance-Locked Loop Embedded Digital Low Dropout Regulator in 40 nm CMOS With 80.5% Power Supply Rejection Improvement. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 59–69. [Google Scholar] [CrossRef]
- Choi, Y.; Tak, W.; Yoon, Y.; Roh, J.; Kwon, S.; Koh, J. A 0.018% THD+N, 88-dB PSRR PWM Class-D Amplifier for Direct Battery Hookup. IEEE J. Solid-State Circuits 2012, 47, 454–463. [Google Scholar] [CrossRef]
- Halonen, K.A.I.; Sansen, W.M.C.; Steyaert, M. A micropower fourth-order elliptical switched-capacitor low-pass filter. IEEE J. Solid-State Circuits 1987, 22, 164–173. [Google Scholar] [CrossRef]
- Razavi, B. Design of Analog CMOS Integrated Circuits; Tsinghua University Press: Beijing, China, 2001. [Google Scholar]
- Allen, P.E.; Holberg, D.R. CMOS Analog Circuit Design, 2nd ed.; Publishing House of Electronics Industry: Beijing, China, 2005; pp. 232–234. [Google Scholar]
- Gray, P.R.; Hurst, P.J.; Lewis, S.H.; Meyer, R.G. Analysis and Design of Analog Integrated Circuits, 4th ed.; Higher Education Press: Beijing, China, 2005; pp. 410–415. [Google Scholar]
- Zhang, H.; Rozsa, N.N.M.; Berkhout, M.; Fan, Q. A Chopper Class-D Amplifier for PSRR Improvement Over the Entire Audio Band. IEEE J. Solid-State Circuits 2022, 57, 2035–2044. [Google Scholar] [CrossRef]
- Yang, C.; Ye, K.; Tan, M. A 0.5-V Capless LDO With 30-dB PSRR at 10-kHz Using a Lightweight Local Generated Supply. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1785–1789. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, R.K. A cross-coupled cascode feedback design of an area-efficient frequency compensated OTA. Arab. J. Sci. Eng. 2024, 49, 6305–6317. [Google Scholar] [CrossRef]
- Yosefi, G. A special technique for Recycling Folded Cascode OTA to improve DC gain, bandwidth, CMRR and PSRR in 90 nm CMOS process. Ain Shams Eng. J. 2020, 11, 329–342. [Google Scholar] [CrossRef]
- Feizbakhsh, S.V.; Yosefi, G. An enhanced fast slew rate recycling folded cascode Op-Amp with general improvement in 180 nm CMOS process. Int. J. Electron. Commun. (AEÜ) 2019, 101, 200–217. [Google Scholar] [CrossRef]
- Kumngern, M.; Kulej, T.; Khateb, F. 31.3 nW, 0.5 V Bulk-Driven OTA for Biosignal Processing. IEEE Access 2023, 11, 56516–56525. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).