Non-Isolated Ultra-High Step-Up DC-DC Converter Topology Using Coupled-Inductor-Based Inverting Buck-Boost and Voltage Multipliers
Abstract
1. Introduction
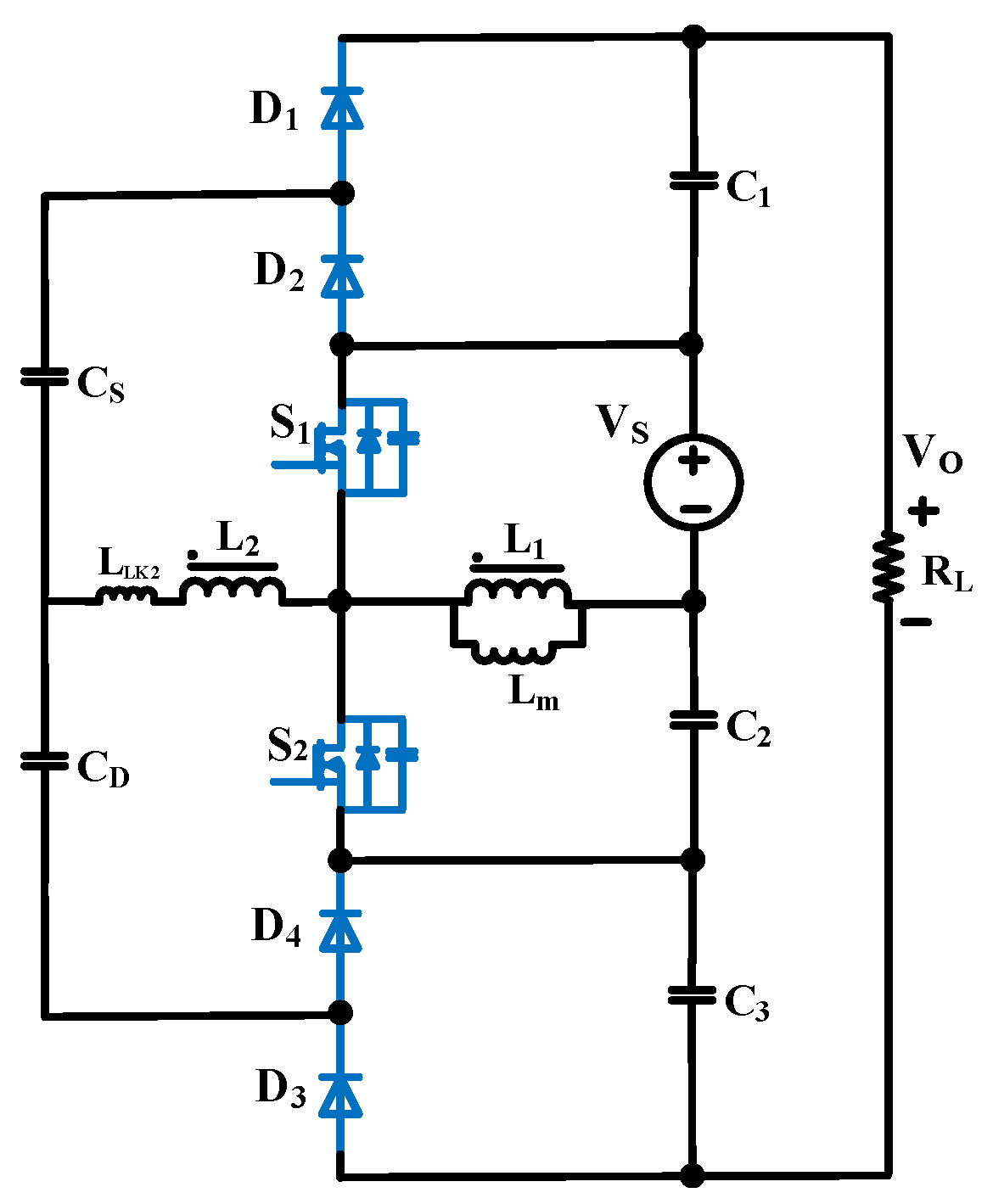
2. Proposed Converter Structure
2.1. Operating Principle
- Steady-state operation with a continuous magnetizing inductor current;
- Ideal components (parasitics neglected);
- Large capacitors maintain constant voltages during switching periods;
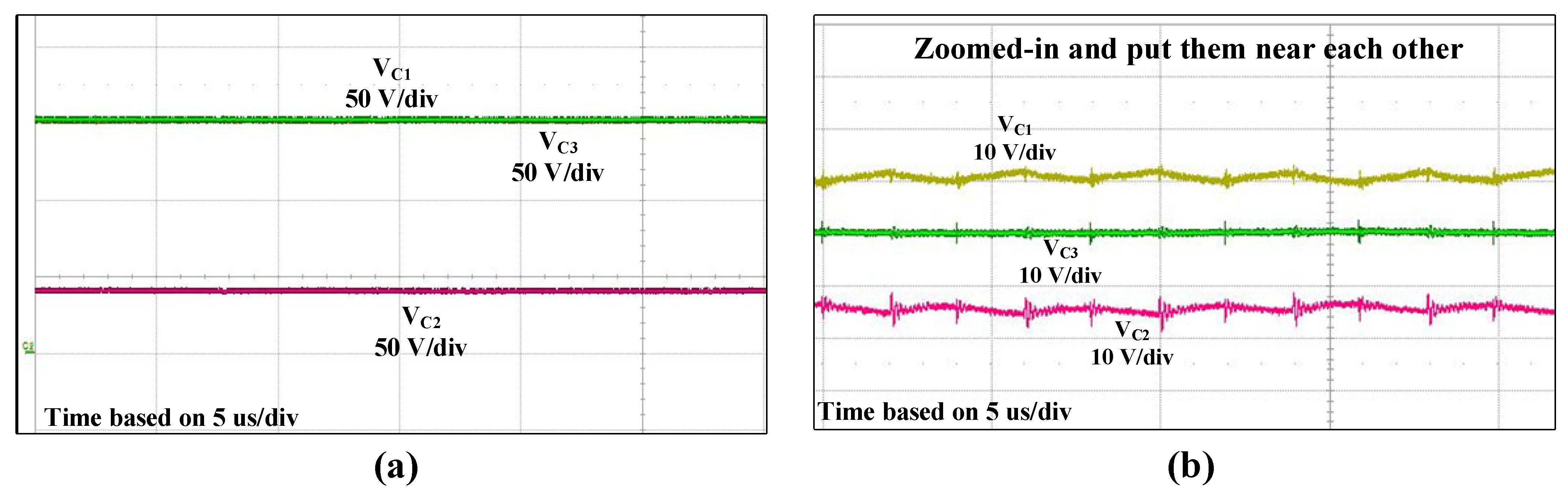
- Symmetrical capacitance values = = and = ;
- The switching period is , where is closed for and open for (1 − D) .
2.2. Steady-State Analysis of the Proposed Converter
2.2.1. Voltage Gain and Voltage Stress on Components
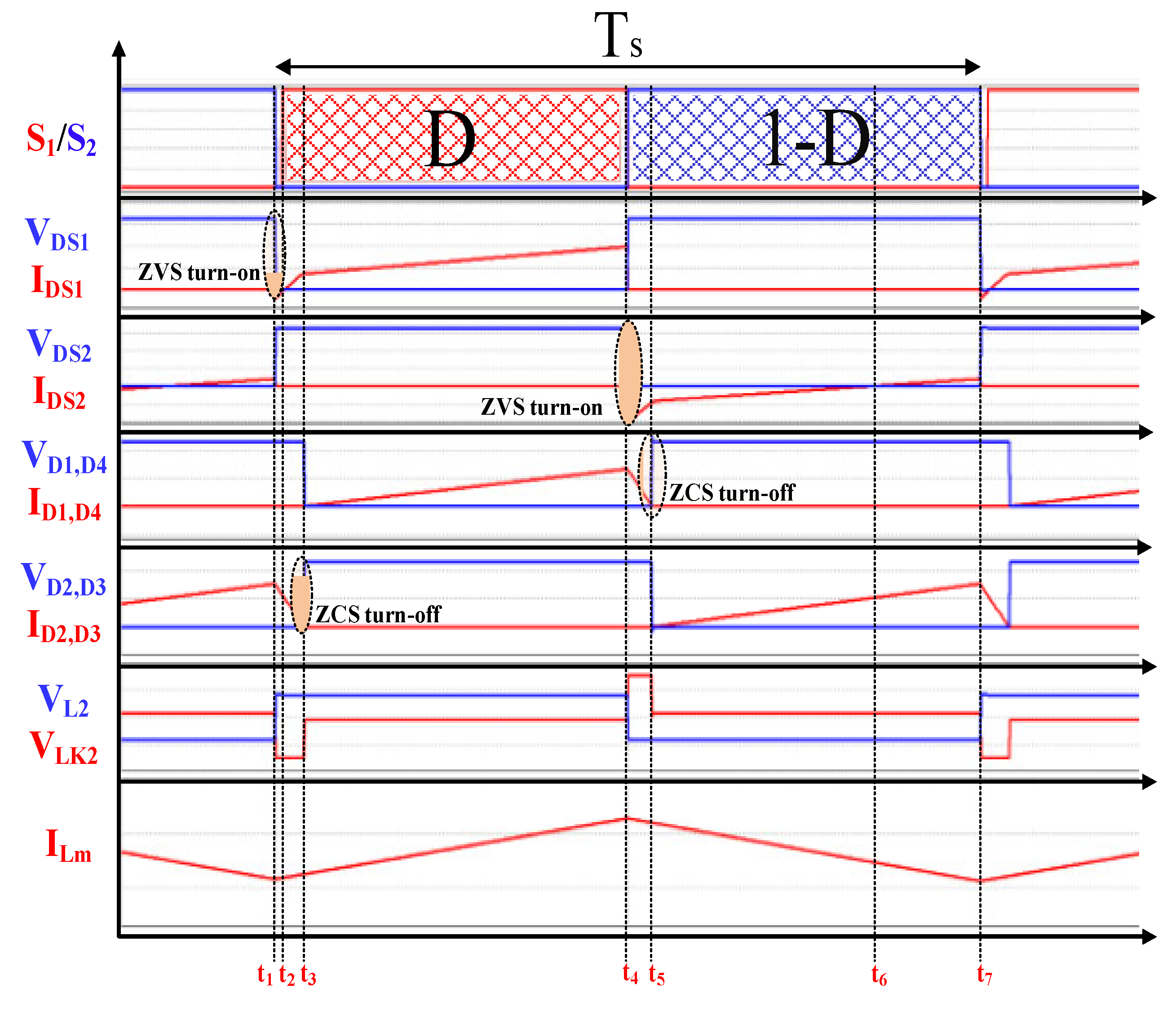
2.2.2. ZVS Condition
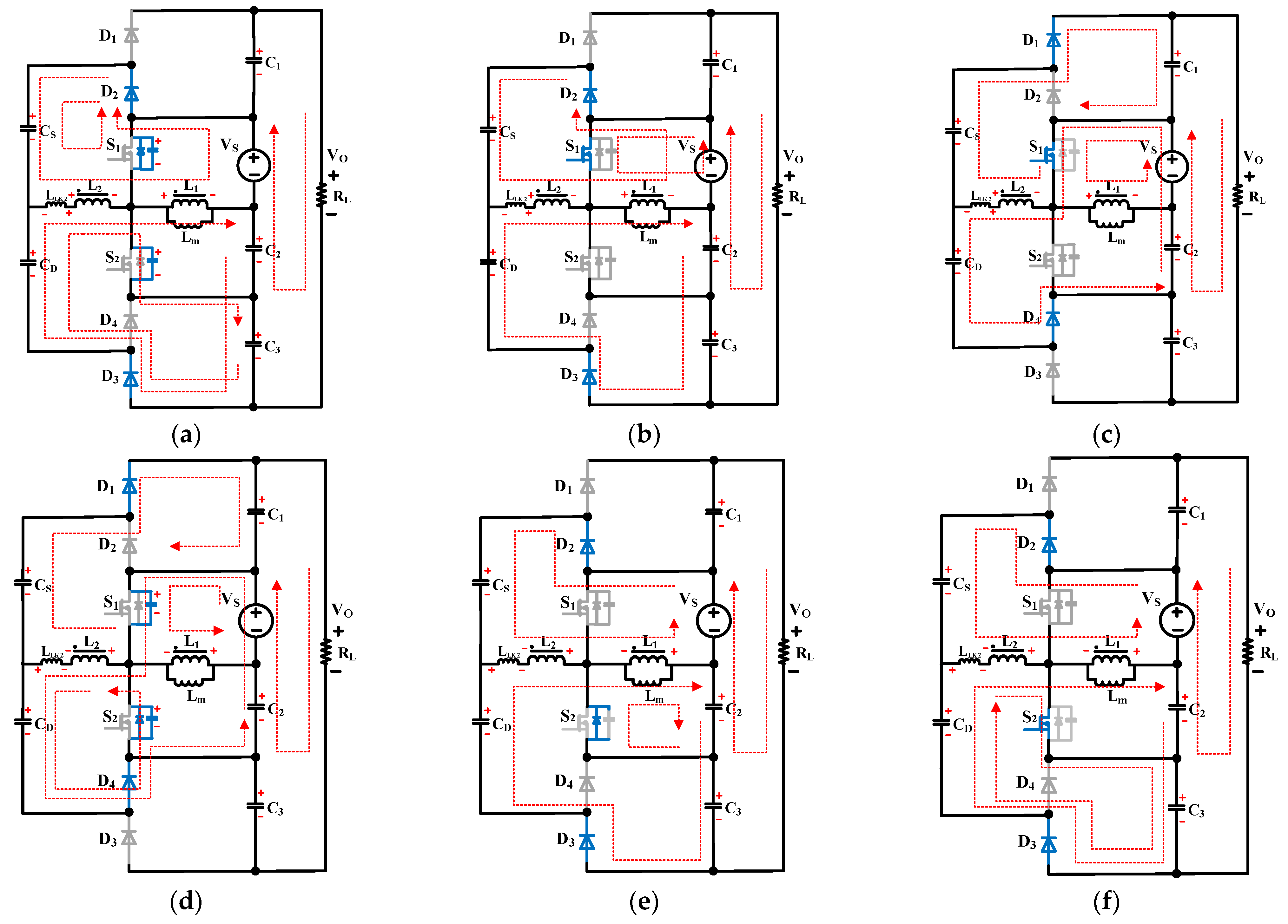
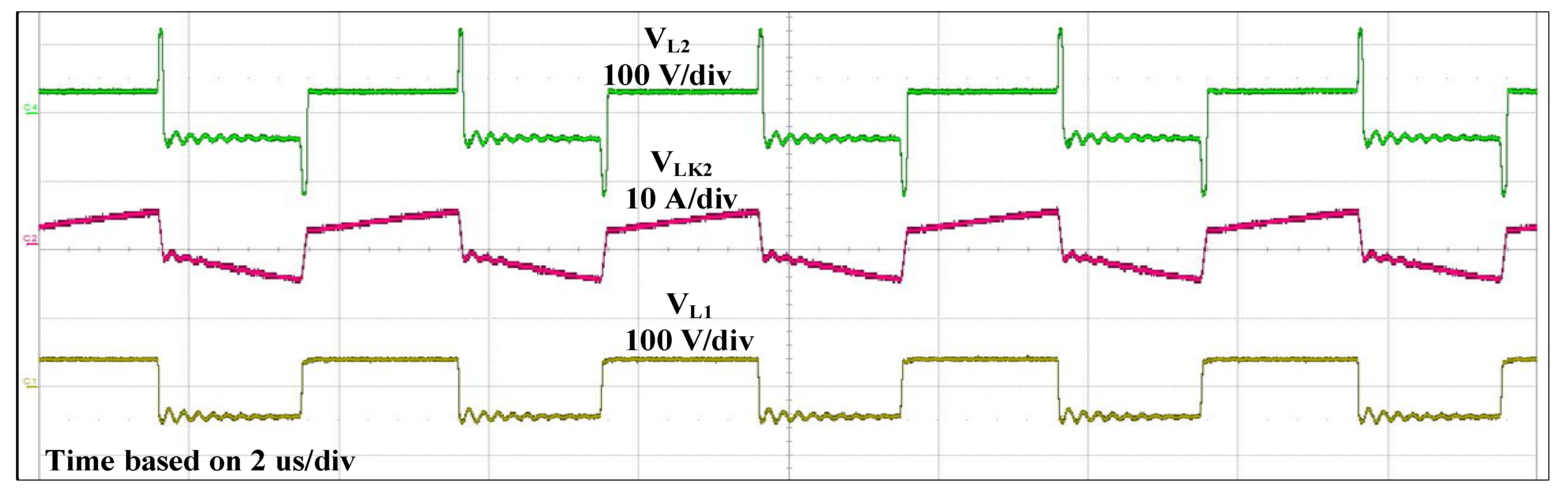
2.3. Converter Operation and Analysis
3. Design of the Proposed Converter
3.1. Design of the Output Capacitors
3.2. Design of the Main Inductor
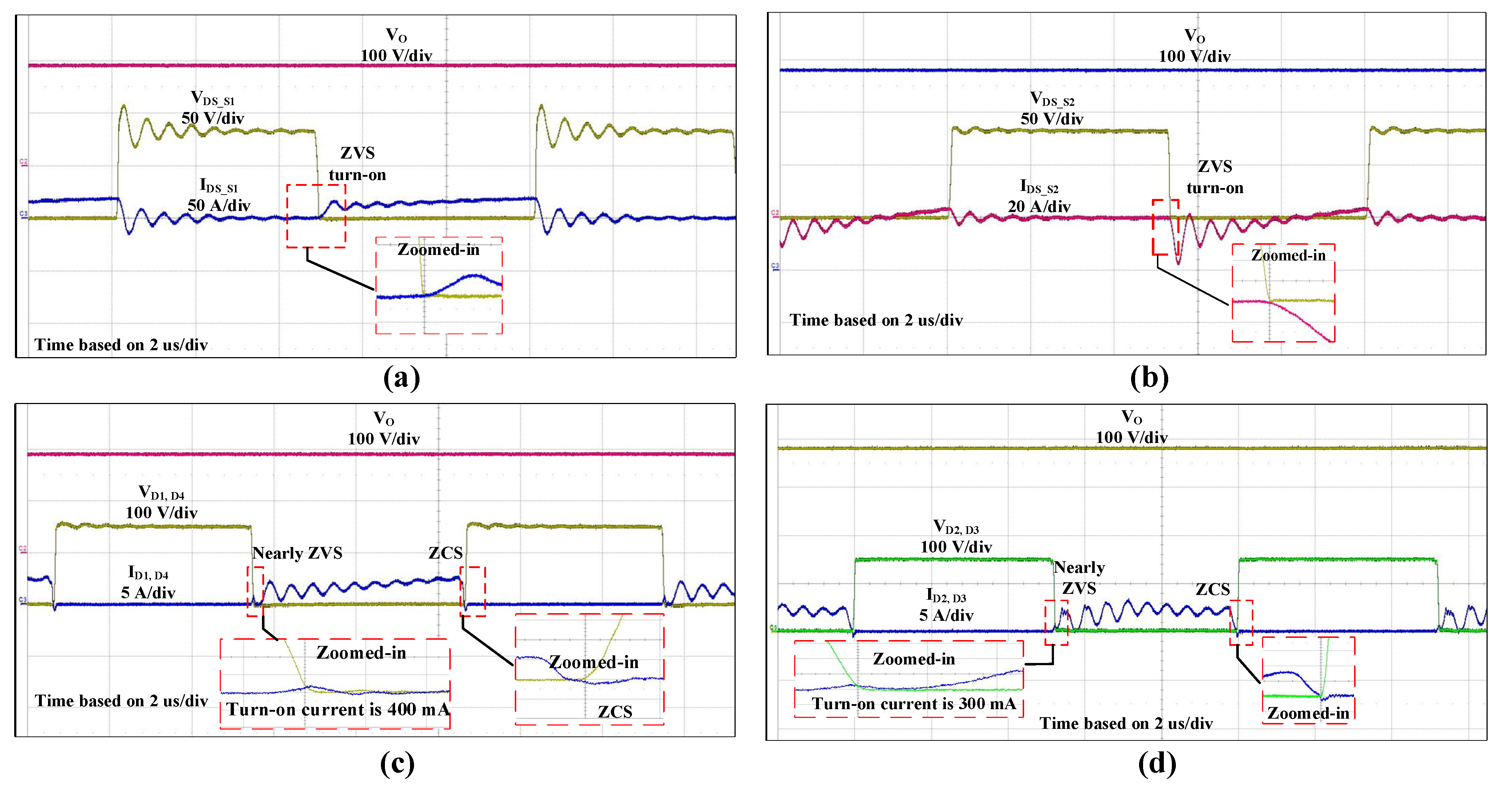
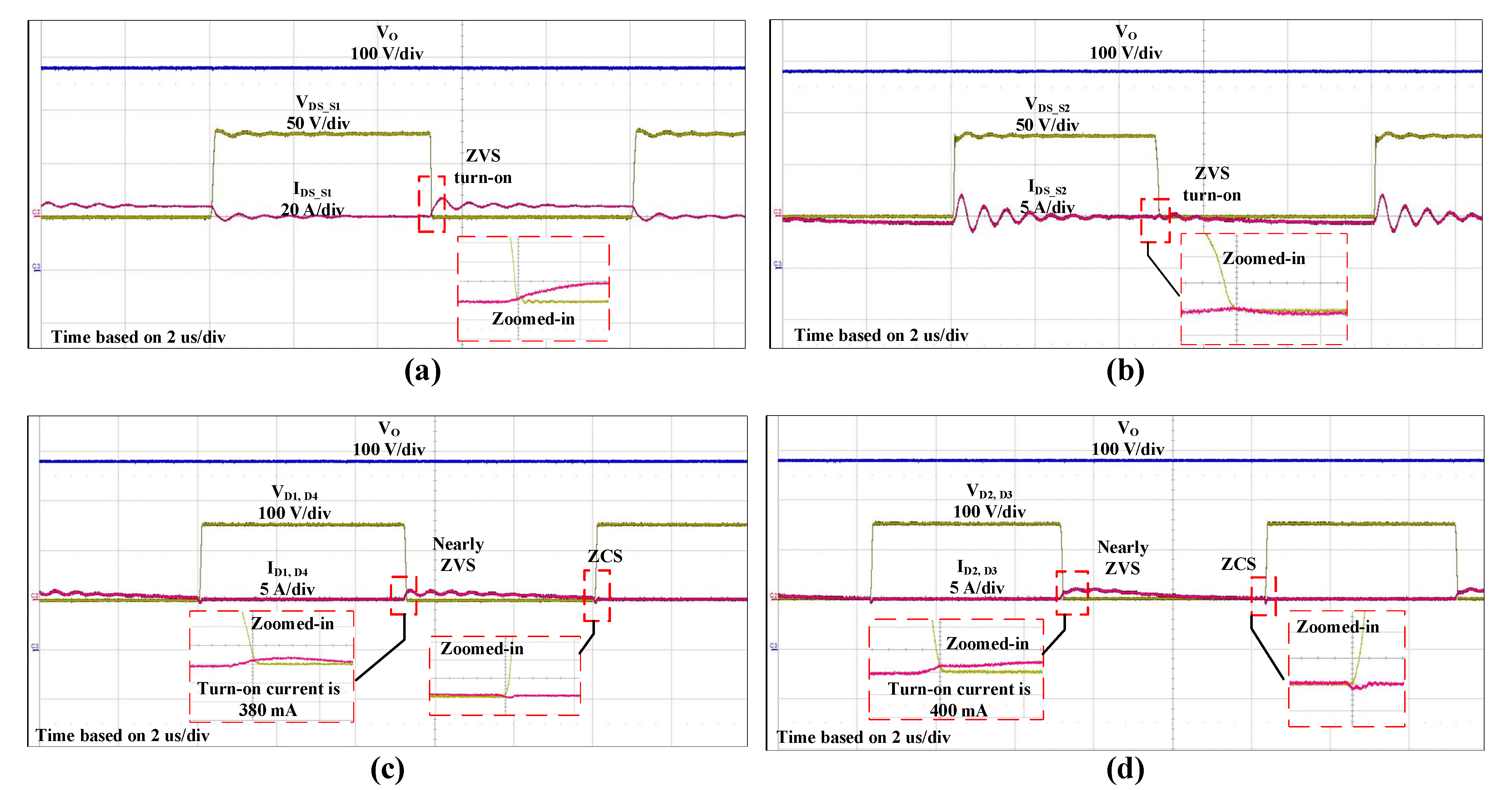
4. Experimental Results
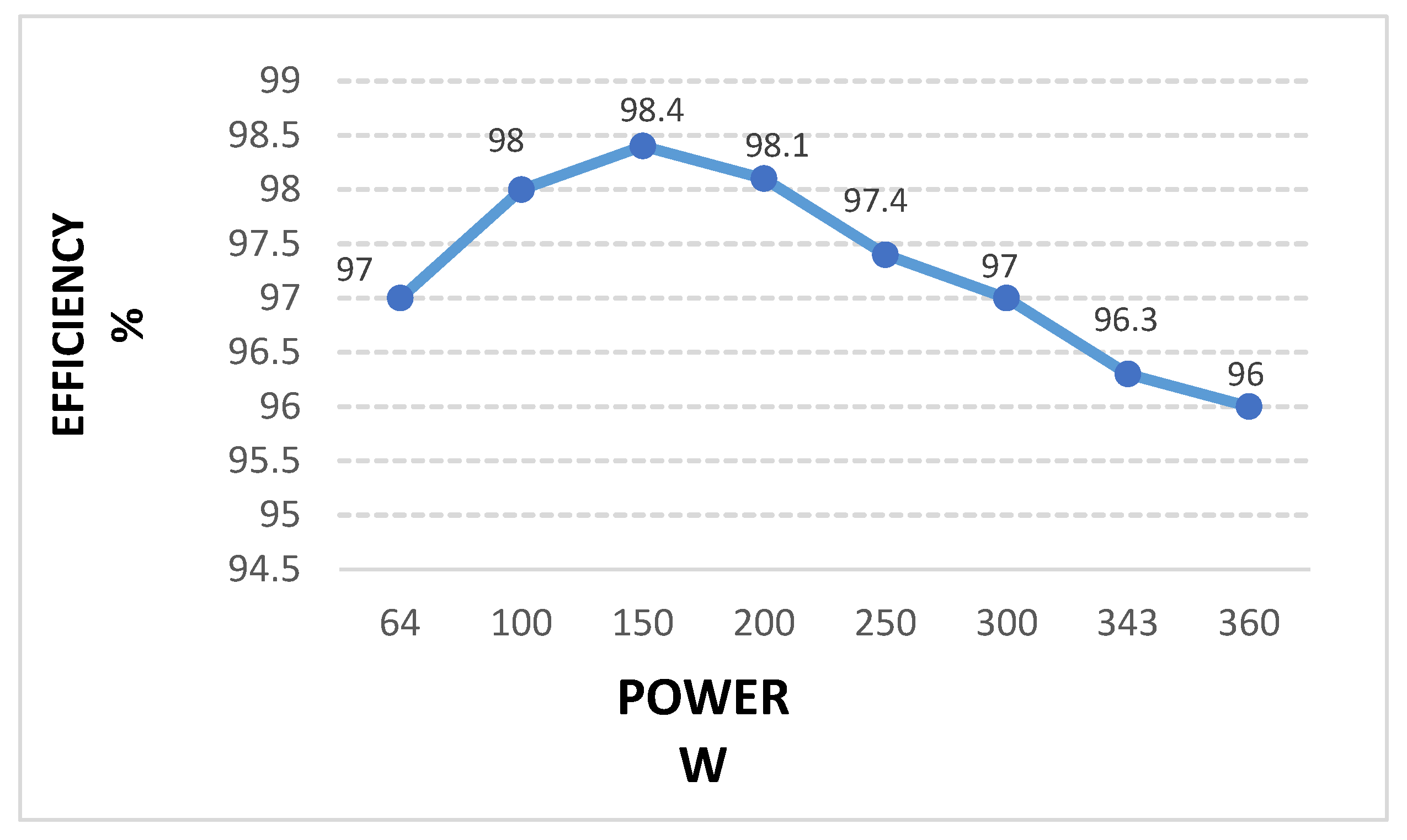
4.1. Losses and Efficiency Analysis
4.2. Scalability Considerations for High Power
5. Comparison Study
- It achieves the highest efficiency (98.4%), outperforming all other referenced converters;
- The voltage stress on both switches and diodes is significantly lower due to the symmetrical configuration of the proposed design;
- The number of components—including switches, diodes, coupled inductors, and capacitors—is moderate, contributing to a lower cost and simplified implementation;
- The output capacitor and diode stress is substantially reduced (to less than 0.5× output voltage), eliminating the need for expensive high-voltage components.
6. Conclusions
- No spike voltage is applied to semiconductor devices and hence there is no need for an extra snubber;
- Very high efficiency with ZVS turn-on for MOSFET and ZVZCS for diodes;
- Reduced voltage stress on the components due to the symmetric configuration;
- Easy to obtain a higher voltage gain by either choosing the turns ratio of the coupled inductor, duty cycle, or cascading more VM stages.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Xu, D.; Wu, B.; Zhao, Y.; Yang, H.; He, X. Zero-voltage-switching dual-boost converter with multi-functional inductors and improved symmetrical rectifier for distributed generation systems. ET Power Electron. 2012, 5, 969–977. [Google Scholar] [CrossRef]
- Zhou, L.W.; Zhu, B.X.; Luo, Q.M.; Chen, S. Interleaved non-isolated high step-up DC/DC converter based on the diode–capacitor multiplier. IET Power Electron. 2014, 7, 390–397. [Google Scholar] [CrossRef]
- Cheng, H.; Smedley, K.M.; Abramovitz, A. A Wide-Input–Wide-Output (WIWO) DC–DC Converter. IEEE Trans. Power Electron. 2010, 25, 280–289. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, H.; Wang, W.; Zhang, B.; Zheng, T.Q. High-Efficient High-Voltage-Gain Capacitor Clamped DC–DC Converters and Their Construction Method. IEEE Trans. Ind. Electron. 2021, 68, 3992–4003. [Google Scholar] [CrossRef]
- Alzahrani, A.; Ferdowsi, M.; Shamsi, P. A Family of Scalable Non-Isolated Interleaved DC-DC Boost Converters with Voltage Multiplier Cells. IEEE Access 2019, 7, 11707–11721. [Google Scholar] [CrossRef]
- Lin, G.; Zhang, Z. Low Input Ripple High Step-Up Extendable Hybrid DC-DC Converter. IEEE Access 2019, 7, 158744–158752. [Google Scholar] [CrossRef]
- Wu, B.; Li, S.; Liu, Y.; Smedley, K.M. A New Hybrid Boosting Converter for Renewable Energy Applications. IEEE Trans. Power Electron. 2016, 31, 1203–1215. [Google Scholar] [CrossRef]
- Luo, F.L.; Ye, H. Positive output super-lift converters. IEEE Trans. Power Electron. 2003, 18, 105–113. [Google Scholar] [CrossRef]
- Sayed, S.; Elmenshawy, M.; Elmenshawy, M.; Ben-Brahim, L.; Massoud, A. Design and analysis of high-gain medium-voltage DC-DC converters for high-power PV applications. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ismail, E.H.; Al-Saffar, M.A.; Sabzali, A.J.; Fardoun, A.A. A Family of Single-Switch PWM Converters with High Step-Up Conversion Ratio. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 1159–1171. [Google Scholar] [CrossRef]
- Wu, G.; Ruan, X.; Ye, Z. Nonisolated High Step-Up DC–DC Converters Adopting Switched-Capacitor Cell. IEEE Trans. Ind. Electron. 2015, 62, 383–393. [Google Scholar] [CrossRef]
- Tran, V.-T.; Nguyen, M.-K.; Choi, Y.-O.; Cho, G.-B. Switched-Capacitor-Based High Boost DC-DC Converter. Energies 2018, 11, 987. [Google Scholar] [CrossRef]
- Prudente, M.; Pfitscher, L.L.; Emmendoerfer, G.; Romaneli, E.F.; Gules, R. Voltage Multiplier Cells Applied to Non-Isolated DC–DC Converters. IEEE Trans. Power Electron. 2008, 23, 871–887. [Google Scholar] [CrossRef]
- Alcazar, Y.J.A.; de Souza Oliveira, D.; Tofoli, F.L.; Torrico-Bascopé, R.P. DC–DC Nonisolated Boost Converter Based on the Three-State Switching Cell and Voltage Multiplier Cells. IEEE Trans. Ind. Electron. 2013, 60, 4438–4449. [Google Scholar] [CrossRef]
- Prudente, M.; Pfitscher, L.; Gules, R. A Boost Converter with Voltage Multiplier Cells. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 2716–2721. [Google Scholar] [CrossRef]
- Ai, J.; Lin, M.; Yin, M. A Family of High Step-Up Cascade DC–DC Converters with Clamped Circuits. IEEE Trans. Power Electron. 2020, 35, 4819–4834. [Google Scholar] [CrossRef]
- Sedaghati, F.; Pourjafar, S. Analysis and implementation of a boost DC–DC converter with high voltage gain and continuous input current. IET Power Electron. 2020, 13, 798–807. [Google Scholar] [CrossRef]
- Zheng, Y.; Smedley, K.M. Analysis and Design of a Single-Switch High Step-Up Coupled-Inductor Boost Converter. IEEE Trans. Power Electron. 2020, 35, 535–545. [Google Scholar] [CrossRef]
- Moradpour, R.; Ardi, H.; Tavakoli, A. Design and Implementation of a New SEPIC-Based High Step-Up DC/DC Converter for Renewable Energy Applications. IEEE Trans. Ind. Electron. 2018, 65, 1290–1297. [Google Scholar] [CrossRef]
- Andrade, A.M.S.S.; Schuch, L.; da Silva Martins, M.L. Analysis and Design of High-Efficiency Hybrid High Step-Up DC–DC Converter for Distributed PV Generation Systems. IEEE Trans. Ind. Electron. 2018, 66, 3860–3868. [Google Scholar] [CrossRef]
- Poorali, B.; Adib, E. Soft-Switched High Step-Up Quasi-Z-Source DC–DC Converter. IEEE Trans. Ind. Electron. 2020, 67, 4547–4555. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, S.; Yi, Y. Switched-Capacitor and Coupled-Inductor Based High Step-Up Converter with Improved Voltage Gain. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 754–764. [Google Scholar] [CrossRef]
- Kothapalli, K.R.; Ramteke, M.R.R.; Suryawanshi, H.M.; REDDI, N.K.; Kalahasthi, R.B. A Coupled Inductor Based High Step—Up Converter for DC Microgrid Applications. in IEEE Transactions on Industrial Electronics. IEEE Trans. Ind. Electron. 2020, 68, 4927–4940. [Google Scholar] [CrossRef]
- Chen, S.; Yang, S.; Huang, C.; Chen, Y. High Step-Up Interleaved Converter with Three-Winding Coupled Inductors and Voltage Multiplier Cells. In Proceedings of the 2019 IEEE International Conference on Industrial Technology (ICIT), Melbourne, Australia, 13–15 February 2019; pp. 458–463. [Google Scholar] [CrossRef]
- Wu, G.; Ruan, X.; Ye, Z. High Step-Up DC–DC Converter Based on Switched Capacitor and Coupled Inductor. IEEE Trans. Ind. Electron. 2018, 65, 5572–5579. [Google Scholar] [CrossRef]
- Hu, X.; Liu, X.; Zhang, Y.; Yu, Z.; Jiang, S. A Hybrid Cascaded High Step-Up DC-DC Converter with Ultra-low Voltage Stress. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1824–1836. [Google Scholar] [CrossRef]
- Upadhyay, P.; Kumar, R.; Sathyan, S. Coupled-inductor-based high-gain converter utilising magnetising inductance to achieve soft-switching with low voltage stress on devices. IET Power Electron. 2020, 13, 576–591. [Google Scholar] [CrossRef]
- Zaoskoufis, K.; Tatakis, E.C. An Improved Boost-based DC/DC Converter with High Voltage step-up ratio for DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1837–1853. [Google Scholar] [CrossRef]
- Mirzaee, A.; Moghani, J.S. Coupled Inductor-Based High Voltage Gain DC–DC Converter For Renewable Energy Applications. IEEE Trans. Power Electron. 2020, 35, 7045–7057. [Google Scholar] [CrossRef]
- Wu, G.; Ruan, X.; Ye, Z. Non-isolated high step-up DC-DC converter adopting auxiliary capacitor and coupled inductor. J. Mod. Power Syst. Clean Energy 2018, 6, 384–398. [Google Scholar] [CrossRef]
- Molavi, N.; Adib, E.; Farzanehfar, H.d. Soft-switched non-isolated high step-up DC–DC converter with reduced voltage stress. IET Power Electron. 2016, 9, 1711–1718. [Google Scholar] [CrossRef]
- Ding, X.; Zhou, M.; Cao, Y.; Li, B.; Sun, Y.; Hu, X. A High Step-Up Coupled-Inductor-Integrated DC–DC Multilevel Boost Converter with Continuous Input Current. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7346–7360. [Google Scholar] [CrossRef]
- Abbasi, V.; Rostami, S.; Hemmati, S.; Ahmadian, S. Ultrahigh Step-Up Quadratic Boost Converter Using Coupled Inductors with Low Voltage Stress on the Switches. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 7733–7743. [Google Scholar] [CrossRef]
- Abbasi, V.; Talebi, N.; Rezaie, M.; Arzani, A.; Moghadam, F.Y. Ultrahigh Step-Up DC–DC Converter Based on Two Boosting Stages with Low Voltage Stress on Its Switches. IEEE Trans. Ind. Electron. 2023, 70, 12387–12398. [Google Scholar] [CrossRef]
- Maalandish, M.; Babaei, E.; Abolhasani, P.; Gheisarnejad, M.; Khooban, M. Ultra high step-up soft-switching DC/DC converter using coupled inductor and interleaved technique. IET Power Electron. 2023, 16, 1320–1338. [Google Scholar] [CrossRef]
- Rahimi, R.; Habibi, S.; Ferdowsi, M.; Shamsi, P. An Interleaved Quadratic High Step-Up DC-DC Converter with Coupled Inductor. IEEE Open J. Power Electron. 2021, 2, 647–658. [Google Scholar] [CrossRef]
- Hashemzadeh, S.M.; Babaei, E.; Hosseini, S.H.; Sabahi, M.; Eslami, M. Design and Analysis of a New Coupled Inductor-Based Interleaved High Step-Up DC-DC Converter for Renewable Energy Applications. Int. Trans. Electr. Energy Syst. 2022, 2022, 7618242. [Google Scholar] [CrossRef]
- Alonso, J.M. Resonant Passive Snubber for High-Efficiency Coupled-Inductor DC–DC Converters. IEEE Trans. Power Electron. 2023, 38, 9152–9165. [Google Scholar]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC–DC Converters: A Comprehensive Review of Voltage-Boosting Techniques, Topologies, and Applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Ali, A.; Mousa, H.H.H.; Shaaban, M.F.; Azzouz, M.A.; Awad, A.S.A. A Comprehensive Review on Charging Topologies and Power Electronic Converter Solutions for Electric Vehicles. J. Mod. Power Syst. Clean Energy 2024, 12, 675–694. [Google Scholar] [CrossRef]
- Wang, S.; Meynard, T.A. Advanced ZVS/ZCS Techniques for High-Frequency High-Gain DC-DC Converters. IEEE Trans. Power Electron. 2024, 39, 1735–1748. [Google Scholar]



| Parameter | Designator | Value |
|---|---|---|
| Input voltage | 40 V | |
| Output voltage | 380 V | |
| Maximum output voltage ripple | 0.8% | |
| Output power | 360 W | |
| Switching frequency | 100 KHz |
| Component | Part # | Specification |
|---|---|---|
| MOSFETs | IPP039N10N5 | 200 V/80 A |
| ) | DSSK10-18A | 180 V/10 A |
| 106MMR250K | 10 µF/250 V | |
| Coupled inductor turns ratio | ―― | 17:18 |
| ―― | 4.5 µH | |
| ―― | 103 µH | |
| ―― | 115 µH |
| Component | Peak Voltage Stress | Peak Current Stress | Relative to Output |
|---|---|---|---|
| MOSFETs (S1, S2) | VS/(1 − D) = 83.3 V | ILm + ΔILm/2 | 0.22 × VO |
| Diodes (D1–D4) | VC1 = VC3 ≈ 127 V | IO/2 ≈ 0.47 A | 0.33 × VO |
| Output Capacitors (C1–C3) | 127 V each | Ripple current | 0.33 × VO |
| Coupled Inductor | Primary: 40 V Secondary: 42 V | Peak magnetizing current | - |
| Component | Loss Type | Equation | Contribution (%) |
|---|---|---|---|
| MOSFETs (S1, S2) | Conduction | 45% | |
| Switching | 15% | ||
| Diodes (D1–D4) | Conduction | 5% | |
| Coupled Inductor | Core Loss | 20% | |
| Copper Loss | 10% | ||
| Capacitors (C1–C3) | ESR Loss | 5% |
| Topology | Voltage Gain | Voltage Stress on Switches (Vs/Vin) | Voltage Stress on Diodes | Voltage Stress on Output Capacitors | Conduction Mode | Soft-Switching Status | S/D/CI/I/C/T | Efficiency |
|---|---|---|---|---|---|---|---|---|
| [23] | NI | CCM | ZVS for MOSFETs, ZCS for diodes | 2/3/2/0/5/12 | 96.5% | |||
| [28] | CCM | ZVS (switch) and ZCS (diode) via active clamp | 2/3/1/1/5/12 | 96.8% | ||||
| [18] | CCM | None | 1/2/1/1/3/8 | 94.1% | ||||
| [21] | CCM | ZVS (switches) and ZVZCS (diodes) | 2/2/1/1/4/10 | 95.6% | ||||
| [24] | NI | CCM | None | 2/6/2/0/6/16 | 96.7% | |||
| [16] (Figure 4a) | CCM and DCM | None | 1/6/1/1/5/14 | 94.4% | ||||
| [22] | CCM | ZCS (switch) only | 1/4/1/0/4/10 | 97.1% | ||||
| [30] (Figure 6b) | NI | CCM | None | 1/4/1/1/5/12 | 95% | |||
| [25] (Figure 4) | CCM | None | 1/3/1/0/3/8 | 96.4% | ||||
| [19] | CCM | None | 1/4/1/1/5/12 | 96.2% | ||||
| [20] | CCM | None | 1/8/1/0/8/18 | 97.6% | ||||
| [31] | CCM | ZVS for main and clamp switches; ZCS on diodes | 2/4/1/0/5/12 | 96.3% | ||||
| [33] | NI | CCM | None | 2/5/2/5/14 | 95.2% | |||
| [34] | CCM | None | 2/5/1/1/5/14 | 94.2% | ||||
| [35] | NI | CCM | ZCS on diodes only | 2/8/2/0/8/20 | 94.6% | |||
| [36] | CCM | None | 2/4/2/0/4/12 | 94.4% | ||||
| [37] | NI | CCM | None | 2/5/3/0/5/15 | 95.96% | |||
| Proposed converter | (24) | (22) | (22) | CCM | ZVS for switches, ZCS for diodes | 2/4/2/0/5/13 | 98.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duong, V.-T.; Waheed, Z.; Choi, W. Non-Isolated Ultra-High Step-Up DC-DC Converter Topology Using Coupled-Inductor-Based Inverting Buck-Boost and Voltage Multipliers. Electronics 2025, 14, 2519. https://doi.org/10.3390/electronics14132519
Duong V-T, Waheed Z, Choi W. Non-Isolated Ultra-High Step-Up DC-DC Converter Topology Using Coupled-Inductor-Based Inverting Buck-Boost and Voltage Multipliers. Electronics. 2025; 14(13):2519. https://doi.org/10.3390/electronics14132519
Chicago/Turabian StyleDuong, Van-Tinh, Zeeshan Waheed, and Woojin Choi. 2025. "Non-Isolated Ultra-High Step-Up DC-DC Converter Topology Using Coupled-Inductor-Based Inverting Buck-Boost and Voltage Multipliers" Electronics 14, no. 13: 2519. https://doi.org/10.3390/electronics14132519
APA StyleDuong, V.-T., Waheed, Z., & Choi, W. (2025). Non-Isolated Ultra-High Step-Up DC-DC Converter Topology Using Coupled-Inductor-Based Inverting Buck-Boost and Voltage Multipliers. Electronics, 14(13), 2519. https://doi.org/10.3390/electronics14132519








