High-Frequency Link Analysis of Enhanced Power Factor in Active Bridge-Based Multilevel Converters
Abstract
1. Introduction
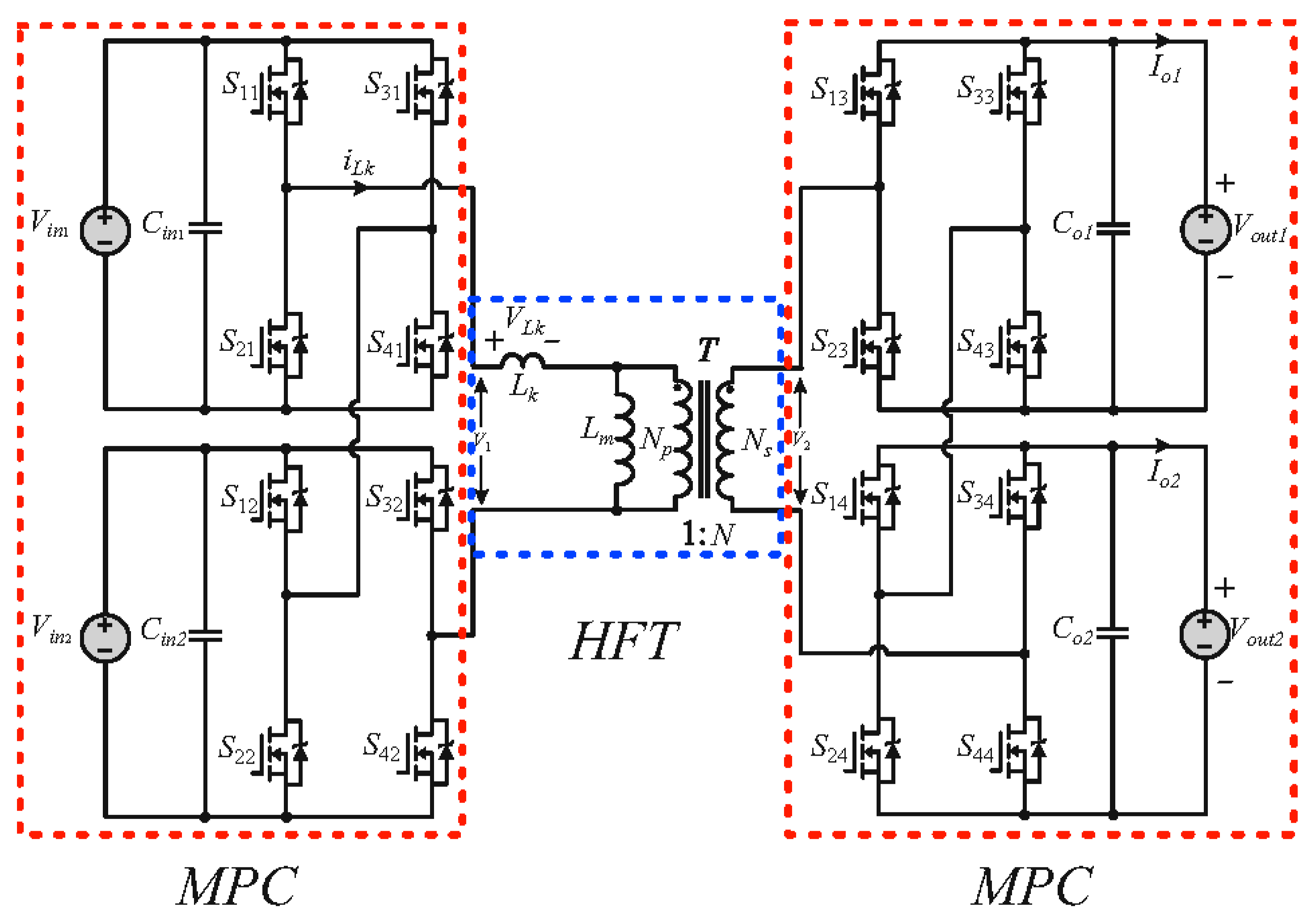
2. Structure of the Proposed MAB Converter
3. High-Frequency Link Characterization
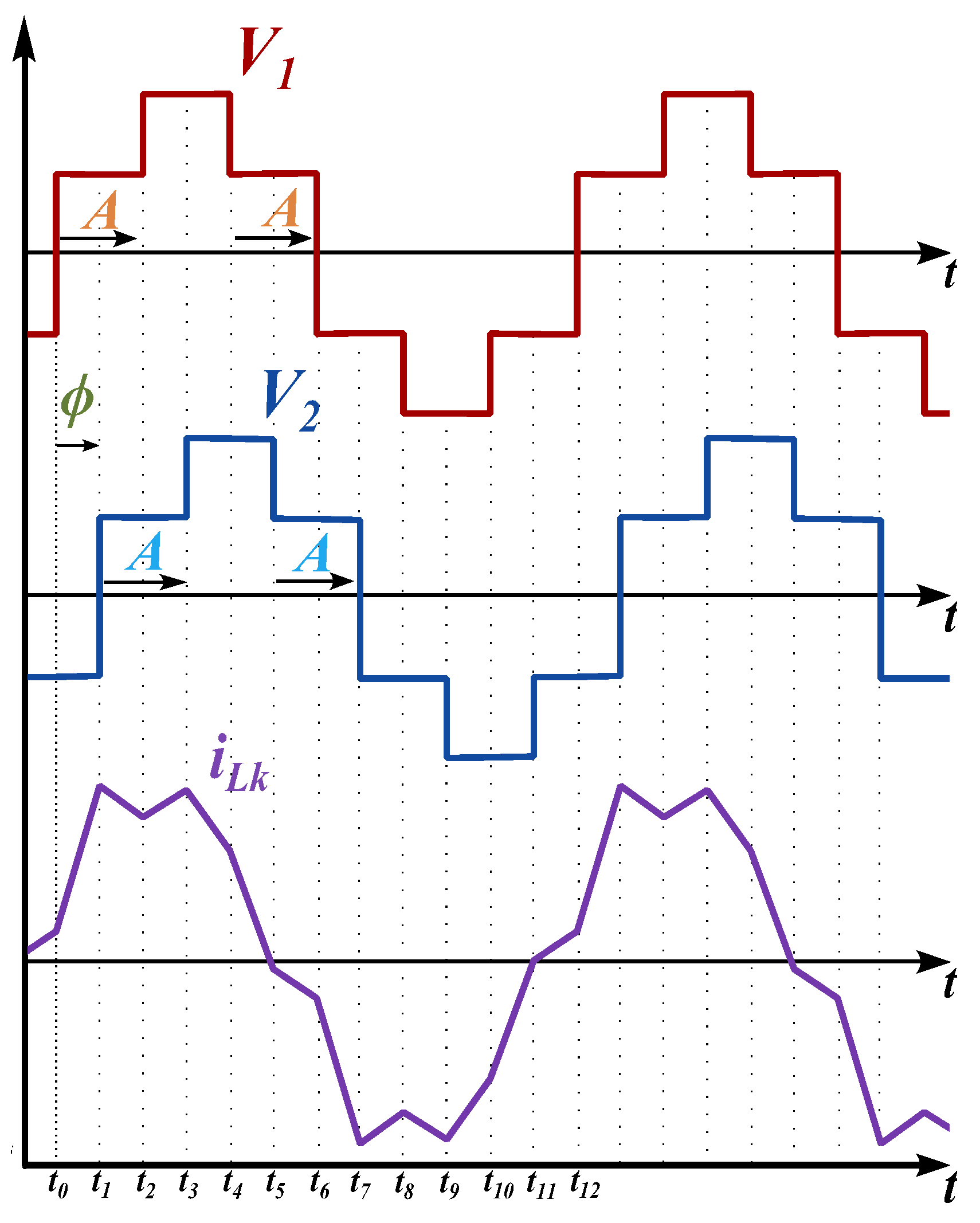
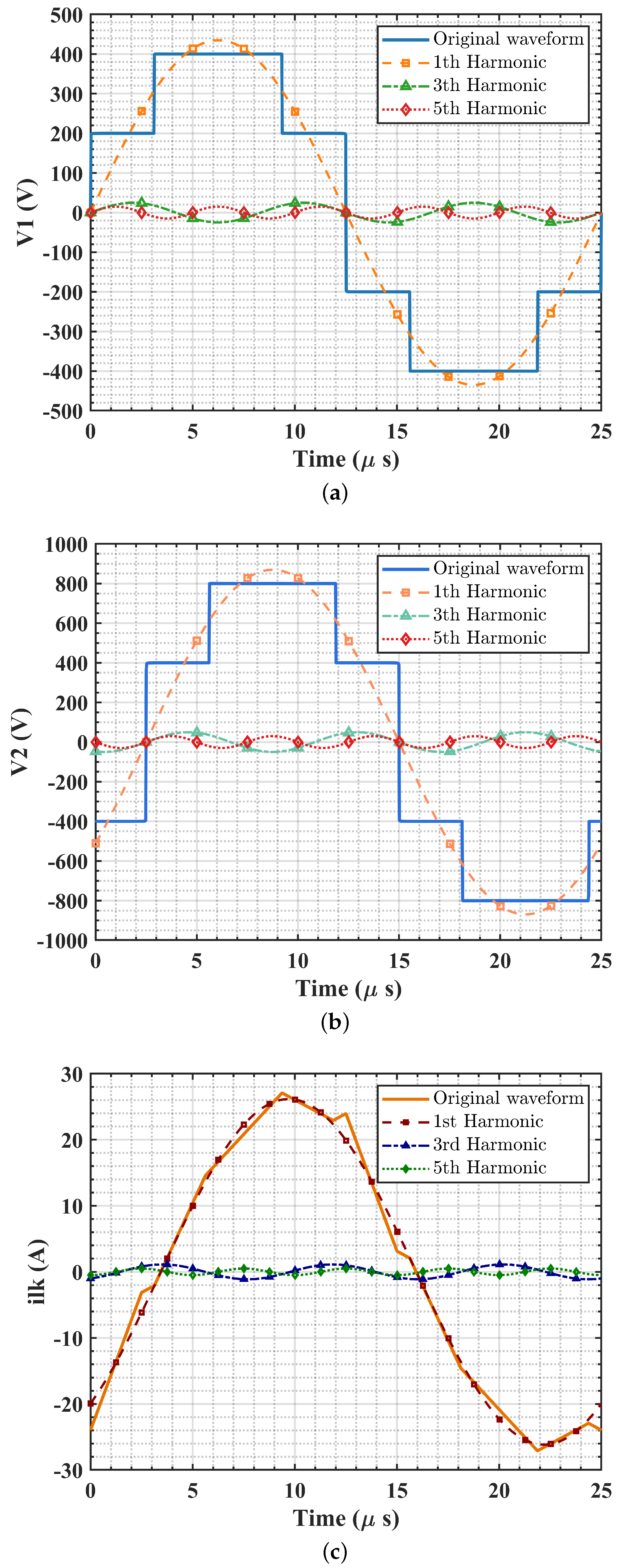
3.1. Voltage and Current Characterization
3.2. Active Power Characterization
4. Analysis of HFL Circulating Current
4.1. HFL Reactive Power in MAB Converter
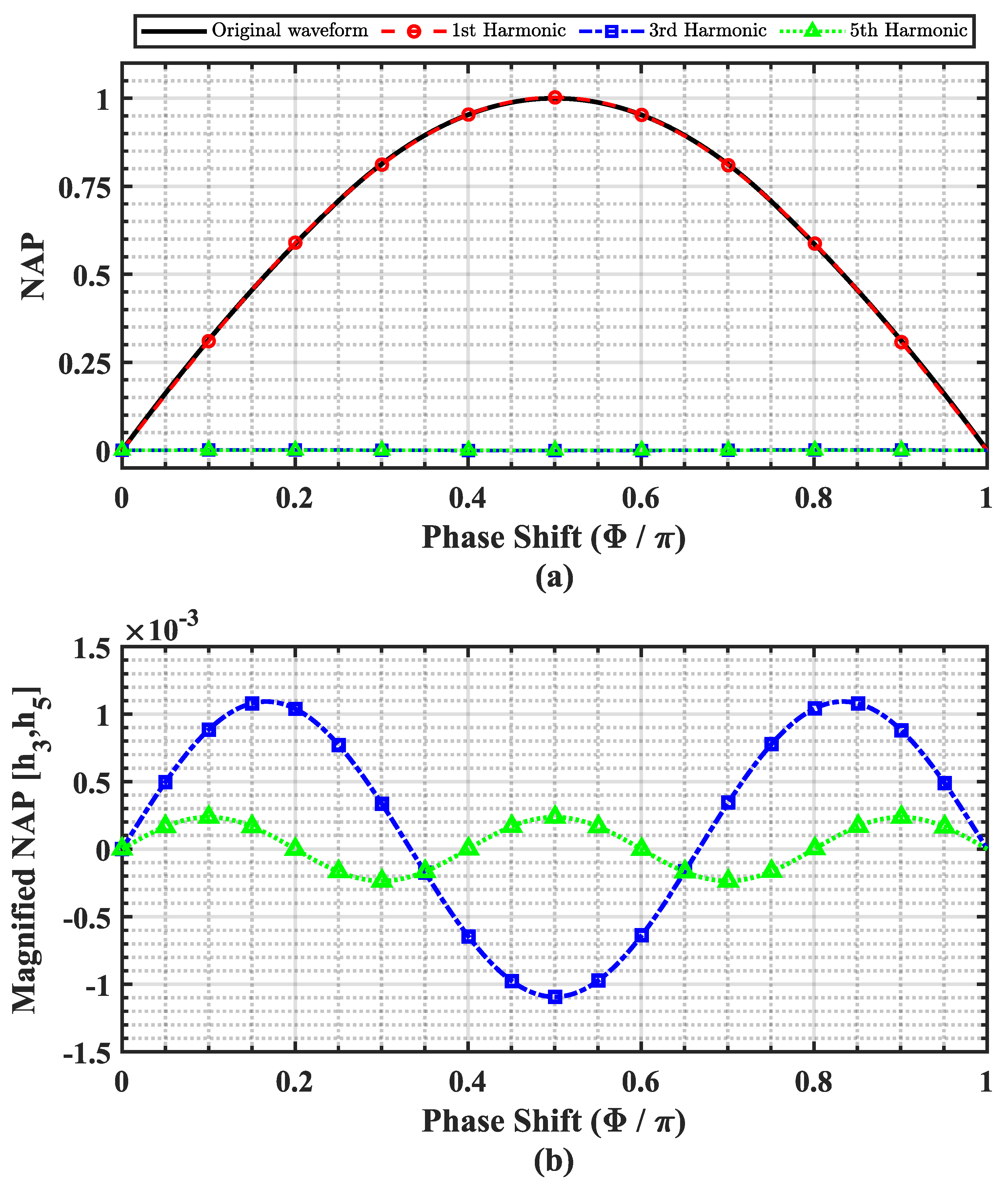
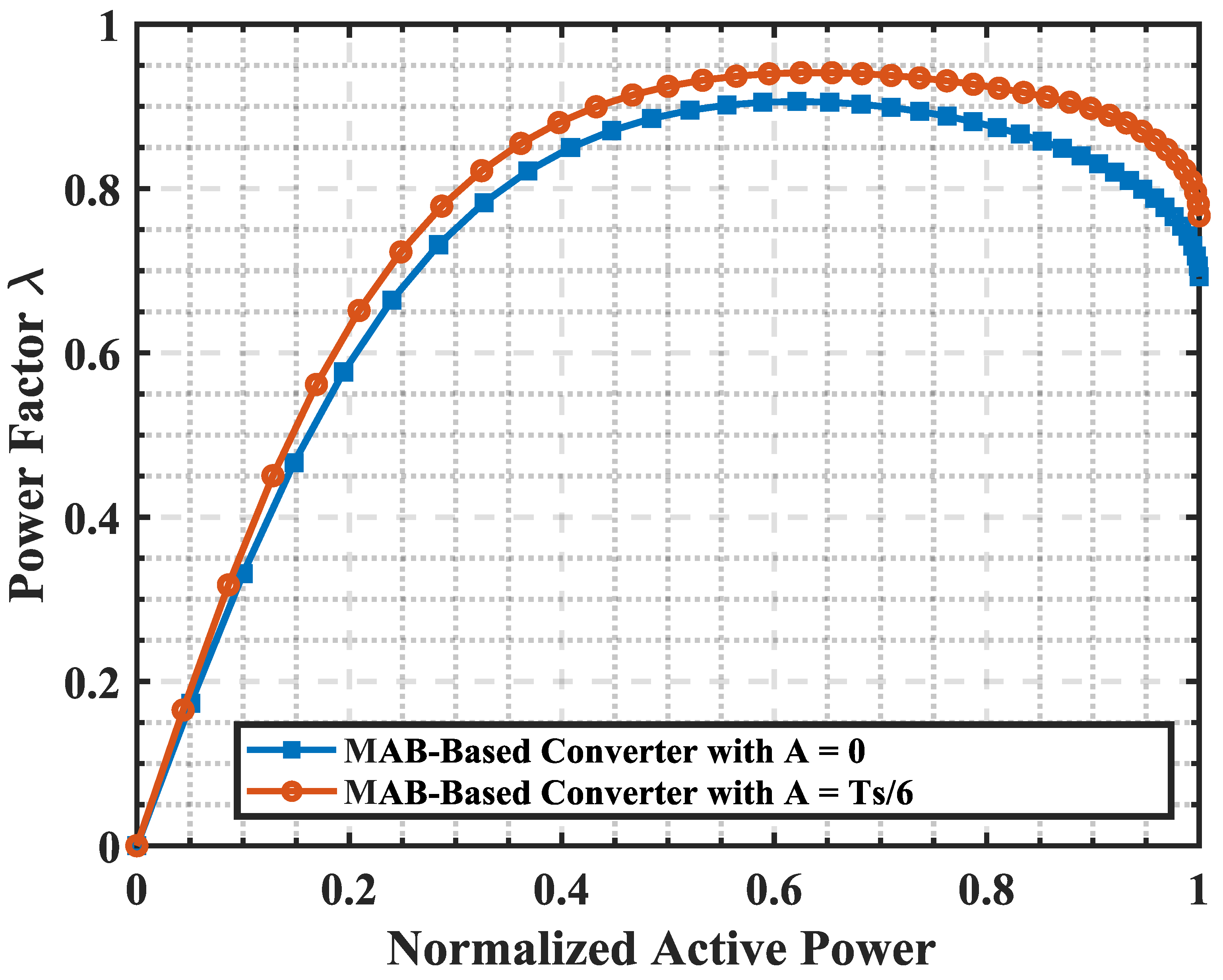
4.2. Circulating Current and HFL Power Factor
5. Power Loss Modeling and Optimization
5.1. Theoretical Basis for Power Loss
5.2. RMS Current Derivations
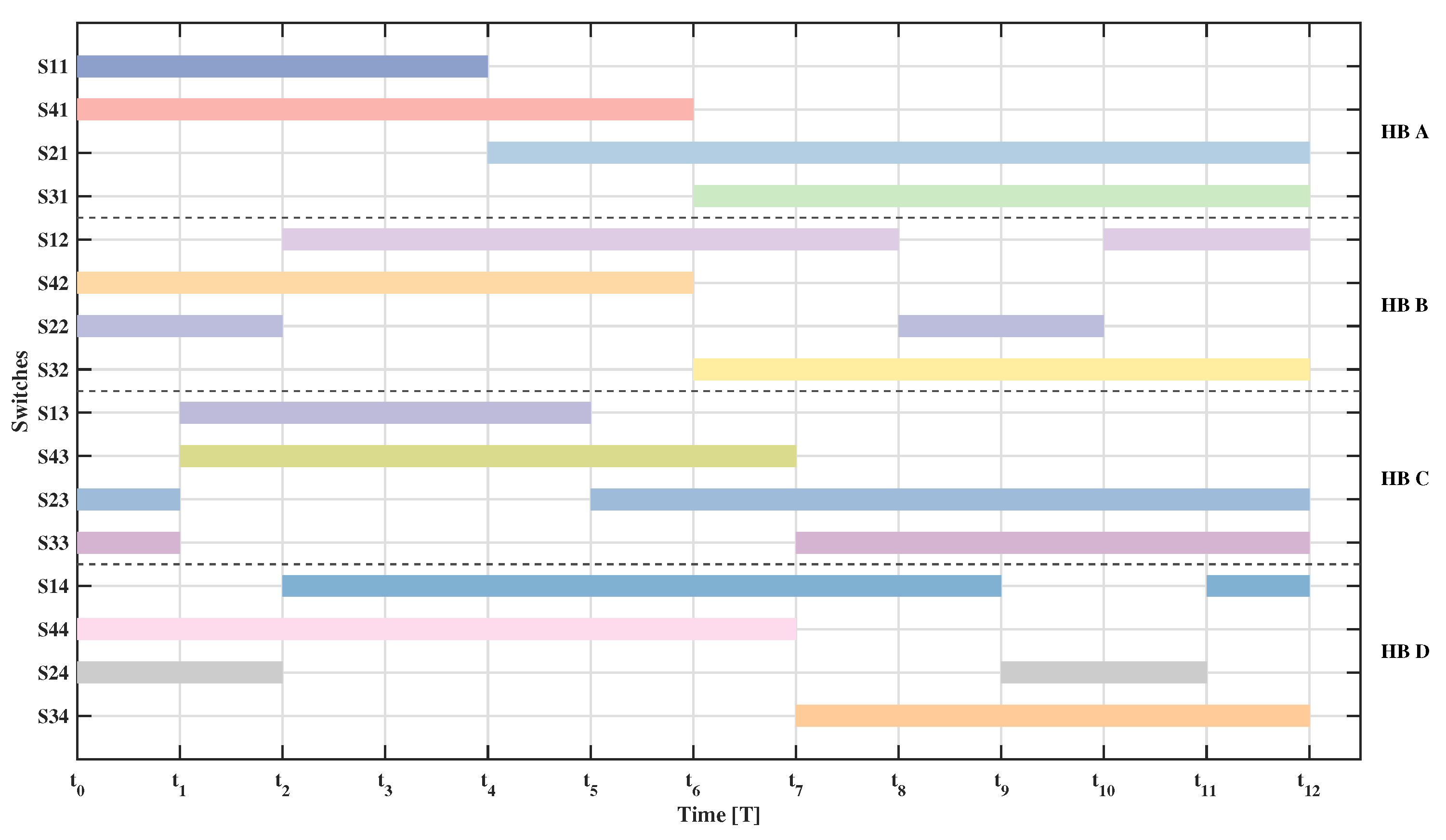
5.2.1. Switching Patterns
5.2.2. Generalized RMS Current Formulas
5.2.3. Body Diode RMS Currents
5.2.4. Leakage Inductance Current
5.3. Parameters Related to Conduction and Switching Losses of the Devices
5.4. Transformer Loss Calculations
5.5. Semiconductor Losses
5.5.1. Conduction Losses
5.5.2. Switching Losses
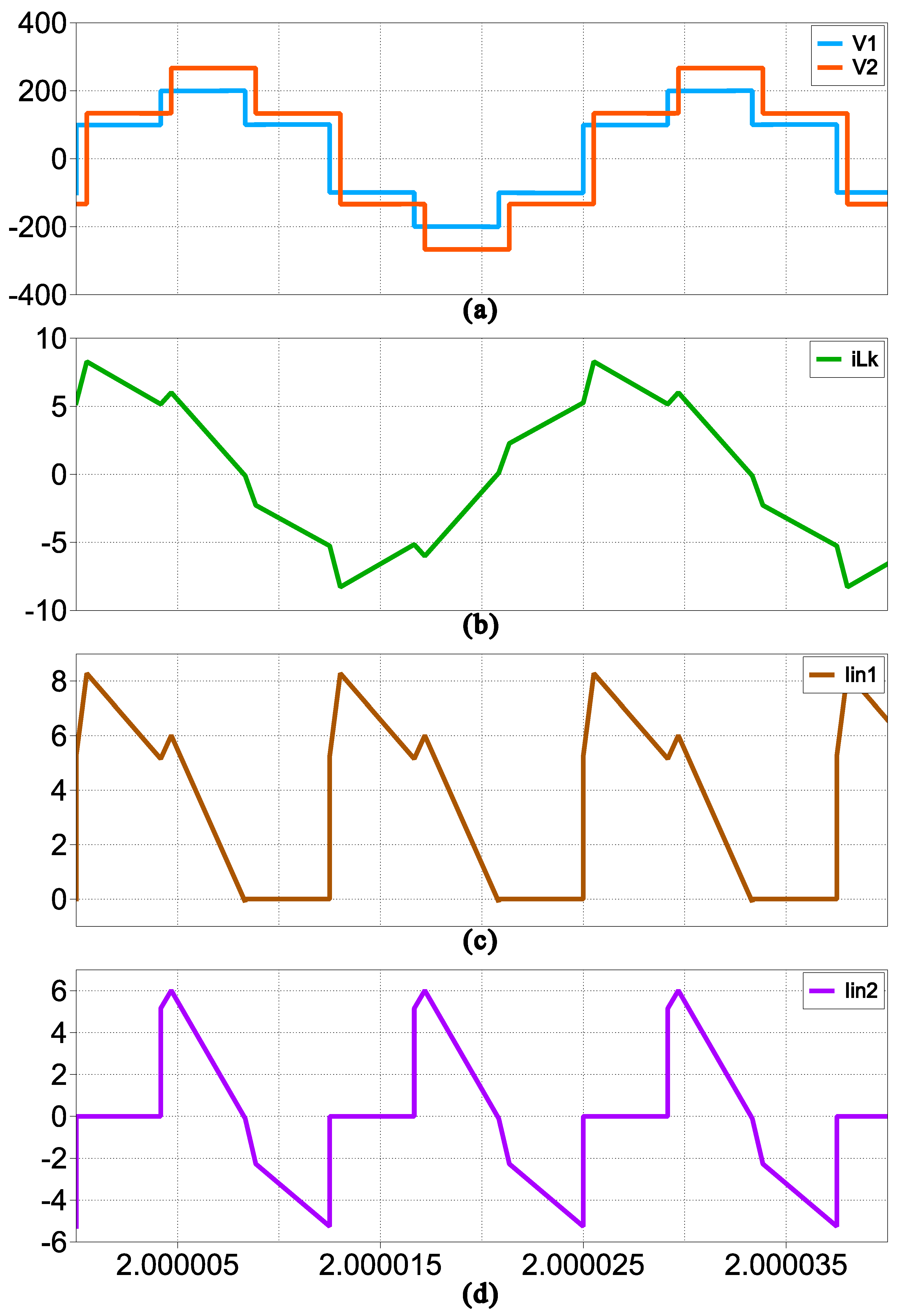
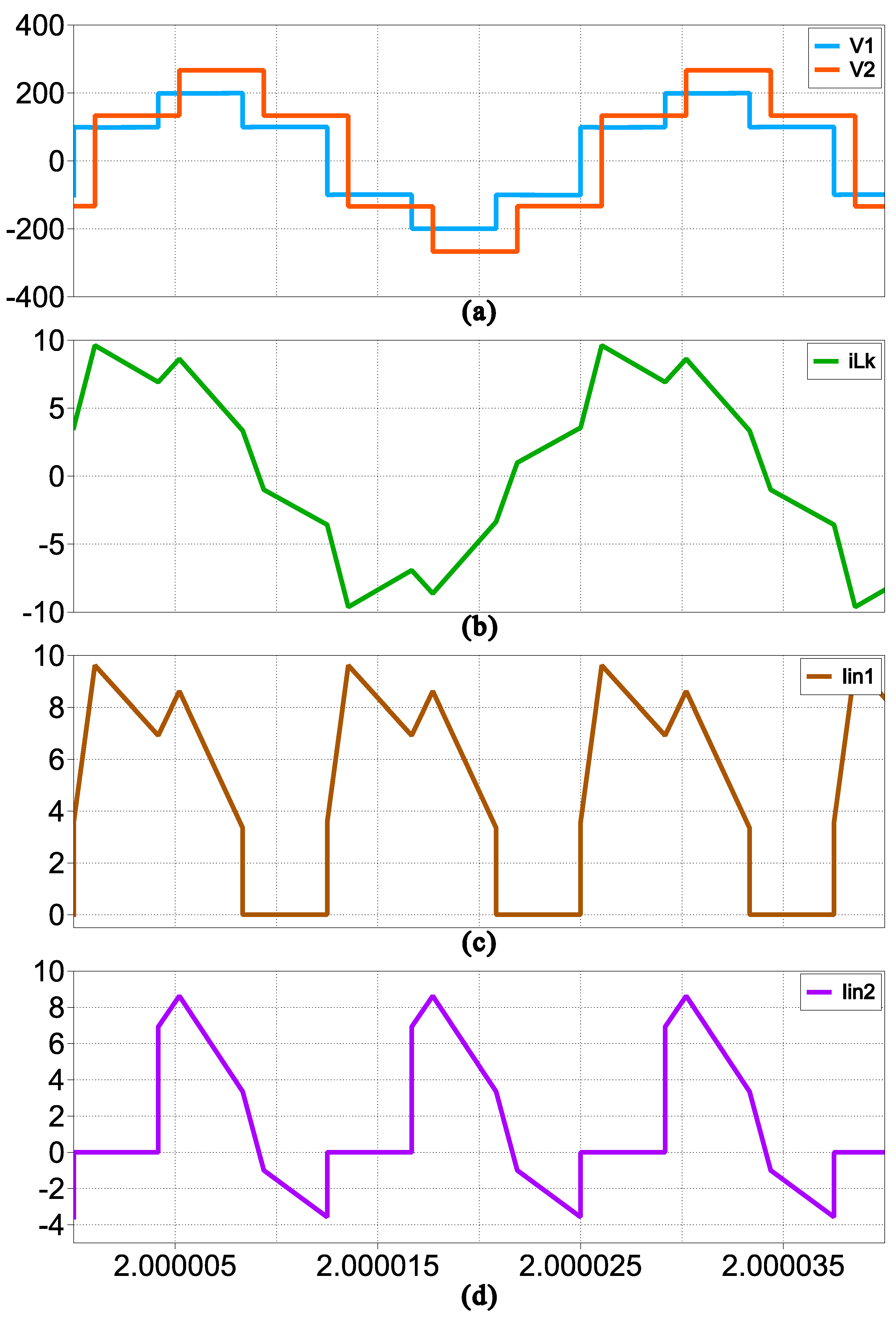
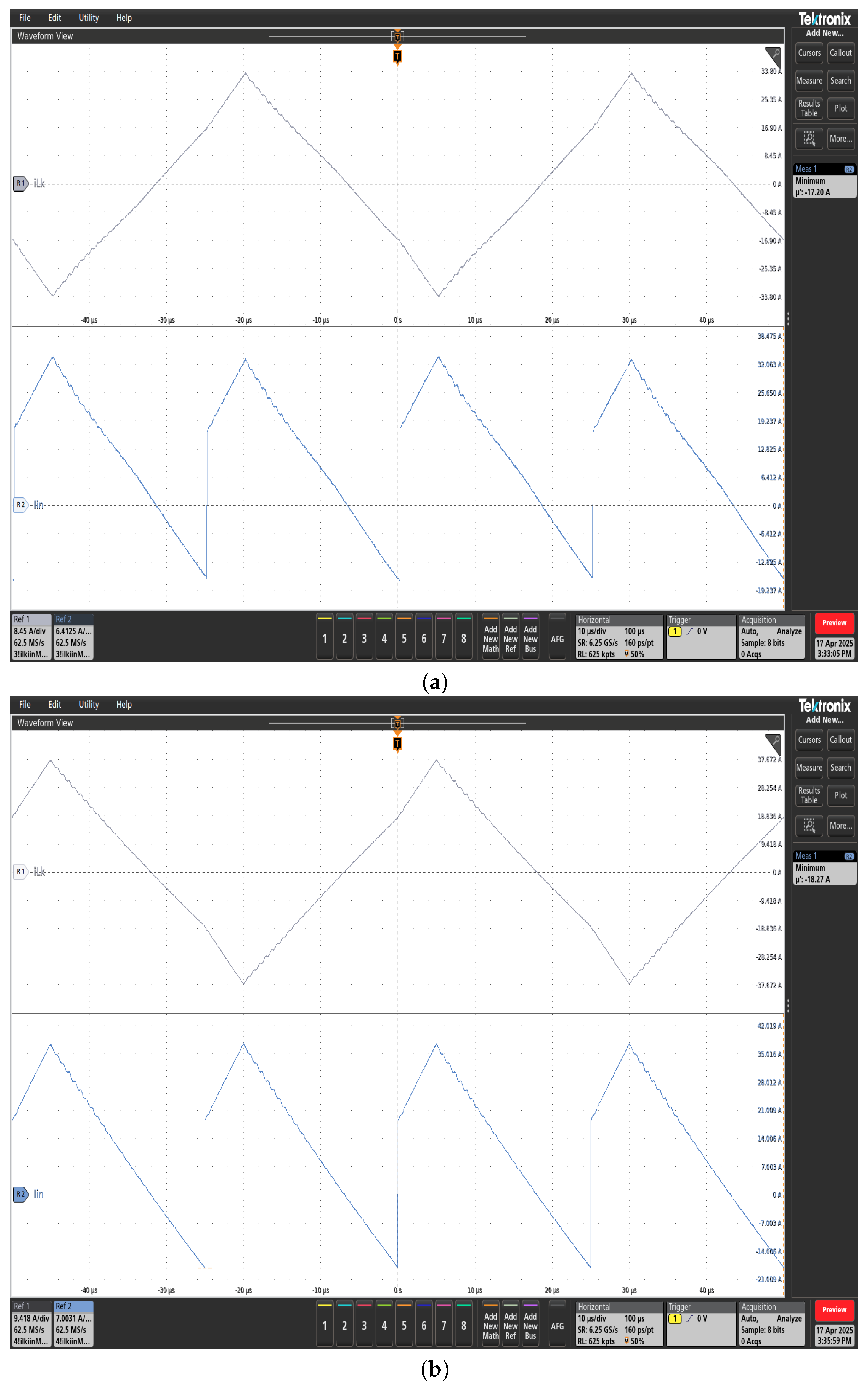
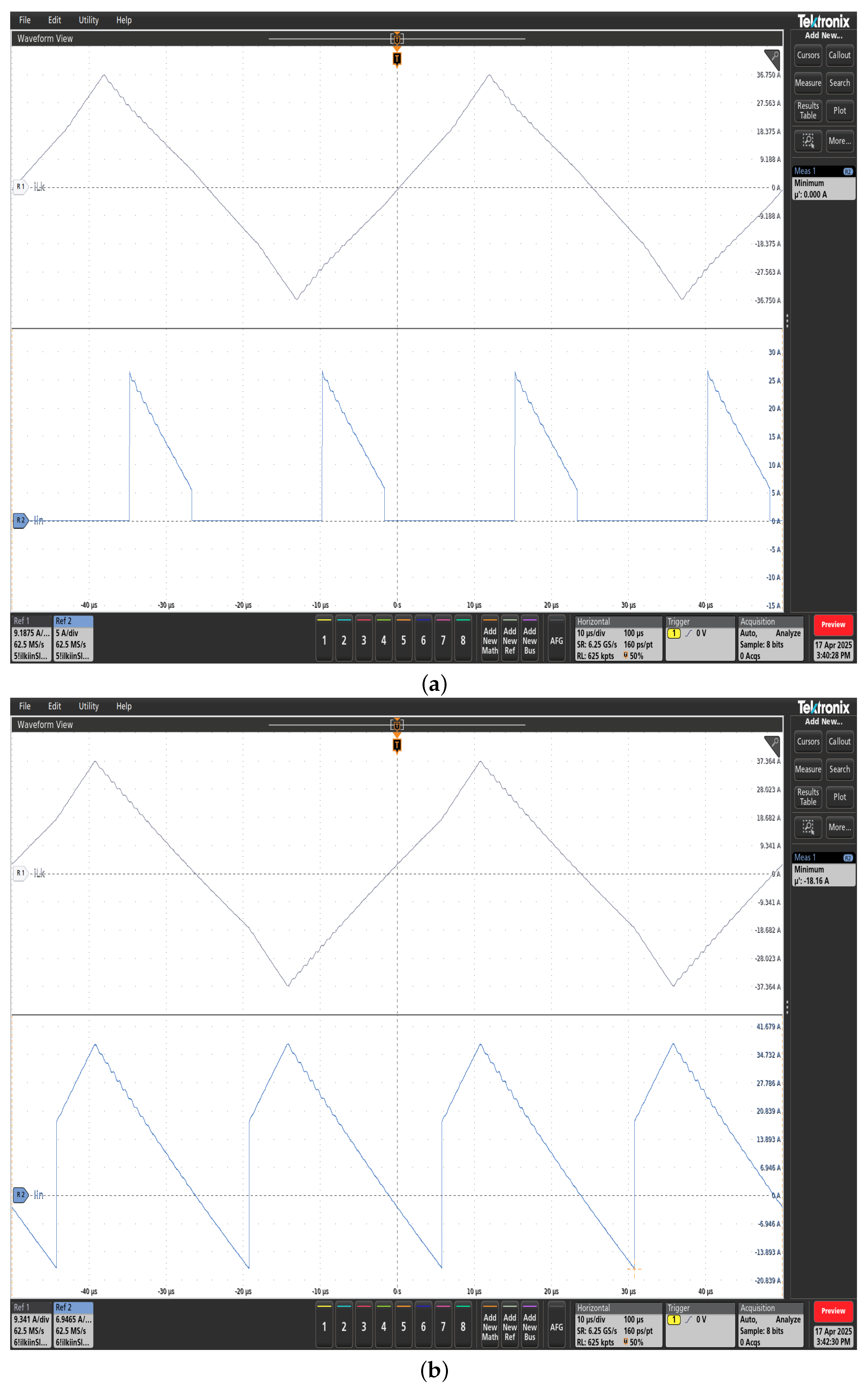
6. Simulation Results
7. Experimental Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| A | Modulation index |
| B | Total number of switch operation modes |
| DAB | Dual active bridge |
| f | Switching frequency |
| HFL | High-frequency link |
| HFT | High-frequency transformer |
| Peak current | |
| Root mean square current | |
| Initial current | |
| Leakage inductance current | |
| j | Number of turn-on modes |
| Leakage inductance | |
| Magnetizing inductance | |
| M | Modulation-related term |
| MAB | Multiple active bridge |
| MV | Medium voltage |
| MPC | Multiple port converters |
| N | Transformer turn ratio |
| n | Number of harmonics |
| NAP | Normalized active power |
| P | Nominal power |
| Conduction loss | |
| Switching loss | |
| Power factor | |
| Phase shift angle | |
| PV | Photovoltaics |
| QAB | Quadruple active bridge |
| Q | Reactive power |
| On-state resistance of MOSFET | |
| RMS | Root mean square |
| S | Apparent power |
| TAB | Triple active bridge |
| Switching period | |
| THD | Total harmonic distortion |
| Rise time and fall time of MOSFET | |
| Voltage (drain to source) | |
| Input voltages | |
| Output voltages | |
| Transformer’s primary and secondary voltages | |
| Voltage supplied in the specified interval | |
| Angular frequency | |
| x | Particular switch within the converter |
References
- Kumar, L.; Jain, S. Multiple-input DC/DC converter topology for hybrid energy system. IET Power Electron. 2013, 6, 1483–1501. [Google Scholar] [CrossRef]
- Dezhbord, M.; Babalou, M.; Mohammadsalehian, S.; Rabiul Islam, M. SIMO DC-DC Converter with a Multi-Winding Coupled Inductor to Reduce Input Current Ripple. In Proceedings of the 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET), Arad, Romania, 20–22 May 2022; pp. 1043–1048. [Google Scholar] [CrossRef]
- Bossi, G.; Buccella, C.; Cecati, C.; Damiano, A.; Floris, A.; Simonetti, F. A Converter Topology for Auxiliary Power System of an All Electric Aircraft. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 1605–1612. [Google Scholar] [CrossRef]
- Costa, L.F.; Buticchi, G.; Liserre, M. Quadruple Active Bridge DC-DC converter as the basic cell of a modular Smart Transformer. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2449–2456. [Google Scholar] [CrossRef]
- Bai, H.; Nie, Z.; Mi, C.C. Experimental Comparison of Traditional Phase-Shift, Dual-Phase-Shift, and Model-Based Control of Isolated Bidirectional DC–DC Converters. IEEE Trans. Power Electron. 2010, 25, 1444–1449. [Google Scholar] [CrossRef]
- Dezhbord, M.; Mohamadian, S.; Ghasemian, A.; Buccella, C.; Cecati, C. Enhancing Voltage Gain and Assessing Current THD in Transformer of Photovoltaic Applications through a New Triple Active Bridge Converter. In Proceedings of the 2024 IEEE 33rd International Symposium on Industrial Electronics (ISIE), Quebec City, QC, Canada, 18–21 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, Z.; Thomsen, O.C.; Andersen, M.A.E. Analysis and Design of a Bidirectional Isolated DC–DC Converter for Fuel Cells and Supercapacitors Hybrid System. IEEE Trans. Power Electron. 2012, 27, 848–859. [Google Scholar] [CrossRef]
- Beiranvand, H.; Hoffmann, F.; Pascal, Y.; Hahn, F.; Liserre, M. Multiwinding Transformer Leakage Inductance Optimization for Power Flow Decoupling in Multiport DC-DC Converters. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14–16 July 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Liu, G.; Zhao, Y. Universal High-Frequency-Link Characterization and Practical Fundamental-Optimal Strategy for Dual-Active-Bridge DC-DC Converter Under PWM Plus Phase-Shift Control. IEEE Trans. Power Electron. 2015, 30, 6488–6494. [Google Scholar] [CrossRef]
- Yang, H.; Xu, W.; Wang, H.; Narayanan, M. Investigation of reverse current for crystalline silicon solar cells—New concept for a test standard about the reverse current. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference (PVSC), Honolulu, HI, USA, 20–25 June 2010; pp. 2806–2810. [Google Scholar] [CrossRef]
- Jamshed, J.; Mastromauro, R.A. LV DC/MV AC Power Conversion Interface Based on Asymmetrical Multilevel Converters. In Proceedings of the 2025 IEEE 19th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Lisbon, Portugal, 18–20 June 2025; pp. 1–7. [Google Scholar] [CrossRef]
- Jamshed, J.; Mastromauro, R.A. Filter-Less Sub-Multilevel DC/AC Power Converters for MV Connection. In Proceedings of the 2024 IEEE 18th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Capri, Italy, 19–21 June 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Kurm, S.; Agarwal, V. Dual Active Bridge Based Reduced Stage Multiport DC/AC Converter for PV-Battery Systems. IEEE Trans. Ind. Appl. 2022, 58, 2341–2351. [Google Scholar] [CrossRef]
- Kolahian, P.; Tarzamni, H.; Nikafrooz, A.; Hamzeh, M. Multi-port DC–DC converter for bipolar medium voltage DC micro-grid applications. IET Power Electron. 2019, 12, 1841–1849. [Google Scholar] [CrossRef]
- Mukherjee, S.; Ruiz, J.M.; Barbosa, P. A High Power Density Wide Range DC–DC Converter for Universal Electric Vehicle Charging. IEEE Trans. Power Electron. 2023, 38, 1998–2012. [Google Scholar] [CrossRef]
- Bossi, G.; Buccella, C.; Cecati, C.; Simonetti, F.; Damiano, A. A Battery-Based Auxiliary Power System for an All-Electric Aircraft: A Novel Converter Configuration. IEEE Trans. Ind. Appl. 2025, 1–13. [Google Scholar] [CrossRef]
- Pamujula, M.; Ohja, A.; Kulkarni, R.; Swarnkar, P. Cascaded ‘H’ Bridge based Multilevel Inverter Topologies: A Review. In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Meng, X.; Duan, Q.; Sha, G.; Zhao, C.; Wang, H.; Wang, X.; Lan, Z. An Efficiency Improvement Strategy for Triple-Active-Bridge-Based DC Energy Routers in DC Microgrids. Electronics 2024, 13, 1172. [Google Scholar] [CrossRef]
- Das, D.; Weise, N.; Basu, K.; Baranwal, R.; Mohan, N. A Bidirectional Soft-Switched DAB-Based Single-Stage Three-Phase AC–DC Converter for V2G Application. IEEE Trans. Transp. Electrif. 2019, 5, 186–199. [Google Scholar] [CrossRef]
- Costa, L.F.; Buticchi, G.; Liserre, M. Quad-Active-Bridge DC–DC Converter as Cross-Link for Medium-Voltage Modular Inverters. IEEE Trans. Ind. Appl. 2017, 53, 1243–1253. [Google Scholar] [CrossRef]
- Han, J.; Li, X.; Sun, Y.; Gong, S.; Huang, S. Quadruple-active-bridge based unified power quality conditioner-L with fault current limiting capability. Electr. Power Syst. Res. 2022, 206, 107780. [Google Scholar] [CrossRef]
- Adam, A.H.A.; Chen, J.; Xu, M.; Kamel, S.; Ali, G. Model predictive control for quad active bridge DC-DC converter for more electric aircraft applications. Sci. Rep. 2025, 15, 13653. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tu, C.; Xiao, F.; Liu, B.; Li, P. Method for Classification and Optimization of Modes in Triple-Active-Bridge Converter Based on Waveform Structural Characteristics Analysis. Electronics 2025, 14, 187. [Google Scholar] [CrossRef]
- Wolfspeed. C3M0030090K Silicon Carbide Power MOSFET Datasheet. Wolfspeed Technical Datasheet. 2025, pp. 1–10. Available online: https://www.wolfspeed.com/products/power/c3m0030090k/ (accessed on 21 July 2025).
- Wolfspeed. C3M0065090D Silicon Carbide Power MOSFET Datasheet. Wolfspeed Technical Datasheet. 2025, pp. 1–10. Available online: https://www.wolfspeed.com/products/power/sic-mosfets/900v-silicon-carbide-mosfets/c3m0065090d/ (accessed on 21 July 2025).
- Dezhbord, M.; Mohseni, P.; Hosseini, S.H.; Mirabbasi, D.; Islam, M.R. A High Step-Up Three-Port DC–DC Converter With Reduced Voltage Stress for Hybrid Energy Systems. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 998–1009. [Google Scholar] [CrossRef]



| Switch | Current Expressions | Switch | Current Expressions |
|---|---|---|---|
| Parameter | Symbol | Value and Description |
|---|---|---|
| On-state resistance at 25 °C | , 25 | C3M0030090K: 30 m typ, 39 m max at = 15 V, = 35 A. C3M0065090D: 65 m typ, 78 m max at = 15 V, = 20 A. |
| Temperature coefficient of | - | C3M0030090K: ≈1.3× at 100 °C, ≈1.7–1.8× at 150 °C relative to 25 °C. C3M0065090D: ≈1.25–1.3× at 100 °C, ≈1.6–1.7× at 150 °C. |
| Turn-on energy | (I,V) | C3M0030090K: 133 µJ typ at = 600 V, = 35 A. C3M0065090D: 250 µJ typ at = 400 V, = 20 A. |
| Turn-off energy | (I,V) | C3M0030090K: 111 µJ typ. C3M0065090D: 48 µJ typ. |
| Output capacitance energy | (V) | C3M0030090K: ~30 µJ typ from Eoss curve. C3M0065090D: ~16 µJ typ from Eoss curve. |
| Total gate charge | C3M0030090K: 74 nC typ. C3M0065090D: 33 nC typ. | |
| Forward voltage drop | C3M0030090K: ≈4.5 V typ. C3M0065090D: ≈4.4 V typ. | |
| Reverse recovery charge and energy | C3M0030090K: Qrr ≈ 536 nC, trr ≈ 24 ns. C3M0065090D: Qrr ≈ 185 nC, trr ≈ 28 ns. |
| Parameter | Symbol | Value and Description |
|---|---|---|
| Switching frequency | 300 kHz | |
| Saturation flux density | 0.51 (25 °C), 0.39 (100 °C) | |
| Initial permeability (25 °C) | 2400 ± 25% | |
| Core area | ||
| Winding resistance at 40 kHz | 0.240, 0.520 | |
| Magnetic path length | ||
| Core volume |
| Power Loss Distribution | (Loss/Total Loss) | Power Loss |
|---|---|---|
| Conduction Losses of the Input Side of HB_A | 8.69% | 4.9621 W |
| Switching Losses of the Input Side of HB_A | 0.89% | 0.5089 W |
| Conduction Losses of the Input Side of HB_B | 8.62% | 4.9235 W |
| Switching Losses of the Input Side of HB_B | 3.51% | 2.0036 W |
| Conduction Losses of the Output Side of HB_A | 2.23% | 1.2732 W |
| Switching Losses of the Output Side of HB_A | 1.62% | 0.9230 W |
| Conduction Losses of the Output Side of HB_B | 2.20% | 1.2586 W |
| Switching Losses of the Output Side of HB_B | 1.46% | 0.8326 W |
| Total Conduction Losses | 21.74% | 12.4174 W |
| Total Switching Losses | 7.47% | 4.2683 W |
| Transformer Loss | 70.79% | 40.44 W |
| Total Loss | - | 57.1257 W |
| Efficiency | - | 97.61% |
| Parameter | Value |
|---|---|
| Leakage inductance | |
| Turn ratio of the transformer | 3 |
| Frequency | |
| Modulation index |
| Parameter | Value |
|---|---|
| Leakage inductance | |
| Turn ratio of the transformer | 2 |
| Frequency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dezhbord, M.; Rehman, F.U.; Ghasemian, A.; Cecati, C. High-Frequency Link Analysis of Enhanced Power Factor in Active Bridge-Based Multilevel Converters. Electronics 2025, 14, 3551. https://doi.org/10.3390/electronics14173551
Dezhbord M, Rehman FU, Ghasemian A, Cecati C. High-Frequency Link Analysis of Enhanced Power Factor in Active Bridge-Based Multilevel Converters. Electronics. 2025; 14(17):3551. https://doi.org/10.3390/electronics14173551
Chicago/Turabian StyleDezhbord, Morteza, Fazal Ur Rehman, Amir Ghasemian, and Carlo Cecati. 2025. "High-Frequency Link Analysis of Enhanced Power Factor in Active Bridge-Based Multilevel Converters" Electronics 14, no. 17: 3551. https://doi.org/10.3390/electronics14173551
APA StyleDezhbord, M., Rehman, F. U., Ghasemian, A., & Cecati, C. (2025). High-Frequency Link Analysis of Enhanced Power Factor in Active Bridge-Based Multilevel Converters. Electronics, 14(17), 3551. https://doi.org/10.3390/electronics14173551






