An Improved CNN-Based Algorithm for Quantitative Prediction of Impact Damage Depth in Civil Aircraft Composites via Multi-Domain Terahertz Spectroscopy
Abstract
1. Introduction
- By combining THz multi-domain features with the defect depth obtained via CLSM, an innovative “THz Spectral Features-Defect Depth” (TSF-DD) dataset for CFRP was systematically constructed, providing a solid foundation for the precise quantitative analysis of low-velocity impact damage depth in CFRP materials.
- We propose a novel deep learning model, FEN-CNN-BiLSTM, which represents the innovative application of this hybrid model specifically to the depth regression prediction of CFRP defects in civil aircraft. The proposed method achieves high-accuracy prediction of continuous depth values for CFRP impact damage defects, providing new perspectives and methodologies for non-destructive testing within the field of civil aviation.
- The improved FEN-CNN-BiLSTM model is specifically designed to address THz spectral characteristics and incorporates an innovative FEN module. This module achieves feature recombination and purification through a simplified encoder-decoder-like architecture, effectively mitigating information loss. Additionally, the BiLSTM bidirectional modeling mechanism comprehensively investigates the inter-feature correlations, enhancing the model’s capability to understand complex features. Consequently, this model significantly enhances the accuracy and stability of predictions regarding the depth of impact damage defect.
2. Theory and Methods
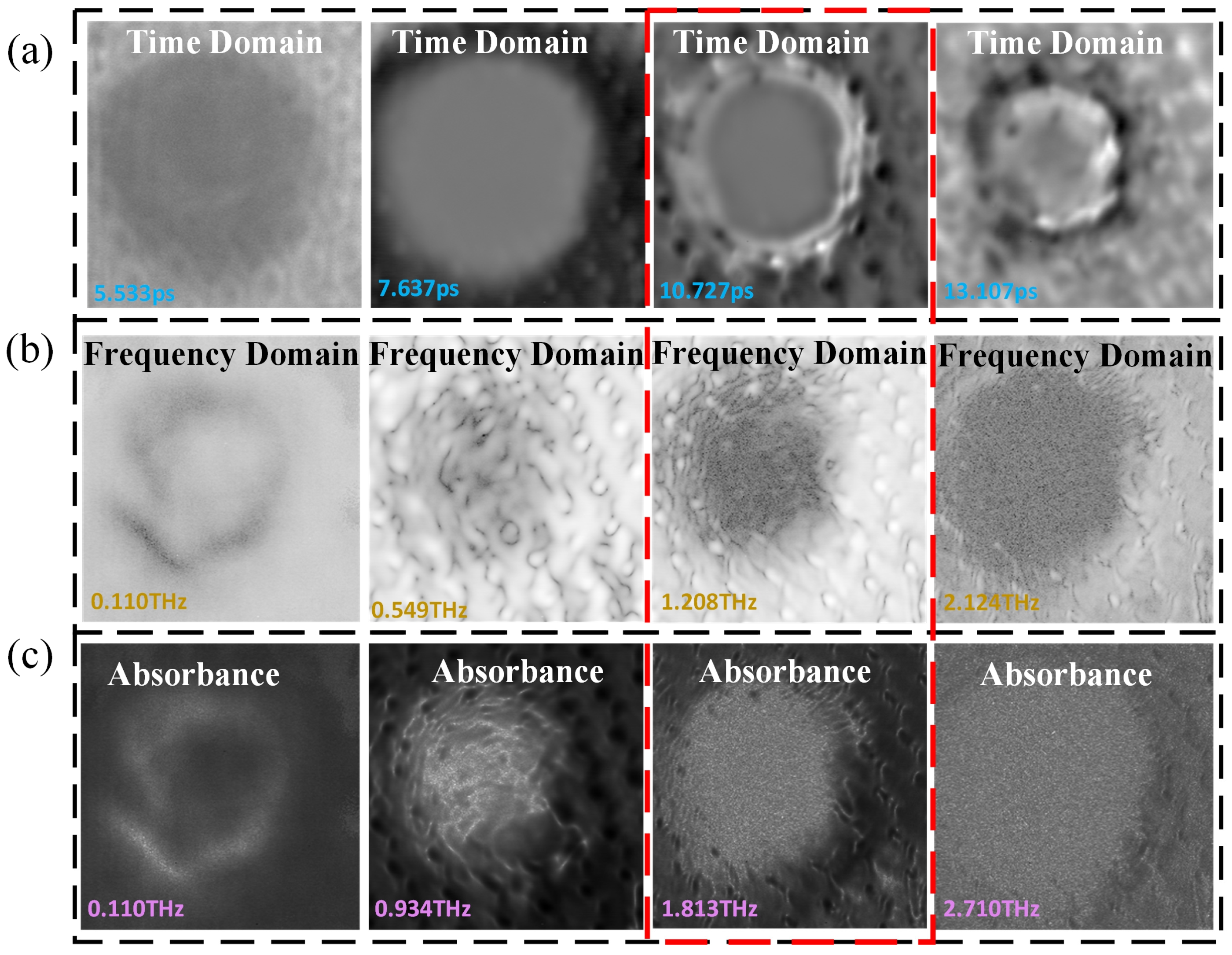
2.1. Time-Domain Signal
2.2. Frequency-Domain Signal
2.3. Absorbance Signal
3. Experiment and Data Analysis
3.1. Sample Preparation
3.2. THz Imaging Results and Multi-Feature Depth Analysis
3.2.1. Imaging Analysis
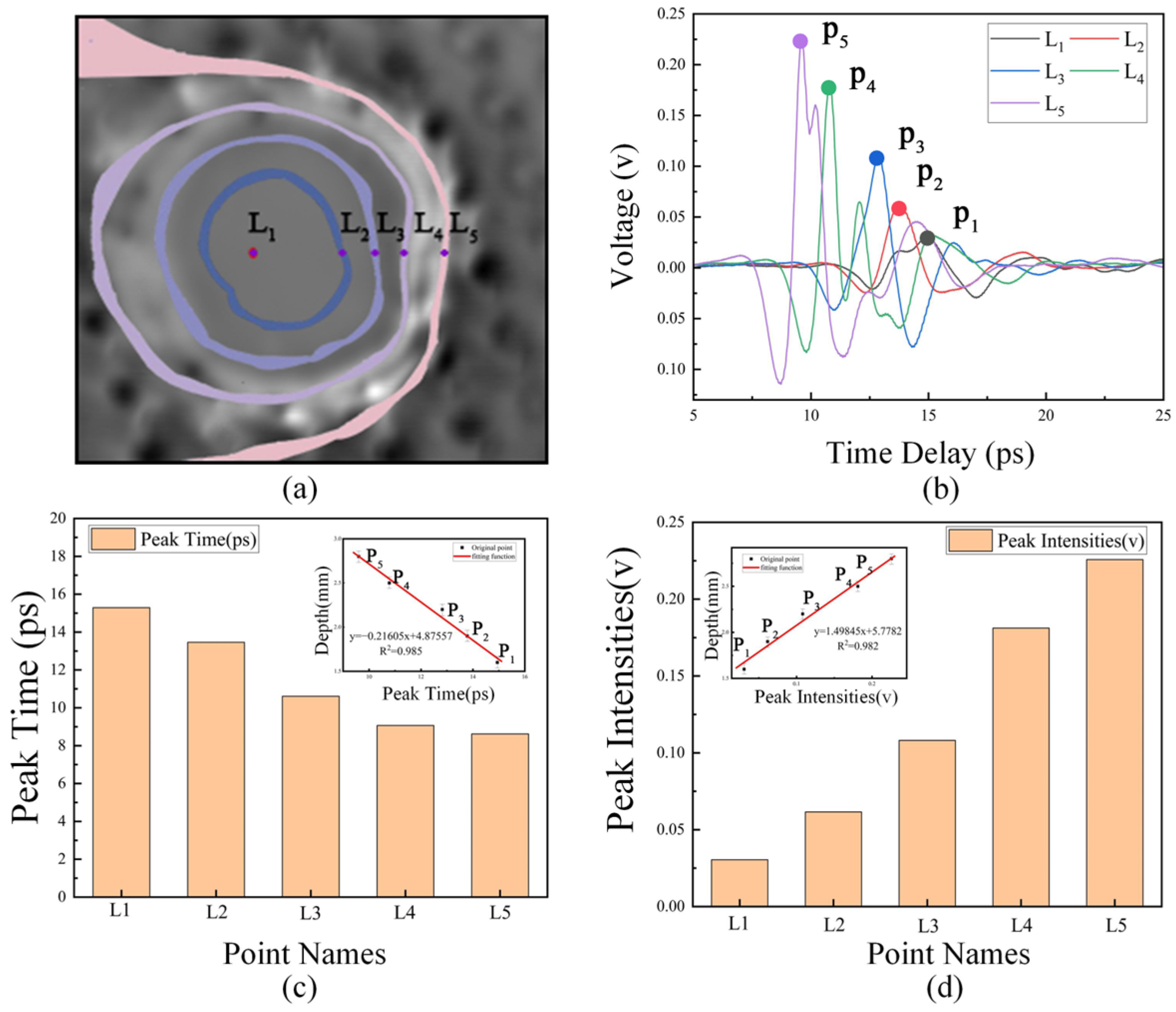
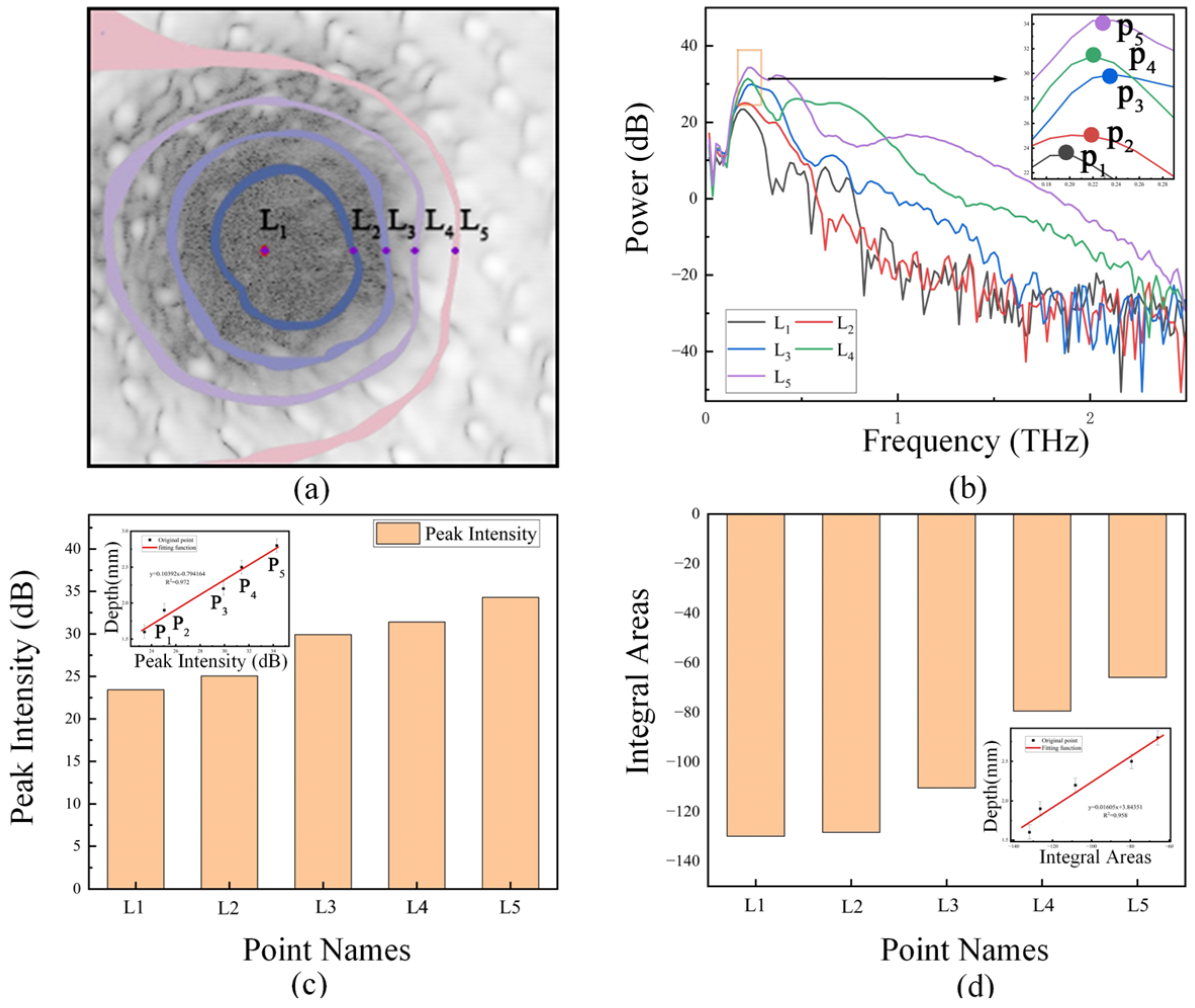
3.2.2. Depth-Based Spectral Point Selection
3.2.3. THz Multi-Feature Depth Analysis
4. Multi-Feature Depth Prediction Model
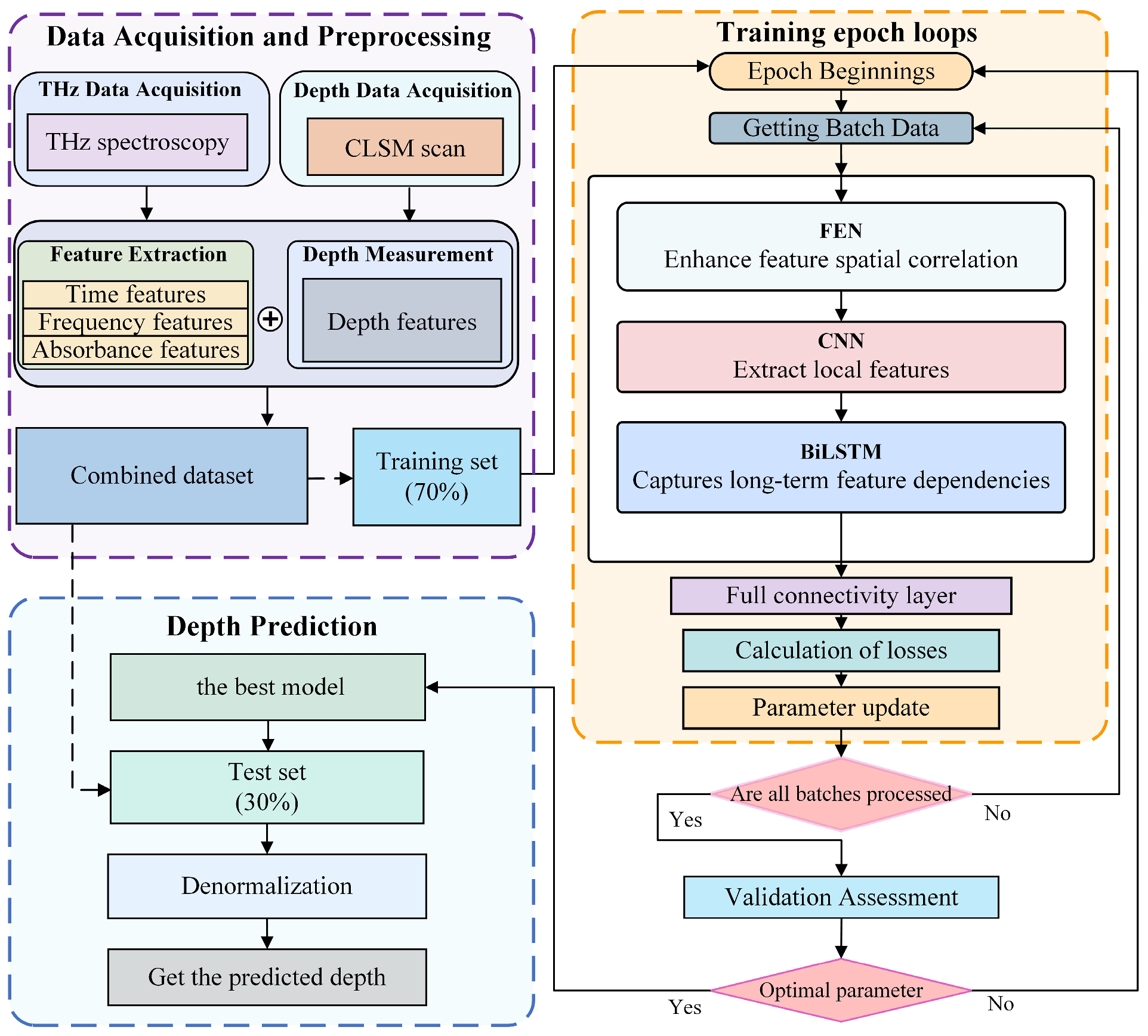
4.1. Dataset Preparation
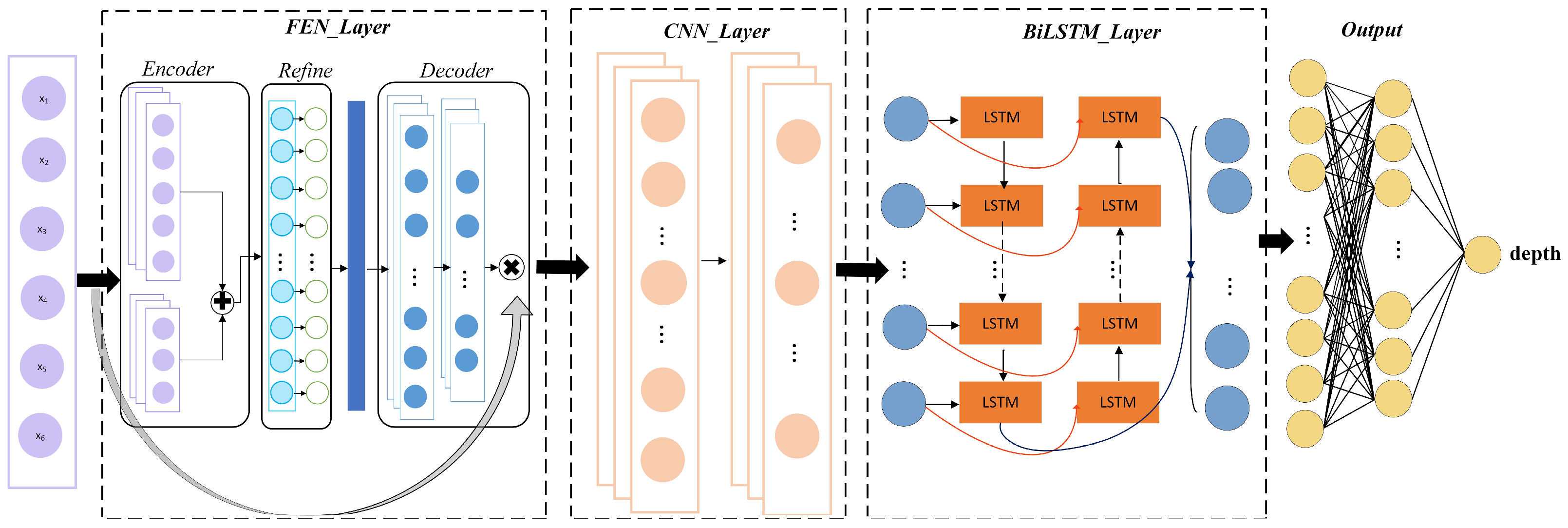
4.2. Model Design Overview
4.2.1. FEN Module
4.2.2. CNN Algorithm
4.2.3. BiLSTM Structure
4.2.4. FEN-CNN-BiLSTM Hybrid Model
- THz data and CLSM depth scanning data were systematically collected. From these datasets, six important features are extracted: time-domain peak time, time-domain peak value, frequency-domain peak intensities, frequency-domain integral areas, absorbance peak intensity, and baseline absorbance. These extracted features were then integrated with corresponding depth labels to construct a comprehensive dataset. The dataset was normalized using the MinMaxScaler method. Finally, the dataset is divided into training set and testing subset at a ratio of 70% and 30%, respectively, to facilitate model development and evaluation.
- The input features of the model are initially processed by the FEN structure, which performs feature enhancement while effectively suppressing noise interference.
- After undergoing FEN processing, the enhanced and recombined features are subsequently output to the CNN module for local features of the signal.
- The features processed by the CNN module are input to the BiLSTM module, which captures inter-feature relationships from both forward and backward directions. Finally, the output of the BiLSTM module is mapped to depth labels through fully connected layers.
- To identify the optimal parameters, the model undergoes rigorous evaluation via cross-validation. The best-performing model is then assessed on a held-out 30% test set to determine its final performance metrics.
4.2.5. Parameter Settings and Evaluation Metrics
5. Experimental Analyses
5.1. Model Result Analysis
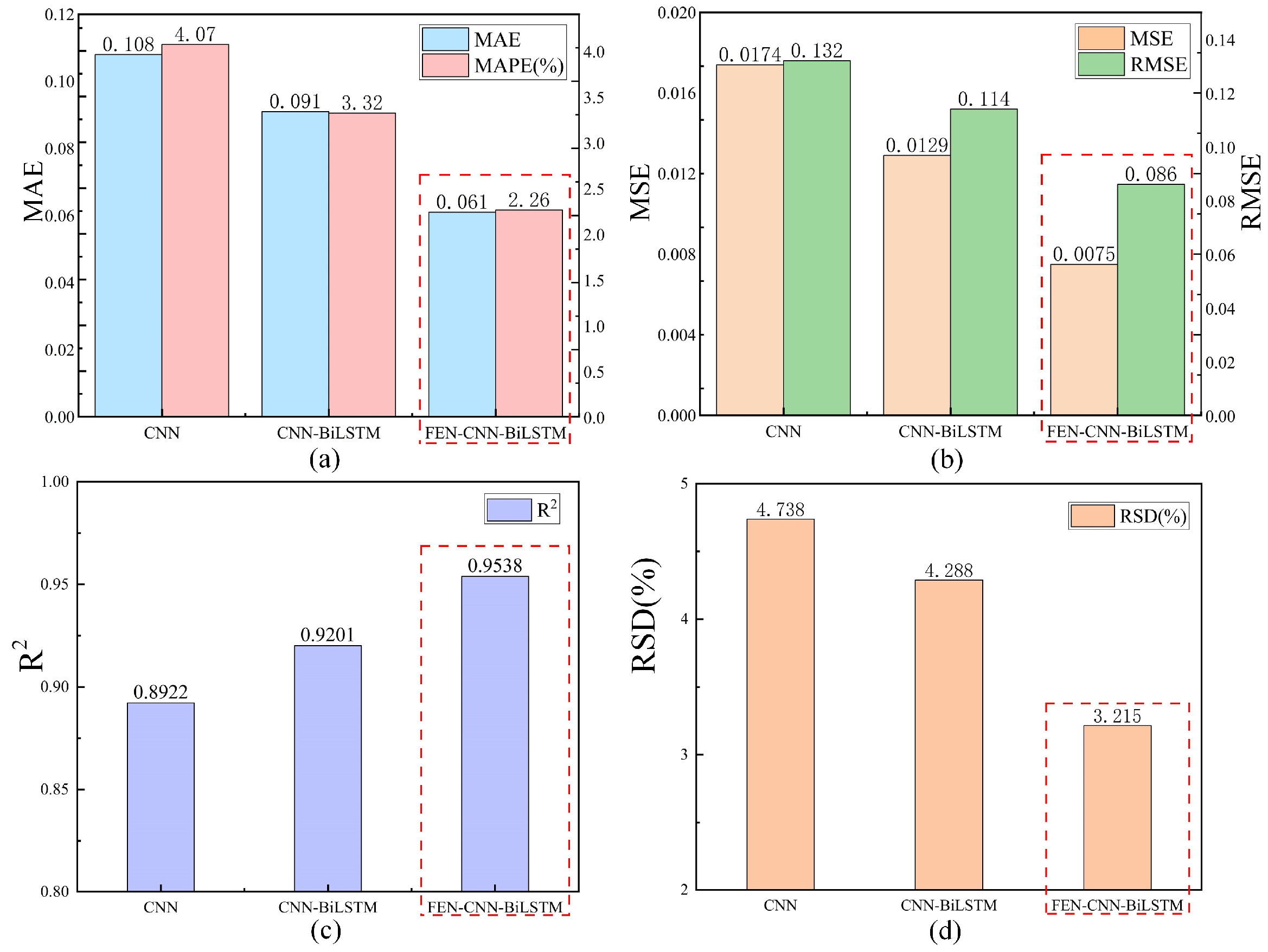
5.1.1. Ablation Experiments
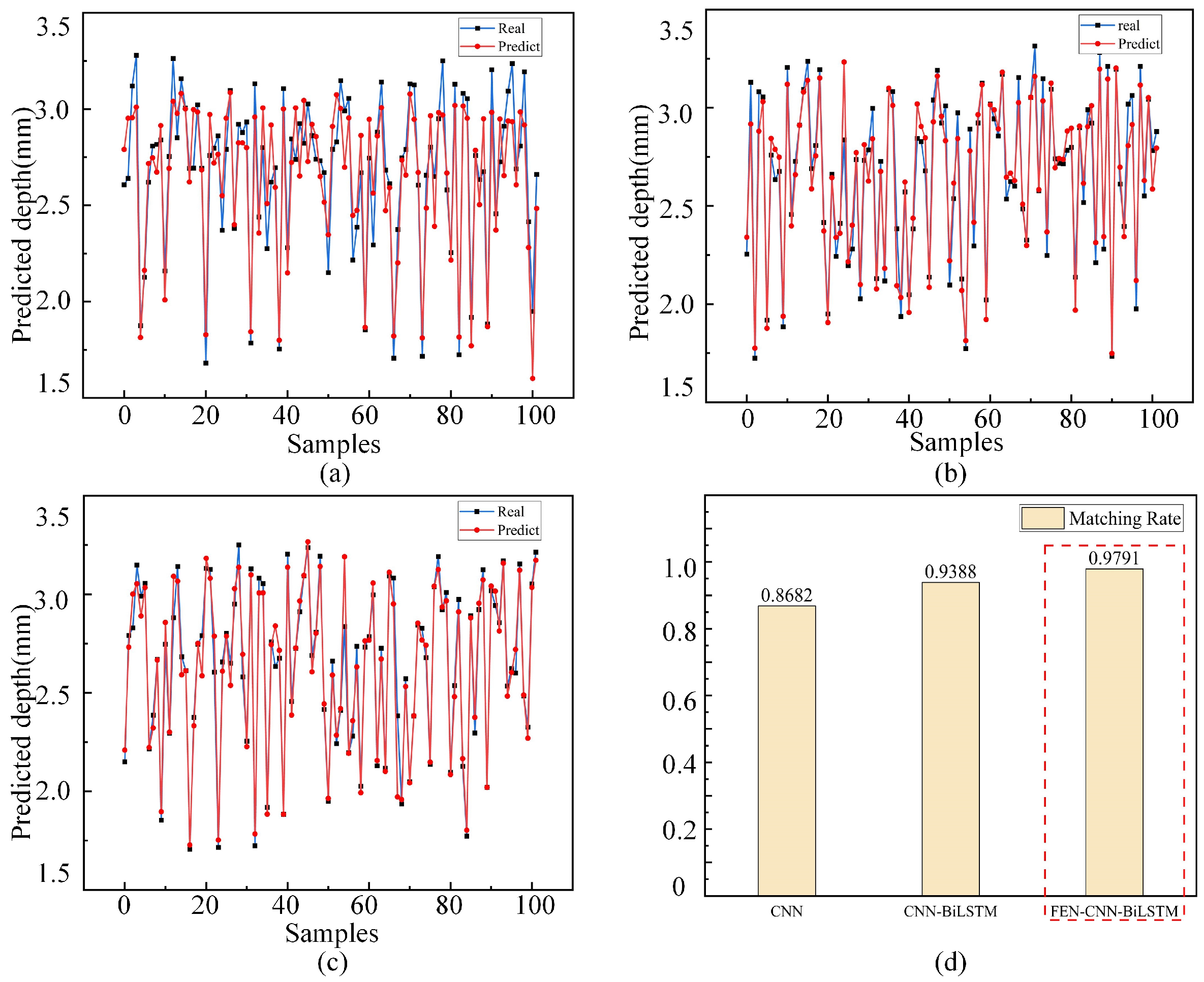
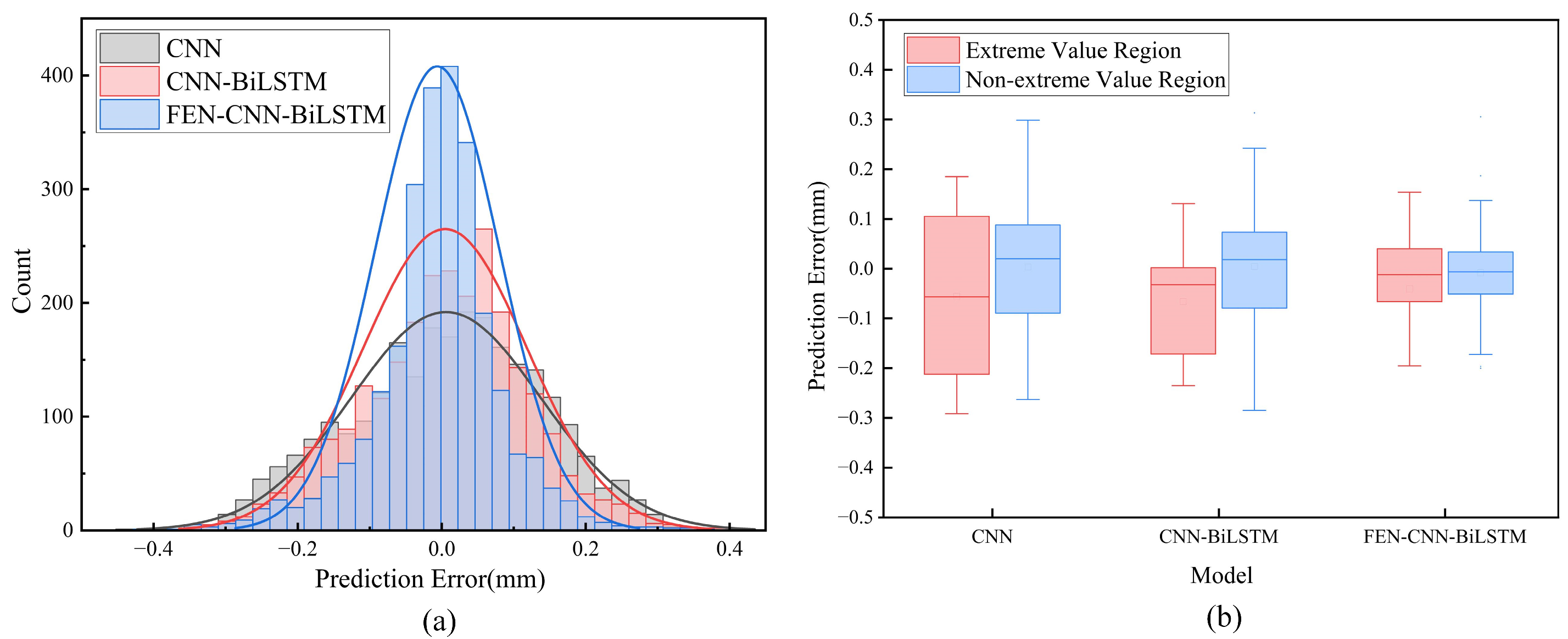
5.1.2. Analysis of Prediction Results
5.2. Comparative Analysis
5.3. External Dataset Verification Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFRP | Carbon Fiber Reinforced Polymer |
| THz | Terahertz |
| CLSM | Confocal Laser Scanning Microscopy |
| TOF | Time of Flight |
| CNN | Convolutional Neural Network |
| FEN | Feature Extraction Network |
| BiLSTM | Bidirectional Long Short-Term Memory |
References
- Xu, X.; Peng, G.; Zhang, B.; Shi, F.; Gao, L.; Gao, J. Material performance, manufacturing methods, and engineering applications in aviation of carbon fiber reinforced polymers: A comprehensive review. Thin-Walled Struct. 2024, 209, 112899. [Google Scholar] [CrossRef]
- Li, J.; Su, X.; Wang, F.; Zhang, D.; Wang, Y.; Song, H.; Xu, J.; Guo, B. Effect of laser processing parameters on the quality of titanium alloy cladding layer on carbon fiber-reinforced polymer. Polymers 2025, 17, 1195. [Google Scholar] [CrossRef]
- Chua, C.Y.X.; Liu, H.-C.; Trani, N.D.; Susnjar, A.; Ho, J.; Scorrano, G.; Rhudy, J.; Sizovs, A.; Lolli, G.; Hernandez, N.; et al. Carbon fiber reinforced polymers for implantable medical devices. Biomaterials 2021, 271, 120719. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, G.; Vaidy, U.; Wang, H. Past, present and future prospective of global carbon fibre composite developments and applications. Compos. Part B Eng. 2022, 250, 110463. [Google Scholar] [CrossRef]
- Parveez, B.; Kittur, M.I.; Badruddin, I.A.; Kamangar, S.; Hussien, M.; Umarfarooq, M.A. Scientific advancements in composite materials for aircraft applications: A review. Polymers 2022, 14, 5007. [Google Scholar] [CrossRef]
- Chen, L.; Lin, X.; Bai, R.; Zhao, Z.; Guo, Z. Anti-bird-strike behavior of M40J carbon fiber reinforced plastic laminates. Compos. Struct. 2024, 339, 118094. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, M.; Liu, K.; Yuan, K.; He, J. Experimental analysis and prediction of CFRP delamination caused by ice impact. Eng. Fract. Mech. 2022, 273, 108757. [Google Scholar] [CrossRef]
- Chen, S.Y.; van de Waerdt, W.; Castro, S.G.P. Design for bird strike crashworthiness using a building block approach applied to the Flying-V aircraft. Heliyon 2023, 9, e14723. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.H.; Fitzgerald, A.J.; Wallace, V.P. Non-contact, non-destructive testing in various industrial sectors with terahertz technology. Sensors 2020, 20, 712. [Google Scholar] [CrossRef]
- Wu, Y.Q.; Chen, M.Y.; Dai, Z.J. Review on the terahertz transmission devices and their applications: From metal waveguides to terahertz fibers. Opt. Laser Technol. 2025, 183, 112339. [Google Scholar] [CrossRef]
- Amenabar, I.; Lopez, F.; Mendikute, A. In introductory review to THz non-destructive testing of composite mater. J. Infrared Millim. Terahertz Waves 2013, 34, 152–169. [Google Scholar] [CrossRef]
- Bauer, M.; Friederich, F. Terahertz and millimeter wave sensing and applications. Sensors 2022, 22, 9693. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Yang, X.K.; Ren, J.J.; Li, L.J.; Zhang, D.D.; Gu, J.; Xiong, W.H. Terahertz recognition of composite material interfaces based on ResNet-BiLSTM. Measurement 2024, 233, 114771. [Google Scholar] [CrossRef]
- Nüßler, D.; Jonuscheit, J. Terahertz based non-destructive testing (NDT) making the invisible visible. Tech. Mess 2021, 88, 199–210. [Google Scholar] [CrossRef]
- Zhong, M.; Xu, H.X.; Li, F.; Yang, M.; Li, S.Q.; Lei, X.; Tu, X.G.; Wang, Z.Q.; Li, C.; Zhao, X.; et al. Nondestructive testing and predictability of microcracks in carbon fiber-reinforced composites via terahertz time-domain spectroscopy. Russ. J. Nondestruct. Test. 2024, 60, 96–103. [Google Scholar] [CrossRef]
- Li, R.; Ye, D.; Zhang, Q.K.; Xu, J.F.; Pan, J.B. Nondestructive evaluation of thermal barrier coatings’ porosity based on terahertz multi-feature fusion and a machine learning approach. Appl. Sci. 2023, 13, 8988. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Q.H.; Xia, R.C.; Zhang, P.T.; Zhou, H.B.; Zhao, B.Y.; Li, G.Y. Automatic defect prediction in glass fiber reinforced polymer based on THz-TDS signal analysis with neural networks. Infrared Phys. Technol. 2021, 115, 103673. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Peng, G.Z.; Tan, Y.P.; Pu, T.J.; Wang, L.M. THz wave detection of gap defects based on a convolutional neural network improved by a residual shrinkage network. CSEE J. Power Energy Syst. 2020, 9, 1078–1089. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Cui, H.L.; Shi, C.C.; Han, X.H.; Ma, Y.T.; Chen, J.D.; Chang, T.Y.; Wei, D.S.; Zhang, Y.M.; et al. Nondestructive evaluation of carbon fiber reinforced polymer composites using reflective terahertz imaging. Sensors 2016, 16, 875. [Google Scholar] [CrossRef]
- Zhou, C.L.; Lin, H.J.; Jia, X.L.; Yang, Z.; Zhang, G.; Xia, L.; Li, X.; Li, M.L. Impact morphology characteristics and damage evolution mechanisms in CFRP laminates for hydrogen storage cylinders. Int. J. Hydrogen Energy 2024, 77, 110–125. [Google Scholar] [CrossRef]
- Yang, S.H.; Kim, K.B.; Oh, H.G.; Kang, J.S. Non-contact detection of impact damage in CFRP composites using millimeter-wave reflection and considering carbon fiber direction. NDT E Int. 2013, 57, 45–51. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Z.H.; Zhang, T.Y.; Zhao, X.Y.; Chen, Y.; Cao, C.; Li, Y.; Xu, K.K. Effects of surface roughness on terahertz transmission spectra. Opt. Quantum Electron. 2020, 52, 240. [Google Scholar] [CrossRef]
- Kumar, V.; Cecconi, V.; Cutrona, A.; Peters, L.; Olivieri, L.; Gongora, J.S.T.; Pasquazi, A.; Peccianti, M. Terahertz microscopy through complex media. Sci. Rep. 2025, 15, 11706. [Google Scholar] [CrossRef]
- Koch, M.; Mittleman, D.M.; Ornik, J.; Castro-Camus, E. Terahertz time-domain spectroscopy. Nat. Rev. Methods Primers 2023, 3, 48. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Huang, Y.; Zhong, S.C.; Lin, T.L.; Zhong, Y.J.; Zeng, Q.M.; Nsengiyumva, W.; Yu, Y.J.; Peng, Z.K. Time of flight improved thermally grown oxide thickness measurement with terahertz spectroscopy. Front. Mech. Eng. 2022, 17, 49. [Google Scholar] [CrossRef]
- Neu, J.; Schmuttenmaer, C.A. Tutorial: An introduction to terahertz time domain spectroscopy (THz-TDS). J. Appl. Phys. 2018, 124, 231101. [Google Scholar] [CrossRef]
- Wang, Q.F.; Wang, Q.C.; Yang, Z.F.; Wu, X.; Peng, Y. Quantitative analysis of industrial solid waste based on terahertz spectroscopy. Photonics 2022, 9, 184. [Google Scholar] [CrossRef]
- Makhloughi, F. Artificial intelligence-based non-invasive bilirubin prediction for neonatal jaundice using 1D convolutional neural network. Sci. Rep. 2025, 15, 11571. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, X.H.; Zhong, Z.W. Ultra-short-term photovoltaic power prediction based on BiLSTM with wavelet decomposition and dual attention mechanism. Electronics 2025, 14, 306. [Google Scholar] [CrossRef]
- Xiong, L.; Su, L.; Zeng, S.; Li, X.; Wang, T.; Zhao, F. Generalized spatial–temporal regression graph convolutional transformer for traffic forecasting. Complex Intell. Syst. 2024, 10, 7943–7964. [Google Scholar] [CrossRef]




| Category | Parameter | Value |
|---|---|---|
| THz Scanning Parameters | Instrument Model | CCT-1800 |
| Spectral Range | 0.06 THz–4 THz | |
| Dynamic Range | 80 dB | |
| Minimum Step Size | 0.08 mm | |
| Positioning Accuracy | 2 μm | |
| CLSM Scanning Parameters | Instrument Model | OLS4100 |
| Light Source | 405 nm semiconductor laser | |
| Z-axis Travel Range | 10 mm | |
| Accuracy error | <0.5 μm | |
| Positioning Resolution | 10 nm | |
| Scanning Environment | Temperature/Humidity | 23 °C/45% |
| Feature Category | Features Name | Pearson Coefficient | Correlation Strength |
|---|---|---|---|
| Time-domain | Peak Time | 0.993 | strong positive correlation |
| Peak Value | −0.991 | strong negative correlation | |
| Frequency-domain | Peak Intensities | −0.986 | strong negative correlation |
| Integral Areas | −0.979 | strong negative correlation | |
| Absorbance | Peak Intensity | 0.994 | strong positive correlation |
| Baseline absorbance | 0.942 | strong positive correlation |
| Sampling Interval | MNND | ME | MV |
|---|---|---|---|
| 1 | 0.548772 | 1.8007367 | 34,376.13 |
| 2 | 0.831841 | 1.8162872 | 34,383.62 |
| 3 | 1.043408 | 1.8572339 | 34,877.77 |
| 4 | 1.313768 | 1.8755792 | 34,795.24 |
| 5 | 1.594213 | 1.8863185 | 35,572.18 |
| Hyperparameter | Applicable Scope | Value | Remarks |
|---|---|---|---|
| Optimizer | FEN-CNN-BiLSTM | AdamW [30] | Optimization Algorithm of the Model |
| Initial Learning Rate | FEN-CNN-BiLSTM | 0.001 | Learning Rate |
| Epochs | FEN-CNN-BiLSTM | 500 | Maximum Training Epochs |
| Batch Size | FEN-CNN-BiLSTM | 64 | Number of Samples per Training Batch |
| Loss Function | FEN-CNN-BiLSTM | SmoothL1Loss | Function for Calculating Model Prediction Error |
| Activation Function | FEN-CNN-BiLSTM | GELU | Activation Function |
| Hidden Layer Dimension | FEN Layer | 32 | Feature Dimension of FEN Hidden Layer |
| Encoder Kernel Sizes | FEN Layer | [3,5] | List of kernel sizes for the two parallel convolutional paths |
| Attention Reduction Factor | FEN Layer | 4 | Convolutional Kernel Size |
| Decoder Kernel Size | FEN Layer | 3 | Convolutional Kernel Size |
| Number of Convolutional Layer Filters | CNN Layer | 32/6 | The first CNN layer uses 32 filters, the second CNN layer uses 6 filters. |
| Convolutional Kernel Size | CNN Layer | 3 | Convolutional Kernel Size |
| Unidirectional Hidden Layer Dimension | BiLSTM | 32 | Unidirectional Hidden State Dimension |
| Model | MSE | RMSE | MAE | MAPE% | R2 | RSD% | FLOPs | Params |
|---|---|---|---|---|---|---|---|---|
| Decision Tree | 0.021558 | 0.14683 | 0.11793 | 4.4308 | 0.8667 | 4.8291 | ||
| RNN | 0.018962 | 0.1377 | 0.11606 | 4.3592 | 0.8827 | 5.1373 | 21.776K | 3.265K |
| MLP | 0.019198 | 0.13856 | 0.11774 | 4.4281 | 0.8813 | 4.8291 | 17.280K | 17.537K |
| CNN | 0.017421 | 0.13199 | 0.10755 | 4.0668 | 0.8923 | 4.7381 | 25.856K | 8.039K |
| CNN-transformer | 0.013398 | 0.11575 | 0.09524 | 3.6029 | 0.9131 | 3.8492 | 80.704K | 13.633K |
| CNN-RESNET | 0.013575 | 0.11651 | 0.0946 | 3.6987 | 0.916 | 3.6585 | 310.016K | 51.009K |
| CNN-BiLSTM | 0.012907 | 0.11361 | 0.09141 | 3.3288 | 0.9202 | 4.2886 | 194.664K | 32.919K |
| FEN-CNN-BiLSTM | 0.00746 | 0.08637 | 0.06122 | 2.2611 | 0.9539 | 3.2153 | 266.416K | 43.809K |
| CNN-BilLSTM-Attention | 0.01174 | 0.10835 | 0.08162 | 3.0567 | 0.9274 | 4.0038 | 238.584K | 34.892K |
| CNN-BilLSTM-Transformer | 0.008541 | 0.09242 | 0.07059 | 2.6351 | 0.9472 | 3.4492 | 247.216K | 41.875K |
| ResNet-CNN-BiLSTM | 0.010873 | 0.10427 | 0.08149 | 3.0257 | 0.9328 | 3.8909 | 364.256K | 104.289K |
| ECA-CNN-BiLSTM | 0.011787 | 0.10857 | 0.08518 | 3.1733 | 0.9271 | 4.0491 | 237.564K | 38.634K |
| SelfAttention-CNN-BiLSTM | 0.011597 | 0.10721 | 0.08278 | 3.1313 | 0.9226 | 4.0226 | 242.254K | 37.757K |
| Model | MSE | RMSE | MAE | MAPE (%) | R2 | RSD% |
|---|---|---|---|---|---|---|
| FEN-CNN-BiLSTM | 0.010365 | 0.10181 | 0.07568 | 2.82620 | 0.93879 | 3.8171 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yin, H.; Lei, X.; Xing, X.; Zhong, M.; Yang, R.; Liu, Z.; Li, S.; Mo, Z. An Improved CNN-Based Algorithm for Quantitative Prediction of Impact Damage Depth in Civil Aircraft Composites via Multi-Domain Terahertz Spectroscopy. Electronics 2025, 14, 2412. https://doi.org/10.3390/electronics14122412
Zhang H, Yin H, Lei X, Xing X, Zhong M, Yang R, Liu Z, Li S, Mo Z. An Improved CNN-Based Algorithm for Quantitative Prediction of Impact Damage Depth in Civil Aircraft Composites via Multi-Domain Terahertz Spectroscopy. Electronics. 2025; 14(12):2412. https://doi.org/10.3390/electronics14122412
Chicago/Turabian StyleZhang, Huazhong, Hongbiao Yin, Xia Lei, Xiaoqing Xing, Mian Zhong, Rong Yang, Zeguo Liu, Shouqing Li, and Zhenguang Mo. 2025. "An Improved CNN-Based Algorithm for Quantitative Prediction of Impact Damage Depth in Civil Aircraft Composites via Multi-Domain Terahertz Spectroscopy" Electronics 14, no. 12: 2412. https://doi.org/10.3390/electronics14122412
APA StyleZhang, H., Yin, H., Lei, X., Xing, X., Zhong, M., Yang, R., Liu, Z., Li, S., & Mo, Z. (2025). An Improved CNN-Based Algorithm for Quantitative Prediction of Impact Damage Depth in Civil Aircraft Composites via Multi-Domain Terahertz Spectroscopy. Electronics, 14(12), 2412. https://doi.org/10.3390/electronics14122412






