Hardware Accelerator for Approximation-Based Softmax and Layer Normalization in Transformers
Abstract
1. Introduction
- We present a unified hardware architecture that integrates Softmax and LayerNorm operations into a single computational path within Transformer models. By analyzing their shared computational flows, the proposed design improves overall hardware utilization.
- PLA is applied to the exponential function in Softmax, while Newton–Raphson iteration is used for the square root computation in LayerNorm. The approximation strength is adjustable via parameters h and N, enabling fine-grained control over the trade-off between accuracy and speed.
- The proposed accelerator was implemented on a Xilinx VU37P FPGA and applied to BERT and GPT-2 models for practical evaluation. It achieved speedups of up to 7.6× for Softmax and 2.0× for LayerNorm, with Softmax delivering up to 4.6× faster execution compared to GPU baselines.
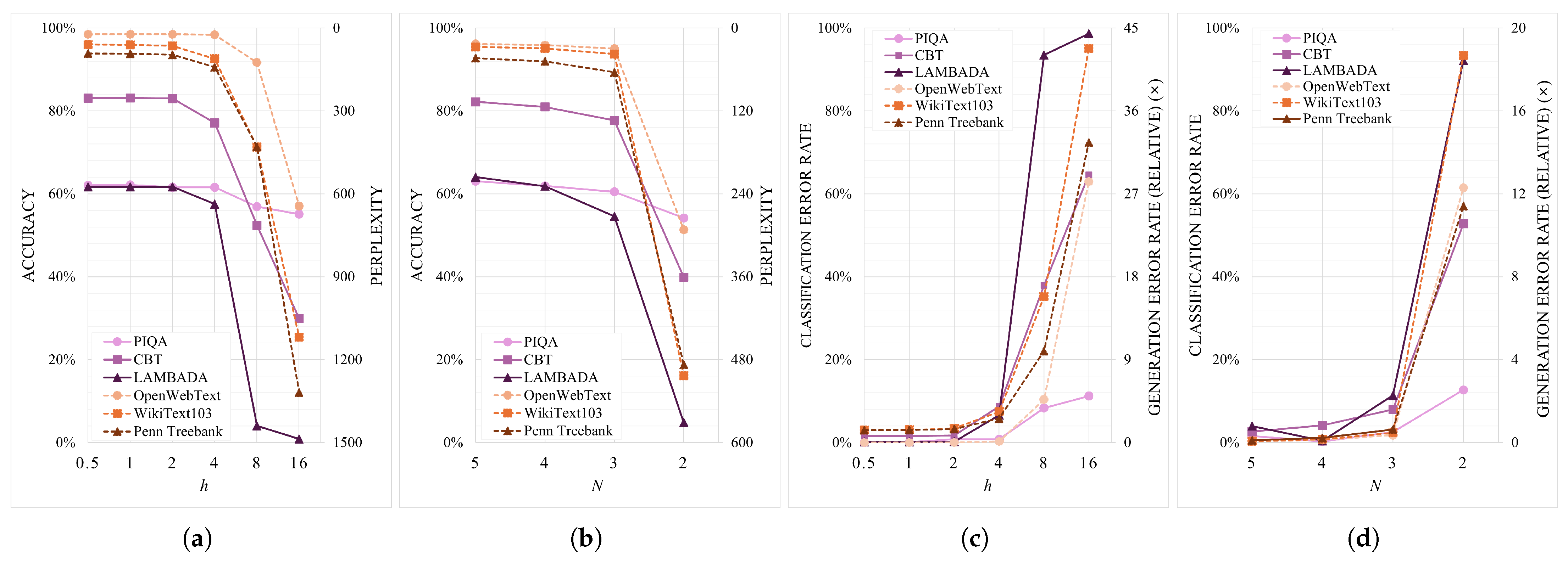
- To assess the impact on model accuracy, we performed extensive evaluation across eleven benchmark datasets spanning classification and generation tasks. When and , classification performance was preserved with less than 1% degradation. In contrast, generation tasks were more sensitive to approximation, particularly in Softmax, necessitating more conservative parameter choices.
2. Background
2.1. Transformer Overview
2.2. Non-Linear Functions in Transformer
2.2.1. Softmax
2.2.2. Layer Normalization
2.3. Latency Breakdown Analysis
3. Related Works
3.1. Normalization Acceleration in Transformers
3.2. Softmax Approximation Techniques
3.3. Joint Optimization of Softmax and LayerNorm
4. Proposed Methods
4.1. Piecewise Linear Approximation
4.2. Newton–Raphson Method
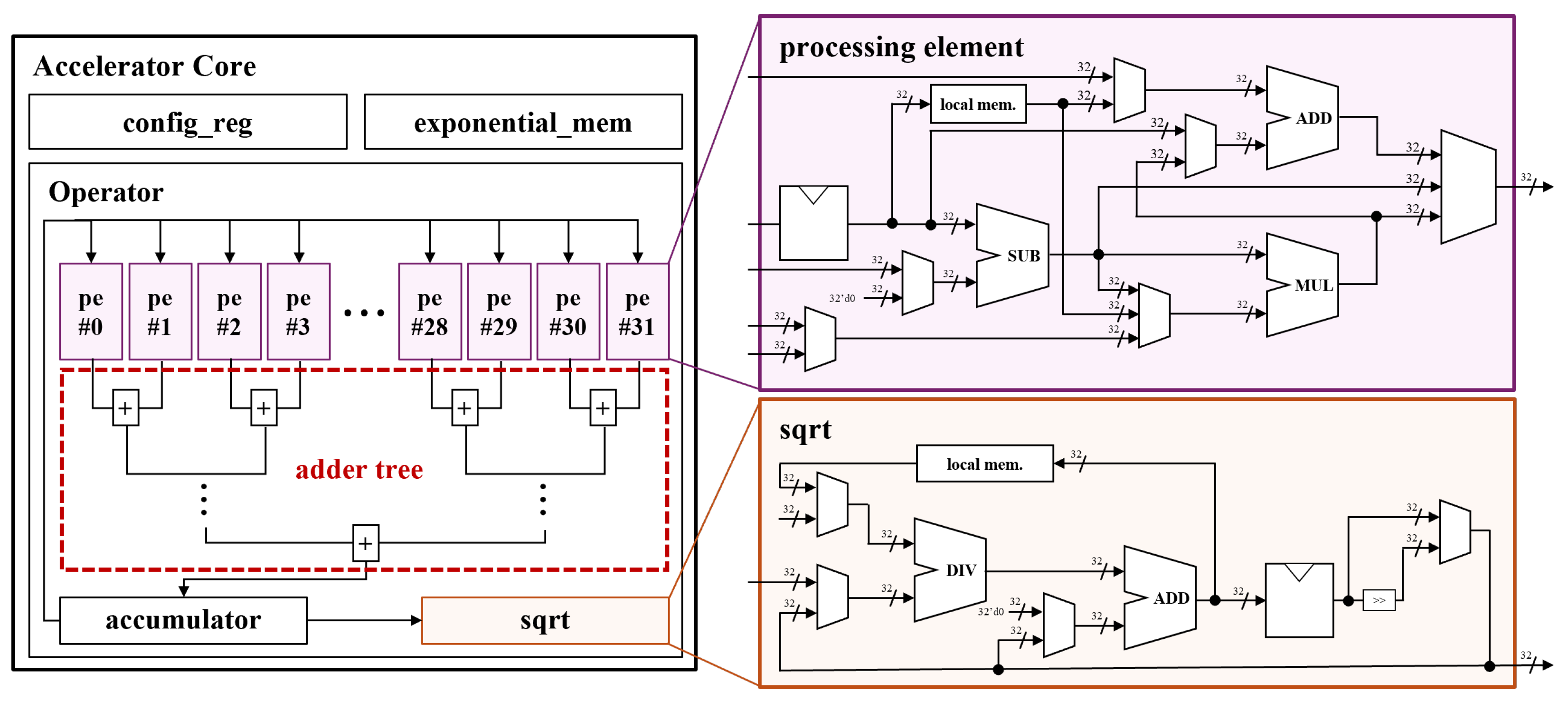
5. Hardware Implementation
5.1. Processing Element (PE)
- LayerNorm: the FSM performs mean and variance computation (LN_MEAN, LN_VAR), computes the standard deviation (LN_STD), normalizes the input (LN_NORM), and applies the learnable scale and bias (LN_WGT, LN_BIAS).
- Softmax: the FSM applies the exponential function (SM_EXP), computes the normalization term via division (SM_DIV), and outputs the result (SM_RSLT).
5.2. Accumulator
5.3. Square Root and Division
- LayerNorm: The input to the square root is generally less than 2. The LUT stores reciprocals of values in the range using uniform intervals or linear interpolation.
- Softmax: The normalization term can be large, ranging from 1 to , depending on sequence length and input scale. A separate LUT covering is used, with log-uniform spacing to maintain precision across a wide dynamic range.
6. Experiments and Results
6.1. Experimental Setup
6.2. Accuracy and Perplexity
6.3. Execution Time
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| BatchNorm | Batch Normalization |
| BN | Batch Normalization |
| BERT | Bidirectional Encoder Representations from Transformers |
| CNN | Convolutional Neural Network |
| CPU | Central Processing Unit |
| DSP | Digital Signal Processor (or Digital Signal Processing slice) |
| FF | Flip-Flop |
| FFN | Feed-Forward Network |
| FPGA | Field-Programmable Gate Array |
| FP32 | 32-bit Floating Point |
| GPT | Generative Pre-trained Transformers |
| GPU | Graphics Processing Unit |
| GELU | Gaussian Error Linear Unit |
| INT8 | 8-bit Integer |
| LayerNorm | Layer Normalization |
| LUT | Look-Up Table |
| LN | Layer Normalization |
| LAMBADA | LAnguage Modeling Benchmark with Analysis of Discourse Across Discourse |
| LUT | Look-Up Table |
| MHA | Multi-Head Attention |
| NLP | Natural Language Processing |
| PE | Processing Element |
| PLA | Piecewise Linear Approximation |
| Q | Query |
| K | Key |
| V | Value |
| RNN | Recurrent Neural Network |
| RTE | Recognizing Textual Entailment |
| SDPA | Scaled Dot-Product Attention |
| SM | Softmax |
| SST-2 | Stanford Sentiment Treebank 2 |
| TEA-S | Transformer Exponential Approximation-Softmax |
| VU37P | Xilinx Virtex UltraScale+ VU37P FPGA |
| “intN” | N-bit Integer (e.g., int8, int16, etc.) |
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar] [CrossRef]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Khan, A.; Rauf, Z.; Sohail, A.; Khan, A.R.; Asif, H.; Asif, A.; Farooq, U. A survey of the vision transformers and their CNN-transformer based variants. Artif. Intell. Rev. 2023, 56, 2917–2970. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Wu, Y.; Wang, X.; Yang, X.; Li, S. Learning adaptive and view-invariant vision transformer for real-time UAV tracking. In Proceedings of the 41st International Conference on Machine Learning, ICML’24, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Anwar, A.; Khalifa, Y.; Coyle, J.L.; Sejdic, E. Transformers in biosignal analysis: A review. Inf. Fusion 2025, 114, 102697. [Google Scholar] [CrossRef]
- Vafaei, E.; Hosseini, M. Transformers in EEG analysis: A review of architectures and applications in motor imagery, seizure, and emotion classification. Sensors 2025, 25, 1293. [Google Scholar] [CrossRef]
- Kachris, C. A survey on hardware accelerators for large language models. Appl. Sci. 2025, 15, 586. [Google Scholar] [CrossRef]
- Du, J.; Jiang, J.; Zheng, J.; Zhang, H.; Huang, D.; Lu, Y. Improving computation and memory efficiency for real-world transformer inference on GPUs. ACM Trans. Archit. Code Optim. 2023, 20, 46. [Google Scholar] [CrossRef]
- Chen, Q. Research on inference and training acceleration of large language model. In Proceedings of the 2024 7th International Conference on Computer Information Science and Artificial Intelligence, CISAI ’24, Shaoxing, China, 13–15 September 2024; pp. 303–307. [Google Scholar] [CrossRef]
- Wu, J.; Song, M.; Zhao, J.; Gao, Y.; Li, J.; So, H.K.H. TATAA: Programmable mixed-precision transformer acceleration with a transformable arithmetic architecture. ACM Trans. Reconfig. Technol. Syst. 2025, 18, 14. [Google Scholar] [CrossRef]
- Park, J.; Shin, J.; Kim, R.; An, S.; Lee, S.; Kim, J.; Oh, J.; Jeong, Y.; Kim, S.; Jeong, Y.R.; et al. Accelerating strawberry ripeness classification using a convolution-based feature extractor along with an edge AI processor. Electronics 2024, 13, 344. [Google Scholar] [CrossRef]
- Jeong, Y.; Park, J.; Kim, R.; Lee, S.E. SEAM: A synergetic energy-efficient approximate multiplier for application demanding substantial computational resources. Integration 2025, 101, 102337. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Li, X.; Yang, H.; Liu, Y. ULSeq-TA: Ultra-long sequence attention fusion transformer accelerator supporting grouped sparse softmax and dual-path sparse layernorm. Trans. Comp.-Aided Des. Integ. Cir. Sys. 2024, 43, 892–905. [Google Scholar] [CrossRef]
- Sadeghi, M.E.; Fayyazi, A.; Azizi, S.; Pedram, M. PEANO-ViT: Power-efficient approximations of non-linearities in vision transformers. In Proceedings of the 29th ACM/IEEE International Symposium on Low Power Electronics and Design, ISLPED ’24, Newport Beach, CA, USA, 5–7 August 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Bao, Z.; Li, H.; Zhang, W. A vision transformer inference accelerator for KR260. In Proceedings of the 2024 8th International Conference on Computer Science and Artificial Intelligence, CSAI ’24, Beijing China, 6–8 December 2024; pp. 245–251. [Google Scholar] [CrossRef]
- Dong, Q.; Xie, X.; Wang, Z. SWAT: An efficient swin transformer accelerator based on FPGA. In Proceedings of the 2024 29th Asia and South Pacific Design Automation Conference (ASP-DAC), Incheon, Republic of Korea, 22–25 January 2024; pp. 515–520. [Google Scholar] [CrossRef]
- Amin, H.; Curtis, K.; Hayes-Gill, B. Piecewise linear approximation applied to nonlinear function of a neural network. IEE Proc.-Circuits Devices Syst. 1997, 144, 313–317. [Google Scholar] [CrossRef]
- Geng, X.; Lin, J.; Zhao, B.; Kong, A.; Aly, M.M.S.; Chandrasekhar, V. Hardware-aware softmax approximation for deep neural networks. In Computer Vision—ACCV 2018, Proceedings of the 14th Asian Conference on Computer Vision, Perth, Australia, 6–8 December 2018; Jawahar, C., Li, H., Mori, G., Schindler, K., Eds.; Springer: Cham, Switzerland, 2019; pp. 107–122. [Google Scholar]
- Soydaner, D. Attention mechanism in neural networks: Where it comes and where it goes. Neural Comput. Appl. 2022, 34, 13371–13385. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Xiong, R.; Yang, Y.; He, D.; Zheng, K.; Zheng, S.; Xing, C.; Zhang, H.; Lan, Y.; Wang, L.; Liu, T.Y. On layer normalization in the transformer architecture. arXiv 2020, arXiv:2002.04745. [Google Scholar] [CrossRef]
- Tay, Y.; Dehghani, M.; Bahri, D.; Metzler, D. Efficient transformers: A survey. ACM Comput. Surv. 2022, 55, 109. [Google Scholar] [CrossRef]
- Pearce, T.; Brintrup, A.; Zhu, J. Understanding softmax confidence and uncertainty. arXiv 2021, arXiv:2106.04972. [Google Scholar] [CrossRef]
- Holm, A.N.; Wright, D.; Augenstein, I. Revisiting softmax for uncertainty approximation in text classification. Information 2023, 14, 420. [Google Scholar] [CrossRef]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Guo, J.; Chen, X.; Tang, Y.; Wang, Y. SLAB: Efficient transformers with simplified linear attention and progressive re-parameterized batch normalization. In Proceedings of the 41st International Conference on Machine Learning, ICML’24, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Stevens, J.R.; Venkatesan, R.; Dai, S.; Khailany, B.; Raghunathan, A. Softermax: Hardware/software co-design of an efficient softmax for transformers. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 469–474. [Google Scholar] [CrossRef]
- Zhu, D.; Lu, S.; Wang, M.; Lin, J.; Wang, Z. Efficient precision-adjustable architecture for softmax function in deep learning. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3382–3386. [Google Scholar] [CrossRef]
- Mei, Z.; Dong, H.; Wang, Y.; Pan, H. TEA-S: A tiny and efficient architecture for PLAC-based softmax in transformers. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3594–3598. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, W.; Lombardi, F. Design and implementation of an approximate softmax layer for deep neural networks. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, S.; Sun, W.; Sun, P.; Liu, Y. SOLE: Hardware-software co-design of softmax and layernorm for efficient transformer inference. In Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, CA, USA, 28 October–2 November 2023; pp. 1–9. [Google Scholar] [CrossRef]
- Cha, M.; Lee, K.; Nguyen, X.T.; Lee, H.J. A low-latency and scalable vector engine with operation fusion for transformers. In Proceedings of the 2024 IEEE 6th International Conference on AI Circuits and Systems (AICAS), Abu Dhabi, United Arab Emirates, 22–25 April 2024; pp. 307–311. [Google Scholar] [CrossRef]
- Lu, S.; Wang, M.; Liang, S.; Lin, J.; Wang, Z. Hardware accelerator for multi-head attention and position-wise feed-forward in the transformer. In Proceedings of the 2020 IEEE 33rd International System-on-Chip Conference (SOCC), Las Vegas, NV, USA, 8–11 September 2020; pp. 84–89. [Google Scholar] [CrossRef]
- Thorp, J.; Lewine, R. Exponential approximation with piecewise linear error criteria. J. Frankl. Inst. 1968, 286, 308–320. [Google Scholar] [CrossRef]
- Korzilius, S.; Schoenmakers, B. Divisions and square roots with tight error analysis from newton–raphson iteration in secure fixed-point arithmetic. Cryptography 2023, 7, 43. [Google Scholar] [CrossRef]
- Galántai, A. The theory of Newton’s method. J. Comput. Appl. Math. 2000, 124, 25–44. [Google Scholar] [CrossRef]
- Wang, A.; Singh, A.; Michael, J.; Hill, F.; Levy, O.; Bowman, S. GLUE: A multi-task benchmark and analysis platform for natural language understanding. In Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP; Linzen, T., Chrupała, G., Alishahi, A., Eds.; Association for Computational Linguistics: Brussels, Belgium, 2018; pp. 353–355. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level convolutional networks for text classification. In Proceedings of the 29th International Conference on Neural Information Processing Systems, NIPS’15, Montreal, QC, Canada, 7–12 December 2015; Volume 1, pp. 649–657. [Google Scholar]
- Årup Nielsen, F. A new ANEW: Evaluation of a word list for sentiment analysis in microblogs. arXiv 2011, arXiv:1103.2903. [Google Scholar] [CrossRef]
- Merity, S.; Xiong, C.; Bradbury, J.; Socher, R. Pointer sentinel mixture models. arXiv 2016, arXiv:1609.07843. [Google Scholar] [CrossRef]
- Marcus, M.P.; Santorini, B.; Marcinkiewicz, M.A. Building a large annotated corpus of English: The Penn Treebank. Comput. Linguist. 1993, 19, 313–330. [Google Scholar]
- Bisk, Y.; Zellers, R.; Bras, R.L.; Gao, J.; Choi, Y. PIQA: Reasoning about physical commonsense in natural language. arXiv 2019, arXiv:1911.11641. [Google Scholar] [CrossRef]
- Hill, F.; Bordes, A.; Chopra, S.; Weston, J. The goldilocks principle: Reading children’s books with explicit memory representations. arXiv 2016, arXiv:1511.02301. [Google Scholar] [CrossRef]
- Paperno, D.; Kruszewski, G.; Lazaridou, A.; Pham, N.Q.; Bernardi, R.; Pezzelle, S.; Baroni, M.; Boleda, G.; Fernández, R. The LAMBADA dataset: Word prediction requiring a broad discourse context. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Erk, K., Smith, N.A., Eds.; Association for Computational Linguistics: Berlin, Germany, 2016; pp. 1525–1534. [Google Scholar] [CrossRef]

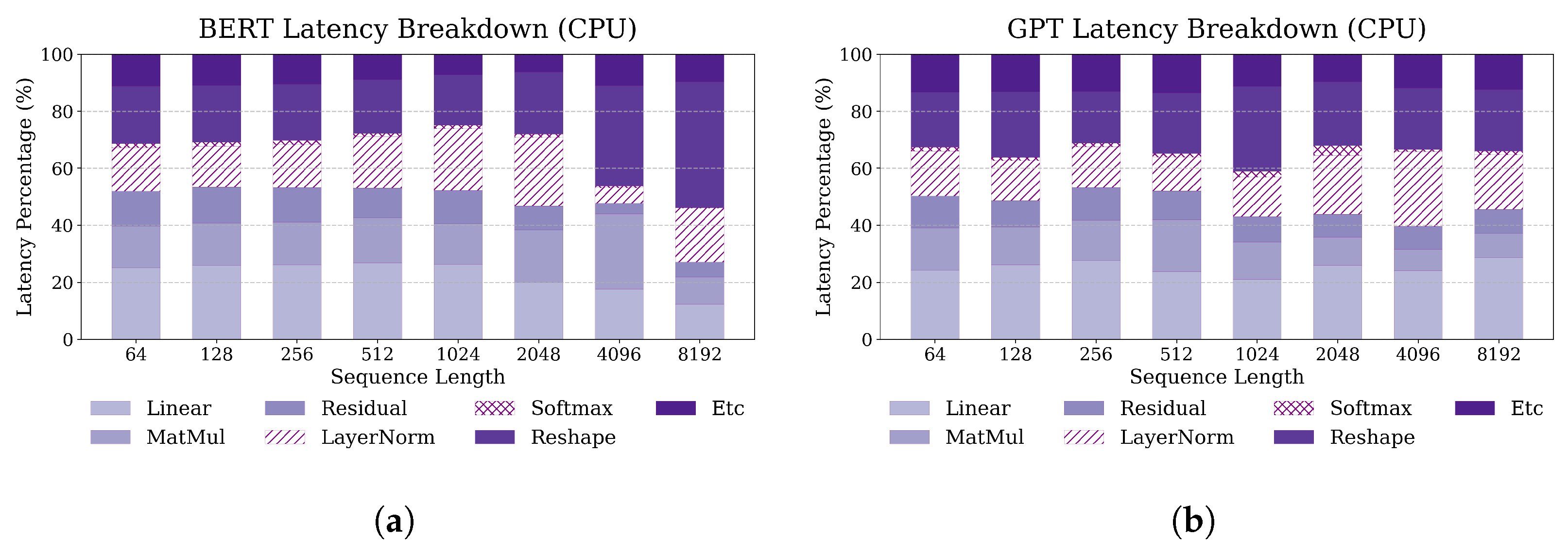
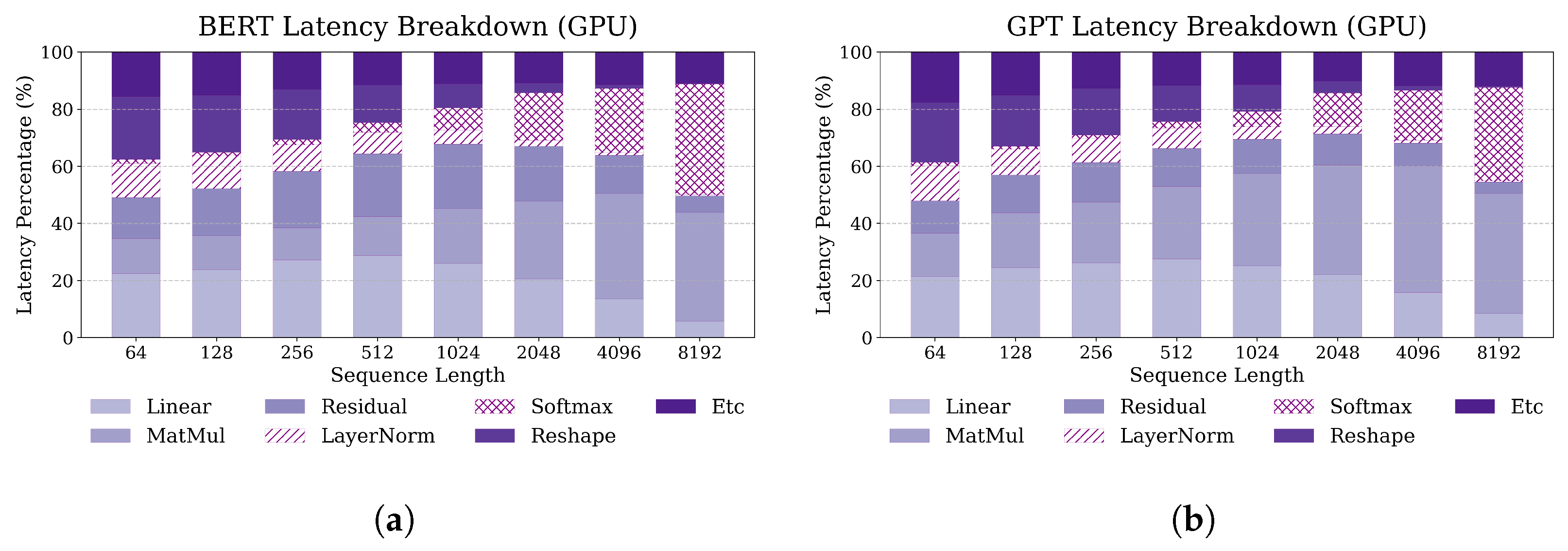
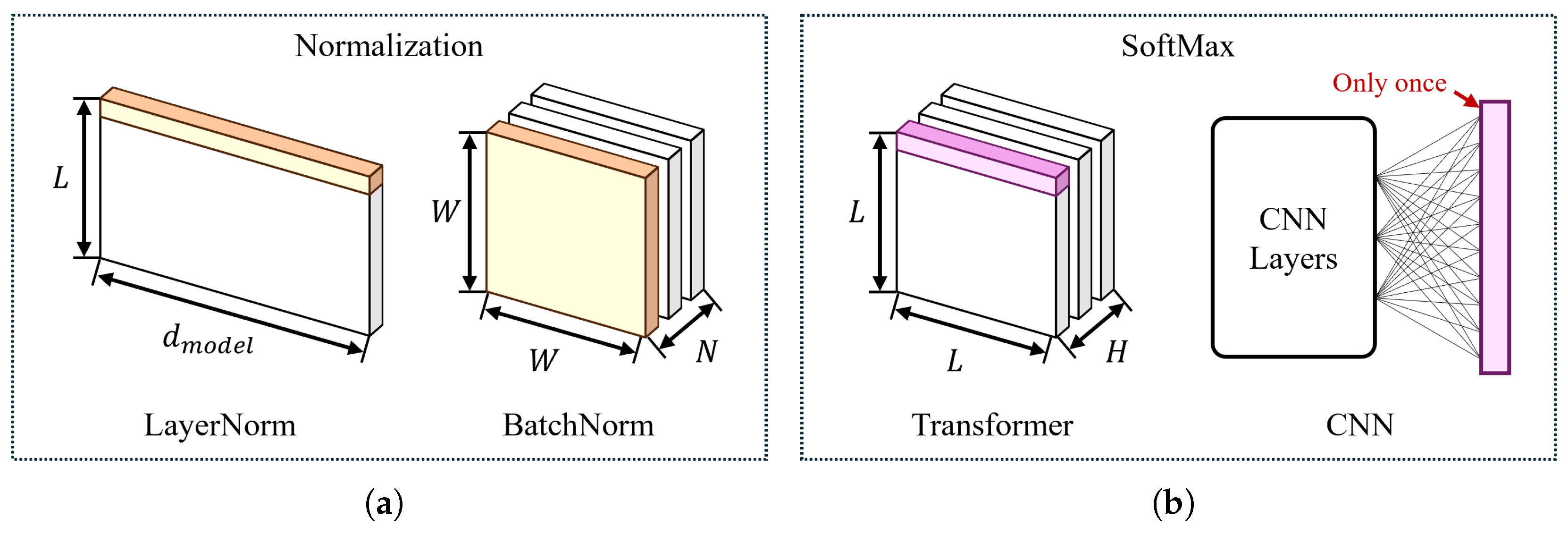
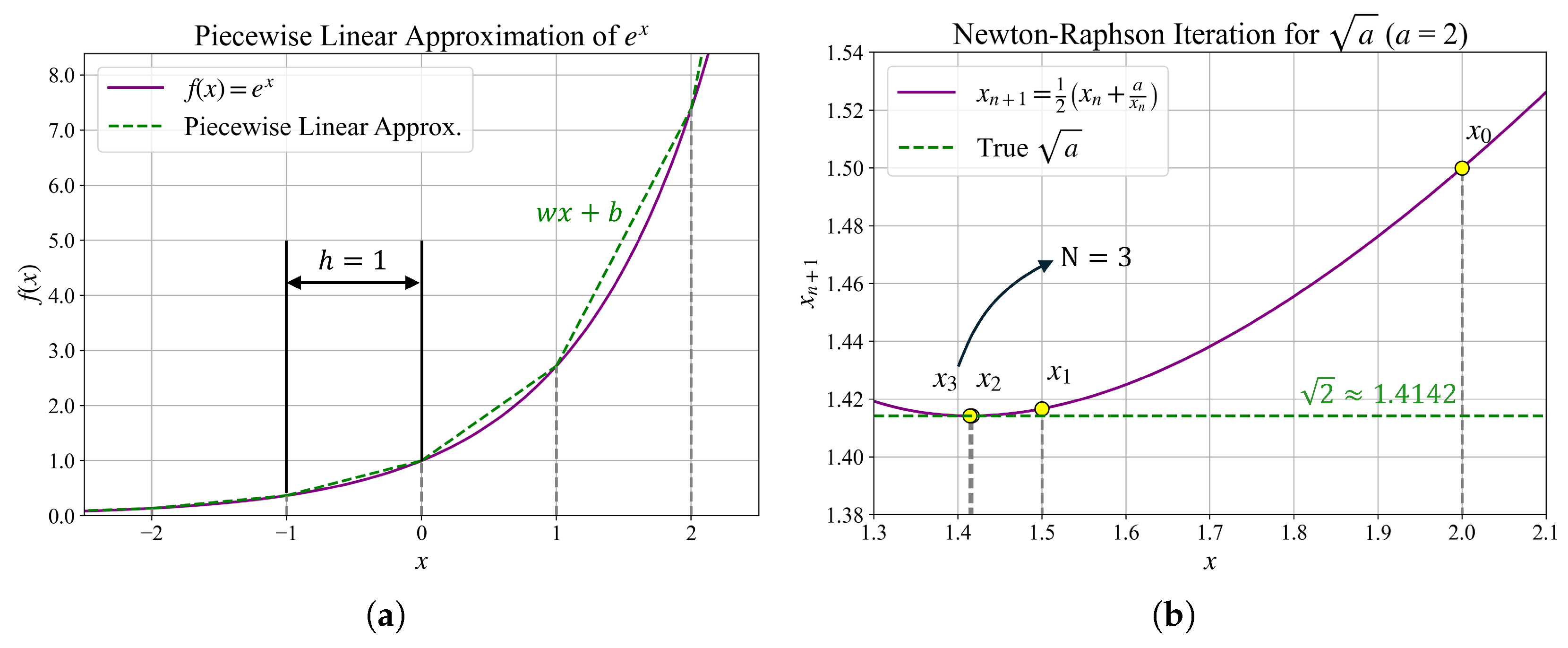


| Paper | Target | Technique | Precision | HW-Int. | Config. |
|---|---|---|---|---|---|
| Dong et al. [17] | LN | Replace LN with BN for inference | Fixed-point | No | No |
| Guo et al. [27] | LN | Gradual LN-to-BN replacement during training | Mixed (BN + LN) | No | Yes |
| Stevens et al. [28] | SM | Use base-2 exp and online normalization | Fixed-point | No | No |
| Zhu et al. [29] | SM | Simplified log-sum-exp with tunable parameter | Fixed-point | No | Yes |
| Mei et al. [30] | SM | PLAC-based approximation in one-pass pipeline | INT8 | No | No |
| Gao et al. [31] | SM | Use LUT and Taylor series for exp/log | Fixed-point | No | No |
| Wang et al. [32] | SM + LN | Log2-based SM and integer stats LN | INT4–INT8 | No | No |
| Lu et al. [34] | SM + LN | Log-sum-exp SM and parallel LN accumulation | Fixed-point | No | No |
| Cha et al. [33] | SM + LN | Parallel mean/var and loop fusion optimization | FP32 Accumulator | Yes | No |
| State | Operation Description |
|---|---|
| LayerNorm | |
| LN_MEAN | Compute mean of input vector |
| LN_VAR | Compute variance using squared deviation |
| LN_STD | Apply square root to obtain standard deviation |
| LN_NORM | Normalize vector by subtracting mean and dividing by std |
| LN_WGT | Multiply normalized values by scale (weight) |
| LN_BIAS | Add learned bias term |
| Softmax | |
| SM_EXP | Apply exponential function to each element |
| SM_DIV | Divide each exponential by the total exponential sum |
| SM_RSLT | Output final Softmax result |
| Paper | Hardware Platform | LUT | FF | DSP |
|---|---|---|---|---|
| Cha et al. [33] | Xilinx ZCU106 FPGA | 129,772 | 117,365 | 1033 |
| Lu et al. [34] | Xilinx XCVU13P FPGA | 32,741 | 37,948 | 129 |
| Ours | Xilinx VCU128 FPGA | 22,654 | 4345 | 128 |
| Wang et al. [32] | ASIC (simulated) | N/A | N/A | N/A |
| Platform | BERT | GPT-2 | ||
|---|---|---|---|---|
| Softmax | LayerNorm | Softmax | LayerNorm | |
| CPU | 272.30 | 154.10 | 249.05 | 130.30 |
| GPU | 160.75 | 117.35 | 150.85 | 103.15 |
| Ours (FPGA) | 69.10 | 109.45 | 32.75 | 66.70 |
| Platform | BERT | GPT-2 | ||
|---|---|---|---|---|
| Softmax | LayerNorm | Softmax | LayerNorm | |
| CPU | 1.000× | 1.000× | 1.000× | 1.000× |
| GPU | 1.694× | 1.313× | 1.651× | 1.263× |
| Ours (FPGA) | 3.940× | 1.408× | 7.605× | 1.954× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, R.; Lee, D.; Kim, J.; Park, J.; Lee, S.E. Hardware Accelerator for Approximation-Based Softmax and Layer Normalization in Transformers. Electronics 2025, 14, 2337. https://doi.org/10.3390/electronics14122337
Kim R, Lee D, Kim J, Park J, Lee SE. Hardware Accelerator for Approximation-Based Softmax and Layer Normalization in Transformers. Electronics. 2025; 14(12):2337. https://doi.org/10.3390/electronics14122337
Chicago/Turabian StyleKim, Raehyeong, Dayoung Lee, Jinyeol Kim, Joungmin Park, and Seung Eun Lee. 2025. "Hardware Accelerator for Approximation-Based Softmax and Layer Normalization in Transformers" Electronics 14, no. 12: 2337. https://doi.org/10.3390/electronics14122337
APA StyleKim, R., Lee, D., Kim, J., Park, J., & Lee, S. E. (2025). Hardware Accelerator for Approximation-Based Softmax and Layer Normalization in Transformers. Electronics, 14(12), 2337. https://doi.org/10.3390/electronics14122337









