Abstract
Satellite Internet is the key to integrated air–space–ground communication, while the design of waveforms with high spectrum efficiency is an intrinsic requirement for high-speed data transmission in satellite Internet. Time-domain synchronous orthogonal frequency division multiplexing (TDS-OFDM) technology can significantly improve spectrum utilization efficiency by using PN sequences instead of traditional CP cyclic prefixes. However, it also leads to time-domain aliasing between PN sequences and data symbols, posing a serious challenge to channel estimation. To solve this problem, a compressive sensing-based coding iterative channel estimation method for the TDS-OFDM system is proposed in this paper. This method innovatively combines compressive sensing channel estimation technology with the Reed–Solomon low-density parity-check cascade coding (RS-LDPC) scheme, and achieves performance improvements as follows: (1) Construct the iterative optimization mechanism for the compressive sensing algorithm and equalization feedback loop. (2) RS-LDPC cascaded coding is employed to enhance the anti-interference and error correction capability of system. (3) Design the recoding link of error-corrected data to improve the accuracy of sensing matrix. The simulation results demonstrate that compared with conventional methods, the proposed method can obviously converge on the mean squared errors (MSEs) of channel estimation and significantly reduce the bit error rate (BER) of the system.
1. Introduction
Satellite platforms, which feature wide coverage and little impact from ground, serve as the key nodes of integrated air–space–ground communication network in the future. With the rapid development of communication technologies in recent years, ground 5G network is integrated with satellite communication network to form a seamlessly connected and fully covered space–ground communication network. This is an important development direction for new-generation communication systems [1,2,3,4,5]. TDS-OFDM is a multi-carrier communication system that can solve the problems of multipath fading and high-bit-rate transmission in wireless channels [6]. Different from conventional OFDM systems, the TDS-OFDM system cancels pilot signals and uses all subcarriers to transmit data and improve spectrum efficiency [7]. Additionally, it adopts a pseudorandom PN sequence as the guard interval and utilizes its good autocorrelation to realize channel estimation and synchronization [8]. However, after time-domain signals pass through a multipath channel, data smearing occurs, which causes the aliasing between the PN sequence and its adjacent valid data. It affects the accuracy of channel estimation and restricts the extensive applications of the TDS-OFDM system [9].
The key issue in TDS-OFDM channel estimation lies in the processing of the PN sequence as the guard interval. A large number of domestic studies have been conducted and mainly focused on the design and extraction of interference-free regions in the PN sequence as well as the separation and reconstruction of PN sequence and transmission data. Since aliasing interference usually occurs at the head and tail of the PN sequence and does not cover the entire sequence, it is an effective technique to estimate the channel using the non-aliasing part of the PN sequence. Ref. [10] proposed a sparse channel estimation technique based on forward-backtracking orthogonal matching pursuit (OMP), which estimates the channel impulse response using the PN sequence in the inter-symbol interference-free (ISI-free) regions to reduce channel interference. However, when the delay spread of the channel impulse response is approximated using the duration of the guard interval, the number of samples in the ISI-free regions was insufficient, leading to incomplete channel information estimation. Ref. [11] introduced a dual PN sequence method in which the first PN sequence was used as the guard interval, and the part of the second PN sequence that was not interfered by the data blocks was used for channel estimation to reduce the complexity of eliminating inter-block interference (IBI) and to improve channel estimation efficiency. However, this was carried out at the expense of some spectrum resources to some extent. To solve the above problems and improve the spectrum efficiency of the system, researchers turned their attention to the separation and reconstruction of the PN sequence and transmission data. Ref. [12] proposed a compressive sensing-based iterative channel estimation method in which a sensing matrix was constructed using a PN sequence and data affected by ISI; high-accuracy channel estimation was realized by the iterative optimization of compressive sensing channel estimation. Ref. [13] combined the least squares estimation (LS) method and RefineNet neural network to design a channel estimator. This estimator can accurately learn the characteristics of time-varying channels, and its estimation accuracy is significantly better than traditional LS estimation. However, the training data for this algorithm are based on the specific basis expansion model (BEM), differing from the actual channel and consuming many resources.
The compressive sensing reconstruction algorithm is used to solve the L1 norm minimum solution, which can be mainly divided into three categories based on the type of reconstruction:
Convex optimization algorithm or optimal approximation algorithm: Converting non-convex problems into convex problems to find the approximation of the signal, such as the Basic Pursit (BP) algorithm. Bayesian algorithm: First, determine the sparse prior distribution of the signal, and reconstruct the signal that satisfies this partition from the randomly observed data information using Bayesian probability distribution criteria, such as Bayesian Compressed Sensing (BCS) and Variational Bayesian Compressed Sensing (VBCS). Among the two algorithms mentioned above, convex optimization method and Bayesian algorithm require complex matrix operations and have strong dependence on parameters, resulting in high hardware resource consumption. To avoid such problems, this article uses the greedy iterative algorithm, iteratively finding the support set of sparse vectors, i.e., directly selecting the most relevant atoms in the perception matrix to form new samples, and using constrained support least squares estimation to reconstruct the signal. Examples include Matching Pursuit (MP), Orthogonal Matching Pursuit (OMP), Compressed Sampling Matching Pursuit (CoSaMP), etc. Among them, the MP algorithm converges slowly and may repeatedly select the same atoms. OMP is sensitive to noise and requires precise knowledge of sparsity. The CoSaMP algorithm has strong noise resistance and can adapt to sparsity. Therefore, in the case of accurately reconstructing the original sparse signal while balancing computational complexity and noise environment, the CoSaMP algorithm in greedy iterative algorithms is a good choice.
To sum up, the channel estimation method based on the interference-free region in the PN sequence is limited by the short PN data length, which easily leads to incomplete channel information estimation. The channel estimation method based on the separation and reconstruction of a complete PN sequence has a better channel estimation capability. However, this method brings noise interference during data reconstruction in this method, which increases the errors in channel estimation. To solve the above problems, this paper proposes a cyclic compressive sensing channel estimation algorithm based on channel coding. It combines cascaded channel coding technology with compressive sensing channel estimation to realize channel estimation through the iterative optimization of compressive sensing and an equalization feedback loop. After cascaded channel coding is employed to correct the data errors, compressive sensing is iterated again to further improve the accuracy of channel estimation. This paper attempts to make the following contributions:
- There is a problem of insufficient samples when using PN sequences without IBI regions for wireless sparse channel reconstruction. This article utilizes the CoSaMP algorithm in greedy algorithms to construct an equilibrium feedback loop, achieving sparse channel iterative estimation using all PN sequences. It solves the limitation of small non-IBI areas in PN sequences, and improves channel estimation accuracy in multipath fading environments.
- In this paper, RS-LDPC cascaded coding is introduced, and the accuracy of decoded data is improved through the correction of received data errors. Moreover, the accuracy of the sensing matrix is effectively improved by designing the recoding link of error-corrected data, and the accuracy of channel estimation in a multipath fading environment is improved through repeated iterative optimizations. Meanwhile, RS-LDPC cascaded coding enhances the anti-interference of data and improves the bit error rate (BER) of the system.
2. Construction of TDS-OFDM System
The TDS-OFDM system uses all subcarriers to transmit data, which effectively improves spectrum efficiency. To realize channel estimation and synchronization, the system utilizes the PN sequence with good autocorrelation as the guard interval. However, the PN sequence causes the symbol data to lose its cycle performance, bringing serious interference between adjacent symbols [14]. In addition, the autocorrelation function of the PN sequence is not an ideal impulse function, which will cause errors in channel estimation. Therefore, the processing of PN sequence pairs is key for TDS-OFDM systems. The time-domain modulation signal for the length of N points in the TDS-OFDM system is
where represents the complex modulation symbol on the subcarrier.
After adding the PN sequence with a length of sampling points, the frame structure z of the TDS-OFDM system is shown in the following equation:
The wireless channel can be modeled as a multi-delay tap filter, and its mathematical expression is given below:
where denotes the total channel impulse response of all paths at n, is the amplitude gain of impulse response in the sub-path, is the fixed Doppler shift, and is the time delay.
To simplify the system complexity, the effect of the Doppler shift is not taken into consideration. Then, the TDS-OFDM signal, after passing through the channel , is
where denotes the noise. The PN sequence is assumed to be and the valid data to be . Due to the effect of the multipath channel, smearing and aliasing occur between and y, as shown in Figure 1.
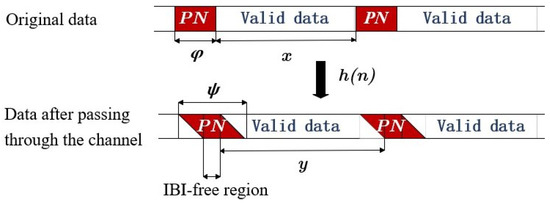
Figure 1.
Schematic diagram of data aliasing in a multipath channel.
3. Cyclic Compressive Sensing Channel Estimation Algorithm Based on Channel Coding
To solve the aliasing problem of the PN sequence and valid data in the TDS-OFDM system, we adopt the compressive sensing method [15] to accurately estimate the channel frequency response, and we improve the accuracy of received data by making use of the error correction capability of cascaded channel coding [16]. Then, the received data after error correction is used to construct a sensing matrix. Finally, the compressive sensing algorithm is applied again to estimate the channel. Figure 2 shows the system chart.
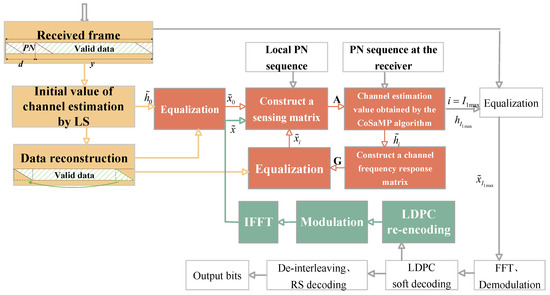
Figure 2.
TDS-OFDM system chart based on the coding cyclic compressive sensing channel estimation algorithm.
The system chart is composed of three sections: the yellow section represents the process of separating and reconstructing the valid data from the aliased data; the orange red section represents the iterative channel estimation process based on the CoSaMP algorithm; and the green section represents the LDPC re-encoding process.
3.1. Separation and Reconstruction of Valid Data from the Aliased Data
The conventional TDS-OFDM system can only conduct channel estimation in the IBI-free region of the PN sequence, which leads to inaccurate and incomplete channel estimation results and thus greatly affects the symbol detection performance. To overcome this problem, we separate and reconstruct the aliased data, and we then employ the compressive sensing algorithm to improve the accuracy of channel estimation.
The symbol vector of the frame at the receiver is expressed as
Since the TDS-OFDM system uses the PN sequence as the guard interval, the cycle performance of data is disrupted. Under the effect of the multipath channel, the sampling points of valid data at the tail of the received frame will alias with the first sampling points of the PN sequence in the frame, which causes IBI. Therefore, the TDS-OFDM system cannot apply the frequency domain equalization method commonly used in conventional OFDM systems, and it must splice the tail and head data of the received data to reconstruct the received data. The algorithm process is given below (Algorithm 1):
- Extract the IBI-free regions of the PN sequence from the received data , and conduct channel estimation by LS to obtain the channel estimation value ;
- Use obtained in Step (1) to calculate the PN sequence affected by the multipath channel, where is the matrix of ;
- Delete the first lines of data from the received data of the frame, and mark the remaining data as , where is the matrix of ;
- Remove the first lines of the PN sequence data (i.e.,: the to lines of the matrix ) in to obtain the valid data , where is the matrix of ;
- Repeat Steps (1) and (2) to obtain the updated channel estimation value and the PN sequence affected by the multipath channel;
- Delete the lines of data from the received data of the frame, and mark the remaining data as , where is the matrix of ;
- Remove the PN sequence in to obtain , where is the matrix of ;
- Splice in Step (7) at the tail of in Step (4) to obtain the reconstructed valid data , where is the matrix of ;
- Splice the lines of data at the tail of to the head of , and transform linear convolution into cyclic convolution so that data can be equalized in the frequency domain.
| Algorithm 1 Data reconstruction. |
Input:
|
The realization process is shown in Figure 3.
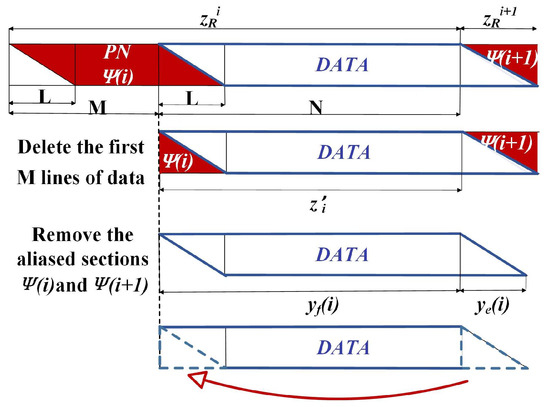
Figure 3.
Schematic diagram of data reconstruction.
3.2. Channel Estimation Based on CoSaMP Compressive Sensing
In the actual wireless environment, most of the channels are sparse channels. The sparse channels can be reconstructed according to a small number of observation values using the compressive sensing theory. The compressive-sensing based channel estimation method can reduce the expenditure and improve the channel estimation performance [17]. In this paper, the CoSaMP algorithm in the greedy iterative algorithm is selected to obtain a solution.
The CoSaMP algorithm has the same effect as the optimization methods. This algorithm is rather effective for practical problems, for it only needs to multiply the matrix vector by the sampling matrix. The algorithm adopts a backtracking method, selects multiple best-matching atoms in each iteration, and discards some atoms with a low correlation after each iteration. Therefore, it has good stability.
Figure 4 shows the comparison of the channel estimation MSE of the system using different compressive sensing reconstruction algorithms in sparse Rayleigh channels. According to simulation data, the CoSaMP algorithm has the best MSE performance under different SNR conditions.
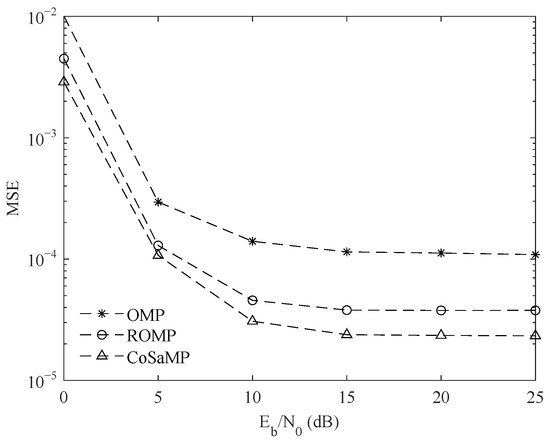
Figure 4.
Comparisonof cyclic compression sensing performance based on different reconstruction algorithms.
The input of the CoSaMP algorithm includes sensing matrix , observation vector y and signal sparsity K. The CoSaMP algorithm requires a sensing matrix, and the initial sensing matrix is unknown. Therefore, after data reconstruction , the initial value of channel estimation obtained by LS is used to equalize the reconstructed data and obtain the equalized data . can be used to construct the sensing matrix required by the CoSaMP algorithm.
If the measurement vector for the first lines in is defined, the expression of is shown in (6).
where the expression of sensing matrix is shown in (7).
where represents the time-domain data after equalization. The error exists between the equalized data and the real data, and it is marked as .
The channel estimation value of the frame can be obtained by (6). Assuming that the channel is of a slow varying characteristic, it can be considered that the data of the channel displays no changes in three consecutive frames. The channel estimation value of the frame is interpolated by using the channel estimation values of the previous two frames, as shown in (8).
where , k denotes the discrete time.
Then, a channel frequency response matrix is constructed by using , and the data are equalized again to obtain .
3.3. RS-LDPC Cascaded Coding and Decoding
Since the TDS-OFDM system brings noise interference during data reconstruction in 3.1, the error is caused in the equalized data. Meanwhile, the correlation function of the PN sequence is not an ideal function, and it will also cause errors during channel estimation. In order to reduce the effect of system errors and improve the reliability of the communication system, we adopt RS-LDPC as cascaded channel coding in this study. LDPC code has excellent performance close to the Shannon limit, while RS code is good at correcting sudden errors. The RS-LDPC cascaded code corrects the error bits that may remain after the decoding of inner code (LDPC code) through the outer code (RS code), thereby improving the error correction capability of the system [18].
The basic idea of RS code is to select an appropriate generating polynomial so that the polynomial on the information side is a multiple of a generating polynomial. The generating polynomial of RS code is as follows:
where a is a primitive element in , and m is the order of RS code [19].
The encoding of LDPC codes depends on the sparse check matrix . That is, the number of non-zero elements in the matrix is very small. Due to the sparsity of the check matrix, the check matrix can be transformed into the following form by Gaussian elimination and column rearrangement.
where is the unit matrix.
Since the relationship between the generating matrix and the check matrix is , the generating matrix is expressed as
After receiving the data, the receiver first parallelizes the data and conducts LDPC soft decoding on corresponding data according to the noise variance of the channel [20]. Soft decision information is mainly represented by the LLR value, and the accuracy of logarithmic likelihood ratio information (LLR) directly affects the reliability of decoding.
The conditional probability density function of the received symbol in the process of soft decision is shown in (12) when the noise variance of the received data x is .
If the soft decision information per bit is represented as and the symbol sets with the bits of 1 and 0 are represented by and , respectively, is shown in (13) [21]:
where and are defined in (14).
After obtaining , the soft information is entered into the LDPC soft decoder for the inner decoding of LDPC codes.
It should be noted that the data reconstruction in 3.2 destroys the position relationship between information bit and parity bit in the channel coding. Demodulation and decoding cannot be conducted directly, and the entire received frame needs to be equalized in the frequency domain before this.
Figure 5 shows the simulation curves comparing the communication performance of uncoded systems, single RS and LDPC coding systems, Bose–Chaudhuri–Hocquenghem low-density parity-check (BCH-LDPC) cascaded coding systems, and RS-LDPC cascaded coding systems in sparse Rayleigh fading channels. It shows that in sparse Rayleigh fading channels, the RS-LDPC cascaded coding system still has the best performance compared to uncoded systems, single coding systems, and BCH-LDPC cascaded systems. When the SNR is 20 dB, the BER of single RS coding and LDPC coding systems is not less than , the BER of BCH-LDPC cascaded coding system is , and the BER of RS-LDPC cascaded coding system is .
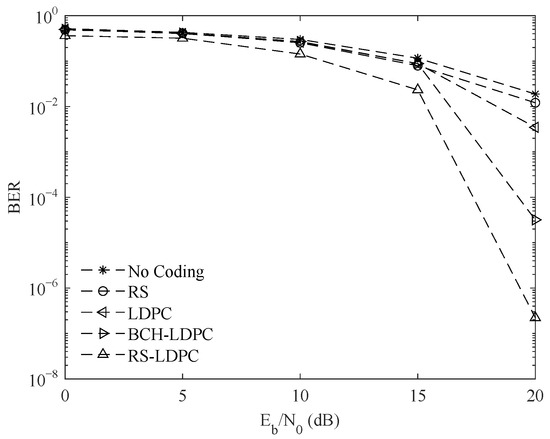
Figure 5.
BER of different encoding methods.
3.4. Process of the Coding Cyclic Compressive Sensing Channel Estimation Algorithm
Combining the compressive sensing-based channel estimation in 3.2 with the cascaded coding in 3.3, this section improves the accuracy of the equalized data using RS-LDPC. The error-corrected data with a high accuracy is used to form a sensing matrix , and then (6) is used to improve the accuracy of channel estimation through iterative computation.
The process of the coding cyclic compressive sensing channel estimation algorithm is given below (Algorithm 2):
| Algorithm 2 Coding cyclic compressive sensing channel estimation. |
Input:
|
- After receiving the data, the receiver conducts the signal estimation by LS according to 3.1 and separates and reconstructs the valid data.
- Use the initial value of channel estimation by LS obtained in (1) to initially equalize the reconstructed data , and then send the equalized data, the received PN sequence and the local PN sequence to the compressive sensing module.
- For the input data in (2), the compressive sensing module adopts the channel estimation method based on CoSaMP compressive sensing and the interpolation processing according to 3.2 to obtain the channel estimation value .
- Use the channel estimation value obtained in Step (3) to construct a channel frequency response matrix , set a cycle threshold , and return to Step (2) when the number of cycles is , and obtain the data again. When , stop the cycle, and then proceed to the next step.
- Average the channel estimation values obtained after the loop of step (4) is completed, and then equalize the received original data frames.
- Complete FFT processing and soft demodulation of the QAM signal after obtaining the equalized original data frames. Furthermore, conduct LDPC soft decoding according to 3.3. First, set the threshold for maximum iterations. When the number of iterations is , conduct LDPC coding and QAM modulation for the data decoded by LDPC, send the data to the compressive sensing module, and then repeat Step (3). When the number of iterations is , go to Step (7).
- Conduct de-interleaving and RS decoding for the data decoded by LDPC, and then output the final bit stream.
The flowchart is shown in Figure 6:
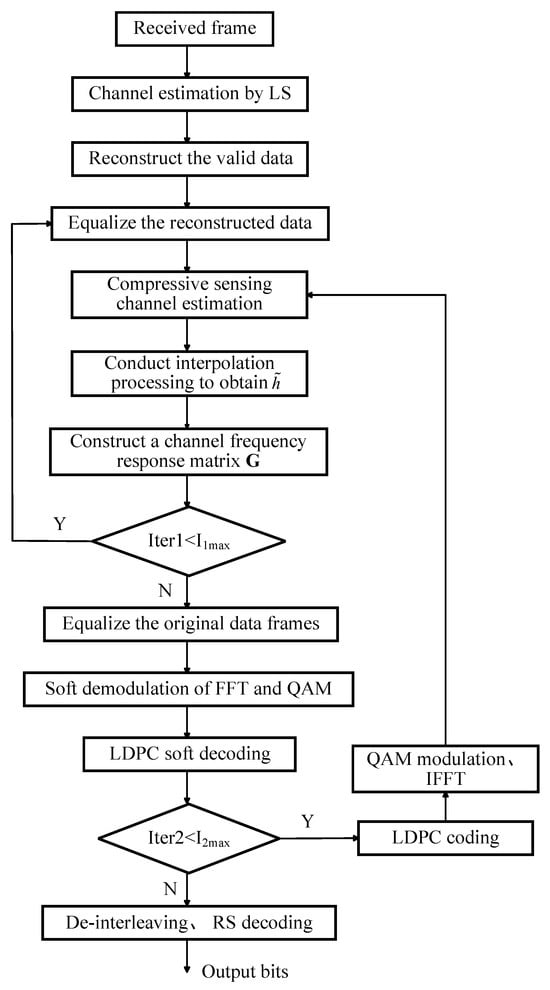
Figure 6.
Flowchart of the receiver.
4. Simulation Results and Analysis
To verify the effectiveness of the proposed method, this section compares and simulates the proposed method, the traditional channel estimation method based on IBI-free compressive sensing (LCS-IBI-free), and the cyclic compressive sensing channel estimation method based on all PN sequences without coding (LCS), and analyzes their channel estimation and BER performances.
4.1. Settings of Simulation Parameters
Simulation parameters include baseband system parameters and multipath channel parameters. The typical measurement of channel variability is Doppler spread. The relationship between the Doppler spread and the duration of OFDM symbols is limited as . The parameters of the baseband system are set as follows: The number of subcarriers is 1024, the length of the PN sequence is 256, the total number of frames is 30, and the number of OFDM symbols per frame is 30. The baseband modulation mode is 64QAM. The RS code rate is 11/15, and the LDPC code rate is 1/2. The interleaving mode is row–column interleaving. The numbers of their encoding cycles are set as 0, 1 and 2, respectively, and the effect of cyclic encoding is compared.
In order to verify the applicability of this system, performance simulation analysis is conducted in different channel environments, and multiple verifications are carried out under sparse multipath channels with different path numbers. The amplitude and delay of the channel follow a uniform distribution between 0 and the maximum value. Figure 7 shows the impulse response histograms of channels with different path numbers, and the channel amplitude satisfies the Rayleigh fading condition.
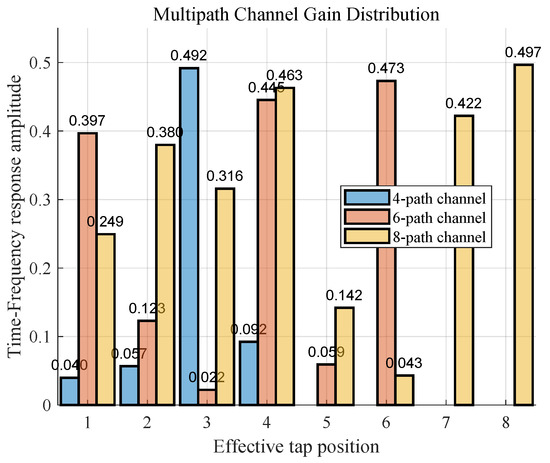
Figure 7.
Histogram of impulse response distribution in multipath channel.
4.2. Complexity Analysis
The main module complexity of the algorithm is shown in Table 1:

Table 1.
Main module complexity of the algorithm.
The time complexity of the method proposed in this article compared to traditional LS channel estimation is shown in Table 2.

Table 2.
Complexity of the algorithm proposed.
4.3. MSE Performance Simulation
Figure 8 is a comparison diagram of channel estimation MSEs for different methods. It can be seen from the experimental results that the channel estimation effect of LCS-IBI-free is not ideal due to the short measurement vector. When the signal-to-noise ratio (SNR) is 15 dB, the MSE is . The measurement vector of LCS increases significantly. When the SNR is 15 dB, the MSE is . Therefore, the channel estimation effect is improved significantly. The proposed method adopts RS-LDPC cascaded coding to enhance the correction capability of transmission data errors and effectively enhance the channel estimation performance. Therefore, the channel estimation effect of the proposed method is significantly better than another two methods. The channel estimation effect is improved obviously with the increase of iterations. When the SNR is 15 dB, the MSE of the proposed method after one iteration is , and the MSE of the proposed method after two iterations is . When iterating twice or more, its performance is better than the LS+RetineNet method using neural networks.
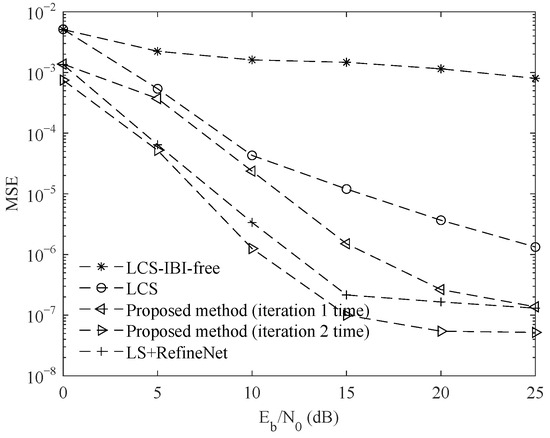
Figure 8.
Comparison of channel estimation MSEs for different methods.
Since the channel estimation effect of LCS-IBI-free is not ideal, this section compares the channel estimation MSEs between the proposed method and the cyclic compressive sensing method (LCS). Figure 9, Figure 10 and Figure 11 are the simulation comparison curves for the four-path channel, six-path channel and eight-path channel, respectively. According to the experimental data, compared with the traditional cyclic compressive sensing methods, the proposed method provides better channel estimation performance in different multiple paths. The channel estimation effect is improved obviously with the increase in iterations. When the SNR is 15 dB, the MSEs of the proposed method after one iteration and two iterations are and in the four-path channel, respectively. When the SNR is 15 dB, the MSEs of the proposed method after one iteration and two iterations are and in the six-path channel, respectively. When the SNR is 15 dB, the MSEs of the proposed method after one iteration and two iterations are and in the eight-path channel, respectively. Therefore, the coding cyclic compressive sensing channel estimation method is superior to the cyclic compressive sensing channel estimation method.
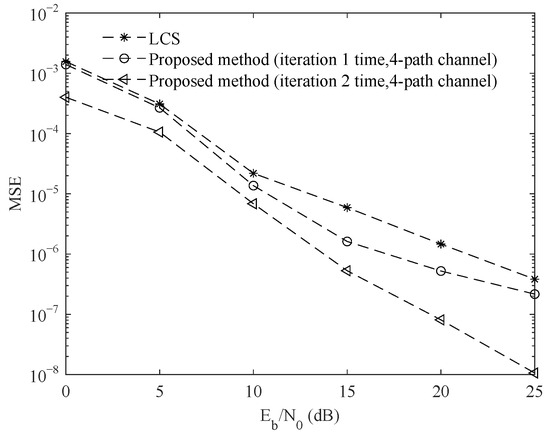
Figure 9.
Comparison of channel estimation MSEs for different iterations in a 4-path channel.
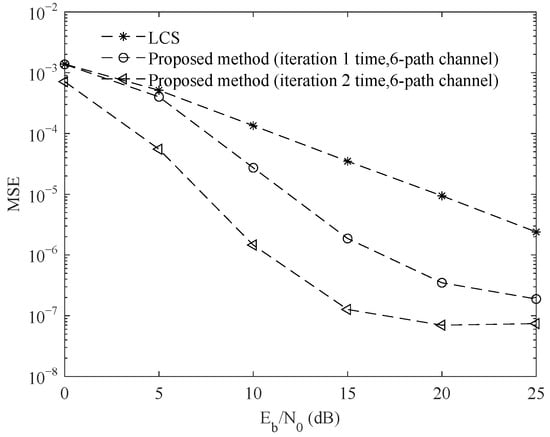
Figure 10.
Comparison of channel estimation MSEs for different iterations in a 6-path channel.
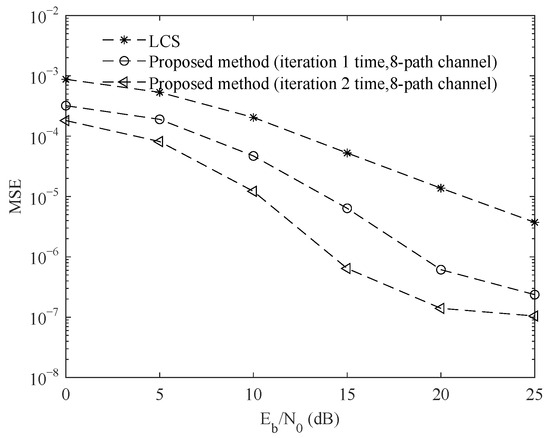
Figure 11.
Comparison of channel estimation MSEs for different iterations in a 8-path channel.
4.4. BER Performance Simulation
Figure 12, Figure 13 and Figure 14 are the BER comparison curves for the four-path channel, six-path channel and eight-path channel, respectively. When the SNR is 15 dB, BERs of the proposed method after one iteration, two iterations and the LCS method are 0.124, 0.097 and 0.182 in the four-path channel, respectively. When the SNR is 15 dB, BERs of the proposed method one iteration, two iterations and the LCS method are 0.111, 0.058 and 0.177 in the six-path channel, respectively. When the SNR is 15 dB, BERs of the proposed method after iteration one iteration, two iterations and the LCS method are 0.065, 0.051 and 0.108 in the eight-path channel, respectively. According to the experimental data, compared with the system without coding cyclic compressive sensing, the BER performance of the system with coding cyclic compressive sensing is enhanced obviously, and the BER after two iterations is lower than that after one iteration. With the increase in multiple paths, the effect of the BER is enhanced.
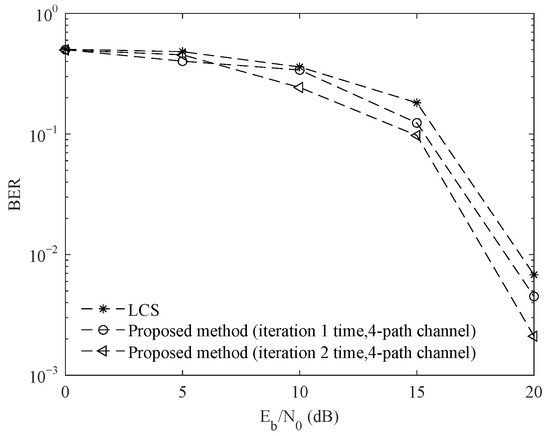
Figure 12.
Comparison of system communication performance in a 4-path channel.
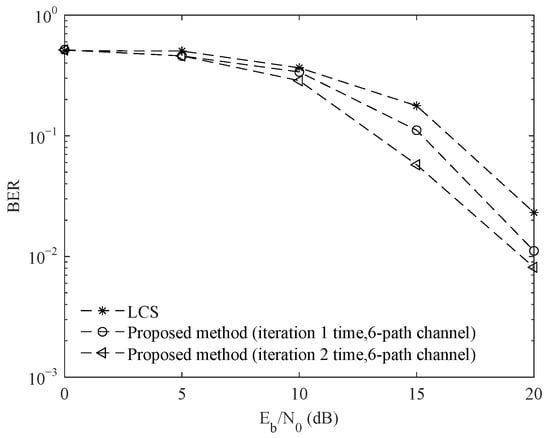
Figure 13.
Comparison of system communication performance in a 6-path channel.
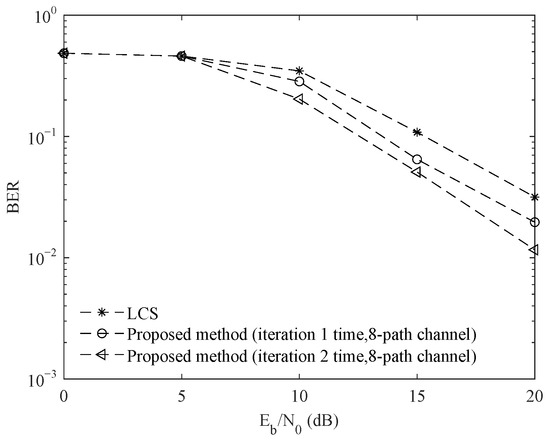
Figure 14.
Comparison of system communication performance in a 8-path channel.
5. Conclusions
In this paper, we study the TDS-OFDM system with high spectrum efficiency based on the requirement of high spectrum efficiency in satellite Internet communication. In this study, RS-LDPC cascaded channel coding is combined with compressive sensing iterative channel estimation to improve the data accuracy of a sensing matrix in the compressive sensing channel estimation algorithm and solve the problem that all PN sequences cannot be used for channel estimation in traditional methods. Based on the accurate recovery of the aliased data, the proposed method utilizes the iterative optimization of the compressive sensing algorithm and equalization feedback loop to realize the channel estimation and improve the anti-interference and error correction capabilities of the data through RS-LDPC cascaded channel coding. Furthermore, in order to improve the accuracy of the sensing matrix, the error-corrected data are re-encoded, and then the compressive sensing iterative channel estimation is conducted again to enhance the compressive sensing channel estimation performance and the communication performance of the TDS-OFDM system. The simulation results demonstrate that the cyclic compressive sensing channel estimation module based on all PN sequences provides better MSE performance and BER performance in a complex multipath channel, and the performance of the cyclic compressive sensing channel estimation method combined with RS-LDPC coding is superior to the simple cyclic compressive sensing channel estimation method. It realizes high-accuracy channel estimation in a multipath fading environment, and verifies the applicability and effectiveness of the proposed method. In this paper, we do not consider the modules of filtering and frequency conversion at the transmitter. However, we will consider the data rate limitation and the large frequency offset caused by high-frequency carriers in the future.
Author Contributions
Conceptualization, Y.Y. and H.W.; validation, Y.Y. and X.Z.; writing—original draft preparation, Y.Y. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, C.X.; Huang, J.; Wang, H.; Gao, X.; You, X.; Hao, Y. 6G Wireless Channel Measurements and Models: Trends and Challenges. IEEE Veh. Technol. Mag. 2020, 15, 22–32. [Google Scholar] [CrossRef]
- Chen, S.; Sun, S.; Kang, S. System integration of terrestrial mobile communication and satellite communication—The trends, challenges and key technologies in B5G and 6G. China Commun. 2020, 17, 156–171. [Google Scholar] [CrossRef]
- Ding, R.; Chen, T.; Liu, L.; Zheng, Z.; Hao, Y.; Zheng, H.; Wang, W.; You, L. 5G Integrated Satellite Communication Systems: Architectures, Air Interface, and Standardization. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 702–707. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, S.; Liu, Z.; Lin, J.; Wang, S.; Xing, C. An overview of multi-antenna technologies for space-ground integrated networks. Sci. China Inf. Sci. 2016, 59, 121301. [Google Scholar] [CrossRef][Green Version]
- Ray, P.P. A review on 6G for space-air-ground integrated network: Key enablers, open challenges, and future direction. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 6949–6976. [Google Scholar] [CrossRef]
- Zheng, Z.W. Improved Frame Head mode detection and symbol detection scheme for Chinese TDS-OFDM-based DTTB systems. In Proceedings of the 2010 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16–18 April 2010; pp. 27–30. [Google Scholar] [CrossRef]
- Jing, C.; Tang, X.; Zhang, X.; Xi, L.; Zhang, W. Time domain synchronous OFDM system for optical fiber communications. China Commun. 2019, 16, 155–164. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Z.X.; Pan, C.Y.; Song, J.; Yang, L. Iterative padding subtraction of the PN sequence for the TDS-OFDM over broadcast channels. IEEE Trans. Consum. Electron. 2005, 51, 1148–1152. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L. Pre-processing filter design at transmitters for IBI mitigation in an OFDM system. J. Syst. Eng. Electron. 2013, 24, 722–728. [Google Scholar] [CrossRef]
- Ur Rehman Junejo, N.; Esmaiel, H.; Zhou, M.; Sun, H.; Qi, J.; Wang, J. Sparse Channel Estimation of Underwater TDS-OFDM System Using Look-Ahead Backtracking Orthogonal Matching Pursuit. IEEE Access 2018, 6, 74389–74399. [Google Scholar] [CrossRef]
- Fu, J.; Wang, J.; Song, J.; Pan, C.Y.; Yang, Z.X. A Simplified Equalization Method for Dual PN-Sequence Padding TDS-OFDM Systems. IEEE Trans. Broadcast. 2008, 54, 825–830. [Google Scholar] [CrossRef]
- Dziwoki, G.; Izydorczyk, J. Iterative Identification of Sparse Mobile Channels for TDS-OFDM Systems. IEEE Trans. Broadcast. 2016, 62, 384–397. [Google Scholar] [CrossRef]
- Zhu, Y.; Fan, D.; Mu, Y.; Wang, G. Model-driven Time-varying Channel Estimation Method for OFDM System Based on Neural Network. In Proceedings of the 2024 IEEE 24th International Conference on Communication Technology (ICCT), Chengdu, China, 18–20 October 2024; pp. 1520–1524. [Google Scholar] [CrossRef]
- Qasem, Z.A.H.; Leftah, H.A.; Sun, H.; Qi, J.; Esmaiel, H. X-Transform Time-Domain Synchronous IM-OFDM-SS for Underwater Acoustic Communication. IEEE Syst. J. 2022, 16, 1984–1995. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, C.; Pan, C. Priori-Information Hold Subspace Pursuit: A Compressive Sensing-Based Channel Estimation for Layer Modulated TDS-OFDM. IEEE Trans. Broadcast. 2018, 64, 119–127. [Google Scholar] [CrossRef]
- Fu, C.; Gong, C.; Huang, N.; Luo, J.; Xu, Z. Concatenated RS-LDPC Coding for Water-to-Air Visible Light Communication Through Wavy Water Surface. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Altabbaa, M.T. Double Focusing: A New Sparse Channel Estimation Algorithm for Doubly Selective SFBC-OFDM-Based Underwater Acoustic Systems. IEEE Wirel. Commun. Lett. 2020, 9, 2040–2044. [Google Scholar] [CrossRef]
- Zhang, X.; Siegel, P.H. Quantized Iterative Message Passing Decoders with Low Error Floor for LDPC Codes. IEEE Trans. Commun. 2014, 62, 1–14. [Google Scholar] [CrossRef]
- Qiu, J.; Chen, L.; Liu, S. A Novel Concatenated Coding Scheme: RS-SC-LDPC Codes. IEEE Commun. Lett. 2020, 24, 2092–2095. [Google Scholar] [CrossRef]
- Summers, T.; Wilson, S. SNR mismatch and online estimation in turbo decoding. IEEE Trans. Commun. 1998, 46, 421–423. [Google Scholar] [CrossRef]
- Ferrari, M.; Tomasoni, A.; Bellini, S. Analysis of practical LDPC decoders in tanner graphs with absorbing sets. In Proceedings of the 2017 IEEE Information Theory Workshop (ITW), Kaohsiung, Taiwan, 6–10 November 2017; pp. 141–145. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).