Fuzzy Logic in Smart Meters to Support Operational Processes in Energy Management Systems
Abstract
1. Introduction
1.1. Energy Management Algorithms for Home Energy Management Systems
1.2. Home Energy Management System
1.3. Smart Energy Meters
1.4. The Application of Fuzzy Logic to Energy Management Algorithms
1.5. Research Issues, Limitations, and Gaps
1.6. Contributions
- A novel decision-making system for energy management in smart energy meters with a FIS tailored for HEMS. This contribution specifically targets the under-explored area of implementing fuzzy logic-based energy management within residential smart energy meters, moving beyond broader applications in grid-level control and optimization.
- A detailed mathematical description of the low-cost decision-making system, explicitly considering resource constraints. Unlike prior work that may not have focused on the practical limitations of embedded devices, this paper provides a comprehensive mathematical formulation of the proposed FIS-based system, designed with the computational capabilities of low-cost smart energy meter hardware in mind.
- Comprehensive simulation studies and experimental verification carried out on both a PC and representative low-cost resource-constrained devices. To directly address the lack of validation on target hardware, this study includes rigorous simulations and real-world experiments conducted not only on a standard PC but also on embedded platforms representative of the resource limitations of smart energy meters intended for residential deployment.
- Empirical confirmation of the justification for the need to optimize algorithms for practical deployment in smart energy meters. Through the simulation and experimental results obtained on low-cost devices, this paper provides concrete evidence supporting the critical necessity of algorithm optimization to ensure the feasibility and real-time performance of advanced energy management functionalities within commercially viable smart energy meters.
1.7. Paper Organisation
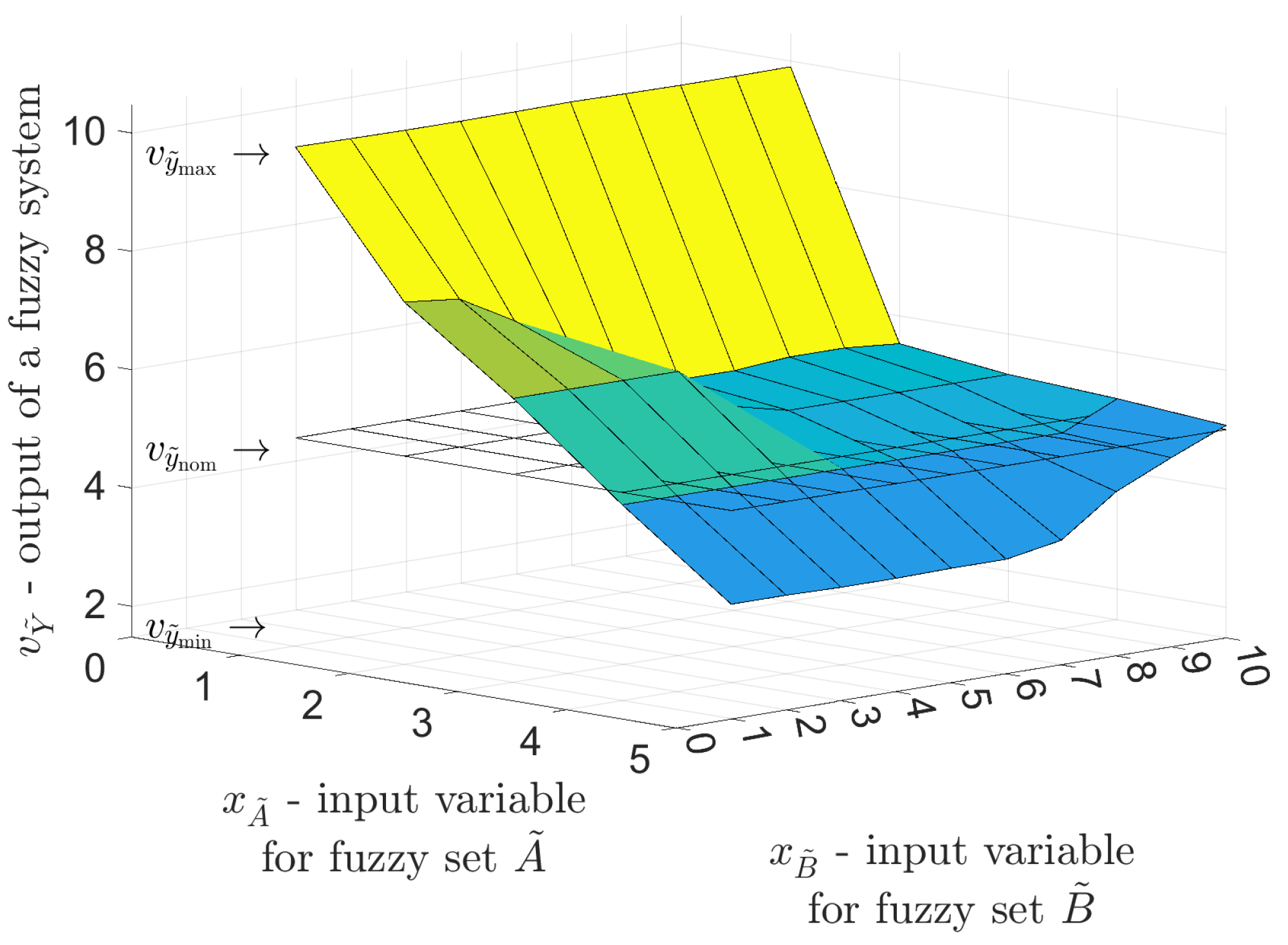
2. Mathematical Modeling
Fuzzy Inference System Model for Smart Energy Meters
3. Case Studies
4. Experimental Verification
- There was no compilation to machine code, optimization, no low-level access to C/C++ libraries, or no parallelization was used. This situation is visible in the case of comparing the execution of the proposed FIS model algorithm in the Matlab environment from m files in the configuration of device and from mex files in device .
- The device had the weakest hardware resource configuration (random access memory and central processing unit), as was the case with .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMI | advanced metering infrastructure |
| AI | artificial intelligence |
| BEMS | Building Energy Management Systems |
| CES | conventional electricity suppliers |
| DSO | distribution system operators |
| EPS | electric power system |
| FIS | fuzzy inference system |
| HVAC | heating, ventilation, air conditioning systems |
| HEMS | home energy management systems |
| IoT | Internet of Things |
| RTP | real-time pricing |
| RES | renewable energy sources |
| SA | smart appliances |
| SG | smart grid |
| TSO | transmission system operators |
References
- Khalili, M.; Dashtaki, M.A.; Nasab, M.A.; Hanif, H.R.; Padmanaban, S.; Khan, B. Optimal instantaneous prediction of voltage instability due to transient faults in power networks taking into account the dynamic effect of generators. Cogent Eng. 2022, 9, 2072568. [Google Scholar] [CrossRef]
- Cunningham, J.D.; Aved, A.; Ferris, D.; Morrone, P.; Tucker, C.S. A Deep Learning Game Theoretic Model for Defending Against Large Scale Smart Grid Attacks. IEEE Trans. Smart Grid 2023, 14, 1188–1197. [Google Scholar] [CrossRef]
- Feng, S.; Cucuzzella, M.; Bouman, T.; Steg, L.; Scherpen, J.M.A. An Integrated Human–Cyber–Physical Framework for Control of Microgrids. IEEE Trans. Smart Grid 2023, 14, 3388–3400. [Google Scholar] [CrossRef]
- Nasab, M.A.; Zand, M.; Padmanaban, S.; Bhaskar, M.S.; Guerrero, J.M. An efficient, robust optimization model for the unit commitment considering renewable uncertainty and pumped-storage hydropower. Comput. Electr. Eng. 2022, 100, 107846. [Google Scholar] [CrossRef]
- Mischos, S.; Dalagdi, E.; Vrakas, D. Intelligent energy management systems: A review. Artif. Intell. Rev. 2023, 56, 11635–11674. [Google Scholar] [CrossRef]
- Yan, D.; Li, T.; Ma, C.; LAI, L.L.; Fung TSANG, K. Cost Effective Energy Management of Home Energy System with Photovoltaic-Battery and Electric Vehicle. In Proceedings of the IECON 2020—The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 3611–3616. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, P.; Zhang, H. Privacy-Preserving Regulation Capacity Evaluation for HVAC Systems in Heterogeneous Buildings Based on Federated Learning and Transfer Learning. IEEE Trans. Smart Grid 2023, 14, 3535–3549. [Google Scholar] [CrossRef]
- Fink, J.; Hurink, J.L. Minimizing costs is easier than minimizing peaks when supplying the heat demand of a group of houses. Eur. J. Oper. Res. 2015, 242, 644–650. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Yazdaninejadi, A.; Golshannavaz, S. Decentralized prioritization of demand response programs in multi-area power grids based on the security considerations. ISA Trans. 2023, 134, 396–408. [Google Scholar] [CrossRef]
- Halinga, M.S.; Nshama, E.W.; Schäfle, T.R.; Uchiyama, N. Time and energy optimal trajectory generation for coverage motion in industrial machines. ISA Trans. 2023, 138, 735–745. [Google Scholar] [CrossRef]
- Alvarado-Barrios, L.; Álvarez Arroyo, C.; Escaño, J.M.; Gonzalez-Longatt, F.M.; Martinez-Ramos, J.L. Two-Level Optimisation and Control Strategy for Unbalanced Active Distribution Systems Management. IEEE Access 2020, 8, 197992–198009. [Google Scholar] [CrossRef]
- da Silva, E.C.; Melgar-Dominguez, O.D.; Romero, R. Simultaneous Distributed Generation and Electric Vehicles Hosting Capacity Assessment in Electric Distribution Systems. IEEE Access 2021, 9, 110927–110939. [Google Scholar] [CrossRef]
- Hadian, E.; Akbari, H.; Farzinfar, M.; Saeed, S. Optimal Allocation of Electric Vehicle Charging Stations With Adopted Smart Charging/Discharging Schedule. IEEE Access 2020, 8, 196908–196919. [Google Scholar] [CrossRef]
- Son, Y.J.; Lim, S.H.; Yoon, S.G.; Khargonekar, P.P. Residential Demand Response-Based Load-Shifting Scheme to Increase Hosting Capacity in Distribution System. IEEE Access 2022, 10, 18544–18556. [Google Scholar] [CrossRef]
- Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement Learning for Selective Key Applications in Power Systems: Recent Advances and Future Challenges. IEEE Trans. Smart Grid 2022, 13, 2935–2958. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Wadud, Z.; Khan, I.; Usman, M.; Qazi, A.B.; Khan, F.A. An Innovative Optimization Strategy for Efficient Energy Management With Day-Ahead Demand Response Signal and Energy Consumption Forecasting in Smart Grid Using Artificial Neural Network. IEEE Access 2020, 8, 84415–84433. [Google Scholar] [CrossRef]
- Rehman, A.U.; Hafeez, G.; Albogamy, F.R.; Wadud, Z.; Ali, F.; Khan, I.; Rukh, G.; Khan, S. An Efficient Energy Management in Smart Grid Considering Demand Response Program and Renewable Energy Sources. IEEE Access 2021, 9, 148821–148844. [Google Scholar] [CrossRef]
- Liu, C.H.; Gu, J.C.; Yang, M.T. A Simplified LSTM Neural Networks for One Day-Ahead Solar Power Forecasting. IEEE Access 2021, 9, 17174–17195. [Google Scholar] [CrossRef]
- Kou, X.; Li, F.; Dong, J.; Olama, M.; Starke, M.; Chen, Y.; Zandi, H. A Comprehensive Scheduling Framework Using SP-ADMM for Residential Demand Response With Weather and Consumer Uncertainties. IEEE Trans. Power Syst. 2021, 36, 3004–3016. [Google Scholar] [CrossRef]
- Zhen, J.; Khayatnezhad, M. Optimum pricing of smart home appliances based on carbon emission and system cost. Energy Rep. 2022, 8, 15027–15039. [Google Scholar] [CrossRef]
- Azimi Nasab, M.; Zand, M.; Eskandari, M.; Sanjeevikumar, P.; Siano, P. Optimal Planning of Electrical Appliance of Residential Units in a Smart Home Network Using Cloud Services. Smart Cities 2021, 4, 1173–1195. [Google Scholar] [CrossRef]
- Raza, M.H.; Rind, Y.M.; Javed, I.; Zubair, M.; Mehmood, M.Q.; Massoud, Y. Smart Meters for Smart Energy: A Review of Business Intelligence Applications. IEEE Access 2023, 11, 120001–120022. [Google Scholar] [CrossRef]
- Çimen, H.; Çetinkaya, N.; Vasquez, J.C.; Guerrero, J.M. A Microgrid Energy Management System Based on Non-Intrusive Load Monitoring via Multitask Learning. IEEE Trans. Smart Grid 2021, 12, 977–987. [Google Scholar] [CrossRef]
- Lin, Y.H.; Tang, H.S.; Shen, T.Y.; Hsia, C.H. A Smart Home Energy Management System Utilizing Neurocomputing-Based Time-Series Load Modeling and Forecasting Facilitated by Energy Decomposition for Smart Home Automation. IEEE Access 2022, 10, 116747–116765. [Google Scholar] [CrossRef]
- Sami, B.S. A Survey of Hydrogen Energy and I-Energy Applications: Household Intelligent Electrical Power Systems. IEEE Access 2020, 8, 55181–55203. [Google Scholar] [CrossRef]
- Hadi, A.A.; Silva, C.A.S.; Hossain, E.; Challoo, R. Algorithm for Demand Response to Maximize the Penetration of Renewable Energy. IEEE Access 2020, 8, 55279–55288. [Google Scholar] [CrossRef]
- Gupta, R.; Al-Ali, A.R.; Zualkernan, I.A.; Das, S.K. Big Data Energy Management, Analytics and Visualization for Residential Areas. IEEE Access 2020, 8, 156153–156164. [Google Scholar] [CrossRef]
- Chin, J.X.; Tinoco De Rubira, T.; Hug, G. Privacy-Protecting Energy Management Unit Through Model-Distribution Predictive Control. IEEE Trans. Smart Grid 2017, 8, 3084–3093. [Google Scholar] [CrossRef]
- Luo, F.; Ranzi, G.; Wang, X.; Dong, Z.Y. Social Information Filtering-Based Electricity Retail Plan Recommender System for Smart Grid End Users. IEEE Trans. Smart Grid 2019, 10, 95–104. [Google Scholar] [CrossRef]
- Monaco, R.; Liu, X.; Murino, T.; Cheng, X.; Nielsen, P.S. A non-functional requirements-based ontology for supporting the development of industrial energy management systems. J. Clean. Prod. 2023, 414, 137614. [Google Scholar] [CrossRef]
- Desai, J.P. Smart Grid and Energy Management. In Electric Vehicle Charging Infrastructures and Its Challenges; Giri, A.K., Singh, M., Eds.; Springer Nature: Singapore, 2025; pp. 103–126. [Google Scholar] [CrossRef]
- Wijesingha, J.; Hasanthi, B.R.; Wijegunasinghe, I.; Perera, M.; Hemapala, K. Smart Residential Energy Management System (REMS) Using Machine Learning. In Proceedings of the 2021 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), Dubai, United Arab Emirates, 17–18 March 2021; pp. 90–95. [Google Scholar] [CrossRef]
- Yang, J.; Dai, J.; Gooi, H.B.; Nguyen, H.D.; Paudel, A. A Proof-of-Authority Blockchain-Based Distributed Control System for Islanded Microgrids. IEEE Trans. Ind. Inform. 2022, 18, 8287–8297. [Google Scholar] [CrossRef]
- Soni, R.; Mehta, B. Diagnosis and prognosis of incipient faults and insulation status for asset management of power transformer using fuzzy logic controller and fuzzy clustering means. Electr. Power Syst. Res. 2023, 220, 109256. [Google Scholar] [CrossRef]
- Ain, N.U.; Mahmood, F.; Tong, C.; Vagasky, C.; Rizk, M.E. Lightning nowcasting using fuzzy logic—A risk assessment framework for resilience of microgrids. Electr. Power Syst. Res. 2024, 230, 110253. [Google Scholar] [CrossRef]
- Usman, H.M.; ElShatshat, R.; El-Hag, A.H. Energy management for smart residential homes: A real-time fuzzy logic approach. Electr. Power Syst. Res. 2025, 238, 111057. [Google Scholar] [CrossRef]
- Loia, V.; Vaccaro, A.; Vaisakh, K. A Self-Organizing Architecture Based on Cooperative Fuzzy Agents for Smart Grid Voltage Control. IEEE Trans. Ind. Inform. 2013, 9, 1415–1422. [Google Scholar] [CrossRef]
- Mahmud, N.; Zahedi, A.; Mahmud, A. A Cooperative Operation of Novel PV Inverter Control Scheme and Storage Energy Management System Based on ANFIS for Voltage Regulation of Grid-Tied PV System. IEEE Trans. Ind. Inform. 2017, 13, 2657–2668. [Google Scholar] [CrossRef]
- Narendra Babu, P.; Guerrero, J.M.; Siano, P.; Peesapati, R.; Panda, G. A Novel Modified Control Scheme in Grid-Tied Photovoltaic System for Power Quality Enhancement. IEEE Trans. Ind. Electron. 2021, 68, 11100–11110. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. A Stochastic Multi-Objective Framework for Optimal Scheduling of Energy Storage Systems in Microgrids. IEEE Trans. Smart Grid 2017, 8, 117–127. [Google Scholar] [CrossRef]
- Ali, M.; Hossain, M.I.; Shafiullah, M. Fuzzy Logic for Energy Management in Hybrid Energy Storage Systems Integrated DC Microgrid. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 25–27 February 2022; pp. 424–429. [Google Scholar] [CrossRef]
- Sahoo, S.; Sekhar Dash, S.; Jena, N.K.; Sahu, B.K.; Patel, N.C.; Bayindir, R. SHO designed fuzzy logic based controller for AGC study with capacitor energy storage. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 845–850. [Google Scholar] [CrossRef]
- Alfaverh, F.; Denaï, M.; Sun, Y. Demand Response Strategy Based on Reinforcement Learning and Fuzzy Reasoning for Home Energy Management. IEEE Access 2020, 8, 39310–39321. [Google Scholar] [CrossRef]
- Thirugnanam, K.; Moursi, M.S.E.; Khadkikar, V.; Zeineldin, H.H.; Al Hosani, M. Energy Management of Grid Interconnected Multi-Microgrids Based on P2P Energy Exchange: A Data Driven Approach. IEEE Trans. Power Syst. 2021, 36, 1546–1562. [Google Scholar] [CrossRef]
- Kakouche, K.; Oubelaid, A.; Mezani, S.; Rekioua, T.; Bajaj, M.; Jurado, F.; Kamel, S. Energy Management Strategy of Dual-Source Electric Vehicles Based on Fuzzy Logic Control Considering Driving Cycles. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkiye, 14–16 June 2023; pp. 92–97. [Google Scholar] [CrossRef]
- Rifai, N.; Sabor, J.; Alaoui, C.; Gualous, H. Fuzzy Logic Based Energy Management Strategy for Fuel Cell/Supercapacitor Electric Vehicles. In Proceedings of the 2021 9th International Renewable and Sustainable Energy Conference (IRSEC), Tetouan, Morocco, 23–27 November 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Sah, B.; Kumar, P.; Rayudu, R.; Bose, S.K.; Inala, K.P. Impact of Sampling in the Operation of Vehicle to Grid and Its Mitigation. IEEE Trans. Ind. Inform. 2019, 15, 3923–3933. [Google Scholar] [CrossRef]
- Cheng, F.; Qu, L.; Qiao, W.; Hao, L. Enhanced Particle Filtering for Bearing Remaining Useful Life Prediction of Wind Turbine Drivetrain Gearboxes. IEEE Trans. Ind. Electron. 2019, 66, 4738–4748. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K.; Lehtonen, M. Reliable Solar Irradiance Forecasting Approach Based on Choquet Integral and Deep LSTMs. IEEE Trans. Ind. Inform. 2021, 17, 1873–1881. [Google Scholar] [CrossRef]
- Hassani, H.; Razavi-Far, R.; Saif, M. Fault Location in Smart Grids Through Multicriteria Analysis of Group Decision Support Systems. IEEE Trans. Ind. Inform. 2020, 16, 7318–7327. [Google Scholar] [CrossRef]
- Shao, N.; Chen, Q.; Dong, Y.; Ding, W.; Wang, L. Power System Fault Diagnosis Method Based on Intuitionistic Fuzzy Sets and Incidence Matrices. IEEE Trans. Power Deliv. 2023, 38, 3924–3938. [Google Scholar] [CrossRef]
- Pan, C.Y.; Hsu, H.C.; Huang, K.W. Real-Time Control of the Air Volume in Ventilation Facilities by Limiting CO2 Concentration With Cluster Algorithms. IEEE Trans. Ind. Electron. 2023, 70, 12894–12903. [Google Scholar] [CrossRef]
- Sushma, N.; Suresh, H.N.; Lakshmi, J.M.; Srinivasu, P.N.; Bhoi, A.K.; Barsocchi, P. A Unified Metering System Deployed for Water and Energy Monitoring in Smart City. IEEE Access 2023, 11, 80429–80447. [Google Scholar] [CrossRef]
- DEGEFA, M.Z.; Lundkvist, H.; Sanchez-Acevedo, S.; Gregertsen, K.N. Challenges of TSO-DSO Voltage Regulation Under Real-Time Data Exchange Paradigm. IEEE Open J. Ind. Electron. Soc. 2023, 4, 75–84. [Google Scholar] [CrossRef]
- Powroźnik, P.; Szcześniak, P. Energy Management of Home Devices With Smart Response for the Energy Generation Profile. IEEE Trans. Ind. Inform. 2024, 20, 6995–7007. [Google Scholar] [CrossRef]
- Flynn, C.; Pengwah, A.B.; Razzaghi, R.; Andrew, L.L.H. An Improved Algorithm for Topology Identification of Distribution Networks Using Smart Meter Data and Its Application for Fault Detection. IEEE Trans. Smart Grid 2023, 14, 3850–3861. [Google Scholar] [CrossRef]
- Sajid, M.; Tanveer, M.; Suganthan, P.N. Ensemble Deep Random Vector Functional Link Neural Network Based on Fuzzy Inference System. IEEE Trans. Fuzzy Syst. 2025, 33, 479–490. [Google Scholar] [CrossRef]
- Wang, T.; Qiu, Y.; Xie, S.; Li, Q.; Chen, W.; Breaz, E.; Ravey, A.; Gao, F. Energy Management Strategy Based on Optimal System Operation Loss for a Fuel Cell Hybrid Electric Vehicle. IEEE Trans. Ind. Electron. 2024, 71, 2650–2661. [Google Scholar] [CrossRef]
- Madhu, C.; Sudhakar, M.S. An Interpretable Fuzzy Graph Learning for Label Propagation Assisting Data Classification. IEEE Trans. Fuzzy Syst. 2024, 32, 1331–1345. [Google Scholar] [CrossRef]







| Refs. | RES | Electric Vehicles | Frequency Regulation | Voltage Control | Energy Cost | HEMS | Weather and Environment |
|---|---|---|---|---|---|---|---|
| [11] | ✓ | ||||||
| [12,13] | ✓ | ||||||
| [14] | ✓ | ✓ | |||||
| [15] | ✓ | ✓ | |||||
| [16] | ✓ | ✓ | |||||
| [17] | ✓ | ✓ | ✓ | ✓ | |||
| [18] | ✓ | ||||||
| [19] | ✓ | ✓ |
| Refs. | Data Processing and IoT | AI and Energy Management Algorithms | Demand Side Management | Electric Vehicles | Energy Cost | RES | User Comfort | RTP |
|---|---|---|---|---|---|---|---|---|
| [22] | ✓ | ✓ | ✓ | ✓ | ||||
| [23] | ✓ | ✓ | ✓ | |||||
| [24] | ✓ | ✓ | ||||||
| [25] | ✓ | ✓ | ✓ | ✓ | ||||
| [26] | ✓ | ✓ | ✓ | |||||
| [27] | ✓ | ✓ | ||||||
| [28] | ✓ | ✓ | ||||||
| [29] | ✓ | ✓ | ✓ |
| Type | Description | Key Smart Energy Meter Functionalities Utilized | Primary Goals |
|---|---|---|---|
| HEMS | Focus on managing energy consumption and generation within residential buildings. | Real-time energy consumption monitoring, providing data for home automation, enabling response to dynamic pricing signals, supporting integration of residential renewable energy (e.g., solar PV), facilitating demand response participation. | Reducing household energy bills, increasing energy efficiency, optimizing self-consumption of generated energy, enhancing user comfort, and contributing to grid stability. |
| BEMS | Manage energy use in commercial and institutional buildings (offices, hospitals, schools, etc.). | Detailed energy consumption monitoring across various building systems (HVAC, lighting, etc.), occupancy detection data, real-time reporting, fault detection, and providing data for automated control and optimization strategies. | Minimizing energy waste in buildings, reducing operational costs, improving building sustainability, ensuring occupant comfort, and complying with energy regulations. |
| IEMS | Focus on optimizing energy consumption in industrial facilities and manufacturing plants. | Real-time monitoring of energy usage in production processes, machinery, and other industrial equipment, identifying energy-intensive processes, providing data for process optimization, enabling demand-side management in industrial settings, and integrating with on-site generation. | Lowering energy costs in industrial operations, improving production efficiency, optimizing energy distribution within the facility, and enhancing sustainability. |
| SGEMS | Encompasses systems used by utilities and grid operators to manage energy flow, stability, and efficiency across the entire power grid. | Real-time data acquisition from numerous smart energy meters across the grid, load forecasting based on consumption patterns, voltage and frequency monitoring, enabling demand response programs, facilitating the integration of distributed renewable energy sources, and supporting grid automation and control. | Ensuring grid stability and reliability, optimizing energy distribution, managing peak demand, integrating renewable energy effectively, reducing transmission losses, and improving overall grid efficiency. |
| REMS | Focus on managing the generation, storage, and integration of renewable energy sources (solar, wind, etc.) into the grid or local energy systems. While not solely reliant on smart energy meters, they utilize data from them for demand-side management and grid interaction. | Monitoring renewable energy generation in real-time, forecasting generation output, managing energy storage systems, coordinating with smart grid operations based on demand data from smart energy meters, and optimizing the dispatch of renewable energy. | Maximizing the utilization of renewable energy, ensuring grid stability with variable generation sources, reducing reliance on fossil fuels, and optimizing energy storage operations. |
| Refs. | Voltage Control | RES | Energy Storage | RTP | User Comfort | Demand Side Management | Energy Cost | Electric Vehicles | Locating Faults in SGs | HEMS |
|---|---|---|---|---|---|---|---|---|---|---|
| [37] | ✓ | |||||||||
| [38] | ✓ | ✓ | ||||||||
| [39] | ✓ | ✓ | ||||||||
| [40,41,42] | ✓ | |||||||||
| [43] | ✓ | ✓ | ✓ | ✓ | ||||||
| [44] | ✓ | ✓ | ✓ | |||||||
| [45,46,47] | ✓ | |||||||||
| [48,49] | ✓ | |||||||||
| [50,51] | ✓ | |||||||||
| [52] | ✓ |
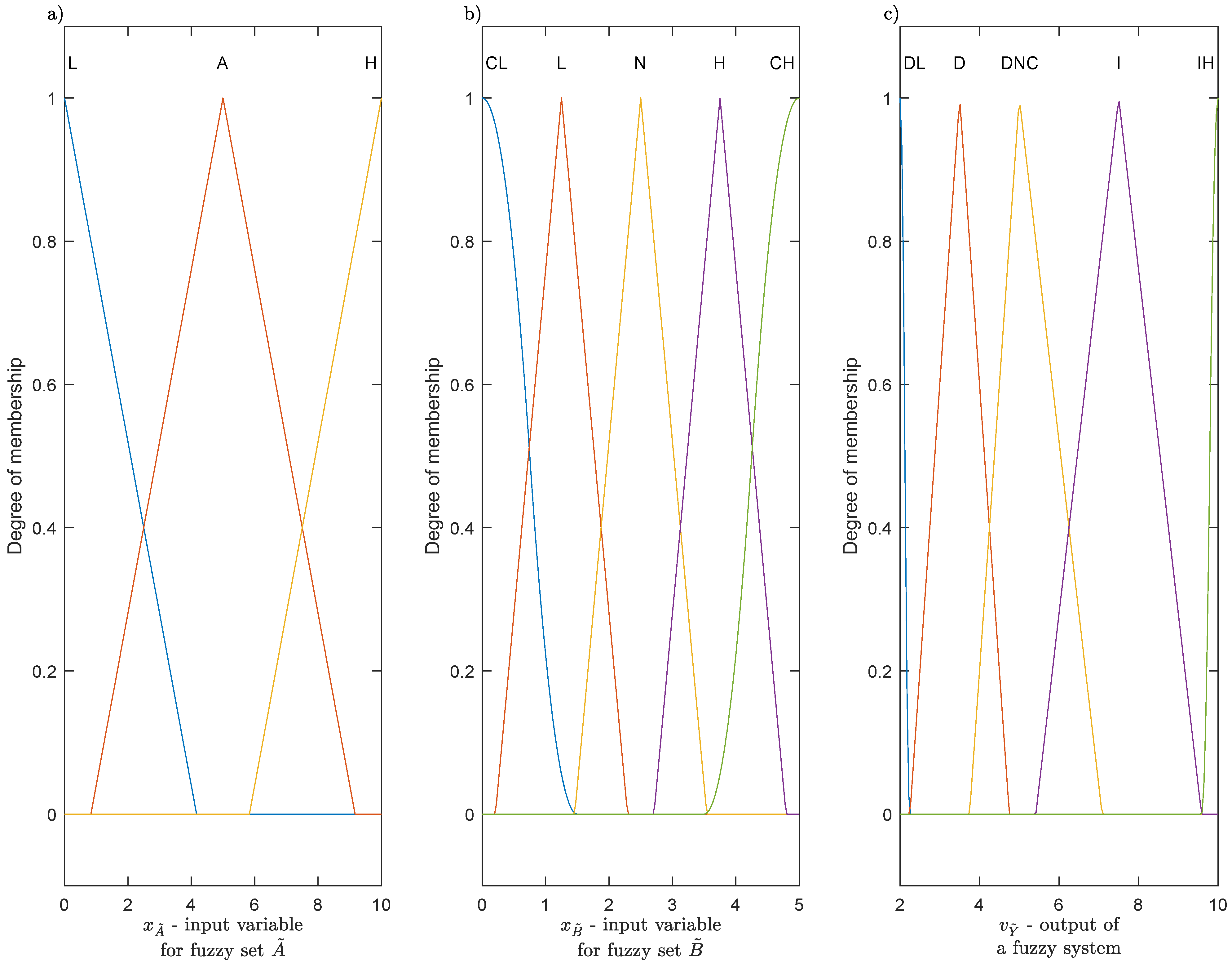
| Fuzzy Sets | Linguistic Term | Membership Function | |
|---|---|---|---|
| Type | |||
| L | Triangular | ||
| A | Triangular | ||
| H | Triangular | ||
| CL | Z-shaped | ||
| L | Triangular | ||
| N | Triangular | ||
| H | Triangular | ||
| CH | S-shaped | ||
| DL | Z-shaped | ||
| D | Triangular | ||
| DNC | Triangular | ||
| I | Triangular | ||
| IH | S-shaped | ||
| Rule No. | Parameters | |||
|---|---|---|---|---|
| Input | Output | |||
| Operator | ||||
| 1 | L | AND | CL | IH |
| 2 | A | AND | CL | IH |
| 3 | H | AND | CL | IH |
| 4 | L | AND | L | I |
| 5 | A | AND | L | DNC |
| 6 | H | AND | L | DNC |
| 7 | L | AND | N | DNC |
| 8 | A | AND | N | DNC |
| 9 | H | AND | N | DNC |
| 10 | L | AND | H | D |
| 11 | A | AND | H | D |
| 12 | H | AND | H | DNC |
| 13 | L | AND | CH | DL |
| 14 | A | AND | CH | DL |
| 15 | H | AND | CH | DL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Powroźnik, P.; Szcześniak, P.; Suliga, M. Fuzzy Logic in Smart Meters to Support Operational Processes in Energy Management Systems. Electronics 2025, 14, 2336. https://doi.org/10.3390/electronics14122336
Powroźnik P, Szcześniak P, Suliga M. Fuzzy Logic in Smart Meters to Support Operational Processes in Energy Management Systems. Electronics. 2025; 14(12):2336. https://doi.org/10.3390/electronics14122336
Chicago/Turabian StylePowroźnik, Piotr, Paweł Szcześniak, and Mateusz Suliga. 2025. "Fuzzy Logic in Smart Meters to Support Operational Processes in Energy Management Systems" Electronics 14, no. 12: 2336. https://doi.org/10.3390/electronics14122336
APA StylePowroźnik, P., Szcześniak, P., & Suliga, M. (2025). Fuzzy Logic in Smart Meters to Support Operational Processes in Energy Management Systems. Electronics, 14(12), 2336. https://doi.org/10.3390/electronics14122336








