Abstract
Accurate and timely estimation of the root-mean-square (RMS) voltage is essential for grid-connected inverter systems, where it underpins reference generation, synchronization, and protection functions. Conventional RMS estimation methods, based on squaring, averaging, and taking the square root of values over full-cycle windows, achieve high accuracy but incur significant latency and computational overhead, thereby limiting their suitability for real-time control. Frequency-domain approaches, such as the FFT or wavelet analysis offer harmonic decomposition but are too complex for cost-sensitive embedded controllers. To address these challenges, this paper proposes an averaging-based RMS estimation method that exploits the proportionality between the mean absolute value of a sinusoidal waveform and its RMS. The method computes a moving average of the absolute voltage over a half-cycle window synchronized to the phase-locked loop (PLL) frequency, followed by a fixed scaling factor. This recursive implementation reduces the computational burden to a few arithmetic operations per sample while maintaining synchronization with off-nominal frequencies. Time-domain simulations under nominal (60 Hz) and deviated frequencies (57 Hz and 63 Hz) demonstrate that the proposed estimator achieves steady-state accuracy comparable to that of conventional and adaptive methods but with convergence within a half-cycle, thereby reducing latency by nearly 50%. These results confirm the method’s suitability for fast, reliable, and resource-efficient real-time inverter control in modern distribution grids. To provide a comprehensive evaluation, the paper first reviews conventional RMS estimation methods and their inherent limitations, followed by a detailed presentation of the proposed averaging-based approach. Simulation results under both nominal and off-nominal frequency conditions are then presented, along with a comparative analysis highlighting the advantages of the proposed method.
1. Introduction
In grid-connected inverter systems, accurate estimation of the root-mean-square (RMS) voltage is fundamental for functions such as reference generation, synchronization, and protection [1,2]. RMS estimation underpins various control strategies, including voltage-oriented control (VOC) and power-based regulation [3]. While the conventional RMS definition—squaring the instantaneous waveform, averaging over a full window, and taking the square root—ensures high accuracy, it is computationally demanding and introduces latency proportional to the window length [4,5]. This latency becomes critical in low-frequency grid conditions, where a full-cycle measurement may span tens of milliseconds, limiting the controller’s ability to react promptly to dynamic disturbances [6,7].
In embedded control platforms with constrained processing power, such as digital signal processors (DSPs) and microcontrollers, the combination of high computational load and latency can compromise transient performance [8]. This challenge is exacerbated in modern grids, where voltage fluctuations, harmonic distortion, and frequency deviations are increasingly common due to the integration of renewable energy sources [9,10]. Consequently, there is a strong demand for RMS estimation methods that retain sufficient accuracy while significantly reducing latency and computational cost [11,12].
True RMS estimation inherently accounts for harmonic distortion, making it robust in non-ideal conditions. However, its reliance on long data windows results in a slow response to sudden voltage changes [13]. Frequency-domain approaches, such as fast Fourier transform (FFT) or wavelet-based analysis, can provide harmonic decomposition but require high sampling rates, complex filtering, and substantial memory, making them less suitable for cost-sensitive real-time controllers [14].
For real-time inverter control, the primary objective is not to obtain a metrologically exact RMS value but rather to acquire a sufficiently accurate estimate quickly enough to be useful within the control loop. In this context, latency reduction is often more beneficial for system stability than marginal improvements in absolute accuracy [15]. This trade-off motivates the development of simplified RMS estimation strategies tailored specifically for control purposes.
This paper proposes an averaging-based RMS estimation method that approximates the RMS voltage using a moving average of the absolute voltage waveform, followed by scaling. The proposed method substantially reduces computational overhead and estimation latency, making it particularly suitable for real-time control in grid-connected inverters.
In summary, the critical literature review highlights the following points:
- Conventional RMS estimation methods [4,5,6,7,11,12,13] provide high accuracy but suffer from long latency and heavy computational demand, which limit their suitability for real-time inverter control.
- Frequency-domain approaches [14] enable harmonic decomposition but require high sampling rates and large memory, making them impractical for cost-sensitive embedded platforms.
- Current global research lacks simplified RMS estimation strategies that achieve both low latency and low computational cost while maintaining sufficient accuracy under grid disturbances.
- To address this gap, the present work proposes an averaging-based RMS estimation method that exploits the proportionality between mean absolute value and RMS, offering reduced complexity and faster response.
- The proposed solution directly concerns real-time inverter control functions such as reference generation, synchronization, and protection [1,2,3], providing a practical pathway to improve transient performance in modern renewable-integrated grids [8,9,10,15].
The rest of this paper is organized as follows. Section 2 reviews conventional RMS estimation methods and their limitations in real-time applications. Section 3 introduces the proposed averaging-based RMS estimation method, covering its conceptual foundation, algorithmic implementation, and integration into inverter control. Section 4 presents simulation results under nominal and off-nominal frequency conditions, followed by a comparative evaluation. Finally, Section 5 concludes the paper and outlines future research directions.
2. Analysis of Conventional RMS Estimation Methods
2.1. Definition of RMS and Its Importance in Power Conversion Systems
The RMS value of a voltage or current waveform is a fundamental metric in power conversion systems [16,17,18]. It represents the equivalent DC quantity that delivers the same power to a resistive load as the given AC waveform. Mathematically, for a periodic voltage v(t) with fundamental period T, the RMS value VRMS is defined as follows:
This definition guarantees that RMS values directly capture the thermal and power-related effects in electrical components, which is why they are indispensable for monitoring, protection, and control of grid-connected inverters. However, implementing this definition in practice requires continuous-time integration over one or more cycles, introducing significant computational delay that makes it unsuitable for real-time control [19].
2.2. Conventional Moving-Window RMS Estimation
A widely used approach in digital controllers is the moving-window RMS estimator. In this method, the waveform is sampled at discrete instants, and the RMS value is obtained from a finite set of N samples corresponding to one or multiple cycles:
Here, N denotes the number of samples within the chosen window, and k represents the discrete-time index corresponding to the current sampling instant. This method achieves high accuracy and inherently filters out high-frequency noise when multiple cycles are included. However, it requires storing many samples and recomputing the squared sum at every update, leading to high memory demand and computational burden [20,21]. Moreover, it introduces a latency equal to the window length, which can be substantial in low-frequency grids [22]. Its performance also degrades under non-stationary conditions, such as frequency deviations or voltage dips, since the integration interval assumes stationarity.
2.3. Frequency-Locked and Adaptive RMS Estimation
To address frequency variation, adaptive RMS algorithms have been developed. These synchronize the estimation window with the instantaneous grid frequency, typically obtained from a phase-locked loop (PLL) [23]. For a grid period Tgrid, the RMS value VRMS is computed as follows:
By dynamically adjusting the window length to match the actual grid period, the estimator avoids bias caused by off-nominal frequencies. This improves accuracy under frequency deviations. However, the method requires tight coupling with PLL dynamics and frequent recalculation of variable-length sums, which increases computational complexity [23,24,25]. As a result, the adaptive approach improves accuracy but often at the expense of responsiveness in real-time control.
2.4. Limitations in Real-Time Control
Although the methods above provide mathematically accurate values for metering, they exhibit several limitations when applied to inverter control. First, there is a mismatch in objectives: metering-oriented RMS estimation includes the entire spectrum—fundamental, harmonics, and noise—to ensure compliance and monitoring. Control-oriented RMS estimation, by contrast, requires only the fundamental component to regulate active and reactive power. This distinction means that conventional RMS estimators may provide information unnecessary or even detrimental for real-time control.
Second, all window-based methods introduce latency, as they must accumulate data over at least one cycle before producing an accurate value. This delay can hinder the inverter’s response to rapid grid disturbances.
Finally, the recursive or integration-heavy computations of conventional approaches impose an additional burden on digital controllers, especially at high switching frequencies where updates must occur every few microseconds.
These drawbacks motivate the exploration of simplified estimation methods that reduce latency and computational effort while still delivering sufficient accuracy for real-time inverter control [26,27,28,29,30,31].
3. The Proposed Averaging-Based RMS Estimation Method
3.1. Concept
The proposed method approximates the RMS value by exploiting the relationship between the average magnitude of a sinusoidal signal and its RMS value. For an ideal sinusoidal waveform , the average value VAVG of its absolute value over a half cycle is given by
Since the RMS value VRMS of a sinusoid is calculated as follows
constant proportionality k exists between the mean value VAVG and the RMS value VRMS, expressed as follows:
where .
This proportionality forms the core of the proposed method: by computing a moving average of the absolute waveform and applying a fixed scaling factor, an accurate RMS estimate can be obtained without the need for squaring, integration, or square root operations.
3.2. Algorithm Implementation
To compute the proposed RMS estimator, a direct implementation can be expressed as a moving-window average of the absolute voltage samples, scaled to approximate the RMS value. Specifically, for a window of length N, the direct formula is as follows:
While mathematically straightforward, this formulation requires summing N samples at every update, leading to a computational complexity of O(N). Such repeated summations are inefficient for real-time inverter controllers, particularly under high sampling frequencies.
To address this issue, the summation can be reformulated in a recursive manner. By reusing the previous accumulated sum, the improved rule becomes the following:
This recursive update reduces the complexity to O(1), as only one addition and one subtraction are required per new sample. Since the recursive form is directly derived from the original definition, both methods are mathematically equivalent, but the recursive algorithm is far better suited for embedded digital controllers, where memory and computation are constrained.
Accordingly, the recursive formulation will be used in the implementation and performance evaluation throughout this paper, while the direct expression serves to highlight the theoretical foundation of the proposed RMS estimator.
3.3. Integration into Inverter Control
The proposed averaging-based RMS estimator can be seamlessly integrated into the control framework of grid-connected inverters. The RMS voltage serves as a critical signal for reference generation, synchronization, and protection mechanisms, as shown in Figure 1. In particular, the estimated RMS value defines the magnitude of voltage or current references used in power regulation, providing a stable amplitude reference that complements the phase information obtained from a phase-locked loop (PLL). Protection functions such as over-voltage and under-voltage detection also rely on fast and reliable RMS tracking to ensure grid code compliance. By delivering low-latency and computationally efficient estimates, the proposed method enables the controller to respond promptly to grid disturbances without the delay inherent in conventional RMS estimation techniques.
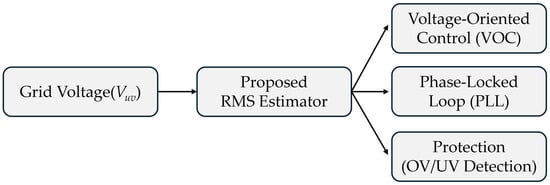
Figure 1.
Functional block diagram of the proposed RMS estimator in a grid-connected inverter controller.
Within voltage-oriented control (VOC) schemes, the accurate and timely estimation of the RMS voltage is essential for the normalization of d–q components of measured quantities, which directly influences the regulation of active and reactive power. With the proposed estimator, the RMS value can be updated at every sampling instant, thereby reducing the latency in reference updates and enhancing the transient response during events such as voltage sags, swells, or harmonic distortions. The recursive update mechanism further ensures that the method can be implemented efficiently in digital controllers such as DSPs or FPGAs, where computational resources are often constrained.
The proposed estimator also enhances the performance of inverter protection mechanisms. Conventional moving-window estimators typically require at least one cycle of the fundamental frequency to provide accurate RMS values, resulting in detection delays of approximately 16.7 ms for a 60 Hz grid. Such delays may be insufficient to satisfy modern grid-code requirements for low-voltage ride-through or fault ride-through. In contrast, the averaging-based method reduces the detection time to a fraction of the grid period, enabling faster protective actions and improving compliance with grid stability requirements.
Compared to conventional approaches, the proposed method offers three primary advantages: lower latency, reduced computational complexity, and adequate robustness under practical harmonic conditions. While conventional estimators may achieve slightly higher accuracy in idealized conditions, their computational burden and inherent delay limit their suitability for real-time control. The proposed method, by contrast, strikes an effective balance between speed and accuracy, making it highly suitable for real-time inverter control applications.
4. Simulation Results
To validate the performance of the proposed averaging-based RMS estimation method, time-domain simulations were conducted under conditions representative of low-voltage grid-connected inverters. The grid voltage was modeled as a pure sinusoid with a nominal RMS value of 220 V. To account for frequency deviations around the nominal value, three cases were considered: 57 Hz, 60 Hz, and 63 Hz. These scenarios correspond to approximately ±5% variation relative to nominal operation and provide a realistic benchmark for assessing estimator performance.
The simulations were discretized with a sampling frequency of 10 kHz, which provides sufficient resolution for RMS estimation. Each run lasted over 50 ms, equivalent to about three cycles at 60 Hz, allowing for the observation of both initial transients and steady-state convergence. The short horizon also captures the impact of partially filled averaging windows at startup, which directly affects estimation latency.
For the conventional moving-window RMS estimator, the window length was fixed to one nominal cycle, corresponding to 167 samples at 60 Hz. This configuration does not adapt when the frequency deviates from its nominal value, and its performance therefore degrades under off-nominal conditions. The adaptive RMS estimator, by contrast, dynamically adjusts its window length based on the instantaneous grid period provided by the PLL, yielding 175, 167, and 159 samples for 57, 60, and 63 Hz, respectively. The proposed averaging-based estimator employs a half-cycle window synchronized to the PLL frequency, corresponding to 88, 83, and 79 samples for the three cases. In all implementations, the early-time estimate uses only the available samples—that is, k + 1 samples at time index k—until the target window length is reached. This ensures that the transient performance of each method is evaluated consistently.
After averaging the absolute voltage over the PLL-synchronized half-cycle window, the proposed method applies the theoretical scaling factor to obtain the RMS estimate. This design preserves the method’s computational simplicity and inherently short latency while ensuring synchronization with the actual grid frequency.
The three estimators were benchmarked against the analytical RMS reference of the modeled sinusoidal waveform. Their performance was evaluated in terms of (i) steady-state accuracy and (ii) latency, defined as the time required for the estimated RMS to enter and remain within a specified error band relative to the true RMS for at least 0.5 ms. This framework provides a consistent basis for comparing the proposed approach with conventional and adaptive RMS estimation techniques under realistic inverter operating conditions.
4.1. Results at Nominal Frequency (60 Hz)
Figure 2 illustrates the comparison of three RMS estimation methods under a pure sinusoidal grid voltage of 220 V at 60 Hz, sampled at 10 kHz. The figure shows the instantaneous voltage v(t), its absolute value ∣v(t)∣, the true RMS (220 V), and the estimated RMS values from three methods. The conventional moving-window method uses a fixed window of one cycle (N1 = 167 samples), while the adaptive method dynamically adjusts the window length N2 according to the instantaneous grid frequency provided by the PLL, which is 167 samples at 60 Hz. The proposed averaging-based method uses a PLL-synchronized half-cycle window (N3 = 83 samples) and applies a scaling factor of to the mean absolute value to obtain the RMS estimate. Results confirm that the proposed method converges to the true RMS once the PLL-synchronized half-cycle averaging window is fully populated (~8.3 ms), whereas both the conventional and adaptive methods require a full cycle before achieving steady-state accuracy.
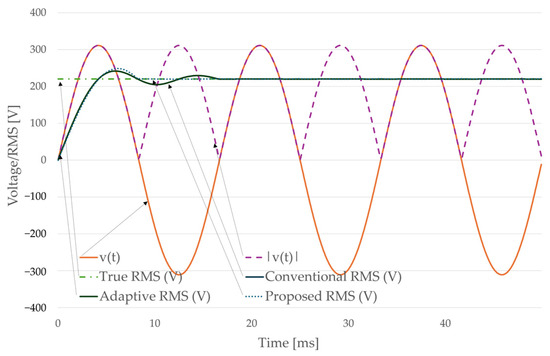
Figure 2.
RMS estimation under pure sinusoidal grid (220 V, 60 Hz).
Figure 3 presents the estimation errors of the three methods relative to the true RMS value of 220 V. Both the moving-window and adaptive approaches exhibit transient errors up to 2% during the initial cycle, reflecting the one-cycle averaging horizon. In contrast, the proposed estimator shows negligible error once its half-cycle averaging window is filled, corresponding to the end of the first half-cycle. This improvement arises from its reduced window length and the direct mathematical relation between the mean absolute value and the RMS for sinusoidal waveforms.
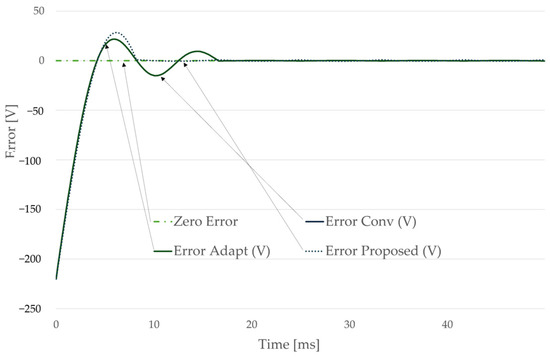
Figure 3.
Estimation errors relative to the true RMS value (220 V, 60 Hz).
Latency is defined as the time required for the RMS estimate to enter and remain within a predefined error band relative to the true RMS for at least 0.5 ms. Figure 4 summarizes latency performance under two thresholds: ±1% (2.2 V) and ±0.5% (1.1 V). The proposed half-cycle estimator reaches both thresholds in 8.2 ms, consistent with its half-cycle averaging window. In contrast, the conventional and adaptive methods exhibit longer delays of approximately 12.3 ms (±1%) and up to 16.5 ms (±0.5%), reflecting their reliance on a full-cycle averaging process. These results demonstrate that the proposed method not only achieves accurate steady-state RMS estimation but also provides a clear latency advantage, making it particularly suitable for fast and stable real-time inverter control.
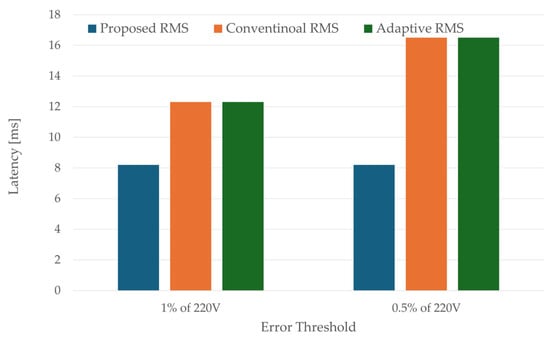
Figure 4.
Latency in entering and remaining within error thresholds (220 V, 60 Hz).
4.2. Results Under Lower Frequency Deviation (57 Hz)
To investigate the impact of frequency deviation, simulations were performed for a grid voltage of 220 V RMS at 57 Hz, representing approximately a 5% deviation from the nominal operating frequency. The sampling frequency was maintained at 10 kHz, and the analytical reference RMS value was fixed at 220 V. Three RMS estimation strategies were evaluated under these conditions: the conventional moving-window method, which uses a fixed one-cycle window of 167 samples corresponding to 60 Hz; the adaptive estimator, which adjusts its window length to 175 samples based on the PLL-tracked 57 Hz period; and the proposed averaging-based estimator, which employs a PLL-synchronized half-cycle window of 88 samples.
Figure 5 illustrates the RMS estimation trajectories for the three methods. The proposed estimator rapidly converges to the true RMS value within a half-cycle (≈8.8 ms), consistent with its reduced averaging interval. The adaptive estimator achieves accurate results but requires a full cycle (≈17.5 ms) to settle. By contrast, the conventional method, operating with a mismatched 60 Hz window, exhibits a persistent steady-state offset of approximately 0.5–0.7 V, demonstrating its sensitivity to off-nominal frequencies.
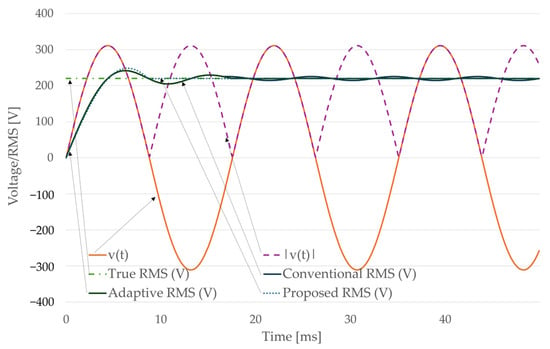
Figure 5.
RMS estimation under a sinusoidal grid with lower frequency deviation (220 V, 57 Hz).
Figure 6 presents the corresponding estimation errors relative to the true RMS. Both the adaptive and proposed estimators achieve steady-state accuracy within 0.05%. The conventional approach, however, remains biased because its fixed one-cycle window does not align with the actual 57 Hz grid period. The proposed estimator further distinguishes itself by eliminating transient errors after only one half-cycle, highlighting its superior responsiveness.
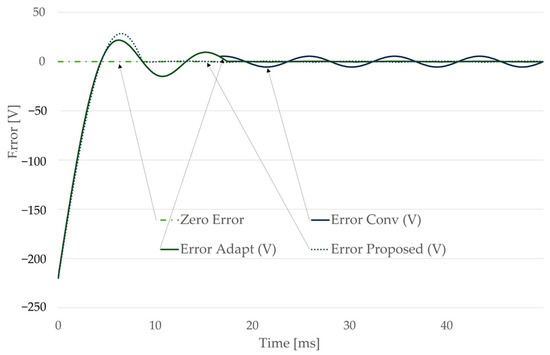
Figure 6.
Estimation errors relative to the true RMS value (220 V, 57 Hz).
Figure 7 shows the latency analysis. Latency is defined as the time required for the RMS estimate to enter and remain within a specified error threshold for at least 0.5 ms. Two thresholds were considered: ±1% (2.2 V) and ±0.5% (1.1 V). The proposed half-cycle estimator reached both thresholds in approximately 8.6–8.7 ms, reflecting its inherent half-cycle averaging design. The adaptive estimator required 12.9 ms to satisfy the ±1% threshold and 17.3 ms for the ±0.5% threshold. The conventional method exhibited comparable delays to the adaptive approach, but with the additional drawback of a steady-state bias.
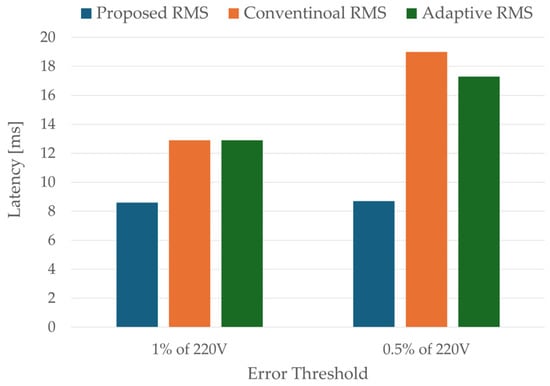
Figure 7.
Latency in entering and remaining within error thresholds (220 V, 57 Hz).
These results demonstrate that, under significant frequency deviation, the proposed averaging-based estimator provides both fast transient convergence and robust steady-state accuracy. Compared with the conventional and adaptive approaches, it offers the most favorable balance of simplicity, low computational cost, and suitability for real-time inverter control.
4.3. Results Under Higher Frequency Deviation (63 Hz)
To further evaluate the effect of frequency deviation, simulations were conducted for a grid voltage of 220 V RMS at 63 Hz, representing approximately a +5% deviation from the nominal frequency. The sampling frequency was set to 10 kHz, and the analytical RMS reference was fixed at 220 V. As in previous cases, three RMS estimation methods were compared: the conventional moving-window estimator, with a fixed one-cycle window of 167 samples corresponding to 60 Hz; the adaptive estimator, which adjusts its window to 159 samples based on the PLL-tracked 63 Hz period; and the proposed averaging-based estimator, which uses a PLL-synchronized half-cycle window of 79 samples.
Figure 8 presents the RMS estimation trajectories for the three approaches under the 63 Hz grid condition. The proposed estimator rapidly converges to the true RMS within a half-cycle (~7.9 ms), maintaining both accuracy and responsiveness. The adaptive estimator eliminates steady-state bias but requires a full cycle (~15.9 ms) to reach a stable state. By contrast, the conventional method, operating with a mismatched window based on 60 Hz, introduces a systematic bias of approximately 0.6–0.8 V, again reflecting its sensitivity to off-nominal frequencies.
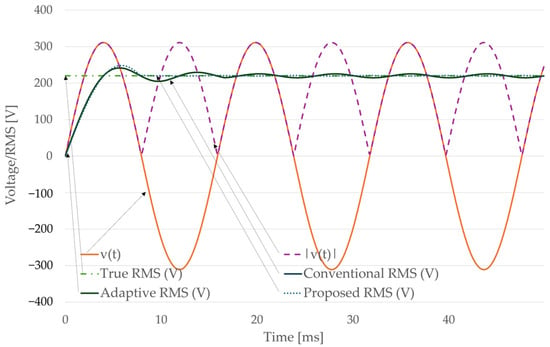
Figure 8.
RMS estimation under a sinusoidal grid with higher frequency deviation (220 V, 63 Hz).
Figure 9 shows the estimation errors relative to the true RMS value. The proposed method maintains an error below 0.05% once its half-cycle window is filled, while the adaptive estimator exhibits a similar steady-state accuracy after a full cycle. The conventional approach, however, retains a persistent bias due to its fixed window assumption. The superior transient performance of the proposed method is evident in its ability to reduce errors to negligible levels after only half a cycle.
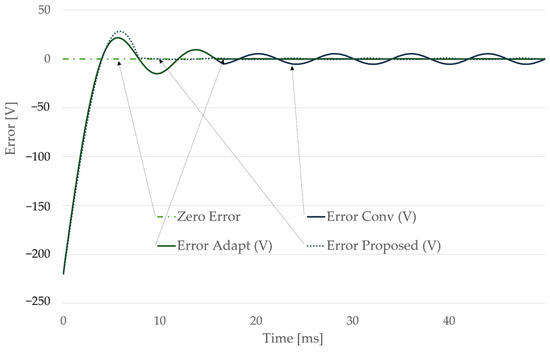
Figure 9.
Estimation errors relative to the true RMS value (220 V, 63 Hz).
Figure 10 presents the latency analysis, using thresholds of ±1% (2.2 V) and ±0.5% (1.1 V). The proposed estimator satisfied both thresholds in approximately 7.9–8.0 ms, reflecting its PLL-synchronized half-cycle averaging. The adaptive estimator required about 12.5 ms to satisfy the ±1% condition and 15.8 ms for the ±0.5% threshold. The conventional method displayed similar delays to the adaptive approach but with the additional drawback of steady-state bias, making it less suitable for real-time control.
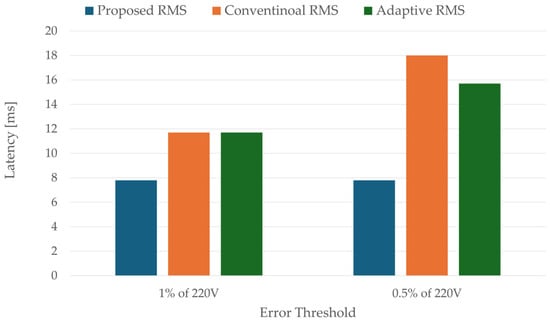
Figure 10.
Latency in entering and remaining within error thresholds (220 V, 63 Hz).
Overall, the results at 63 Hz confirm that the proposed averaging-based estimator maintains accuracy and low latency even under higher frequency deviations. Compared to both conventional and adaptive methods, it provides the most favorable trade-off between transient response, computational simplicity, and suitability for fast inverter control loops.
4.4. Comparative Evaluation
To consolidate the findings across nominal and off-nominal frequency conditions, the three RMS estimation methods are compared in Table 1, which reports steady-state accuracy, latency to reach defined error thresholds, sensitivity to frequency deviation, and computational burden. Latency values are now shown for both ±1% and ±0.5% thresholds to ensure consistency across all methods.

Table 1.
Comparative summary of RMS estimation methods.
The comparison yields several insights. First, in terms of steady-state accuracy, both the adaptive and proposed estimators achieve near-identical performance across nominal and off-nominal frequencies, while the conventional method suffers from a persistent bias under frequency deviation due to its fixed 60 Hz window. Second, when considering latency, the proposed averaging-based estimator consistently outperforms both alternatives. It reaches the ±1% and ±0.5% thresholds in roughly half a cycle (≈8 ms), whereas both the conventional and adaptive methods require a full cycle (12–17 ms). Third, regarding robustness to frequency deviation, the adaptive and proposed methods maintain accurate operation by leveraging PLL synchronization, while the conventional method degrades due to window mismatch. Finally, the computational burden of the proposed method is substantially lower than that of both conventional and adaptive estimators, since it avoids recursive integration and large memory storage, relying instead on a simple averaging and scaling step.
In summary, the proposed averaging-based method provides the most favorable trade-off across all relevant metrics: accuracy comparable to state-of-the-art methods, substantially lower latency, robustness against frequency deviation, and minimal computational cost. These attributes reinforce its suitability for real-time inverter control applications, where simplicity and responsiveness are of paramount importance.
5. Conclusions
This paper has introduced an averaging-based RMS estimation method tailored for real-time control of grid-connected inverters. By exploiting the proportional relationship between the mean absolute value of a sinusoidal waveform and its RMS, the method provides accurate voltage estimates with substantially reduced computational effort. The recursive implementation requires only minimal arithmetic operations per sample, ensuring efficient operation even on resource-constrained embedded controllers.
Simulation studies under nominal and off-nominal frequency conditions (57, 60, and 63 Hz) have shown that the proposed estimator achieves steady-state accuracy comparable to that of conventional and adaptive RMS methods, while converging within a half-cycle. This low-latency behavior enables faster response to grid disturbances and enhances stability in inverter control loops. Unlike conventional estimators, which exhibit systematic bias under frequency deviations, the proposed method maintains accuracy through PLL synchronization. For example, Figure 3, Figure 6, and Figure 9 clearly illustrate how the proposed method eliminates steady-state bias within a half-cycle, while Figure 4, Figure 7, and Figure 10 demonstrate its latency advantage compared to conventional and adaptive approaches. These graphical observations directly support the claim that the method achieves both rapid convergence and robust accuracy in the presence of frequency deviations.
Beyond technical performance, the proposed estimator has clear industrial relevance. In modern distribution grids with increasing penetration of renewable energy sources, rapid and reliable RMS estimation supports voltage-oriented control, active and reactive power regulation, and fast protection mechanisms such as low-voltage ride-through (LVRT) compliance. By reducing computational burden and response delay, the method can be implemented in cost-sensitive inverter hardware without compromising control performance. In practical terms, the proposed method can be applied to inverter control in microgrids, rapid detection of voltage sags and swells in protection devices, and the optimization of algorithms for systems with limited computing power. This makes it well aligned with practical deployment in distributed generation, microgrid systems, and renewable-integrated power electronics.
In summary, the proposed averaging-based method achieves a favorable balance between accuracy, speed, and simplicity. These qualities establish it as a strong candidate for real-time inverter applications today, while future research will extend its validation to harmonic-rich environments, unbalanced voltages, and noisy conditions through further simulation-based studies.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RMS | Root Mean Square |
| VOC | Voltage-Oriented Control |
| PLL | Phase-Locked Loop |
| DSP | Digital Signal Processor |
| FPGA | Field-Programmable Gate Array |
References
- Bastos, A.F.; Lao, K.W.; Todeschini, G.; Santoso, S. Novel Moving Average Filter for Detecting RMS Voltage Step Changes in Triggerless PQ Data. IEEE Trans. Power Deliv. 2018, 33, 2920–2929. [Google Scholar] [CrossRef]
- Geiger, D.L.; Halpin, S.M. Assessing Voltage Fluctuations and Lamp Flicker Using RMS Voltages. IEEE Trans. Power Deliv. 2017, 32, 2481–2488. [Google Scholar] [CrossRef]
- Bollen, M.H.J.; Goossens, P.; Robert, A. Assessment of Voltage Dips in HV-Networks: Deduction of Complex Voltages from the Measured RMS Voltages. IEEE Trans. Power Deliv. 2004, 19, 783–790. [Google Scholar] [CrossRef]
- Santoso, S.; Powers, E.J.; Grady, W.M.; Parsons, A.C. Power Quality Disturbance Waveform Recognition Using Wavelet-Based Neural Classifier. IEEE Trans. Power Deliv. 2000, 15, 222–228. [Google Scholar] [CrossRef]
- Yang, J.; Shu, Z.; Wang, T.; Xiang, S.; Nie, J.; Wang, S. Online Digital Implementation of Wide Voltage Range RMS-Current-Optimized Control With Voltage Balancing Capability for DAB Converter. IEEE Trans. Power Electron. 2023, 38, 4360–4377. [Google Scholar] [CrossRef]
- Pogliano, U.; Trinchera, B.; Francone, F. Reconfigurable Unit for Precise RMS Measurements. IEEE Trans. Instrum. Meas. 2009, 58, 827–831. [Google Scholar] [CrossRef]
- Shenil, P.S.; George, B. Development of a Nonintrusive True-RMS AC Voltage Measurement Probe. IEEE Trans. Instrum. Meas. 2019, 68, 3899–3906. [Google Scholar] [CrossRef]
- Zacchigna, F.G. Methodology for CNN Implementation in FPGA-Based Embedded Systems. IEEE Embed. Syst. Lett. 2023, 15, 85–88. [Google Scholar] [CrossRef]
- Yu, Y.; Ju, P.; Peng, Y.; Lou, B.; Huang, H. Analysis of Dynamic Voltage Fluctuation Mechanism in Interconnected Power Grid with Stochastic Power Disturbances. J. Mod. Power Syst. Clean Energy 2020, 8, 38–45. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, K.; Li, X.; Li, Y.; Song, P. A Control Strategy for Suppressing Submodule Capacitor Voltage Fluctuation of MMC Based on Circulating Current Voltage Drop Balance. IEEE Access 2021, 9, 9130–9141. [Google Scholar] [CrossRef]
- Mauritzen, D.W.; Alam, M.S. Comments on “Accurate Measurement of Power, Energy, and True RMS Voltage Using Synchronous Counting”. IEEE Trans. Instrum. Meas. 1997, 46, 1300–1301. [Google Scholar] [CrossRef]
- Lapuh, R.; Svetik, Z. Evaluation of a Voltage Source with Three Calculable RMS Outputs. IEEE Trans. Instrum. Meas. 1997, 46, 784–788. [Google Scholar] [CrossRef]
- Xu, G.; Tang, J.; Zhang, L.; Xiong, W.; Sun, Y.; Su, M. A Hybrid Extended Phase Shift Modulation Strategy for DAB Converter With DC Blocking Capacitor to Extend ZVS Range and Reduce RMS Current. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6192–6207. [Google Scholar] [CrossRef]
- Luo, Z.; Yao, J.; Sang, Y.; Ioinovici, A. Photovoltaic-Powered High-Performance Common-Ground Switched-Capacitor Inverter With Ultra-Wide Input Voltage Range and Constant RMS Output Voltage and Level Count. IEEE Trans. Ind. Electron. 2025, 72, 9071–9081. [Google Scholar] [CrossRef]
- Haberman, M.A.; Spinelli, E.M. A Noncontact Voltage Measurement System for Power-Line Voltage Waveforms. IEEE Trans. Instrum. Meas. 2020, 69, 2790–2797. [Google Scholar] [CrossRef]
- Gill, L.; Garcia Rodriguez, L.A.; Kaplar, R.; Michaels, A.J. Novel On-State Voltage Measurement Circuit Topology, Operation, and Performance for High-Voltage Wide-Bandgap Devices. IEEE Trans. Power Electron. 2025, 40, 15433–15449. [Google Scholar] [CrossRef]
- Gallo, D.; Landi, C.; Luiso, M. Accuracy Analysis of Algorithms Adopted in Voltage Dip Measurements. IEEE Trans. Instrum. Meas. 2010, 59, 2652–2659. [Google Scholar] [CrossRef]
- Pogliano, U.; Bosco, G.C.; Lanzillotti, M. Generalized Automatic System for AC/DC Transfer, AC Voltage, and AC Current Measurements. IEEE Trans. Instrum. Meas. 2006, 55, 1747–1751. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Qu, Z.; Cheng, R. A High-Accuracy Ultrasonic Flow Measurement Method Based on Voltage Amplitude Difference. IEEE Trans. Instrum. Meas. 2025, 74, 7507912. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Harmonic Distortion Compensation in Voltage Transformers for Improved Power Quality Measurements. IEEE Trans. Instrum. Meas. 2019, 68, 3823–3830. [Google Scholar] [CrossRef]
- P1564/D19; July 2013—IEEE Guide for Voltage Sag Indices. IEEE: New York, NY, USA, 2014. Available online: https://ieeexplore.ieee.org/servlet/opac?punumber=6781508 (accessed on 15 June 2015).
- Yang, Y.; Wang, H. RMS Calculation Model for Variable Frequency AC and FPGA Implementation. In Proceedings of the 2024 10th Asia Conference on Mechanical Engineering and Aerospace Engineering (MEAE), Taichang, China, 18–20 October 2024; IEEE: New York, NY, USA, 2025. [Google Scholar] [CrossRef]
- Cho, S.-H.; Park, C.-H.; Han, J.; Jang, G. A Waveform Distortion Evaluation Method Based on a Simple Half-Cycle RMS Calculation. IEEE Trans. Power Deliv. 2012, 27, 1461–1467. [Google Scholar] [CrossRef]
- Kostakis, G.T.; Manias, S.N.; Margaris, N.I. A Generalized Method for Calculating the RMS Values of Switching Power Converters. IEEE Trans. Power Electron. 2000, 15, 616–625. [Google Scholar] [CrossRef][Green Version]
- Wang, F.; Bollen, M.H.J. Frequency-Response Characteristics and Error Estimation in RMS Measurement. IEEE Trans. Power Deliv. 2004, 19, 1569–1578. [Google Scholar] [CrossRef]
- Langella, R.; Testa, A. The Effects of Integration Intervals on Recursive RMS Value and Power Measurement in Nonsinusoidal Conditions. IEEE Trans. Instrum. Meas. 2011, 60, 3047–3057. [Google Scholar] [CrossRef]
- Kashif, M.; Singh, B. Multi-Resonant Third-Order Generalized Integrator Based PLL for Seamless Control of Solar-Battery Fed Grid Synchronized Water Pumping System. IEEE Trans. Energy Convers. 2023, 38, 355–366. [Google Scholar] [CrossRef]
- Ciobotaru, M.; Agelidis, V.G.; Teodorescu, R.; Blaabjerg, F. Accurate and Less-Disturbing Active Antiislanding Method Based on PLL for Grid-Connected Converters. IEEE Trans. Power Electron. 2010, 25, 1576–1584. [Google Scholar] [CrossRef]
- Luna, A.; Rocabert, J.; Candela, J.I.; Hermoso, J.R.; Teodorescu, R.; Blaabjerg, F. Grid Voltage Synchronization for Distributed Generation Systems Under Grid Fault Conditions. IEEE Trans. Ind. Appl. 2015, 51, 3414–3425. [Google Scholar] [CrossRef]
- Sun, H.; Wang, S.; Xu, S.; Bi, J.; Wang, Y. Synchronization Stability Analysis of PLL-Based Grid-Connected VSC System by Voltage Space Vectors. CSEE J. Power Energy Syst. 2024, 10, 2055–2064. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, L.; Duan, J. A New Two-Phase Stationary-Frame-Based Enhanced PLL for Three-Phase Grid Synchronization. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 251–255. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).