Efficient GPU Parallel Implementation and Optimization of ARIA for Counter and Exhaustive Key-Search Modes
Abstract
1. Introduction
- 1.
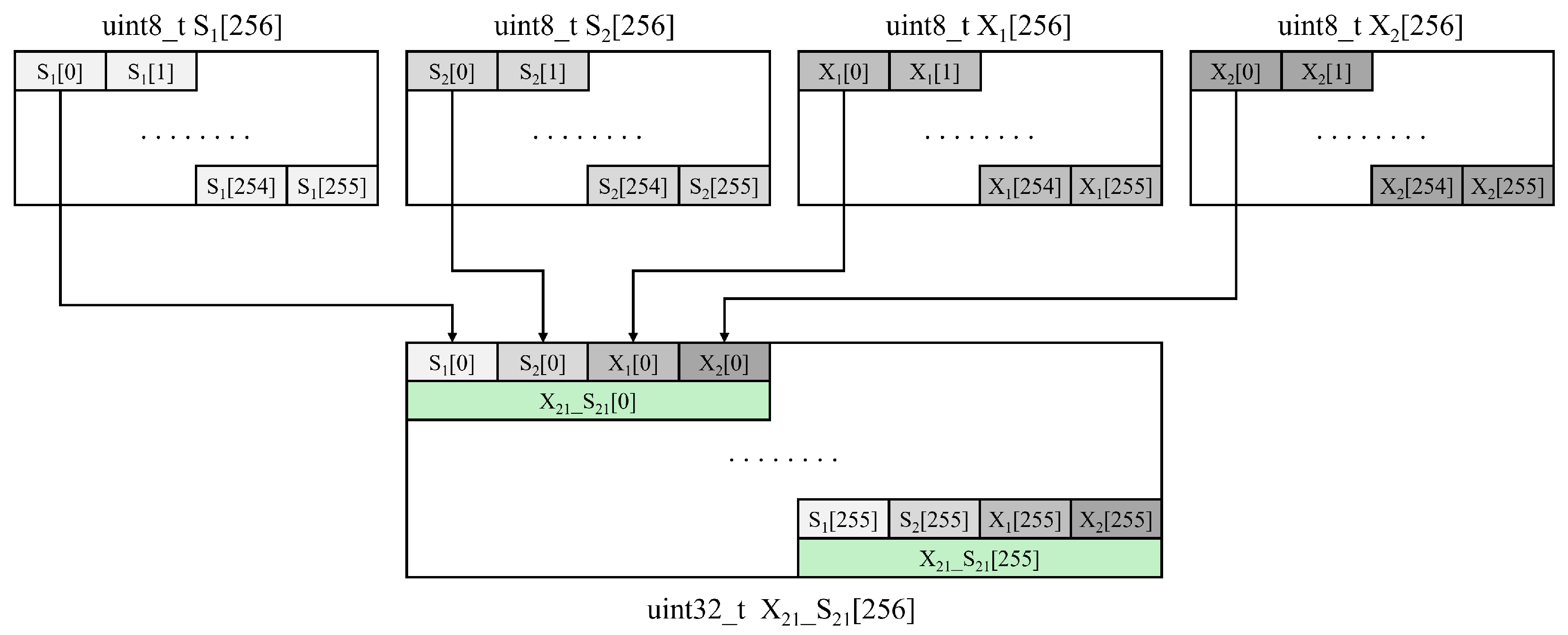
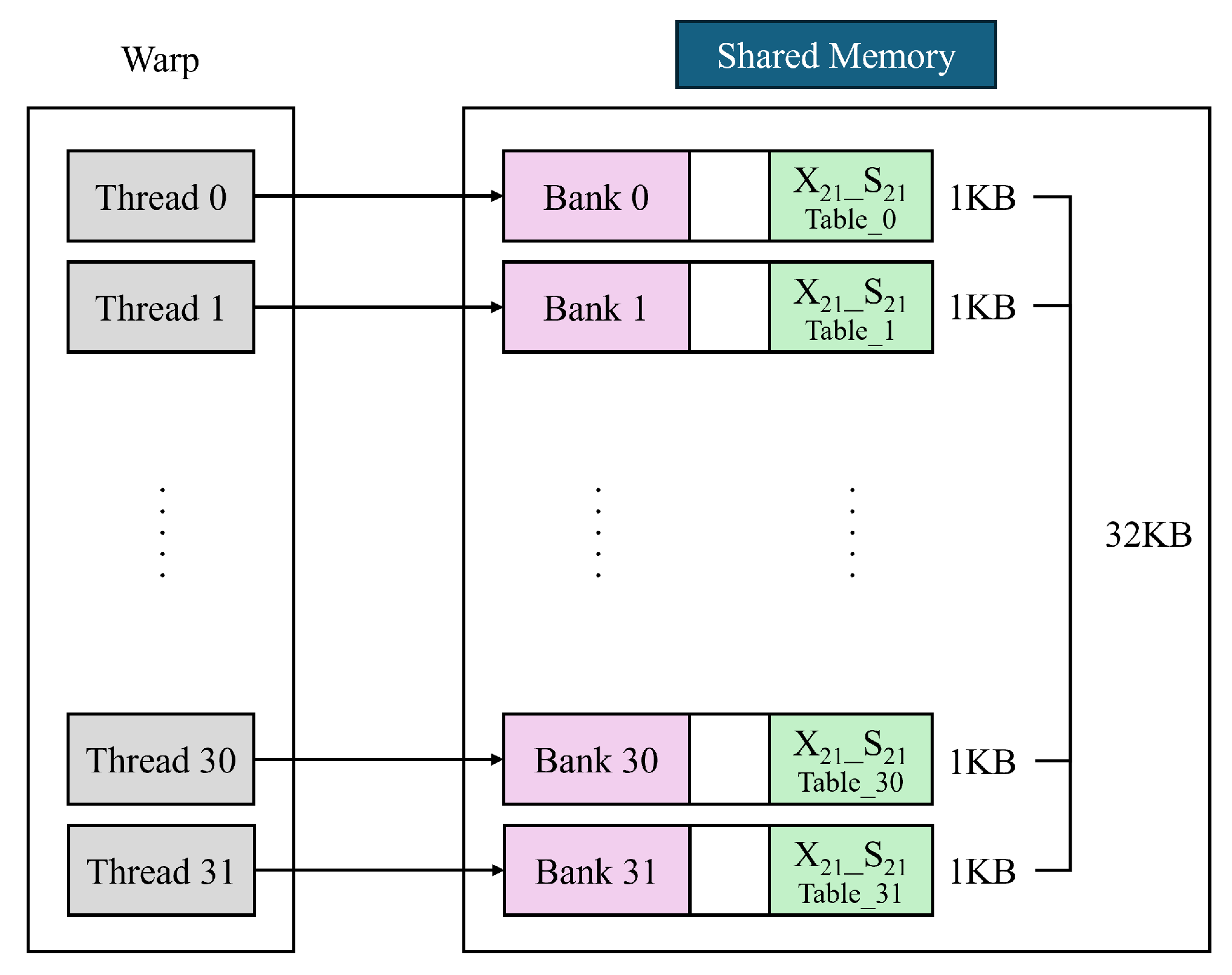
- We implement an optimized CTR mode for the ARIA algorithm. Previous research [7] could not employ a table-copying technique to avoid bank conflicts due to the large size of the S-box table. In this work, we reduce the size of the S-box table from 4 KB to 1 KB so that it can be replicated in shared memory as many times as the number of banks, effectively preventing bank conflicts and maximizing shared memory efficiency. To provide an accurate comparison of performance improvements, we also conduct a detailed profiling analysis based on the storage location of the S-box table. Specifically, we evaluate and compare performance when the table is stored in global memory, shared memory, and shared memory with our proposed bank conflict minimization technique.
- 2.
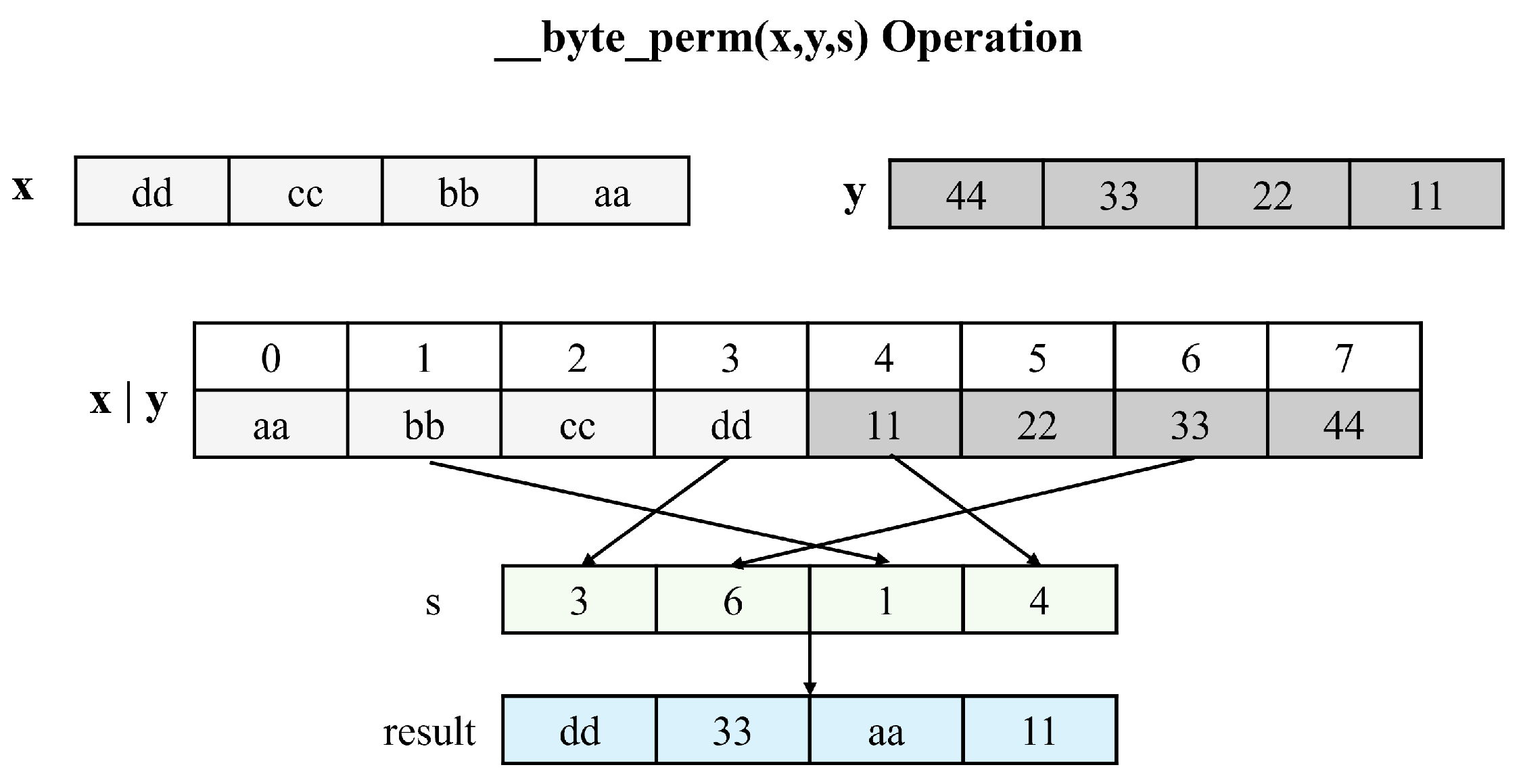
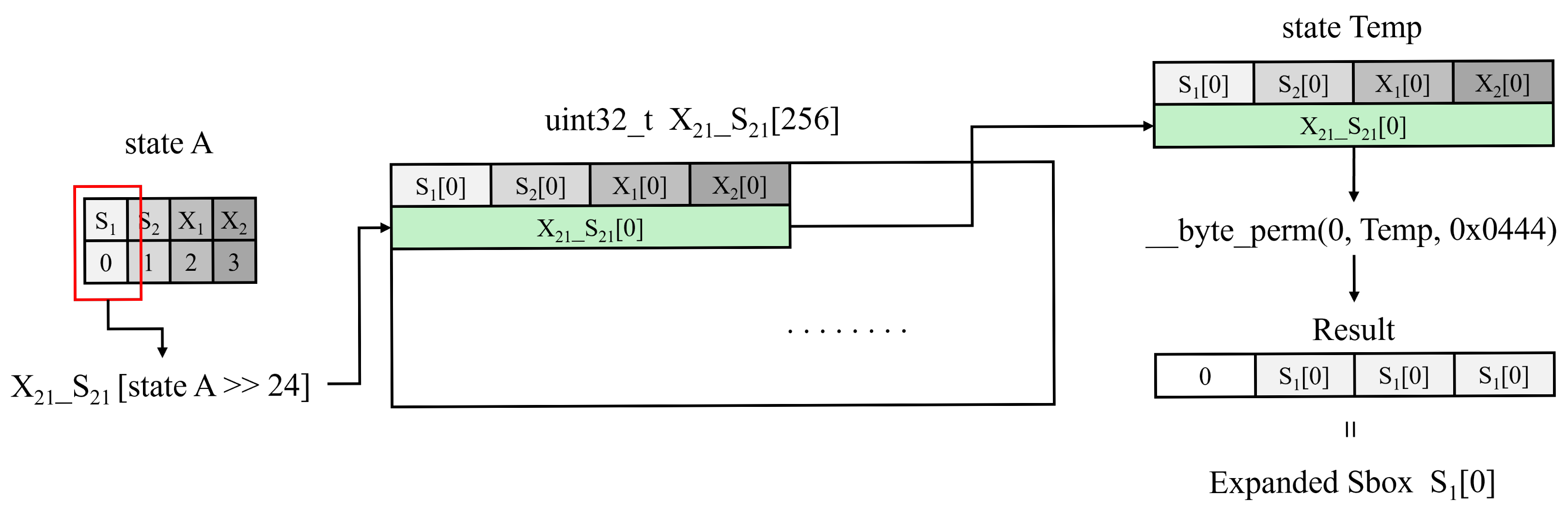
- We extensively utilize CUDA’s built-in function __byte_perm(). Encryption processes often require state transformations such as permutations, which we efficiently implement using __byte_perm() instructions. Furthermore, we reconstruct the outputs of the reduced S-box table using __byte_perm(), achieving the same results as the original S-box with minimal additional overhead.
- 3.
- Exhaustive key searches (ES) in block cipher modes like CTR are suitable for parallel implementations due to their independent block computations. However, performing key expansion for each thread individually creates a memory burden for storing round keys. To address this, we implement an on-the-fly approach that computes round keys as needed. This method significantly reduces memory usage and minimizes memory accesses, resulting in performance improvements. To the best of our knowledge, this work presents the first optimization and performance analysis of ARIA ES operation.
- 4.
- Experiments on the RTX 3060 Mobile and RTX 4080 GPUs show notable performance gains. The RTX 4080 reaches 1532.42 Gbps in ARIA-CTR mode and 1365.84 Gbps in exhaustive search, while the RTX 3060 achieves a 2.34× speedup over prior implementations.
2. Background
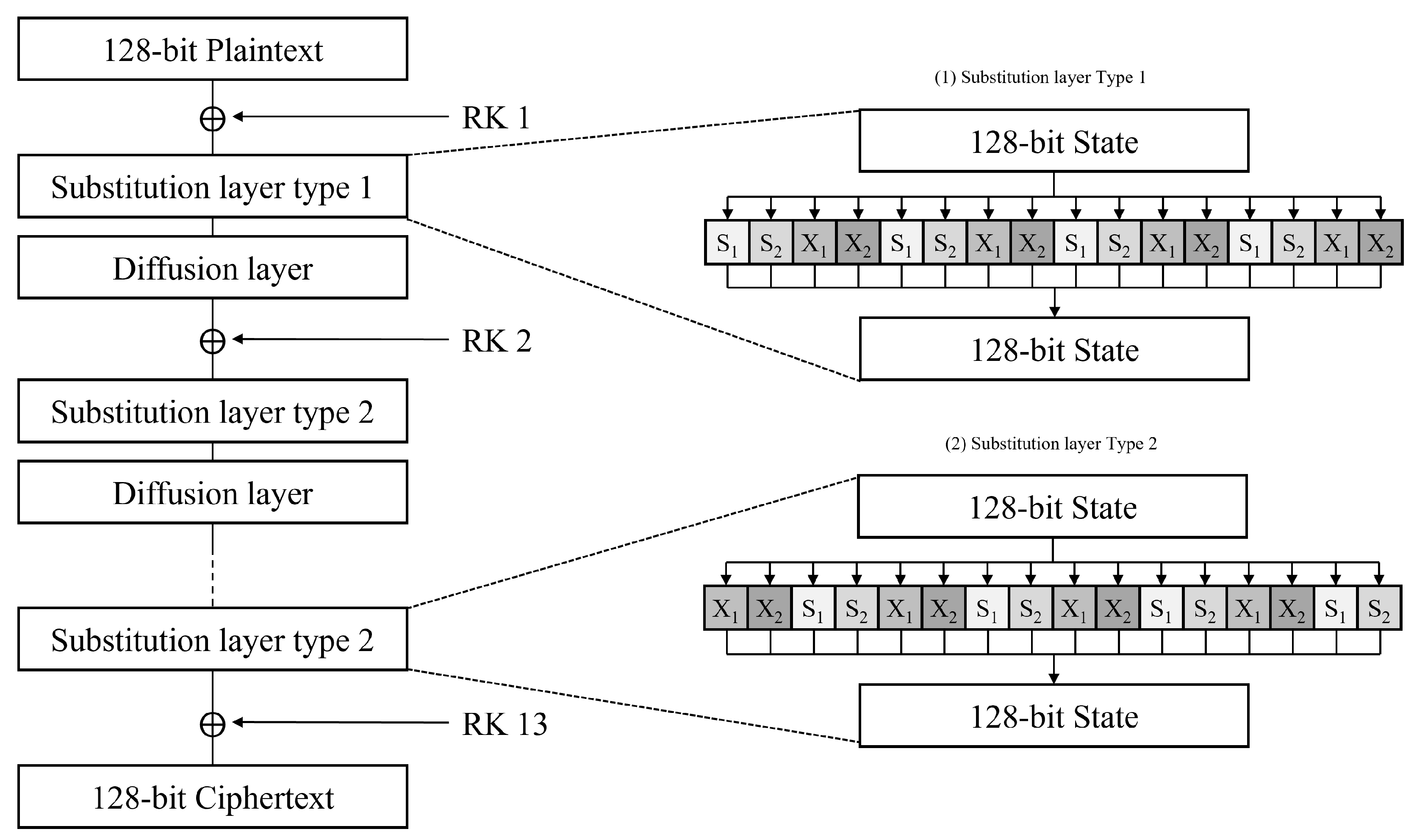
2.1. Overview of the ARIA Block Cipher
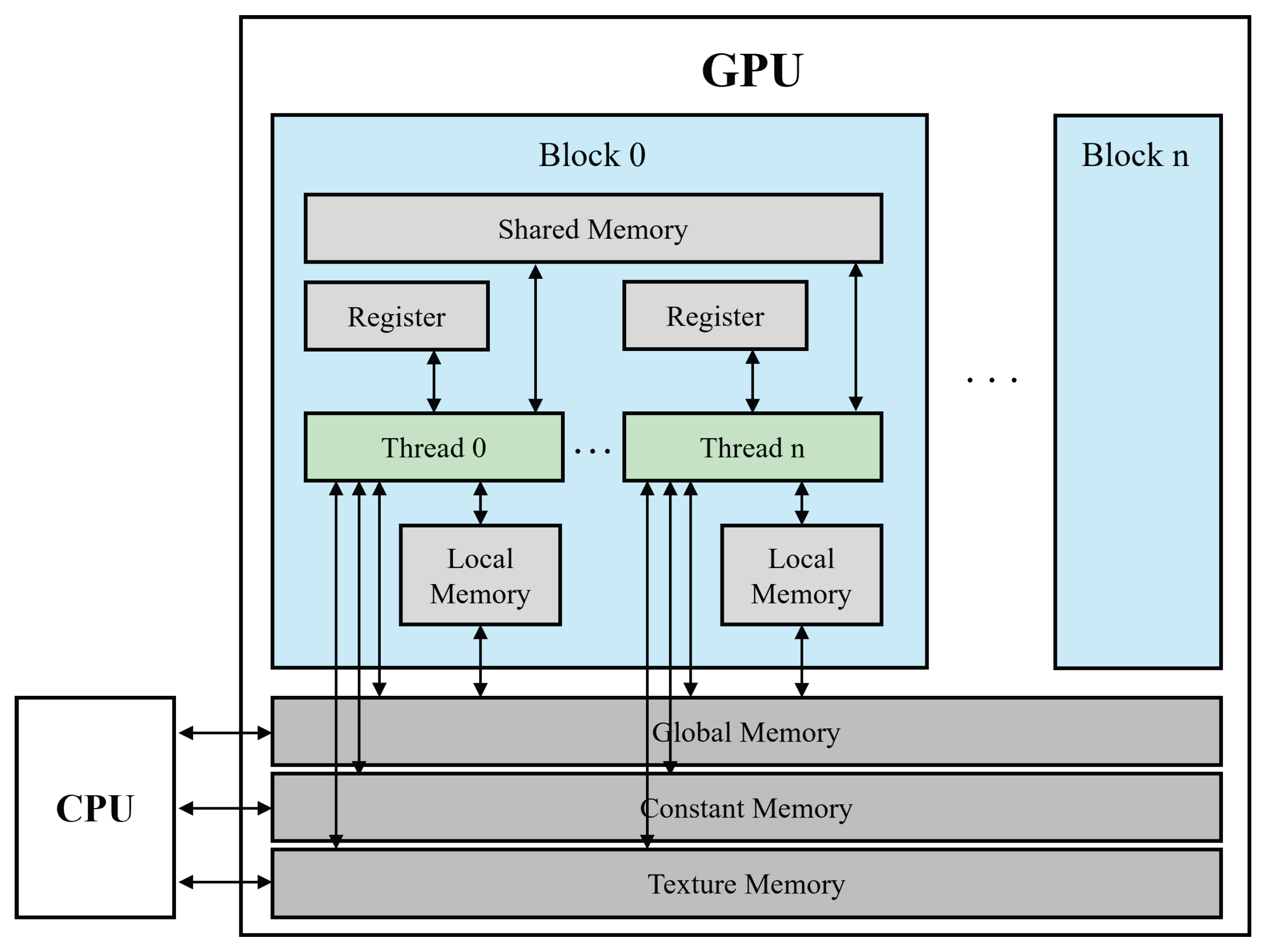
2.2. Graphics Processing Units and CUDA Basics
2.3. CTR Mode Encryption and Exhaustive Key Searches
2.4. Related Works
3. Optimization Strategy of ARIA on GPU
3.1. Shared Memory Utilization Through Optimized S-box Table
| Algorithm 1 x21_s21 Table construction |
Input: Output: 1: for to 255 do 2: 3: 4: 5: 6: 7: end for |
3.2. Efficient Output Reconstruction Using the __byte_perm() Function
3.3. Overall Structure of the Proposed Optimization Technique
| Algorithm 2 Shared memory table initialization |
1: for to in parallel do 2: for to do 3: 4: end for 5: end for |
| Algorithm 3 Algorithmic description of device_SBL1_M_func |
1: procedure device_SBL1_M_func() 2: for to 3 do 3: 4: 5: 6: 7: 8: 9: 10: 11: end for 12: end procedure |
3.4. Memory Optimization for Exhaustive Key Searches
4. Evaluation
4.1. Performance Measurement Environment and Measurement Method
4.2. Profiling Results Analysis
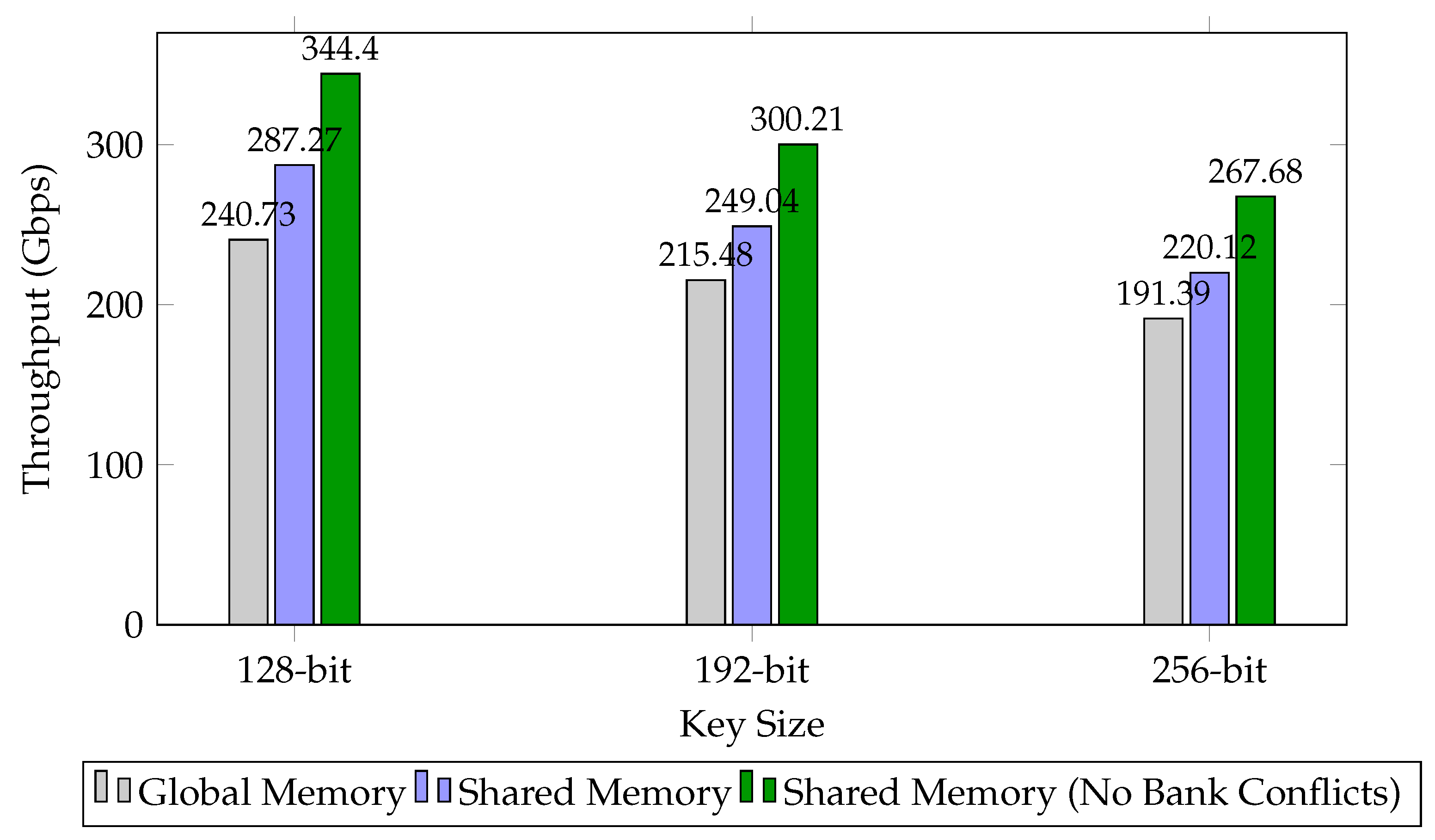
4.3. ARIA-CTR Performance Evaluation
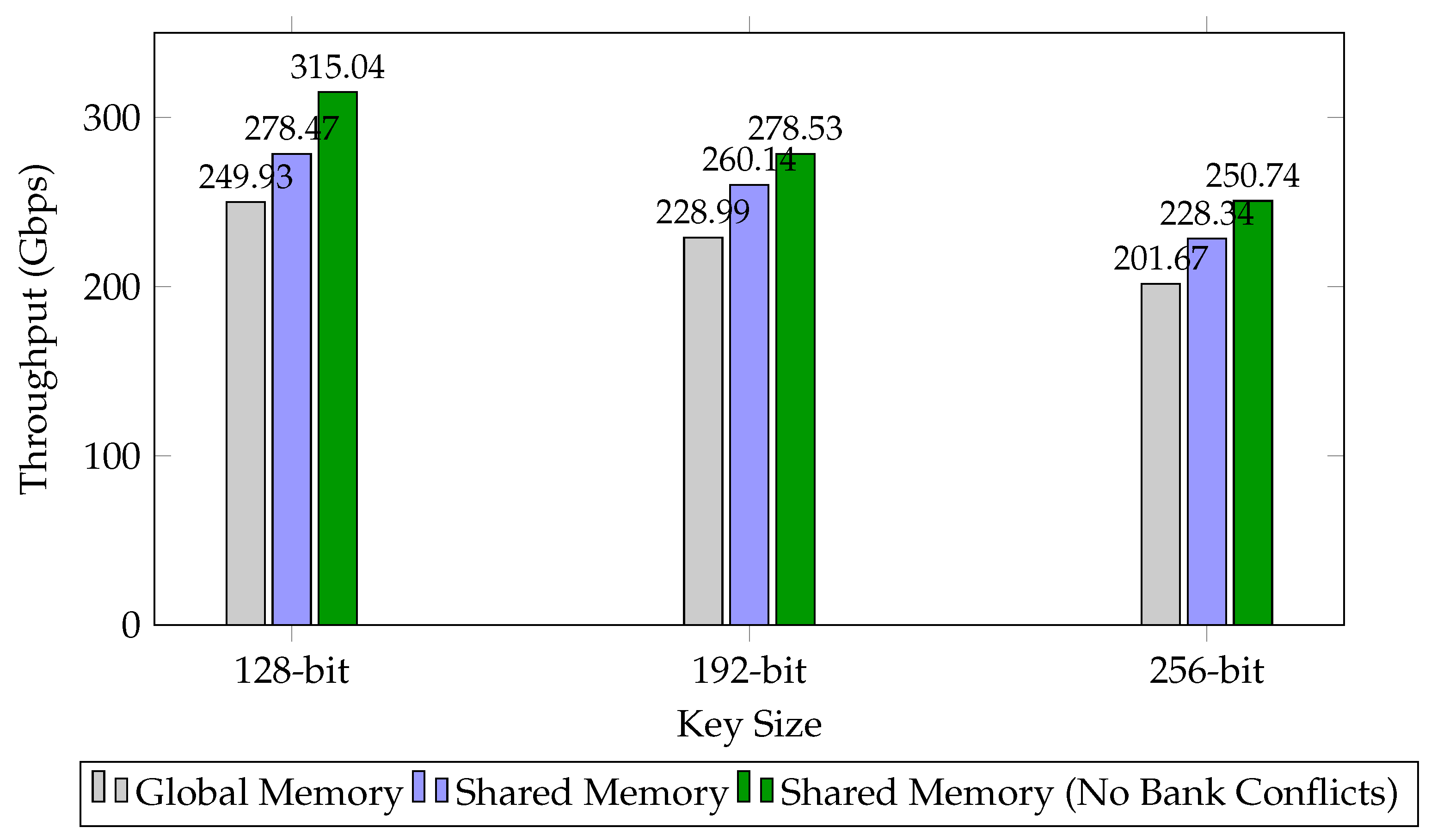
4.4. ARIA-ES Performance Evaluation
4.5. Overall Performance Comparison of ARIA-CTR/ES Modes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- KS X 1213-1; Information Technology—Security Techniques—128-Bit Block Cipher Algorithm ARIA—Part 1: General. Korean Agency for Technology and Standards (KATS): Seoul, Republic of Korea, 2004.
- Kwon, D.; Kim, J.; Park, S.; Sung, S.H.; Sohn, Y.; Song, J.H.; Yeom, Y.; Yoon, E.J.; Lee, S.; Lee, J.; et al. New block cipher: ARIA. In Proceedings of the International Conference on Information Security and Cryptology, Seoul, Republic of Korea, 27–28 November 2003; pp. 432–445. [Google Scholar]
- Kim, J.; Lee, J.; Kim, C.; Lee, J.; Kwon, D. A Description of the ARIA Encryption Algorithm. RFC 5794. 2010. Available online: https://www.rfc-editor.org/info/rfc5794 (accessed on 14 May 2025).
- Daemen, J.; Rijmen, V. AES Proposal: Rijndael. 1999. Available online: https://www.cs.miami.edu/home/burt/learning/Csc688.012/rijndael/rijndael_doc_V2.pdf (accessed on 14 May 2025).
- Song, J.; Seo, S.C. Efficient parallel implementation of CTR mode of ARX-based block ciphers on ARMv8 microcontrollers. Appl. Sci. 2021, 11, 2548. [Google Scholar] [CrossRef]
- Tezcan, C. Optimization of advanced encryption standard on graphics processing units. IEEE Access 2021, 9, 67315–67326. [Google Scholar] [CrossRef]
- Eum, S.; Kim, H.; Kwon, H.; Sim, M.; Song, G.; Seo, H. Parallel implementations of ARIA on ARM processors and graphics processing unit. Appl. Sci. 2022, 12, 12246. [Google Scholar] [CrossRef]
- Xiao, L.; Li, Y.; Ruan, L.; Yao, G.; Li, D. High performance implementation of aria encryption algorithm on graphics processing units. In Proceedings of the 2013 IEEE 10th International Conference on High Performance Computing and Communications & 2013 IEEE International Conference on Embedded and Ubiquitous Computing, Zhangjiajie, China, 13–15 November 2013; pp. 504–510. [Google Scholar]
- Fang, M.; Fang, J.; Zhang, W.; Zhou, H.; Liao, J.; Wang, Y. Benchmarking the GPU memory at the warp level. Parallel Comput. 2018, 71, 23–41. [Google Scholar] [CrossRef]
- NVIDIA. CUDA Toolkit Documentation 12.8. 2025. Available online: https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#shared-memory-3-0 (accessed on 1 April 2025).
- Eum, S.; Kim, H.; Song, M.; Seo, H. Optimized Implementation of Argon2 Utilizing the Graphics Processing Unit. Appl. Sci. 2023, 13, 9295. [Google Scholar] [CrossRef]
- Mei, X.; Zhao, K.; Liu, C.; Chu, X. Benchmarking the memory hierarchy of modern GPUs. In Proceedings of the Network and Parallel Computing: 11th IFIP WG 10.3 International Conference, NPC 2014, Ilan, Taiwan, 18–20 September 2014; Proceedings 11. Springer: Berlin/Heidelberg, Germany, 2014; pp. 144–156. [Google Scholar]
- Mei, X.; Chu, X. Dissecting GPU memory hierarchy through microbenchmarking. IEEE Trans. Parallel Distrib. Syst. 2016, 28, 72–86. [Google Scholar] [CrossRef]
- Eum, S.W.; Kim, H.J.; Kwon, H.D.; Jang, K.B.; Kim, H.J.; Seo, H.J. Implementation of SM4 block cipher on CUDA GPU and its analysis. In Proceedings of the 2022 International Conference on Platform Technology and Service (PlatCon), Jeju, Republic of Korea, 22–24 August 2022; pp. 71–74. [Google Scholar]
- Lipmaa, H.; Rogaway, P.; Wagner, D. CTR-mode encryption. In First NIST Workshop on Modes of Operation; Citeseer: College Park, MD, USA, 2000; Volume 39. [Google Scholar]
- Yeom, Y.; Cho, Y.; Yung, M. High-Speed Implementations of Block Cipher ARIA Using Graphics Processing Units. In Proceedings of the 2008 International Conference on Multimedia and Ubiquitous Engineering (MUE 2008), Busan, Republic of Korea, 24–26 April 2008; pp. 271–275. [Google Scholar] [CrossRef]
- Lee, W.K.; Seo, H.J.; Seo, S.C.; Hwang, S.O. Efficient implementation of AES-CTR and AES-ECB on GPUs with applications for high-speed FrodoKEM and exhaustive key search. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2962–2966. [Google Scholar] [CrossRef]
- NVIDIA. GeForce RTX 30 Series Laptops. 2025. Available online: https://www.nvidia.com/en-us/geforce/laptops/30-series/#specs (accessed on 9 April 2025).
- NVIDIA. GeForce RTX 4080 Series. 2025. Available online: https://www.nvidia.com/ko-kr/geforce/graphics-cards/40-series/rtx-4080-family/ (accessed on 9 April 2025).

| Parameter | Value |
|---|---|
| CUDA Blocks | 1024 |
| Threads per Block | 512 |
| Total Thread Count | 524,288 |
| Key Range () | |
| Key Range (decimal) | 34,359,738,368 |
| Key Range per Thread | 65,536 |
| Total Encryptions | 34,359,738,368 |
| Metric | Global Memory S-Box | Shared Memory S-Box | Shared Mem. + Bank Conflict Removal |
|---|---|---|---|
| Memory Throughput (%) | 90.69 | 96.76 | 95.71 |
| Compute (SM) Throughput (%) | 67.27 | 73.53 | 95.71 |
| Placement | Key Size | Time (s) | Throughput (Gbps) |
|---|---|---|---|
| Global Memory | 128-bit | 18.27 | 240.73 |
| 192-bit | 20.41 | 215.48 | |
| 256-bit | 22.98 | 191.39 | |
| Shared Memory | 128-bit | 15.31 | 287.27 |
| 192-bit | 17.66 | 249.04 | |
| 256-bit | 19.98 | 220.12 | |
| Shared Memory (No Bank Conflicts) | 128-bit | 12.77 | 344.40 |
| 192-bit | 14.65 | 300.21 | |
| 256-bit | 16.43 | 267.68 |
| Placement | Key Size | Time (s) | Throughput (Gbps) |
|---|---|---|---|
| Global Memory | 128-bit | 17.60 | 249.93 |
| 192-bit | 19.21 | 228.99 | |
| 256-bit | 21.81 | 201.67 | |
| Shared Memory | 128-bit | 15.79 | 278.47 |
| 192-bit | 16.91 | 260.14 | |
| 256-bit | 19.26 | 228.34 | |
| Shared Memory (No Bank Conflicts) | 128-bit | 13.96 | 315.04 |
| 192-bit | 15.79 | 278.53 | |
| 256-bit | 17.54 | 250.74 |
| GPU | Key Size | Time (s) | Throughput (Gbps) |
|---|---|---|---|
| RTX 3060 [7] | 128-bit | – | 135.06 |
| 128-bit | – | 146.67 | |
| RTX 3060 * | 128-bit | 12.77 | 344.40 |
| 192-bit | 14.65 | 300.21 | |
| 256-bit | 16.43 | 267.68 | |
| RTX 4080 * | 128-bit | 2.87 | 1532.42 |
| 192-bit | 3.28 | 1340.87 | |
| 256-bit | 3.70 | 1188.66 |
| GPU | Key Size | Time (s) | Throughput (Gbps) |
|---|---|---|---|
| RTX 3060 * | 128-bit | 13.96 | 315.04 |
| 192-bit | 15.79 | 278.53 | |
| 256-bit | 17.54 | 250.74 | |
| RTX 4080 * | 128-bit | 3.22 | 1365.84 |
| 192-bit | 3.67 | 1198.37 | |
| 256-bit | 4.05 | 1085.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eum, S.; Song, M.; Kim, S.; Seo, H. Efficient GPU Parallel Implementation and Optimization of ARIA for Counter and Exhaustive Key-Search Modes. Electronics 2025, 14, 2021. https://doi.org/10.3390/electronics14102021
Eum S, Song M, Kim S, Seo H. Efficient GPU Parallel Implementation and Optimization of ARIA for Counter and Exhaustive Key-Search Modes. Electronics. 2025; 14(10):2021. https://doi.org/10.3390/electronics14102021
Chicago/Turabian StyleEum, Siwoo, Minho Song, Sangwon Kim, and Hwajeong Seo. 2025. "Efficient GPU Parallel Implementation and Optimization of ARIA for Counter and Exhaustive Key-Search Modes" Electronics 14, no. 10: 2021. https://doi.org/10.3390/electronics14102021
APA StyleEum, S., Song, M., Kim, S., & Seo, H. (2025). Efficient GPU Parallel Implementation and Optimization of ARIA for Counter and Exhaustive Key-Search Modes. Electronics, 14(10), 2021. https://doi.org/10.3390/electronics14102021






