Advanced Intelligent Frame Generation Algorithm for Differentiated QoS Requirements in Advanced Orbiting Systems

Abstract

In order to efficiently transmit spatial data with diversified service types, this paper proposes an Advanced Intelligent Framing Algorithm (AIFG) for Advanced Orbiting System (AOS), based on the virtual channel multiplexing AOS technology, aiming to meet differentiated quality of service (QoS) requirements. To enable the timely transmission of delay-sensitive services, the optimal time threshold for framing such services is modeled as a Markov decision process (MDP). The algorithm utilizes Proximal Policy Optimization (PPO), achieving an optimal solution based on performance metrics such as frame multiplexing efficiency, average framing time, and average packet delay. To improve the multiplexing efficiency of non-delay-sensitive services, this type of traffic is transmitted only after completely filling a frame. Simulation results show that, compared to traditional frame generation algorithms, the AIFG algorithm reduces the average queuing delay of services by an average of 32%. Moreover, the AIFG algorithm increases throughput by an average of 32%, and improves multiplexing efficiency by an average of 61%. Thus, the AIFG algorithm balances the transmission requirements of both real-time and non-real-time services, and enhances the QoS of the AOS.

1. Introduction

In recent years, space exploration activities such as deep space exploration, manned spaceflight, and satellite development have become increasingly active globally. The returned data cover various services, including engineering telemetry, physiological telemetry, engineering control, scientific observation, scientific experiments, delayed playback, audio, video, etc. [1]. These data exhibit significant heterogeneity in service types, transmission rates, and QoS requirements. These developments have placed higher demands on the real-time performance and reliability of space data systems. In response, the Consultative Committee for Space Data Systems (CCSDS) established the Advanced Orbiting System (AOS) protocol. The AOS protocol allows multiple data packets with a similar QoS to be multiplexed within the same virtual channel. These data packets are segmented and encapsulated into fixed-length Multiplexing Protocol Data Units (MPDUs), which are then assembled into complete frames with added control information to improve the spatial link multiplexing efficiency.

To provide a comprehensive background and highlight the motivation for this study, we first review the existing research on AOS framing algorithms, which can be broadly categorized into three types as follows: isochronous, high-efficiency, and adaptive framing algorithms. The principle of isochronous frame generation is to set a fixed framing threshold. Regardless of the number of incoming packets, the framing occurs once the set framing time is reached. If the total number of incoming packets does not meet the MPDU length, idle packets are used for padding [2,3,4]. For example, for the ON/OFF source arrival model obeying the Pareto distribution in an AOS, Zhao et al. established the isochronous frame generation method. They obtained the calculation formulas of average packet delay and MPDU average multiplexing efficiency, which verified the feasibility of the isochronous frame generation algorithm in AOS [3]. However, for non-delay-sensitive packets, using the isochronous frame generation algorithm may result in a low frame multiplexing efficiency due to the less stringent timing requirements. As a result, high-efficiency frame generation algorithms were proposed. The principle of high-efficiency frame generation is that, in continuous packet arrival scenarios, a frame is generated and transmitted only when the accumulated packet length reaches the length of an MPDU [5,6,7]. For example, Zhang et al. studied the simplified calculation method of the average frame generation time and the average packet delay in the efficient frame generation algorithm. For the case where the packet arrival rate is the Poisson distribution, they used the Erlang distribution to obtain a clearer correlation between performance indicators [7]. However, the standards for the framing algorithms in the aforementioned two methods are too rigid. In contrast, the adaptive frame generation algorithm can be controlled by pre-setting the framing threshold and MPDU length. Specifically, when the frame waiting time is less than the set threshold value or the MPDU area has been filled with arriving packets, the frame is encapsulated and sent immediately. When the frame waiting time reaches the maximum threshold and the MPDU buffer is not filled, the idle packet is used to complete the entire transmission frame [8,9,10,11]. Tian et al. studied the adaptive frame generation algorithm in the AOS protocol and provided an effective method of calculating the information transmission rate [9]. Dai Changhao et al. proposed an adaptive frame generation algorithm based on wavelet neural network traffic prediction. Under certain delay constraints, the algorithm can adaptively adjust the frame time according to the traffic prediction results [11]. However, most of these algorithms need to set relevant parameters in advance, such as framing time threshold, number of iterations, etc., which cannot interact with the environment in real time. These algorithms result in a low application efficiency in space systems with various types of services and time-varying network states.

Reinforcement learning (RL) is an intelligent method used to achieve the iterative optimization of a policy through a continuous interaction with the environment. This method ensures that the agent selects the best action that is suitable for task requirements under different network conditions. RL does not need to predefine a large number of rules, and it has strong adaptability. Typical RL algorithms include value-based Q-learning and SARSA [12,13,14], policy-based REINFORCE and Actor–Critic methods, and Proximal Policy Optimization (PPO), which is popular recently [15,16,17]. PPO introduces restrictive optimization when updating strategies to ensure stability and efficiency. It is an advanced algorithm in deep reinforcement learning, which is widely used in robot control, autonomous driving, intelligent recommendation systems and other fields [18,19,20,21].

To this end, in this paper, we introduce the PPO algorithm in reinforcement learning into the framing process. We propose the advanced intelligent frame generation (AIFG) algorithm in Advanced Orbiting Systems for differentiated QoS requirements. The main contributions are as follows:

• For massive heterogeneous services in AOS, we establish a service classification framework for delay-sensitive services and non-delay-sensitive services. Among them, delay-sensitive services include audio data, telemetry data, telecommand data, etc., while non-delay-sensitive services include video data, remote control data, observation data, experimental data, etc. Based on this, we design real-time framing algorithms for delay-sensitive services and efficient framing algorithms for non-delay-sensitive services, which are discussed in detail in Section 2 and Section 5.
• In order to effectively reduce the queuing delay of delay-sensitive services, we model the problem of calculating the optimal time threshold for framing such services as a Markov decision process. This model captures the sequential decision-making nature of the problem. Then, we employ the PPO algorithm to obtain the optimal solution based on performance indicators such as frame multiplexing efficiency, average framing time, and average packet delay. This modeling and optimization process is elaborated in Section 4.
• We develop a joint simulation platform based on NS-3 and PyTorch, which enables a comprehensive performance evaluation of the proposed AIFG algorithm under realistic network conditions. The results show that compared with the traditional frame generation algorithm, the average queuing delay of the service under the AIFG algorithm is reduced by an average of 31.69%, the average multiplexing efficiency is increased by an average of 60.88%, and the average throughput is increased by an average of 31.92%. The AIFG algorithm accommodates different transmission needs of real-time and non-real-time services, enhancing the network QoS of the AOS. The detailed simulation setup and performance analysis are presented in Section 6.

This article is organized as follows. In Section 2, the system model is established, including the data arrival model, service classification, and queuing structures for different service types. Section 3 describes the materials and methods of this paper. Then, Section 4 formulates the optimal frame generation time threshold calculation as a Markov decision process and presents a solution based on the Proximal Policy Optimization algorithm. Section 5 introduces the design of the advanced intelligent frame generation (AIFG) algorithm to address differentiated QoS requirements. Section 6 details the simulation setup, parameter settings, and performance evaluation of the proposed algorithm compared with baseline methods. The results of the simulation and theoretical analysis are given in Section 6. Finally, Section 7 concludes this article and highlights potential future research directions.

2. System Model

In this section, we establish the system model for an AOS environment, which provides the foundation for subsequent algorithm design and performance evaluations. The model describes the integration of heterogeneous data sources, the classification of services based on their delay sensitivity, and the differentiated frame generation processes to meet various QoS requirements.

In the AOS, various types of data are received from spacecraft payloads. As shown in Figure 1, the system input integrates six types of heterogeneous data sources. Among them, telemetry data monitor device states, while telecommand data issue control instructions with the highest operational priority. Voice data are real-time streaming media, requiring stringent low-latency transmission. Non-real-time bulk data, such as video, observation and experimental data generated from scientific tasks, allow for flexible delay tolerance. After classification, data packets are separated into two service queues. Voice, telemetry, and telecommand data, which are highly delay-sensitive, are directed into the delay-sensitive service queue and processed using the real-time framing algorithm to generate complete frames. The real-time frame generation process operates within a time-slotted framework. Each frame period collects the arrived packets and supplements idle packets if necessary. Each frame carries both the arrived packets during each time window and dynamically generated idle packets to maintain frame structure integrity under bandwidth fluctuations. In contrast, video, observation, and experimental data, which are less delay-sensitive, enter the non-delay-sensitive service queue and are processed using the high-efficiency framing algorithm. After framing, all data frames are scheduled and transmitted through the virtual channel scheduling module for subsequent transmission within the AOS network. The overall structure of the system model is illustrated in Figure 1, showing the classification of incoming data, the queuing and the framing mechanisms.

We construct a dual-queue framing model to accommodate both delay-sensitive and non-delay-sensitive traffic in AOS. Two distinct traffic models are employed to more accurately reflect real-world service characteristics. First, we define two types of data: real-time data $U_h=\{u_{h0},u_{h1},\dots ,u_{hH}\}$ and non-real-time data $U_l=\{u_{l0},u_{l1},\dots ,u_{lL}\}$. Among them, real-time data include audio data, telemetry data, etc. Non-real-time data include video data, remote control data, observation data, experimental data, etc. After the arrival of all data packets, real-time data enter the delay-sensitive service queue, and non-real-time data enter the non-delay-sensitive service queue.

On the one hand, the framing task of packets in the delay-sensitive service queue is primarily handled by the real-time framing (RTFG) module. Delay-sensitive data such as telemetry, telecommand, and voice traffic typically consist of short-duration flows with limited burstiness and minimal long-range dependence. These characteristics have been extensively validated in the literature, which supports modeling such traffic using Poisson arrival processes. We establish a packet arrival model. We assume that the packet arrival process follows a Poisson distribution with arrival rate parameter $\lambda$. In this case, the probability of receiving exactly k packets during a time interval t is characterized by the Poisson distribution, as given by Equation (1):

$$P(X=k)={\displaystyle \frac{{\left(\lambda t\right)}^k}{k!}}{e}^{-\lambda t}k=0,1,2,3,\dots$$

(1)

where X denotes the number of packet arrivals within time duration t, and $\lambda$ is the average arrival rate.

Assuming that each packet has a fixed size $l_s$, the number of packets which can be accommodated in an MPDU is n, and the length of the MPDU is $l_{ms}=n\times l_s$. Thus, incoming packets can exactly fill the MPDU data area, avoiding the issue of incomplete packet filling.

The maximum number of packets that can be packed into the MPDU data area is set to be N, and the time required to generate a frame is denoted as $t_{sw}$. As shown in Equation (2), the probability density function for framing time $t_{sw}$ within the interval $\left(0,T\right]$ is

$$f_{sw}\left(t\right)=\lambda e^{-\lambda t}{\displaystyle \frac{{\left(\lambda t\right)}^{N-1}}{(N-1)!}}$$

(2)

The probability that the framing time $t_{sw}$ is below the threshold value $T_{th}=T$ is

$$P(t_{sw}=T)={\int }_T^{+\infty }\lambda e^{-\lambda t}{\displaystyle \frac{{\left(\lambda t\right)}^{N-1}}{\left(N-1\right)!}}dt$$

(3)

The average framing time for the RTFG module is

$$\mathrm{\Phi }\left(S_w\right)={\int }_0^{T}t{f}_{sw}\left(t\right)dt+TP(t_{sw}=T)={\int }_0^{T}t\lambda e^{-\lambda t}{\displaystyle \frac{{\left(\lambda t\right)}^{N-1}}{\left(N-1\right)}}dt+T{\int }_T^{+\infty }\lambda e^{-\lambda t}{\displaystyle \frac{{\left(\lambda t\right)}^{N-1}}{\left(N-1\right)}}dt$$

(4)

Let $l_s$ be the packet length and $l_{ms}$ be the packet length of the MPDUs. The average multiplexing efficiency for the RTFG module is

$$E\left(ef{f}_m\right)=P(t_{SW}<T)+\sum _{n=0}^{N-1}{\displaystyle \frac{n{l}_s}{l_{ms}}}P(A\left(T\right)=n)={\int }_0^{T}t\lambda e^{-\lambda t}{\displaystyle \frac{{\left(\lambda t\right)}^{N-1}}{\left(N-1\right)}}dt+\sum _{n=0}^{N-1}{\displaystyle \frac{n{l}_s}{l_{ms}}}{\displaystyle \frac{e^{-\lambda t}{\left(\lambda T\right)}^n}{n!}}$$

(5)

Let $T_d$ be the packet delay, $P\left(A\right(t)=n)$ be the probability of reaching n packets in $\left[\begin{array}{c}0,T\end{array}\right]$ time, and $P\left(A\right(t)=N+x)$ be the probability of reaching $N+x$ packets in $\left[\begin{array}{c}0,T\end{array}\right]$ time, with the average packet delay of the RTFG module when i packets arrive being

$$\vartheta \left(T_d\right)={\displaystyle \frac{1}{N·E\left(ef{f}_m\right)}}·\left(\sum _{n=1}^{N-1}P(A\left(t\right)=n)·{\displaystyle \frac{T}{2}}·n+\sum _{x=0}^{\infty }P(A\left(t\right)=N+x)·\sum _{i=1}^N{\displaystyle \frac{(N-i)·T}{N+x+1}}\right)$$

(6)

On the other hand, the framing task of packets in the non-delay-sensitive service queue is handled by the high-efficiency framing (HEFG) module. The non-real-time packets are framed according to the maximum number of packets in the MPDU. Non-delay-sensitive traffic, such as observation or scientific payload data, often exhibits bursty behavior, long-range dependence, and variable flow sizes. To better model such phenomena, we introduce a self-similar ON/OFF traffic model, where each of the M sources alternates between ON (sending packets) and OFF (idle) periods.

Both ON durations ${\tau }_l$ and OFF durations ${\theta }_l$ follow Pareto distributions, with tail behavior:

$$P(\tau >t)\sim t^{-\alpha },1<\alpha <2$$

(7)

The aggregate active source count $\xi$ at time t follows a binomial distribution with success probability $p={\displaystyle \frac{E\left[\tau \right]}{E\left[\tau \right]+E\left[\theta \right]}}$, and it can be approximated by a Poisson process with intensity $\lambda =M·p$ as $M\to \infty$. In the queue model, we set $S_w$ as the time required to generate a frame. Then, the average frame time of the HEFG module is

$$\mathrm{\Phi }\left(S_w\right)={\int }_0^{\infty }t·f_{\mathrm{ON}}\left(t\right)dt$$

(8)

where $f_{\mathrm{ON}}\left(t\right)$ is the empirically derived arrival distribution during ON periods. The average queuing delay $\vartheta \left(T_d\right)$ for non-delay-sensitive services under self-similar ON/OFF traffic is obtained in a manner analogous to that for Poisson arrivals, but it is adapted to capture long-range dependence and burstiness. Assuming an aggregated arrival rate ${\lambda }_{\mathrm{eff}}$, the average frame generation time in this case is

$$\mathrm{\Phi }\left(S_w\right)={\displaystyle \frac{N}{{\lambda }_{\mathrm{eff}}}}$$

(9)

Then, the average queuing delay can be estimated as

$$\vartheta \left(T_d\right)\approx {\displaystyle \frac{\rho ·{\sigma }^2}{2(1-\rho )}}·{\displaystyle \frac{1}{\mathrm{\Phi }\left(S_w\right)}}$$

(10)

or, in simplified form,

$$\vartheta \left(T_d\right)\approx {\displaystyle \frac{N·l_s}{2·{\lambda }_{\mathrm{eff}}·(1-\rho )}}$$

(11)

where $\rho$ is the queue utilization factor. This formulation captures the impact of long-term correlations in bursty traffic on the frame queuing behavior.

Finally, all the encapsulated transmission frames subsequently enter the virtual channel scheduling process and carry out the next transmission.

3. Materials and Methods

In this section, we detail the research methodology adopted to develop and validate the proposed advanced intelligent frame generation (AIFG) algorithm. The complete process is structured into several key steps, as illustrated in Figure 2.

• Queuing System Modeling: We establish the system model for the AOS environment, integrating heterogeneous data sources. The system architecture includes service classification (delay-sensitive and non-delay-sensitive), queuing structures, and differentiated framing processes, as described in Section 2.
• Problem Formulation: The framing problem for delay-sensitive services is formulated as a Markov decision process, where the agent selects optimal frame generation times to minimize queuing delay and maximize the transmission efficiency. Key mathematical models include the Poisson arrival model (Equation (1)), average frame generation time and packet delay equations (Equations (2)–(6)), and the self-similar traffic model formula (Equations (7)–(11)). The above content is displayed in Section 2.
• Algorithm Design: First, a model algorithm for Optimal Frame Generation Time Threshold Calculation was developed, based on which the RTFG was subsequently derived. A real-time framing algorithm (RTFG) is designed for delay-sensitive queues to satisfy strict latency constraints. A high-efficiency framing algorithm (HEFG) is applied to non-delay-sensitive queues for maximizing frame utilization. Then, an advanced intelligent frame generation algorithm (AIFG) is composed of the RTFG and HEFG. Reinforcement learning-based adaptive framing using the PPO algorithm optimizes frame generation thresholds dynamically based on real-time traffic conditions. The above content is displayed in Section 2 and Section 4.
• Simulation Setup: We implement the AIFG algorithm using NS-3 and PyTorch. The simulation experiments are conducted under varying traffic intensities and service mixes. The key simulation parameters include a fixed frame capacity, delay threshold for real-time services, and maximum tolerable delay for non-delay-sensitive services. More than 300-round simulation runs are performed to ensure statistical reliability, and average values along with standard deviations are reported. The above content is shown in Section 5.
• Performance Evaluation: The performance metrics used for evaluation include the following: average queuing delay, frame multiplexing efficiency and system throughput. Comparative analyses are performed against conventional isochronous framing and high-efficiency framing baselines. Additionally, the proposed AIFG algorithm is evaluated alongside a DQN+HEFG algorithm to further demonstrate its advantages in learning stability, convergence efficiency, and QoS adaptability.

The complete research process is summarized in Figure 2, showing the sequence from system modeling, problem formulation, algorithm design, and simulation implementation to the performance evaluation.

4. Optimal Frame Generation Time Threshold Calculation

Real-time frame generation in AOS faces a fundamental trade-off between latency and transmission efficiency. Fixed threshold-based strategies are unable to adapt to dynamic traffic patterns and often fail to meet delay constraints for delay-sensitive services such as voice and control commands. Therefore, this section investigates a dynamic threshold adjustment method that minimizes queuing delay while maintaining high frame utilization. Among them, the determination of the optimal framing time threshold is the basic condition for the implementation of the real-time framing algorithm. Therefore, we first explain the framing time threshold calculation algorithm. To this end, we formulate the frame generation problem as a Markov decision process and propose a reinforcement learning-based solution using the Proximal Policy Optimization algorithm. The agent learns to select the optimal frame generation threshold dynamically by interacting with the queuing environment and receiving feedback based on performance metrics, such as delay and frame efficiency.

4.1. Overall Structure

In the real-time frame generation (RTFG) module, under the condition that the system buffer capacity is fixed, if the frame generation waiting time threshold $T_{th}$ is set too small, the average packet delay will decrease. However, this will require the addition of a large number of idle packets in the MPDU, leading to a reduction in the frame multiplexing efficiency. On the other hand, if $T_{th}$ is set too large, the frame multiplexing efficiency will improve, but the average packet delay will increase, which will negatively impact real-time data with stringent delay requirements. Therefore, it is necessary to calculate the optimal frame generation time threshold $T_{th}$.

In this paper, the problem is modeled as a Markov decision process $M=(S,A,P,R)$ and solved with the Proximal Policy Optimization algorithm. The overall structure of the optimal frame generation time threshold calculation model is shown in Figure 3. The model involves three main components: state space, action space, and reward.

As illustrated in Figure 3, the proposed framework consists of three main interacting modules: the agent, the environment, and the reward computation module.

• Agent: The agent module contains the actor network, critic network, and the weight parameter vector of the policy function. The agent implements a Proximal Policy Optimization algorithm with an actor–critic structure. The actor network generates actions $a_t$, representing the selected frame generation threshold based on the current state $s_t$, while the critic network evaluates the expected return of each action. These networks are trained using a clipped surrogate loss function, value function regression, and policy entropy regularization.
• Environment: The environment models the delay-sensitive queuing system and real-time frame generation process in the AOS scenario. It includes idle packet filling and transmission scheduling based on traffic load and queue conditions. At each time step, the environment produces a new state $s_t$, capturing features such as packet arrival rate, queue length, frame generation time, and frame length.
• Reward: The reward module quantifies the QoS outcome of each action by combining parameters such as frame multiplexing efficiency and average delay into a composite reward signal $r_t$. This reward is used to reinforce beneficial actions and suppress suboptimal ones, guiding the agent to converge toward optimal framing policies.

Moreover, the buffer stores critical transition data collected during agent–environment interactions. Specifically, it logs tuples of ($s_k$, $a_k$, ${\pi }_{old}(a_k\mid s_k)$, $r_k$), including the current state, selected action, action probability under the old policy, and corresponding reward. These stored experiences are used for batch policy updates, enabling efficient and stable training.

These components operate in a closed feedback loop where the agent continuously observes the environment, takes action, receives rewards, stores transitions in a buffer, and updates its policy through backpropagation. The integrated design ensures adaptive, real-time optimization of framing behavior in delay-sensitive service transmission.

4.1.1. State Space

In this paper, the training cycle is divided into several continuous time slots. At time slot t, the agent observes and collects the environment state $s_t$, and the state space for all time slots is represented as $S=[s_1,s_2,\dots ,s_t]$, $s_t$, defined as Equation (12):

$$s_t=\{R_s,L_s,T_f,L_f\}$$

(12)

where $R_s$ represents the average arrival rate of packets in time slot t, and $L_s$ represents the average queue length in time slot t, which is used to determine the current load status. Specifically, if the queue length is large, it indicates that the current queue is in a state of congestion. Thus, the next round should be framed as soon as possible, and the frame threshold should be reduced. $T_f$ represents the average frame generation time in time slot t, and $L_f$ represents the average frame length in time slot t.

This state space representation is independently constructed by us, taking into account the queuing dynamics and framing requirements specific to the AOS environment.

4.1.2. Action Space

After each time slot, the agent makes decisions based on the environment state and the reward function. The action space in the current time slot is $A=\left[\begin{array}{c}{a}_1,a_2,\dots ,a_t\end{array}\right]$, where the action $a_t$ represents the frame generation threshold for the RTFG algorithm. The decision on the threshold value determines when the real-time data packets in the queue will be framed. The action impacts the environment and interacts with the environment based on the chosen threshold. The range of actions is $a_t\in [0,T_m]$, where $T_m$ is the maximum allowed average queue delay for real-time business. In time slot t, after the algorithm’s decision, a fixed frame generation threshold $T_{th}$ is set, and a fixed frame length $L_{th}$ is also established. According to the rules of the real-time frame generation algorithm, the data packets in the real-time data service queue are combined into a data frame and sent only when at least one of these two conditions is met. Obviously, the threshold value of one round will affect the decision of the next round.

In continuous action space, the standard deviation $\sigma$ of the action decays gradually to a minimum value ${\sigma }_{\min }$. This parameter controls the randomness of action selection. The update rule for the standard deviation is as shown in Equation (13):

$${\sigma }_{t+1}=max({\sigma }_t-{\rm Y},{\sigma }_{min})$$

(13)

where ${\sigma }_t$ is the standard deviation of the action after the t time interval update, ${\rm Y}=\alpha t$ is the decay rate, $\alpha$ is the proportional coefficient of the decay rate, and ${\sigma }_{\min }$ is the minimum standard deviation of the action. The constraint condition for the standard deviation of the action is

$${\sigma }_t\ge {\sigma }_{min}$$

(14)

This ensures that the standard deviation of the action will not be lower than the set minimum value, thus ensuring continuous exploration of the agent.

The definition of the action space, including the mapping between the selected threshold and frame generation behavior, is tailored to reflect the control objectives of our system model.

4.1.3. Reward Function

During each training step, the agent receives the current reward value $r_t$ based on the composite function $R(s_t,a_t)$, which indicates the reward for the action $a_t$ taken at state $s_t$ of the current slot t. The reward function value $r_t$ is obtained by feedback after setting the threshold value. Moreover, $r_t$ provides an effective signal for the agent to guide its decision making in the next training step. The reward function defined in this paper is

$$R(s_t,a_t)=\left\{\begin{array}{c}\alpha L_f-\beta T_f\dots \gamma T_h\le T_f\le \delta T_h\hfill \\ \beta L_f-\alpha T_f\dots \dots \dots otherwise\hfill \end{array}\right.$$

(15)

where $L_f$ is the normalized average effective frame length (excluding idle packets), $T_f$ is the normalized average frame generation time, and $\alpha$ and $\beta$ are the adjustable weights for the average effective frame length and average frame generation time, respectively, with $\alpha +\beta =1$.

The reward function in Equation (15) is specifically formulated in this work, combining delay and frame utilization in a custom composite formulation to reflect the QoS needs of real-time services in the AOS.

4.2. Algorithm Design

The optimal frame generation time threshold is derived based on the policy. The policy is typically represented by ${\pi }_{\theta }$. When the state is $s_t$, the probability of the agent executing action $a_t$ based on the parameters $\theta$ is given by Equation (16):

$${\pi }_{\theta }(a\mid s)=p[a_t=a\mid s_t=s,\theta ]$$

(16)

where $\theta$ is the weight parameter vector of the policy function; π_θ (a∣s) is the policy function obtained by function fitting of the parameter vector $\theta$. When the policy gradient is $\nabla \widehat{E}\left({\theta }_t\right)$ and the learning rate is $\alpha$, the formula for updating the policy parameter $\theta$ of the objective function by using the gradient rise method is as shown in Equation (17):

$${\theta }_{t+1}={\theta }_t+\alpha \nabla \widehat{E}\left({\theta }_t\right)$$

(17)

In this paper, the transition function $P\left(s_{t+1}\right|s_t,a_t)$ is used to represent the probability that the environment state is transferred from $s_t$ to $s_{t+1}$. The actions made by the agent will affect the state of the environment and the related reward values. For example, the frame time threshold calculated by the time slot $t-1$ will affect the average queue length, average frame time and average frame length in the time slot t. If the threshold value is large, the number of packets combined in the data frame will increase, and the average queue length will decrease. At the same time, the average frame time and average frame length will also increase.

The policy optimization and loss function structure presented in this section is formulated by the authors to support stable training in the context of real-time adaptive framing. The specific expressions for the surrogate objective, critic loss, and entropy term reflect our design choices.

4.2.1. Clipped Surrogate Objective

The clipped surrogate objective function ${\kappa }^{CLIP}\left(\theta \right)$ defined in this paper is

$${\kappa }^{CLIP}\left(\theta \right)={\mathbb{E}}_t\left[min\left(r_t\left(\theta \right){\widehat{A}}_t,clip\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right){\widehat{A}}_t\right)\right]$$

(18)

where $r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{\mathrm{old}}}(a_t\mid s_t)}}$ represents the probability ratio of the current policy and the old policy. ${\widehat{A}}_t$ represents the advantage estimation of the time interval t, and the advantage function represents the advantage of taking action $a_t$ under the state $s_t$. $ϵ$ is a clipping coefficient used to limit the range of policy updates, which is used to limit the range of policy updates. $clip\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right)$ limits $r_t\left(\theta \right)$ to the range of $[1-ϵ,1+ϵ]$. This shearing mechanism ensures that the policy update does not cause the $r_t\left(\theta \right)$ to be too large or too small, thereby avoiding excessively deviating from the old policy. At the same time, the clipping constraint of the policy update range is

$$1-ϵ\le r_t\left(\theta \right)\le 1+ϵ$$

(19)

The difference between the new policy and the old policy is limited to a small range, avoiding the instability caused by excessive policy updates.

4.2.2. Mean Squared Error (MSE) of the State Value Function

The mean squared error (MSE) of the state value function ${\kappa }_{\mathrm{critic}}\left(\theta \right)$ is defined as

$${\kappa }_{\mathrm{critic}}\left(\theta \right)={\displaystyle \frac{1}{N}}\sum ^N{(G_t-V_{\theta }\left(s_t\right))}^2$$

(20)

This formula shows the mean square error between the predicted state value function $V_{\theta }\left(s_t\right)$ and the actual return $G_t$. $V_{\theta }\left(s_t\right)$ is the estimated state value of the state $s_i$ evaluation network under the current policy, and $G_t$ is the return estimated by the Monte Carlo method. The specific formula for the total return with the time step of t is given by Equation (21):

$$G_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+...$$

(21)

where $\gamma$ is the discount factor, typically set between $[0,1]$, representing the weight of future rewards. The agent learns more accurate state value estimation by minimizing the mean square error (MSE).

4.2.3. Policy Entropy Reward Function

The policy entropy reward function ${\kappa }^S\left(\theta \right)$ defined in this paper is

$${\kappa }^S\left(\theta \right)={\mathbb{E}}_t\left[\mathcal{H}\left({\pi }_{\theta }(·|s_t)\right)\right]$$

(22)

The policy entropy reward function can improve the degree of divergence of reinforcement learning policy exploration and achieve optimal decision generation through a more comprehensive decision test. $\mathcal{H}\left({\pi }_{\theta }(·|s_t)\right)$ represents the entropy of the policy ${\pi }_{\theta }$ under the state $s_t$, which represents the randomness of the policy. The larger the entropy, the higher the randomness of the policy and the stronger the exploration.

Finally, the loss function combines these three parts of functions to obtain

$$\kappa \left(\theta \right)=-{\kappa }^{CLIP}\left(\theta \right)+c_1{\kappa }_{\mathrm{critic}}\left(\theta \right)-c_2{\kappa }^S\left(\theta \right)$$

(23)

In this formula, $c_1$ and $c_2$ are hyperparameters that weigh the value function loss and entropy reward, respectively, and $c_1$ and $c_2$ control the weight of the value function loss and entropy penalty term, respectively. The overall goal of the algorithm is to maximize the expected return by optimizing the proximal policy objective and the entropy term, while minimizing the value function loss. At the same time, the policy updates are constrained to ensure stable training.

The entropy-based regularization and its integration into the total loss function are designed by the authors to balance exploration and stability in the decision-making process.

The pseudo-code of the optimal frame generation time threshold calculation algorithm is as shown in Algorithm 1.

Algorithm 1 Optimal Frame Generation Time Threshold Calculation

Require: PPO hyperparameters, number of iterations Ensure: Optimal frame generation time threshold $T_h$ Initialize network parameters $\theta$, and buffer $\mathcal{D}$ for each episode do    Initialize PPO hyperparameters    for each Delay Sensitive Queue do      Construct the state space $s_k$ for current time slot      According to $s_k$, the action $a_k$ is selected by ${\pi }_{old}$, and save action probability $P\left({\pi }_{old}(a_k\mid s_k)\right)$      if Execute $a_k$, $r_t\left(\theta \right)>1$ then         Abandon the threshold value result derived from this action         Break         Execute $a_k$, $s_k\leftarrow s_{k+1}$, obtain the reward function         Store the current dataset $\{s_k,a_k,P\left({\pi }_{old}(a_k\mid s_k)\right),r_k\}$ in buffer $\mathcal{D}$         if $a_k\ne a_1$ (not the first action) then           for $n_{update}$ do              if time step reaches $update\_\mathrm{timestep}$ then                Calculate objective function ${\kappa }^{\mathrm{CLIP}}\left(\theta \right)$ using Equation (18), update PPO policy loss function                Calculate the mean squared error using Equations (20) and (21), update the critic network              end if              if action space is sufficient & time step = $\mathrm{action}\mathrm{std}\mathrm{decay}\mathrm{freq}$ (action standard deviation decay frequency) then                Update action standard deviation according to Equation ${\sigma }_{t+1}=max({\sigma }_t-{\rm Y},{\sigma }_{min})$              end if              Complete a series of updates of the agent           end for           Calculate cumulative reward $sum\left(r_k\right)$ and store it         end if         if the amount of data in buffer $\mathcal{D}$ exceeds maximum capacity $>K$ then           Update network parameters ${\theta }_{\mathrm{old}}\leftarrow \theta$, clear buffer $\mathcal{D}$         end if         $s_k\leftarrow s_{k+1}$      end if    end for end for

5. Advanced Intelligent Frame Generation Algorithm

As described in the system model in Section 2 of this paper, for the RTFG module, when the frame generation waiting time for the delay-sensitive queue reaches the threshold $T_h$, the data packets arriving during this period are encapsulated into frames. On the contrary, if the number of packets in the delay-sensitive queue has filled the MPDU packet area before the threshold value $T_h$ arrives, it is also encapsulated into a frame. For the HEFG module, if the packet size of the non-delay sensitive queue reaches the maximum length $L_h$ of an MPDU packet area, it is encapsulated into a frame without filling the idle packet. The pseudo-code of the advanced intelligent framing generation algorithm in Advanced Orbiting Systems designed for differentiated QoS requirements is as shown in Algorithm 2.

Algorithm 2: Advanced Intelligent Frame Generation Algorithm for Differentiated QoS Demands in Advanced Orbiting Systems

Require: Average packet arrival rate $\lambda$; number of iterations $\mathrm{G}$; decay frequency $\alpha$; policy update period $T_c$; discount factor $\gamma$; clipping parameter $\mathrm{c}$; number of policy updates per training episode $n_{update}$; policy optimization network learning rate $\rho$; training sample size $\mathrm{N}$ Ensure: Average frame generation time $\mathrm{\Phi }\left(S_w\right)$, frame multiplexing efficiency $E\left(ef{f}_m\right)$, average packet delay $\vartheta \left(T_d\right)$, throughput Initialize network simulation environment based on network parameters and create simulation topology if $U_{\mathrm{integerValue}}=1$ (indicating real-time business) then    Generate a data stream that follows a Poisson distribution based on the real-time business requirements    Initialize network parameters $\theta$    Use Algorithm 1 to obtain the optimal frame generation time threshold $T_h$    Set the real-time frame generation threshold $T_{th}=T_h$ and set maximum MPDU length for the transmission frame $L_{th}=L_h$    if the number of packets arriving within $T_1$ exceeds the threshold $n=N$ then      Encapsulate $\mathrm{n}$ packets into the MPDU packet area      Set $T_{th}=T_1$      Calculate $\mathrm{\Phi }\left(S_w\right)$, $E\left(ef{f}_m\right)$ and $\vartheta \left(T_d\right)$ by using Equations (4), (5) and (6), respectively    else if the number of packets arriving in $\mathrm{T}$$n<N$ then      Encapsulate packets into the MPDU packet area      Fill the idle packets, and set $T_{th}=T$      Calculate $\mathrm{\Phi }\left(S_w\right)$, $E\left(ef{f}_m\right)$ and $\vartheta \left(T_d\right)$ by using Equations (4), (5) and (6) respectively      End the time slot, get the reward $r_t$ and the new state $s_{t+1}$      Release the current frame and send it to the virtual channel scheduler    end if else if  $U_{\mathrm{integerValue}}=2$ (indicating non-real-time business) then    Generate a data stream that conforms to a self-similar traffic model, in accordance with the characteristics of non-real-time service requirements    Initialize $\theta$    Set $L_{th}=L_h$, and observe the MPDU packet area status    if the arriving packet length $L=L_h$, MPDU packet area is filled then      Encapsulate the data into the transmission frame and calculate $\mathrm{\Phi }\left(S_w\right)$ and $\vartheta \left(T_d\right)$ for the HEFG module by using Equations (8)–(11)    end if end if The iteration is completed. Return $\mathrm{\Phi }\left(S_w\right)$ for both delay-sensitive and non-delay-sensitive queues, $E\left(ef{f}_m\right)$ of the delay-sensitive queue, and $\vartheta \left(T_d\right)$ for both delay-sensitive and non-delay-sensitive queues

The advanced intelligent frame generation algorithm described in this section, including the modeling of action, reward, and policy structure, is proposed by the authors as an original design for the specific requirements of AOS.

6. Simulation Results and Analysis

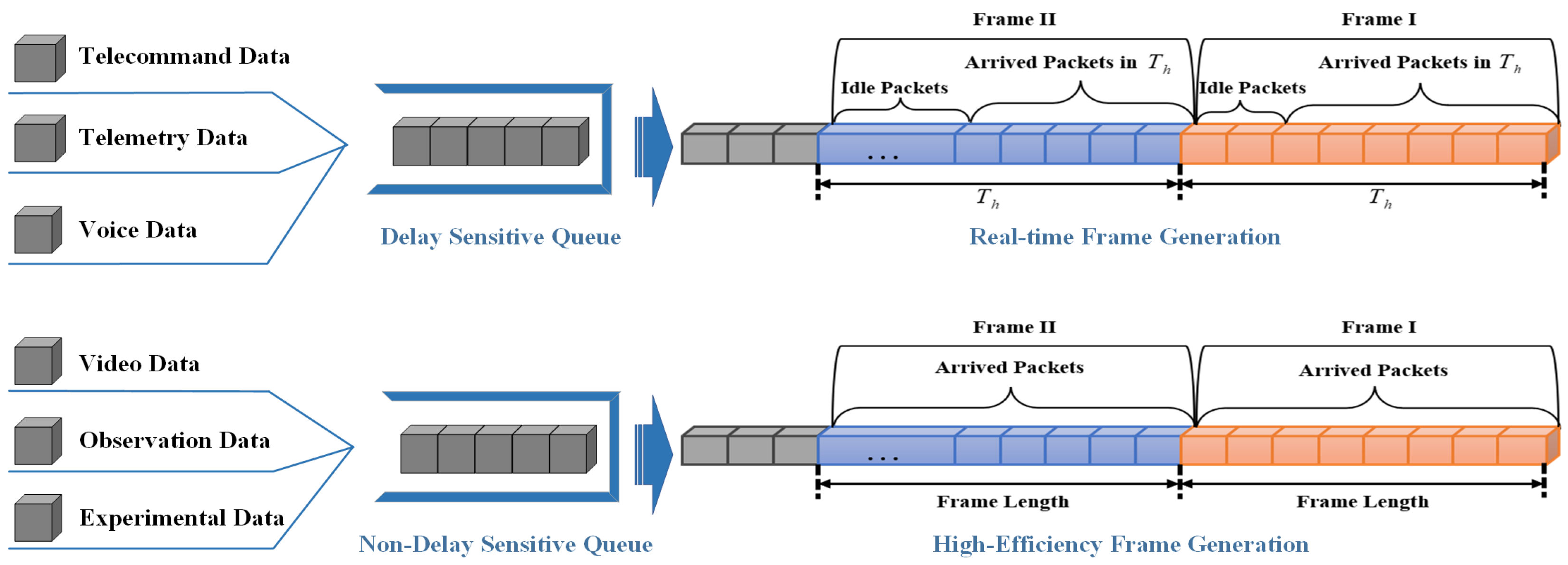
This section presents the simulation results that evaluate the effectiveness of the proposed advanced intelligent frame generation (AIFG) algorithm under different delay constraints. The main goals of the simulation are to validate the adaptability of AIFG in varying network conditions, and to compare its performance against three benchmark algorithms: AFG + HEFG, IFG + HEFG, and FIFO + FIFO. Additionally, to strengthen the evaluation from the perspective of reinforcement learning methodologies, we introduce a Deep Q-Network-combined framing policy (DQN + HEFG) as an additional comparative baseline. This inclusion supplements the analysis with a machine learning-based benchmark, allowing for a more comprehensive performance assessment of AIFG against both traditional and contemporary intelligent algorithms. The simulation scenario emulates data traffic in an AOS, incorporating delay-sensitive and non-delay-sensitive services with dynamic arrival patterns.

The evaluation focuses on three critical performance indicators: average queue delay, frame multiplexing efficiency, and throughput. To explore the robustness of AIFG, the simulations are conducted under four different delay threshold settings: 5 ms, 10 ms, 15 ms, and 20 ms.

Beyond the standard evaluations, this section further investigates the scalability and practical applicability of AIFG. We extend the simulation environment by varying the number of network nodes (from 25 up to 200), altering the MPDU payload length (ranging from 800 to 1800 bytes), and adjusting satellite link bandwidth (from 3 Mbps to 20 Mbps). These additional experiments serve to analyze the computational overhead, convergence behavior, and performance resilience of AIFG under more realistic and heterogeneous system conditions.

The results demonstrate that AIFG can dynamically adjust its frame generation policy based on real-time feedback from the system environment, effectively balancing delay and efficiency. The subsequent subsections provide detailed discussions of the simulation setup, algorithm configurations, and quantitative comparisons under each experimental scenario.

6.1. Simulation Scenario and Parameter Settings

The topology of the simulation system designed for this study is shown in Figure 4. The simulation system consists of 50 transmitting nodes representing spacecraft probe loads and 50 receiving nodes representing simulated ground terminal devices. After collecting various types of data and encapsulating and processing the data accordingly, the payloads divide the data packets into real-time data packets and non-real-time data packets. Then, the payloads send them to the communication satellite, respectively, entering the time-sensitive and non-time-sensitive service queues. Afterwards, corresponding to different service type queues, different frame generation algorithms are applied to complete the data transmission between communication satellites. Ultimately, based on the business type, the satellite transmits the data to multiple ground terminal devices for further analysis and processing. In order to simulate the complex space links and various services in the AOS, the communication satellite nodes transmit typical acquisition data and communication information collected by aerospace payloads to the receiving terminal nodes. The simulation focuses on the frame generation module in the system. Based on the random data generated by the ON/OFF source model, the link is simulated as the link type of the communication satellite. At the same time, AIFG in the AOS for differentiated QoS requirements is deployed on the transmitting communication satellite to perform data transmission between two satellite nodes.

To evaluate the performance of the proposed AIFG algorithm, a simulation environment was configured to emulate the data transmission scenario of Advanced Orbiting Systems. The specific simulation parameters settings are shown in

Table 1. Simulation parameters.

Simulation Parameter	Value
Simulation Time	50 s
Real-time Data Traffic	100 streams
Non-real-time Data Traffic	110 streams
Bottleneck Link Bandwidth	1 Mbps
Satellite Link Bandwidth	6 Mbps
Time Slot Size	50 ms
Maximum MPDU Size in RTFG/IFG/HEFG	1500 bytes

, and they are summarized as follows. The simulation runs for 50 s, during which 100 real-time data streams and 110 non-real-time data streams are simultaneously transmitted. Real-time data include delay-sensitive services, such as voice or telemetry data, while non-real-time data include observation and video information. The bottleneck link bandwidth is set to 1 Mbps to model constrained access segments, while the satellite link bandwidth is configured as 6 Mbps, simulating higher-capacity backbone transmission. The simulation operates in discrete time steps, with each time slot spanning 50 ms, during which the agent observes system states and decides frame generation thresholds. The maximum MPDU size for all framing algorithms (RTFG, IFG, HEFG) is unified at 1500 bytes, corresponding to a standard Ethernet MTU, ensuring consistency across different service types.

The main simulation parameters of the PPO algorithm are set as shown in

Table 2. PPO algorithm parameters.

Algorithm Parameter	Definition
Standard Deviation of Initial Action Distribution $\sigma$	$2.0$
Linear Decay Frequency $\xi$	$0.2$ Hz
Minimum Action Standard Deviation ${\sigma }_{\min }$	$0.4$
Action Standard Deviation Decay Frequency (per time step)	5000 Hz
Discount Factor $\gamma$	$0.99$
Clipping Parameter c	$0.2$
Policy Update Frequency	100 Hz
Model Saving Frequency	$1\times {10}^5$ Hz
Number of Running Rounds per PPO Update Cycle	1
Evaluation Network Learning Rate	$0.001$
Proximal Policy Action Network Learning Rate $\rho$	$0.0003$

.

In the simulation case, to demonstrate the performance advantages of the proposed algorithm in terms of network multiplexing efficiency, average queue delay, and throughput, the proposed algorithm is compared with the following four algorithms:

• AFG + HEFG: The adaptive frame generation (AFG) algorithm is used for time-sensitive service queues, and the high-efficiency frame generation (HEFG) algorithm is used for non-time-sensitive service queues. Because of the requirements of AOS transmission frames, the frame generation length for the HEFG algorithm is fixed at 1500 bytes.
• IFG + HEFG: For delay-sensitive business queues, the isochronous frame generation (IFG) algorithm is applied. For non-delay-sensitive business queues, the HEFG algorithm is used. The frame generation length for HEFG is also fixed at 1500 bytes.
• FIFO + FIFO: No frame generation algorithm is applied for either the delay-sensitive or non-delay-sensitive business queues. Instead, the standard First-In First-Out (FIFO) algorithm is used.
• DQN + HEFG: The Deep Q-Network (DQN) algorithm dynamically selects the delay threshold for real-time service queues, while HEFG continues to handle non-delay-sensitive services.

6.2. Simulation Results and Analysis

Under different delay requirements, the AOS automatically adjusts and produces varying network performance results, leading to changes in parameters such as the final threshold values, delay, multiplexing efficiency, and throughput. To achieve more accurate results from the advanced intelligent frame generation algorithm, the simulation sets four different delay requirements $T_h$: 5 ms, 10 ms, 15 ms, and 20 ms. At the same time, according to the delay requirements, iteration parameters, reward function parameters, and final reward values of the old and new policy are flexibly adjusted to train the agent to obtain a more optimized delay threshold.

In the simulation of this algorithm, the change in the delay requirement combined with adjustments to the reward function parameters can guide the correct training and learning of the agent, which makes the agent complete. Then, the agent is able to make the optimal policy. The difference in the four parameter settings in the reward function will greatly affect the performance of the algorithm. Therefore, the numerical selection of the parameter group is particularly important. This simulation takes the setting delay requirement of 5 ms as an example. Multiple parameter sets of reward functions are as shown in

Table 3. Reward function parameters (delay requirement: 5 ms).

Parameter Set Number	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	$\mathit{\delta }$
1	0.7	0.3	0.2	1.20
2	0.4	0.6	0.4	0.75
3	0.9	0.5	0.8	1.50
4	0.5	0.5	0.5	1.20

. For each case, the reward function, throughput, average delay, and multiplexing efficiency are observed. The optimal parameter group value is obtained via a comparison, and the reward value convergence curve changes as shown in Figure 5.

Different parameter settings will bring different changes in the value of the reward function. Figure 5 clearly shows the mainstream trend of the reward function, which gradually rises in the early stage of training. When the number of iterations is about 40, it begins to stabilize and enters the platform period, indicating the convergence of the reward function. Among the four parameter groups selected, the growth rate of the convergence function is the fastest in the case of Parameter Group 3, and the growth rate of the Parameter Group 2 is slower. At the same time, the convergence effect of Parameter Groups 1, 3 and 4 is better, but the convergence effect of Parameter Group 2 is poor.

From Figure 6, it can be observed that the average delay and throughput are optimal for Parameter Group 3, while the multiplexing efficiency is highest for Parameter Group 4. Overall, selecting Parameter Group 3 for AIFG algorithm training is the most optimal choice.

For the four different network processing strategies, different simulation performances are observed under varying delay threshold requirements. Except for the FIFO + FIFO algorithm, which cannot accurately set delay requirements, the other strategies produce a single result under each delay requirement. In this simulation, the parameter groups of the optimal reward function are set for the four delay requirements, and the specific values are shown in

Table 4. Reward function parameters (different delay threshold requirements).

Parameter	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	$\mathit{\delta }$
5 ms	0.9	0.5	0.8	1.50
10 ms	0.8	0.2	0.5	1.10
15 ms	0.6	0.4	0.5	0.90
20 ms	0.8	0.2	0.4	0.75

. These sets determine the weights for delay and efficiency trade-offs in the agent’s learning process. The detailed values of $\alpha$, $\beta$, $\gamma$, and $\delta$ for each delay condition are summarized in Table 4, covering thresholds of 5 ms, 10 ms, 15 ms, and 20 ms, respectively. The following series of figures provides the frame generation delay, throughput, and multiplexing efficiency for the four strategies under different delay requirements.

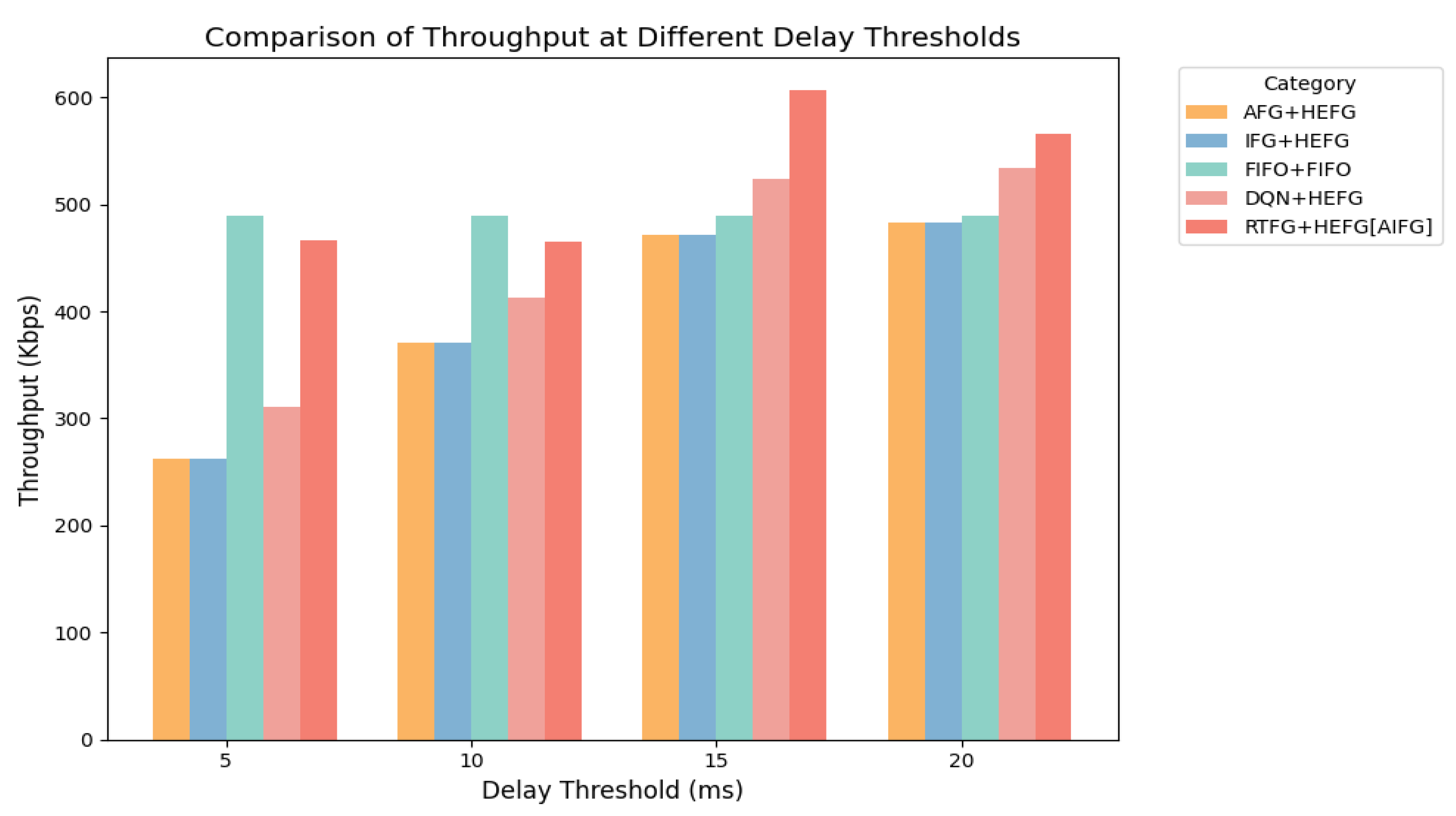
From Figure 7, it can be seen that the throughput of the AIFG algorithm is generally higher compared to other frame generation algorithms. When the delay requirement is 5 ms, the throughput of the AIFG algorithm is 466 Kbps, which is an increase of 78.05% over both the AFG + HEFG and IFG + HEFG algorithms. With a delay requirement of 10 ms, the throughput of AIFG is 464 Kbps, which is an increase of 25.37% compared to that of AFG + HEFG and IFG + HEFG. When the delay requirement is 15 ms, the AIFG algorithm achieves the maximum throughput of 606.456 Kbps, which is 28.66% higher than that of the AFG + HEFG and IFG + HEFG algorithms. At a delay requirement of 20 ms, the throughput of AIFG also improves, with an increase of 17.18% compared to both AFG + HEFG and IFG + HEFG. The AIFG consistently exhibits superior throughput, especially under 5 ms and 10 ms delay thresholds, where it outperforms DQN + HEFG by margin of 49.9% and 12.7% respectively. Under 15 ms and 20 ms delay thresholds, the throughput of AIFG is 15.8% and 6.1% higher than that of DQN + HEFG, respectively. When the delay requirement is low, AIFG shows a higher throughput improvement rate, and its performance change is optimal. Conversely, when the delay requirement is high, AIFG is able to achieve a larger throughput value. This highlights the effectiveness of PPO in guiding reward shaping and decision making over longer time horizons.

Due to the FIFO transmission mechanism, the queue’s multiplexing efficiency is always 100%. As shown in Figure 8, the multiplexing efficiency of the AIFG algorithm is higher compared to the IFG + HEFG, AFG + HEFG and DQN + HEFG algorithms under smaller delay requirements. With a delay requirement of 5 ms, AIFG’s multiplexing efficiency is 69.25%, which is an increase of 92.36% over both AFG + HEFG and IFG + HEFG, and an increase of 63.2% over DQN + HEFG. Under a delay requirement of 10 ms, the multiplexing efficiency of the AIFG algorithm is 69.1%, which is 52.47% higher than that of the AFG + HEFG and IFG + HEFG algorithms, and an increase of 35.5% over DQN + HEFG. At a 15 ms delay requirement, AIFG’s multiplexing efficiency is 12.26% higher than that of AFG + HEFG and IFG + HEFG, while it is only 3.2% higher than that of DQN + HEFG. When the delay requirement is 20 ms, the multiplexing efficiency of AIFG reaches its maximum value of 94.7%, with an increase of 1.4% compared to DQN + HEFG, but with a slight decrease compared to AFG + HEFG and IFG + HEFG. When the delay requirement is high, the multiplexing efficiency improvement rate of AIFG decreases. This is constrained by the time threshold and influenced by the fixed AOS transmission frame size. Nevertheless, the overall trend in multiplexing efficiency remains upward. Among learning-based methods, AIFG shows better multiplexing efficiency than DQN + HEFG, especially under strict delay conditions (5 ms, 10 ms), indicating a more refined policy learned through PPO.

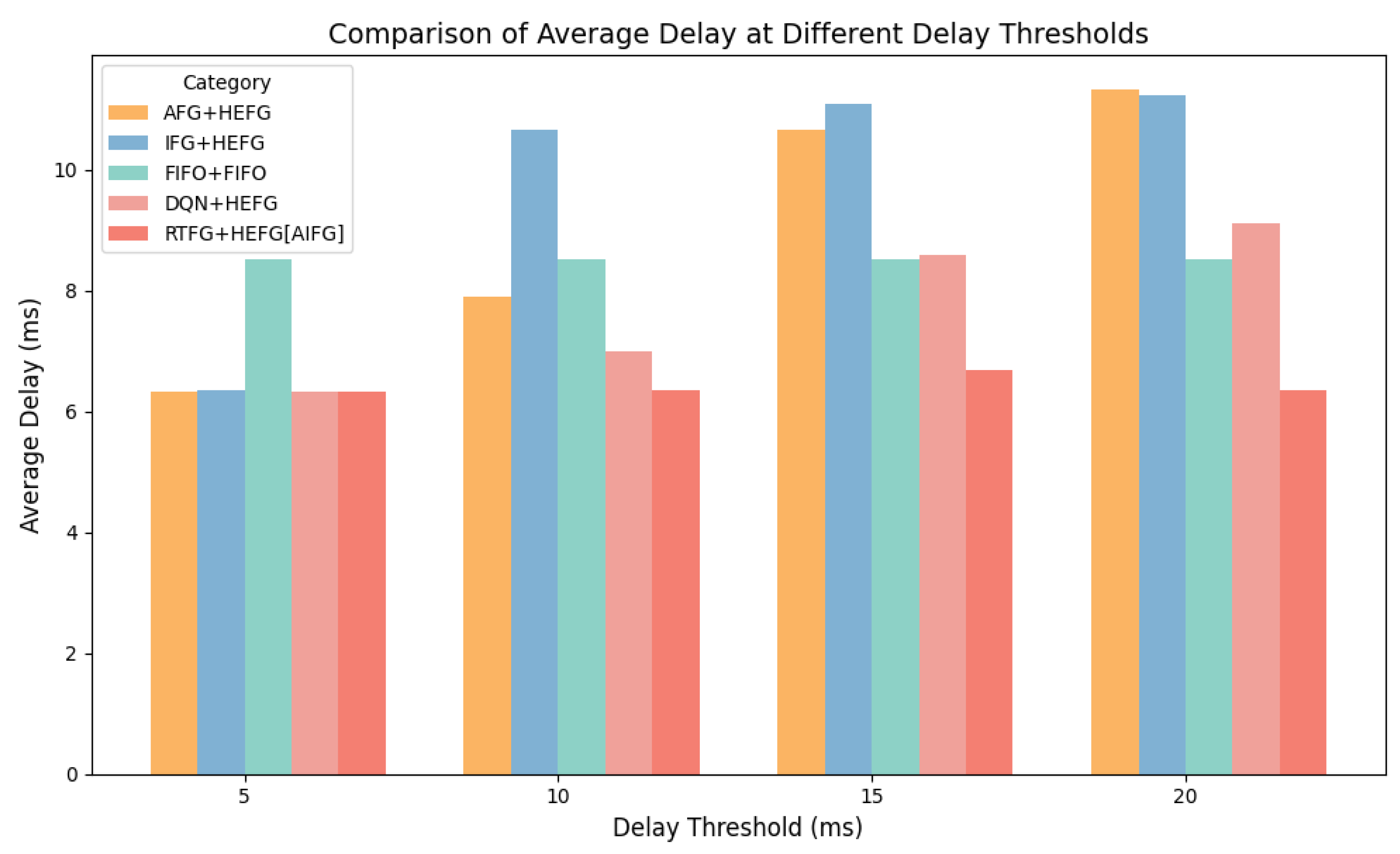
Figure 9 shows that AIFG consistently exhibits the lowest delay across all time requirements, outperforming all other methods. This is especially noticeable under higher time requirements (15 ms and 20 ms), where the delay is substantially smaller. Meanwhile, the FIFO-based method exhibits slower processing times due to its inherent characteristics. With a delay requirement of 5 ms, the average queue delay for AIFG, DQN + HEFG, AFG + HEFG, and IFG + HEFG is almost the same, ranging from 6 to 7 ms. However, at a 10 ms delay requirement, AIFG’s average queue delay is reduced by 19.39% compared to AFG + HEFG and by 40.33% compared to IFG + HEFG and by 8.9% compared to DQN + HEFG. At a 15 ms delay requirement, AIFG’s average queue delay decreases by 37.30% compared to AFG + HEFG and by 39.62% compared to IFG + HEFG and by 22.1% compared to DQN + HEFG. At a 20 ms delay requirement, AIFG’s average queue delay is 43.90% lower than AFG + HEFG and 43.45% lower than IFG + HEFG and 30.3% lower than DQN + HEFG. When the delay requirement is low (e.g., 5 ms), the queue length typically does not exceed the AFG threshold, so the algorithm’s performance is similar to that of AFG, and the advantages of AIFG are not fully manifested. However, when the delay requirement is high, AIFG dynamically optimizes the gap between frames, reducing delays and improving overall performance by adapting to changing conditions in the transmission environment. In this part, DQN + HEFG performs better than traditional rule-based approaches (AFG/IFG + HEFG) but does not reach the stability and optimization level of PPO-based AIFG. The simulation results validate the adaptability of the AIFG algorithm under varying delay requirements and the advantage of AIFG in reducing average queue delay.

Based on the analysis of the above results, in the face of time-sensitive service queues, the AIFG algorithm proposed in this paper can effectively adjust the framing threshold according to the queue state. Compared with the traditional algorithm, it achieves a better multiplexing efficiency and a lower queuing delay while ensuring excellent throughput, which is an effective performance improvement. In terms of throughput performance, the AIFG algorithm has an average increase of 31.92% compared with the AFG + HEFG, IFG + HEFG and DQN + HEFG algorithms. In terms of the multiplexing efficiency, the AIFG algorithm has an average increase of 74.93% compared with the AFG + HEFG, IFG + HEFG and DQN + HEFG algorithms when the delay requirement is below 5 ms. In terms of the average queuing delay, the AIFG algorithm is 33.53% lower than the AFG + HEFG algorithm and 41.13% lower than the IFG + HEFG algorithm and 20.43% lower than the DQN + HEFG algorithm when the delay requirement is above 5 ms. In reinforcement learning applications, while DQN provides improvements over heuristic baselines, the PPO-based AIFG exhibits higher adaptability, stability, and better global optimization performance, making it more suitable for diverse and dynamic space network environments.

To evaluate the scalability and robustness of the proposed AIFG algorithm under varying network sizes, we expand the simulation to assess performance across different network sizes, including 25–25, 50–50, 100–100, and 200–200 transmitter–receiver pairs. We maintain the same satellite relay architecture. These different simulation situations are all performed under the condition that the delay requirement is 20 ms. To further validate the scalability of the proposed AIFG algorithm, we specifically focus on the PPO training time, training memory consumption, convergence iterations, and resulting performance metrics such as delay, multiplexing efficiency, and throughput. The key performance metrics observed include the following:

• Training computational overhead, measured as the cumulative time and training memory consumption required for PPO training to reach a stable policy.
• Convergence time, quantified as the number of iterations needed for the reward function to stabilize within a defined tolerance range.

As shown in Figure 10, the reward sum becomes negative in large-scale cases due to an increased queuing delay. In contrast, for smaller networks (25 and 50 nodes), the algorithm achieves convergence within fewer episodes and yields positive reward values. Notably, the algorithm’s accumulated reward converges well even in large-scale environments.

As summarized in

Table 5. Performance metrics and computational overhead of AIFG under different network scales (delay requirement: 20 ms).

Network Size (T-R Pairs)	PPO Training Time (s)	PPO Training Memory Consumption (MB)	Convergence Iterations	Average Delay (ms)	Multiplexing Efficiency (%)	Throughput (Kbps)
25–25 Nodes	98.52	260.64	45	8.64923	86.3845	389.417
50–50 Nodes	41.46	261.61	40	10.28250	98.6160	554.862
100–100 Nodes	365.48	261.09	68	52.43700	95.4074	643.059
200–200 Nodes	797.71	259.97	80	70.74900	95.4598	643.448

, the training time increases with the node scale, reaching approximately 798 s in the 200-node configuration, compared to just 41.5 s for 50 nodes. Similarly, the number of PPO training iterations required for reward convergence increases from 40 to 80. Nonetheless, AIFG still delivers high efficiency and throughput across all scenarios. Although the computational cost increases as the network grows, the performance in delay remains acceptable.

These results, summarized in Figure 10 and Table 5, demonstrate that AIFG remains computationally viable and robust under scale expansion, offering consistent performance and QoS adaptability even in dense satellite constellations. In summary, the AIFG algorithm demonstrates strong scalability with a predictable computational cost growth and robust convergence behavior, indicating its feasibility in large-scale deployment.

To further investigate the robustness and adaptability of the proposed AIFG algorithm under varying network configurations, two additional simulation scenarios were conducted. The first scenario explores the influence of different MPDU sizes on system performance. Specifically, MPDU sizes were varied across 800, 1200, 1500 (default), and 1800 bytes. As shown in

Table 6. Performance comparison under different MPDU sizes (delay requirement: 20 ms).

MPDU Size (Bytes)	Average Delay (ms)	Multiplexing Efficiency (%)	Throughput (Kbps)
800	7.23457	96.110	559.608
1200	9.27896	98.992	566.066
1500 (Default)	10.77100	99.494	566.453
1800	12.05860	97.593	525.173

, the AIFG algorithm maintains consistently high throughput and multiplexing efficiency across different MPDU sizes. The results show that while increasing MPDU size improves multiplexing efficiency up to a point, overly large frame sizes (e.g., 1800 bytes) lead to degraded throughput, likely due to transmission and fragmentation inefficiencies. The default size of 1500 bytes strikes a good balance among the average delay (10.77 ms), efficiency (99.49%), and throughput (566.45 Kbps), confirming the appropriateness of the default setting. Interestingly, even when reducing the frame size to 800 bytes, the algorithm achieves strong performance with an average delay of only 7.23 ms and a throughput of 559.61 Kbps. These results indicate that the AIFG algorithm is capable of dynamically adjusting the frame threshold to maintain high performance, even under less efficient framing conditions.

In the second scenario, the satellite link bandwidth was adjusted across 3, 6 (default), 9, 15, and 20 Mbps to simulate the variability caused by orbital distance, channel fading, or dynamic scheduling. As summarized in

Table 7. Performance comparison under different satellite link bandwidth (delay requirement: 20 ms).

Relay Link Bandwidth (Between Satellites) (Mbps)	Average Delay (ms)	Multiplexing Efficiency (%)	Throughput (Kbps)
3	11.0130	96.588	566.859
6 (Default)	11.3376	99.523	575.183
9	11.0255	97.558	569.503
15	11.0319	96.951	567.063
20	11.2763	99.044	574.157

, the AIFG algorithm continues to demonstrate resilient performance, with stable average delay and throughput across all bandwidth conditions. Although slight improvements in throughput are observed as bandwidth increases, the average delay and efficiency remain within a narrow and acceptable range. The default configuration of 6 Mbps achieved the highest throughput at 575.18 Kbps and the best multiplexing efficiency at 99.52%. Even in constrained link scenarios (e.g., 3 Mbps), the algorithm sustains efficient operation, with a throughput of 566.86 Kbps. These findings confirm the algorithm’s robustness under dynamic bandwidth constraints and validate its practical applicability in real-world spaceborne communication environments.

These extended experiments further support that the AIFG algorithm not only provides adaptive framing under differentiated QoS demands but also maintains high levels of delay control, bandwidth efficiency, and throughput under fluctuating MPDU configurations and varying relay link conditions. This reinforces the algorithm’s suitability for deployment in dynamic space networking environments with heterogeneous service profiles.

6.3. Results

Based on the simulation results described in Section 6.2, the proposed AIFG algorithm demonstrates significant advantages over traditional framing algorithms across multiple dimensions:

• Reduction in Queue Delay: As claimed in the abstract, AIFG effectively reduces the average queuing delay for delay-sensitive services. Simulation results show a reduction of at least 8.90%, and up to 43.90%, compared to benchmark methods such as AFG + HEFG, IFG + HEFG, and DQN + HEFG. It demonstrated effective delay control under diverse QoS constraints.
• Improvement in Throughput: The throughput achieved by AIFG increases by at least 6.10%, with improvements up to 78.05% under low delay constraints, confirming its efficiency in data delivery across time-sensitive and non-sensitive flows.
• Enhancement of Multiplexing Efficiency: AIFG demonstrates improved frame utilization, with the multiplexing efficiency increasing by, at most, 92.36% in comparison with traditional methods, especially under stricter time thresholds.

These quantitative results fully support the core contributions presented in the abstract and validate the effectiveness of AIFG algorithm in adapting to differentiated QoS requirements in Advanced Orbiting Systems.

It is important to note that in the proposed AIFG algorithm, the framing time threshold is not statically set. Instead, it is dynamically adjusted at runtime by the reinforcement learning agent. The PPO algorithm continuously updates the threshold value based on the observed system state, including packet arrival rate, queue length, and frame generation time. As such, the threshold evolves differently under each delay requirement scenario (e.g., 5 ms, 10 ms, 15 ms, 20 ms), and there is no single fixed optimal value applicable across all conditions. During simulation, different delay requirement environments are used to train the agent, and reward parameters are tuned accordingly.

The performance improvements reported in this section—such as higher throughput, reduced average queue delay, and increased multiplexing efficiency—are the result of adaptive threshold selection throughout the simulation. The reward function parameters used to guide this adaptive process are provided in Table 3 and Table 4. These results demonstrate the effectiveness of using policy-based learning to dynamically regulate the frame generation process. AIFG achieves superior performance not through a static configuration but via a policy-driven dynamic adjustment under varying QoS conditions.

6.4. Discussion

Although the proposed AIFG algorithm has demonstrated substantial improvements in reducing queue delay, increasing throughput, and enhancing the multiplexing efficiency, several limitations and open challenges remain:

• Simulation-Based Validation: The current evaluation is based solely on a simulation platform using NS-3 (version 3.33) and PyTorch (version 2.2.2). Real-world satellite communication environments introduce complexities, such as hardware constraints, channel fading, and protocol interoperability, which are not modeled here.
• Static Traffic Model: The number of service streams and their classifications were fixed during the simulations. In practical deployments, service types and loads are often time-varying and mission-dependent, which may impact the algorithm’s adaptability.
• Energy Efficiency Not Considered: This study focuses on QoS metrics without evaluating energy consumption, which is a critical constraint in space systems. Future work should explore low-power optimization and computational efficiency.
• Algorithm Scalability and Convergence: Although PPO provides stable learning, its convergence speed and computational cost may become significant in larger-scale AOS. Exploring more lightweight or distributed RL techniques would be beneficial.
• Cross-Layer Optimization: Integrating AIFG with transport-layer protocols or application-layer protocols, or co-designing with physical-layer resource adaptation, could further enhance end-to-end QoS.

These limitations provide a roadmap for future research and guide the further refinement of the AIFG framework toward deployment in practical aerospace communication systems.

7. Conclusions

To further enhance the service quality of the AOS for handling massive heterogeneous services, this paper proposes an advanced intelligent frame generation (AIFG) algorithm designed to meet differentiated QoS requirements. Based on the classification framework for delay-sensitive and non-delay-sensitive services, real-time frame generation and high-efficiency frame generation algorithms are designed for each type of service. In the real-time framing algorithm, this paper models the optimal framing time threshold calculation problem of delay-sensitive services as a Markov decision process and uses the reinforcement learning algorithm to obtain the optimal solution. For non-delay-sensitive services, the high-efficiency frame generation algorithm ensures that the frame is filled before transmission and it is adopted to maximize frame utilization. Simulation results show that compared to traditional frame generation algorithms and the learning-based DQN algorithm, the proposed algorithm accommodates the different transmission needs of real-time and non-real-time services, reduces the average queue delay for real-time services, increases the average multiplexing efficiency for services, and improves the overall network service quality of the AOS. For future work, efforts can focus on extending AIFG to real-world scenarios with more complex environmental dynamics and hardware constraints. The algorithm’s reinforcement learning-based structure and modular framing design also provide a flexible foundation for further research in intelligent communications across other delay-constrained or resource-limited network environments.