Efficient Data Reduction Through Maximum-Separation Vector Selection and Centroid Embedding Representation
Abstract
1. Introduction
- To propose a systematic data reduction framework that enables effective sentiment classification with minimal labeled samples.
- To demonstrate that models trained on carefully selected subsets (as few as two or 100 samples) can achieve performance comparable to full-dataset training.
- To show that data-efficient models, by minimizing overfitting to dataset-specific artifacts, can exhibit improved generalization across different domains and datasets.
2. Related Work
2.1. Early Methods for Sentiment Analysis
2.2. Transformer Models and Data Efficiency Challenges
2.3. Data Reduction and Sample Selection Strategies
2.4. Embedding Space Geometry and Sentiment Representation
2.5. Extending Prior Work with Geometric Data Reduction
- HDSV (High-Distance Sentiment Vectors) selects maximally separated sentiment pairs based on pairwise distance in the embedding space, enabling compact yet diverse training sets inspired by active learning but adapted for one-shot use.
- CSEV (Centroid Sentiment Embedding Vectors) constructs representative class prototypes guided by the CSR metric, which balances inter-class separation and intra-class cohesion to ensure discriminative representation.
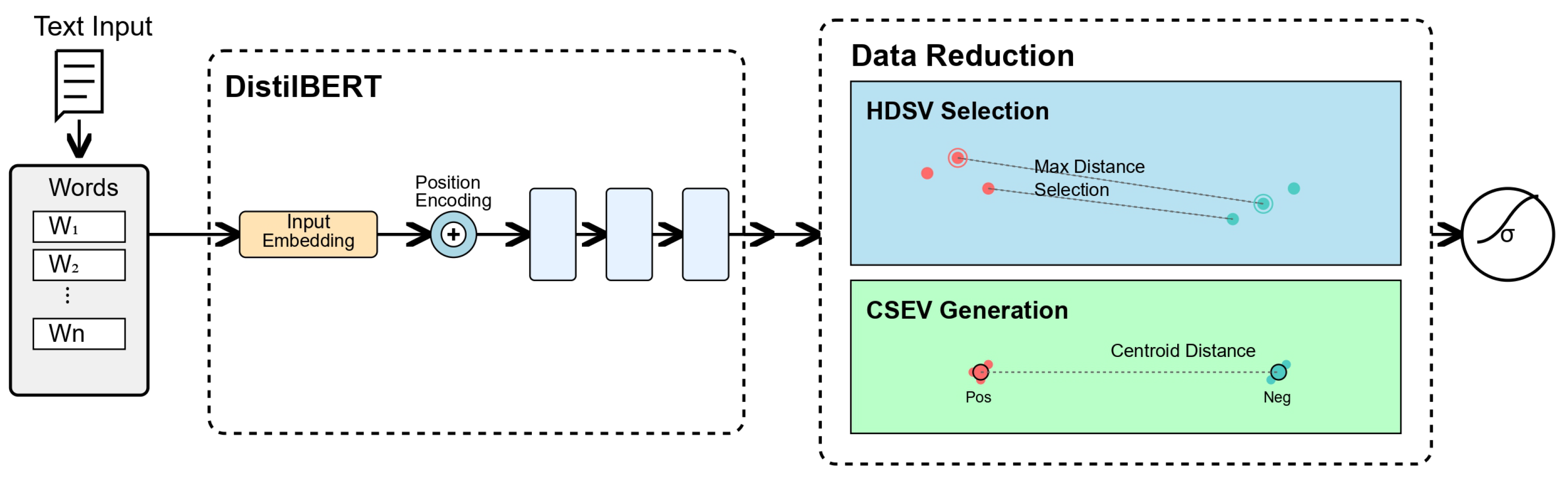
3. Methodology
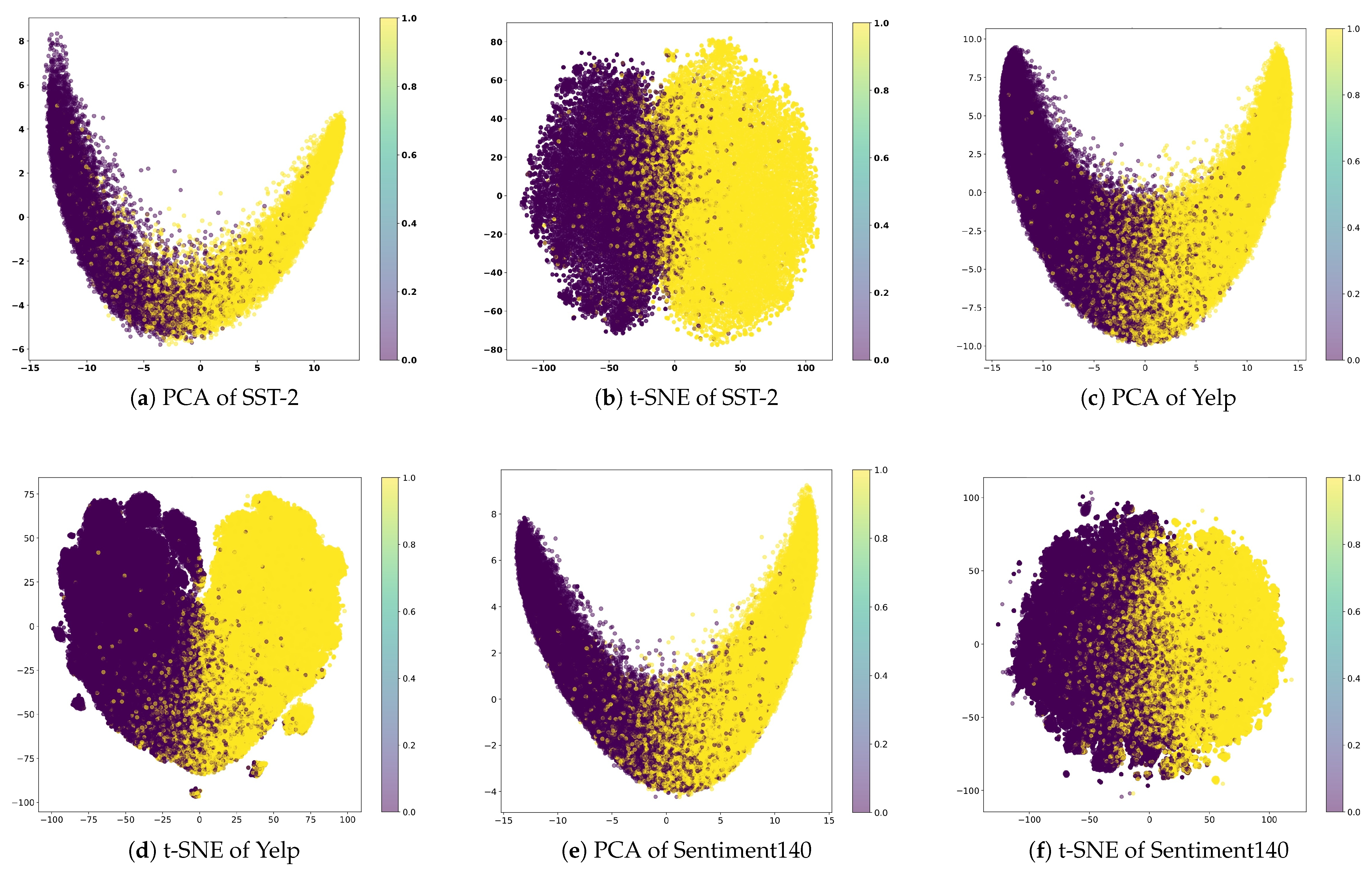
3.1. Embedding Space Analysis
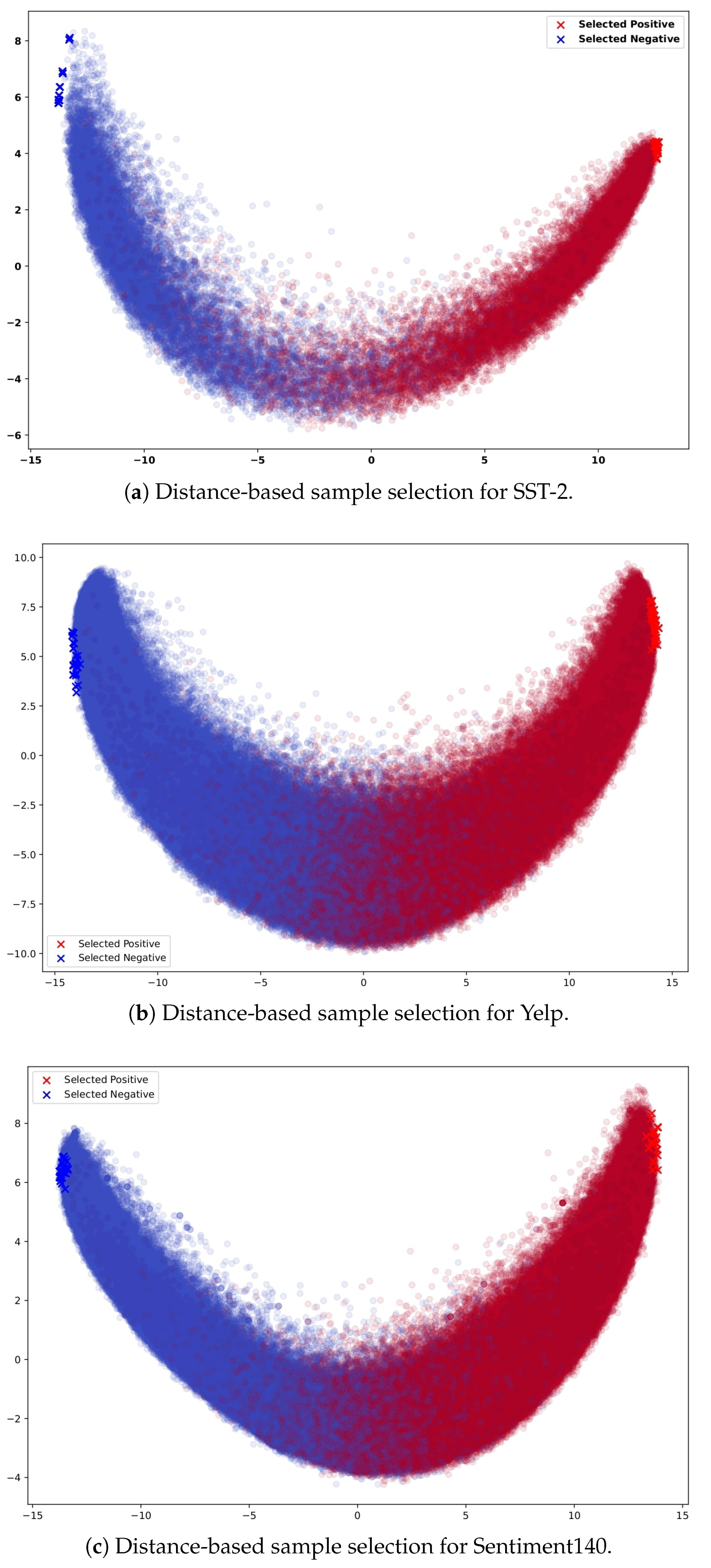
3.2. High-Distance Sentiment Vectors (HDSV)
3.3. Centroid Sentiment Embedding Vector (CSEV)
3.4. Fine-Tuning Process
4. Results
4.1. Dataset Size Reduction Analysis
4.2. Model Performance Analysis
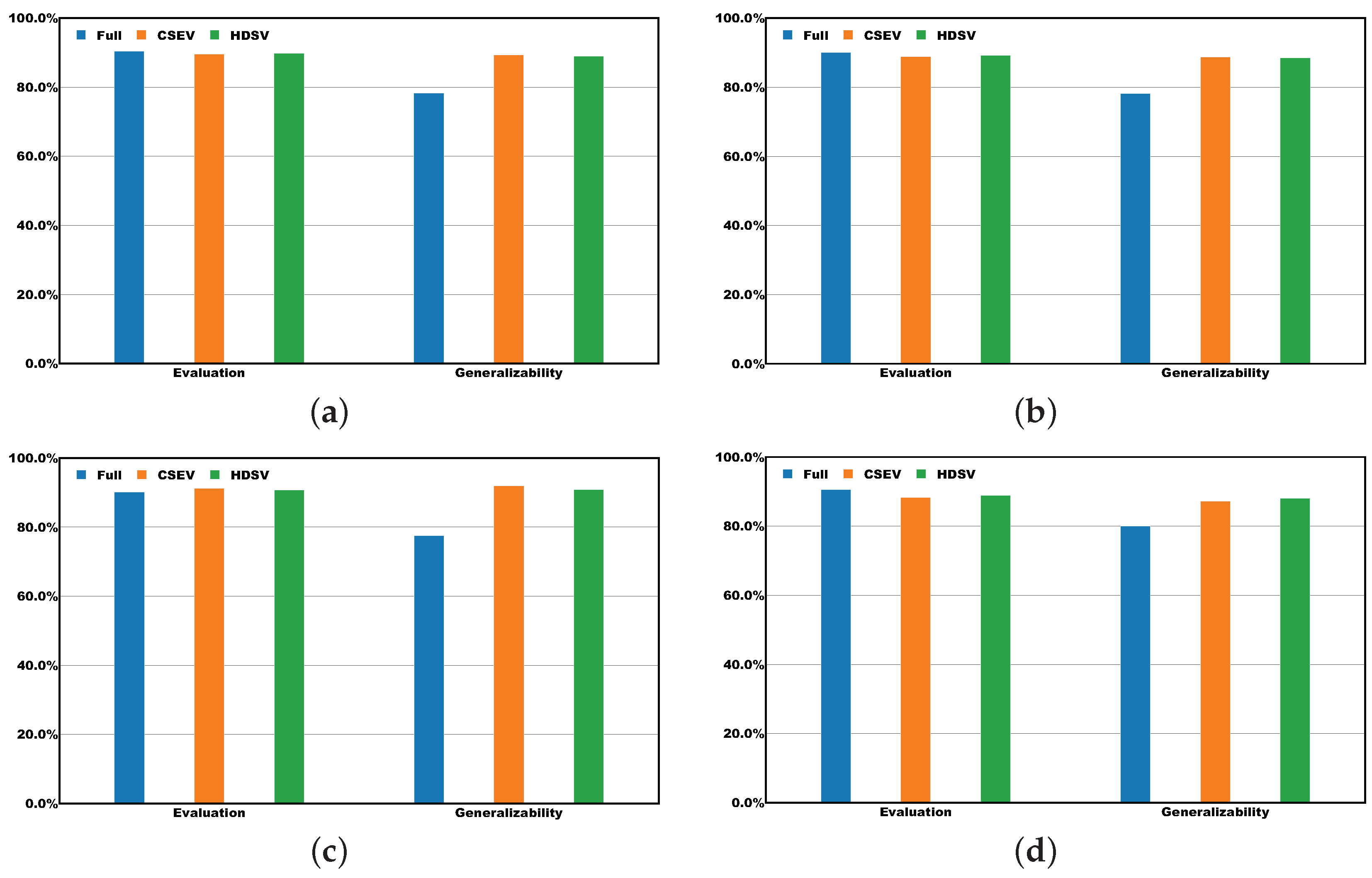
4.2.1. Direct Evaluation Performance
4.2.2. Generalizability Analysis
4.2.3. Metric-Specific Analysis
4.2.4. Comparison with Established Data Reduction Methods
5. Discussion
5.1. Data Reduction and Efficiency
5.2. Performance and Robustness
5.3. Cross-Domain Generalization
5.4. Limitations and Future Work
5.5. Practical Implications
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaiser, C.; Ahuvia, A.; Rauschnabel, P.A.; Wimble, M. Social media monitoring: What can marketers learn from Facebook brand photos? J. Bus. Res. 2020, 117, 707–717. [Google Scholar] [CrossRef]
- Kim, J.H.; Sabherwal, R.; Bock, G.W.; Kim, H.M. Understanding social media monitoring and online rumors. J. Comput. Inf. Syst. 2021, 61, 507–519. [Google Scholar] [CrossRef]
- de Oliveira Santini, F.; Ladeira, W.J.; Pinto, D.C.; Herter, M.M.; Sampaio, C.H.; Babin, B.J. Customer engagement in social media: A framework and meta-analysis. J. Acad. Mark. Sci. 2020, 48, 1211–1228. [Google Scholar] [CrossRef]
- Choi, J.; Yoon, J.; Chung, J.; Coh, B.Y.; Lee, J.M. Social media analytics and business intelligence research: A systematic review. Inf. Process. Manag. 2020, 57, 102279. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019, Minneapolis, MN, USA, 2–7 June 2019; Burstein, J., Doran, C., Solorio, T., Eds.; Long and Short Papers. Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; Volume 1, pp. 4171–4186. [Google Scholar] [CrossRef]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Lankford, S.; Afli, H.; Way, A. adaptmllm: Fine-tuning multilingual language models on low-resource languages with integrated llm playgrounds. Information 2023, 14, 638. [Google Scholar] [CrossRef]
- Ding, N.; Qin, Y.; Yang, G.; Wei, F.; Yang, Z.; Su, Y.; Hu, S.; Chen, Y.; Chan, C.M.; Chen, W.; et al. Parameter-efficient fine-tuning of large-scale pre-trained language models. Nat. Mach. Intell. 2023, 5, 220–235. [Google Scholar] [CrossRef]
- Sanh, V. DistilBERT, a distilled version of BERT: Smaller, faster, cheaper and lighter. arXiv 2019, arXiv:1910.01108. [Google Scholar]
- Gou, J.; Yu, B.; Maybank, S.J.; Tao, D. Knowledge distillation: A survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Y.; Fang, Y.; Liu, Y.; Sun, S.; Xu, R.; Zhu, C.; Zeng, M. Training Data is More Valuable than You Think: A Simple and Effective Method by Retrieving from Training Data. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), ACL 2022, Dublin, Ireland, 22–27 May 2022; Muresan, S., Nakov, P., Villavicencio, A., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2022; pp. 3170–3179. [Google Scholar] [CrossRef]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 2020, 21, 1–67. [Google Scholar]
- Peters, M.E.; Neumann, M.; Zettlemoyer, L.; Yih, W. Dissecting Contextual Word Embeddings: Architecture and Representation. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; Riloff, E., Chiang, D., Hockenmaier, J., Tsujii, J., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 1499–1509. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; Cohen, T.; Veličković, P. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv 2021, arXiv:2104.13478. [Google Scholar]
- Ethayarajh, K. How Contextual are Contextualized Word Representations? Comparing the Geometry of BERT, ELMo, and GPT-2 Embeddings. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; Inui, K., Jiang, J., Ng, V., Wan, X., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 55–65. [Google Scholar] [CrossRef]
- Tharwat, A.; Schenck, W. A survey on active learning: State-of-the-art, practical challenges and research directions. Mathematics 2023, 11, 820. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, H.; Ming, X.; Cui, L.; Yin, H.; Xu, G. Where are we in embedding spaces? In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021; pp. 2223–2231. [Google Scholar]
- Socher, R.; Perelygin, A.; Wu, J.; Chuang, J.; Manning, C.D.; Ng, A.; Potts, C. Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, Seattle, WA, USA, 18–21 October 2013; pp. 1631–1642. [Google Scholar]
- Zhang, X.; Zhao, J.; LeCun, Y. Character-Level Convolutional Networks for Text Classification. arXiv 2015, arXiv:1509.01626 [Cs]. [Google Scholar]
- Go, A.; Bhayani, R.; Huang, L. Twitter sentiment classification using distant supervision. Cs224N Proj. Rep. Stanf. 2009, 1, 2009. [Google Scholar]
- Barnes, J.; Øvrelid, L.; Velldal, E. Sentiment Analysis Is Not Solved! Assessing and Probing Sentiment Classification. In Proceedings of the 2019 ACL Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP, Florence, Italy, 1 August 2019; Linzen, T., Chrupała, G., Belinkov, Y., Hupkes, D., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 12–23. [Google Scholar] [CrossRef]
- Taboada, M.; Brooke, J.; Tofiloski, M.; Voll, K.; Stede, M. Lexicon-based methods for sentiment analysis. Comput. Linguist. 2011, 37, 267–307. [Google Scholar] [CrossRef]
- Kim, J.; Lee, M. Robust lane detection based on convolutional neural network and random sample consensus. In Proceedings of the International Conference on Neural Information Processing, Montreal, QC, Canada, 8–13 December 2014; Springer: Cham, Switzerland, 2014; pp. 454–461. [Google Scholar]
- Aquino-Brítez, S.; García-Sánchez, P.; Ortiz, A.; Aquino-Brítez, D. Towards an Energy Consumption Index for Deep Learning Models: A Comparative Analysis of Architectures, GPUs, and Measurement Tools. Sensors 2025, 25, 846. [Google Scholar] [CrossRef]
- Khalil, M.; McGough, A.S.; Pourmirza, Z.; Pazhoohesh, M.; Walker, S. Machine Learning, Deep Learning and Statistical Analysis for forecasting building energy consumption—A systematic review. Eng. Appl. Artif. Intell. 2022, 115, 105287. [Google Scholar] [CrossRef]
- Xie, Q.; Dai, Z.; Hovy, E.; Luong, T.; Le, Q. Unsupervised data augmentation for consistency training. Adv. Neural Inf. Process. Syst. 2020, 33, 6256–6268. [Google Scholar]
- Feldman, D. Core-sets: Updated survey. In Sampling Techniques for Supervised or Unsupervised Tasks; Springer: Cham, Switzerland, 2020; pp. 23–44. [Google Scholar]
- Lorenzoni, G.; Portugal, I.; Alencar, P.; Cowan, D. Exploring Variability in Fine-Tuned Models for Text Classification with DistilBERT. arXiv 2024, arXiv:2501.00241. [Google Scholar]
- Reyad, M.; Sarhan, A.M.; Arafa, M. A modified Adam algorithm for deep neural network optimization. Neural Comput. Appl. 2023, 35, 17095–17112. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, J.; Ding, X.; Huai, T.; Liu, S.; Chen, Q.; Xie, Y.; He, L. Recent advances of foundation language models-based continual learning: A survey. ACM Comput. Surv. 2025, 57, 112. [Google Scholar] [CrossRef]
- Liang, P.; Bommasani, R.; Lee, T.; Tsipras, D.; Soylu, D.; Yasunaga, M.; Zhang, Y.; Narayanan, D.; Wu, Y.; Kumar, A.; et al. Holistic evaluation of language models. arXiv 2022, arXiv:2211.09110. [Google Scholar]
- Liu, J.; Zheng, S.; Xu, G.; Lin, M. Cross-domain sentiment aware word embeddings for review sentiment analysis. Int. J. Mach. Learn. Cybern. 2021, 12, 343–354. [Google Scholar] [CrossRef]
- Ramanujan, V.; Nguyen, T.; Oh, S.; Farhadi, A.; Schmidt, L. On the connection between pre-training data diversity and fine-tuning robustness. Adv. Neural Inf. Process. Syst. 2024, 36, 66426–66437. [Google Scholar]
- Zhu, R.; Guo, D.; Qi, D.; Chu, Z.; Yu, X.; Li, S. A Survey of Trustworthy Representation Learning Across Domains. ACM Trans. Knowl. Discov. Data 2024, 18, 173. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, X.; Zhao, L.; Liang, Y.; Zhang, P.; Jin, B. Hybrid embedding-based text representation for hierarchical multi-label text classification. Expert Syst. Appl. 2022, 187, 115905. [Google Scholar] [CrossRef]
- Yuan, M.; Mengyuan, Z.; Jiang, L.; Mo, Y.; Shi, X. stce at semeval-2022 task 6: Sarcasm detection in english tweets. In Proceedings of the 16th International Workshop on Semantic Evaluation (SemEval-2022), Virtual, 14–15 July 2022; pp. 820–826. [Google Scholar]
- Walker, T.; Wendt, S.; Goubran, S.; Schwartz, T. Artificial Intelligence for Sustainability: An Overview. In Artificial Intelligence For Sustainability: Innovations In Business And Financial Services; Palgrave Macmillan: Cham, Switzerland, 2024; pp. 1–10. [Google Scholar]
| Dataset | Type | Size (MB) | Relative Size (%) | Training Samples |
|---|---|---|---|---|
| Sentiment140 | HDSV | 117.66 | 1% | 100 |
| CSEV | 2.59 | Less than 1% | 2 | |
| Full | 10,608.69 | 100% | 1,600,000 | |
| SST-2 | HDSV | 117.66 | 19% | 100 |
| CSEV | 2.59 | Less than 1% | 2 | |
| Full | 613.57 | 100% | 67,349 | |
| Yelp | HDSV | 117.66 | Less than 1% | 100 |
| CSEV | 2.59 | Less than 1% | 2 | |
| Full | 42,153.33 | 100% | 560,000 |
| Type | Testing Method | Accuracy | F1-Score | Precision | Recall | MCC |
|---|---|---|---|---|---|---|
| Full | Evaluation | 90.14% | 90.36% | 90.57% | 90.16% | 80.73% |
| Generalizability | 78.20% | 78.30% | 80.00% | 77.50% | 57.80% | |
| CSEV | Generalizability | 88.79% | 89.30% | 87.21% | 91.92% | 78.46% |
| Evaluation | 88.93% | 89.55% | 88.27% | 91.20% | 78.99% | |
| HDSV | Generalizability | 88.56% | 88.97% | 88.11% | 90.80% | 78.42% |
| Evaluation | 89.30% | 89.76% | 88.94% | 90.79% | 79.42% |
| # Samples | Reduction Method | Testing Method | Accuracy | Precision | Recall | F1 |
|---|---|---|---|---|---|---|
| 100 | Uncertainty | Evaluation | 62.85% | 61.83% | 84.80% | 71.03% |
| Sampling | Generalizability | 54.63% | 54.18% | 96.17% | 69.77% | |
| 100 | Random | Evaluation | 59.38% | 62.00% | 82.93% | 69.74% |
| Sampling | Generalizability | 53.88% | 68.89% | 34.40% | 25.13% | |
| 2 | Uncertainty | Evaluation | 52.19% | 54.53% | 63.93% | 51.61% |
| Sampling | Generalizability | 50.48% | 52.88% | 65.78% | 58.33% | |
| 2 | Random | Evaluation | 53.66% | 58.25% | 59.16% | 48.78% |
| Sampling | Generalizability | 47.86% | 34.24% | 54.08% | 43.65% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshamrani, S. Efficient Data Reduction Through Maximum-Separation Vector Selection and Centroid Embedding Representation. Electronics 2025, 14, 1919. https://doi.org/10.3390/electronics14101919
Alshamrani S. Efficient Data Reduction Through Maximum-Separation Vector Selection and Centroid Embedding Representation. Electronics. 2025; 14(10):1919. https://doi.org/10.3390/electronics14101919
Chicago/Turabian StyleAlshamrani, Sultan. 2025. "Efficient Data Reduction Through Maximum-Separation Vector Selection and Centroid Embedding Representation" Electronics 14, no. 10: 1919. https://doi.org/10.3390/electronics14101919
APA StyleAlshamrani, S. (2025). Efficient Data Reduction Through Maximum-Separation Vector Selection and Centroid Embedding Representation. Electronics, 14(10), 1919. https://doi.org/10.3390/electronics14101919






