Single Trace Analysis of Visible vs. Invisible Leakage for Comparison-Operation-Based CDT Sampling

Abstract

The emergence of quantum computers poses a significant threat to the security of conventional public-key cryptosystems, driving the demand for quantum-resistant cryptographic solutions. In response, the National Institute of Standards and Technology (NIST) conducted a multi-year competition, ultimately selecting four ciphers. Among these, Falcon employs cumulative distribution table (CDT) sampling, which produces arrays of random values derived from a discrete Gaussian distribution during the signature generation phase. This array is then used with secret key information, forming the core of Falcon. Enhanced variants of Falcon, such as Mitaka, SOLMAE, and Antrag, implemented CDT sampling using comparison operations. Previous research by Choi et al. proposed a single trace analysis and countermeasure for CDT sampling, which exploited a non-constant-time vulnerability in 8-bit AVR microcontrollers. However, this vulnerability is specific to certain environments, and a potential vulnerability in comparison-operation-based constant-time CDT sampling remains unstudied. This paper is an extension of that study. This paper investigates the constant-time operation of comparison-operation-based CDT sampling on Arm Cortex-M4-based chips and proposes a deep learning-based side-channel analysis to recover the sampling values using a novel vulnerability. The proposed model achieves an F1 score of 1.0 and a recovery success rate of 99.97%.

1. Introduction

Public-key cryptography is widely used in areas such as digital signatures and mobile communication. However, it has proven that it will be vulnerable in the future with the advent of quantum computers [1,2]. To address this issue, the U.S. National Institute of Standards and Technology (NIST) has been running a post-quantum cryptography (PQC) competition since 2016, with four final algorithms selected in 2022 and additional algorithm competitions underway. The quantum-resistant ciphers of the future will replace the public-key ciphers we use today, so they need to be tested for security on real devices. Falcon is one of the algorithms selected in the competition. In other words, Falcon [3] was proposed as a digital signature, and models are needed to evaluate the security of Falcon and its improved crypto algorithms when operating on embedded devices. Proposed ciphers that improve on Falcon are Mitaka [4] and Antrag [5], and a variation of it is SOLMAE, one candidate of Korean post-quantum cryptography (KPQC) [6]. KPQC is a quantum-resistant cryptography competition held in South Korea.

The core of Falcon and its variants is quickly generating arrays of random values drawn from a discrete Gaussian distribution table. The generated random values are the signature values after working using the secret values. Thus, Falcon and its variants are interested in speed sampling. However, the leakage of extracted random values from Gaussian sampling can contribute to the indirect leakage of secret information. The intermediate value generated by the computation of the sampled value and the secret value can be leaked using side-channel analysis, etc. Cumulative distribution table (CDT) sampling is a method that stores discrete Gaussian probabilities in a table and uses comparisons between the input and stored values to determine output. There is extensive research on side-channel vulnerabilities associated with different implementations of CDT sampling [7,8,9,10]. CDT sampling based on subtraction operations is vulnerable due to the discrepancy between positive and negative Hamming weights, with successful attacks demonstrated on schemes such as Lizard and FrodoKEM [11,12].

However, there is a lack of studies on side-channel analysis of CDT sampling based on comparison operations used in Falcon-based PQC algorithms. We proposed a single trace analysis (STA) of CDT sampling based on comparison operations in the International Conference on Information Security and Cryptology (ICISC 2023) [10]. It is a single trace analysis using vulnerability for CDT sampling with a non-constant time. The study was performed with a CDT operating on a 8-bit AVR microcontroller unit (MCU). A comparison-operation-based CDT sampling algorithm that satisfies constant time was proposed as a countermeasure. However, 8-bit AVR MCUs are not realistic enough for Falcon and Mitaka, which deal with 64-bit-sized operators. To our knowledge, there is no study on the safety of CDT sampling based on comparison operations on MCUs with constant time. This paper extends the work of Choi et al. to study the safety of CDT sampling based on comparison operations in more practical environments.

The following is a contribution to this paper. In this paper, we propose a single trace analysis for each visible and invisible vulnerability to CDT sampling based on comparison operations.

• Single trace analysis for visible vulnerability: This is the non-constant-time vulnerability we proposed in ICISC 2023. We studied that CDT sampling based on comparison operation has a visible vulnerability in the 8-bit AVR environment, which can be used to recover sampled values using only a single trace. We investigated the cause of this in depth. The reason is that comparison operations in AVR can operate on operands larger than the compiler’s unit of operation, causing them to operate early stop.
• The countermeasure that constant-time CDT sampling is based on comparison operations: We proposed a comparison-operation-based CDT sampling algorithm that divides the operands by the compiler’s unit of operation and stores and processes them. We have experimentally shown that it satisfies constant time in the AVR environment. Of course, depending on the implementation method, branching statements may be generated, and we proposed an implementation method to eliminate them.
• Single trace analysis of an invisible vulnerability: We investigated the fact that CDT sampling is already constant-time on a 32-bit ARM Cortex-M4, a common environment. We were deeply interested in invisible vulnerabilities. Through reverse engineering, we traced the behavior of CDT on ARM and found a vulnerability that caused Hamming weight differences depending on the result of the comparison operation. We proposed a novel safety evaluation model using power consumption traces for when CDT sampling operates on ARM. The proposed model can recover the value of CDT sampling with a single trace. The recovery accuracy is 99.97%, and the test results show that the F1 score is 1 for both micro and macro.

This work is structured as follows: Section 2 explores the crucial role of CDT sampling in quantum-resistant cryptography and reviews ongoing research on its security. Section 3 describes the power consumption acquisition environment that occurs when CDT is operating. Section 4 addresses single trace analysis and countermeasures for visible vulnerabilities in 8-bit AVR microcontrollers. Section 5 examines single trace analysis and mitigation strategies for invisible vulnerabilities in the 32-bit ARM Cortex-M4. Finally, Section 6 presents the conclusions and future work.

2. Preliminaries

This section highlights the importance of CDT sampling, a method used to sample values from a discrete Gaussian distribution, and its role in lattice-based cryptosystems. Additionally, it reviews research on side-channel analysis related to CDT sampling, focusing on the limitations of comparison-based CDT sampling in non-constant-time environments. The discussion emphasizes the necessity for further security studies in more generalized environments.

2.1. Lattice-Based Cryptosystems: LWE and NTRU

Quantum-resistant ciphers designed as lattice-based problems, such as learning with error (LWE) [13] and NTRU [14,15], which are NP-hard, have been submitted to NIST [3,11,12]. Many cryptographic algorithms based on LWE and NTRU use Gaussian sampling. Gaussian sampling generates either the secret value or random values related to the secret value. This means that Gaussian sampling is closely linked to security in most of the ciphers we studied. The equations for the lattice, LWE, and NTRU are as follows:

Definition 1. 

Lattice: Let $b_1,b_2,\dots ,b_n\in {\mathbb{R}}^m$ be a set of linearly independent vectors. The Lattice $\mathcal{L}(b_1,b_2,\dots ,b_n)$ is defined as the set of all linear combinations of $b_1,b_2,\dots ,b_n$ with integer coefficients, that is,

$$\mathcal{L}(b_1,b_2,\dots ,b_n)=\left\{\sum _{i=1}^n{x}_i{b}_i\mid x_i\in \mathbb{Z}\right\}$$

Here, $(b_1,b_2,\dots ,b_n)$ is called the basis of the lattice.

Definition 2. 

NTRU: Let q be a positive integer and $z\left(x\right)\in \mathbb{Z}\left[x\right]$ be a monic polynomial. A set of NTRU secrets consists of four polynomials $f,g,F,G\in \mathbb{Z}\left[x\right]/z\left(x\right)$, and they satisfy the following equation:

$$fG-gF\equiv q(modz(x\left)\right)$$

And define h as $h\leftarrow g·f^{-1}modq$. Then, given h, find f and g.

Definition 3. 

LWE distribution: Let n be a positive integer, q be a prime number, and χ be a probability distribution over the integers. For a secret vector $s\in {\mathbb{Z}}_q^n$, the LWE distribution $A_{s,\chi }$ over ${\mathbb{Z}}_q^n\times {\mathbb{Z}}_q$ is sampled by choosing a random vector $a\in {\mathbb{Z}}_q^n$ uniformly at random, selecting an error term $e\leftarrow \chi$, and generating the pair

$$(a,\langle s,a\rangle +emodq).$$

2.2. Discrete Gaussian Distribution Sampling Using CDT

Falcon is an NTRU-based quantum-resistant cipher that uses Gaussian sampling and has been selected as an NIST standard. In this paper, we are interested in the Gaussian sampling used in Mitaka, Antrag, and SOLMAE [3,4,5,6]. Gaussian sampling is as follows:

Definition 4. 

Discrete Gaussian distribution over lattices: For an arbitrary $c\in {\mathbb{R}}^n$ and $\sigma \in {\mathbb{R}}^{+}$, the Gaussian function ${\rho }_{\sigma ,c}\left(x\right)$ is defined as

$$\forall x\in {\mathbb{R}}^n,{\rho }_{\sigma ,c}\left(x\right)=exp\left(-\pi {\displaystyle \frac{{\parallel x-c\parallel }^2}{{\sigma }^2}}\right).$$

Then, for $c\in {\mathbb{R}}^n$, $\sigma \in {\mathbb{R}}^{+}$, and an n-dimensional lattice $\mathcal{L}$, the discrete Gaussian distribution over $\mathcal{L}$ is defined as

$$\forall x\in \mathcal{L},D_{\mathcal{L},\sigma ,c}\left(x\right)={\displaystyle \frac{{\rho }_{\sigma ,c}\left(x\right)}{{\rho }_{\sigma ,c}\left(\mathcal{L}\right)}}.$$

CDT sampling is an efficient, table-based technique that implements discrete Gaussian sampling. It leverages a cumulative distribution function (CDF) to construct a lookup table. During encryption or signing, random values produced by a random number generator serve as inputs to this table. Utilizing the CDF, the table returns the corresponding index for each input value. The CDF of a random variable X is defined as follows.

Definition 5. 

Cumulative distribution function (CDF): For a given random variable X, the cumulative distribution function $F_X$ is defined as

$$F_X=P(X\le x)$$

In this paper, we conduct a single trace analysis of CDT sampling implemented through comparison operations in Mitaka. We clearly distinguish that CDT sampling is combined with rejection sampling to perform a hybrid form of Gaussian sampling. Mitaka, Antrag, and SOLMAE, a variant of Falcon, also employ CDT sampling using comparison operations.

2.3. Side-Channel Analysis on Implementations of CDT Sampling

CDT sampling performs a comparison against the values stored in a table. CDT sampling is implemented differently in Listings 1–3, but the basics are similar. Generate a random value $rnd$, compare it to a value stored in a table, and store how many times the random $rnd$ value is greater than the value stored in the table. This value becomes the sampled value. A substantial body of research on single trace analysis has focused on various implementations of CDT sampling [7,8,9]. CDT sampling operates by generating a random value, $rnd$, which is then compared to values in a pre-stored table. The result of these cumulative comparisons is returned as the sampled value. Listings 1–3 present different implementation approaches. Listing 1 employs a while loop, terminating the comparison operation when $rnd$ is smaller than a value in the table. In this case, not all values in the table are compared. In other words, Listing 1 operates in non-constant time, rendering it vulnerable to timing attacks. Listing  2 is a constant-time algorithm in which all elements of the stored table are compared. However, it is also a weak algorithm for single trace analysis. Kim et al. proposed a single trace analysis of Listing 2 based on subtraction operations. The power consumption in this method differs depending on whether the resulting value is negative or positive. Zhang et al. further investigated the side-channel vulnerabilities of rejection sampling after CDT sampling in Mitaka.

Listing 1. CDT sampling C Code with early stop vulnerability.

int Early_Stop_CDT() { uint64_t rnd = random_bytes(); //Extract random values for 8 bytes int S = 0; int i = 0; while (rnd > CDT_TABLE[i]) i++; S = i; return S; }

Listing 2. Subtraction-based CDT sampling C code known to be vulnerable.

int Hamming Weight Differentially Attacked CDT() { uint64_t rnd = random_bytes(); //Extracting random values for 8 bytes. int S = 0; int i = 0; for (i = 0; i < CDT_TABLE_SIZE; i++) S += (CDT[i] - rnd) >> 63; //Extracting the sign bit. return S; }

Listing 3 illustrates the comparison-operation-based CDT sampling used in Mitaka. CDT sampling based on comparison operations does not weaken the vulnerability proposed by Kim et al. It uses a comparison operation instead of subtraction, so there is no difference between negative and positive numbers. However, as far as we know, it has yet to be discovered if this is safe. In other words, we must evaluate whether the comparison operation CDT sampling is safe.

Listing 3. CDT Sampling C code based on comparison operations used in Falcon’s variant ciphers.

int Comparions_operation_based_CDT() { uint64_t rnd = random_bytes(); //Extracting random values for 8 bytes. int S = 0; int i = 0; for (i = 0; i < CDT_TABLE_SIZE; i++) S += (rnd >= CDT[i]); // Adding the result (0 or 1). return S; }

3. Experiment Setup

This paper investigates the vulnerabilities that occur when comparative CDT sampling operates in embedded devices used in the real world. This section describes the power consumption acquisition environment and its two targets. It also describes the main instruction set used in each target.

3.1. Power Consumptions Acquisition

In this paper, we validate CDT sampling operating on two target MCUs. Target 1 is a board with an 8-bit AVR MCU, and target 2 has a 32-bit Arm Cortex-M4 MCU. In Figure 1, the target MCU board was mounted on the ChipWhisperer CW308 UFO board and used in conjunction with the ChipWhisperer Lite (CW-Lite) to measure power consumption traces for the security evaluation of CDT sampling. The ChipWhisperer Lite incorporates an analog-to-digital converter (ADC) that digitizes fluctuations in the applied voltage. The ADC operates at a sampling rate of 4 samples per clock cycle. During the experiment, the CW308 UFO board supplied the voltage across the shunt resistor to the ChipWhisperer Lite via a connecting cable. The resulting digital values from the ChipWhisperer Lite were controlled through the Python API (ChipWhisperer 5.7.0) provided by NewAE [16], enabling data transfer to a PC. The CW308 UFO is a board made for side-channel analysis. The power collected by the CW308 UFO is low noise.

3.2. Instruction Sets of Each Target

The 8-bit AVR MCU and the 32-bit Arm Cortex-M4 used in this study use different instruction sets to perform various operations [17,18]. The instructions can be categorized according to their role as follows.

• Data transfer instructions: Instructions used to move and transfer data between registers or between memory and registers.
• Arithmetic instructions: Instructions for basic operations such as addition and subtraction.
• Logical operations instructions: Instructions used to perform bitwise logical operations such as AND, OR, and XOR.
• Comparison and branch instructions: Instructions that change the flow of the program according to conditions, such as comparing two values and acting differently depending on the result.
• Control instructions: Instructions that handle interrupts.
• I/O instructions: Instructions that control data transmission to and from external devices.

The number of clocks may vary or be fixed depending on the execution of the instruction. In this paper, we are interested in determining whether the number of clocks in the entire program changes according to the four compare and branch instructions. This is because changing the number of clocks creates a visible vulnerability. This paper’s main compare and branch instructions are ’cp’, ’brcs’, ’brne’, etc., for AVR and ’cmp’ for Arm Cortex-M4.

4. Single Trace Analysis Using Visible Leakage in 8-bit AVR

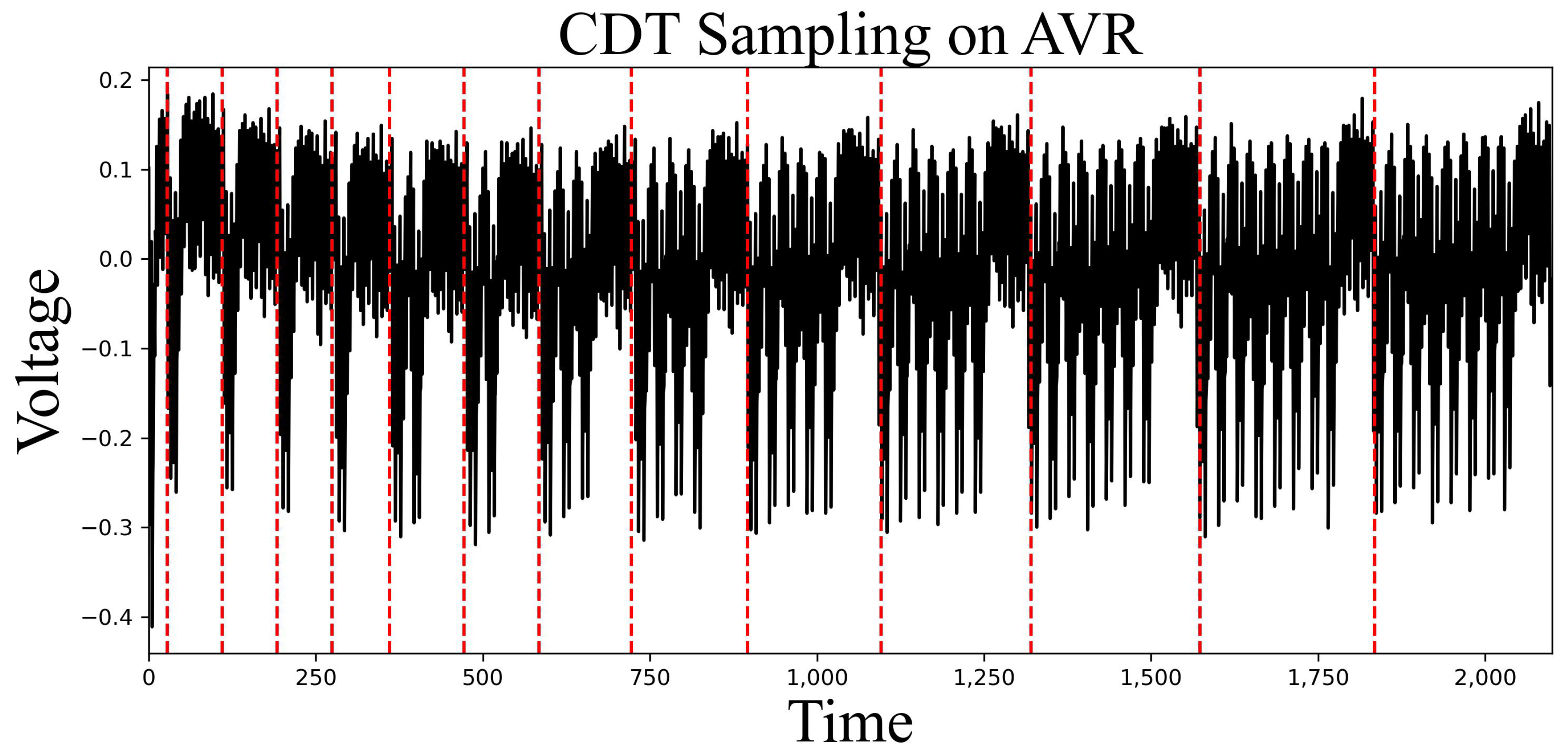
To verify the safety of CDT sampling, we gathered the power consumption of CDT sampling operation on an 8-bit AVR. Figure 2 is the power consumption trace gathered when 13 comparison operations of CDT sampling were operated. This means that the x-axis is time, and the y-axis is the intensity of the power consumption. A red line separates each comparison operation. If the comparison operations were constant-time, the time taken for each should be the same, but Figure 2 shows otherwise; i.e., CDT sampling is non-constant-time operating. It can be seen that the time of each comparison operation is different. In other words, CDT operates with non-constant time in 8-bit AVR. Therefore, in this section, we analyze the reasons for this in detail, propose a single trace analysis based on it, and propose and evaluate a comparison-operation-based CDT sampling that satisfies constant time.

4.1. Comparison-Operation-Based CDT on 8-bit AVR

The word size is 8 bits, which is the unit that the 8-bit AVR compiler operates on. Additional work is required for the compiler to perform operations on numbers larger than the word size. An example is separating large numbers into word-sized pieces and storing them separately. Mitaka’s CDT deals with 64-bit-sized data. The compiler must split the data into eight units before any operations. Algorithm 1 is the procedure by which the 8-bit AVR compiler compares 64-bit sized data A, B. The $Compare$ function on line 4 performs the comparison operation in 8-bit units. $Compare$ returns the result of the comparison operation for the i-th block. It returns 1 if $A_i$ is greater than $B_i$, 0 if they are equal, and −1 if it is less. If the result is 1 or −1, the result of the comparison operation on A and B is determined. This means that the remaining (i+1)-th, …, 7-th comparison operations do not need to be performed. This means that a premature stop vulnerability can exist.

Algorithm 1 Comparison operations that divide 64-bit data into 8-bit units

Require:  A = ($A_0\left|\right|A_1\left|\right|\dots \left|\right|A_7$), B = ($B_0\left|\right|B_1\left|\right|\dots \left|\right|B_7$) Ensure:  The result of the comparison operation is RES.   1: RES = 0   2: TEMP = 0   3: for For i = 0 to 7 do do   4:    TEMP = Compare($A_i$, $B_i$) //Return 1 if $A_i>B_i$, 0 if equal, −1 if less than.   5:    if TEMP $\ne 0$ then   6:      break   7:    end if   8: end for   9: RES = TEMP 10: return RES

The assembly code depicted in Listing 4 illustrates the part of Listing 3 for the optimized s-level. Comparison operations operate like Algorithm 1. We verified that it behaves similarly to Algorithm 1 for all compile options. Depending on the result of the comparison operation, the behavior varies in three cases. The three colors represent different cases in Listing 4. Red lines mean that the value in the table is greater than the input value. This terminates the operation after the first comparison. Black lines mean that the input value is greater than the value in the table. This terminates the operation after the second comparison. This adds 1 to the result to be output. Blue lines suggest that the next block is compared if the two values are equal. It loads the next blocks, and the computation continues. Different comparison operations take different amounts of time to run, so consume different amounts of power. Therefore, by analyzing the power consumption trace, you can guess the result of the operation.

We described the AVR’s instruction set in Section 3. Section 3 emphasized that branching instructions result in different clock counts. Listing 4 has many branching statements. ’cp’ is a comparison instruction that must precede a branch statement [17]. ’cp’ stores the result in Z-flags, C-flags, etc. In line 252, we have the instruction ’cp r25, r24’. If the two values are equal, the Z-flag will be 0. If they are different, it will be cleared. The C-flag will be enabled if the value stored in r24 is greater. The branch statements are ’brcs’, ’brne’. ’brcs’ means ’Branch if Carry Set’. The compiler checks the C-flag where the value of carry is stored. If C is enabled, it jumps by the number after the ’brcs’ instruction. If not, it performs the next line. ’brne’ stands for ’Branch if Not Equal’. The compiler checks the value of the Z-flag. If the Z-flag has been cleared, it jumps by the number after ’brne’. This means that CDT sampling performs a minimum of one and a maximum of eight comparison operations on the AVR. This vulnerability is not safe from single trace analysis.

Listing 4. Assembly code analysis of CDT, where different colors mean differnt behaviors (Red: A0 < B0, Black: A0 > B0, Blue: A0 = B0).

<base_sampler>: ... 24c: ldi r22, 0x00 24e: lldi r23, 0x00 250: lldd r24, Z+7 252: lcp r25, r24 254: lbrcs .+74 //Jump to next red line or go to next line. 256: lcp r24, r25 258: lbrne .+66 //Jump to next black line or go to next line. 25a: lldd r24, Z+6 //Load next block 25c: lcp r20, r24 //Recurring tasks 25e: lbrcs .+64 260: lcp r24, r20 262: lbrne .+56 ... 29c: lldi r22, 0x01 //Temporary Result register 0->1 29e: lldi r23, 0x00 2a0: ladd r18, r22 //Increase or maintain result 2a2: ladc r19, r23 ...

4.2. Analyzing the Security of CDTs

CDT performs a total of 13 comparison operations. If you can analyze a trace and then know the results of the 13 comparison operations, you can recover the sampled value. All of the comparison operations are non-constant-time, depending on the result. This means that the computation time can be used to recover the resulting value of CDT sampling. In this paper, we analyze the time that CDT sampling takes to operate using power consumption trace analysis. Listing 3 shows that CDT sampling performs 13 comparison operations. Algorithm 1 is similar to how it behaves when performing each comparison operation. 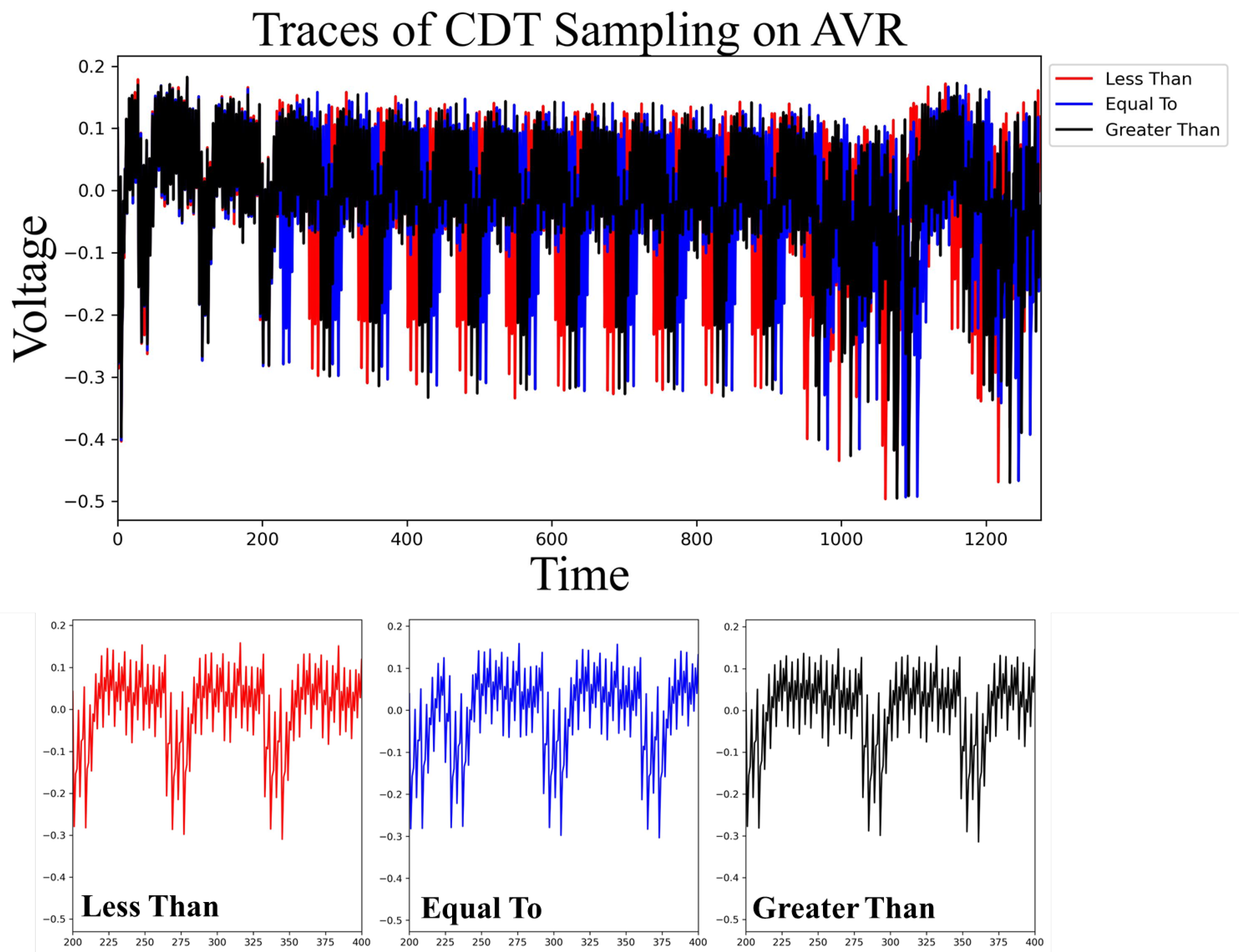Figure 3 is the trace collected when CDT sampling is run repeatedly three times.

The top shows the three traces overlaid, while the bottom shows the individual traces. This means that each trace is different when viewed on top of the other, and each is shown separately to show the differences in detail. The difference between each operation means that Compare($A_0,B_0$) is different. Red means Compare($A_0,B_0$) is −1, blue is 0, and black is 1. In other words, red means when the operands have values less than the table, blue means when they are equal to the table, and black means when they are greater than the table. For our experiments, we made the most significant byte of the input data differ by 1 from the most significant value of the value stored in the CDT table. You can see that the respective power consumption traces change shape. This means that even though the two values being compared are close, the power consumption differs. In other words, we have experimentally demonstrated the vulnerability described in Section 4.1. If CDT sampling had behaved as constant-time, all traces would have had similar shapes [19]. In this paragraph, we have shown that CDT sampling behaves differently depending on the result of the compare operation, which means that single trace analysis is possible using non-constant-time leakage.

4.3. Countermeasure

This paper proposes a CDT sampling based on comparison operations that eliminates visible vulnerabilities and constantly operates in all environments. In this paragraph, we clearly define that our proposed algorithm is a non-constant-time countermeasure. In other words, the goal of our proposed counterpart is CDT sampling, which performs constant-time comparison operations that do not depend on the data of the operands. Algorithm 2 is our proposed constant-time CDT sampling. It contains operations that the compiler performs automatically. In Section 4.1, we described how the compiler divides 8 bytes of data $A,B$ into 8 bytes of $\left(A_0\right|\left|A_1\right||\dots ||A_7,B_0|\left|B_1\right||\dots |\left|B7\right)$ each. This partitioned byte-by-byte comparison, while efficient, is vulnerable to single trace analysis. This emphasizes the need for comparison operations to operate on all bytes to be safe. This paper proposes a countermeasure to prevent security improvements to the algorithm after the compiler’s work. In other words, our proposed algorithm performs a compare operation on every byte. In Algorithm 2, $rnd,CDT$ are random values divided into 8-bit units and stored in a CDT table. Table_size is 13, and $gt,lt$ is used to update the resulting value S. This finally returns the sampled value.

Algorithm 2 Comparison-operation-based constant-time CDT sampling

Require:  NDB Num of data blocks, CDT Table with size CDT_TABLE_SIZE*NDB. Ensure:  Random value S extracted from a constant time CDT sampling.   1: S$\leftarrow 0$   2: rnd← random_bytes() $\left(rn{d}_0\right|\left|rn{d}_1\right||\cdots |\left|rn{d}_{NDB-1}\right)$   3: $i\leftarrow 0$, $j\leftarrow 0$   4: for$i=0$ to CDT_TABLE_SIZE $-1$ do   5:    $gt\leftarrow 0$, $lt\leftarrow 0$   6:    for $j=0$ to NDB $-1$ do   7:      $gt\leftarrow gt\vee (\neg (gt\vee lt)\wedge (\mathbf{rnd}\left[j\right]>\mathbf{CDT}\left[i\right]\left[j\right]\left)\right)$   8:      $lt\leftarrow lt\vee (\neg (gt\vee lt)\wedge (\mathbf{rnd}\left[j\right]<\mathbf{CDT}\left[i\right]\left[j\right]\left)\right)$   9:    end for 10:    S ←S + $(lt\oplus 1)$ 11: end for 12: return S

Listing 5 is part of the assembly code of the proposed countermeasure. This shows that the proposed algorithm runs in constant time on the AVR. The blue and red lines in Listing 5 refer to the comparison operations in lines 7 and 8 of Algorithm 2. Lines 278 and 288 initialize the value of register r18, where the result of the comparison operation will be stored to zero. Lines 27a and 28a compare registers r22 and r23 using ’cp’ commands, respectively, and store the results in the carry flag. Lines 27c and 28c execute an addition operation on the initialized r18 using the ’adc’ (add with carry) instruction. During this operation, the stored carry values are combined, storing the comparison operation’s result within r18. This approach allowed us to eliminate the need for branching instructions, thus removing the previously mentioned vulnerabilities.

Listing 5. Comparison operation of assembly implementation code of countermeasure. (Blue: Comparison operation on line 7 of Algorithm 2, Red: Comparison operation on line 8 of Algorithm 2).

<STA-Resistant CDT sampling>: ... 278: ldi r18, 0x00 //Initialize the result register to 0. 27a: cp r22, r23 //Two values of 8-bit size are compared. 27c: adc r18, r18 //Addition with Carry. (No branch command!) 27e: and r24, r18 280: or r19, r24 282: mov r24, r19 284: or r24, r25 286: com r24 288: ldi r18, 0x00 //Initialize the result register to 0. 28a: cp r23, r22 //Two values of 8-bit size are compared. 28c: adc r18, r18 //Addition with Carry. (No branch command) ...

Figure 4 illustrates the power consumption traces of three different types of Listing 5 operating in the 8-bit AVR MCU. This figure is fully examined by overlapping all the results to represent the corresponding power consumption traces. The trace reveals no discernible variations in the comparison time across different values. This serves as compelling evidence that CDT sampling demonstrates resistance against STA using visible leakage. Eliminating visible vulnerabilities means we are safe from the proposed single trace analysis. However, invisible vulnerabilities are not considered, and we must work on them.

5. Single Trace Analysis of Invisible Leakage in 32-bit Arm Cortex-M4

This section demonstrates that CDT sampling based on comparison operations satisfies constant-time execution on an Arm Cortex-M4-based STM32F3 chip. In the last section, power consumption traces revealed that compiler-generated branch statements in the 8-bit AVR MCU exhibit varying execution times due to differences in clock cycles depending on the result of the comparison operation. In contrast, on the Arm Cortex-M4, although branch statements are present, the clock cycles remain fixed and independent of the comparison result. 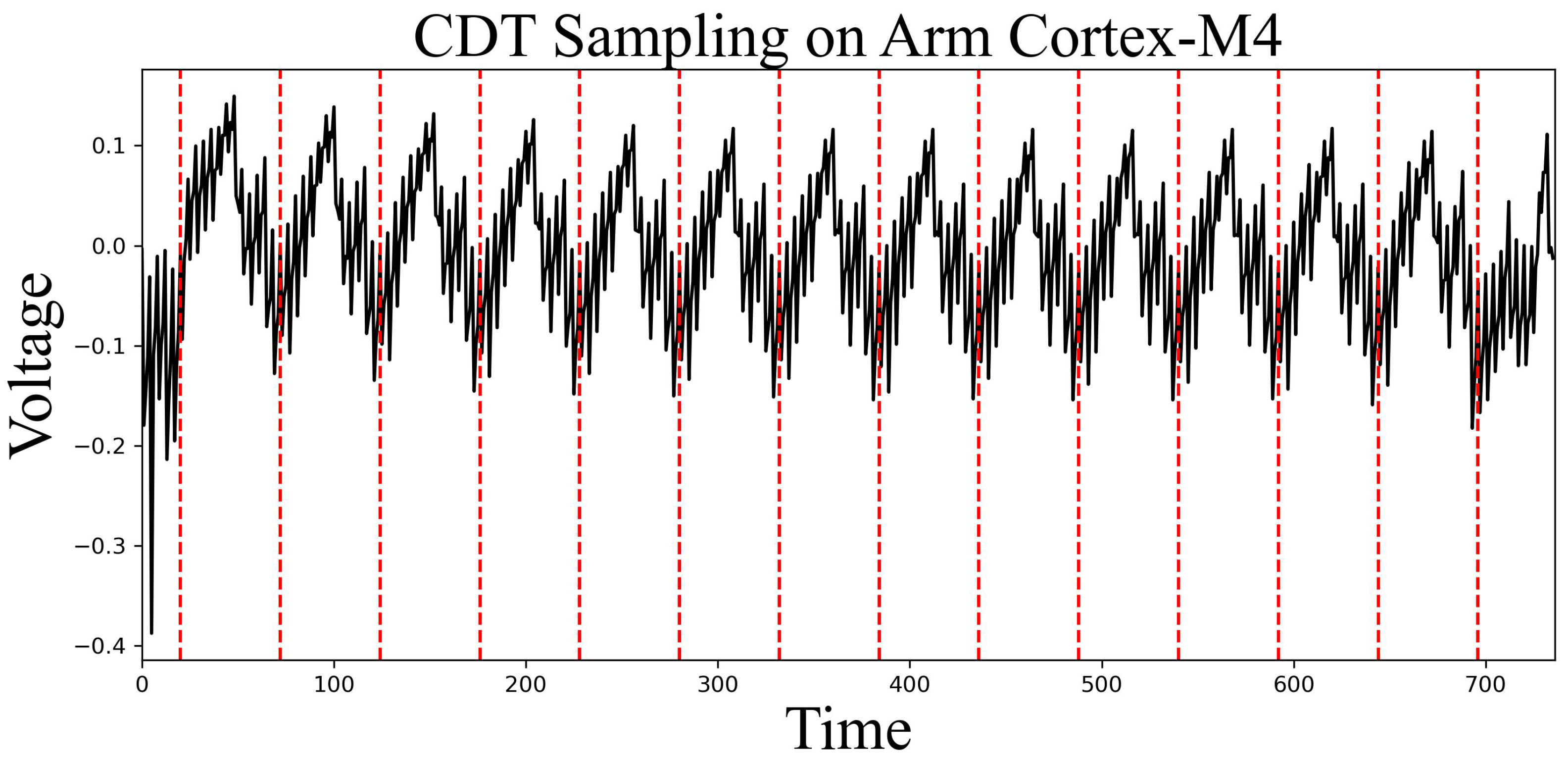Figure 5 shows the power consumption trace of CDT sampling operating on an Arm Cortex-M4. The x-axis represents time, while the y-axis indicates voltage. It can be seen that all of the comparison operations are of the same time length, which proves that CDT sampling on Arm Cortex-M4 is a constant-time algorithm.

5.1. Comparison-Operation-Based CDT on 32-bit Arm Cortex

This study investigates vulnerabilities by analyzing the assembly code. Listing 6 presents the comparison operation section of CDT sampling on the Cortex-M4. The two 32-bit comparisons are performed to handle 64-bit operands, utilizing Z-registers to ensure constant-time execution. The operands are stored in registers r7, r6, and CDT in MSB (most significant bit) order, with one table value loaded into registers r1 and r0. The Arm Cortex-M4 stores the result of the operation in its N, Z, C, and V flags. Specifically, Z is set to 1 if the two values are equal, and C is set to 1 if the left-hand side is greater than or equal to the right-hand side. Line 27e checks whether r7 and r1 are equal, executing line 282 if they match and line 284 if not. At this point, the it instruction is folded with the 16-bit thumb instruction, ensuring that no additional cycles are consumed or, at most, one cycle is used [18]. Consequently, CDT sampling on the Arm Cortex-M4 achieves constant-time execution. However, the values stored in registers r1 and r4, which hold the results of comparison operations on lines 286, 288, and 28c, vary depending on the outcome of the comparison. These variations could potentially expose the results of the comparison operations.

Listing 6. Assembly code for CDT sampling in Arm Cortex-M4.

<base_sampler>: 27a: ldrd r0, r1, [r3, #8]! 27e: cmp r7, r1 280: it eq // The instruction has a variable clock count. 282: cmpeq r6, r0 284: ite cs 286: movcs r1, #1 288: movcc r1, #0 28a: cmp r3, r2 28c: add r4, r1

5.2. Analyzing the Security of CDTs

Power consumption varies due to differences in Hamming weight [19]. We employ profiling analysis, a deep learning-based side-channel analysis technique, to evaluate the security of CDT sampling for comparison operations that adhere to constant-time execution. Profiling analysis involves extracting secret information by utilizing a model trained on a profiled device and applying it to data from the attacked device. This method allows for predicting the attack target value from a single power trace. 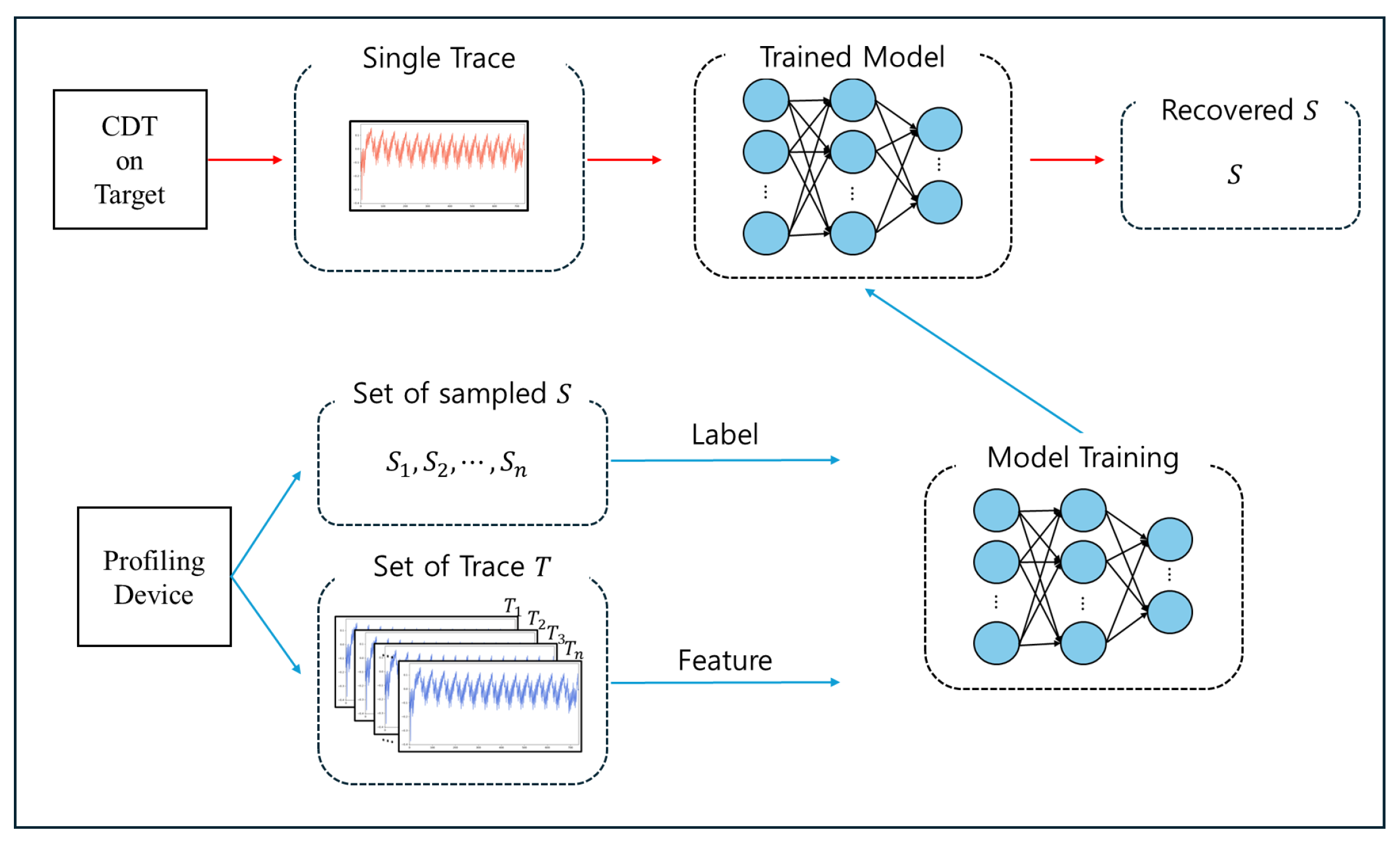Figure 6 illustrates the procedure for applying profiling analysis to CDT sampling. The proposed model labels 14 distinct CDT result types and learns the corresponding power consumption traces collected from the profiling device. The trained model then analyzes power traces from the device under attack during CDT sampling and predicts the output values.

5.2.1. Adversarial Model

The adversary can run the system on profiling devices. This means they have free access and control over the target device and can obtain sampled values. The attacker can also measure the power consumption of the base_sampler() function while Mitaka is running. In our experiments, we directly triggered base_sampler(). However, it could be collected in practical scenarios by activating base_sampler() during Mitaka’s execution or through physical manipulation [20,21]. This scenario closely mirrors the experimental setup described in Section 3. The attacker uses the acquired data to train a model. The trained model can predict sampled values using a single trace. The trained model performs a single trace analysis for new devices to predict the CDT output.

5.2.2. Profiling Phase

The power consumed by the device satisfies the following Equation (1). Therefore, the power consumption is proportional to the Hamming weight information of the data used in the computation [19]. $P_{\mathrm{total}}$ is power consumption, $P_{\mathrm{op}}$ power consumption by operation, $P_{\mathrm{data}}$ power consumption based on data, and $P_{\mathrm{noise}}$ and $P_{\mathrm{const}}$ refer to the noise inherent in the device and the constant power consumption independent of computation and data, respectively.

$$P_{\mathrm{total}}=P_{\mathrm{op}}+P_{\mathrm{data}}+P_{\mathrm{noise}}+P_{\mathrm{const}}$$

(1)

This paper analyzes power consumption to recover the values used in CDT sampling. However, signal noise can interfere with the accuracy of the analysis [8]. For effective evaluation of CDT sampling, it is crucial to distinguish differences in the Hamming weights of operations by a value of 1. Consequently, an analysis method highly sensitive to the data change rate is required. Furthermore, since CDT sampling generates a random value with each execution, the recovery of the sampled value from a single execution’s power consumption should be achievable. To address this, we propose a single-trace analysis using deep learning-based side-channel analysis to assess the security of CDT sampling.

The training data for the profiling analysis consist of power consumption traces obtained by repeatedly executing CDT sampling on random inputs and the corresponding output values for each execution. Specifically, we define a set X of multiple collected power consumption traces and a set Y of sampled values obtained for each run. Each $X_i$ leaks information about its corresponding $Y_i$. Therefore, this study trains a model using pairs $(X_i,Y_i)$$\in (X,Y)$, where $X_i$ serves as the input data and $Y_i$ serves as the label. A total of 10,000 datasets were collected for each label, with the ratio of training data to validation data at 80:20, resulting in a training set of 112,000 traces and a validation set of 28,000 traces. The test dataset comprises 10,000 $(X_i,Y_i)$ pairs generated from random inputs. Recently, side-channel analytics using deep learning has been actively researched [22,23,24,25,26]. We selected MLP as a model to evaluate the safety of CDT. Information on the hyperparameters we tuned can be found in

Table 1. MLP structure.

Layer Type	(In, Out) Shape	# Parameters
Batch Normalization	(736, 736)	2944
Dense	(736, 512)	377,344
Batch Normalization	(512, 512)	2048
Dense	(512, 256)	131,328
Batch Normalization	(256, 256)	1024
Dense	(256, 14)	3598

. The MLP architecture includes an input layer, one hidden layer, and an output layer comprising multiple nodes. The training was conducted with an epoch count of 10 and a batch size of 512, utilizing the ReLU [27] activation function and the Adam [28] optimization algorithm (learning rate = $1\times {10}^{-4}$).

5.2.3. Evaluating Model Performance

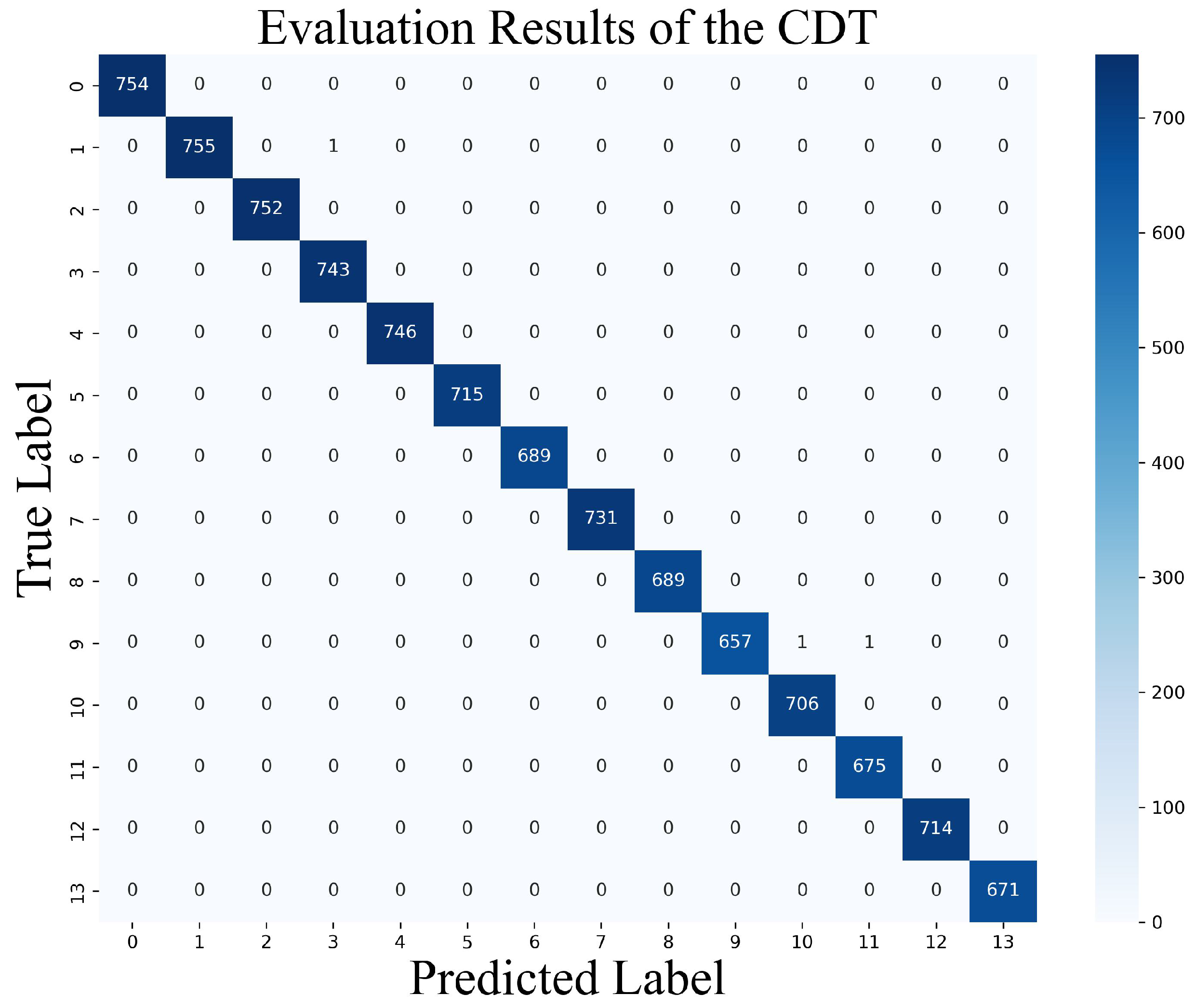
The training results of the model are presented in Figure 7. Model accuracy reflects the accuracy of both the training and validation phases, while model loss represents the corresponding loss during these phases. The model converged to 1 for training and validation accuracy and to 0 for both training and validation loss. As shown in Figure 8, the accuracy on the test dataset is 99.97%. The test dataset consists of 10,000 traces, representing each trace’s classification accuracy. The F1 score for both micro- and macro-averages is 1.0, indicating that the proposed model can accurately predict the CDT sampling output from a single trace of a comparison operation executed on the Cortex-M4.

5.2.4. Leak Point Analysis Through Weight Analysis

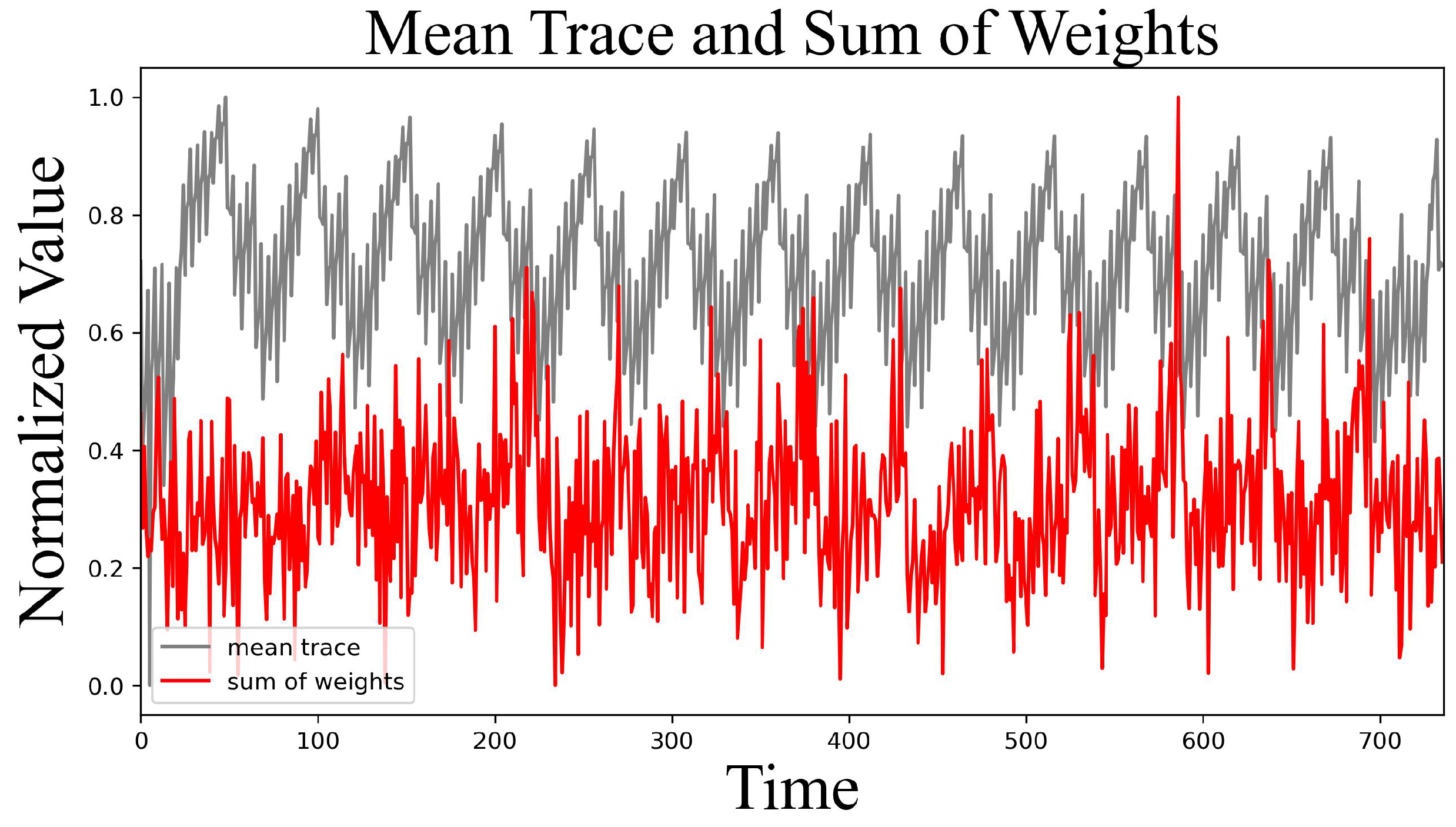
As described in Section 5.1, the difference in Hamming weights during the CDT sampling process results from comparisons between 32-bit words. By examining the weights of the trained model, it is possible to identify the moments when the model successfully classified the sampled value. Figure 9 illustrates the sum of the weights for each node in the first layer of the trained model. The red line represents the sum of the weights, while the gray line shows the average across the entire waveform, normalized for visualization purposes. It demonstrates that the model makes its classification decision when comparing random and table values.

5.3. Countermeasure

CDT sampling is found to have an invisible vulnerability on the 32-bit Arm Cortex-M4, which means that the CDT sampling value of Falcon-based quantum-resistant cryptography is leaking; i.e., there is an indirect leakage of secret information. Therefore, side-channel analysis countermeasures against CDT sampling should be studied. Side-channel analytics has been studied for a long time, and countermeasures have also been studied for a long time. Traditionally, shuffling and masking have been employed in side-channel analysis [29,30], though these methods tend to be computationally slow and memory heavy. Research to improve this and apply masking and shuffling to ciphers has been ongoing [31,32,33,34,35,36,37,38,39,40,41]. Research is needed to apply these methods to CDT sampling. Countermeasures related to CDT sampling have also been studied; the model we propose in Section 4 is a study that satisfies constant time. However, it does not consider the invisible vulnerabilities discussed in Section 5, which have been studied in papers analyzing subtraction-based CDT sampling. Kim et al. proposed a table-based method that requires a minimum-sized table depending on the size of the operands [7]. But, in the case of Mitaka, which operates with 64-bit data, a byte-sized table is required, demanding significant memory resources. Zhang et al. introduced a correspondence technique utilizing a look-up table with a fixed Hamming weight of 1, offering lower memory and speed overhead than other correspondence methods [9]. However, this approach is unsuitable for different structures of quantum-resistant ciphers that employ CDT sampling, as it applies to operations performed after CDT sampling. Therefore, further research is necessary to design secure algorithms against deep learning-based side-channel analysis.

6. Conclusions and Future Work

The growing importance of quantum-resistant cryptography has underscored the need for vulnerability verification research in embedded environments. In this paper, we explore the use of CDT sampling in several quantum-resistant cryptosystems, including Falcon and FrodoKEM. Specifically, we conduct a vulnerability analysis of CDT sampling based on comparison operations used in implementations such as Mitaka, Antrag, and SOLMAE.

Our research shows that CDT sampling has both visible and invisible vulnerabilities, depending on the environment in which it operates. On 8-bit AVRs, CDT sampling has a visible vulnerability. This paper uses reverse engineering to investigate the source of the vulnerability. It was found that AVRs are vulnerable when the size of the operands in a comparison operation is larger than the compiler’s unit of operation. This is due to the premature termination when a comparison operation is performed by splitting the operands into units of operations. This was also revealed through the power consumption trace. We proposed a method to recover the value of CDT sampling from a single power consumption trace. This could indirectly leak the secret information of the Falcon-based PQC algorithm. Since the sampled values are computed with the secret values, new vulnerabilities, such as side-channel analysis, will potentially exist in the future. In this paper, we proposed a CDT sampling algorithm that operates in AVR at constant time. It can be seen that no existing visible vulnerabilities exist.

Furthermore, we investigated the potential vulnerabilities of CDT sampling on ARM Cortex-M4. CDT satisfies constant time on ARM, which means it satisfies constant time like our proposed countermeasure. We investigated the safety of CDT sampling with constant time. We reverse-engineered CDT sampling on ARM to investigate potential leakage points. We found that a Hamming weight difference occurs when the results of the comparison operations are added together. We proposed a model to recover the sampled value from a power consumption trace on ARM. The proposed model evaluates the safety of invisible CDT sampling. The model successfully recovered the sampled values from CDT. Its accuracy is 99.97%, and the F1 score is 1.0 for both micro and macro.

In this paper, we investigated the potential vulnerabilities of Falcon-based PQC algorithms. This means that there is still research to be performed on the physical vulnerabilities of PQC used in IoT devices in the future. This emphasizes the need for further research on the safety of PQC, which is where our work lies. We want to study the leakage of secret information in PQC due to the leakage of the value of the CDT sampling in various environments. We are considering a noisy environment. Environments where only noisy signals are obtained, such as electromagnetic signals and environments with parallel operations, are candidates.