Abstract
As the most popular cryptographic scheme in the post-quantum field, lattices have received extensive attention and research. Not only do they provide quantum-resistant security, they also enable the construction of complex applications. Currently, lattice cryptography schemes based on different difficult problems have been applied in different fields. The threshold secret sharing (TSS) scheme is an important field of cryptography and has important application value and development prospects in key protection, secure multi-party computation, privacy protection, etc. However, with the rapid development of quantum computing, many existing cryptography-underlying technologies are facing huge difficulties and challenges. Therefore, post-quantum TSS has important research significance and value for the future development of cryptography. In this paper, we summarize the existing secret sharing schemes based on lattice-hard problems and the relevant applications of these schemes in the post-quantum realm. We classify existing lattice-based TSS according to different functions and introduce typical solutions. To the best of our knowledge, this is the first review paper on lattice-based TSS schemes.
1. Introduction
The concept of quantum computing was first proposed by physicists David Deutsch and Richard Feynman in the late 1980s and early 1990s [1,2]. They believed that computing with qubits instead of traditional bits could provide supercomputing power in some cases. With the rapid development of information technology, quantum computing technology continues to make breakthroughs. However, with the continuous improvement of computing power, some difficult classical mathematical problems, such as RSA and discrete logarithm problems, are no longer safe, and the security of traditional public key cryptography algorithms will also face huge challenges [3]. Post-quantum cryptography (PQC) is a new generation of cryptographic algorithms that can resist quantum computing attacks on public key cryptography algorithms. It aims to study the security of cryptographic algorithms in quantum environments and is designed to work in both classical and quantum environments [4,5]. All have secure password systems. Compared with traditional cryptography methods, post-quantum cryptography provides a higher level of information security and can withstand the powerful computing power of quantum computers, providing a powerful solution for the field of future information security [6,7]. At present, quantum-resistant cryptography schemes mainly include the following five aspects: hash-based signatures, code-based cryptography, multivariate cryptography, lattice-based cryptography, and homology-based cryptography [7,8,9,10,11].
A lattice is a mathematical structure defined as a linear combination of integer coefficients of a set of linearly independent non-zero vectors [12]. In post-quantum cryptography, the study of lattice-based cryptography is the most active and flexible. Lattice-based algorithms can achieve a better balance in security, public and private key sizes, and calculation speed. The security of the lattice-based algorithm depends on the difficulty of solving the problems in the lattice. When these problems achieve the same security strength, the size of the public and private keys is smaller than other solutions, the calculation speed is faster, and it can be used to construct multiple cryptographic primitives that are more practical for real-world applications. At present, lattice-based algorithms have been used to implement cryptographic constructions for various functions such as encryption, digital signatures, key exchange, attribute encryption, and fully homomorphic encryption [13]. Therefore, lattice-based algorithms are considered to be one of the most promising post-quantum cryptographic algorithms.
TSS is a cryptographic technique used to divide secret information (such as a passwords, private keys, etc.) into multiple shares that are distributed to different participants. Only when certain threshold conditions are met can the original secret information be reconstructed [14,15,16]. Although TSS provides strong guarantees for information security, it also faces some challenges. Currently, most TSS schemes are based on numerical assumptions, such as RSA, factorization, discrete logarithms, etc. [17,18,19]. However, as Shor [20] proposed a quantum algorithm to solve the factorization problem within polynomials in 1994, more and more scholars have proposed research on quantum cracking algorithms for numerical assumptions, demonstrating the vulnerability of schemes based on numerical assumptions. Because of this, with the continuous maturity and improvement of quantum technology, the security of traditional TSS schemes will suffer a great blow. Therefore, it is urgent to study new candidate schemes for post-quantum TSS.
From a practical point of view, lattice-based TSS has important research significance and prospects, especially some special properties, such as verifiability, multiple secrets, etc., that broaden the application of TSS in different scenarios [21,22]. Currently, many lattice-based TSS schemes already exist. However, to our knowledge, there is a lack of review papers focusing on this research direction. Therefore, to give readers a detailed understanding of this direction, we survey the existing lattice-based TSS schemes from the perspective of different functions. Furthermore, we investigate the application of these schemes in different scenarios. The main contributions of the manuscript are summarized as follows:
- We survey and summarize existing TSS schemes based on lattice cryptography to solve the security problems of traditional cryptography in the post-quantum era. Given the unique properties of different TSS, we classify lattice-based TSS according to the different functions they implement and conduct a comparative analysis of these schemes. To the best of our knowledge, this is the first systematic review paper on lattice-based TSS.
- This paper investigates the related applications of lattice-based TSS schemes in different scenarios, including (a) threshold encryption, (b) identity-based encryption, (c) blockchain distributed storage, and (d) privacy-preserving federated learning.
- After studying and summarizing the existing schemes, we introduce the future work and development direction of lattice-based TSS.
The rest of the article is organized as follows. In Section 2, we give the concept of lattices and the definition of some important mathematical problems. In Section 3, we introduce an overview of TSS and several general lattice-based schemes. From Section 4, Section 5 and Section 6, we conduct detailed research on and introduce verifiable threshold secret sharing, threshold multi-secret sharing, and threshold changeable secret sharing according to the different functions of the scheme. In Section 7, we introduce the related applications of lattice-based TSS schemes in different cryptography fields. Finally, we provide a summary of the manuscript and analyze the existing open problems and future work directions in Section 8 and Section 9.
2. Lattice-Based Cryptography
2.1. Lattice
Lattice-based cryptography is a branch of modern cryptography, and its security is based on intractable problems in lattice theory. A lattice is a collection of vectors in mathematics. In cryptography, a lattice can be regarded as a vector space generated by a set of linearly independent vectors [12,23,24].
Definition 1 (Lattice).
Given n linearly independent vectors the lattice generated by these vectors is defined as:
where are called the basis vector of lattice Similarly, we define B as an matrix whose column vectors are ; then the lattice generated by the matrix is defined as:
Both m and n are integers, , m is called the dimension of the lattice, and n is called the rank. Among them, when is satisfied, the lattice is called full-rank. The shortest distance of lattice , denoted as is the minimum distance between any two different lattice points, equal to the length of the non-zero shortest lattice vector. Next, we will introduce some mathematically difficult problems on lattices.
2.2. Cryptographic Assumptions on Lattices
Lattice-based cryptography utilizes mathematical problems defined on lattices to design cryptographic schemes for encryption, signatures, and key exchange, among others. These schemes typically rely on challenging problems such as the shortest vector problem (SVP), closest vector problem (CVP), and learning with errors (LWE) [25,26,27,28]. These problems are generally computationally hard, which provides lattice-based cryptographic schemes with strong security given current computational capabilities.
- A.
- Small Integer Solution
Definition 2 (SIS).
Given m uniformly distributed random vectors, form a matrix whose norm satisfies .
- B.
- Learning with Errors
Definition 3 (LWE).
Given a prime number q, a positive integer n, and a Gaussian distribution on , the input of LWE is a random matrix and , where . The LWE hard problem is to find with non-negligible probability.
- C.
- Shortest Vector Problem
Definition 4 (SVP).
Given is a d-dimensional lattice, is a set of basis vectors on the lattice. The input of SVP is a lattice basis B, and the goal is to find a non-zero vector x in lattice such that .
Definition 5 ().
Given that is a d-dimensional lattice, is a set of basis on the lattice. The input of SVPγ is a lattice basis B and an approximation factor . The goal is to find a non-zero vector x in lattice such that .
Definition 6 ().
Given is a d-dimensional lattice, is a set of basis on the lattice. The input of GapSVPγ is a lattice base B, a rational number r, and an approximation factor . When , the judgment is “NO”, and when , the judgment is “YES”. Other cases randomly return “YES” or “NO”.
- D.
- Closest Vector Problem
Definition 7 (CVP).
Given is a d-dimensional lattice, is a set of basis on the lattice. The input of CVP is a lattice basis B and a target vector t. Find a non-zero vector v, for any non-zero vector , satisfying .
Definition 8 ().
Given is a d-dimensional lattice, is a set of basis on the lattice. The input of CVPγ is a lattice basis B, a target vector t, and an approximation factor . Find a non-zero vector v, for any non-zero vector satisfying .
Definition 9 ().
Given is a d-dimensional lattice, is a set of basis on the lattice. The input of GapCVPγ is a lattice basis B, a target vector t, an approximation factor , and a rational number r. If , the judgment is “NO”; if , the judgment is “YES”. Other cases randomly return “YES” or “NO”.
3. Overview of Threshold Secret Sharing Scheme
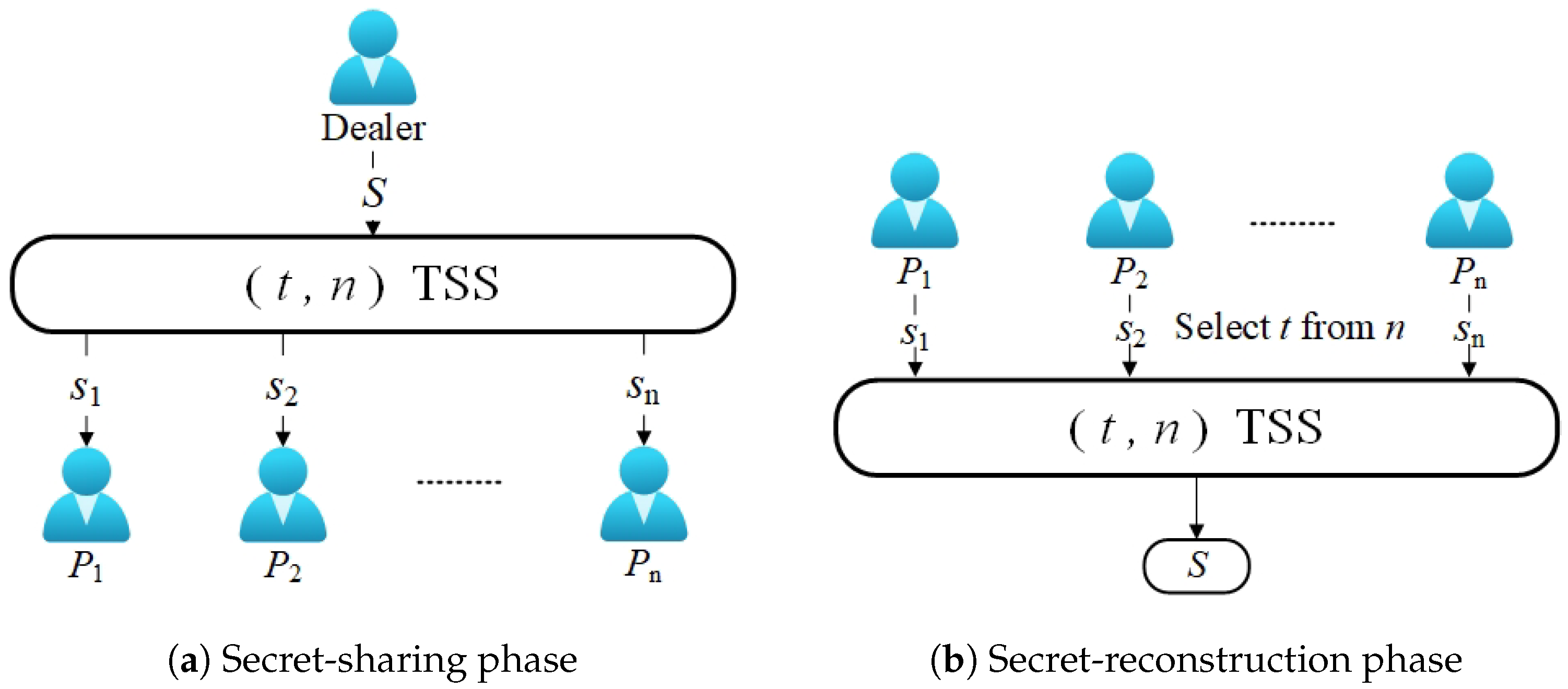
TSS is a technique used to hide a piece of information called the secret by splitting this secret into several parts called shares and spreading them among participants. In a way, the secret can be recovered from certain subsets of the shares [16,22]. The one who produces such shares and privately distributes them to the participants is called the dealer. Since its invention, many different TSS schemes have emerged, such as linear schemes, ideal schemes, verifiable schemes, proactive schemes, multiple schemes, visual schemes, Chinese remainder schemes, quantum schemes, rational schemes, online schemes, etc. The earliest and most widely used (t, n)-TSS was proposed by Shamir in 1979, which allows the dealer to divide the secret into n shares and obtain the original secret information through the reconstruction of the authorized set [29]. As shown in Figure 1 and Definition 10, the general TSS scheme mainly includes two steps: secret sharing and secret reconstruction.
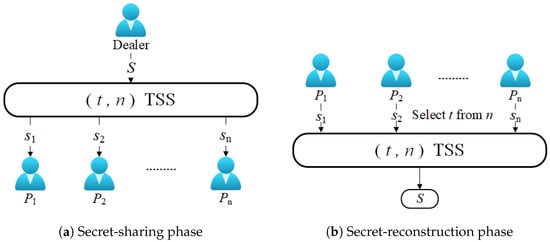
Figure 1.
General threshold secret sharing.
Definition 10 (Threshold Secret Sharing Scheme).
If a threshold secret sharing mechanism includes a secret sharing process and a secret reconstruction process and satisfies the following properties, we call it threshold secret sharing. It contains the following two algorithms: Secret sharing (S, t, n): Input a secret S, a threshold t, and the number of participants n. There exists a secret-sharing algorithm that splits the secret S into several sub-shares, .
: Input at least t secret shares. There is a secret reconstruction algorithm to obtain the original secret .
In addition, the TSS algorithm needs to meet the following security requirements:
: From any number of secret shares smaller than t, the participants cannot obtain any information about the secret S:
With the development of post-quantum computing technology, TSS based on numerical assumptions can no longer provide security, so lattice-based encryption schemes are needed.
3.1. Lattice-Based Threshold Secret Sharing Scheme
In 2014, Hamidreza et al. [30,31] proposed a lattice-based TSS scheme based on the threshold changeable secret sharing (TCSS) of Steinfeld et al. [32]. We will discuss the relevant content of [32] in the TCSS section later. For details, the dealer uses the inner product of two m-dimensional vectors l and a; the share of the secret share is calculated by adding noise. The first item of the vector a is the secret S, and the remaining items are random values. In the secret-reconstruction stage, the reconstructor uses the vectors of t participants to construct a -dimensional lattice basis M and a vector , where elements are part of secret S. Finally, an approximation algorithm is performed to recover the secret. Specifically, in the parameter-generation stage of the scheme, the dealer selects the public parameters, including the prime number random discrete vectors and the upper limit value N of the random number. In the stage of calculating the secret share, to share secret , the dealer selects random integers and assumes that . Then, they add noise e to the vector and calculate the secret share as:
Finally, the reconstructor recovers the secret by collecting t secret shares and constructing -dimensional matrix and executing the CVP approximation algorithm to obtain the recovered secret
where is the output result after running the CVP algorithm. In addition to the construction of an ordinary TSS, the difficulty problem on lattice is more applied to solve some special cases, including verifiable, multi-secret, variable threshold, etc.
3.2. Classification Based on Functions and Properties
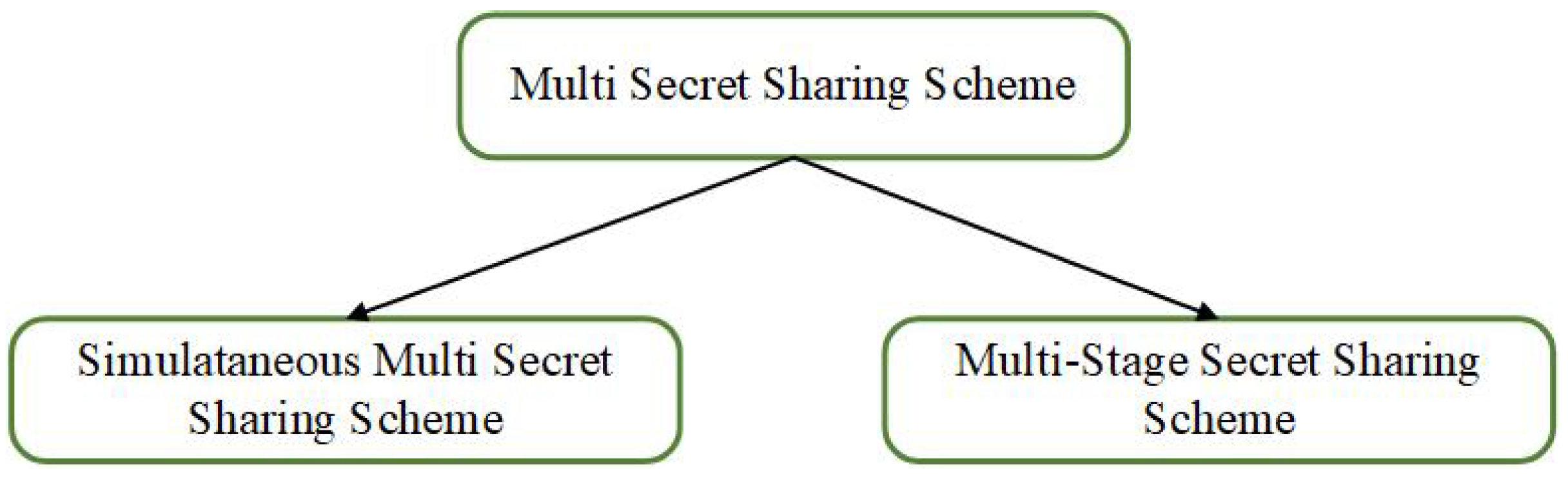
TSS is an important area of information security designed to ensure the secure storage and transmission of sensitive data. In this manuscript, to better understand and study lattice-based TSS, we divide them into the following four categories according to their functions and properties: general secret sharing, verifiable secret sharing (VSS), multi-secret sharing (MSS), and threshold changeable secret sharing (TCSS). We divide multi-secret sharing into two parts: simultaneous multi-secret sharing schemes (SMSS) and multi-stage secret sharing (MSSS). The classification method is shown in Table 1. Among them, we have already introduced lattice-based general TSS in Section 3.1

Table 1.
Classification of lattice-based TSS schemes based on functions.
By classifying lattice-based TSS according to these functions, we can more clearly understand the applicability of different schemes and provide more flexible and effective security solutions for various application scenarios. Each classification has its unique advantages and limitations, and researchers and practitioners can choose the most appropriate solution based on their actual needs. This review paper aims to deeply explore the principles and algorithms of each classification to promote further development and innovation in the field of TSS. In the following sections of this paper, we will discuss each different functional solution in detail.
4. Verifiable Threshold Secret Sharing Scheme
4.1. Overview of VSS
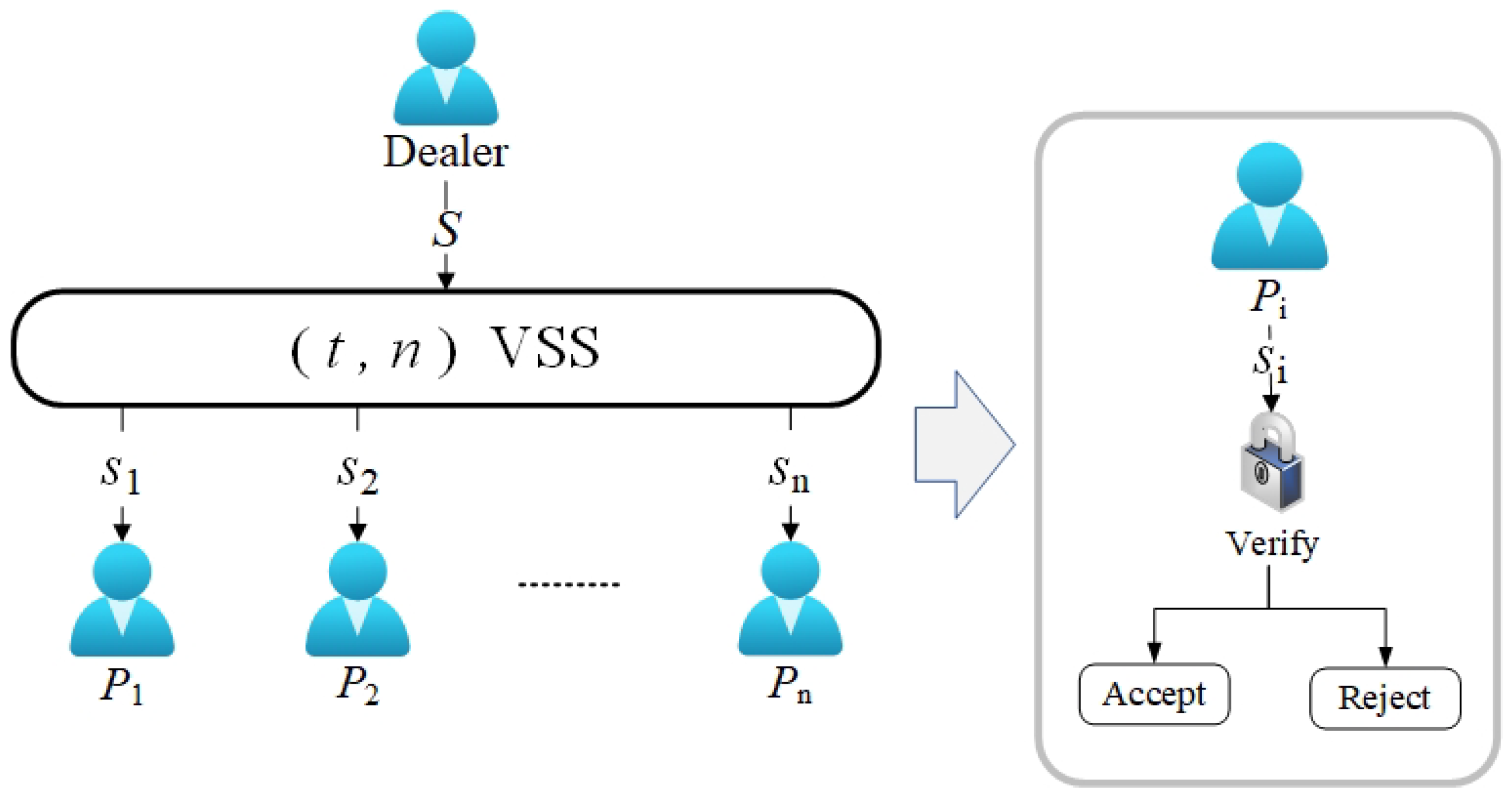
In 1985, Benny Chor et al. [47] proposed the concept of verifiable threshold secret sharing for the first time, with the purpose of making TSS robust to malicious participants. As shown in Figure 2, participants can verify the correctness of shares during the execution of the scheme.
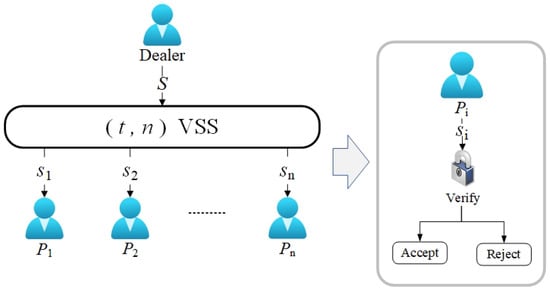
Figure 2.
Verifiable threshold secret sharing.
The development of VSS makes the traditional TSS schemes resistant to dishonest participants, thus effectively preventing distributors and participants from cheating each other. It is ensured that even if there is a malicious party, there must be a definite secret share value to be able to complete the secret-recovery process.
In 1996, Stadler [48] introduced the concept of publicly verifiable secret sharing (PVSS), allowing anyone (not only the dealer) to verify the accuracy of the scheme shares. This notion was implicitly present in earlier research, where the VSS proposed by Chor et al. coincidentally possessed the property of public verifiability.
Most of the existing VSS schemes are mainly based on discrete logarithm, elliptic curve cryptography, one-way function, and other difficult cryptographic problems. However, a large number of studies have proved that these mainstream cryptographic algorithms are unable to resist quantum attacks; that is to say, the VSS scheme designed based on these difficult problems is not safe in the post-quantum era. Pedersen presented an unconditionally secure VSS [49] protocol that builds upon Feldman’s work [50]. Unlike other VSS schemes that rely on mathematical problems like the discrete logarithm for security, Pedersen’s approach ensures the confidentiality of sub-shares even in the event of a discrete logarithm solution. But once this happens, although the security of sub-shares can be guaranteed, the scheme will not be able to maintain validity, the verification process can be arbitrarily forged, and the scheme is no longer valid. In contrast, lattice-based VSS schemes can encrypt larger scalars, and the security will not be threatened by quantum attacks.
4.2. Lattice-Based VSS
Adela Georgescu proposed an LWE-based -VSS [35] in 2011. The construction of the scheme is elegantly simple, and it possesses the valuable property of verifiability, enabling participants to independently confirm the accuracy of their shares. Additionally, the size of each share in the scheme is equivalent to the size of the secret being shared. Based on the LWE problem, n secret shares are added to each other to cancel the error vector. For the offset share information, the final secret value can be obtained through Gaussian elimination. Specifically, in order to generate the secret shares of n participants, the dealer performs the following calculations in the secret share construction phase:
- (1)
- For , the dealer first randomly selects a vector ai from and selects based on the error probability distribution X. They calculate secret share value .
- (2)
- For , they choose uniform at random from and calculate , such that the last secret share is defined as: .
To verify the share’s correctness, the dealer calculates the verification message in the distribution phase and makes it public. After receiving the secret share , the participant judges whether the secret share value is valid according to the public information. In the secret-recovery phase, they collect the shares of all n participants to obtain and finally, obtain the secret S through Gaussian elimination.
In 2012, Bansarkhani and Meziani [39] designed an -VSS using a lattice-based one-way hash function. The scheme is designed to be verifiable, which means it can effectively detect any dishonest behavior from both the dealer and participants involved. Its security relies on the computational hardness of the n-approximate SVP, with n representing the dimension of the lattice utilized in the scheme, and c being a positive constant.
In the secret-distribution stage, the dealer first selects an lattice basis B and selects a vector with length n and weight . They compute shares and forward them secretly to the participants. Simultaneously, they broadcast the public parameters , where is the vector of lattice basis B. After receiving the shares, the participants verify the equation . If the value is valid, the participant sends a confirmation to the dealer.
In the secret-restoration phase, n participants secretly send their shares to the combiner. These n shares can be combined and expressed as an square matrix . Subsequently, the combiner calculates:
They solve to obtain the unknown vector group , expressed as a matrix , where represents the n-dimensional unit vector of . Through the unknown matrix A and the secret matrix C, we can calculate and restore the initial lattice base .
The secret is obtained by calculating the public value V. The combiner judges by the public parameters. The secret is then sent back to each participant over a secure channel.
However, the construction of -VSS cannot satisfy most usage scenarios. For example, participants may be disconnected or even attacked during the secret-recovery process, so that they cannot upload the secret share value correctly. Therefore, a -VSS based on lattice-hard problems is necessary.
In 2009, Shanyue Bu et al. [43] proposed a new -VSS based on Shamir’s Lagrange interpolation polynomial TSS scheme. The scheme is constructed based on the NTRU algorithm, and there is no need to establish a special secure channel between the participants and the server during the secret-sharing process. This makes the scheme more lenient on the environment and can effectively resist cheating among members. In this scheme, the dealer first constructs the parameters of the NTRU algorithm and assigns a pair of keys to each member in the scheme, where N is the maximum number of polynomials in the NTRU algorithm (usually a prime number), p and q are the large modulus and small modulus, respectively, in the NTRU algorithm, are polynomials used to generate the NTRU algorithm key, r is the NTRU algorithm polynomial used for encryption, and represent the non-zero coefficients in the , and r polynomials, respectively. Then, the secret share of participant is calculated using a polynomial, and the public verification information V is calculated using a one-way hash function . Finally, in the secret-recovery stage, Lagrange’s interpolation formula is used to calculate the original secret information. During the verification process, participants can check the correctness of the secret share through calculation, specifically:
In the scheme-initialization phase, the dealer selects NTRU parameters according to the security level requirements, where . Then, they generate polynomials and through the parameters, letting , and calculate:
The dealer secretly sends to participant , asks them to keep it secret, and then announces . Subsequently, in the secret share calculation stage, the dealer randomly generates mutually identical vectors and constructs a polynomial:
Then, they select n different values on the finite field to calculate the secret share:
and use the one-way hash function to calculate the verification share:
They send to and publish . After participant receives the secret share information, they calculate the equation:
by calculating whether the two sides of the formula are equal to determine whether there is fraud or forgery. Finally, any t members in the scheme can share their secret shares to reconstruct the polynomial .
Rajabi and Eslami also proposed a VSS scheme based on Shamir’s TSS in 2019 [22]. In this scheme, the authors first propose a general-purpose VSS, which requires a set of collision-resistant hash functions that maintain homomorphism to verify shares. They use the GCk function proposed by Micciancio [51] to construct a lattice-based VSS.
The dealer uses an integer m, secret , and random number to construct a polynomial and a one-way function . They expose .
If the dealer is honest to implement the agreement, then the following equation holds:
This means everyone can check that the dealer distributed the correct shares of the secret. At the same time, if a participant tries to join the secret-reconstruction phase, the shares they offer should also satisfy the equation, and everyone can check the compatibility of the slave participant’s shares with the public new one. Finally, if t or more participants provide their own secret share, the original secret can be constructed through the Lagrangian interpolation formula.
To support very large committees with tens of thousands of participants, the scheme’s communication and computation need to be sufficiently efficient. To this end, Gentry et al. [52] proposed a non-interactive PVSS scheme based on the LWE. To further save bandwidth, they use the PVW encryption scheme in the multi-receiver setting along with bulletproofs to obtain compact proofs of correct share encryption and decryption.
Given a security parameter and the number of participants n, then the PVSS protocol they proposed only requires dealers and participants to perform power operations and broadcast scalars in and group elements. Furthermore, each side needs to perform scalar multiplications in .
Different from [22], Yong Peng et al. [45] used the Ajtai one-way function to construct the verification process of the VSS scheme. After receiving the secret share sent by the dealer and the public information, the participant uses the public matrix to check to determine the correctness of the share. is an Ajtai one-way function, and the probability of reverse calculation is negligible. and are randomly selected. Besides the secret-sharing phase, the scheme also achieves verifiability in the secret-reconstruction phase. When participants cooperate to restore the secret S, the shareholders can mutually verify the legitimacy of the share:
They determine the identity of each participant and determine who is the illegal participant with the following calculation:
In addition, the generation and reconstruction process of secret shares are designed based on Shamir’s TSS. Simultaneously, this scheme can be applied to TSS constructed in any way, such as SS based on Lagrange’s interpolation formula, CRT, hyperplane space, and other cryptographic schemes.
Hidden structure is a technique that can remain secret until some authorized subset of participants collaborate, introduced by Sehrawat and Desmedt in 2020 [53]. A new hidden VSS supporting all monotonic access structures was proposed by Vipin et al. [46]. The scheme begins by establishing the access structure for the lattice-based TSS and introduces a novel variant of the LWE problem, termed PRIM-LWE. Leveraging PRIM-LWE, they devised the first VSS scheme with graph-based access structure concealment. Notably, this VSS is the first of its kind to support the detection of malicious behavior and sharing verifiability even in a malicious majority context. Moreover, the unique construction of the scheme contributes to smaller share sizes.
The summary of Section 4.2 is shown in Table 2.

Table 2.
Lattice-based verifiable threshold secret sharing schemes.
5. Threshold Multi-Secret Sharing Scheme
5.1. Overview of MSS
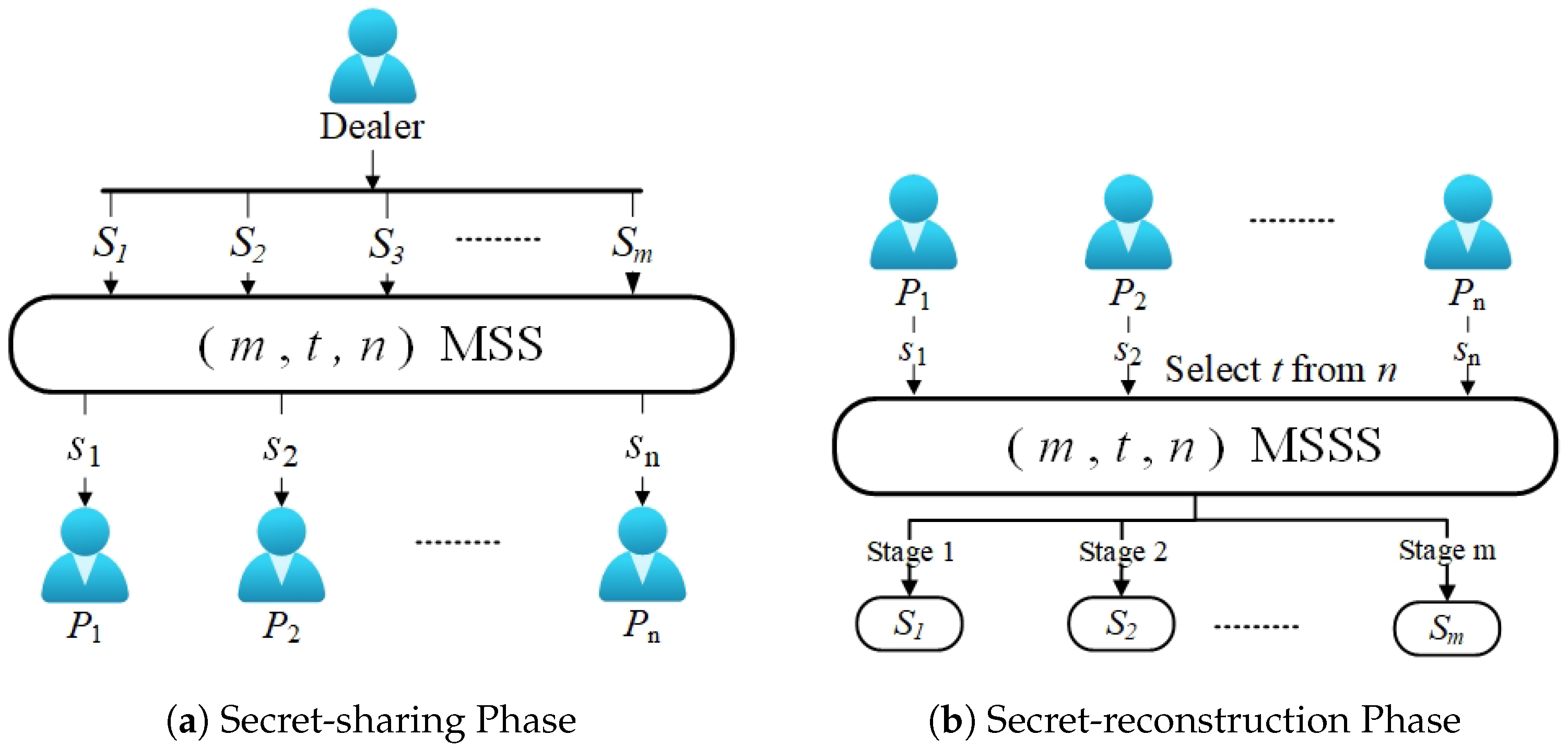
Because the traditional schemes can only share one secret, scholars have proposed the MSS scheme to solve this problem. As shown in Figure 3, MSS can share and reconstruct multiple secrets. Dawson [54] proposed the first MSS. The scheme uses an MSS to share multiple secrets simultaneously, with each participant holding a secret share. However, during the recovery phase, the secrets must be retrieved in a predefined order to ensure the security of other unrecovered secrets. Deviating from this order may compromise the confidentiality of the shared information.
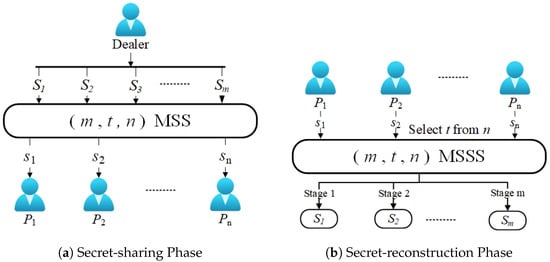
Figure 3.
Threshold multi-secret sharing.
Generally speaking, according to the order of secret recovery, MSS can be generally categorized into three categories: (1) the simultaneous multi-secret sharing scheme (SMSS) [55]; (2) the multi-stage secret sharing scheme recovering secrets in a predefined order (MSSSPO) [56]; (3) the multi-stage secret sharing scheme recovering secrets in any order (MSSSAO) [57]. Most of the existing MSS are based on difficult problems such as one-way hash functions, which cannot resist the threat of quantum algorithms very well.
Harn proposed a verifiable MSS scheme [58]. After the proposal of verifiable multiple secret sharing (VMSS), almost all new MSS schemes will have verifiable properties. The verifiable property has become an integral part of TSS, especially in multi-secret schemes. As far as we know, all current lattice-based MSS have the verifiable property. Therefore, we summarize and study the MSS under the VSS, because to some extent, verifiability is an important basic property of the MSS.
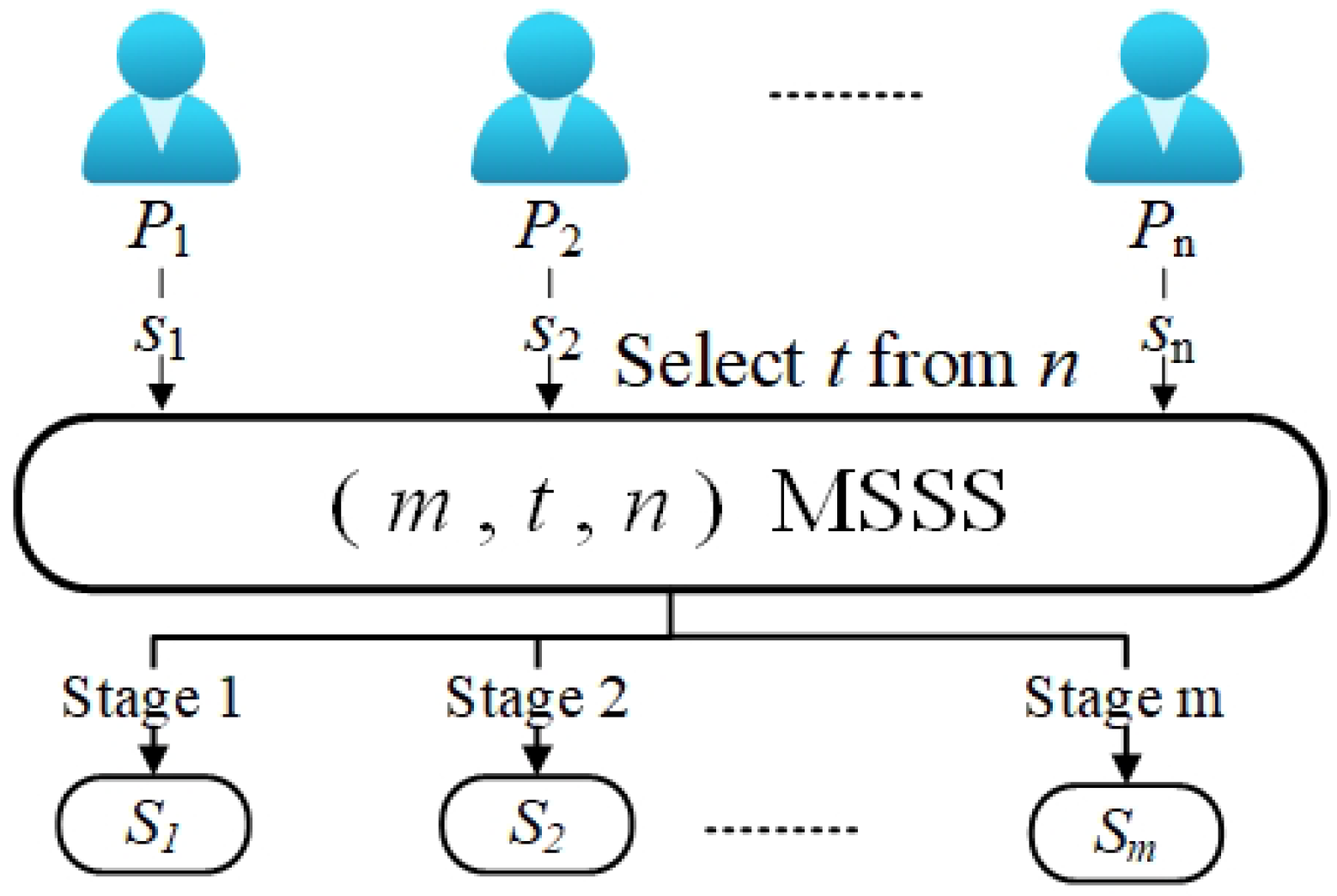
The threshold multi-stage secret sharing scheme is a significant component of the broader concept of MSS. In traditional MSS, all secrets are reconstructed simultaneously in a single stage. Figure 4 shows the secret-reconstruction process of MSSS. In the MSSS [57,59], secrets have different attributes and importance levels, which requires that any authorized subset of participants can only reconstruct one of the secrets in each stage. If the reconstructed secret does not reveal any other secret information when multiple secrets are reconstructed, then the MSS is called an MSSS. To extend the MSS to be multi-stage, participants must provide pseudo-secret shares to the aggregator based on the original shares. However, most of the existing MSSSs are designed based on a one-way hash function and discrete logarithm.
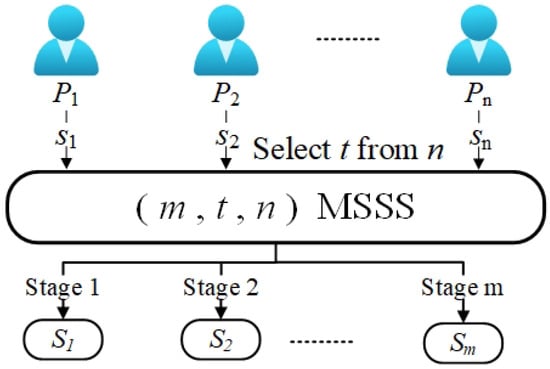
Figure 4.
Threshold multi-stage secret sharing.
In the remainder of this section, we summarize and analyze existing lattice-based MSS schemes. As shown in Figure 5, we divide lattice-based MSS into two types: lattice-based simultaneous multi-secret sharing scheme and lattice-based multi-stage secret sharing scheme.
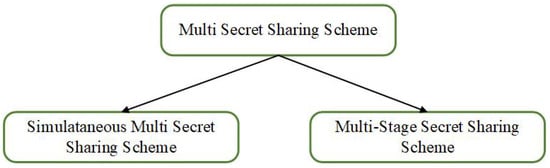
Figure 5.
Classification of multi-secret sharing schemes.
5.2. Lattice-Based Simultaneous Multi-Secret Sharing Scheme
In the traditional MSS, only one secret can be used for construction, and when the secret value changes, the system must recalculate the secret share and resend the share information to the participants. This would consume a lot of additional resources and may not be practical in many application environments. In 2017, Amroudi et al. [33] proposed a -SMSS based on the NTRU difficulty problem. In their scheme, the authors define an MP to construct multivariate polynomials, where multiple secrets are kept secret and distributed as coefficients of the polynomial.
In addition, the scheme realizes the verification function through the hash function. The scheme does not require a secure channel, and all public parameters are resistant to quantum attacks. In addition, the author defines different secret share verification schemes for different relationships between the number of secrets and the number of participants. However, the proposed scheme must recover the complete polynomial during the reconstruction phase, which means that all secrets need to be reconstructed at once. This is not friendly to many complex application environments, and the scheme of recovering secrets in stages and sequentially has more application value and prospects in real scenarios.
In 2022, Fulin LI et al. [36] also proposed an SMSS that can verify shares during the secret-generation and -reconstruction phases based on the SIS difficulty problem. The scheme employs symmetric binary polynomials for generating secret shares:
To hide the secrets and encrypt valid information during transmission:
where . The dealer utilizes binary polynomials to calculate shares , which are sent to participant over a secure channel. To verify the accuracy of the shared shares during the secret-generation and -reconstruction stages, a one-way collision-resistant hash function is used to realize the verifiability of the scheme, where represents a matrix that contains m linear independent column vectors with dimension In the verification phase, the participants use the public parameters disclosed by the dealer and the one-way hash function to verify their shares. In addition, under appropriate parameters, this paper reduces the pressure of memory consumption by reducing the public value and the share size of each secret. The scheme based on the LWE hard problem also provides post-quantum security. In the scheme [40], the author proposes a SMSS based on the search-LWE difficult problem and proves the security of the scheme under the standard model. Furthermore, the scheme can provide non-interactive verifiability [60], and during the verification phase, no additional communication is required between the participant and the dealer.
5.3. Lattice-Based Multi-Stage Secret Sharing Scheme
In 2011, Shanyue Bu et al. [34] proposed an MSSS algorithm based on NTRU. In order to extend and improve the scheme, Bu et al. proposed a verifiable multi-secret threshold cipher scheme based on the original scheme in 2011. The scheme is also based on Shamir’s TSS, using Lagrange’s interpolation formula for secret segmentation and reconstruction. It uses an NTRU algorithm and one-way hash function to verify the validity of new data.
In the specific implementation process of the scheme, in order to share multiple secrets the dealer selects different random numbers and generates a binary secret credential for each secret using NTRU public parameters r and h:
Next, they generate a shadow subkey for each secret and public . To reconstruct the secret, any authorized subset can compute and verify the authenticity of through public parameters.
If the above verification is correct, then the secret can be recovered according to the formula:
It is worth noting that is the subkey generated by Shamir’s TSS, v is the verification vector for , f is generated by the NTRU algorithm, and is the identity of participating member i.
In the paper [37], the authors proposed an MSSS based on the SIS problem and its corresponding verifiable version. In their scheme, any secret information is recovered in an indeterminate order during the recovery phase. To offer an efficient verification protocol for the scheme, the authors modify Vadim’s identity authentication protocol [61] and use it in the scheme.
Specifically, the authors use the function for secret sharing and calculate to achieve different secrets’ reconstruction, where . Moreover, the scheme ensures the robustness of the dealer by means of public parameter information verification. During the secret-reconstruction phase, it employs the Vadim identity authentication protocol to verify the participants’ shares. The scheme realizes an efficient secret sharing and verification algorithm with a low number of parameters.
In 2017, Pilaram et al. [41] designed an MSSS based on the Ajtai one-way function. The scheme has the characteristics of being multi-stage, multi-purpose, and verifiable, which expands the application prospect of the scheme. In this scheme, the shared secret share is a vector in an lattice, and t participants realize secret reconstruction by jointly maintaining an matrix. Specifically, for m secrets , the dealer needs to randomly select a vector in the preparation stage and make it public, where the last entry is equal to 1. For each secret , the dealer prepares a lattice basis , where , such that:
Then, the dealer needs to select n public vector , public matrix , and secret vector so that the equation holds true. In the secret-distribution phase, the dealer sends the share vector to participant through the secret channel and makes public the public matrix and the vector . In the secret-reconstruction stage, t participants use their shares to calculate , and jointly maintain an matrix . Using the public parameters, we can calculate to obtain the lattice basis , where . Finally, based on the lattice basis and the public vector v, the secret can be calculated using the formula.
In addition, in the secret-distribution stage, the dealer can disclose a random matrix and use the one-way hash function to verify the secret share. The participants can verify the secret shares and the reconstruction secret after receiving the secret shares and during the reconstruction stage.
In 2022, Peng Xu et al. [62] adapted the scheme, applied it to the aggregation of security models in federated learning, and constructed a post-quantum secure privacy-preserving federated learning framework. We will elaborate on this part in the application of Section 7.3.
In 2022, Jing Yang et al. [44] proposed a computationally secure MSSS for quantum computers using inhomogeneous linear recursion (ILR) and the Ajtai function. Furthermore, their proposed scheme is verifiable, dynamic, and reusable. In this paper, ILR is divided into two types, Type-t and Type-l. Combined with ILR and the Ajtai function, four MSSS schemes are designed. Specifically, the scheme uses ILR to generate relevant shares of secret information and uses Lagrange’s interpolation formula to realize secret reconstruction in the secret-reconstruction stage. In addition, the scheme realizes efficient share verification based on the Ajtai function. The four schemes in this paper require more memory consumption than other known schemes but reduce the consumption in terms of time.

Table 3.
Lattice-based simultaneous multi-secret sharing schemes.

Table 4.
Lattice-based multi-stage secret sharing schemes.
6. Threshold Changeable Secret Sharing Scheme
6.1. Overview of TCSS
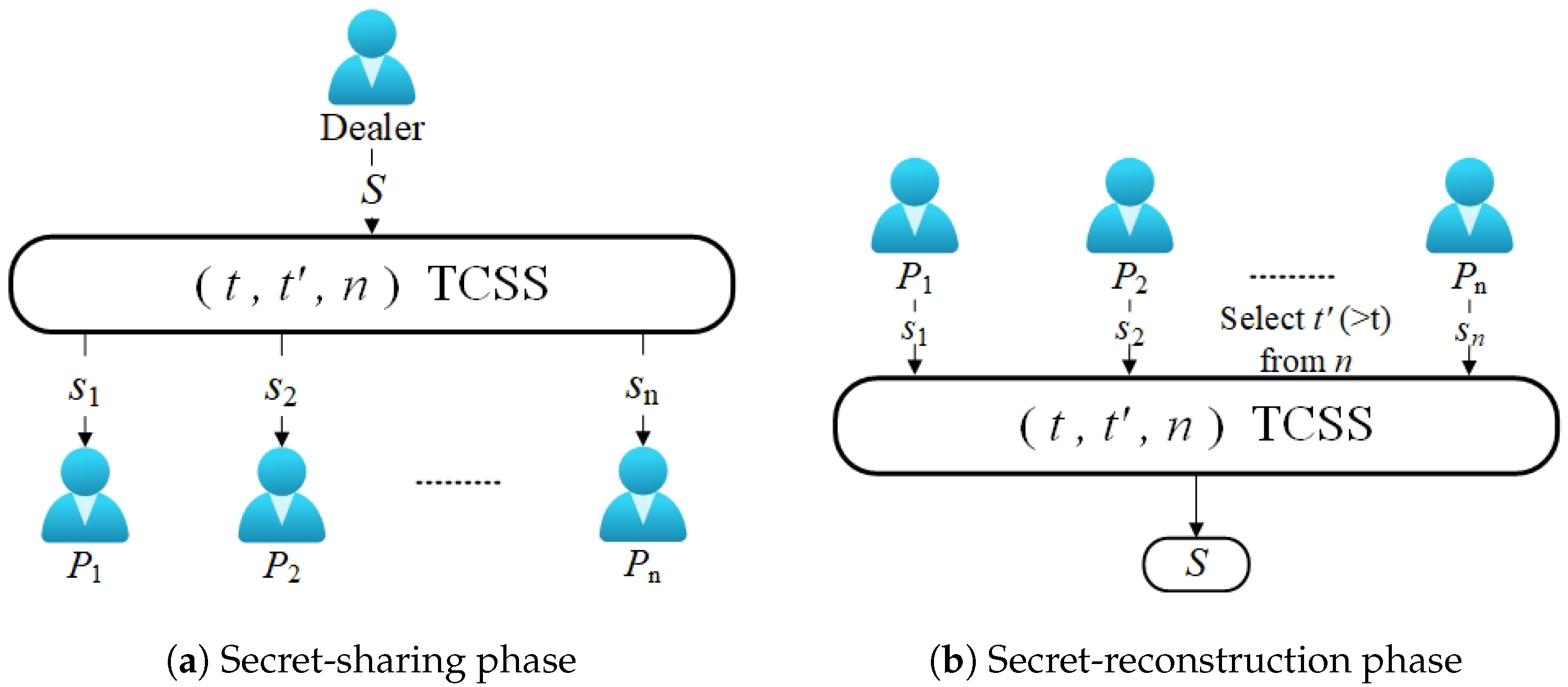
In the life cycle of a TSS scheme, some unpredictable changes are often encountered, such as the increase in distrust among the participants, the joining and withdrawal of the participants, and the strengthening of the adversary’s attack ability, etc. Indeed, various application scenarios and evolving requirements may lead to changes over time, necessitating adjustments to the threshold parameter t to ensure the privacy protection capability of the TSS. Specifically, after an initial setting with a relatively low threshold value, an increase in system size or potential attacker capabilities may demand raising the threshold parameter to a higher value . The longer the system’s lifespan, the more probable it becomes to require such adjustments. This adaptability ensures the ongoing security and effectiveness of the TSS as the system evolves.
For the problem of increasing the threshold parameter from t to in -TSS, a simple solution is to let the participants discard their old shares and have the dealer distribute new shares of the -TSS to all the new participants. However, this solution may not be very appealing due to the requirement of the dealer’s continued involvement after the establishment phase, along with the need for communication between the dealer and each participant (which might be challenging to establish after the initial setup phase). This ongoing dependency and communication overhead can pose practical difficulties and limit the scalability of the scheme. Another approach is for the dealer to generate for each future possible threshold value during the distribution phase and distribute each share of the TSS to the participants. This means that as a participant, one would receive shares from the dealer. However, these methods would bring significant computational and communication overheads. Therefore, a more efficient and economical solution is needed to provide some flexibility to traditional TSS, so that threshold value adjustments can be made at a smaller cost when encountering changes.
In this case, the threshold changeable secret sharing scheme is proposed. As shown in Figure 6, its goal is to dynamically adjust the threshold value of the scheme after the share of secret sharing is distributed and before the secret is reconstructed. The generation of the TCSS scheme further promotes the application of TSS in wider scenarios. In 1999, Martin et al. [63] proposed the first TCSS. Later, different TCSS systems were proposed. This format can be divided into three categories: based on linear polynomials [64], based on hyperplane geometry [63], and based on Chinese remainder theorem [65]. However, the traditional variable threshold scheme often has problems, such as large amounts of calculation, secure channels between participants in the process of threshold adjustment, and inability to resist post-quantum attacks. TSS schemes based on lattice-hard problems are provably secure, and they only require linear computation on relatively small integers. Therefore, it is extremely valuable to study the TCSS based on lattice-hard problems.
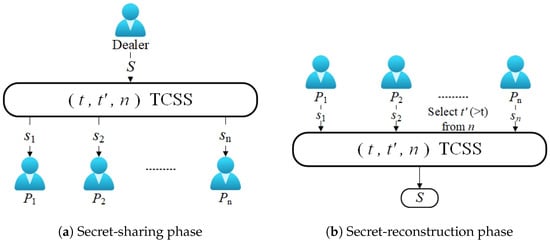
Figure 6.
Threshold changeable secret sharing.
6.2. Lattice-Based TCSS
Steinfeld et al. first improved on the standard Shamir’s TSS and proposed the first lattice-based TCSS [32]. Their scheme focuses on the problem of increasing the threshold parameter t of the TSS after the secret-distribution phase, and the scheme only needs to broadcast some public parameters to instruct participants to modify their shares, without requiring further communication between the dealer and participants. In order to increase the threshold t by so that , this paper designs a TCSS scheme based on the lattice “error-correction” algorithm and using the lattice reduction technique. The dealer introduces a moderate amount of random noise into their shares to generate new secret shares that carry partial information about the original shares. As the new secret shares contain only partial information about the original shares, it is possible that a set of sub-shares might no longer be enough to reconstruct the secret if the threshold t is altered.
Specifically, in the initialization phase of the scheme, the dealer runs Shamir’s TSS to calculate the initial shares of the secret. We will not expand on this part but focus on the threshold-changing part of the scheme. The change in the threshold t in the scheme is mainly realized through the CVP algorithm, where the sub-share combiner algorithm runs an efficient CVP-approximation algorithm with -approximation factory on a lattice of dimension . In order to obtain the share of the new -TSS scheme, it is necessary to first determine the correct noise bound , where
The participants use the public parameters to update their secret shares to obtain .
where is a random integer and . In the secret-reconstruction phase, the threshold-changed secret shares are used to construct full-rank lattice , whose rows form a basis for a full-rank lattice in :
Define . Finally, run a CVP-approximation algorithm on lattice to obtain secret .
Subsequently, Steinfeld designed a new threshold-varying method for a TSS scheme based on the CRT, also based on the CVP hardness problem. Similar to [38], neither of these schemes necessitates communication between the dealer and the participants after the initial stage. They can be applied to existing threshold schemes, even if these schemes were originally designed without considering potential future threshold increases. The schemes maintain their functionality and effectiveness without requiring additional modifications to accommodate higher threshold values.
In 2017, Pilaram et al. [42] improved their previously proposed MSSS scheme [41]. In addition to the function of increasing the threshold, the functions already supported, such as multi-stage, multi-use, and verifiability, remain unchanged. To achieve the function of increasing threshold such that , the authors use a zero-addition protocol [66]. When updating the threshold, the updater uses the new threshold to share zero secrets among the participants and combines the result with the original -TSS to achieve an increase in the threshold and obtain a new -TSS. Specifically, their scheme mainly consists of the following steps:
Step 1: Extend the size of the original matrix threshold parameter from t to , and extend the matrix with zero vectors:
where and are chosen randomly from and is chosen randomly from
Step 2: Use the new threshold parameter to share the zero secret according to the original -TSS:
Step 3: By combining the above formulas, we can obtain the new scheme:
Additionally, define the parameters:
Through the above definition, after updating the threshold , the following formula holds:
After the new -TSS is generated, the method of the secret-reconstruction phase is similar to [41]. After collecting the secret information of participants, the public parameters and secret information can be used to restore the secret matrix and calculate secret S. It is worth noting that during the process of changing the threshold t, the attributes in the original scheme will not change, and multi-stage, multi-use, and verifiability can still be guaranteed. Not only that, on the basis of Lindner and Peikert’s encryption scheme, the author proposes an improved lattice-based threshold decryption algorithm using the secret-sharing algorithm.
The summary of Section 6.2 is shown in Table 5.

Table 5.
Lattice-based threshold changeable secret sharing schemes.
7. Application of Lattice-Based Secret Sharing
Initially, TSS has been widely used in key management, shared access to important resources, and other fields. However, with the continuous development of information technology and communication technology, TSS has also shown a strong ability to protect privacy in various fields. In addition, with the occurrence of data privacy leaks in various countries, more and more people have begun to pay more attention to personal data security, especially in the fields of medical care and finance, which has further promoted the development and application of TSS. In this section, we will discuss the application scenarios of lattice-based TSS, including threshold cryptosystem, threshold signature, blockchain distributed storage, and privacy-preserving federated learning.
7.1. Threshold Cryptosystems
In the traditional cryptosystem, the key realizes various operations in the system, and the safe storage of the key is also the security core. However, systems based on traditional public-key cryptography suffer from several serious problems. With the introduction of TSS technology, the concept of a threshold has been gradually introduced into the traditional cryptosystem, which greatly improves the security and robustness of the original system. Desment et al. [67] introduced the concept of threshold cryptosystems after Shamir’s TSS was proposed. Security is improved by sharing secret information with multiple users for decentralized storage, and the cryptographic system can even be completed collaboratively by at least a threshold number of users. Similar to encryption and signatures in traditional cryptography, a threshold cryptosystem generally includes two aspects, threshold encryption and threshold signature. Next, we will carry out specific research on the content of these two parts and summarize the relevant applications of the current lattice-based TSS schemes in this field.
7.1.1. Threshold Encryption
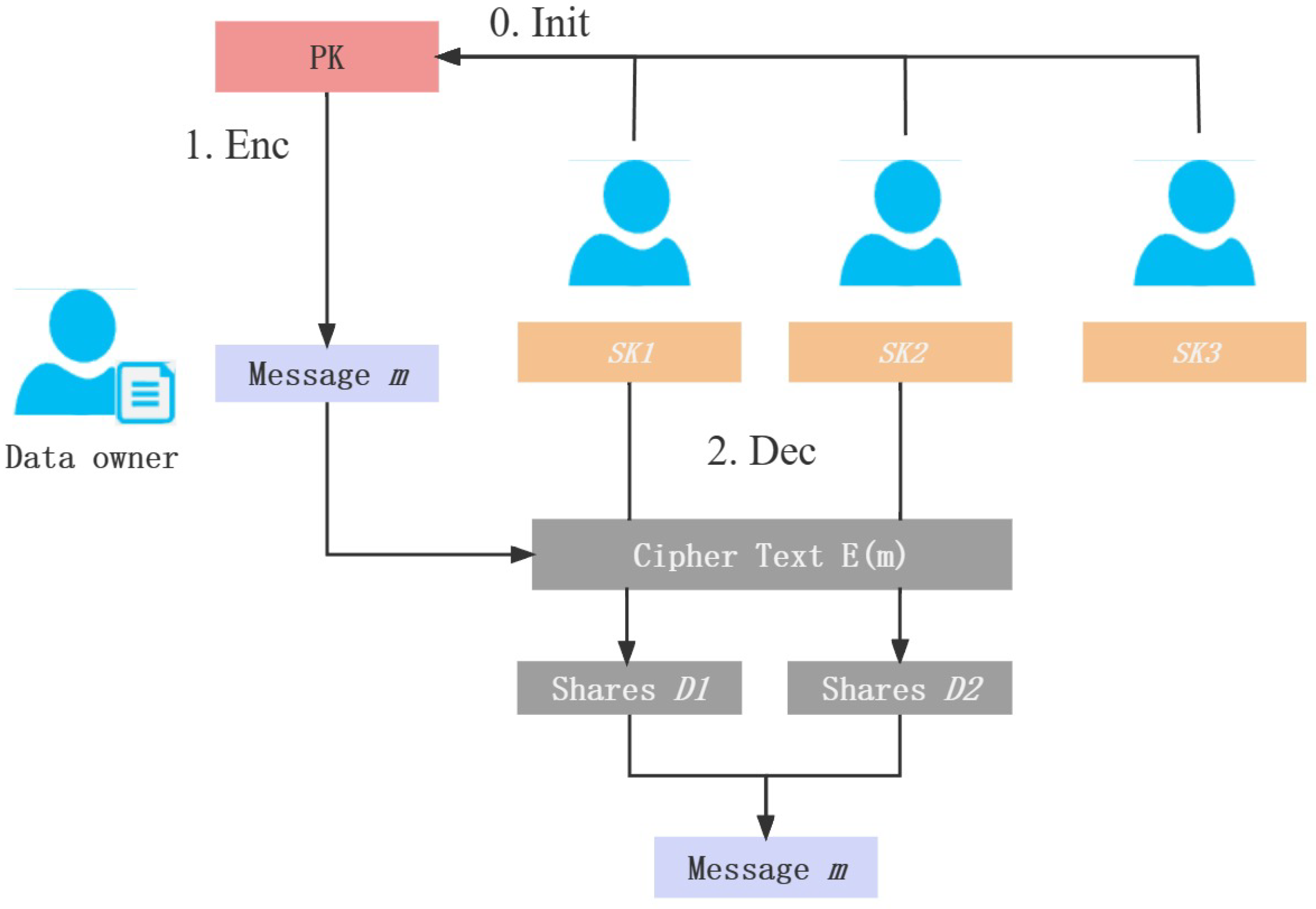
As shown in Figure 7, threshold encryption generally includes key generation, encryption and decryption processes, and a message combiner. In the process of decrypting a ciphertext, participants use their own private keys to decrypt the ciphertext and upload the ciphertext to the combiner. The message combiner can combine the original plaintext content after collecting decrypted messages greater than the threshold t. In general, the threshold encryption scheme generally includes the following four algorithms:
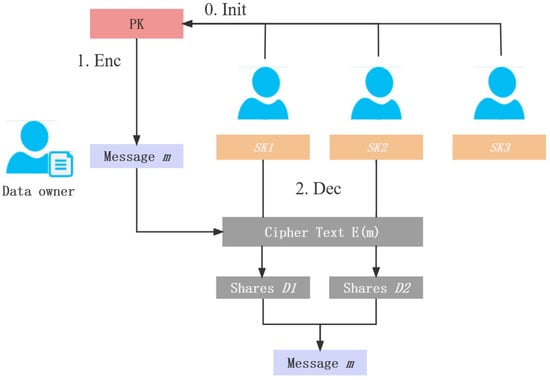
Figure 7.
Threshold encryption.
KeyGen : The key-generation algorithm inputs the security parameter , the number of users n, and the threshold t. It outputs the public key and private key shares .
Enc : The encryption algorithm inputs the public key and the message m encrypts the message m and outputs the ciphertext.
Dec : The decryption algorithm inputs the private key share of any user and the ciphertext c and outputs the decryption share .
Combine : The message-combination algorithm inputs any threshold t decryption shares and combines them to obtain the original message m.
In 2010, Bendline and Damgard [68] proposed the first lattice-based single-bit threshold pk encryption scheme based on the LWE encryption system [69], using pseudorandom secret sharing technology to split the private key. Under quantum attack, their scheme prevents passive adversaries from corrupting all but one player and is also resistant to active adversaries from corrupting up to a third of the players. Furthermore, their scheme includes a highly efficient non-interactive decryption protocol. Additionally, toward the end of the scheme, they introduce a zero-knowledge protocol designed to enhance the information pertaining to the plaintext contained within the provided ciphertext. Subsequently, Frederiksen extended the scheme and promoted the original single-bit scheme to a multi-bit scheme.
In 2013, in order to shorten the length of the for threshold encryption, Sunwar Singh et al. [70] designed an efficient threshold scheme and constructed a repeatable threshold encryption scheme [71] based on it. Compared with Bendline’s single-bit threshold encryption scheme, in the case of the same ciphertext size, the size of the is reduced from to , where represents the number of bits required for elements.
In order to study the application of anti-quantum threshold technology in distributed cloud computing platforms, Zhang et al. proposed a lattice-based TSS (LB-SSA) in 2015 to ensure cloud security properties in post-quantum environments [72]. In their scheme, each share can independently generate its own to without interaction with other participants, which is especially important for distributed environments that require less interaction. In this paper, the authors explore the application of LB-SSA to lattice-based threshold decryption schemes. In addition, the authors also study the related application of this scheme in multi-agency identity-based encryption (MA-IBE).
Identity-based encryption (IBE) is an optimization for traditional infrastructure (PKI) technology. Unlike the traditional concept based on digital certificates, IBE uses a user’s unique identity as the , while the private key is generated by a central authority. In short, IBE is a encryption system that allows for arbitrary selection of public keys. The concept of IBE was initially proposed by Shamir [73], but it was only in 2001 that Boneh and Franklin formally introduced the first IBE scheme based on bilinear mapping [74].
In IBE, the private key generator and the certificate authority are systems that perform high-value operations. Using threshold encryption technology can enhance the robustness of the system and distribute trust. In addition, from a security point of view, many existing schemes are not resistant to quantum attacks. In 2008, Gentry and Peikert et al. [75] first proposed the IBE scheme based on the LWE difficulty problem in the lattice. Since then, more IBE schemes based on lattice-hard problems have been proposed [76]. However, these proposed schemes are quite complex in algorithm. In order to simplify the efficiency of key generation and other stages, Bendlin et al. proposed a lattice-based threshold protocol in 2013 [77]. The optimal threshold for this scheme is for a semi-honest adversary and for a malicious adversary. Finally, this paper constructs a secure IBE scheme based on the threshold protocol.
In 2015, Zhang et al. [72] proposed LB-SSA, the content of which we have explained in the previous article. Based on LB-SSA, they proposed the first lattice-based multi-agent IBE (MA-IBE) and proved that the scheme is secure under the random oracle model.
7.1.2. Threshold Signature
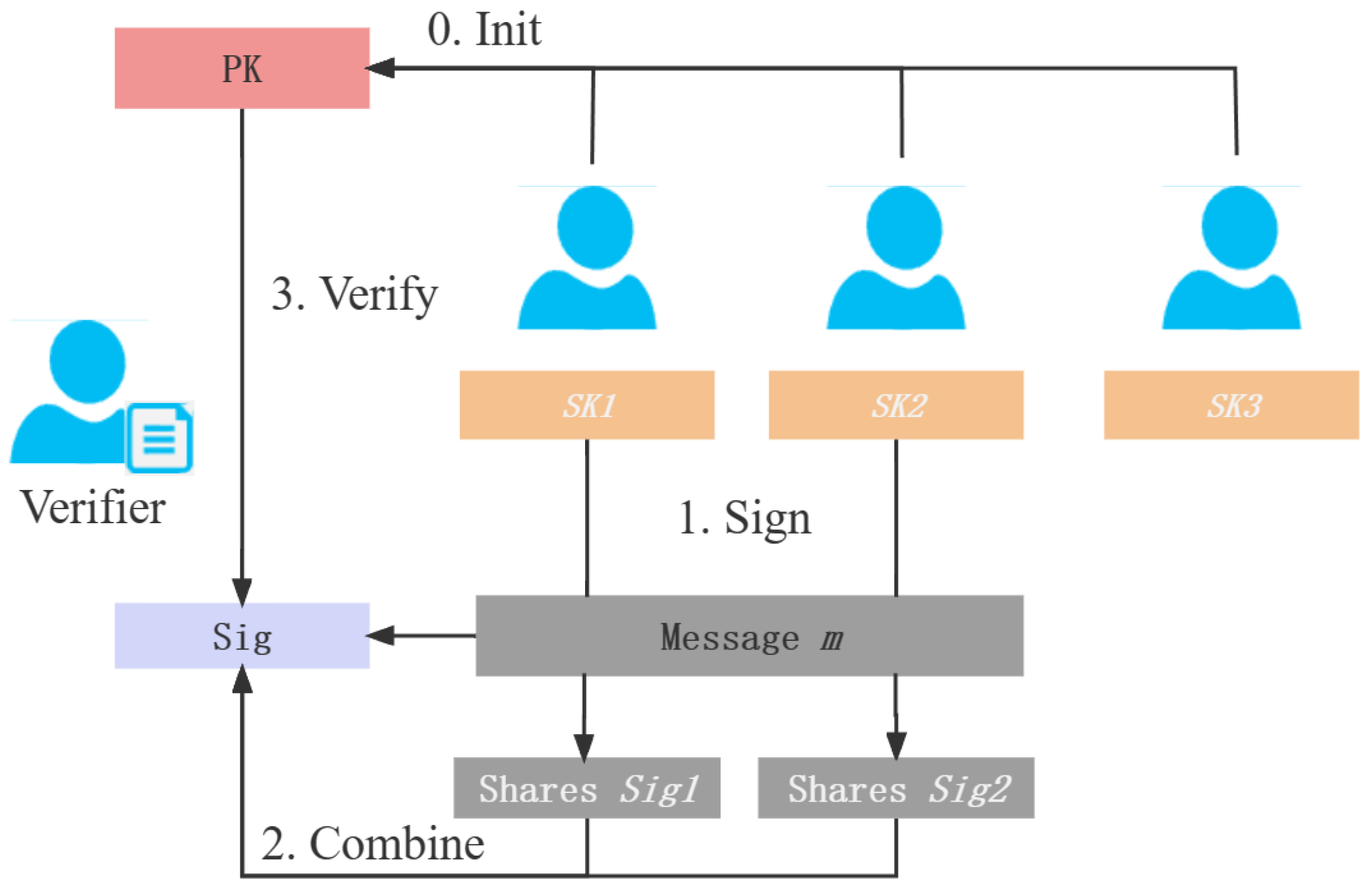
Figure 8 shows the execution process of the threshold signature. Similar to threshold encryption, the threshold signature mainly includes three steps of key generation, signature, and verification. The participants complete the signing with their private keys and upload the combiner. Waiting for the signature information of users greater than the threshold t, the combiner can combine the complete signature of the message.
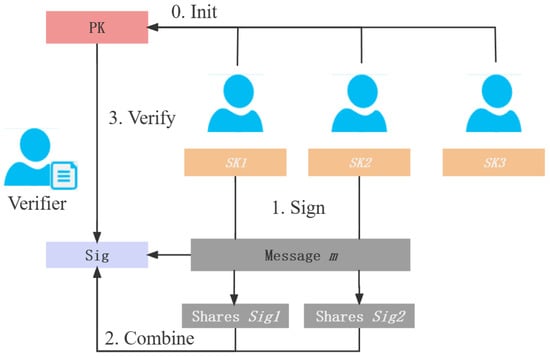
Figure 8.
Threshold signature.
KeyGen : The key-generation algorithm inputs the security parameters , the number of users n, and the threshold t. It outputs the public key and private key shares .
Sign : The signature algorithm inputs the private key share of any user and the message m. It outputs the signature share .
Combine : The signature-combination algorithm inputs any threshold t signature shares and combines the output signature .
Verify : The verification algorithm inputs the public key , message m, and signature for signature verification and outputs 1 when the signature verification is correct; otherwise, it outputs ⊥.
In 1991, Desmedt et al. [78] designed a TSS scheme operating on the Abelian group and designed a threshold signature scheme based on the RSA assumption for the first time. Since then, the research on threshold signature schemes [79,80] has attracted the attention of many scholars. Among them, the lattice-based signature scheme is also a popular research direction in recent years. In 2010, Cayrel et al. [81] presented a lattice-based threshold ring signature scheme that necessitates the collaboration of at least t participants to generate an anonymous signature. In this system, each member possesses its own , and the verification time scales linearly with the number of participating members. In addition, Tao Feng et al. [82] also proposed a threshold signature scheme with a variable threshold. Its signature algorithm goes through each member of the group in turn. The program is highly interactive and the program is based on NTRU-Sign. Unfortunately, NTRU-Sign has been proven to be unsafe as research on lattice ciphers continues to deepen [83].
In 2013, Bendlin et al. [77] improved Gentry’s scheme [75] by thresholding the lattice-based signature scheme. They separately constructed a threshold encryption scheme based on lattices that achieves chosen-ciphertext security and a threshold signature scheme that is unforgeable. They also provided security proofs under the general framework. However, in the process of non-interactive decryption and signature generation, the scheme requires a large amount of interactive computation among the participants, which limits its application in some special scenarios.
In 2022, Damgard et al. [84], following the Fiat–Shamir with Aborts (FSWA) paradigm, constructed several low-complexity distributed signature schemes and proposed a complete security proof based on the difficulty of SIS and LWE problems. However, the main disadvantage of the scheme proposed by Damgard et al. is that the threshold of the message signature cannot be changed; that is, only all participants in the system can sign the message. Based on this scheme, Anton et al. [85] proposed a new threshold signature scheme in 2023 and allowed a change in the threshold of the message signature, thus improving the flexibility of the original scheme. To provide functional interchangeability of threshold signature schemes, Tang et al. [21] proposed a lattice-based t-out-of-n threshold signature scheme in 2023. In order to build a special access structure, the authors first proposed a lattice-based TSS scheme and based on this, designed a secure multi-party computation protocol to obtain a higher signature efficiency. In addition, the author also designed a periodic key update mechanism for the threshold signature scheme to further improve the security of the system.
7.2. Data Storage and Transmission in Blockchain
One of the important features of blockchain is distributed storage. In the traditional concept, distributed storage is essentially a centralized system that disperses and stores data across multiple independent devices, utilizing numerous storage servers to distribute the storage load. However, this method still relies on the server to record the data address and conduct unified management and does not achieve distributed data storage in the true sense. In addition, if the server goes down or fails, it will cause a large amount of data loss and leakage.
The blockchain-based distributed storage technology can effectively solve this problem. Relying on technologies such as distributed ledgers, real distributed data storage and joint maintenance and management can be realized. In addition, the digital records on the blockchain are non-tamperable and unforgeable, which protects the security and correctness of data. All participants are efficiently coordinated through smart contracts to establish a credible new digital economic order. While breaking the data silos [86], it improves the efficiency of data flow, thereby creating a new storage model.
In recent years, leveraging TSS technology to reduce the storage cost of all nodes in the blockchain network has emerged as a prominent and trending research topic [87]. Diverse secret-sharing techniques are utilized to distribute block data among nodes within a blockchain network. In 2020, Sihem Mesnager et al. [88] applied the threshold scheme based on the grid difficulty problem to blockchain-distributed storage for the first time. In their scheme, the authors propose a post-quantum secure VMSS based on Feldman VSS, using quantum-resistant algorithms (such as the knapsack function) to ensure the security of the share-verification phase. This scheme aims to decrease the communication cost within the blockchain network while simultaneously enhancing the system’s robustness. In addition, the scheme does not require secret channels between nodes and also has a quantum-safe verification algorithm. In order to improve the high cost and network congestion problems in the execution of blockchain smart contracts, Yu et al. [89] designed a lattice-based threshold signcryption for blockchain oracle data transmission . This scheme not only guarantees the threshold characteristics of TSS, but also has the characteristics of unforgeability, confidentiality, and small amount of calculation, which is suitable for application in blockchain scenarios.
7.3. Privacy-Preserving Federated Learning
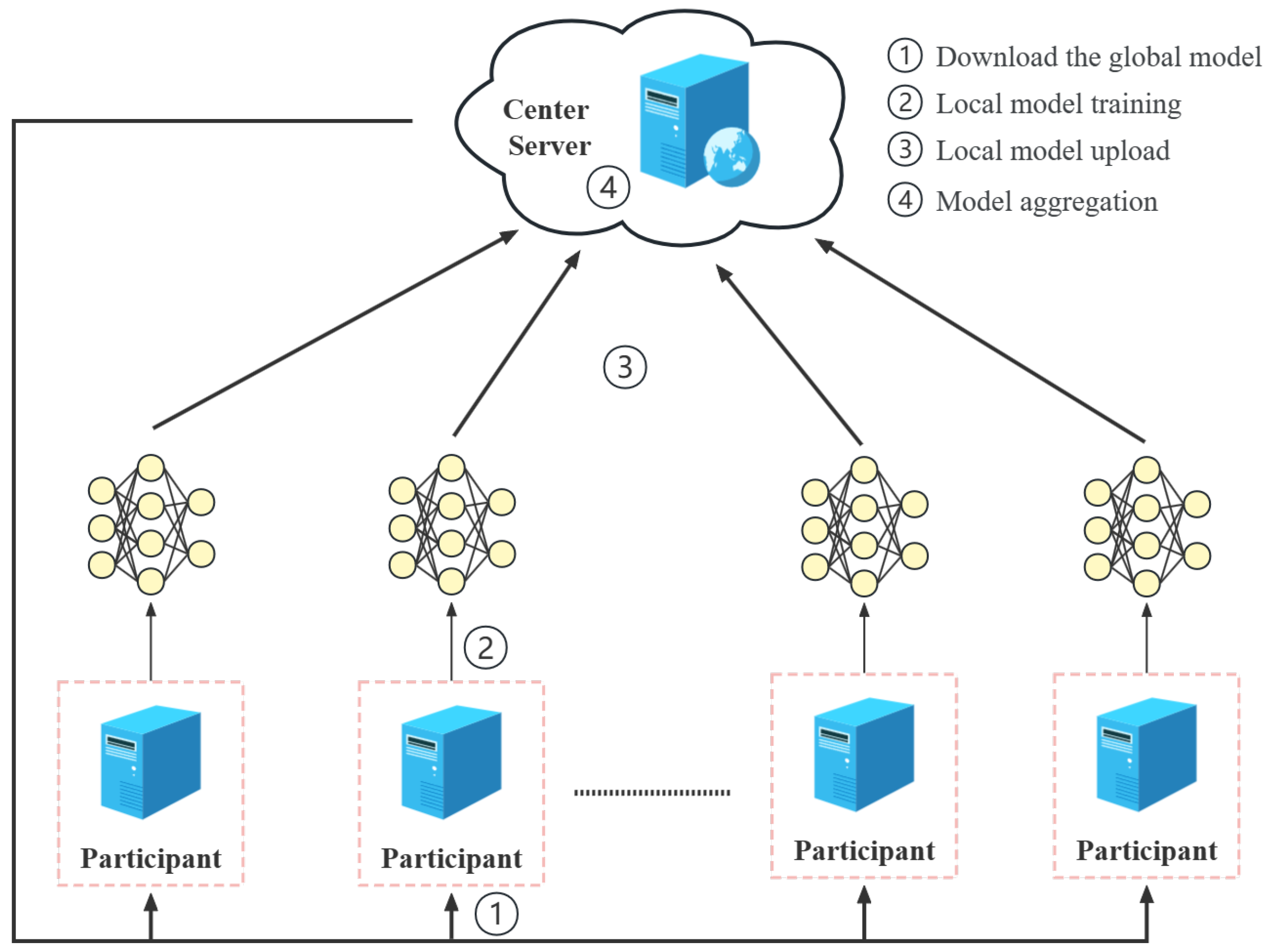
In 2017, Google first proposed federated learning, a distributed ML technology. As shown in Figure 9, FL transfers the model-training phase of ML to local participants and jointly maintains a global model by uploading gradient parameters. The privacy security of participants is effectively guaranteed only by uploading partial models, and the distributed training method will not greatly damage the accuracy of model training. In recent years, federated learning has emerged as a prominent research area within the field of network security, garnering significant attention and interest.
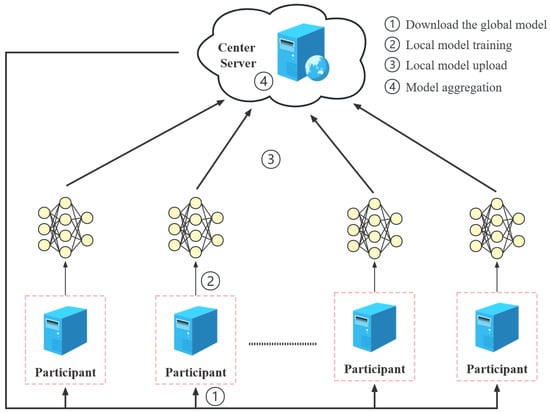
Figure 9.
Federated learning framework.
However, after continuous research, a large number of studies have proved that federated learning cannot protect the privacy of local data sets very well. Using the model parameters uploaded by the participants, the server can launch a reverse attack to restore the contents of the local data set or determine whether a certain record exists in the data set. Currently, privacy preservation in federated learning is primarily centered around three key aspects: homomorphic encryption (HE), secure multi-party computation (SMPC), and differential privacy (DH) [60].
In 2017, Google proposed a scheme to ensure the security of the federated learning model, using double masking and TSS to ensure that the local gradients during the learning process will not be leaked. However, this method is not effective against quantum attacks, and the process of computing the mask and unmasking requires a lot of communication between the parties. In order to solve the problem, Xu et al. [62] proposed a post-quantum secure federated learning privacy protection framework based on Pilaram et al.’s scheme [41] in 2022. In each training session of federated learning, participants modify their own secret share information by updating the public parameters. In addition, Laf uses the NewHope anti-quantum key agreement scheme to replace the original DH key agreement to ensure the security of the mask. Compared with Google’s scheme, Laf’s solution saves communication overhead in privacy-preserving federated learning and provides post-quantum security.
8. Summary and Open Problems
8.1. Summary
With the emergence of quantum computers and the increasing computing power of computers, the security of traditional cryptography algorithms will no longer be guaranteed. Lattices are an important field in post-quantum cryptography and have always received widespread attention and research. At present, based on the difficult problems of lattice cryptography, relatively mature public key encryption and digital signature schemes have been proposed.
TSS schemes are one group of the most important primitives of modern cryptography. As technology is evolving and more multi-computations are used, we need to have secure schemes that will protect our data. However, with the continuous development of quantum technology, the TSS scheme based on traditional cryptography assumptions is no longer safe. This paper comprehensively summarizes the existing lattice-based TSS schemes and related applications. To the best of our knowledge, this is the first review paper in this direction.
Based on the difficult problem of lattice cryptography, many schemes have been designed. After summarizing the lattice-based secret sharing schemes, we observe that LWE and SIS are widely used in modern cryptography, mainly due to their ability to provide a solid security foundation while maintaining high practicality. On the other hand, SVP and CVP are mainly concentrated in the fields of theoretical research and cryptanalysis. Their high computing resources and low efficiency have limited their application in actual encryption protocols. Finally, NTRU stands out among lattice-based encryption algorithms, especially in terms of encryption and decryption speed, making it a viable choice in practical encryption and key-exchange systems. However, the choice of these different algorithms mainly depends on the specific security requirements and application scenarios, so that they can play a key role in the development of the field of lattice cryptography.
8.2. Open Problems and Future Work
Lattice-based TSS technology has made significant progress in the field of information security, but there are still some shortcomings. For example, the threshold t of some schemes is equal to n. Unless such a solution is feasible in an environment with extremely high security requirements, it is not suitable for widespread popularization and application. In addition, the current solutions are relatively independent and not related to each other, which will hinder the popularization and use of technology.
After conducting systematic research on lattice-based TSS, we have summarized the problems and future development directions of existing schemes:
- (1)
- Reduce computational and communication costs: Lattice-based TSS schemes usually involve substantial computational and communication overhead, which may limit their use in practical applications. Future development directions will focus on improving performance, including finding more efficient algorithms, optimizing communication protocols, and reducing the need for computing resources, thereby making these solutions more attractive.
- (2)
- Key-management complexity: In applications such as multi-party secure computing, key management is a challenge. Lattice-based approaches require efficient management of multiple keys, which can lead to key-management complexity. Future work should focus on streamlining the key-management process.
- (3)
- Standardization and interoperability: To ensure interoperability between different systems and implementations, standardization efforts may occur. This will help facilitate the widespread adoption of lattice-based TSS schemes, as different systems can work with each other without being tied to a particular implementation.
- (4)
- Practical application: With the continuous growth of data and the increasing demand for data security, the lattice-based secret sharing scheme will be adopted in a wider range of applications. For example, financial institutions might use these schemes to protect customers’ sensitive data, healthcare organizations might use it to share patient data, governments might use it to protect sensitive government information, and cloud computing providers might use it to provide more secure service.
- (5)
- Security assumptions: Some lattice-based TSS technologies are based on specific security assumptions, such as the LWE assumption. While these assumptions are widely considered safe under current circumstances, more in-depth future research is needed to assess their durability, especially with the rise of quantum computing.
In general, the current lattice-based secret sharing scheme is still in the early stages of development, and no lattice-based solution has yet achieved the universality and scalability of traditional schemes (such as Shamir’s TSS). With the continuous development of quantum computers, lattice-based key agreement and signature schemes are becoming increasingly mature. Considering the characteristics of post-quantum keys, it is crucial to design a secret sharing scheme. At the same time, the design of solutions for different fields and different security requirements is also one of the issues that needs to be considered in future development. Finally, improving the performance of the solution and reducing overhead is also a topic that requires long-term research.
9. Conclusions
This manuscript systematically summarizes and studies lattice-based threshold secret sharing schemes. To the best of our knowledge, this paper is the first review paper on lattice-based threshold secret sharing. This paper classifies secret sharing schemes according to their different functions and compares and analyzes each part of them. In addition, this article also deeply explores the application research of TSS schemes in different fields, including threshold cryptography, blockchain, and federated learning. At present, lattice-based secret sharing is still in the development stage, and a more adaptable and secure solution needs to be proposed. At the same time, the optimization of the solution’s performance and storage overhead also requires further research. We hope that through this review paper, we can provide readers with a more comprehensive research investigation and determine future research directions.
Author Contributions
Conceptualization, J.C.; methodology, J.C. and H.S.; writing—original draft preparation, H.D. and H.S.; writing—review and editing, H.D. and Y.R.; supervision, Y.R.; project administration, M.Y.; funding acquisition, Y.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 62072249).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no potential conflicts of interest with respect to the research, authorship, and publication of this article.
References
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A Math. Phys. Sci. 1985, 400, 97–117. [Google Scholar]
- Feynman, R.P. Quantum mechanical computers. Opt. News 1985, 11, 11–20. [Google Scholar] [CrossRef]
- Chamola, V.; Jolfaei, A.; Chanana, V.; Parashari, P.; Hassija, V. Information security in the post quantum era for 5G and beyond networks: Threats to existing cryptography, and post-quantum cryptography. Comput. Commun. 2021, 176, 99–118. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Chen, L.; Jordan, S.; Liu, Y.K.; Moody, D.; Peralta, R.; Perlner, R.A.; Smith-Tone, D. Report on Post-Quantum Cryptography; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016; Volume 12.
- Fernandez-Carames, T.M.; Fraga-Lamas, P. Towards post-quantum blockchain: A review on blockchain cryptography resistant to quantum computing attacks. IEEE Access 2020, 8, 21091–21116. [Google Scholar] [CrossRef]
- Fernández-Caramés, T.M. From pre-quantum to post-quantum IoT security: A survey on quantum-resistant cryptosystems for the Internet of Things. IEEE Internet Things J. 2019, 7, 6457–6480. [Google Scholar] [CrossRef]
- Suhail, S.; Hussain, R.; Khan, A.; Hong, C.S. On the role of hash-based signatures in quantum-safe internet of things: Current solutions and future directions. IEEE Internet Things J. 2020, 8, 1–17. [Google Scholar] [CrossRef]
- Cheng, C.; Lu, R.; Petzoldt, A.; Takagi, T. Securing the Internet of Things in a quantum world. IEEE Commun. Mag. 2017, 55, 116–120. [Google Scholar] [CrossRef]
- Ravi, P.; Howe, J.; Chattopadhyay, A.; Bhasin, S. Lattice-based key-sharing schemes: A survey. ACM Comput. Surv. 2021, 54, 1–39. [Google Scholar] [CrossRef]
- Koziel, B.; Azarderakhsh, R.; Kermani, M.M.; Jao, D. Post-quantum cryptography on FPGA based on isogenies on elliptic curves. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 64, 86–99. [Google Scholar] [CrossRef]
- Micciancio, D.; Regev, O. Lattice-based cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 147–191. [Google Scholar]
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-quantum lattice-based cryptography implementations: A survey. ACM Comput. Surv. 2019, 51, 1–41. [Google Scholar] [CrossRef]
- Tassa, T. Hierarchical threshold secret sharing. J. Cryptol. 2007, 20, 237–264. [Google Scholar] [CrossRef]
- Kurihara, J.; Kiyomoto, S.; Fukushima, K.; Tanaka, T. A new (k, n)-threshold secret sharing scheme and its extension. In Proceedings of the Information Security: 11th International Conference, ISC 2008, Taipei, Taiwan, 15–18 September 2008; Proceedings 11. Springer: Berlin/Heidelberg, Germany, 2008; pp. 455–470. [Google Scholar]
- Kumar, P.; Banerjee, K.; Singhal, N.; Kumar, A.; Rani, S.; Kumar, R.; Lavinia, C.A. Verifiable, Secure Mobile Agent Migration in Healthcare Systems Using a Polynomial-Based Threshold Secret Sharing Scheme with a Blowfish Algorithm. Sensors 2022, 22, 8620. [Google Scholar] [CrossRef] [PubMed]
- Hazay, C.; Mikkelsen, G.L.; Rabin, T.; Toft, T.; Nicolosi, A.A. Efficient RSA key generation and threshold paillier in the two-party setting. J. Cryptol. 2019, 32, 265–323. [Google Scholar] [CrossRef]
- Velumani, R.; Sudalaimuthu, H.; Choudhary, G.; Bama, S.; Jose, M.V.; Dragoni, N. Secured Secret sharing of QR codes based on nonnegative matrix factorization and regularized super resolution convolutional neural network. Sensors 2022, 22, 2959. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Li, L. A fully dynamic secret sharing scheme. Inf. Sci. 2019, 496, 42–52. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Tang, G.; Pang, B.; Chen, L.; Zhang, Z. Efficient Lattice-Based Threshold Signatures with Functional Interchangeability. IEEE Trans. Inf. Forensics Secur. 2023, 18, 4173–4187. [Google Scholar] [CrossRef]
- Rajabi, B.; Eslami, Z. A verifiable threshold secret sharing scheme based on lattices. Inf. Sci. 2019, 501, 655–661. [Google Scholar] [CrossRef]
- Regev, O. New lattice-based cryptographic constructions. J. ACM 2004, 51, 899–942. [Google Scholar] [CrossRef]
- Khalid, A.; McCarthy, S.; O’Neill, M.; Liu, W. Lattice-based cryptography for IoT in a quantum world: Are we ready? In Proceedings of the 2019 IEEE 8th International Workshop on Advances in Sensors and Interfaces (IWASI), Otranto, Italy, 13–14 June 2019; pp. 194–199. [Google Scholar]
- Pradhan, P.K.; Rakshit, S.; Datta, S. Lattice based cryptography: Its applications, areas of interest & future scope. In Proceedings of the 2019 3rd International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 27–29 March 2019; pp. 988–993. [Google Scholar]
- Wang, A.; Xiao, D.; Yu, Y. Lattice-based cryptosystems in standardisation processes: A survey. IET Inf. Secur. 2023, 17, 227–243. [Google Scholar] [CrossRef]
- Zheng, Z. Lattice-Based Cryptography. In Modern Cryptography Volume 1: A Classical Introduction to Informational and Mathematical Principle; Springer: Singapore, 2022; pp. 253–351. [Google Scholar]
- Albrecht, M.; Ducas, L. Lattice Attacks on NTRU and LWE: A History of Refinements. 2021. Available online: https://eprint.iacr.org/2021/799 (accessed on 5 January 2024).
- Bogdanov, D. Foundations and Properties of Shamir’s Secret Sharing Scheme Research Seminar in Cryptography; University of Tartu, Institute of Computer Science: Tartu, Estonia, 2007. [Google Scholar]
- Khorasgani, H.A.; Asaad, S.; Eghlidos, T.; Aref, M. A lattice-based threshold secret sharing scheme. In Proceedings of the 2014 11th International ISC Conference on Information Security and Cryptology, Tehran, Iran, 3–4 September 2014; pp. 173–179. [Google Scholar]
- Asaad, S.; Khorasgani, H.A.; Eghlidos, T.; Aref, M. Sharing secret using lattice construction. In Proceedings of the 7’th International Symposium on Telecommunications (IST’2014), Tehran, Iran, 9–11 September 2014; pp. 901–906. [Google Scholar]
- Steinfeld, R.; Pieprzyk, J.; Wang, H. Lattice-based threshold changeability for standard shamir secret-sharing schemes. IEEE Trans. Inf. Theory 2007, 53, 2542–2559. [Google Scholar] [CrossRef]
- Amroudi, A.N.; Zaghain, A.; Sajadieh, M. A verifiable (k, n, m)-threshold multi-secret sharing scheme based on ntru cryptosystem. Wirel. Pers. Commun. 2017, 96, 1393–1405. [Google Scholar] [CrossRef]
- Ogata, W.; Araki, T. Computationally secure verifiable secret sharing scheme for distributing many secrets. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2017, 100, 103–114. [Google Scholar] [CrossRef]
- Georgescu, A. A LWE-based secret sharing scheme. IJCA Spec. Issue Netw. Secur. Cryptogr. NSC 2011, 3, 27–29. [Google Scholar]
- Li, F.; Yan, J.; Zhu, S.; Hu, H. A Verifiable Multi-Secret Sharing Scheme Based on Short Integer Solution. Chin. J. Electron. 2023, 32, 556–563. [Google Scholar] [CrossRef]
- Hadian Dehkordi, M.; Ghasemi, R. A lightweight public verifiable multi secret sharing scheme using short integer solution. Wirel. Pers. Commun. 2016, 91, 1459–1469. [Google Scholar] [CrossRef]
- Steinfeld, R.; Pieprzyk, J.; Wang, H. Lattice-based threshold-changeability for standard CRT secret-sharing schemes. Finite Fields Their Appl. 2006, 12, 653–680. [Google Scholar] [CrossRef]
- El Bansarkhani, R.; Meziani, M. An efficient lattice-based secret sharing construction. In Information Security Theory and Practice. Security, Privacy and Trust in Computing Systems and Ambient Intelligent Ecosystems, Proceedings of the 6th IFIP WG 11.2 International Workshop, WISTP 2012, Egham, UK, 20–22 June 2012; Proceedings 6; Springer: Berlin/Heidelberg, Germany, 2012; pp. 160–168. [Google Scholar]
- Kiamari, N.; Hadian, M.; Mashhadi, S. Non-interactive verifiable LWE-based multi secret sharing scheme. Multimed. Tools Appl. 2023, 82, 22175–22187. [Google Scholar] [CrossRef]
- Pilaram, H.; Eghlidos, T. An efficient lattice based multi-stage secret sharing scheme. IEEE Trans. Dependable Secur. Comput. 2015, 14, 2–8. [Google Scholar] [CrossRef]
- Pilaram, H.; Eghlidos, T. A lattice-based changeable threshold multi-secret sharing scheme and its application to threshold cryptography. Sci. Iran. 2017, 24, 1448–1457. [Google Scholar] [CrossRef]
- Bu, S.; Zhou, H. A secret sharing scheme based on NTRU algorithm. In Proceedings of the 2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009; pp. 1–4. [Google Scholar]
- Yang, J.; Fu, F.W. Post-quantum Multi-stage Secret Sharing Schemes using Inhomogeneous Linear Recursion and Ajtai’s Function. arXiv 2022, arXiv:2202.09026. [Google Scholar]
- Liu, Q.; Gao, S.; Xu, L.; Yue, W.; Zhang, C.; Kan, H.; Li, Y.; Shen, G. Nanostructured perovskites for nonvolatile memory devices. Chem. Soc. Rev. 2022, 51, 3341–3379. [Google Scholar] [CrossRef]
- Sehrawat, V.S.; Yeo, F.Y.; Desmedt, Y. Extremal set theory and LWE based access structure hiding verifiable secret sharing with malicious-majority and free verification. Theor. Comput. Sci. 2021, 886, 106–138. [Google Scholar] [CrossRef]
- Chor, B.; Goldwasser, S.; Micali, S.; Awerbuch, B. Verifiable secret sharing and achieving simultaneity in the presence of faults. In Proceedings of the 26th Annual Symposium on Foundations of Computer Science (sfcs 1985), Portland, OR, USA, 21–23 October 1985; pp. 383–395. [Google Scholar]
- Stadler, M. Publicly verifiable secret sharing. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Saragossa, Spain, 12–16 May 1996; Springer: Berlin/Heidelberg, Germany, 1996; pp. 190–199. [Google Scholar]
- Pedersen, T.P. Non-interactive and information-theoretic secure verifiable secret sharing. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1991; Springer: Berlin/Heidelberg, Germany, 1991; pp. 129–140. [Google Scholar]
- Feldman, P. A practical scheme for non-interactive verifiable secret sharing. In Proceedings of the 28th Annual Symposium on Foundations of Computer Science (sfcs 1987), Los Angeles, CA, USA, 12–14 October 1987; pp. 427–438. [Google Scholar]
- Lyubashevsky, V.; Micciancio, D. Generalized compact knapsacks are collision resistant. In Proceedings of the International Colloquium on Automata, Languages, and Programming, Venice, Italy, 10–14 July 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 144–155. [Google Scholar]
- Gentry, C.; Halevi, S.; Lyubashevsky, V. Practical non-interactive publicly verifiable secret sharing with thousands of parties. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2022; Springer: Cham, Switzerland, 2022; pp. 458–487. [Google Scholar]
- Sehrawat, V.S.; Desmedt, Y. Access structure hiding secret sharing from novel set systems and vector families. In Proceedings of the International Computing and Combinatorics Conference, Atlanta, GA, USA, 29–31 August 2020; Springer: Cham, Switzerland, 2020; pp. 246–261. [Google Scholar]
- He, J.; Dawson, E. Multistage secret sharing based on one-way function. Electron. Lett. 1994, 30, 1591–1592. [Google Scholar] [CrossRef]
- Mashhadi, S.; Dehkordi, M.H. Two verifiable multi secret sharing schemes based on nonhomogeneous linear recursion and LFSR public-key cryptosystem. Inf. Sci. 2015, 294, 31–40. [Google Scholar] [CrossRef]
- Mashhadi, S. New multi-stage secret sharing in the standard model. Inf. Process. Lett. 2017, 127, 43–48. [Google Scholar] [CrossRef]
- Chen, D.; Lu, W.; Xing, W.; Wang, N. An efficient verifiable threshold multi-secret sharing scheme with different stages. IEEE Access 2019, 7, 107104–107110. [Google Scholar] [CrossRef]
- Harn, L. Efficient sharing (broadcasting) of multiple secrets. IEE Proc.-Comput. Digit. Tech. 1995, 142, 237–240. [Google Scholar] [CrossRef]
- Hadian Dehkordi, M.; Mashhadi, S.; Oraei, H. A proactive multi stage secret sharing scheme for any given access structure. Wirel. Pers. Commun. 2019, 104, 491–503. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, B.; Cheng, X.; Binh, H.T.T.; Yu, S. PoisonGAN: Generative poisoning attacks against federated learning in edge computing systems. IEEE Internet Things J. 2020, 8, 3310–3322. [Google Scholar] [CrossRef]
- Lyubashevsky, V. Lattice-based identification schemes secure under active attacks. In Proceedings of the International Workshop on Public Key Cryptography, Barcelona, Spain, 9–12 March 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 162–179. [Google Scholar]
- Xu, P.; Hu, M.; Chen, T.; Wang, W.; Jin, H. Laf: Lattice-based and communication-efficient federated learning. IEEE Trans. Inf. Forensics Secur. 2022, 17, 2483–2496. [Google Scholar] [CrossRef]
- Martin, K.M.; Safavi-Naini, R.; Wang, H. Bounds and techniques for efficient redistribution of secret shares to new access structures. Comput. J. 1999, 42, 638–649. [Google Scholar] [CrossRef]
- Zhang, Z.; Chee, Y.M.; Ling, S.; Liu, M.; Wang, H. Threshold changeable secret sharing schemes revisited. Theor. Comput. Sci. 2012, 418, 106–115. [Google Scholar] [CrossRef]
- Lou, T.; Tartary, C. Analysis and design of multiple threshold changeable secret sharing schemes. In Proceedings of the Cryptology and Network Security: 7th International Conference, CANS 2008, Hong Kong, China, 2–4 December 2008; Proceedings 7. Springer: Berlin/Heidelberg, Germany, 2008; pp. 196–213. [Google Scholar]
- Nojoumian, M.; Stinson, D.R. On dealer-free dynamic threshold schemes. Adv. Math. Commun. 2013, 7, 39–56. [Google Scholar] [CrossRef]
- Desmedt, Y. Society and group oriented cryptography: A new concept. In Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Santa Barbara, CA, USA, 16–20 August 1987; Springer: Berlin/Heidelberg, Germany, 1988; pp. 120–127. [Google Scholar]
- Bendlin, R.; Damgård, I. Threshold decryption and zero-knowledge proofs for lattice-based cryptosystems. In Proceedings of the Theory of Cryptography Conference, Zurich, Switzerland, 9–11 February 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 201–218. [Google Scholar]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. J. ACM 2009, 56, 1–40. [Google Scholar] [CrossRef]
- Singh, K.; Rangan, C.P.; Banerjee, A. Lattice Based Efficient Threshold Public Key Encryption Scheme. J. Wirel. Mob. Netw. Ubiquitous Comput. Dependable Appl. 2013, 4, 93–107. [Google Scholar]
- Singh, K.; Rangan, C.P.; Banerjee, A. Lattice-based identity-based resplittable threshold public key encryption scheme. Int. J. Comput. Math. 2016, 93, 289–307. [Google Scholar] [CrossRef]
- Zhang, G.; Qin, J. Lattice-based threshold cryptography and its applications in distributed cloud computing. Int. J. High Perform. Comput. Netw. 2015, 8, 176–185. [Google Scholar] [CrossRef]
- Shamir, A. Identity-based cryptosystems and signature schemes. In Proceedings of the Advances in Cryptology: Proceedings of the CRYPTO 84, Santa Barbara, CA, USA, 19–22 August 1984; Springer: Berlin/Heidelberg, Germany, 1985; pp. 47–53. [Google Scholar]
- Boneh, D.; Franklin, M. Identity-based encryption from the Weil pairing. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 213–229. [Google Scholar]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for hard lattices and new cryptographic constructions. In Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; pp. 197–206. [Google Scholar]
- Cash, D.; Hofheinz, D.; Kiltz, E.; Peikert, C. Bonsai trees, or how to delegate a lattice basis. J. Cryptol. 2012, 25, 601–639. [Google Scholar] [CrossRef]
- Bendlin, R.; Krehbiel, S.; Peikert, C. How to share a lattice trapdoor: Threshold protocols for signatures and (H) IBE. In Proceedings of the Applied Cryptography and Network Security: 11th International Conference, ACNS 2013, Banff, AB, Canada, 25–28 June 2013; Proceedings 11. Springer: Berlin/Heidelberg, Germany, 2013; pp. 218–236. [Google Scholar]
- Desmedt, Y.; Frankel, Y. Shared generation of authenticators and signatures. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1991; Springer: Berlin/Heidelberg, Germany, 1991; pp. 457–469. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J.H. NSS: An NTRU lattice-based signature scheme. In Proceedings of the Advances in Cryptology—EUROCRYPT 2001: International Conference on the Theory and Application of Cryptographic Techniques, Innsbruck, Austria, 6–10 May 2001; Proceedings 20. Springer: Berlin/Heidelberg, Germany, 2001; pp. 211–228. [Google Scholar]
- Lyubashevsky, V. Lattice signatures without trapdoors. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 738–755. [Google Scholar]
- Cayrel, P.L.; Lindner, R.; Rückert, M.; Silva, R. A lattice-based threshold ring signature scheme. In Proceedings of the International Conference on Cryptology and Information Security in Latin America, Puebla, Mexico, 8–11 August 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 255–272. [Google Scholar]
- Feng, T.; Gao, Y.; Ma, J. Changeable threshold signature scheme based on lattice theory. In Proceedings of the 2010 International Conference on E-Business and E-Government, Guangzhou, China, 7–9 May 2010; pp. 1311–1315. [Google Scholar]
- Nguyen, P.Q.; Regev, O. Learning a parallelepiped: Cryptanalysis of GGH and NTRU signatures. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, St. Petersburg, Russia, 28 May–1 June 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 271–288. [Google Scholar]
- Damgård, I.; Orlandi, C.; Takahashi, A.; Tibouchi, M. Two-round n-out-of-n and multi-signatures and trapdoor commitment from lattices. J. Cryptol. 2022, 35, 14. [Google Scholar] [CrossRef]
- Leevik, A.; Davydov, V.; Bezzateev, S. Threshold Lattice-Based Signature Scheme for Authentication by Wearable Devices. Cryptography 2023, 7, 33. [Google Scholar] [CrossRef]
- Zhang, J.; Ge, C.; Hu, F.; Chen, B. RobustFL: Robust federated learning against poisoning attacks in industrial IoT systems. IEEE Trans. Ind. Inform. 2021, 18, 6388–6397. [Google Scholar] [CrossRef]
- Raman, R.K.; Varshney, L.R. Distributed storage meets secret sharing on the blockchain. In Proceedings of the 2018 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 11–16 February 2018; pp. 1–6. [Google Scholar]
- Mesnager, S.; Sınak, A.; Yayla, O. Threshold-based post-quantum secure verifiable multi-secret sharing for distributed storage blockchain. Mathematics 2020, 8, 2218. [Google Scholar] [CrossRef]
- Yu, H.; Wang, H. Lattice-Based Threshold Signcryption for Blockchain Oracle Data Transmission. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11057–11065. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).