Hardware-in-the-Loop Simulation of Flywheel Energy Storage Systems for Power Control in Wind Farms
Abstract
1. Introduction
2. Structure of Wind Farms with FESSs
3. The Structure of HIL Testing Systems
4. Modeling of FESSs
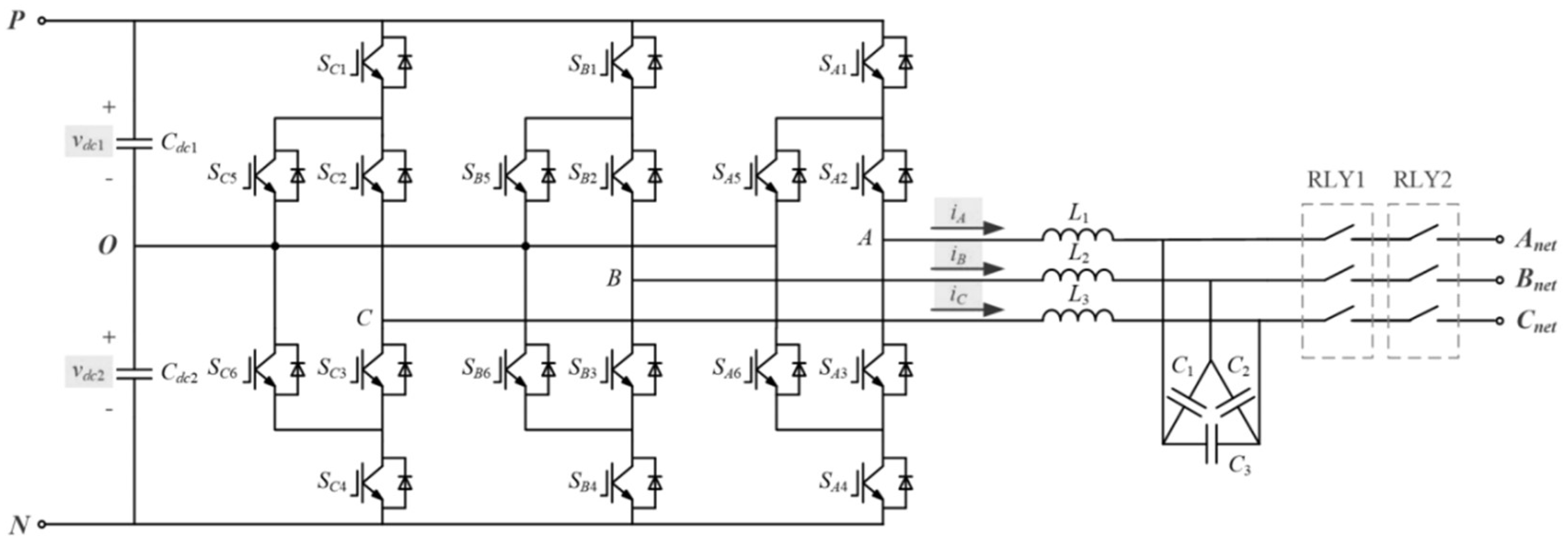
4.1. Modeling of the Main Circuit
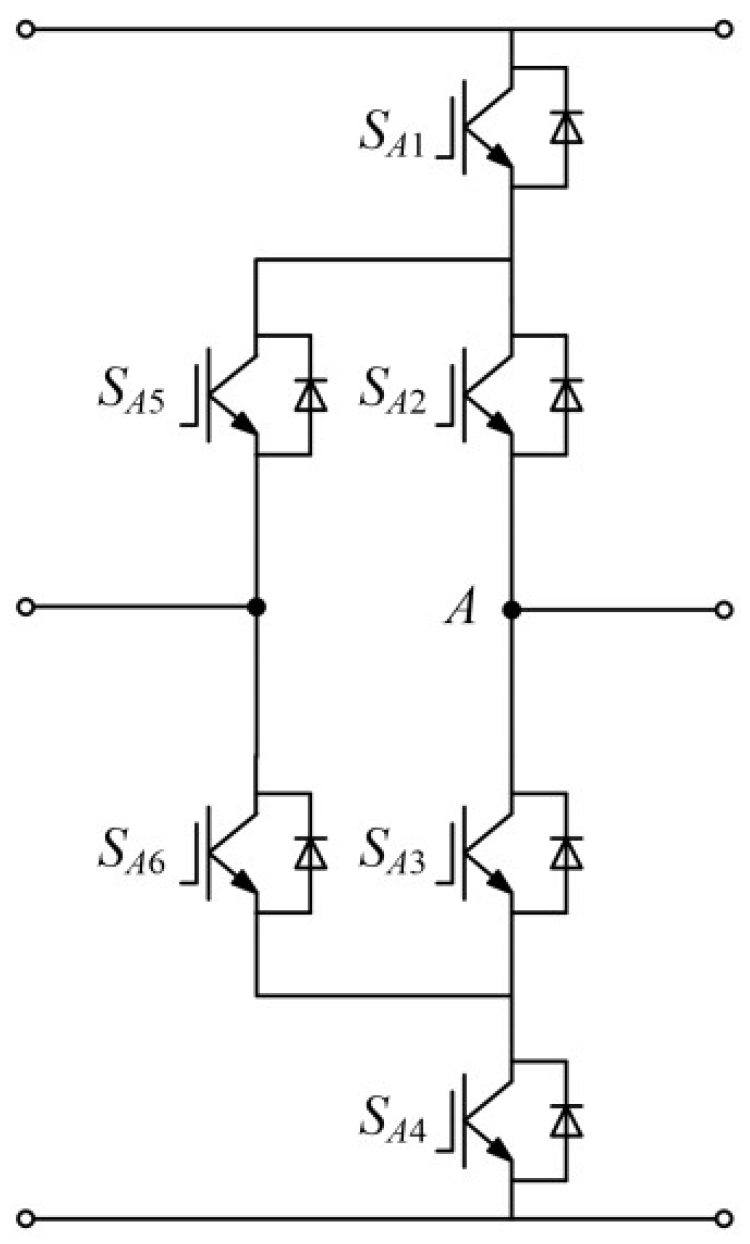
4.1.1. Modeling of ANPC Topology
- Step 1: Let the circuit time interval (simulation step) be 1 × 10−8 s.
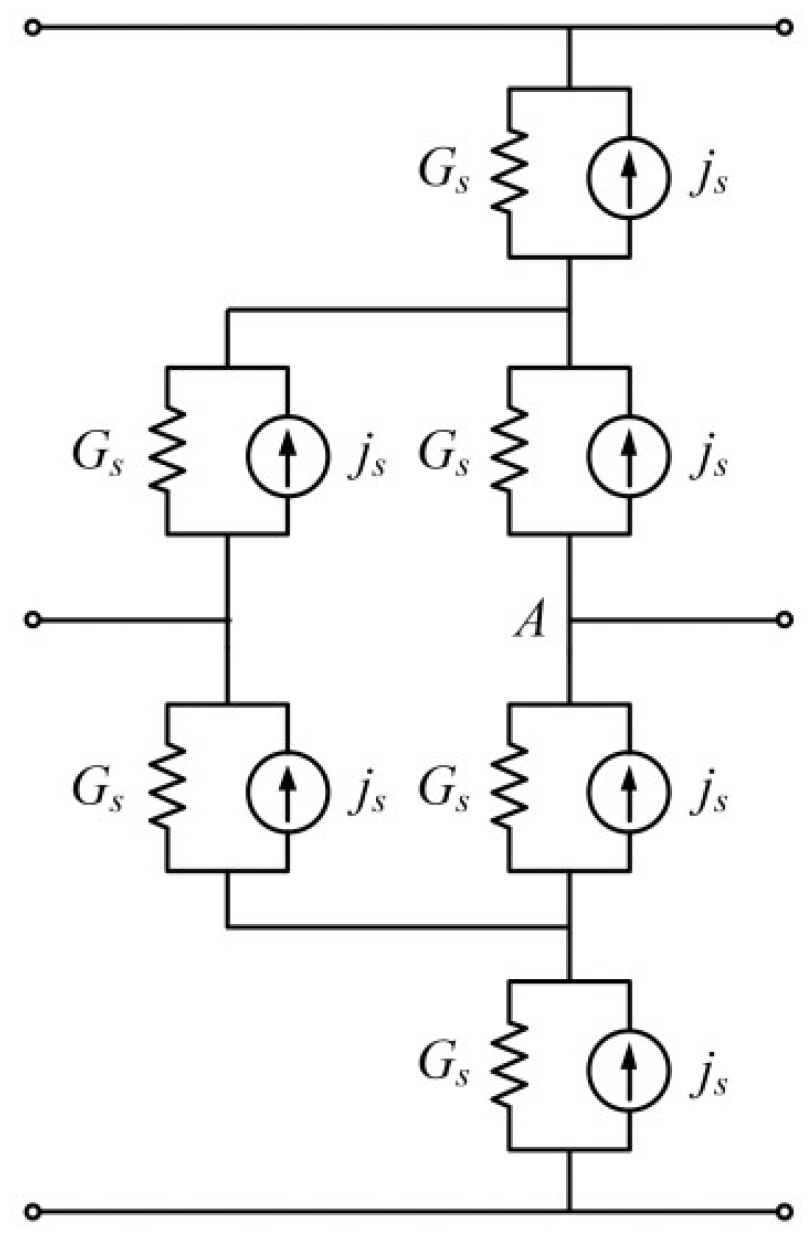
- Step 2: At each time interval, a single IGBT is replaced with its discrete model.
- Step 3: According to the discrete model, the adjoint network corresponding to the original circuit is constructed.
- Step 4: According to the single IGBT equivalent circuit, the equivalent circuit of the A-phase bridge arm is obtained, as shown in Figure 6.
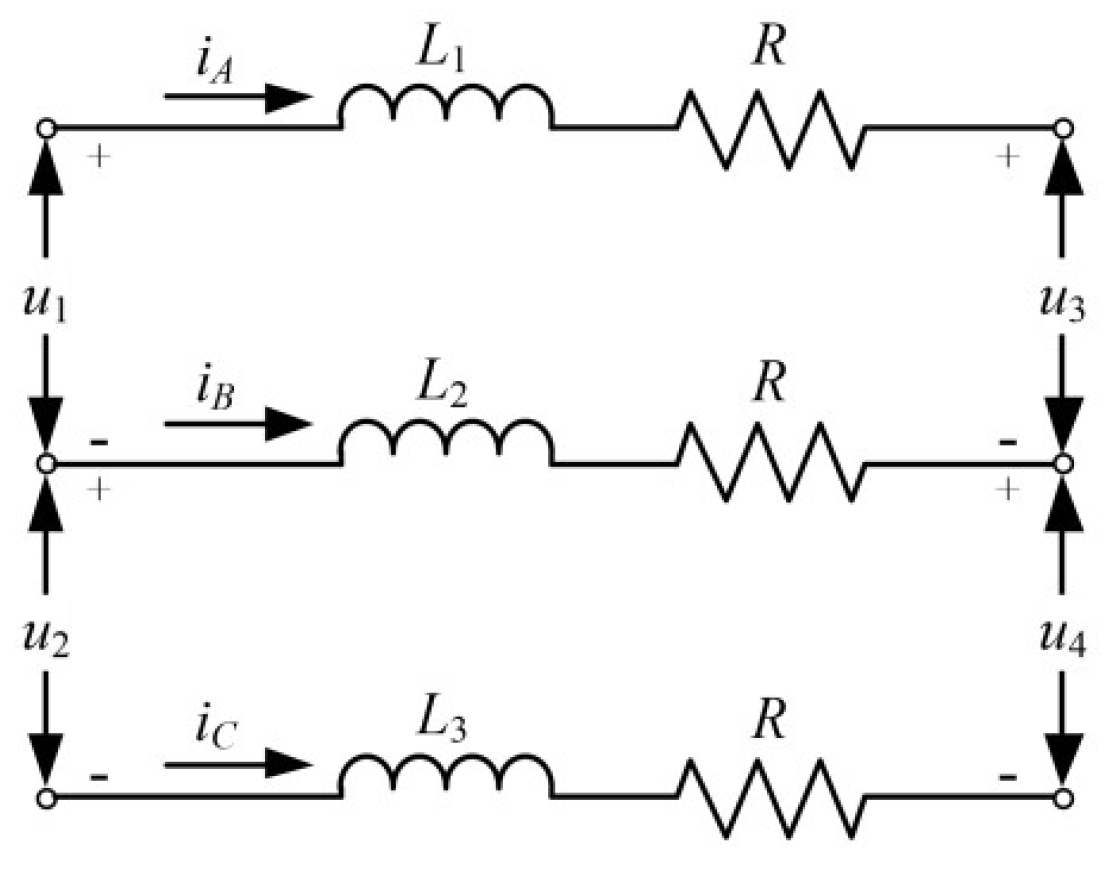
4.1.2. Modeling of Inductive Filter
4.1.3. Modeling of the Capacitive Filter
4.1.4. Modeling of the DC Support Capacitor
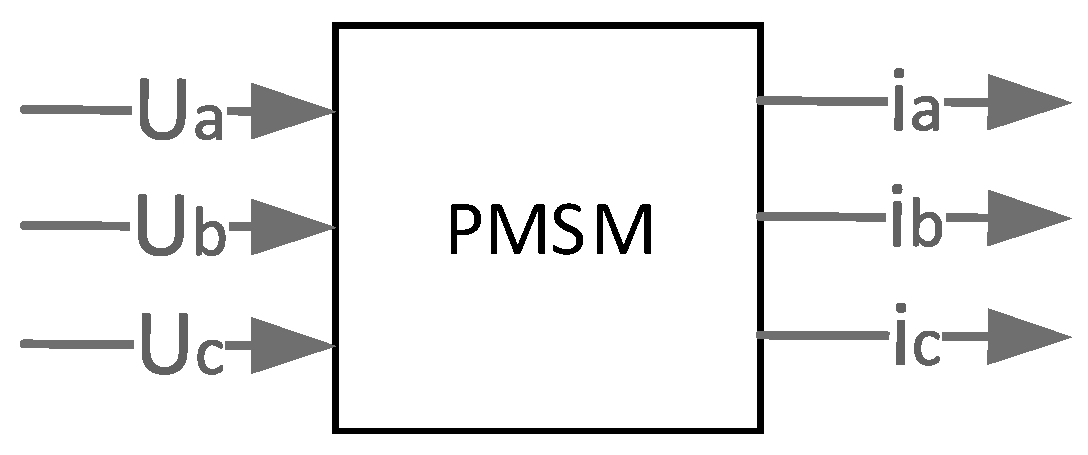
4.2. Modeling of PMSMs
- Step 1: The finite element method is used to obtain the relation curve of , , and , changing with and , respectively. It should be noted that the finite element calculation method is the work of other members of the team, and the specific process is not described in this paper.
- Step 2: Using the relationship curve obtained in step 1, the three parameters , , and are obtained by looking up the table according to the current values and .
- Step 3: The nonlinear model of the PMSM is obtained by substituting parameters , , and into Equation (12).
4.3. Modeling of Flywheel
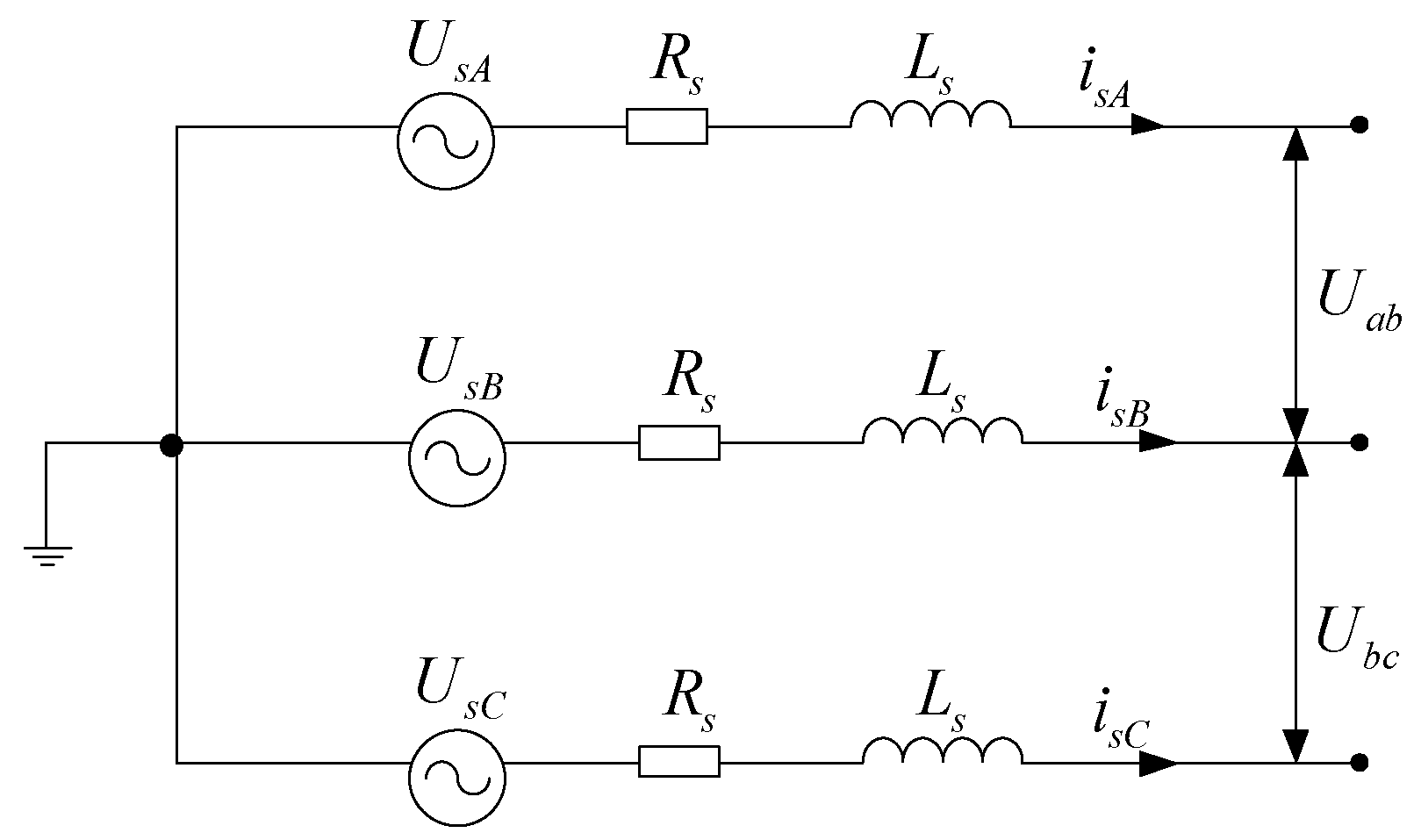
5. Modeling of Power Grids and Wind Farms
- Modeling of power grids
- Modeling of wind farms
6. HIL Testing System Experiment
- The correctness of the motor-side models in FESSs;
- The correctness of the network-side models in FESSs;
- The effectiveness of the power control function of FESSs for wind farms.
6.1. Verification of Motor-Side Models
6.2. Verification of Network-Side Models
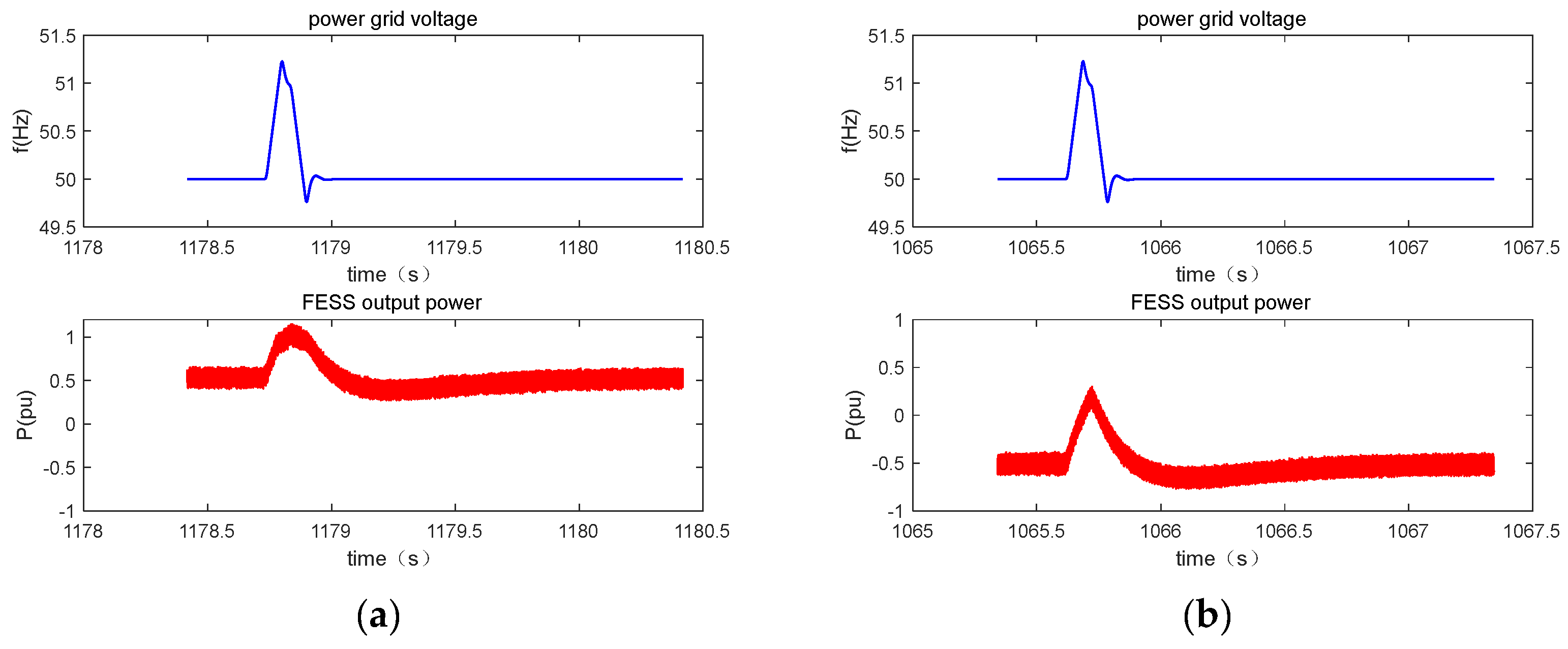
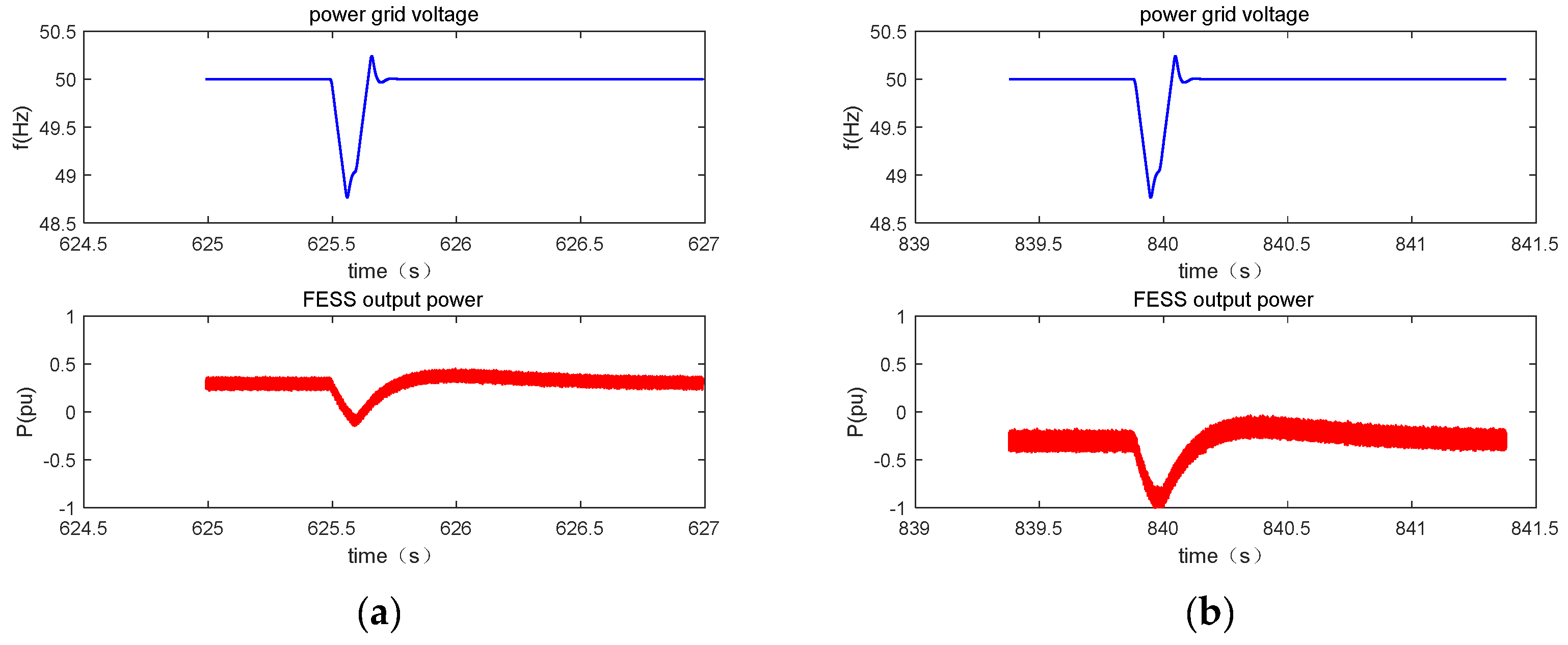
- Positive disturbance
- Negative disturbance
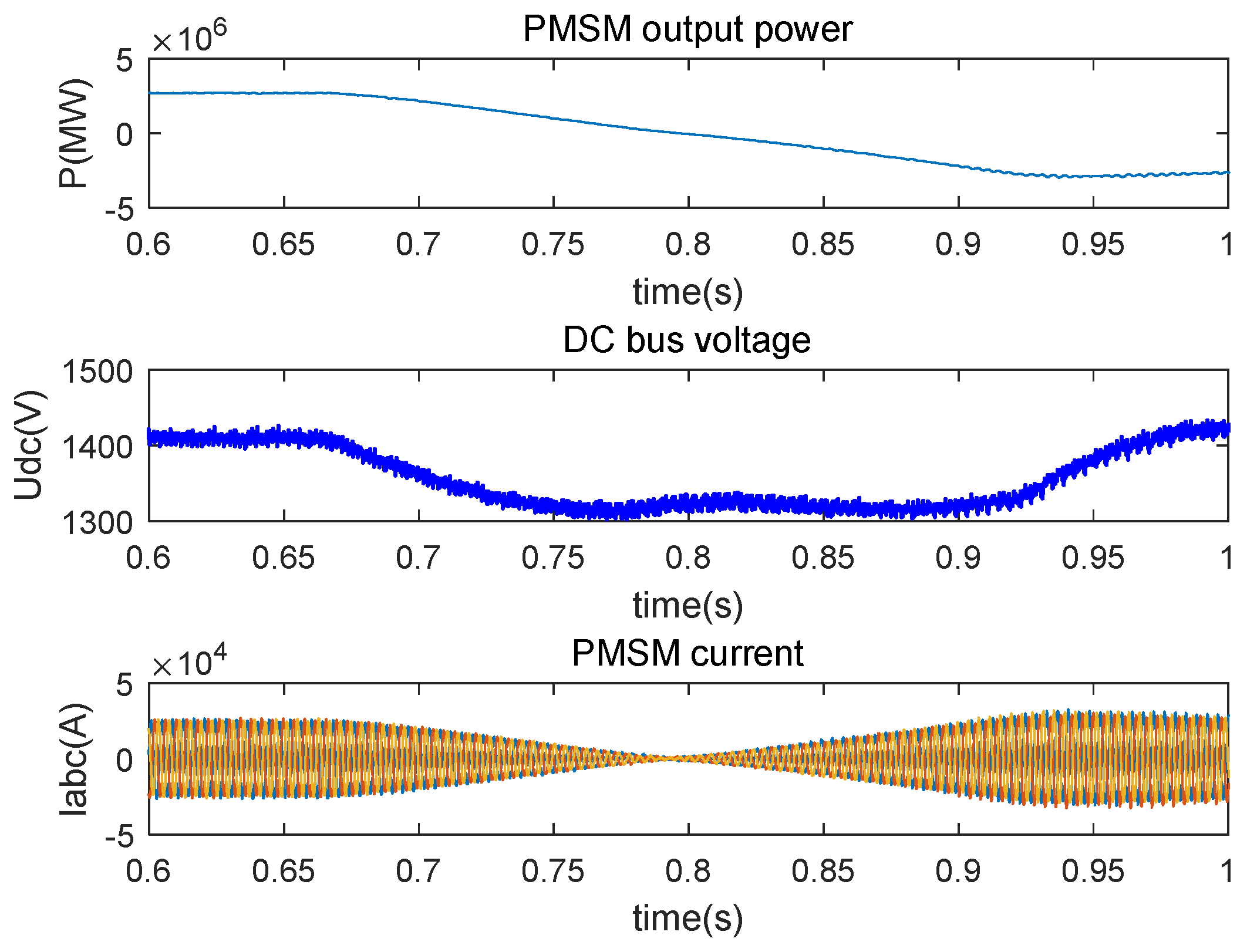
6.3. Verification of Power Control in Wind Farms
7. Conclusions
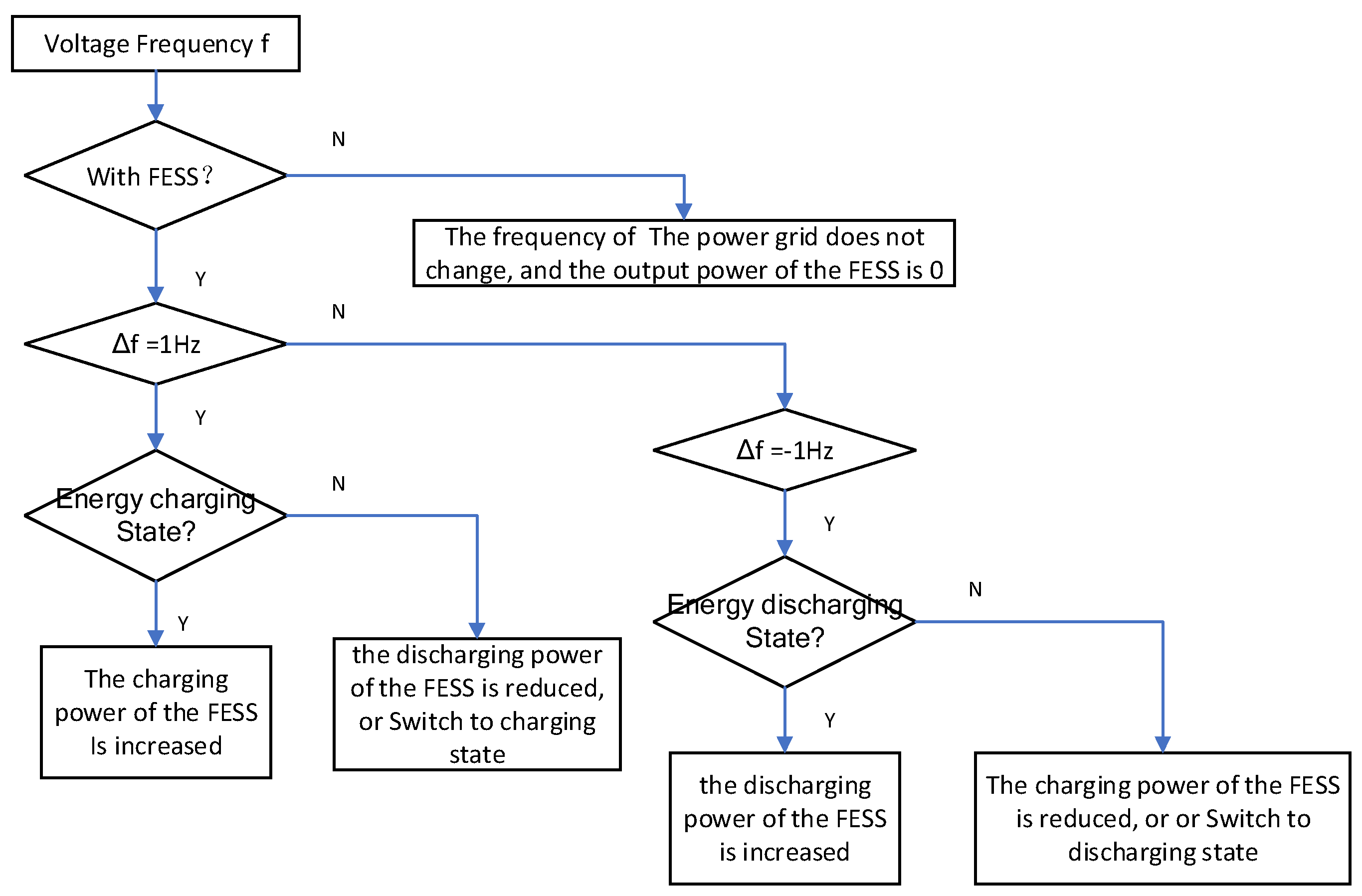
- The constructed FESS model can realize the switching of three states—energy charging, energy discharging, and energy retention—which is in agreement with the expected theory.
- The output power of FESS can be adjusted according to the voltage fluctuations of the power grid, and finally, the rapid fluctuations of the output power of the wind farm can be smoothed via the FESS, which is conducive to improving the wind farm’s grid connection rate.
- The smoothing effect on wind farm output power indicates the reliability of the FESS algorithm in this experiment.
- In general, the HIL testing system built in this article can provide a more convenient environment for the optimization of the team’s FESS control algorithm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| FESS | Flywheel energy storage system |
| HIL | Hardware-in-the-loop |
| PMSM | Permanent magnet synchronous motor |
| AC | Alternating current |
| IGBT | Insulate gate bipolar transistor |
| ANPC | Active neutral point clamped |
| PLL | Phase-locked loop |
| Electrical angular velocity of the PMSM | |
| Angular position of the PMSM | |
| Voltage angle of the power grid | |
| Three-phase stator current of the PMSM | |
| Three-phase phase voltage of the PMSM | |
| Three-phase current of the network-side inverter | |
| Three-phase voltage of the network-side inverter | |
| Three-phase voltage of the power grid | |
| PWM control signals of the motor-side inverter | |
| PWM control signals of the network-side inverter | |
| The d-axis current of the network-side inverter | |
| The q-axis current of the network-side inverter | |
| The given d-axis voltage of the network-side inverter | |
| The given q-axis voltage of the network-side inverter | |
| The d-axis stator current of the PMSM | |
| The q-axis stator current of the PMSM | |
| The given d-axis stator current of the PMSM | |
| The given q-axis stator current of the PMSM | |
| The given active power of the PMSM | |
| The given active power of the wind farm | |
| The given reactive power of the PMSM | |
| The given torque of the PMSM | |
| The voltage of the DC bus |
References
- The Law of the People’s Republic of China on Statistics Bulletin of the National Economy and Social Development in 2023. Available online: https://www.gov.cn/lianbo/bumen/202402/content_6934935.htm (accessed on 19 August 2024).
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A.; Ramadan, M. Critical Review of Flywheel Energy Storage System. Energies 2021, 14, 2159. [Google Scholar] [CrossRef]
- Xu, K.; Guo, Y.; Lei, G.; Zhu, J. A Review of Flywheel Energy Storage System Technologies. Energies 2023, 16, 6462. [Google Scholar] [CrossRef]
- Ji, W.; Hong, F.; Zhao, Y.; Liang, L.; Du, H.; Hao, J.; Fang, F.; Liu, J. Applications of flywheel energy storage system on load frequency regulation combined with various power generations: A review. Renew. Energy 2024, 223, 119975. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.C.; Yong, C.X. Modeling and Application of a Rectifier Transformer with Primary Winding in Series in A Metallurgical Rolling Mill System. Mechatron. Syst. Control 2023, 51, 182–192. [Google Scholar] [CrossRef]
- Zhang, J.W.; Wang, Y.H.; Liu, G.C.; Tian, G.Z. A review of control strategies for flywheel energy storage system and a case study with matrix converter. Energy Rep. 2022, 8, 3948–3963. [Google Scholar] [CrossRef]
- Floris, A.; Porru, M.; Damiano, A.; Serpi, A. Energy Management and Control System Design of an Integrated Flywheel Energy Storage System for Residential Users. Appl. Sci. 2021, 11, 4615. [Google Scholar] [CrossRef]
- Wang, B.; Yu, X.; Yang, X.; Zhang, D. Control strategy for high speed flywheel energy storage system based on voltage threshold of DC1500 V transit transportation traction grid. Energy Rep. 2022, 8, 640–647. [Google Scholar] [CrossRef]
- Lei, M.; Meng, K.; Feng, H.; Bai, J.; Jiang, H.; Zhang, Z. Flywheel energy storage controlled by model predictive control to achieve smooth short-term high-frequency wind power. J. Energy Storage 2023, 63, 106949. [Google Scholar] [CrossRef]
- Wang, K.; Tian, L.; Li, N.; Yin, X.; Han, L.; Jiang, T. Adaptive comprehensive control strategy for primary frequency regulation of coal-fired units assisted by flywheel energy storage system. J. Phys. Conf. Ser. 2023, 1, 2592. [Google Scholar] [CrossRef]
- Zheng, X.; Wu, Z.; Jia, Y.; Zhang, J.; Yang, P.; Zhang, Z. Fault-Tolerant Control Strategy for Phase Loss of the Flywheel Energy Storage Motor. Electronics 2023, 12, 3076. [Google Scholar] [CrossRef]
- Song, G.; Wu, Z.; Zheng, X.; Zhang, J.; Yang, P.; Zhang, Z. Control Strategy of Flywheel Energy Storage System for Improved Model Reference Adaptive System Based on Tent-Sparrow Search Algorithm. Electronics 2024, 13, 2699. [Google Scholar] [CrossRef]
- Qin, R.; Chen, J.; Li, Z.; Teng, W.; Liu, Y. Simulation of Secondary Frequency Modulation Process of Wind Power with Auxiliary of Flywheel Energy Storage. Sustainability 2023, 15, 11832. [Google Scholar] [CrossRef]
- Song, H.H.; Tian, D. Study on Hardware-in-the-loop-simulation of Wind Power Based on dSPACE. In Proceedings of the 2010 Second International Conference on Computational Intelligence and Natural Computing (CINC), Wuhan, China, 13–14 September 2010. [Google Scholar]
- Jia, Y.; Wu, Z.; Zhang, J.; Yang, P.; Zhang, Z. Control Strategy of Flywheel Energy Storage System Based on Primary Frequency Modulation of Wind Power. Energies 2022, 15, 1850. [Google Scholar] [CrossRef]
- Young, L.; Zheng, X.; Gao, E. Numerical Modeling and Application of Horizontal-Axis Wind Turbine Arrays in Large Wind Farms. Wind 2023, 3, 459–484. [Google Scholar] [CrossRef]
- Simani, S.; Farsoni, S.; Turhan, C. Hardware-In-The-Loop Assessment of a Fault Tolerant Fuzzy Control Scheme for an Offshore Wind Farm Simulator. IFAC PapersOnLine 2022, 55, 390–395. [Google Scholar] [CrossRef]
- Kikusato, H.; Ustun, T.S.; Suzuki, M.; Sugahara, S.; Hashimoto, J.; Otani, K.; Ikeda, N.; Komuro, I.; Yokoi, H.; Takahashi, K. Flywheel energy storage system based microgrid controller design and PHIL testing. Energy Rep. 2022, 8, 470–475. [Google Scholar] [CrossRef]
- Karrari, S.; De Carne, G.; Noe, M. Adaptive droop control strategy for Flywheel Energy Storage Systems: A Power Hardware-in-the-Loop validation. Electr. Power Syst. Res. 2022, 212, 108300. [Google Scholar] [CrossRef]
- Martínez-Nolasco, J.; Sámano-Ortega, V.; Botello-Álvarez, J.; Padilla-Medina, J.; Martínez-Nolasco, C.; Bravo-Sánchez, M. Development of a Hardware-in-the-Loop Platform for the Validation of a Small-Scale Wind System Control Strategy. Energies 2023, 16, 7813. [Google Scholar] [CrossRef]
- Venturini, S.; Cavallaro, S.P.; Vigliani, A. Windage loss characterisation for flywheel energy storage system: Model and experimental validation. Energy 2024, 307, 132641. [Google Scholar] [CrossRef]
- Huang, M.; Wang, Z.; Guo, Z.; Zeng, Q.; Niu, Y. Wind Tunnel Hardware-in-the-loop Simulation Techniques for Flight Control System Evaluation. In Proceedings of the 2017 2nd International Conference on Control Automation and Artificial Intelligence (CAAI), Sanya, China, 25–26 June 2017. [Google Scholar]
- Mathivanan, V.; Ramabadran, R.; Nagappan, B.; Devarajan, Y. Assessment of photovoltaic powered flywheel energy storage system for power generation and conditioning. Sol. Energy 2023, 264, 112045. [Google Scholar] [CrossRef]
- Wu, X.; Meng, Y.; Hu, S.; Song, B. Hardware-In-the-Loop Simulation of Wind Turbine Based on 6 Degree-of-Freedom Load. In Proceedings of the 2017 International Electrical and Energy Conference (CIEEC), Beijing, China, 25–27 October 2017. [Google Scholar]







| Number | Parameter | Value |
|---|---|---|
| 1 | Rated frequency of power grid | 50 Hz |
| 2 | Rated voltage of power grid | 35 kV |
| 3 | Rated power of PMSM | 4 MW |
| 4 | Rated voltage of PMSM | 3AC 850 V |
| 5 | Rated current of PMSM | 2900 A |
| 6 | Rated frequency of PMSM | 300 Hz |
| 7 | Rated speed of PMSM | 5400 rpm |
| 8 | Rated voltage of FESS | 1140 V |
| 9 | Electric storage capacity of FESS | 125 kWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhao, Q. Hardware-in-the-Loop Simulation of Flywheel Energy Storage Systems for Power Control in Wind Farms. Electronics 2024, 13, 3610. https://doi.org/10.3390/electronics13183610
Yang L, Zhao Q. Hardware-in-the-Loop Simulation of Flywheel Energy Storage Systems for Power Control in Wind Farms. Electronics. 2024; 13(18):3610. https://doi.org/10.3390/electronics13183610
Chicago/Turabian StyleYang, Li, and Qiaoni Zhao. 2024. "Hardware-in-the-Loop Simulation of Flywheel Energy Storage Systems for Power Control in Wind Farms" Electronics 13, no. 18: 3610. https://doi.org/10.3390/electronics13183610
APA StyleYang, L., & Zhao, Q. (2024). Hardware-in-the-Loop Simulation of Flywheel Energy Storage Systems for Power Control in Wind Farms. Electronics, 13(18), 3610. https://doi.org/10.3390/electronics13183610






