Multi-Objective Parameter Configuration Optimization of Hydrogen Fuel Cell Hybrid Power System for Locomotives
Abstract
1. Introduction
2. Fuel Cell Hybrid Power System Design
2.1. Locomotive Hybrid Power System Topology
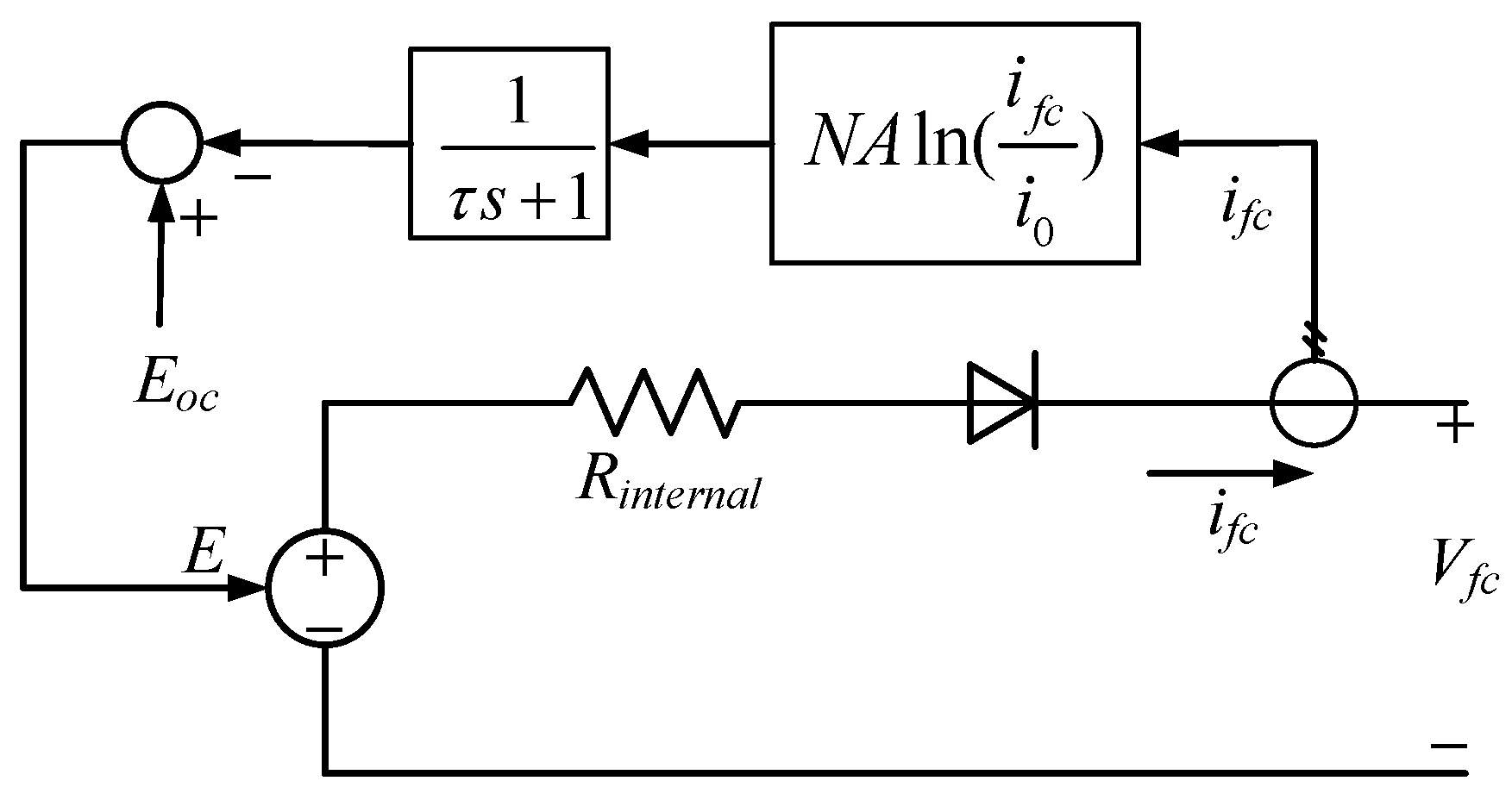
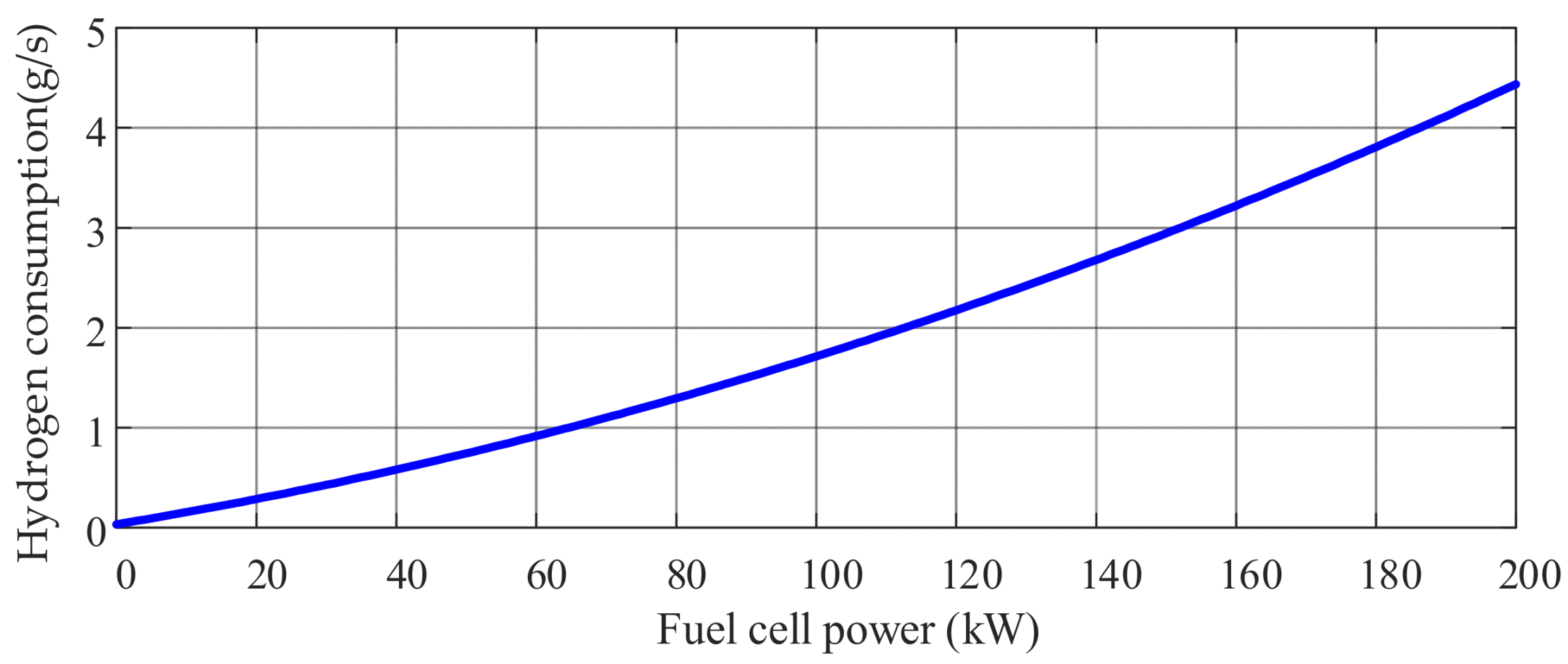
2.1.1. Fuel Cell Modeling
2.1.2. Lithium Battery Models
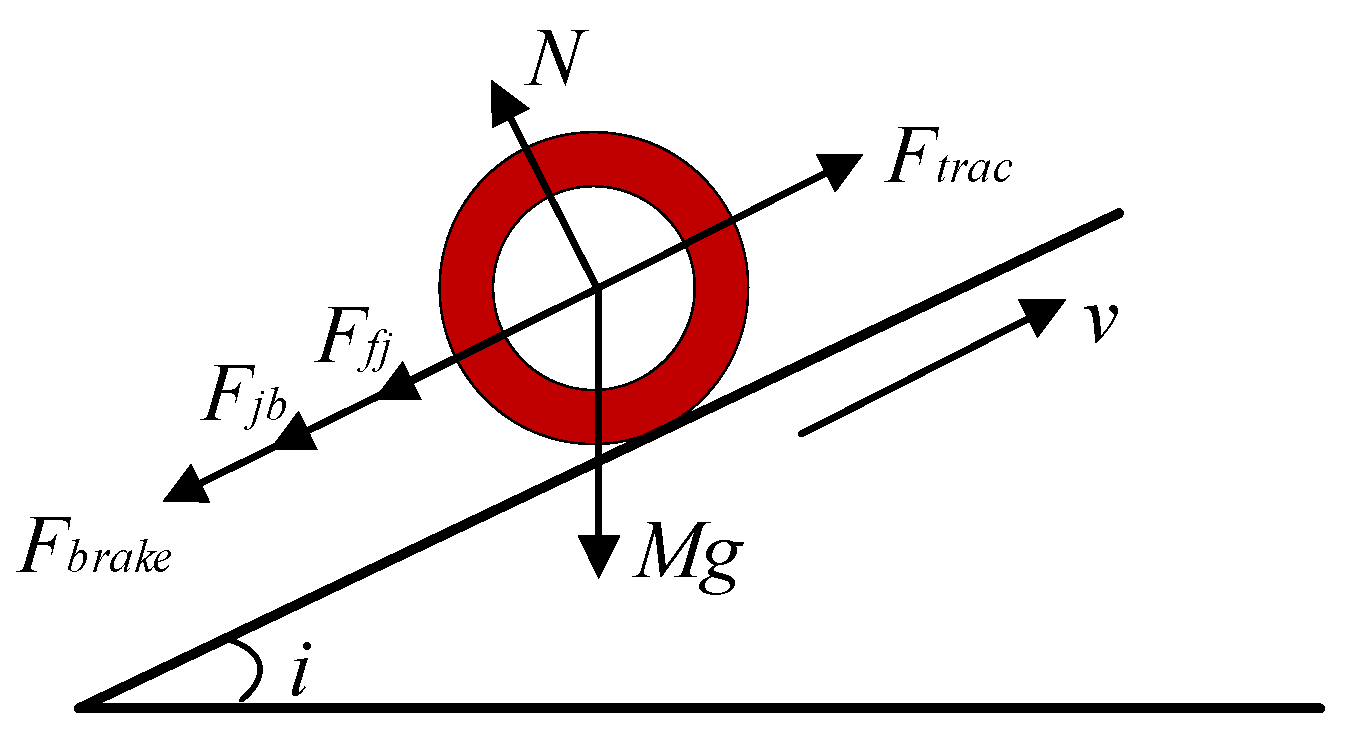
2.2. Dynamic Modeling of Shunting Locomotives
| Parameter | Value |
|---|---|
| Gauge | 1435 mm |
| Axial | C0–C0 |
| Maximum operating speed | 100 km/h |
| Axle weight | 25 t |
| Maximum starting tractive effort | 560 kN |
| Maximum electric braking power | 300 kN |
| Auxiliary system power | 100 kW |
| Transmission efficiency | 0.98 |
| Inverter efficiency | 0.98 |
| DC/DC efficiency | 0.95 |
2.2.1. Locomotive Traction Braking Characteristics
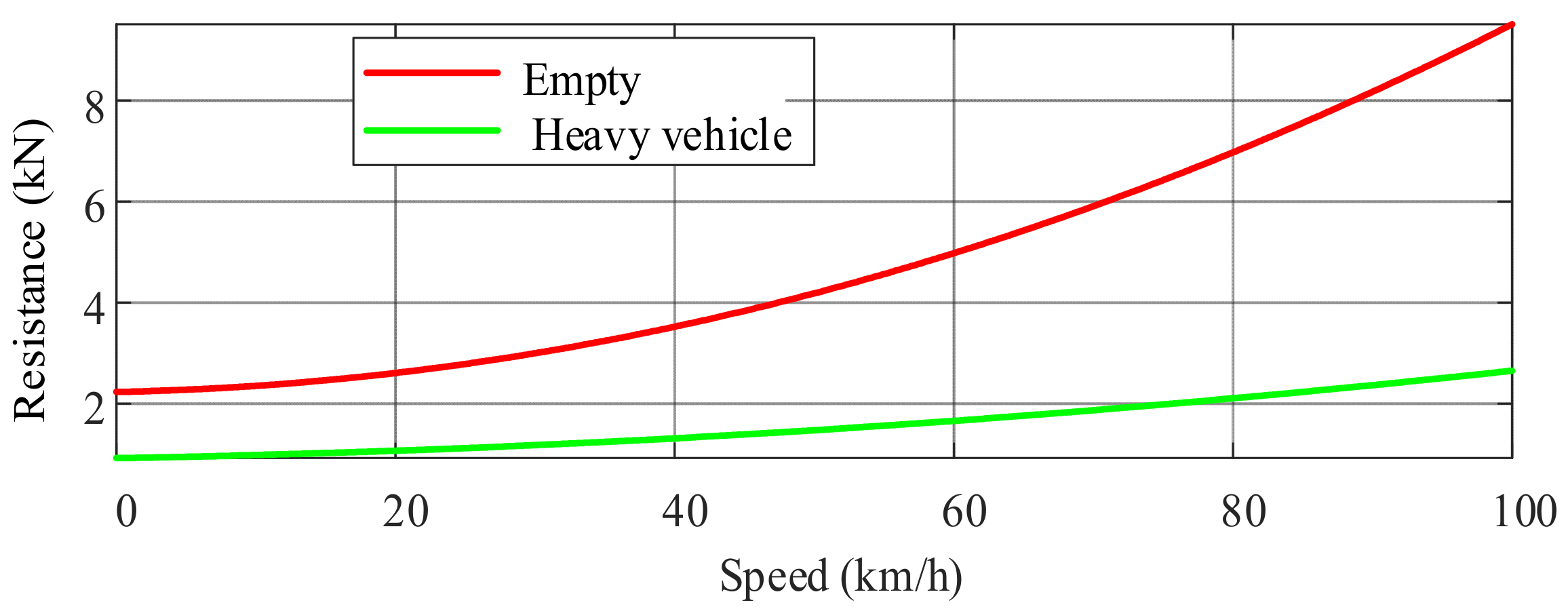
2.2.2. Locomotive Operating Resistance
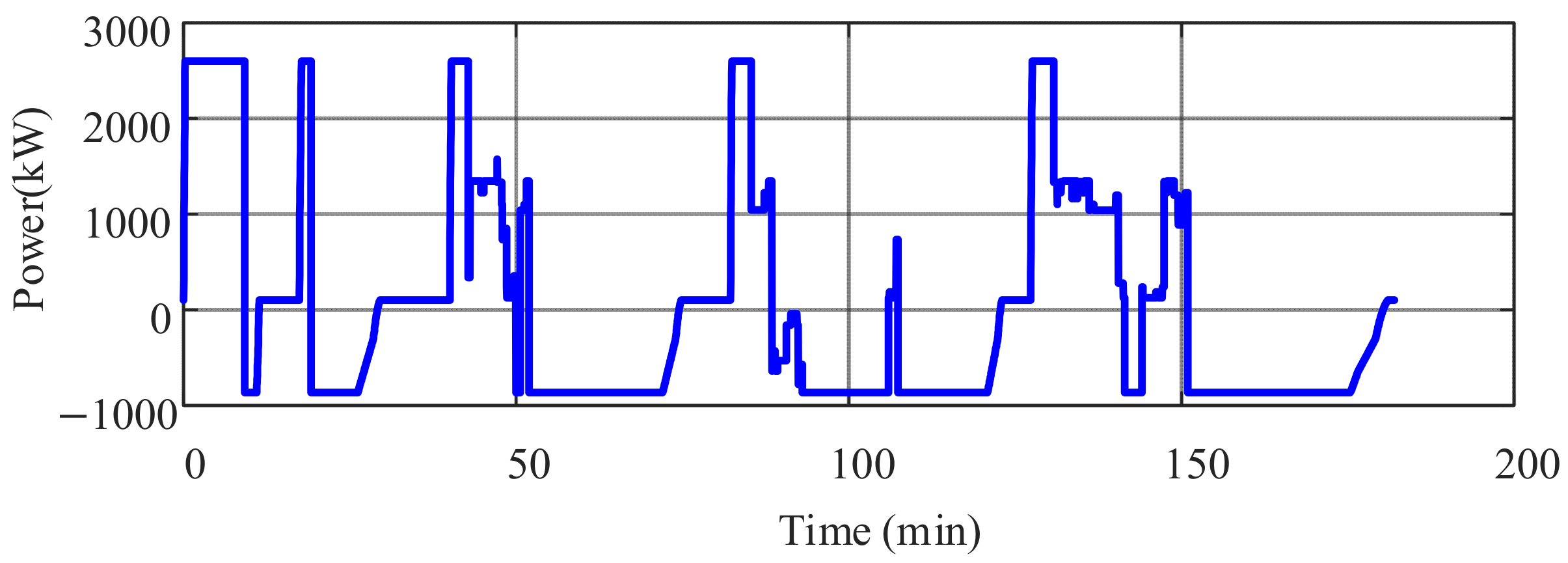
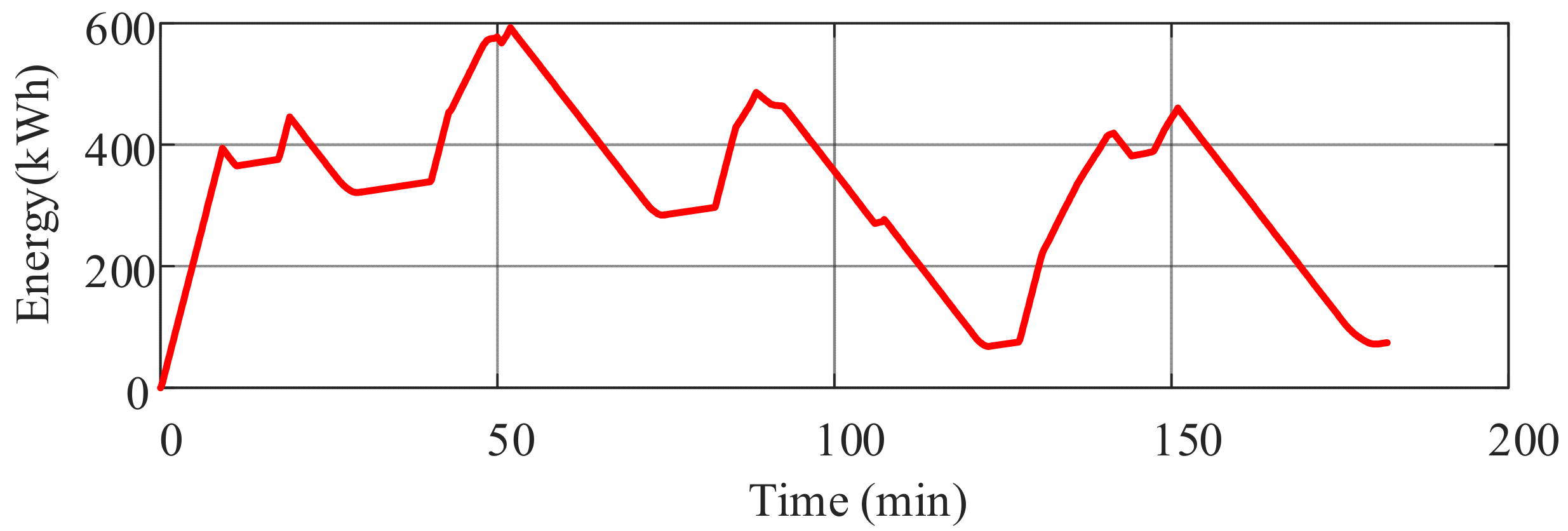
2.3. Train Operating Conditions
3. Optimization of the Parameter Configuration of the FCHPS
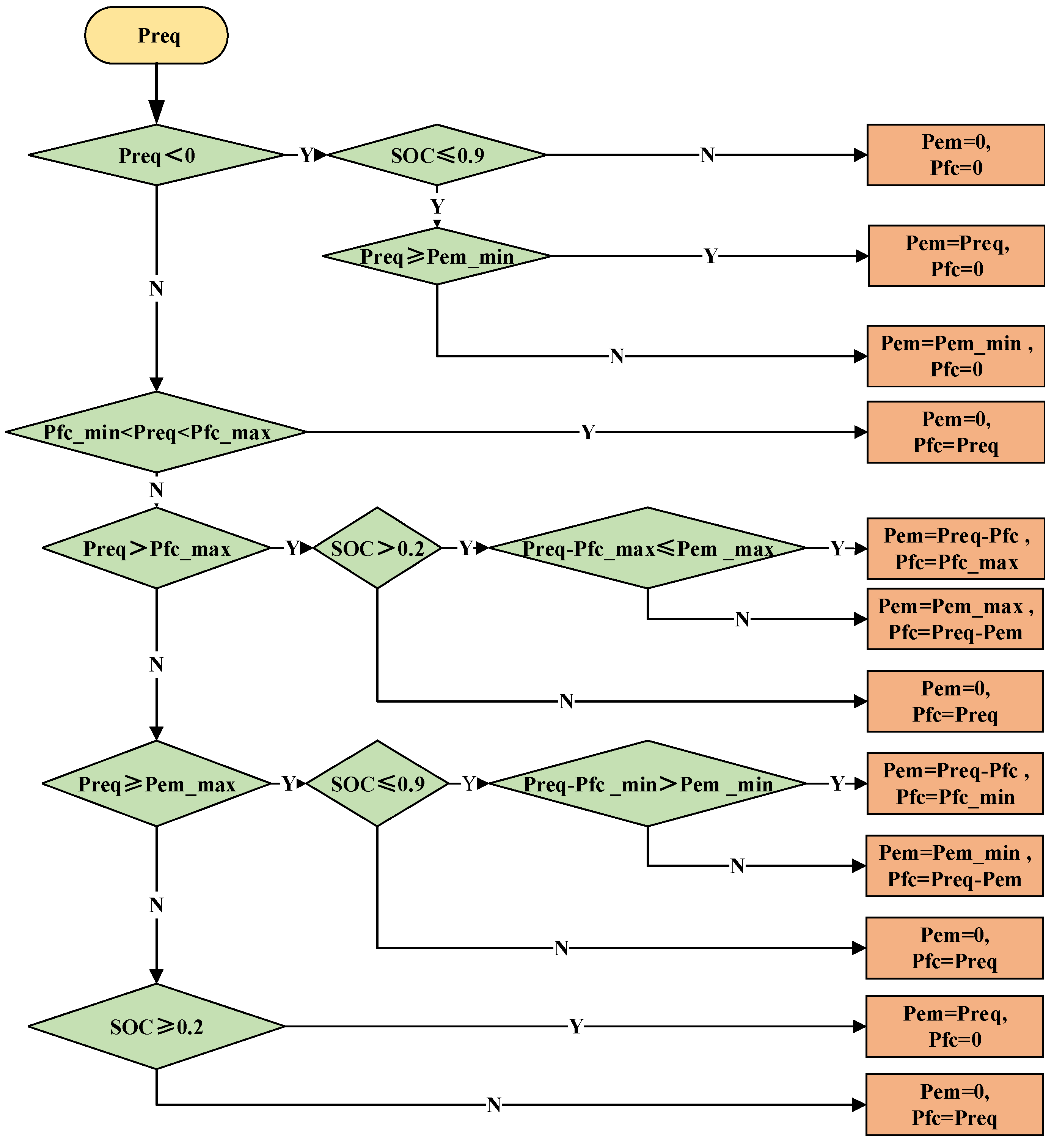
3.1. Rule-Based Energy Management Strategies
3.2. Multi-Objective Configuration Optimization Model
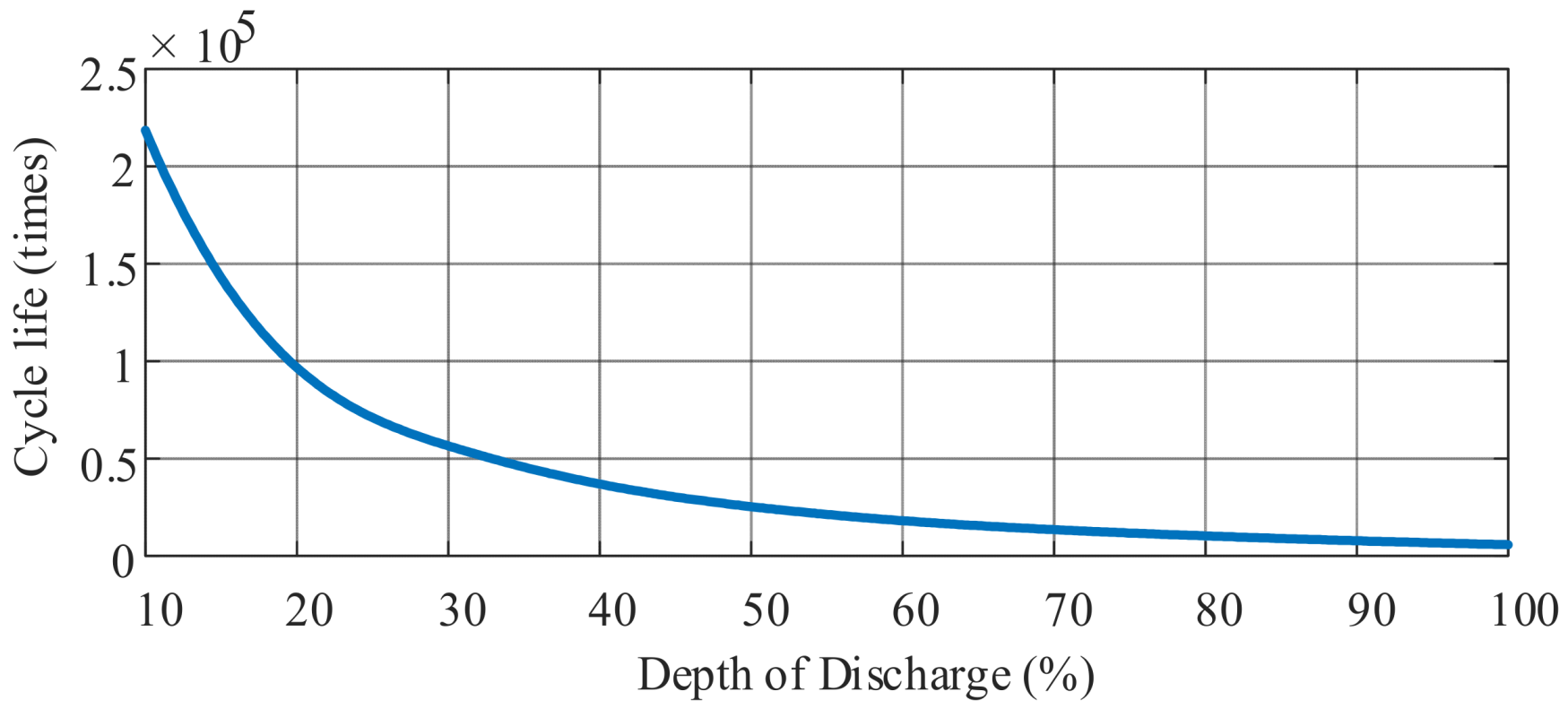
3.2.1. Economic Modeling
- (1)
- Initial acquisition costs
- (2)
- Replacement costs
- 1)
- Fuel cell replacement costs
- 2)
- Energy storage battery replacement costs
- (3)
- Energy costs
3.2.2. Lightweight Modelling
3.3. Overall Optimization Objective Function and Constraints
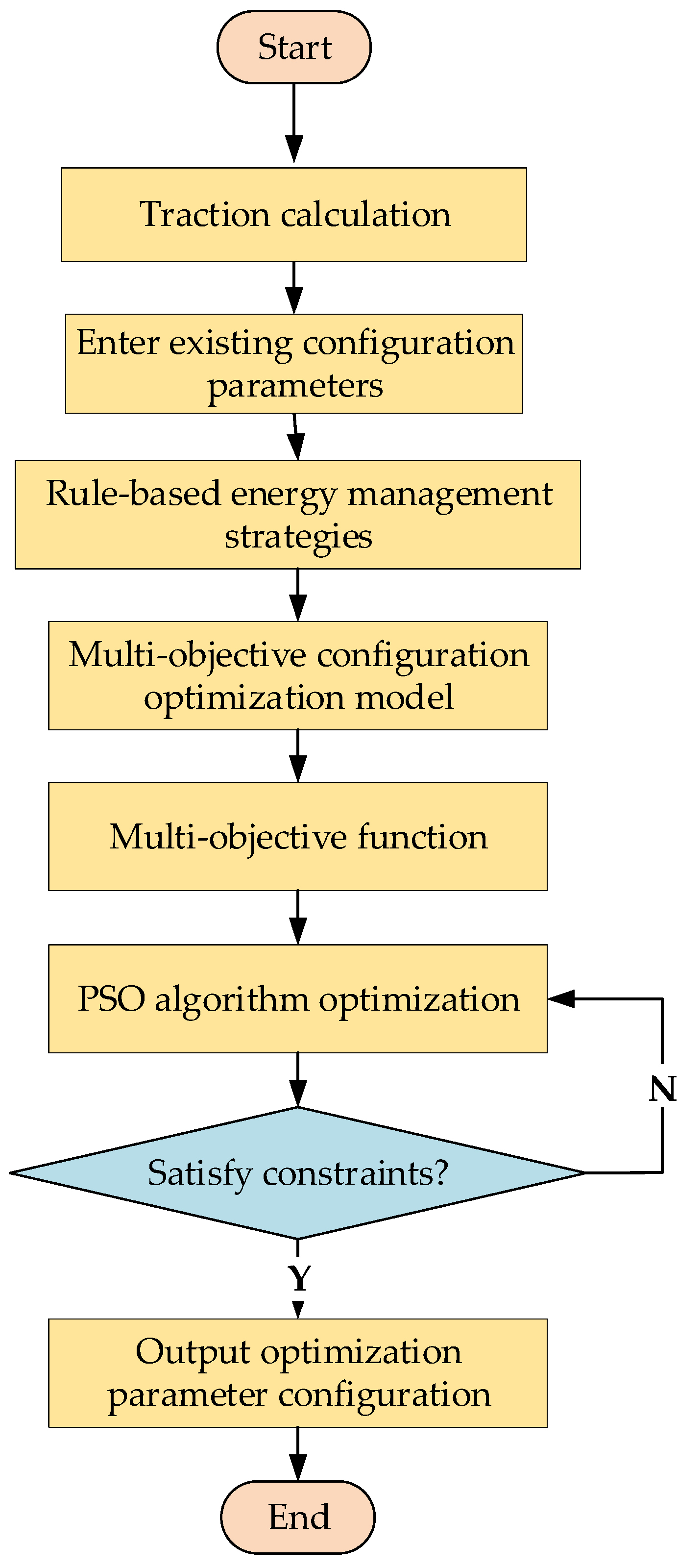
4. Optimization of Configuration Parameters Based on PSO
4.1. Implementation of Optimization Algorithms
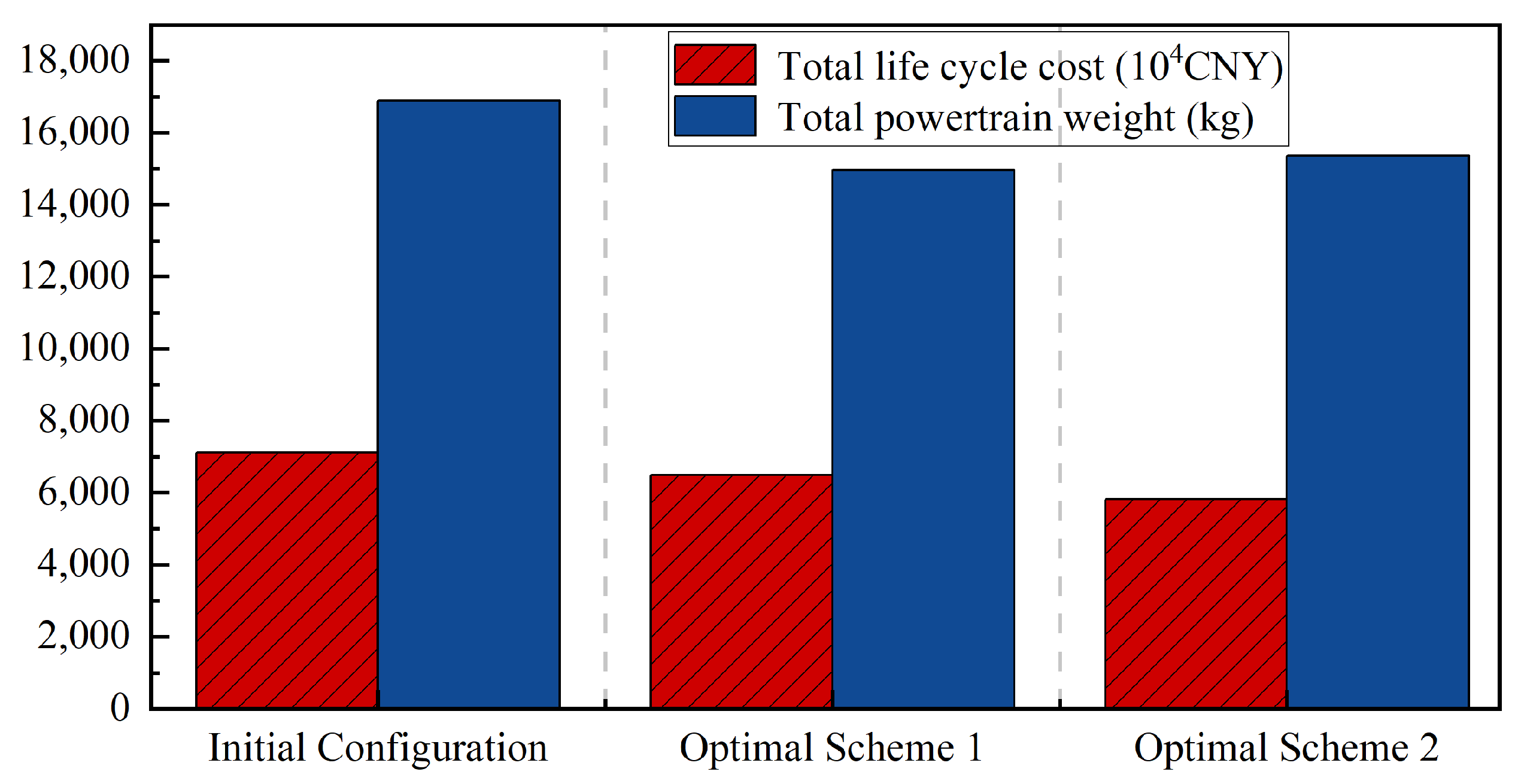
4.2. Analysis of Optimization Results
5. Conclusions
- (1)
- A multi-objective optimization function covering the economic cost and total system weight over the whole life cycle of the vehicle is constructed, and the economy model and lightweight model are established separately. These models can effectively assess the rationality of the configuration of the FCHPS in practical applications and lay a solid foundation for the subsequent parameter optimization.
- (2)
- A method for optimizing a multi-objective function using a PSO algorithm is proposed. By optimally solving two sets of different weight coefficients representing different optimization objectives and comparing the optimization results with the initial configuration, the results of the study show that the optimized economic costs are reduced by 8.76% and 18.05%, while the system weights are reduced by 11.47% and 9.13%, respectively, compared with the initial configuration. This result shows that the optimization methodology can significantly reduce the economic cost over the whole life cycle of the FCHPS and effectively reduce the weight of the system, achieving the desired optimization goal.
- (3)
- The multi-objective optimization method proposed in this paper shows certain advantages. The PSO algorithm is able to globally optimize different sets of weighting coefficients, and in the study of multi-objective configuration optimization of FCHPS, multiple optimal solutions can be obtained by setting different weighting coefficients. Although only one optimal solution can be obtained in each optimization process, more different optimal configurations can be obtained by adjusting the weighting coefficients, thus providing more flexibility and choice space for FCHPS design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Chen, J.; Hissel, D.; Lu, J.; Hou, M.; Shao, Z. Prognostics methods and degradation indexes of proton exchange membrane fuel cells: A review. Renew. Sustain. Energy Rev. 2020, 123, 109721. [Google Scholar] [CrossRef]
- Rokni, M. Performance comparison on repowering of a steam power plant with gas turbines and solid oxide fuel cells. Energies 2016, 9, 399. [Google Scholar] [CrossRef]
- Yaghoubi, E.; Yaghoubi, E.; Khamees, A.; Razmi, D.; Lu, T. A systematic review and meta-analysis of machine learning, deep learning, and ensemble learning approaches in predicting EV charging behavior. Eng. Appl. Artif. Intell. 2024, 135, 108789. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Han, Y.; Li, M.; Chen, W. A state machine strategy based on droop control for an energy management system of PEMFC-battery-supercapacitor hybrid tramway. Int. J. Hydrogen Energy 2016, 41, 16148–16159. [Google Scholar] [CrossRef]
- Fernandez, L.M.; Garcia, P.; Garcia, C.A.; Jurado, F. Hybrid electric system based on fuel cell and battery and integrating a single dc/dc converter for a tramway. Energy Convers. Manag. 2011, 52, 2183–2192. [Google Scholar] [CrossRef]
- Council, H. Hydrogen Scaling Up: A Sustainable Pathway for the Global Energy Transition; Hydrogen Council: Brussels, Belgium, 2017. [Google Scholar]
- Calvert, C.; Allan, J.; Amor, P.; Hillmansen, S.; Roberts, C.; Weston, P. Concept development and testing of the UK’s first hydrogen-hybrid train (HydroFLEX). Railw. Eng. Sci. 2021, 29, 248–257. [Google Scholar] [CrossRef]
- Mustafa, M.Y.; Al-Mahadin, A.; Calay, R.K. Fuel cell technology application for Dubai rail systems. In Proceedings of the 2018 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 6 February–5 April 2018; pp. 1–7. [Google Scholar]
- Palmer, C. Hydrogen-powered trains start to roll. Engineering 2022, 11, 9–11. [Google Scholar] [CrossRef]
- Ozawa, A.; Kudoh, Y.; Murata, A.; Honda, T.; Saita, I.; Takagi, H. Hydrogen in low-carbon energy systems in Japan by 2050: The uncertainties of technology development and implementation. Int. J. Hydrogen Energy 2018, 43, 18083–18094. [Google Scholar] [CrossRef]
- Fotopoulou, M.; Pediaditis, P.; Skopetou, N.; Rakopoulos, D.; Christopoulos, S.; Kartalidis, A. A Review of the Energy Storage Systems of Non-Interconnected European Islands. Sustainability 2024, 16, 1572. [Google Scholar] [CrossRef]
- Al Amerl, A.; Oukkacha, I.; Camara, M.B.; Dakyo, B. Real-time control strategy of fuel cell and battery system for electric hybrid boat application. Sustainability 2021, 13, 8693. [Google Scholar] [CrossRef]
- Zhang, Y.; Diao, L.; Xu, C.; Zhang, J.; Wu, Q.; Pei, H.; Huang, L.; Li, X.; Qi, Y. An optimization of new energy hybrid configuration parameters based on GA method. J. Mar. Sci. Eng. 2022, 10, 1747. [Google Scholar] [CrossRef]
- Wu, X.; Hu, X.; Yin, X.; Li, L.; Zeng, Z.; Pickert, V. Convex programming energy management and components sizing of a plug-in fuel cell urban logistics vehicle. J. Power Sources 2019, 423, 358–366. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, W.; Li, Q. Modeling, optimization and control of a FC/battery hybrid locomotive based on ADVISOR. Int. J. Hydrogen Energy 2017, 42, 18568–18583. [Google Scholar] [CrossRef]
- Hu, Z.; Li, J.; Xu, L.; Song, Z.; Fang, C.; Ouyang, M.; Dou, G.; Kou, G. Multi-objective energy management optimization and parameter sizing for proton exchange membrane hybrid fuel cell vehicles. Energy Convers. Manag. 2016, 129, 108–121. [Google Scholar] [CrossRef]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy management of hybrid electric vehicles: A review of energy optimization of fuel cell hybrid power system based on genetic algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar] [CrossRef]
- Hu, X.; Murgovski, N.; Johannesson, L.M.; Egardt, B. Optimal dimensioning and power management of a fuel cell/battery hybrid bus via convex programming. IEEE/ASME Trans. Mechatron. 2014, 20, 457–468. [Google Scholar] [CrossRef]
- De Almeida, S.C.; Kruczan, R. Effects of drivetrain hybridization on fuel economy, performance and costs of a fuel cell hybrid electric vehicle. Int. J. Hydrogen Energy 2021, 46, 39404–39414. [Google Scholar] [CrossRef]
- Hu, H.; Yuan, W.-W.; Su, M.; Ou, K. Optimizing fuel economy and durability of hybrid fuel cell electric vehicles using deep reinforcement learning-based energy management systems. Energy Convers. Manag. 2023, 291, 117288. [Google Scholar] [CrossRef]
- Huynh, T.; Pham, A.T.; Lee, J.; Nguyen-Xuan, H. Optimal parametric design of fuel cell hybrid electric vehicles by balancing composite motion optimization. Int. J. Precis. Eng. Manuf.-Green Technol. 2024, 11, 123–143. [Google Scholar] [CrossRef]
- Meng, X.; Li, Q.; Zhang, G.; Chen, W. Efficient multidimensional dynamic programming-based energy management strategy for global composite operating cost minimization for fuel cell trams. IEEE Trans. Transp. Electrif. 2021, 8, 1807–1818. [Google Scholar] [CrossRef]
- Wu, M.; Qin, L.; Wu, G. State of power estimation of power lithium-ion battery based on an equivalent circuit model. J. Energy Storage 2022, 51, 104538. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Hua, J.; Li, X.; Ouyang, M. Optimal vehicle control strategy of a fuel cell/battery hybrid city bus. Int. J. Hydrogen Energy 2009, 34, 7323–7333. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, J.; Xu, K.; Sun, J.; Wang, Y. Optimal allocation method of source and storage capacity of PV-Hydrogen zero carbon emission microgrid considering the usage cost of energy storage equipment. Energies 2022, 15, 4916. [Google Scholar] [CrossRef]
- Pei, P.; Chang, Q.; Tang, T. A quick evaluating method for automotive fuel cell lifetime. Int. J. Hydrogen Energy 2008, 33, 3829–3836. [Google Scholar] [CrossRef]
- Chen, H.; Pei, P.; Song, M. Lifetime prediction and the economic lifetime of proton exchange membrane fuel cells. Appl. Energy 2015, 142, 154–163. [Google Scholar] [CrossRef]
- Herrera, V.I.; Gaztañaga, H.; Milo, A.; Saez-de-Ibarra, A.; Etxeberria-Otadui, I.; Nieva, T. Optimal energy management and sizing of a battery--supercapacitor-based light rail vehicle with a multiobjective approach. IEEE Trans. Ind. Appl. 2016, 52, 3367–3377. [Google Scholar] [CrossRef]
- Pei, H.; Diao, L.; Jin, Z.; Xu, C.; Zhang, Y.; Fan, Y. A multi-objective optimal sizing scheme for hybrid traction power supply systems onboard shunting locomotive. Alex. Eng. J. 2023, 72, 399–414. [Google Scholar] [CrossRef]
- Herrera, V.; Milo, A.; Gaztañaga, H.; Etxeberria-Otadui, I.; Villarreal, I.; Camblong, H. Adaptive energy management strategy and optimal sizing applied on a battery-supercapacitor based tramway. Appl. Energy 2016, 169, 831–845. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| System output voltage range | DC 450–750 V |
| Output power | 200 kW |
| Working environment temperature | −30~40 °C |
| Working life | ≥10,000 h |
| Weight | 1400 kg |
| Dimensions | 3264 mm × 2600 mm × 830 mm |
| Parameter | Value |
|---|---|
| Nominal capacity | 40 Ah |
| Nominal voltage | 2.35 V |
| Operating voltage range | 1.5 V–2.8 V |
| Operating temperature | −25~55 °C |
| Dimension | 227 mm × 170 mm × 11.5 mm |
| Weight | 0.95 kg |
| Rules and Regulations | Feature Description |
|---|---|
| Efficient fuel cell operation | Try to keep the fuel cell operating in the high-efficiency zone to reduce the degradation of its performance by start–stop, load change, heavy load, no load, and so on. |
| Maximizing braking energy recovery | When the train decelerates, priority is given to absorbing braking energy with the power battery, and resistive braking and mechanical braking are used when the absorption capacity is exceeded. |
| Battery charge and discharge protection | Set the upper and lower limits of power battery charging and discharging to avoid high-power shock and ensure its safety and durability. |
| SOC maintenance | Charge the battery for peak power demand when the fuel cell is rich in power and the battery SOC is low. |
| Variable Name | Description of Variables | Range of Values |
|---|---|---|
| nfc | Number of fuel cell sets (groups) | 1~8 |
| mbat | Number of batteries in series (pcs) | 511~745 |
| nbat | Number of batteries in parallel (pcs) | 1~30 |
| Parameter | Dimension | Maximum Number of Iterations | Population Size | Acceleration Parameter |
|---|---|---|---|---|
| Value | 3 | 2000 | 50 | 2 |
| Weighting Factor | w1 | w2 |
|---|---|---|
| Group I | 0.8 | 0.2 |
| Group II | 0.2 | 0.8 |
| Configuration Scheme | Initial Configuration | Optimal Scheme 1 | Optimal Scheme 2 |
|---|---|---|---|
| Multi-objective function weight coefficients | — | 0.8, 0.2 | 0.2, 0.8 |
| Lithium battery configuration (number of series-parallel connections) | 672S12P | 535S13P | 614S13P |
| Fuel cell configuration (sets) | 2 | 2 | 1 |
| Total life cycle cost (104CNY) | 7110.47 | 6487.37 | 5827.34 |
| Total FCHPS weight (kg) | 16,899.90 | 14,960.82 | 15,356.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Xu, C.; Zhang, Y.; Pei, H.; Dong, K.; Yang, N.; Ma, Y. Multi-Objective Parameter Configuration Optimization of Hydrogen Fuel Cell Hybrid Power System for Locomotives. Electronics 2024, 13, 3599. https://doi.org/10.3390/electronics13183599
Liu S, Xu C, Zhang Y, Pei H, Dong K, Yang N, Ma Y. Multi-Objective Parameter Configuration Optimization of Hydrogen Fuel Cell Hybrid Power System for Locomotives. Electronics. 2024; 13(18):3599. https://doi.org/10.3390/electronics13183599
Chicago/Turabian StyleLiu, Suyao, Chunmei Xu, Yifei Zhang, Haoying Pei, Kan Dong, Ning Yang, and Yingtao Ma. 2024. "Multi-Objective Parameter Configuration Optimization of Hydrogen Fuel Cell Hybrid Power System for Locomotives" Electronics 13, no. 18: 3599. https://doi.org/10.3390/electronics13183599
APA StyleLiu, S., Xu, C., Zhang, Y., Pei, H., Dong, K., Yang, N., & Ma, Y. (2024). Multi-Objective Parameter Configuration Optimization of Hydrogen Fuel Cell Hybrid Power System for Locomotives. Electronics, 13(18), 3599. https://doi.org/10.3390/electronics13183599






