Efficiency Optimization in Parallel LLC Resonant Inverters with Current-Controlled Variable-Inductor and Phase Shift for Induction Heating
Abstract
1. Introduction
2. Parallel LLC Resonant Converter Topology
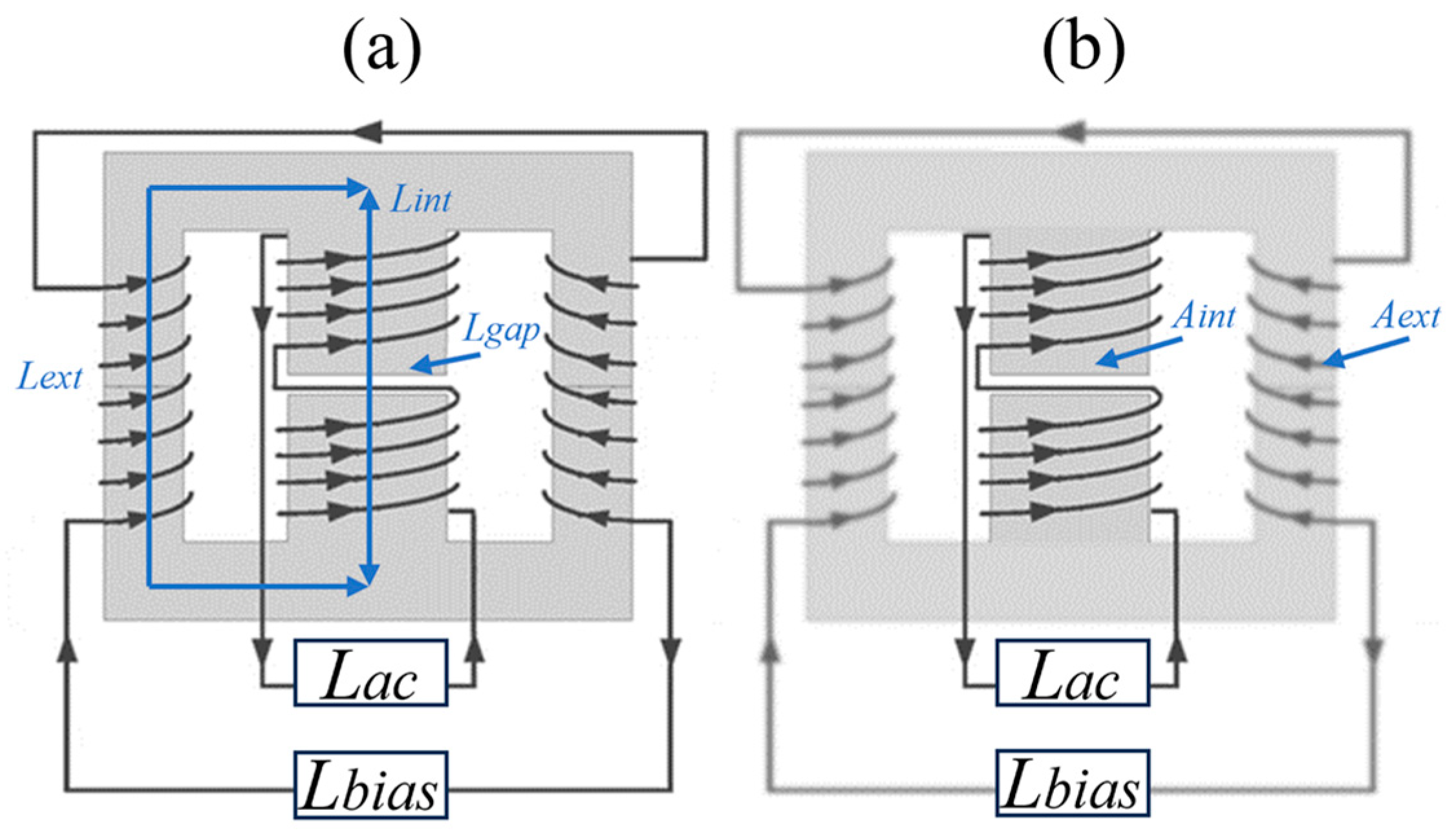
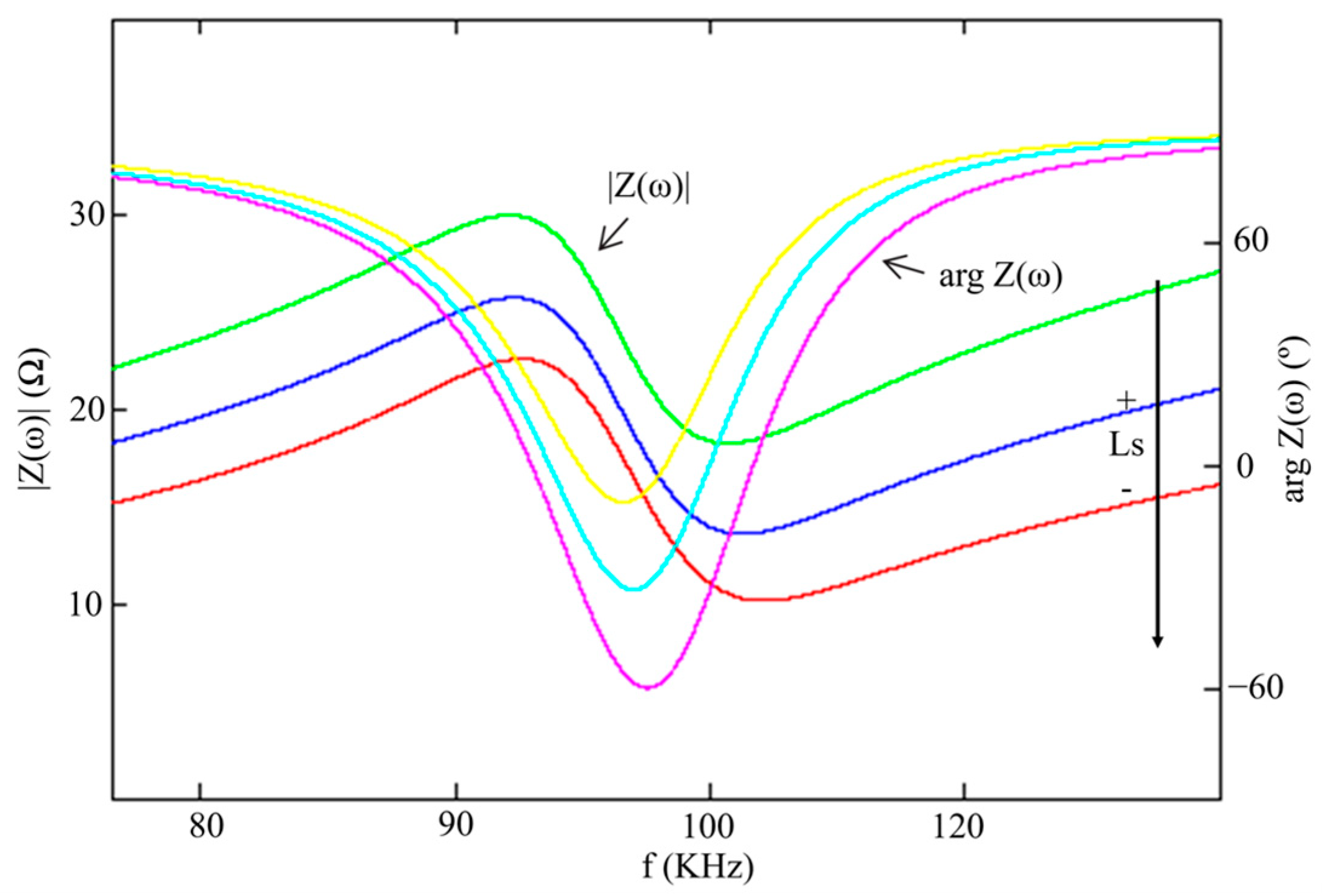
3. Analysis and Application of Current-Controlled Variable Inductor in Parallel LLC Resonant Circuits
4. LLC Resonant Inverter Design
4.1. Design Procedure
4.2. Losses Analysis
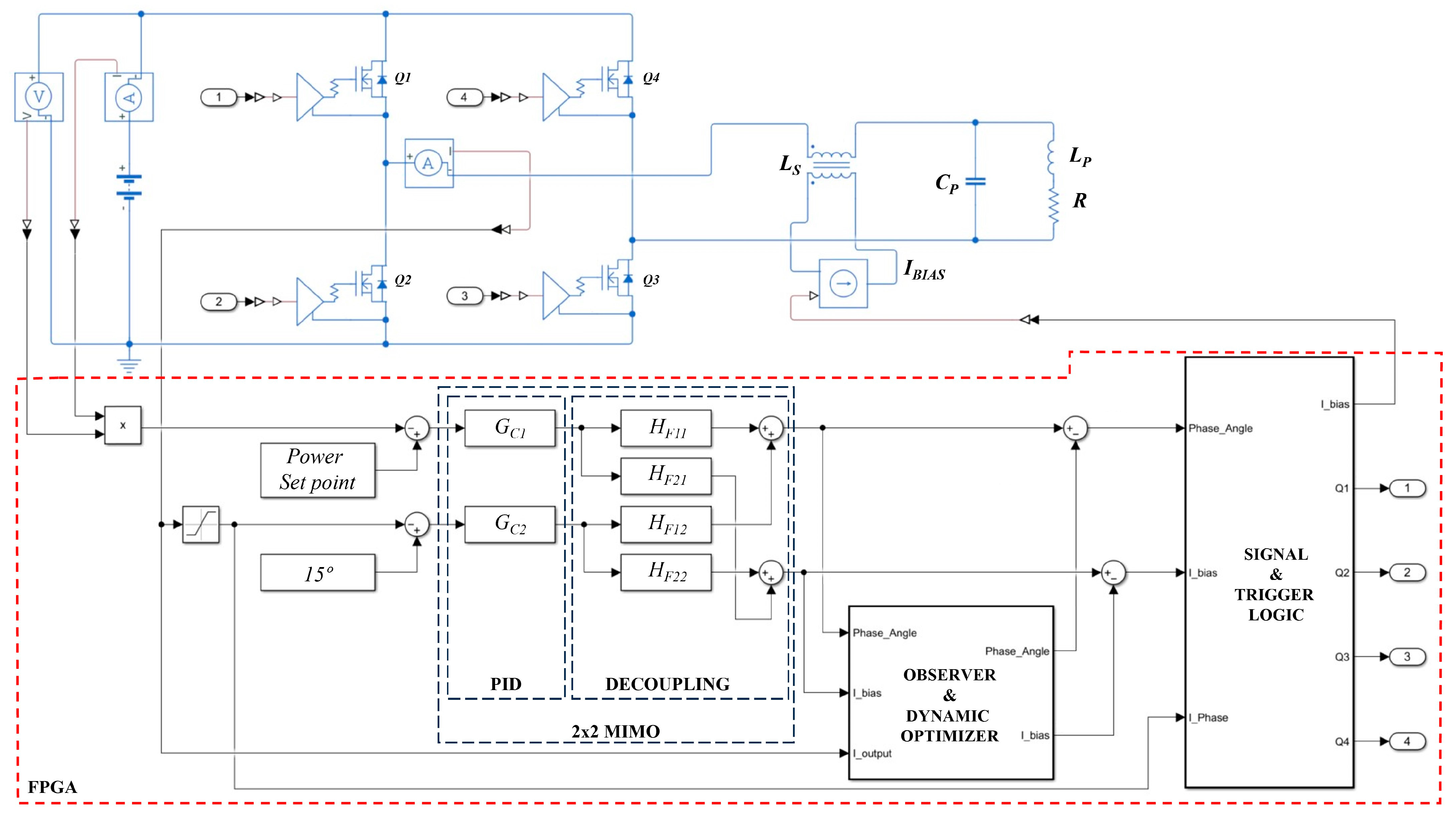
4.3. Control Principles
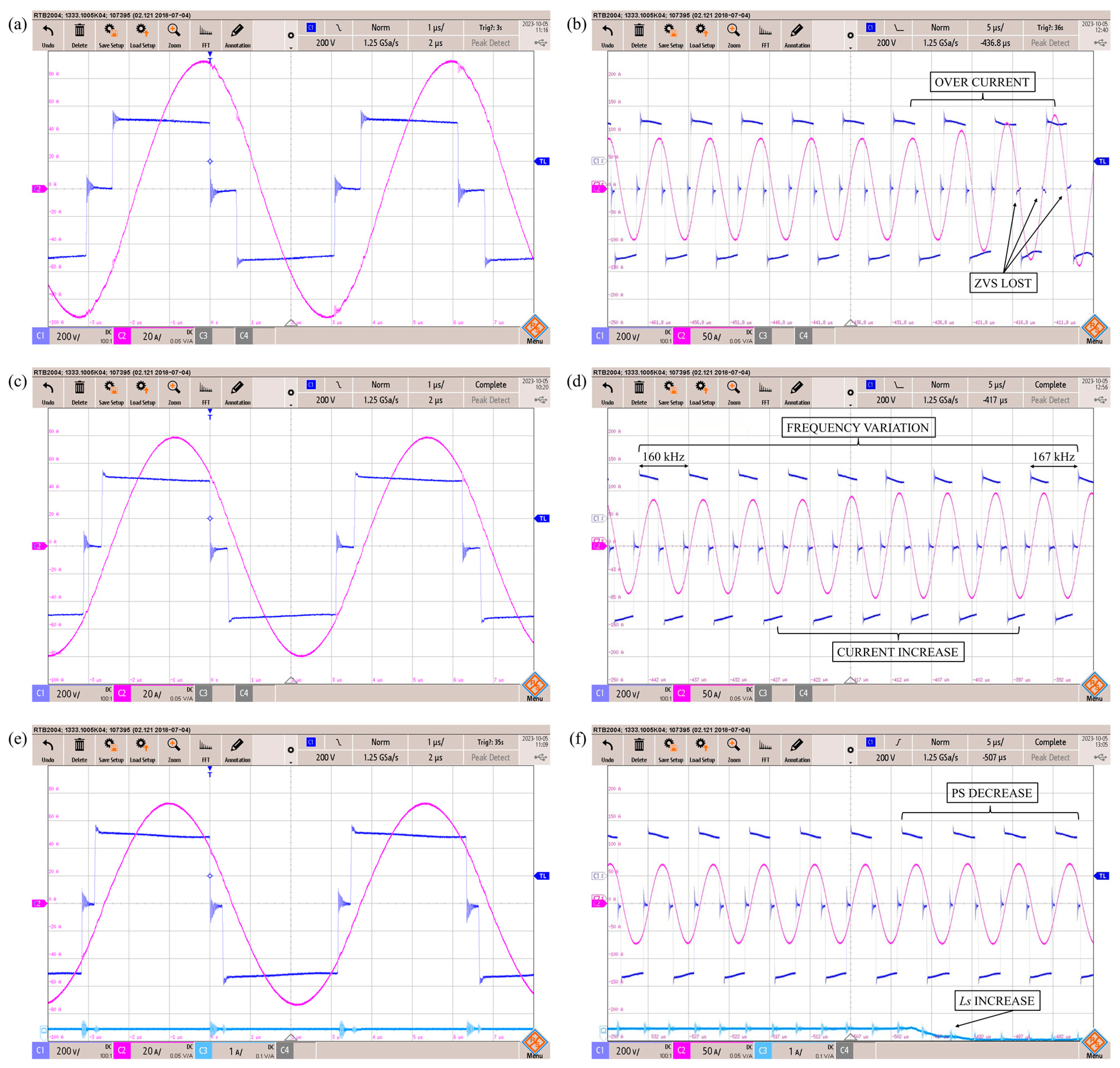
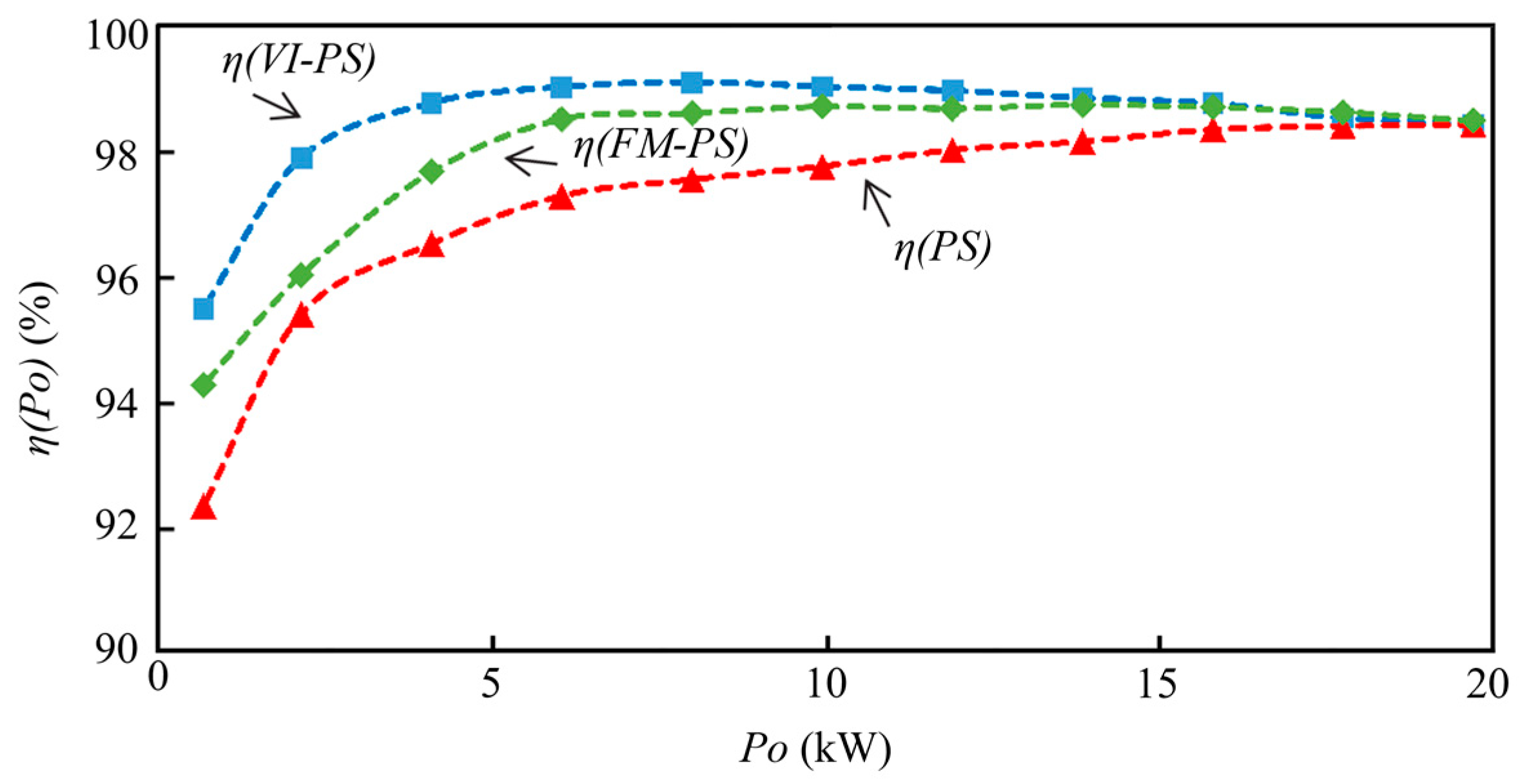
5. Experimental Results with Discussions
- (1)
- Induction heating inverter with four SiC G3R20MT12K;
- (2)
- 300 MHz bandwidth DSO;
- (3)
- Differential voltage probe and Rogowski current probe;
- (4)
- Hall effect probe for DC bias current;
- (5)
- Controllable series inductor (Ls);
- (6)
- Parallel capacitor (Cp);
- (7)
- Parallel inductor (Lp);
- (8)
- Water-cooled load.

6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lucia, O.; Maussion, P.; Dede, E.J.; Burdio, J.M. Induction heating technology and its applications: Past developments, current technology, and future challenges. IEEE Trans. Ind. Electron. 2014, 61, 2509–2520. [Google Scholar] [CrossRef]
- Grajales, L.; Sabaté, J.A.; Wang, K.R.; Tabisz, W.A.; Lee, F.C. Design of a 10 kW, 500 kHz phase-shift controlled series-resonant inverter for induction heating. In Proceedings of the Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; pp. 843–849. [Google Scholar]
- Kamli, M.; Yamamoto, S.; Abe, M. A 50-150 kHz Half-Bridge inverter for induction heating Application. IEEE Trans. Ind. Electron. 1996, 43, 163–172. [Google Scholar] [CrossRef]
- Burdío, J.M.; Barragán, L.A.; Monterde, F.; Navarro, D.; Acero, J. Asymmetrical voltage-cancellation control for full-bridge series resonant inverters. IEEE Trans. Power Electron. 2004, 19, 461–469. [Google Scholar] [CrossRef]
- Esteve, V.; Bellido, J.L.; Jordán, J. Optimal Design of a Single-Phase Bidirectional Rectifier. Energies 2024, 17, 1280. [Google Scholar] [CrossRef]
- Esteve, V.; Bellido, J.L.; Jordán, J.; Dede, E.J. Improving the Efficiency of an Isolated Bidirectional Dual Active Bridge DC–DC Converter Using Variable Frequency. Electronics 2024, 13, 294. [Google Scholar] [CrossRef]
- Ahmed, N. High frequency soft switching AC conversion circuit with dual mode PWM/PDM control strategy for high power IH applications. IEEE Trans. Ind. Electron. 2011, 58, 1440–1448. [Google Scholar] [CrossRef]
- Ramalingam, S.R.; Boopathi, C.S.; Ramasamy, S.; Ahsan, M.; Haider, J.; Shahjalal, M. A Single-Coil Multi-Tapped PDM-Based Induction Heating System for Domestic Applications. Electronics 2023, 12, 404. [Google Scholar] [CrossRef]
- Grajales, L.; Lee, F.C. Control system design and small-signal analysis of a phase-shift controlled series-resonant inverter for induction heating. In Proceedings of the PESC ‘95—Power Electronics Specialist Conference, Atlanta, GA, USA, 18–22 June 1995; pp. 450–456. [Google Scholar]
- Dudrik, J.; Trip, N.-D. Soft-switching PS-PWM DC–DC converter for full-load range applications. IEEE Trans. Ind. Electron. 2010, 57, 2807–2814. [Google Scholar] [CrossRef]
- Viriya, P.; Thomas, T. Power transfer characteristics of a phase-shift controlled ZVS inverter for the application of induction heating. In Proceedings of the International Power Electronics Conference (IPEC), Tokyo, Japan, 3–7 April 2000; pp. 423–428. [Google Scholar]
- Showybul, S.M.; Shakib, I.; Mekhilef, S. A frequency adaptive phase shift modulation control-based LLC series resonant converter for wide input voltage applications. IEEE Trans. Power Electron. 2017, 32, 8360–8370. [Google Scholar]
- Burdío, J.M.; Canales, F.; Barbosa, P.M.; Lee, F.C. A comparison study of fixed-frequency control strategies for ZVS dc/dc series resonant conveters. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference (IEEE Cat. No.01CH37230), Vancouver, BC, Canada, 17–21 June 2001; pp. 427–432. [Google Scholar]
- Yang, X.; Sha, D. Automatic Current Limit Strategy for LLC DC-DC Converter for Overload Operation. EEE Trans. Power Electron. 2024, 39, 9917–9928. [Google Scholar] [CrossRef]
- Scirè, D.; Lullo, G.; Vitale, G. Non-Linear Inductor Models Comparison for Switched-Mode Power Supplies Applications. Electronics 2022, 11, 2472. [Google Scholar] [CrossRef]
- Scirè, D.; Lullo, G.; Vitale, G. Design and Modeling of an Interleaving Boost Converter with Quasi-Saturated Inductors for Electric Vehicles. In Proceedings of the 2020 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 18–20 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chudjuarjeen, S.; Sangswang, A.; Koompai, C. An improved LLC resonant inverter for induction-heating applications with asymmetrical control. IEEE Trans. Ind. Electron. 2011, 58, 2915–2925. [Google Scholar] [CrossRef]
- Espí, J.M.; Dede, E.J.; García-Gil, R.; Castelló, J. Design of the L-LC resonant inverter for induction heating based on its equivalent SRI. IEEE Trans. Ind. Electron. 2007, 54, 3178–3187. [Google Scholar] [CrossRef]
- Lucía, O.; Burdío, J.M.; Millán, I.; Acero, J.; Barragán, L.A. Efficiency oriented design of ZVS half-bridge series resonant inverter with variable frequency duty cycle control. IEEE Trans. Power Electron. 2010, 25, 1671–1674. [Google Scholar] [CrossRef]
- Dede, E.; Gonzalez, J.; Linares, J.; Jordan, J.; Ramirez, D.; Rueda, P. 25-kW/50-kHz generator for induction heating. IEEE Trans. Ind. Electron. 1991, 38, 203–209. [Google Scholar] [CrossRef]
- Lucía, O.; Burdío, J.M.; Millán, I.; Acero, J.; Puyal, D. Load-adaptive control algorithm of half-bridge series resonant inverter for domestic induction heating. IEEE Trans. Ind. Electron. 2009, 56, 3106–3116. [Google Scholar] [CrossRef]
- Czarkowski, D.; Kazimierczuk, M.K. Phase-controlled series-parallel resonant converter. IEEE Trans. Power Electron. 1993, 8, 309–319. [Google Scholar] [CrossRef]
- Barragán, L.A.; Navarro, D.; Acero, J.; Urriza, I.; Burdío, J.M. FPGA implementation of a switching frequency modulation circuit for emi reduction in resonant inverters for induction heating appliances. IEEE Trans. Ind. Electron. 2008, 55, 11–20. [Google Scholar] [CrossRef]
- Esteve, V.; Jordan, J.; Dede, E.J.; Sanchis-Kilders, E.; Martinez, P.J.; Maset, E.; Gilabert, D. Optimal LLC inverter design with SiC MOSFETs and phase shift control for induction heating applications. IEEE Trans. Ind. Electron. 2022, 69, 11100–11111. [Google Scholar] [CrossRef]
- Sewell, H.I.; Stone, D.A.; Bingham, C.M. Dynamic load impedance matching for induction heater systems. COMPEL 2003, 22, 30. [Google Scholar] [CrossRef]
- Medini, D.; Ben-Yaakov, S. A current-controlled variable-inductor for high frequency resonant power circuits. In Proceedings of the 1994 IEEE Applied Power Electronics Conference and Exposition—ASPEC’94, Orlando, FL, USA, 13–17 February 1994. [Google Scholar]
- Ngo-Phi, T.; Nguyen-Quang, N. LLC inverter design procedure for induction heating with quantitative analysis of power transfer. Vnuhcm J. Eng. Technol. 2021, 4, 738–746. [Google Scholar]
- Esteve, V.; Jordán, J.; Dede, E.J.; Martinez, P.J.; Ferrara, K.J.; Bellido, J.L. Comparative analysis and improved design of LLC inverters for induction heating. IET Power Electron. 2023, 16, 1754–1764. [Google Scholar] [CrossRef]
- Wilson, P.R. Modelling and Simulation of Magnetic Components in Electric Circuits. Ph.D. Thesis, Dept. Elect. Comput. Eng., Univ. Southampton, Southampton, UK, November 2001. [Google Scholar]
- Wheeler, H.A. Discussion on simple inductance formulas for radio coils. Proc. Inst. Radio Eng. 1929, 17, 580–582. [Google Scholar]
- Wheeler, H.A. Inductance formulas for circular and square coils. Proc. IEEE 1982, 70, 1449–1450. [Google Scholar] [CrossRef]
- Rudnev, V.; Loveless, D.; Cook, R.; Black, M. Hand Book of Induction Heating; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Brown, G.H.; Hoyler, C.N.; Bierwirth, R.A. Theory and Application of Radio-Frequency Heating; Van Nostrand: New York, NY, USA, 1947. [Google Scholar]
- Esteve, V.; Jordan, J.; Sanchis-Kilders, E.; Dede, E.J.; Maset, E.; Ejea, J.B.; Ferreres, A. Improving the reliability of series resonant inverters for induction heating applications. IEEE Trans. Ind. Electron. 2014, 61, 2564–2572. [Google Scholar] [CrossRef]
- Esteve, V.; Jordán, J.; Dede, E.J.; Bellido, J.L. Enhanced asymmetrical modulation for half-bridge series resonant inverters in induction heating applications. IET Power Electron. 2023, 16, 2482–2491. [Google Scholar] [CrossRef]
- Alonso, J.M.; Perdigão, M.S.; Vaquero, D.G.; Calleja, A.J.; Saraiva, E.S. Analysis, design, and experimentation on constant-frequency DC-DC resonant converters with magnetic control. IEEE Trans. Power Electron. 2012, 27, 1369–1382. [Google Scholar] [CrossRef]
- Rapoport, E.; Pleshivteva, Y. Optimal Control of Induction Heating Process; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- O’Reilly, J. Multivariable Control for Industrial Applications; Peter Peregrinus Ltd.: London, UK, 1987. [Google Scholar]
- Boubaker, O.; Zhu, Q.; Mahmoud, M.S. New Trends in Observer-Based Control: A Practical Guide to Process and Engineering Applications; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]





| Magnitude | Symb. | Eq. | Value | Unit |
|---|---|---|---|---|
| Output power | Po | (36) | 20 | kW |
| Quality factor | Qp | (3) | 10 | |
| Switching frequency | fsw | (27) | 157 | kHz |
| DC input voltage | Vd | (17) | 500 | V |
| Parallel inductor | Lp | (1) | 2 | µH |
| Parallel capacitor | Cp | (25) | 0.66 | µF |
| Minimun series inductor | (26) | 8 | µH | |
| Maximun series inductor | (13) | 14.5 | µH |
| Magnitude | Symb. | Eq. | Value | Unit |
|---|---|---|---|---|
| On resistance | (38) | 17 | mΩ | |
| Turn-OFF losses | a | (39) | 0.0268 | µJ/A2 |
| b | 0.2679 | µJ/A | ||
| c | 18.929 | µJ | ||
| Gate charge | QG | (43) | 180 | nC |
| Magnitude | Symb. | Eq. | PS | VI&PS | Unit |
|---|---|---|---|---|---|
| Conduction losses | (38) | 45.61 | 18.478 | W | |
| Switching losses | (42) | 3.465 | 7.783 | W | |
| Switching losses | 3.238 | 6.075 | W | ||
| Gate losses | (43) | 0.508 | 0.508 | W | |
| Inductor core losses | (44) | 3.57 | 6.12 | W | |
| Inductor wire losses | (45) | 15.499 | 6.279 | W | |
| Total losses | (46) | 216.952 | 116.065 | W |
| Magnitude | Symb. | 12 kW | 20 kW | Unit | ||
|---|---|---|---|---|---|---|
| Theor. | Meas. | Theor. | Meas. | |||
| Phase angle | 15 | 15.1 | 15 | 14.8 | ° | |
| Voltage phase | 52.4 | 51.8 | 39.4 | 40.7 | ° | |
| Output current | 46.6 | 49.5 | 83.5 | 85.1 | A | |
| Upper transistors current | 39.2 | 40 | 55.1 | 55.6 | A | |
| Lower transistors current | 38.6 | 38.3 | 54.3 | 53.7 | A | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellido, J.L.; Esteve, V.; Jordán, J. Efficiency Optimization in Parallel LLC Resonant Inverters with Current-Controlled Variable-Inductor and Phase Shift for Induction Heating. Electronics 2024, 13, 2593. https://doi.org/10.3390/electronics13132593
Bellido JL, Esteve V, Jordán J. Efficiency Optimization in Parallel LLC Resonant Inverters with Current-Controlled Variable-Inductor and Phase Shift for Induction Heating. Electronics. 2024; 13(13):2593. https://doi.org/10.3390/electronics13132593
Chicago/Turabian StyleBellido, Juan L., Vicente Esteve, and José Jordán. 2024. "Efficiency Optimization in Parallel LLC Resonant Inverters with Current-Controlled Variable-Inductor and Phase Shift for Induction Heating" Electronics 13, no. 13: 2593. https://doi.org/10.3390/electronics13132593
APA StyleBellido, J. L., Esteve, V., & Jordán, J. (2024). Efficiency Optimization in Parallel LLC Resonant Inverters with Current-Controlled Variable-Inductor and Phase Shift for Induction Heating. Electronics, 13(13), 2593. https://doi.org/10.3390/electronics13132593













