Survey on Resource Allocation for Future 6G Network Architectures: Cell-Free and Radio Stripe Technologies
Abstract
1. Introduction
- It serves as a comprehensive survey, analyzing current research trends, opportunities, and challenges in CF and RS networks, thereby consolidating knowledge in this rapidly evolving field.
- It delves into emerging RA algorithmic techniques essential for optimizing CF and RS networks. This includes a detailed analysis of algorithms supporting UL and DL power allocation along with AP selection (APS) or AP-UE association.
- It includes a detailed overview specifically focused on RS network architecture, outlining its potential and current research developments.
- It provides a comparative analysis of the computational complexity between CF and RS networks, offering insights into the feasibility and efficiency of RA techniques in these contexts.
2. Massive MIMO
2.1. MIMO System
2.2. Correlated Rayleigh and Rician Fading
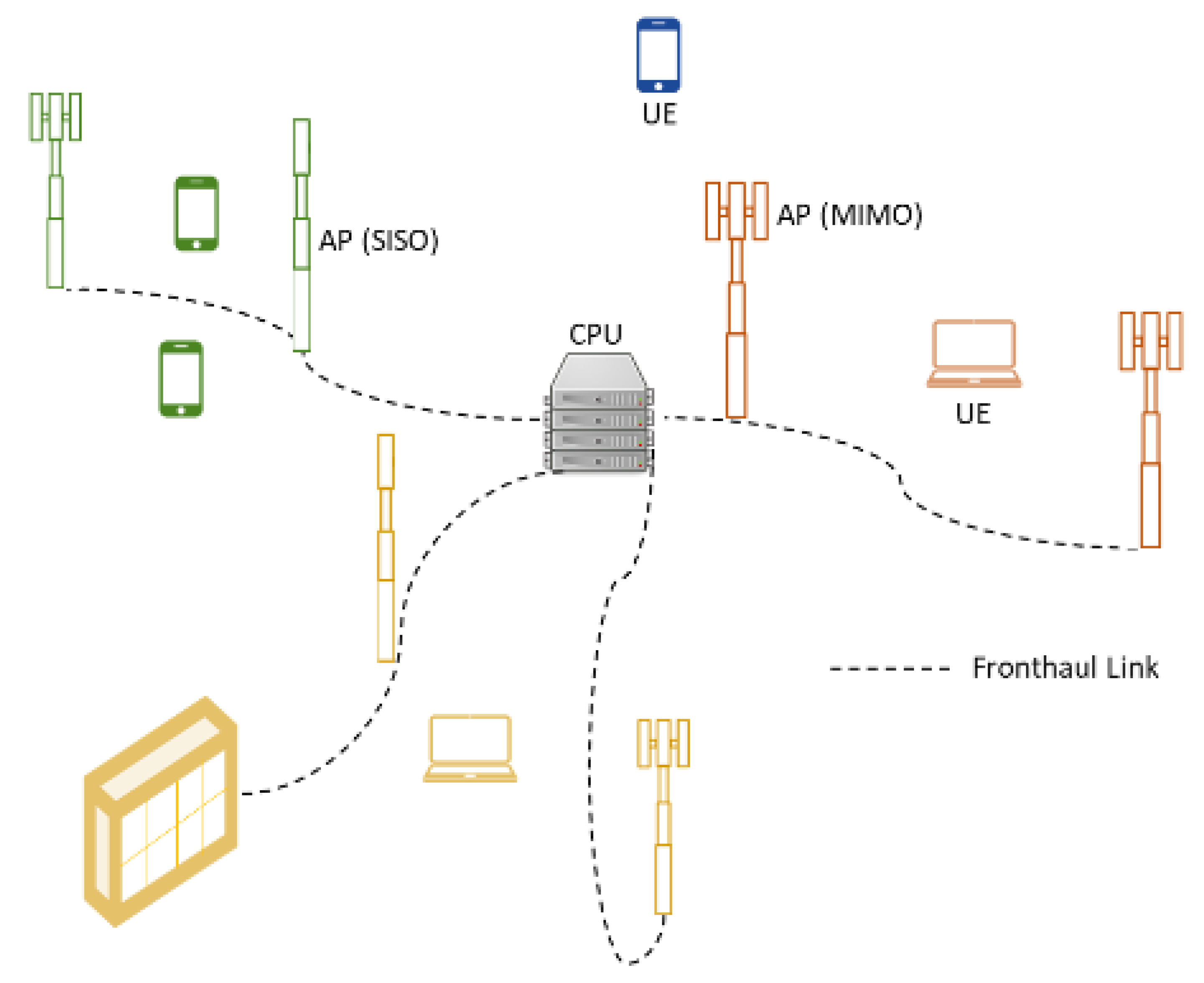
3. Cell-Free Concepts
3.1. Uplink Pilot Transmission and Channel Estimation
3.2. Uplink Data Transmission and Reception
4. Resource Allocation on Cell-Free
4.1. Uplink Power Optimization
4.2. Access Point Selection for Optimized Uplink User Allocation
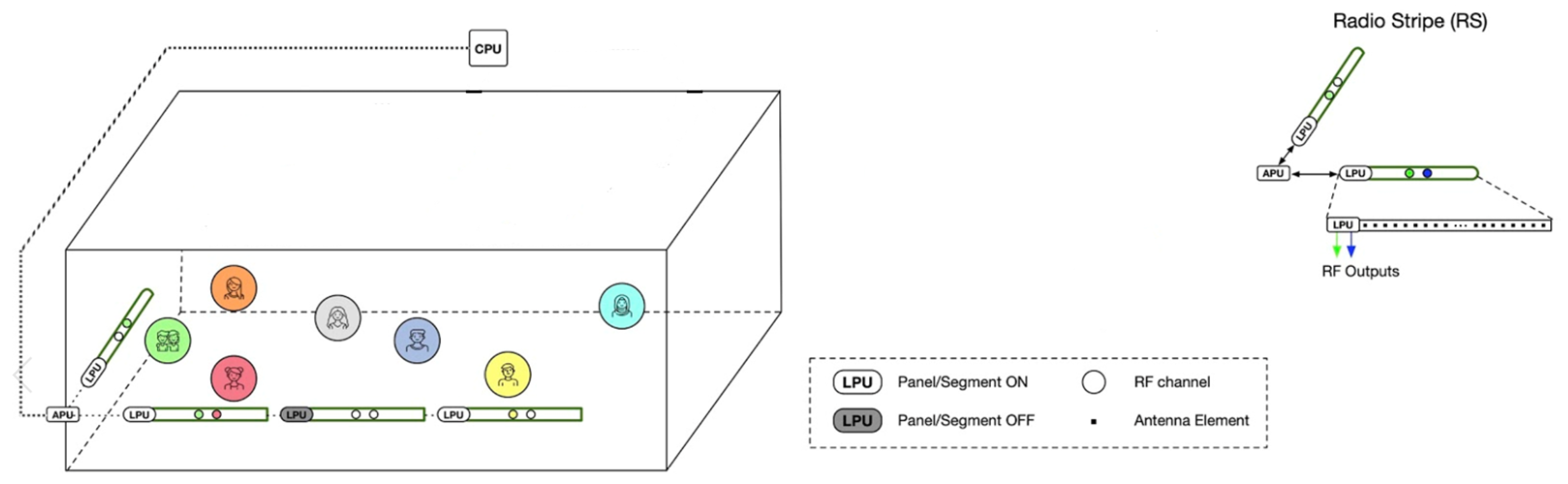
5. Radio Stripe Network Model
- Increasing macro-diversity to enable the cancellation of ICI and reducing the power transmission requirements per antenna;
- Employing massive antenna arrays to achieve gains in system capacity, throughput, PE, and SE;
- Reducing fronthaul overhead by adopting TDD operation, ensuring system scalability and distributed processing;
- Facilitating a more cost-effective deployment with increased robustness, resilience, and lower heat dissipation.
5.1. Channel State Information Estimation
5.2. Uplink and Downlink Payload Transmission
5.3. Uplink Payload Reception
6. Developments on Radio Stripe Technology
7. Research Challenges, Directions, and Open Issues
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CF | Cell-Free |
| RS | Radio Stripe |
| mMIMO | Massive Multiple-Input-Multiple-Output |
| CE | Channel Estimation |
| UL | Uplink |
| DL | Downlink |
| RA | Resource Allocation |
| APS | Access Point Selection |
| 6G | Sixth Generation |
| KPI | Key Performance Indicator |
| SE | Spectral Efficiency |
| PE | Power Efficiency |
| FeMBB | Further Enhanced Mobile Broadband |
| umMTC | Ultra-Massive Machine-Type Communications |
| eURLLC | Enhanced Ultra-Reliable and Low-Latency Communications |
| LDHMC | Long-Distance and High Mobility Communications |
| ELPC | Extremely Low-Power Communications |
| AI | Artificial Intelligence |
| THz | Terahertz |
| QoS | Quality of Service |
| MaL | Machine Learning |
| UE | User Equipment |
| HW | Hardware |
| LIS | Large Intelligent Surface |
| AP | Access Point |
| BS | Base Station |
| FR1 | Frequency Range 1 |
| FR2 | Frequency Range 2 |
| TDD | Time-Division Duplex |
| CSI | Channel State Information |
| 3GPP | Third Generation Partnership Project |
| ICI | Inter-Cell Interference |
| CH | Channel Hardening |
| FP | Favorable Propagation |
| DFT | Discrete Fourier Transform |
| AWGN | Additive White Gaussian Noise |
| nLoS | Non-Line-of-Sight |
| SSF | Small-Scale Fading |
| LSF | Large-Scale Fading |
| PL | Path-Loss |
| LoS | Line-of-Sight |
| RF | Radio Frequency |
| SF | Shadow Fading |
| D-mMIMO | Distributed mMIMO |
| C-RAN | Cloud Radio Access Network |
| CoMP-JT | Coordination Multipoint with Joint Transmission |
| DAS | Distributed Antenna System |
| CPU | Central Processing Unit |
| mmWave | Millimeter Wave |
| IUI | Inter-User Interference |
| LMMSE | Local Minimum Mean Square Error |
| MRC | Maximum Ratio Combining |
| DS | Desired Signal |
| IS | Interference Signal |
| NFM | Network Function Metric |
| OF | Objective Function |
| MMF | Max-Min Fairness |
| NFM | Network Function Metric |
| OF | Objective Function |
| MMF | Max-Min Fairness |
| SOCP | Second-Order Cone Programming |
| ZF | Zero-Forcing |
| GP | Geometric Programming |
| SO | Single-Objective |
| MTP | Minimum Transmission Power |
| MSR | Max-Sum Rate |
| FrP | Fractional Programming |
| SCA | Successive Convex Approximation |
| APG | Accelerated Projected Gradient |
| DeL | Deep Learning |
| DCNN | Deep Convolutional Neural Network |
| DNN | Deep Neural Network |
| MRT | Maximum Ratio Transmission |
| DRL | Deep Reinforcement Learning |
| RZF | Regularized ZF |
| BO | Bi-Objective |
| MH | Meta-Heuristic |
| SINR | Signal-to-Noise-and-Interference Ratio |
| LB | Load Balance |
| OFDM | Orthogonal Frequency Division Multiplexing |
| LPU | Local Processing Unit |
| ADC | Analog-to-Digital Converter |
| DAC | Digital-to-Analog Converter |
| APU | Area Processing Unit |
| NLMMSE | Normalized LMMSE |
| SLP | Sequential Linear Processing |
| OSLP | Optimal Sequential Linear Processing |
| MSE | Mean Square Error |
| IoT | Internet of Things |
| MF | Match Filtered |
| ML | Maximum Likelihood |
| LDPC | Low-Density Parity Check |
| MO | Multi-Objective |
References
- Tataria, H.; Shafi, M.; Molisch, A.F.; Dohler, M.; Sjöland, H.; Tufvesson, F. 6G Wireless Systems: Vision, Requirements, Challenges, Insights, and Opportunities. Proc. IEEE 2021, 109, 1166–1199. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Shahjalal, M.; Ahmed, S.; Jang, Y.M. 6G Wireless Communication Systems: Applications, Requirements, Technologies, Challenges, and Research Directions. IEEE Open J. Commun. Soc. 2020, 1, 957–975. [Google Scholar] [CrossRef]
- Yang, P.; Xiao, Y.; Xiao, M.; Li, S. 6G Wireless Communications: Vision and Potential Techniques. IEEE Netw. 2019, 33, 70–75. [Google Scholar] [CrossRef]
- Giordani, M.; Polese, M.; Mezzavilla, M.; Rangan, S.; Zorzi, M. Toward 6G Networks: Use Cases and Technologies. IEEE Commun. Mag. 2020, 58, 55–61. [Google Scholar] [CrossRef]
- Khan, L.U.; Yaqoob, I.; Imran, M.; Han, Z.; Hong, C.S. 6G Wireless Systems: A Vision, Architectural Elements, and Future Directions. IEEE Access 2020, 8, 147029–147044. [Google Scholar] [CrossRef]
- Xiaohu, Y.; Wang, C.X.; Huang, J.; Gao, X.; Zhang, Z.; Wang, M.; Huang, Y.; Zhang, C.; Jiang, Y.; Wang, J.; et al. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Sci. China Inf. Sci. 2021, 64, 110301. [Google Scholar] [CrossRef]
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, Y.; Ma, Z.; Xiao, M.; Ding, Z.; Lei, X.; Karagiannidis, G.K.; Fan, P. 6G Wireless Networks: Vision, Requirements, Architecture, and Key Technologies. IEEE Veh. Technol. Mag. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Björnson, E.; Chae, C.B.; Heath, R.W., Jr.; Marzetta, T.L.; Mezghani, A.; Sanguinetti, L.; Rusek, F.; Castellanos, M.R.; Jun, D.; Demir, Ö.T. Towards 6G MIMO: Massive Spatial Multiplexing, Dense Arrays, and Interplay between Electromagnetics and Processing. arXiv 2024, arXiv:2401.02844. [Google Scholar] [CrossRef]
- Alsabah, M.; Naser, M.A.; Mahmmod, B.M.; Abdulhussain, S.H.; Eissa, M.R.; Al-Baidhani, A.; Noordin, N.K.; Sait, S.M.; Al-Utaibi, K.A.; Hashim, F. 6G Wireless Communications Networks: A Comprehensive Survey. IEEE Access 2021, 9, 148191–148243. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless Communications and Applications Above 100 GHz: Opportunities and Challenges for 6G and Beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Murroni, M.; Anedda, M.; Fadda, M.; Ruiu, P.; Popescu, V.; Zaharia, C.; Giusto, D. 6G—Enabling the New Smart City: A Survey. Sensors 2023, 23, 7528. [Google Scholar] [CrossRef]
- Dahlman, E.; Parkvall, S.; Skold, J. 5G NR: The Next Generation Wireless Access Technology, 1st ed.; Academic Press, Inc.: Cambridge, MA, USA, 2018. [Google Scholar]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO Versus Small Cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef]
- Hu, S.; Rusek, F.; Edfors, O. Beyond Massive MIMO: The Potential of Data Transmission with Large Intelligent Surfaces. IEEE Trans. Signal Process. 2018, 66, 2746–2758. [Google Scholar] [CrossRef]
- Interdonato, G.; Björnson, E.; Quoc Ngo, H.; Frenger, P.; Larsson, E.G. Ubiquitous cell-free Massive MIMO communications. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 197. [Google Scholar] [CrossRef]
- Hu, S.; Rusek, F.; Edfors, O. Beyond Massive MIMO: The Potential of Positioning with Large Intelligent Surfaces. IEEE Trans. Signal Process. 2018, 66, 1761–1774. [Google Scholar] [CrossRef]
- Ammar, H.A.; Adve, R.; Shahbazpanahi, S.; Boudreau, G.; Srinivas, K.V. User-Centric Cell-Free Massive MIMO Networks: A Survey of Opportunities, Challenges and Solutions. IEEE Commun. Surv. Tutor. 2022, 24, 611–652. [Google Scholar] [CrossRef]
- Elhoushy, S.; Ibrahim, M.; Hamouda, W. Cell-Free Massive MIMO: A Survey. IEEE Commun. Surv. Tutor. 2022, 24, 492–523. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Interdonato, G.; Larsson, E.G.; Caire, G.; Andrews, J.G. Ultradense Cell-Free Massive MIMO for 6G: Technical Overview and Open Questions. Proc. IEEE 2024, 1–27. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.K.; Lee, S.H. Survey Propagation for Cell-Free Massive MIMO Pilot Assignment. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1267–1272. [Google Scholar] [CrossRef]
- Shi, E.; Zhang, J.; Du, H.; Ai, B.; Yuen, C.; Niyato, D.; Letaief, K.B.; Shen, X. RIS-Aided Cell-Free Massive MIMO Systems for 6G: Fundamentals, System Design, and Applications. Proc. IEEE 2024, 112, 331–364. [Google Scholar] [CrossRef]
- Hidayat, B.; Zakia, I. Cell Free Mobile Communication in UAV System as Mobile Infrastructure Solution for Smart System Platforms: A Survey. In Proceedings of the 2023 10th International Conference on ICT for Smart Society (ICISS), Bandung, Indonesia, 6–7 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Andrews, J.G.; Zhang, X.; Durgin, G.D.; Gupta, A.K. Are we approaching the fundamental limits of wireless network densification? IEEE Commun. Mag. 2016, 54, 184–190. [Google Scholar] [CrossRef]
- Marzetta, T.L. Massive MIMO: An Introduction. Bell Labs Tech. J. 2015, 20, 11–22. [Google Scholar] [CrossRef]
- Marzetta, T.L.; Larsson, E.G.; Yang, H.; Ngo, H.Q. Fundamentals of Massive MIMO; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency. Found. Trends® Signal Process. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling Up MIMO: Opportunities and Challenges with Very Large Arrays. IEEE Signal Process. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar] [CrossRef]
- Yang, H.; Marzetta, T.L. Total energy efficiency of cellular large scale antenna system multiple access mobile networks. In Proceedings of the 2013 IEEE Online Conference on Green Communications (OnlineGreenComm), Piscataway, NJ, USA, 29–31 October 2013; pp. 27–32. [Google Scholar] [CrossRef]
- Chen, Z.; Björnson, E. Channel Hardening and Favorable Propagation in Cell-Free Massive MIMO with Stochastic Geometry. IEEE Trans. Commun. 2018, 66, 5205–5219. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. Making Cell-Free Massive MIMO Competitive with MMSE Processing and Centralized Implementation. IEEE Trans. Wirel. Commun. 2020, 19, 77–90. [Google Scholar] [CrossRef]
- Hu, F. Opportunities in 5G Networks: A Research and Development Perspective; CRC Press: Boca Raton, FL, USA, 2016; pp. 1–538. [Google Scholar]
- Fan, W.; Zhang, J.; Bjornson, E.; Chen, S.; Zhong, Z. Performance Analysis of Cell-Free Massive MIMO Over Spatially Correlated Fading Channels. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Demir, Ö.T.; Björnson, E. Joint Power Control and LSFD for Wireless-Powered Cell-Free Massive MIMO. IEEE Trans. Wirel. Commun. 2021, 20, 1756–1769. [Google Scholar] [CrossRef]
- Chiueh, T.D.; Tsai, P.Y. OFDM Baseband Receiver Design for Wireless Communications; Wiley Publishing: Singapore, 2007. [Google Scholar]
- Checko, A.; Christiansen, H.L.; Yan, Y.; Scolari, L.; Kardaras, G.; Berger, M.S.; Dittmann, L. Cloud RAN for Mobile Networks—A Technology Overview. IEEE Commun. Surv. Tutor. 2015, 17, 405–426. [Google Scholar] [CrossRef]
- Chen, C.M.; Blandino, S.; Gaber, A.; Desset, C.; Bourdoux, A.; Van der Perre, L.; Pollin, S. Distributed Massive MIMO: A Diversity Combining Method for TDD Reciprocity Calibration. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Gong, J.; Zhou, S.; Zhou, Z. Networked MIMO with Fractional Joint Transmission in Energy Harvesting Systems. IEEE Trans. Commun. 2016, 64, 3323–3336. [Google Scholar] [CrossRef]
- Boldi, M.; Tölli, A.; Olsson, M.; Hardouin, E.; Svensson, T.; Boccardi, F.; Thiele, L.; Jungnickel, V. Coordinated MultiPoint (CoMP) Systems; Wiley: Hoboken, NJ, USA, 2011; pp. 121–155. [Google Scholar] [CrossRef]
- Nigam, G.; Minero, P.; Haenggi, M. Coordinated Multipoint Joint Transmission in Heterogeneous Networks. IEEE Trans. Commun. 2014, 62, 4134–4146. [Google Scholar] [CrossRef]
- Gesbert, D.; Hanly, S.; Huang, H.; Shamai Shitz, S.; Simeone, O.; Yu, W. Multi-Cell MIMO Cooperative Networks: A New Look at Interference. IEEE J. Sel. Areas Commun. 2010, 28, 1380–1408. [Google Scholar] [CrossRef]
- You, X.H.; Wang, D.; Sheng, B.; Gao, X.; Zhao, X.S.; Chen, M. Cooperative distributed antenna systems for mobile communications [Coordinated and Distributed MIMO]. Wirel. Commun. IEEE 2010, 17, 35–43. [Google Scholar] [CrossRef]
- Heath Jr, R.W.; Wu, T.; Kwon, Y.H.; Soong, A.C.K. Multiuser MIMO in Distributed Antenna Systems with Out-of-Cell Interference. IEEE Trans. Signal Process. 2011, 59, 4885–4899. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, S.; Lin, Y.; Zheng, J.; Ai, B.; Hanzo, L. Cell-Free Massive MIMO: A New Next-Generation Paradigm. IEEE Access 2019, 7, 99878–99888. [Google Scholar] [CrossRef]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Yang, H.; Rao, B.D. Precoding and Power Optimization in Cell-Free Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2017, 16, 4445–4459. [Google Scholar] [CrossRef]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Yang, H. Cell-Free Massive MIMO systems. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; pp. 695–699. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO: Uniformly great service for everyone. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 201–205. [Google Scholar] [CrossRef]
- Bashar, M.; Cumanan, K.; Burr, A.G.; Debbah, M.; Ngo, H.Q. On the Uplink Max–Min SINR of Cell-Free Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2019, 18, 2021–2036. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. Scalable Cell-Free Massive MIMO Systems. IEEE Trans. Commun. 2020, 68, 4247–4261. [Google Scholar] [CrossRef]
- Demir, Ö.T.; Björnson, E.; Sanguinetti, L. Foundations of User-Centric Cell-Free Massive MIMO; Now Foundations and Trends: Boston, MA, USA, 2021; Volume 14, pp. 162–472. [Google Scholar] [CrossRef]
- Polegre, A.Á.; Riera-Palou, F.; Femenias, G.; Armada, A.G. Channel Hardening in Cell-Free and User-Centric Massive MIMO Networks with Spatially Correlated Ricean Fading. IEEE Access 2020, 8, 139827–139845. [Google Scholar] [CrossRef]
- Eddine Hajri, S.; Denis, J.; Assaad, M. Enhancing Favorable Propagation in Cell-Free Massive MIMO Through Spatial User Grouping. In Proceedings of the 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece, 25–28 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Buzzi, S.; D’Andrea, C. Cell-Free Massive MIMO: User-Centric Approach. IEEE Wirel. Commun. Lett. 2017, 6, 706–709. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. Cell-Free versus Cellular Massive MIMO: What Processing is Needed for Cell-Free to Win? In Proceedings of the 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Chakraborty, S.; Björnson, E.; Sanguinetti, L. Centralized and Distributed Power Allocation for Max-Min Fairness in Cell-Free Massive MIMO. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019; pp. 576–580. [Google Scholar] [CrossRef]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Rao, B.D. Performance of cell-free massive MIMO systems with MMSE and LSFD receiversPower allocation in cell-free massive MIMO: A deep learning method. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 203–207. [Google Scholar] [CrossRef]
- Conceição, F.; Antunes, C.H.; Gomes, M.; Silva, V.; Dinis, R. Max-Min Fairness Optimization in Uplink Cell-Free Massive MIMO Using Meta-Heuristics. IEEE Trans. Commun. 2022, 70, 1792–1807. [Google Scholar] [CrossRef]
- Khan, F.; Pi, Z. mmWave mobile broadband (MMB): Unleashing the 3–300GHz spectrum. In Proceedings of the 34th IEEE Sarnoff Symposium, Princeton, NJ, USA, 3–4 May 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Interdonato, G.; Ngo, H.Q.; Larsson, E.G.; Frenger, P. How Much Do Downlink Pilots Improve Cell-Free Massive MIMO? In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Interdonato, G.; Ngo, H.Q.; Frenger, P.; Larsson, E.G. Downlink Training in Cell-Free Massive MIMO: A Blessing in Disguise. IEEE Trans. Wirel. Commun. 2019, 18, 5153–5169. [Google Scholar] [CrossRef]
- Miretti, L.; Björnson, E.; Gesbert, D. Team Precoding Towards Scalable Cell-free Massive MIMO Networks. In Proceedings of the 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 1222–1227. [Google Scholar] [CrossRef]
- Miretti, L.; Björnson, E.; Gesbert, D. Team MMSE Precoding with Applications to Cell-Free Massive MIMO. IEEE Trans. Wirel. Commun. 2022, 21, 6242–6255. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. A New Look at Cell-Free Massive MIMO: Making It Practical with Dynamic Cooperation. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Y.; Qiao, X.; Yang, L. Spatially Correlated Rayleigh Fading for Cell-Free Massive MIMO Systems. IEEE Access 2020, 8, 42154–42168. [Google Scholar] [CrossRef]
- Magueta, R.; Castanheira, D.; Silva, A.; Dinis, R.; Gameiro, A. Hybrid Iterative Space-Time Equalization for Multi-User mmW Massive MIMO Systems. IEEE Trans. Commun. 2017, 65, 608–620. [Google Scholar] [CrossRef]
- Magueta, R.; Castanheira, D.; Silva, A.; Dinis, R.; Gameiro, A. Hybrid Multi-User Equalizer for Massive MIMO Millimeter-Wave Dynamic Subconnected Architecture. IEEE Access 2019, 7, 79017–79029. [Google Scholar] [CrossRef]
- Zhao, Y.; Niemegeers, I.G.; De Groot, S.H. Power Allocation in Cell-Free Massive MIMO: A Deep Learning Method. IEEE Access 2020, 8, 87185–87200. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Tran, L.N.; Duong, T.Q.; Matthaiou, M.; Larsson, E.G. On the Total Energy Efficiency of Cell-Free Massive MIMO. IEEE Trans. Green Commun. Netw. 2018, 2, 25–39. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Tataria, H.; Matthaiou, M.; Jin, S.; Larsson, E.G. On the Performance of Cell-Free Massive MIMO in Ricean Fading. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 980–984. [Google Scholar] [CrossRef]
- Mai, T.C.; Ngo, H.Q.; Duong, T.Q. Uplink Spectral Efficiency of Cell-free Massive MIMO with Multi-Antenna Users. In Proceedings of the 2019 3rd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom), Hanoi, Vietnam, 21–22 March 2019; pp. 126–129. [Google Scholar] [CrossRef]
- Bashar, M.; Cumanan, K.; Burr, A.G.; Debbah, M.; Ngo, H.Q. Enhanced Max-Min SINR for Uplink Cell-Free Massive MIMO Systems. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Bashar, M.; Cumanan, K.; Burr, A.G.; Ngo, H.Q.; Poor, H.V. Mixed Quality of Service in Cell-Free Massive MIMO. IEEE Commun. Lett. 2018, 22, 1494–1497. [Google Scholar] [CrossRef]
- Bashar, M.; Ngo, H.Q.; Burr, A.G.; Maryopi, D.; Cumanan, K.; Larsson, E.G. On the Performance of Backhaul Constrained Cell-Free Massive MIMO with Linear Receivers. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 624–628. [Google Scholar] [CrossRef]
- Bashar, M.; Cumanan, K.; Burr, A.G.; Ngo, H.Q.; Debbah, M.; Xiao, P. Max–Min Rate of Cell-Free Massive MIMO Uplink with Optimal Uniform Quantization. IEEE Trans. Commun. 2019, 67, 6796–6815. [Google Scholar] [CrossRef]
- Bashar, M.; Cumanan, K.; Burr, A.G.; Ngo, H.Q.; Larsson, E.G.; Xiao, P. Energy Efficiency of the Cell-Free Massive MIMO Uplink with Optimal Uniform Quantization. IEEE Trans. Green Commun. Netw. 2019, 3, 971–987. [Google Scholar] [CrossRef]
- Interdonato, G.; Buzzi, S. Joint Optimization of Uplink Power and Computational Resources in Mobile Edge Computing-Enabled Cell-Free Massive MIMO. arXiv 2022, arXiv:2111.04678. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.K.; Han, H.D.; Nguyen, V.D. Optimal Power Control and Load Balancing for Uplink Cell-Free Multi-User Massive MIMO. IEEE Access 2018, 6, 14462–14473. [Google Scholar] [CrossRef]
- Nikbakht, R.; Mosayebi, R.; Lozano, A. Uplink Fractional Power Control and Downlink Power Allocation for Cell-Free Networks. IEEE Wirel. Commun. Lett. 2020, 9, 774–777. [Google Scholar] [CrossRef]
- Sarker, M.; Fapojuwo, A.O. Uplink Power Allocation Scheme for User-Centric Cell-free Massive MIMO Systems. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chakraborty, S.; Demir, Ö.T.; Björnson, E.; Giselsson, P. Efficient Downlink Power Allocation Algorithms for Cell-Free Massive MIMO Systems. IEEE Open J. Commun. Soc. 2021, 2, 168–186. [Google Scholar] [CrossRef]
- Farooq, M.; Ngo, H.Q.; Nam Tran, L. A Low-Complexity Approach for Max-Min Fairness in Uplink Cell-Free Massive MIMO. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 25–28 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Tran, L.N.; Ngo, H.Q. First-Order Methods for Energy-Efficient Power Control in Cell-Free Massive MIMO: Invited Paper. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019; pp. 848–852. [Google Scholar] [CrossRef]
- Bashar, M.; Akbari, A.; Cumanan, K.; Ngo, H.Q.; Burr, A.G.; Xiao, P.; Debbah, M.; Kittler, J. Exploiting Deep Learning in Limited-Fronthaul Cell-Free Massive MIMO Uplink. IEEE J. Sel. Areas Commun. 2020, 38, 1678–1697. [Google Scholar] [CrossRef]
- Rajapaksha, N.; Shashika Manosha, K.B.; Rajatheva, N.; Latva-Aho, M. Deep Learning-based Power Control for Cell-Free Massive MIMO Networks. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Virtual, 14–23 June 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Zhao, Y.; Niemegeers, I.G.; De Groot, S.H. Dynamic Power Allocation for Cell-Free Massive MIMO: Deep Reinforcement Learning Methods. IEEE Access 2021, 9, 102953–102965. [Google Scholar] [CrossRef]
- D’Andrea, C.; Zappone, A.; Buzzi, S.; Debbah, M. Uplink Power Control in Cell-Free Massive MIMO via Deep Learning. In Proceedings of the 2019 IEEE 8th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Le gosier, Guadeloupe, 15–18 December 2019; pp. 554–558. [Google Scholar] [CrossRef]
- Mazhari Saray, A.; Ebrahimi, A. MAX- MIN Power Control of Cell Free Massive MIMO System employing Deep Learning. In Proceedings of the 2022 4th West Asian Symposium on Optical and Millimeter-Wave Wireless Communications (WASOWC), Tabriz, Iran, 12–13 May 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Jin, Y.; Buzzi, S.; Ai, B. Deep Learning-Based Power Control for Uplink Cell-Free Massive MIMO Systems. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zaher, M.; Demir, Ö.T.; Björnson, E.; Petrova, M. Distributed DNN Power Allocation in Cell-Free Massive MIMO. In Proceedings of the 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 722–726. [Google Scholar] [CrossRef]
- Zaher, M.; Demir, Ö.T.; Björnson, E.; Petrova, M. Learning-Based Downlink Power Allocation in Cell-Free Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2023, 22, 174–188. [Google Scholar] [CrossRef]
- Rahmani, M.; Bashar, M.; Dehghani, M.J.; Xiao, P.; Tafazolli, R.; Debbah, M. Deep Reinforcement Learning-based Power Allocation in Uplink Cell-Free Massive MIMO. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; pp. 459–464. [Google Scholar] [CrossRef]
- Doan, T.X.; Nguyen, L.D. Uplink Performance of Cell-Free Massive MIMO with Access Point Selections. EAI Endorsed Trans. Ind. Netw. Intell. Syst. 2018, 5, e2. [Google Scholar] [CrossRef]
- Peng, Q.; Ren, H.; Pan, C.; Liu, N.; Elkashlan, M. Resource Allocation for Cell-free Massive MIMO enabled URLLC Downlink Systems. In Proceedings of the 2022 IEEE/CIC International Conference on Communications in China (ICCC), Foshan, China, 11–13 August 2022; pp. 838–843. [Google Scholar] [CrossRef]
- Vu, T.X.; Chatzinotas, S.; Shahbaz Panahi, S.; Ottersten, B. Joint Power Allocation and Access Point Selection for Cell-free Massive MIMO. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Palhares, V.M.T.; De Lamare, R.; Flores, A.; Landau, L. Iterative AP selection, MMSE precoding and power allocation in cell-free massive MIMO systems. IET Commun. 2021, 14, 3996–4006. [Google Scholar] [CrossRef]
- Dao, H.T.; Kim, S. Effective Channel Gain-Based Access Point Selection in Cell-Free Massive MIMO Systems. IEEE Access 2020, 8, 108127–108132. [Google Scholar] [CrossRef]
- Chien, T.V.; Björnson, E.; Larsson, E.G. Optimal Design of Energy-Efficient Cell-Free Massive Mimo: Joint Power Allocation and Load Balancing. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 5145–5149. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, Q.; Haas, H.; Wang, Z. Joint User Association and Power Allocation for Cell-Free Visible Light Communication Networks. IEEE J. Sel. Areas Commun. 2018, 36, 136–148. [Google Scholar] [CrossRef]
- Biswas, S.; Vijayakumar, P. AP selection in Cell-Free Massive MIMO system using Machine Learning Algorithm. In Proceedings of the 2021 Sixth International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 25–27 March 2021; pp. 158–161. [Google Scholar] [CrossRef]
- Wang, R.; Shen, M.; He, Y.; Zhou, H. Access Point Selection for Cell-free Massive MIMO Over Rician Fading Channels. In Proceedings of the 2020 7th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 18–20 December 2020; pp. 164–168. [Google Scholar] [CrossRef]
- Wei, C.; Xu, K.; Xia, X.; Su, Q.; Shen, M.; Xie, W.; Li, C. User-Centric Access Point Selection in Cell-Free Massive MIMO Systems: A Game-Theoretic Approach. IEEE Commun. Lett. 2022, 26, 2225–2229. [Google Scholar] [CrossRef]
- Jung, S.; Hong, S.E.; Na, J.H. Access Point Selection Schemes for Cell-free Massive MIMO UDN Systems. In Proceedings of the 2022 13th International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 19–21 October 2022; pp. 1601–1603. [Google Scholar] [CrossRef]
- Ranasinghe, V.; Rajatheva, N.; Latva-aho, M. Graph Neural Network Based Access Point Selection for Cell-Free Massive MIMO Systems. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Shakya, I.L.; Ali, F.H. Joint Access Point Selection and Interference Cancellation for Cell-Free Massive MIMO. IEEE Commun. Lett. 2021, 25, 1313–1317. [Google Scholar] [CrossRef]
- Mendoza, C.F.; Schwarz, S.; Rupp, M. Deep Reinforcement Learning for Dynamic Access Point Activation in Cell-Free MIMO Networks. In Proceedings of the WSA 2021—25th International ITG Workshop on Smart Antennas, French Riviera, France, 10–12 November 2021; pp. 1–6. [Google Scholar]
- O’Hurley, S.; Tran, L.N. A Comparison of the Uplink Performance of Cell-Free Massive MIMO using Three Linear Combining Schemes: Full-Pilot Zero Forcing with Access Point Selection, Matched-Filter and Local-Minimum-Mean-Square Error. In Proceedings of the 2020 31st Irish Signals and Systems Conference (ISSC), Letterkenny, Ireland, 11–12 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, W.; Schotten, H.D. Opportunistic AP Selection in Cell-Free Massive MIMO-OFDM Systems. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Ghiasi, N.; Mashhadi, S.; Farahmand, S.; Razavizadeh, S.M.; Lee, I. Energy Efficient AP Selection for Cell-Free Massive MIMO Systems: Deep Reinforcement Learning Approach. IEEE Trans. Green Commun. Netw. 2023, 7, 29–41. [Google Scholar] [CrossRef]
- Wang, J.; Wang, B.; Fang, J.; Li, H. Millimeter Wave Cell-Free Massive MIMO Systems: Joint Beamforming and AP-User Association. IEEE Wirel. Commun. Lett. 2022, 11, 298–302. [Google Scholar] [CrossRef]
- Wang, Z.; Li, M.; Liu, R.; Liu, Q. Joint User Association and Hybrid Beamforming Designs for Cell-Free mmWave MIMO Communications. IEEE Trans. Commun. 2022, 70, 7307–7321. [Google Scholar] [CrossRef]
- Björnson, E.; Ottersten, B. On the principles of multicell precoding with centralized and distributed cooperation. In Proceedings of the 2009 International Conference on Wireless Communications & Signal Processing, Nanjing, China, 13–15 November 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Sanchez, J.R.; Rusek, F.; Sarajlic, M.; Edfors, O.; Liu, L. Fully Decentralized Massive MIMO Detection Based on Recursive Methods. In Proceedings of the 2018 IEEE International Workshop on Signal Processing Systems (SiPS), Cape Town, South Africa, 21–24 October 2018; pp. 53–58. [Google Scholar] [CrossRef]
- Jeon, C.; Li, K.; Cavallaro, J.R.; Studer, C. Decentralized Equalization with Feedforward Architectures for Massive MU-MIMO. IEEE Trans. Signal Process. 2019, 67, 4418–4432. [Google Scholar] [CrossRef]
- Shaik, Z.H.; Björnson, E.; Larsson, E.G. Cell-Free Massive MIMO with Radio Stripes and Sequential Uplink Processing. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Shaik, Z.H.; Björnson, E.; Larsson, E.G. MMSE-Optimal Sequential Processing for Cell-Free Massive MIMO with Radio Stripes. IEEE Trans. Commun. 2021, 69, 7775–7789. [Google Scholar] [CrossRef]
- Miretti, L.; Björnson, E.; Gesbert, D. Precoding for Scalable Cell-free Massive MIMO with Radio Stripes. In Proceedings of the 2021 IEEE 22nd International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 27–30 September 2021; pp. 411–415. [Google Scholar] [CrossRef]
- López, O.L.A.; Kumar, D.; Souza, R.D.; Popovski, P.; Tölli, A.; Latva-Aho, M. Massive MIMO with Radio Stripes for Indoor Wireless Energy Transfer. IEEE Trans. Wirel. Commun. 2022, 21, 7088–7104. [Google Scholar] [CrossRef]
- Ma, Y.; Yuan, Z.; Yu, G.; Chen, Y. Cooperative Scheme for Cell-free Massive MIMO with Radio Stripes. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Yuan, Z.; Ma, Y.; Yu, G. LMMSE Processing for Cell-free Massive MIMO with Radio Stripes and MRC Fronthaul. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; pp. 1336–1340. [Google Scholar] [CrossRef]
- Tominaga, E.N.; L’opez, O.L.A.; Souza, R.D.; Alves, H. Statistical Analysis of Received Signal Strength in Industrial IoT Distributed Massive MIMO Systems. In Proceedings of the 2022 Joint European Conference on Networks and Communications 6G Summit (EuCNC/6G Summit), Grenoble, France, 7–10 June 2022; pp. 100–105. [Google Scholar]
- Mishra, A.K.; Ponnusamy, V. Analytical outage and coverage performance analysis of cell-free massive MIMO system based on radio stripe. Int. J. Commun. Syst. 2021, 34, e4914. [Google Scholar] [CrossRef]
- Chiotis, I.; Moustakas, A.L. On the Uplink Performance of Finite-Capacity Radio Stripes. In Proceedings of the 2022 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Athens, Greece, 5–8 September 2022; pp. 118–123. [Google Scholar] [CrossRef]
- Lakkimsetti, S.; Singh Kshetrimayum, R. Ultra-thin and conformal SSPP based UWB low pass filter for B5G Radio Stripe Networks. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Applied Electromagnetics (APACE), Penang, Malaysia, 20–22 December 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Pathak, B.B.; Kshetrimayum, R.S. Conformal and Compact Low Pass Filter based on SSPP for B5G NR FR1 Radio Stripe Network Application. In Proceedings of the 2023 International Conference on Microwave, Optical, and Communication Engineering (ICMOCE), Bhubaneswar, India, 26–28 May 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ponnusamy, V. Millimeter Wave and Radio Stripe: A Prospective Wireless Technology for 6G and Beyond Networks. In Proceedings of the 2021 Smart Technologies, Communication and Robotics (STCR), Sathyamangalam, India, 9–10 October 2021; pp. 1–3. [Google Scholar] [CrossRef]
- Martins, Ó.; Conceição, F.; Gomes, M.; Silva, V.; Dinis, R. Achievable Capacity for Continuous Radio Stripe LOS Communications. IEEE Commun. Lett. 2023, 27, 2792–2796. [Google Scholar] [CrossRef]
- Conceição, F.; Antunes, C.H.; Gomes, M.; Silva, V.; Dinis, R. User Fairness in Radio Stripes Networks using Meta-Heuristics optimization. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Conceição, F.; Gomes, M.; Silva, V.; Dinis, R.; Antunes, C.H. Bi-Objective Power Optimization of Radio Stripe Uplink Communications. Electronics 2022, 11, 876. [Google Scholar] [CrossRef]
- Conceição, F.; Gomes, M.; Silva, V.; Dinis, R.; Antunes, C.H. Joint Spectral and Power Efficiency Optimization in Uplink Radio Stripes. IEEE Trans. Commun. [CrossRef]
- Conceição, F.; Martins, L.; Gomes, M.; Silva, V.; Dinis, R. Access Point Selection for Spectral Efficiency and Load Balancing Optimization in Radio Stripes. IEEE Commun. Lett. 2023, 27, 2383–2387. [Google Scholar] [CrossRef]
- Frenger, P.; Hederen, J.; Hessler, M.; Interdonato, G. Improved Antenna Arrangement for Distributed Massive MIMO. European. EP3552318B1, 30 September 2020. [Google Scholar]
- Fascista, A.; Deutschmann, B.J.B.; Keskin, M.F.; Wilding, T.; Coluccia, A.; Witrisal, K.; Leitinger, E.; Seco-Granados, G.; Wymeersch, H. Uplink Joint Positioning and Synchronization in Cell-Free Deployments with Radio Stripes. arXiv 2023, arXiv:2302.03387. [Google Scholar] [CrossRef]
- Jo, S.; Lee, H.; Park, S.H. Joint Precoding and Fronthaul Compression for Cell-Free MIMO Downlink with Radio Stripes. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 4945–4951. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, H.; Xia, W.; Wang, Q.; Zhang, Y.; Ni, Y. Energy-Efficient Cell-Free Massive MIMO Systems Based on Radio Stripe. In Proceedings of the 2023 IEEE 23rd International Conference on Communication Technology (ICCT), Wuxi, China, 20–22 October 2023; pp. 1375–1379. [Google Scholar] [CrossRef]
- Gashtasbi, A.; Da Silva, M.M.; Dinis, R. On the Performance of LDPC Codes over Radio Stripes System. In Proceedings of the 2023 Photonics & Electromagnetics Research Symposium (PIERS), Prague, Czech Republic, 3–6 July 2023; pp. 1018–1023. [Google Scholar] [CrossRef]
- Chiotis, I.; Moustakas, A.L. Optimal MMSE Processing for Limited-Capacity Radio Stripes. In Proceedings of the 2023 International Symposium on Networks, Computers and Communications (ISNCC), Doha, Qatar, USA, 23–26 October 2023; pp. 1–6. [Google Scholar]
- Conceição, F.; Pereira, A.; Gomes, M.; Silva, V.; Dinis, R. Active Intelligent Surfaces for Next Generation Radio Systems: An Overview on Large Intelligent Surfaces and Radio Stripes. In Proceedings of the 2024 14th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP 2024), Rome, Italy, 17–19 July 2024; pp. 1–6. [Google Scholar]
- Mishra, A.K.; Vijayakumar, P. AP Switch ON/OFF strategy in Green Cell-Free massive MIMO Based Radio Stripe Network. In Proceedings of the 2021 5th International Conference on Computer, Communication and Signal Processing (ICCCSP), Chennai, India, 24–25 May 2021; pp. 125–130. [Google Scholar] [CrossRef]
- Alves, M.; Antunes, C.; Costa, J. New concepts and an algorithm for multiobjective bilevel programming: Optimistic, pessimistic and moderate solutions. Oper. Res. 2019, 21, 2593–2626. [Google Scholar] [CrossRef]
- Antunes, C.; Alves, M.; Clímaco, J. Multiobjective Linear and Integer Programming; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; TIK Report; ETH Zurich, Computer Engineering and Networks Laboratory: Zurich, Switzerland, 2001; Volume 103. [Google Scholar] [CrossRef]
- Sörensen, K.; Glover, F.W. Metaheuristics. In Encyclopedia of Operations Research and Management Science; Gass, S.I., Fu, M.C., Eds.; Springer: Boston, MA, USA, 2013; pp. 960–970. [Google Scholar]
- Michalewicz, Z. How to Solve It: Modern Heuristics 2e; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gendreau, M.; Potvin, J.Y. Handbook of Metaheuristics, 2nd ed.; Springer Publishing Company, Incorporated: New York, NY, USA, 2010. [Google Scholar]
- Bento, P.; Antunes, C.H.; Gomes, M.; Dinis, R.; Silva, V. Beamforming Optimization for Multiuser Wireless Systems Using Meta-Heuristics. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
| Spectral Efficiency (SE) | |||
|---|---|---|---|
| Max-Sum Rate (MSR) | Max-Min Fairness (MMF) | Power Efficiency (PE) | |
| Successive Convex Approximation (SCA) SO optimization | UL: GP-based [78] LSF-based [80] DL: Weighted MMSE and FrP-based [81], | UL: MRC-based bisection [14] Rician distribution bisection [70] ZF-based bisection [71] GP-based [49,72,78] QoS-constrained [73] Limited backhaul [74] Uniform quantization [75] LSF-based [80] MH-based [58] DL: LSF-based [79] FrP-based [81] | UL: MTP [78,80] DL: HW and backhaul [69] QoS-constrained [76] |
| Non-convex SO optimization | UL: APG-based [82] | DL: First-order method [83] | |
| Deep Learning (DeL) SO optimization | UL: DNN-based [87,88] DL: DNN and MRT-based [56] DNN MRT/RZF [90,91] | UL: DNN-based [87,88] Unsupervised low training MRC-based [89] DL: DNN-based [85] DNN and MRT-based [56,68] | UL: GP and DCNN/LSF-based [84] DL: DRL-based [86] |
| BO optimization | UL: DRL/LSF and SCA-based [92] | UL: SCA MTP and latency-constrained [77] | |
| Paper Reference | Optimization Technique | Computational Complexity |
|---|---|---|
| [14] | SOCP with iterative bisection search | High |
| [69] | Linear programming with bisection method | High |
| [70] | Generalized eigenvalue problem, bisection method | High |
| [71] | Generalized eigenvalue problem | Moderate |
| [72] | GP | Moderate |
| [73] | GP | Moderate |
| [74] | SCA | High |
| [75] | Convex optimization with uniform quantization | High |
| [76] | Convex optimization | High |
| [77] | Convex optimization | High |
| [78] | SCA | High |
| [79] | LSF-based scalable policies | Moderate |
| [80] | Convex optimization | Moderate |
| [81] | FrP | Moderate |
| [82] | Nesterov’s smoothing technique, APG | Moderate |
| [83] | First-order method for non-convex programming | Moderate |
| [84] | DCNN with GP | Moderate |
| [85] | DNN | Low |
| [68] | Heuristic with non-convex iteration, DNN | High (heuristic), Low (DNN) |
| [86] | DRL | High |
| [87] | DeL and DNN | Low |
| [88] | DeL and DNN | Low |
| [89] | Unsupervised low training complexity DeL approach | Low |
| [90] | DNN | Low |
| [91] | DNN | Low |
| [58] | MH approaches | Variable |
| [92] | Twin delayed DRL deterministic policy gradient, SCA | High |
| Capacity Requirements | Load Balance (LB) | Spectral Efficiency (SE) | Power Efficiency (PE) | |
|---|---|---|---|---|
| SO optimization | UL: Fronthaul [93,101] MMSE-based [105] | UL: Power control aided [78] | UL: Game theory-based [102] DL: ZF/LSF-based [94] Power control aided with MMSE [96] Sequential/LSF-based [97] Linear assignment-based [103] Joint beamforming for mmWave [110] mmWave-based [111] | DL: Power control aided with LSF-based [69] QoS-constrained [95] |
| Deep Learning (DeL) SO optimization | UL: Graph neural network-based [104] DL: Cluster-based [100] | UL: DRL/SE QoS-constrained [109] DL: QoS/DRL-based [106] | ||
| BO optimization | UL: Virtual clusters-based [87] DL: SOCP-based [98] Dual projected gradient SCA-based [99] | UL: ZF-based [107] DL: Distance/OFDM-based [108] |
| Paper Reference | Optimization Technique | Computational Complexity |
|---|---|---|
| [69] | DeL with APS (power/control coefficients, LSF) | High |
| [94] | ZF precoding, LSF-based APS | Moderate |
| [95] | DL joint power allocation, APS | High |
| [96] | Iterative APS, MMSE precoding, power allocation | High |
| [97] | Sequential DL APS with LSF, effective channel gain calculation | Moderate |
| [93] | UL APS, novel signal detection method | Moderate |
| [98] | APS for DL SE, LB | Moderate |
| [78] | UL power control, LB | Moderate |
| [99] | Joint APS and power control in visible light CF | Moderate |
| [100] | Cluster-based APS using MaL for DL | Moderate |
| [101] | APS for UL with Rician fading channel | Moderate |
| [102] | UL APS using game theory for AP service cluster formation | Moderate |
| [103] | DL SE prioritization with linear assignment APS | Low |
| [104] | Graph neural network-based UL APS | Low |
| [105] | CE-based APS with SINR assessment for UL | Moderate |
| [106] | DRL-based dynamic AP-UE association for DL | High |
| [107] | Full-pilot ZF combining APS for DL | Moderate |
| [108] | Distance-based DL APS with orthogonal sub-carrier assignment | Moderate |
| [109] | DRL for UL APS optimizing PE with rate constraints | High |
| [87] | Cell-centric clustering of APs, virtual cluster UE association | High |
| [110] | Beamforming combined with DL APS in mmWave | Moderate |
| [111] | AP-UE association, hybrid beamforming, fronthaul compression | Moderate |
| Equalization or Precoding | RF Wireless Energy Transfer | IoT and mmWave | Coverage and Codification | Network Design | Resource Allocation (RA) | |
|---|---|---|---|---|---|---|
| Uplink (UL) | NLMMSE-based [115] OSLP-based [116] RZF-based [119] Quasi-LMMSE-based [120] Clustered-based [123] Cluster-MMSE-based [137] | MRT-based [118] | Spatial Diversity Performance [121] Exploration [126] Integration [127] | Outage Probabilities [122] LDPC codification [136] | Comparison with CF [16] Comparison with LIS [138] Low-pass [124,125] Joint Positioning and synchronization with ML [133] | APS to improve PE [135,139] SO power optimization [128] BO power optimization [129] BO APS to improve SE/LB [131] MO power optimization [130] |
| Downlink (DL) | Team MMSE-based [117] Joint precoding and fronthaul compression [134] | Outage Probabilities [122] | Comparison with CF [16] Low-pass [124,125] | APS to improve PE [139] |
| Metric | CF | RS |
|---|---|---|
| SE | High, improves with the number of antennas and APs; scalable | High, with potential improvements using RA |
| Deployment Complexity | Complex, requires multiple distributed APs | Relatively simpler due to linear arrangement of APs in stripes |
| Interference Management | Better interference management due to distributed nature | Effective interference management due to sequentially connected APs |
| Coverage | Wide coverage with uniform UE distribution | Suitable for medium/small scenarios, enhanced by the linear distribution of APs |
| CH | Weaker than cellular mMIMO, relies on distributed APs | Improved due to the structured deployment of APs |
| PE | High, with proper power control strategies | High, especially with optimized power allocation |
| Scalability | Scalable by adding more APs | Scalable, facilitated by the stripe architecture |
| Latency | Low, but depends on efficient fronthaul and LPU | Medium, with potential improvements from streamlined connectivity of APs |
| Cost | Potentially higher due to more HW and complex deployment | Lower due to simpler and more linear deployment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conceição, F.; Gomes, M.; Silva, V.; Dinis, R. Survey on Resource Allocation for Future 6G Network Architectures: Cell-Free and Radio Stripe Technologies. Electronics 2024, 13, 2489. https://doi.org/10.3390/electronics13132489
Conceição F, Gomes M, Silva V, Dinis R. Survey on Resource Allocation for Future 6G Network Architectures: Cell-Free and Radio Stripe Technologies. Electronics. 2024; 13(13):2489. https://doi.org/10.3390/electronics13132489
Chicago/Turabian StyleConceição, Filipe, Marco Gomes, Vitor Silva, and Rui Dinis. 2024. "Survey on Resource Allocation for Future 6G Network Architectures: Cell-Free and Radio Stripe Technologies" Electronics 13, no. 13: 2489. https://doi.org/10.3390/electronics13132489
APA StyleConceição, F., Gomes, M., Silva, V., & Dinis, R. (2024). Survey on Resource Allocation for Future 6G Network Architectures: Cell-Free and Radio Stripe Technologies. Electronics, 13(13), 2489. https://doi.org/10.3390/electronics13132489








