1. Introduction
In the current communication environment, characterized by an increasing reliance on data and network availability, it is crucial to provide smooth and unrestricted data transmission and communications. Nevertheless, conventional cellular networks encounter obstacles such as signal deterioration and user movement that surpass the coverage zones offered by network operators. In order to tackle these problems, emerging technologies such as blockchain present encouraging possibilities, specifically in the shape of blockchain radio access networks (B-RAN) [
1]. The B-RAN utilizes the distributed ledger technology of blockchain to create a reliable and effective system for network access and authentication, even when dealing with untrusted actors. The use of blockchain technology in radio access networks creates a decentralized environment in which individuals may easily switch roles from being users to providers. This innovative architectural design optimizes network availability, streamlines data offloading across numerous providers, minimizes latency, and guarantees exceptional up time. In order to fully use the advantages of the B-RAN, such as improved network accessibility, less congestion, and minimal latency, a strong incentive mechanism is crucial [
2]. This requires establishing agreements between the providers for mutually beneficial financial incentives [
3]. In this work, we introduce the Smart Pricing Policies (SPP) module, a customized solution designed to tackle this challenge, suggesting an adaptable framework. With the SPP module, we aim to contribute to the overall research and try to reach beyond the state of the art. More specifically, our study aims for the following:
Design and develop the SPP module utilizing reverse auction theory in a deep reinforcement learning environment.
Showcase that SPP can be integrated in smart contracts always adhering to the technical and decentralized requirements of the B-RAN.
Create a fair and democratic procedure to determine a price between the MNOs that maximizes the profit for both the original and temporary operators. This will allow more MNOs to participate in the network, expand its range and services, and provide an uninterrupted experience for the users.
The architectural flexibility of SPP allows for the development of financial incentives tailored to unique contexts, maximizing profit margins for both MNOs, the one that signed a contract with the end user and the one that will act as a temporary provider. The SPP module utilizes the reverse auction theory from the game theory family implemented with reinforcement learning [
4], in order to return the maximum incentive profit for both the original and the new alternative provider. The choice of deep reinforcement learning [
5] to implement the reverse auction theory boosts the scalability and reliability of the system and make it as fair as it can be for all the participants. Additionally, the low complexity of the implementation gives the flexibility for the code to be executed as a smart contract inside the blockchain, securing the tamper-proof procedures and the transparency of the transactions.
The computational complexity of our code is minimal, and it is executed instantly within the smart contract. Therefore, there is no need for latency improvements in our system. Our main objective is to create a stable and democratic system that can provide monetary agreements that meet the needs of all participants, with a particular emphasis on the original MNO. In order to protect democratic values, we allocate a DRL agent to every candidate MNO. This strategy utilizes a blend of incentives and chance, providing each MNO with multiple chances to win the bid. The procedure is regulated by the minimum and maximum bids set by the participants, which ensures that smaller offers do not have an unfair advantage. Within this particular framework, our participation is directed towards attaining societal advantages, rather than exclusively prioritizing the system.
The end customers have agreed to a Service Level Agreement (SLA) and are already enjoying the advantages of the network, which has transferred the duty to the MNOs, who are now maximizing their revenues. In addition, we have created a versatile and adaptable platform for network managers, enabling them to easily customize the code to suit their individual requirements. This encompasses the capacity to modify the incentive structure and the overall number of iterations, thereby establishing a favorable environment customized to their specific needs.
In our decision-making process, we chose to utilize reverse game theory instead of Stackelberg games. This choice was made because our specific problem involves a single buyer, the original MNO, who is looking to purchase goods from multiple sellers at the most favorable price. However, it is important to note that, in our scenario, participants are only allowed to reveal their ranks and not their bids, which is a mandatory condition in Stackelberg games. Our goal is to establish a setting in which the bidding result is economically advantageous for the buyer, accomplished in the most efficient and democratic way feasible.
The structure of the paper is as follows:
Section 2: This section offers a comprehensive analysis of the game theoretic techniques that can be used in smart pricing systems, along side an outline of the B-RAN.
Section 3: We present prior works in the field of smart pricing and the associated techniques.
Section 4: We present our Smart Pricing Policies module implemented with the reverse auction theory and reinforcement theory.
Section 5: In this section, we provide the results of comprehensive tests performed to evaluate the effectiveness of the Smart Pricing Policies module.
Section 6: The last section integrates the results obtained from the experiments, analyzing their significance for both theoretical understanding and practical application. The text provides a critical analysis of the merits and limits of the present solution, as well as identifying opportunities for future research.
2. Background Knowledge
In this section, our goal is to describe the background knowledge required for our work. We sum up the main technologies we incorporated in our research, as well as key theoretical knowledge that is essential in order to understand our motivation and point of view. More specifically, we describe the blockchain and blockchain radio access networks, a number of game theory techniques used extensively in scenarios similar to ours, as well as how reinforcement learning (RL) could prove useful to our work [
6].
2.1. Blockchain
Blockchain is a decentralized and transparent system that enables the recording of transactions between untrusted participants. The ledger is immutable and expands chronologically as new records, known as blocks, are appended to include the latest transactions. Every block includes transaction data, a timestamp, and a hash of the preceding block, among other things. The latter ensures the integrity of the data, as any attempt to edit data in a block will result in erroneous hash values, until all blocks’ hashes are recalculated [
7]. The National Institute of Standards and Technology (NIST) [
8] categorizes blockchain into two basic types: permissioned (private) and permissionless (public). In a permissioned blockchain, participants require authorization from a governing authority to join the network. On the other hand, a permissionless blockchain allows anyone to freely engage without any restrictions. The blockchain offers immutability, as it is not possible to tamper with or delete the data of a block, as even a small modification in the block’s data will change its hash value. This consequently alters the hash value of every subsequent block in the chain, and any changes to the information in a previous block usually necessitate the replacement of all subsequent blocks. The distributed nodes that participate in the network can maintain a duplicate of the ledger, which aids in the building of trust between them. The consensus mechanism is utilized to establish rules for checking and validating blocks, as well as ensuring unanimous agreement among all participants regarding the present state of the chain and the smart contracts, which are programs that run automatically when specific criteria are fulfilled, and its outcome must be unanimously accepted by all involved parties.
2.2. Blockchain Radio Access Network (B-RAN)
Giupponi et al. [
9] introduced a novel O-RAN-based blockchain-enabled architecture that allows mobile operators and others to exchange RAN resources autonomously and dynamically. This integration enhances mobile networks’ reliability and trust, bringing confidence to O-RAN environments. Xu et al. [
10] presented a blockchain-enabled mutual authentication architecture for Open RAN, implementing Blockchain Addresses issued from users’ public keys for secure and effective authentication. Velliangiri et al. [
11] discussed a privacy-preserving framework for increased efficiency and security. The B-RAN architecture, as proposed by them, can improve the performance and sustainability of 5G networks in neglected rural areas. The architecture’s fundamental components include the Proof-of-Connection consensus algorithm, specialized mining software, strict node authentication, and local digital asset staking. The B-RAN is a decentralized architecture designed to improve security and privacy in identification and authentication processes within the growing radio access networks in 5G and beyond. Specifically, the B-RAN offers user-centric identity management for User Equipment and RAN elements, allowing mutual authentication for all entities and permitting on-demand point-to-point communication with accountable billing services over public networks [
1]. The B-RAN protocol offers significant enhancements in terms of communication and computation overheads when compared to current communication authentication technologies.
2.3. Reinforcement Learning
RL is an intriguing field of machine learning that draws inspiration from our ability to learn by engaging in trial and error [
12]. Consider an agent situated within an environment, such as a simulated labyrinth. The agent lacks a map or instructions, yet it possesses a clear objective: to reach a designated location and obtain a prize. The agent engages in exploration by taking actions, observing the response of the environment, and acquiring knowledge from the resulting outcomes. When an RL agent follows a winning strategy, it receives a reward from the system, which strengthens and continues this approach. Conversely, agents that fail to adhere to the intended goal forfeit rewards and are obligated to modify and update their decision-making procedures [
13]. Over time, the agent improves its strategy, developing a decision-making mechanism—a policy—to reliably navigate the maze and obtain the reward. This fundamental notion of acquiring knowledge through firsthand encounters applies to intricate issues. Artificial intelligence systems can employ reinforcement learning methods to train them in various tasks, including game play, robot control, and resource management optimization. This is achieved by iteratively improving their actions based on the feedback they receive. It is an effective technique for promoting intelligent decision-making in machines, enabling them to address situations where the path to success is not always clearly defined [
14]. Standard reinforcement learning often faces challenges when dealing with complex state and action spaces that require discretization or simple linear function approximations. Deep reinforcement learning (DRL) overcomes these limitations by incorporating deep learning techniques. Deep reinforcement learning is capable of properly handling complex, high-dimensional data by utilizing neural networks as function approximators [
15].
2.4. Game Theory
Through our thorough research, we have come to the following conclusion regarding the nature of our problem. Since it involves analyzing strategic interactions between rational decision-makers in situations where the outcome of each player’s action depends on the actions of others, it falls under the umbrella of game theoretic problems. In our scenario, those decision-makers and players are telecommunication providers, data vendors, etc. Below, we examine what we think are the most suitable game theory models for the aforementioned scenario. In the next section, we will demonstrate some related work based on them.
2.4.1. Stackelberg Games
In game theory, Stackelberg games are used to analyze situations where actors, such as corporations in a market, make decisions one after another [
16]. The main difference is that there is a leader and a follower. The leader, known as the Stackelberg leader, gains the benefit of making the first move and committing to a certain action, such as determining a price. After observing the leader’s action, the follower decides on his/her optimal response, which could include determining the appropriate level of production. The sequential nature of this feature provides the leader with an advantage in comparison to games where all participants make their choices simultaneously. Stackelberg games are utilized in diverse domains, ranging from economics, where they simulate leadership dynamics in marketplaces, to security, where defenders strategize before attackers. These games can be solved by employing backward induction, a method that entails examining the follower’s optimal response to each conceivable action taken by the leader, and subsequently determining the leader’s most advantageous move based on this analysis. The leader’s advantage lies in his/her capacity to exert influence on the circumstances prior to the follower’s response, which may result in a more favorable outcome for the leader in contrast to scenarios involving simultaneous decision-making [
17].
2.4.2. Reverse Auction Theory
Reverse auction theory is not an independent notion in game theory, but rather, game theory is a potent instrument for examining the dynamics of these auctions [
18]. In a reverse auction, the seller takes on the role of the buyer, actively seeking to acquire an item or service. Sellers compete by submitting bids with their most competitive pricing for offering that particular commodity or service. The purchaser normally grants the contract to the vendor with the most economical offer that fulfills his/her criteria. This situation presents an opportune strategic scenario that is suitable for examination using game theory. Sellers face the challenge of striking a delicate balance: if they bid excessively high, they risk losing the contract, and if they bid excessively low, they may earn reduced profits. They take into account the potential bids of other vendors and strive to determine the most advantageous price that would secure the contract and maximize their profit. Various variables impact the techniques employed by sellers. The reserve price is the minimal price at which a seller is willing to deliver a good or service. Any bid below this price will lead to a financial loss. Sellers may also attempt to predict the bidding behavior of other sellers by leveraging historical auction data or industry expertise. Moreover, the bidding increments, which refer to the particular amounts by which sellers can decrease their bids, can impact the level of aggressiveness in sellers’ pricing strategies. By comprehending these variables and implementing game theory principles, sellers can create bidding strategies that enhance their likelihood of securing the contract while preserving profitability [
19].
2.4.3. Cournot Oligopoly
The Cournot oligopoly model, derived from game theory, provides insights into the behavior of enterprises in a market characterized by a small number of dominating players [
20]. Consider a scenario of an oligopoly where multiple companies are selling indistinguishable products. In this context, competitiveness is determined by the quantity that each firm chooses to produce, rather than the price. What is the twist? These judgments occur together. Companies in this situation are not unaware of each other’s behavior. Each participant carefully evaluates the impact of others’ output levels on the market price and, consequently, their own profits. Strategic thinking is crucial. In order to optimize its earnings, a company will select an output level that takes into account the anticipated output levels of its rivals. A stable equilibrium arises when each firm selects an ideal production quantity based on the expected output of their competitors. This phenomenon is commonly referred to as the Cournot equilibrium. In this scenario, there is no motivation for any company to alter its production level as it would not result in increased financial gains. Discovering this state of balance frequently entails utilizing response functions, which illustrate the optimal amount of production for a company based on the output chosen by a rival. The Cournot model provides useful insights. It informs us that companies in an oligopoly behave in a logical manner, consistently assessing the actions of their competitors. In addition, the equilibrium achieved in this model leads to a greater overall output compared to a monopoly, but it still falls below the level observed in a totally competitive market. In essence, the Cournot model serves as a fundamental framework for comprehending the strategic decision-making process of enterprises operating in an oligopolistic setting. Nevertheless, it is crucial to recognize the constraints of the model [
21]. It presupposes a singular decision, disregarding the potential for recurring encounters or corporations acquiring knowledge and adjusting their behavior over time. Moreover, the model depicts enterprises as possessing flawless knowledge about the market and the expenses of their competitors, which may not necessarily align with reality. Although there are certain constraints, the Cournot model continues to be a fundamental tool for comprehending oligopolistic rivalry. It enables the development of more intricate game theory models employed in economics to examine strategic decision-making in different market configurations.
2.4.4. Bertrand Model
The Bertrand model explores oligopolies, which are markets characterized by a limited number of dominant enterprises. In this context, the objective of the game is not to determine who can generate the highest quantity, but rather to identify who can present the most competitive price. Companies are engaged in a fierce competition, continuously lowering their prices in order to entice clients [
22]. The model proposed by Joseph Bertrand differs from the Cournot model in that enterprises compete by determining their production levels. Bertrand contended that enterprises will logically reduce prices to a level below the marginal cost, which is the minimal cost required to create an additional unit. The Bertrand paradox is the unexpected result of the Bertrand model. At the point of equilibrium, both firms sell their product at the precise level of their marginal cost, resulting in no profits. This occurs because, if a single company attempts to increase its price even somewhat, consumers will swiftly go to the rival firm that provides a lower price. Although the Bertrand model may appear to be a fight to achieve the lowest price, it provides vital insights into how price competition might reduce prices to the level of production costs, which could potentially be advantageous for consumers [
23]. Nevertheless, it is crucial to bear in mind that the model is based on certain assumptions, including the presence of comparable products and the availability of flawless information for consumers. In reality, other factors such as product differentiation and brand loyalty can complicate matters and have an impact on purchasing choices.
3. Previous Works
In this section, we describe how the theoretical knowledge from
Section 2 has been used to tackle problems similar to ours. We are mostly focused on demonstrating how the models, algorithms, and techniques we described above have been utilized and evaluated so far for the purpose of calculating fair prices among MNOs and data vendors in general.
3.1. Economical and Market Factors in Price Calculation
While we are most interested in the algorithmic point of view, we cannot omit the fact that price calculation also takes into account economic and market factors. These factors can be competition between telecom providers, demand–supply evaluations, client preferences, etc. In [
24], Flamini et al. and, in [
25], Kim et al. employed pricing algorithms that rely on strategic leverage and competition dynamics among operators in the telecoms industry. Operators optimize their prices to maximize their profit, taking into account factors such as client preferences and competition. The analysis encompasses scenarios in which pricing decisions are determined by owners, renters, or regulators with the aim of achieving various objectives, such as maximizing profit or promoting social welfare. The studies also examine the influence of pricing strategies on market dynamics and operator profits in different competitive environments. Another representative example, where researchers focus heavily on the external factors, can be found in [
26]. In this paper, the researchers examined parameters such as demand–supply evaluations, network traffic, latency, end-user figures, and subscriber growth rates in order to ascertain the possible viability of the network. Pricing methods are of utmost importance in these studies, as they utilize models such as the Shapley value, bargaining games, and dynamic pricing to effectively maximize revenue generation and distribute costs among stakeholders.
3.2. The Stackelberg Model
Having in mind the plethora of external factors that should be taken into account, we now need to tackle the issue of calculating the price itself. Since our problem involves analyzing strategic interactions between rational decision-makers in situations where the outcome of each player’s action depends on the actions of others, it falls under the umbrella of game theoretic problems. Indeed, there exists extensive research on this type of mathematical framework used to model and analyze such interactions. Many researchers have adopted the Stackelberg game model in their approaches. In [
27], Zhang et al. examine the application of double-auction and Stackelberg game models in the context of mobile edge computing task offloading. The double-auction concept pairs devices with limited resources with devices that share resources, guaranteeing efficient auctions. The Stackelberg game model is utilized in the context of mining job offloading, wherein the edge server adjusts its pricing techniques in response to the demand from miners. Both models have the objective of enhancing the efficiency of resource allocation, promoting social welfare, and maximizing system utility. Liue et al. also describe a Stackelberg game in [
28] that involves a sequence of subgames between the data consumer and each data owner. The focus is on the price strategies established by data owners with the engagement of market agencies. The objective of the game is to identify the Stackelberg equilibrium in each subgame, where the leader’s utility is maximized by the follower adopting its optimal answer. Backward induction is employed to analyze the Stackelberg game and ascertain the most advantageous pricing schemes and equilibrium points. Finally, in [
29], Datar et al. explore the price and allocation dynamics of strategic resources in a 5G network slicing Stackelberg game. The analysis focuses on market mechanisms, specifically examining the impact of set shares or unbounded budgets on average selling prices.
3.3. Bertrand Games and Cournot Oligopoly
Apart from Stackelberg games, researchers have also tested other models such as Bertrand games and the Cournot oligopoly. In [
30], Luong et al. explore different game theoretical concepts related to the Pricing Model for resource management in 5G. One example of such a model is the Bertrand game model, which enables many entities to compete with each other based on pricing. The game’s equilibrium is established by calculating the first-order derivative of the profit function in relation to price. Two great examples of utilizing Cournot games are found in [
31,
32]. In [
31], the researchers employ a Cournot game model to maximize Mobile Network Operator (MNO) revenues by strategically determining prices and allocating bandwidth resources. The equilibrium study demonstrates that the most effective pricing approach entails a combination of customer willingness to pay and operational costs, highlighting the need for a careful equilibrium to sustain profitability in a competitive market. In [
32], Assila et al. describe the issue of distributing cache storage resources represented as an oligopolistic market employing a Cournot game, in which Content Providers (CPs) aim to maximize profits by adjusting the quantities of content they supply. The Cournot equilibrium is influenced by the number of participants, and an approach based on non-cooperative dynamic game theory is employed to determine the optimal distribution of caching space
3.4. Reinforcement Learning
It has become apparent that game theory has been the preferred approach so far. A part of AI that has shown promising results when it comes to interactions between players and strategy planning is reinforcement learning (RL). In [
33], Nouruzi et al. introduce a new method called Smart Joint Dynamic Pricing and Resource Sharing (SJDPRS) that utilizes deep reinforcement learning (DRL) for MEC services. The suggested approach seeks to dynamically improve resource allocation and pricing strategies, hence improving collaboration among network components in multi-tier slicing networks. Through the application of DRL techniques and the Stackelberg game, the system is able to adjust and accommodate for fluctuations in network circumstances and user mobility. This enables the system to effectively tackle obstacles such as latency, optimizing data rates, and efficiently utilizing resource.
3.5. Auction Techniques in Blockchain Networks
Finally, since our solution is aligned with the B-RAN, we believe that the work in [
34] by Jiao et al. offers valuable insight by describing auction techniques in Cloud–Fog Computing for Public Blockchain Networks. The primary goal is to improve societal welfare by effectively distributing resources among service providers and miners in the blockchain network. The paper examines various bidding systems and suggests auction techniques to maximize societal benefit.
In conclusion, although there is a substantial amount of research in this domain, DRL-based solutions have not been widely implemented despite their demonstrated efficacy and versatility in addressing many situations. This inspired us to investigate DRL for our method.
4. The Smart Pricing Policy Module
Within the realm of 5G and beyond 5G, a notable obstacle comes when customers enter regions where their main service provider does not have signal coverage, requiring uninterrupted connectivity solutions, as shown in
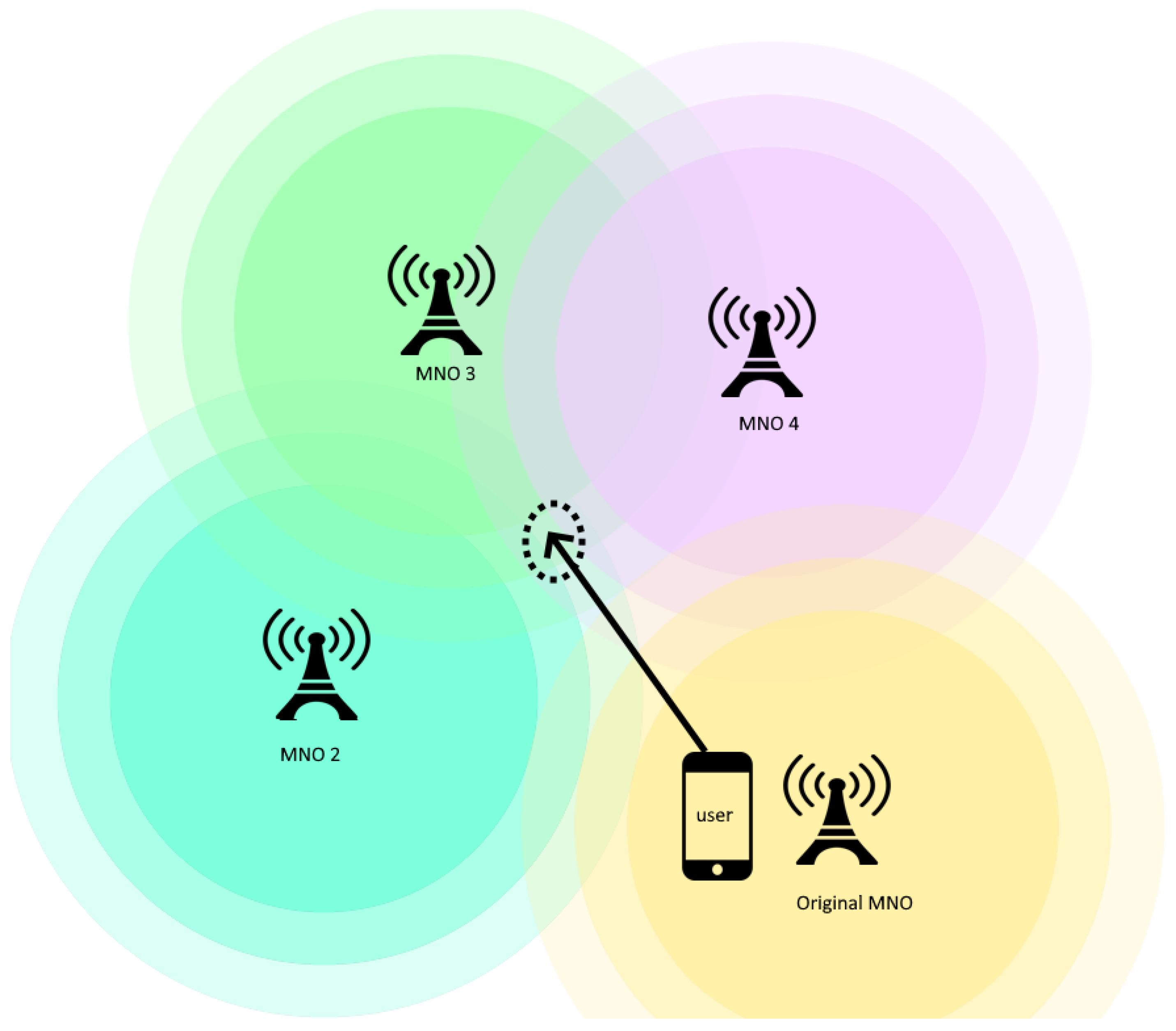
Figure 1, where a user exits his/her original MNO’s (Yellow) coverage and enters in the area of three other MNOs’ coverage. To resolve this issue, our approach implements flexible network sharing and roaming agreements. Hence, this permits alternative providers who have coverage in certain locations to temporarily take on the role of the original provider, guaranteeing uninterrupted service for the user.
Moreover, such a solution enables a unique concept where individuals can serve as temporary providers. This method is especially beneficial in situations where conventional network infrastructure is not feasible, as it enables individuals with adequate connectivity to share their network access with others, forming a user-provided network or mesh network instantaneously. Implementing such solutions necessitates the meticulous deliberation of device interoperability, security, and privacy safeguards, as well as the economic and regulatory consequences of dynamic provider switching and user-provided networks. These procedures are crucial for preserving the authenticity and confidentiality of communications, guaranteeing that users have a smooth experience regardless of their geographical proximity to their major network provider’s infrastructure. When a user switches to a new service provider in an area where his/her original provider has no reception, monetary costs rise since the user has already agreed to a specific Service Level Agreement (SLA) with his/her original provider. In areas with multiple providers, the SPP is responsible for selecting a provider that not only fulfills the user’s resource needs as specified in the SLA, but also negotiates a cost arrangement that is acceptable and financially advantageous for both the original provider and the temporary provider. This guarantees a seamless continuation of service that is in line with the financial and service expectations of all parties involved.
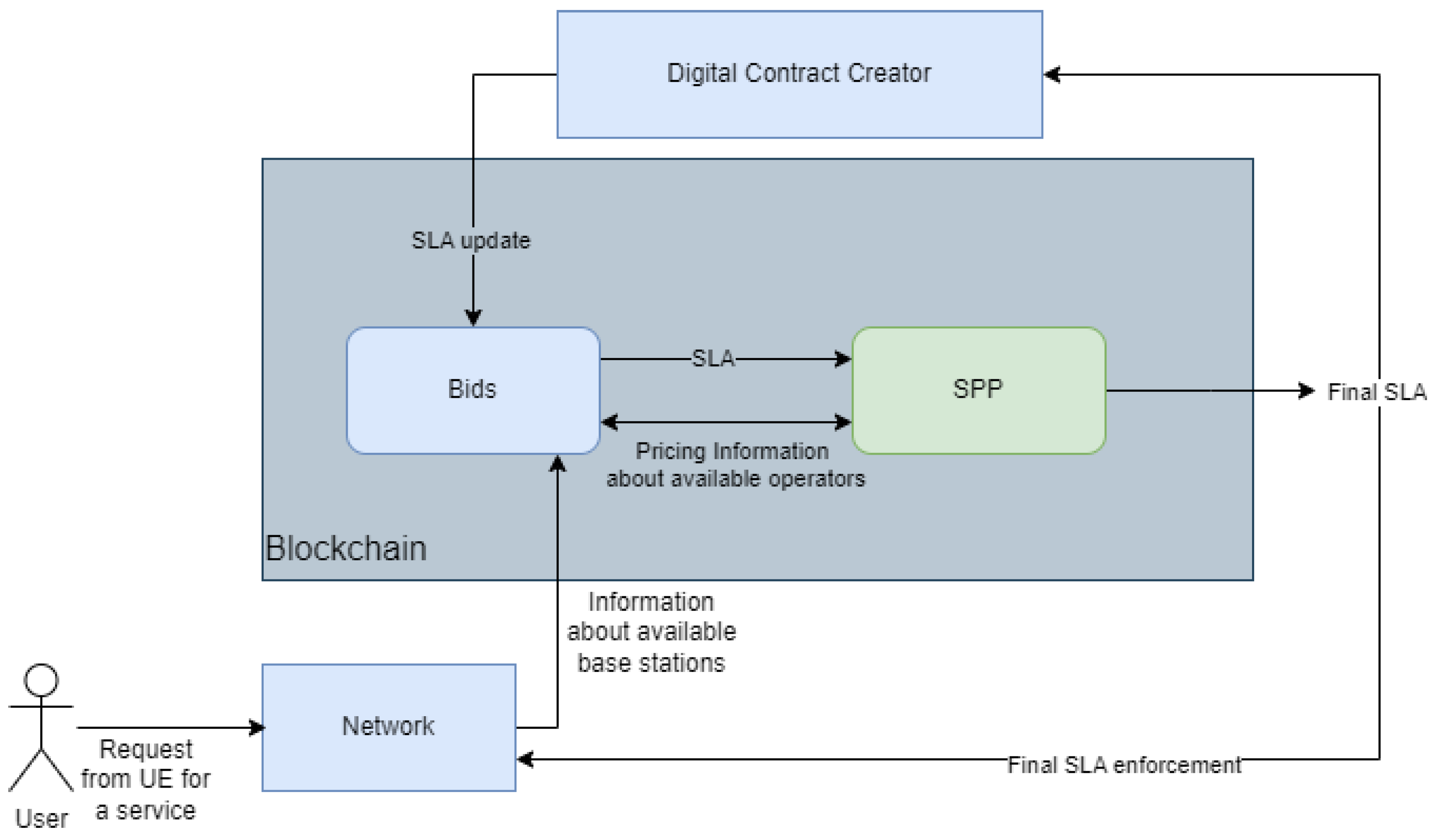
When a user enters an area where his/her original MNO does not offer coverage, the network orchestrator mechanism is triggered. This orchestrator detects all alternative MNOs in the region that can fulfill the user’s SLA needs. The list regarding these accessible MNOs, along with their lowest and highest offers for delivering the service, is then gathered and transmitted to the SPP module. Additionally, the MNOs have previously stated their intention to provide services at specific pricing ranges, which helps to create a competitive and transparent procedure for selecting services. The SPP module determines the winning MNO and the specific bid, which guarantees the contract for service provisioning. After the winning MNO and bid have been selected, this information is transmitted back over the network orchestrator to update the network and to reinforce and update the SLA between the original MNO and the winning temporary MNO; the general architecture can be seen in
Figure 2. This will ensure that all parties have a clear understanding of the terms and conditions for providing the service to the user in the new territory, and the new MNO will be ready to fulfill the agreed obligation regarding the user’s SLA resources at the agreed cost.
4.1. Our Deep Reinforcement Learning Approach
After thoroughly reviewing the relevant literature and previous works, it is clear that the most effective approach for optimizing bidding strategies similar to those used by the SPP is to either use Stackelberg games or reverse auction theory. Unlike Stackelberg Games, the reverse auction theory [
35] we use has not been extensively researched nor applied to address the specific problem our solution aims to solve. This preference is highlighted by the inherent limits of other theories such as Bertrand’s, which relies on a scarcity of bidders, and Cournot’s, which primarily focuses on quantity rather than price considerations. However, it is crucial to recognize that these preferred methods do have their limitations. Instead of using traditional game theory methods, we propose to use the reverse auction theory implemented by reinforcement learning agents for two main reasons. DRL has excellent scalability, which is well suited for the demands of 5G dynamics in the context of the B-RAN. The increase in the number of potential participants, including many users and MNOs, creates a more complicated system, highlighting the appropriateness of DRL. Furthermore, the flexible nature of reinforcement learning algorithms allows for ongoing adjustment based on changing datasets, resulting in a significant level of adaptability when faced with new conditions.
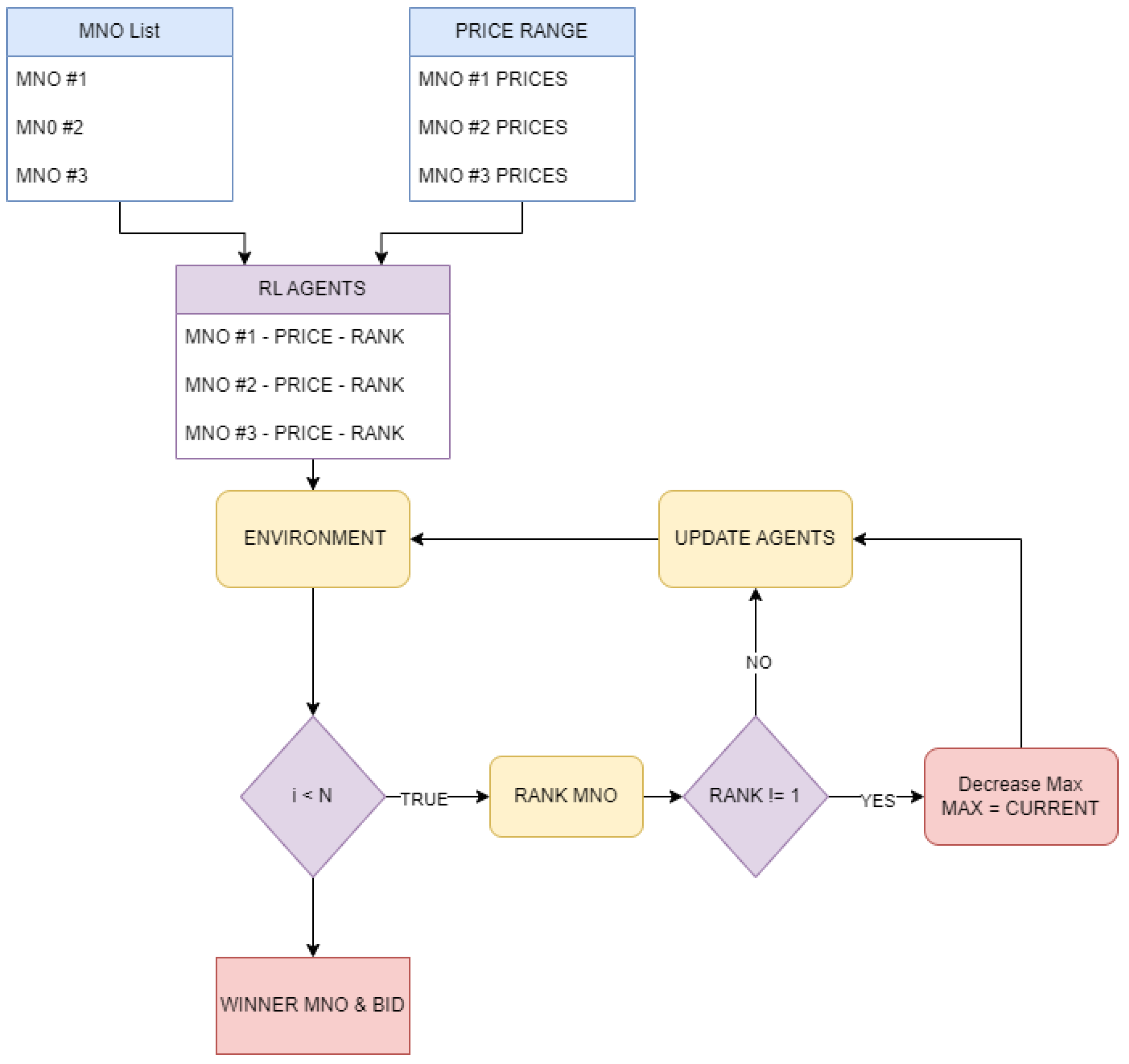
Hence, we decided to focus on a DRL approach as shown in
Figure 3 to implement a reverse auction theory in order to tackle the problem of calculating a fair price between the original and the temporary MNO. By adopting DRL algorithms and techniques, we created an environment where candidate MNOs (other MNOs or users temporarily acting as MNOs) act as agents that compete with each other in a reverse auction simulation environment. Each agent aims to surpass the rest and bid to win the network provisioning. Both the candidate MNOs’ list that can satisfy the original SLA agreement and their respective price ranges act as input to the SPP module. The price range is determined by a lower and upper limit; the lower limit indicates the minimum price a provider can bid, while the upper one defines the maximum. The reverse auction commences once we create the agents. Inside the SPP module, each agent will progressively optimize its pricing strategy by trying to make the “smartest” bids. The goal of this algorithmic effort is to determine a winner among the agents. The winner is the one offering the most favorable price balance, and this price balance will satisfy the needs of both the original MNO and the candidate MNO.
The DRL algorithm begins by evaluating the greatest cost associated with each candidate MNO in the ecosystem, therefore creating a hierarchical ranking based on cost allocation. We assign the highest rank, known as rank 1, to the MNO that offers the most economically beneficial proposal. The next step involves positioning the following MNOs appropriately. Following that, the iterative bidding process begins, when participating companies strategically modify their cost offerings in order to gain a competitive advantage. This iterative process allows the MNOs to evaluate and adjust their pricing strategies, competing against each other for maximum possible gain. As a result, each subsequent bidding round provides an opportunity for MNOs to refine their cost proposals, thus maximizing their competitive position.
where
The bidding procedure consists of an infinite number of iterations, but when the algorithm determines no further improvement is possible, it stops bidding. In the first round, every candidate MNO bids his/her maximum bid, and based on these bids, everyone gets a rank, with rank 1 being the MNO with the lowest bid. From round 2 onwards, each MNO checks if he/she is in rank 1; if not, he/she decreases his/her bid in order to improve his/her competitive position. The decrement strategy for every MNO is shown in Equation (
1) and recalculates the current rank
. The SPP utilizes a decrement strategy to reduce the bids of non-rank-1 MNOs. When the biding auction comes to a state where none of the players can improve their position, the program stops and announces the winning player with the winning bid. A pseudo-code of the procedure can be found in Algorithm 1.
Our thorough experiments have demonstrated that bidding outcomes do not noticeably increase after a certain number of rounds. This means that both MNOs do not increase their profit. This empirical observation highlights the presence of a saturation point in the iterative bidding mechanism when additional refinement leads to diminishing results.
| Algorithm 1 DRL algorithm |
- 1:
While bid ranks changed do - 2:
bid max for every MNO - 3:
rank the MNOs bids - 4:
for every MNO do - 5:
if Rank !=1 then decrease the bid - 6:
max = current max - 7:
else do nothing - 8:
end if - 9:
Re-Rank the MNOs bids - 10:
end for - 11:
Return Winner MNO and final bid
|
4.2. Training Phase and Simulation
In our deep reinforcement learning model, below and in
Table 1 are shown the parameters that can affect the results. These parameters are as follows:
Learning rate (): The parameter in question determines the extent to which the weights of the neural network are adjusted based on the gradient of the loss function. Increasing the learning rate can accelerate the learning process, but may introduce instability, whereas decreasing the learning rate guarantees consistent convergence at the expense of a longer training time.
Discount factor (): This metric quantifies the relative significance of forthcoming benefits in relation to immediate rewards. An agent with a discount factor approaching 1 will prioritize long-term rewards, but a factor approaching 0 will make it focus on immediate rewards
Exploration rate (): The parameter in -greedy policies determines the balance between exploration and exploitation. During the training process, a higher exploration rate guarantees that the agent will attempt various acts in order to uncover their consequences, whereas a lower rate implies that the agent will exploit activities that are already known to result in greater rewards
Replay Buffer Size: This the capacity of the memory buffer utilized for storing experiences to be used in experience replay. A larger buffer has the capacity to hold a greater number of past experiences, hence offering a more varied training set. However, this comes at the cost of requiring additional memory.
Batch size: This is the quantity of samples extracted from the replay buffer during each training iteration. Increasing the size of the batches used in training can lead to more reliable estimations of the gradient, but this comes at the cost of higher processing demands.
Target Network Update Frequency: In algorithms like the DQN, a distinct target network is employed to ensure the stability of the training process. This option specifies the frequency at which the weights of the target network are synchronized with the weights of the main network.
Number of episodes: The agent’s training encompasses the entirety of the episodes. Every episode encapsulates a comprehensive series of activities, observations, and rewards, starting from the initial state and concluding at a terminal state.
Episode Length: The upper limit for the number of steps that can be taken in each episode. This parameter serves to restrict the duration of each training episode, so guaranteeing that the agent encounters a diverse range of states and transitions while staying within realistic computing constraints.
Gradient Clipping: This method effectively mitigates the issue of gradients becoming excessively big, which can lead to instability during the learning process. It establishes a limit for the highest value of gradients
Reward Clipping: Occasionally, rewards are constrained within a specific range to avoid the occurrence of significant rewards that may lead to instability in the training process.
Table 1.
Training parameters.
Table 1.
Training parameters.
| Parameter | Description |
|---|
| Learning Rate () | The weight update of the neural network |
| Discount Factor () | Importance of future rewards |
| Exploration Rate () | Balance between exploration and exploitation |
| Replay Buffer Size | The capacity of the memory buffer |
| Batch Size | The quantity of samples |
| Target Network Update Frequency | Synchronize frequency |
| Number of Episodes | The total number of episodes the agent is trained on |
| Episode Length | Maximum number of steps per episode |
| Gradient Clipping | Limit of gradients |
| Reward Clipping | Reward range |
5. Experimental Results and Discussion
Now that we have established the methodology and defined the different parameters that could potentially affect the results of our experiments, we move to our experimental setup. For the sole reason of creating a fair and scalable SPP model, we ran exhaustive experiments to fine-tune the aforementioned parameters and find the best intersection of these factors. In particular, we tested four agents (players) with fixed Min and Max prices for each one, fine tuning only the Q-Learning factors and the number of rounds. We selected four agents solely for demonstration purposes, aiming to provide a clearer illustration of the variety of outcomes; the total number of agents used does not affect the actual results, as the execution time is very low even with 1000 agents, as shown in
Figure 4. This decision was made in order to demonstrate the differences in behavior and performance among the agents in a more understandable and controllable manner, guaranteeing that the main conclusions can be clearly understood and not overshadowed by an excessive number of variables. To better visualize our results and to make the impact of every parameter more tangible, we assigned user 1 to be the most expensive and user 4 to be the cheapest.
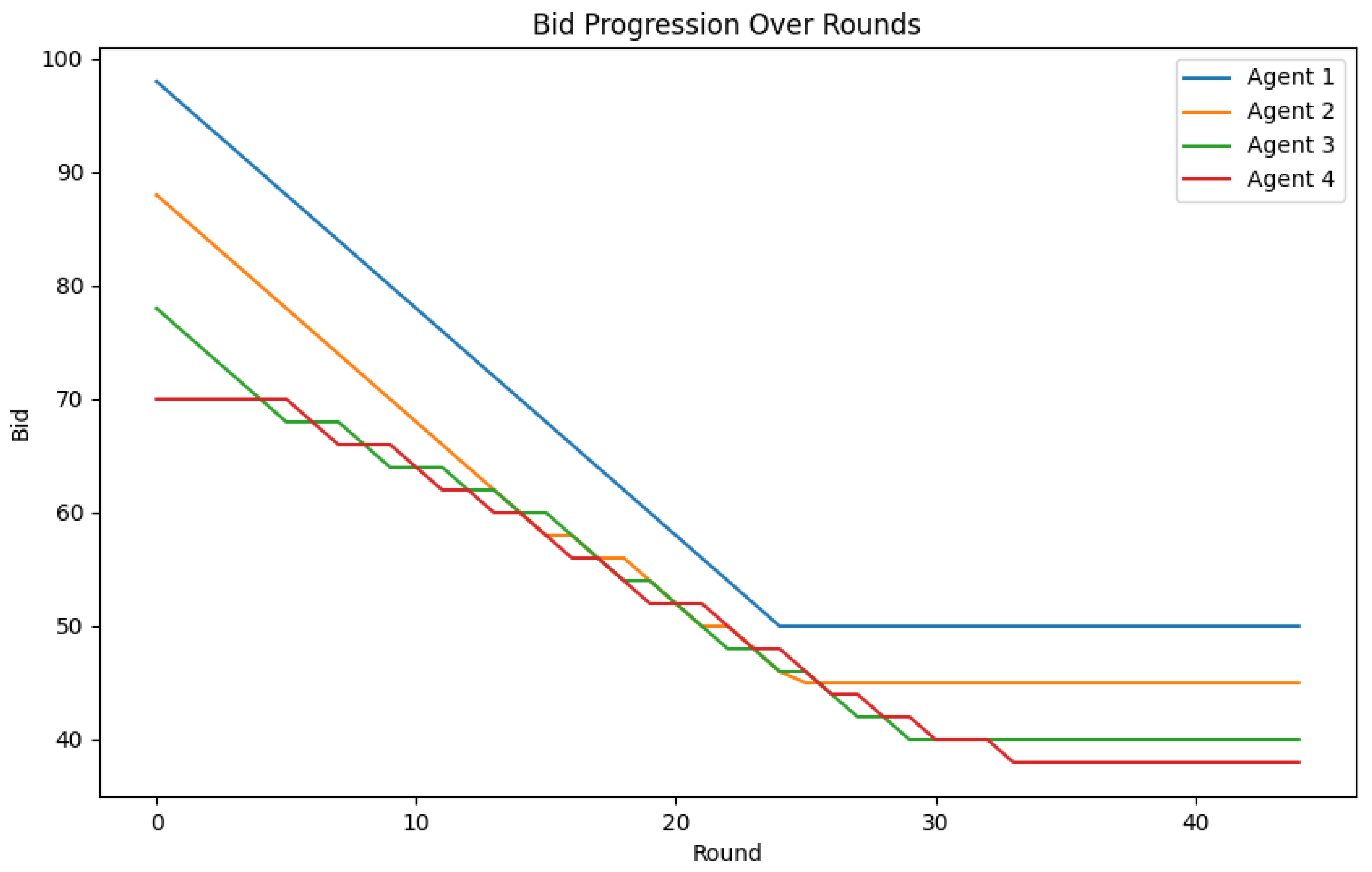
The multi-round bidding mechanism provides a compelling benefit. As depicted in
Figure 5, players generally reach their optimal strategy after only a few rounds. This suggests that players have reached a threshold where they can no longer improve their bids to secure a more advantageous position. This point of convergence provides the system administrator with a potent tool. They can strategically determine the point at which the bidding algorithm should end by analyzing the intended amount of involvement or consensus, which is a key aspect of democracy. The administrator can select a point in the network scenario that guarantees an adequate amount of participation while maintaining the efficiency of the bidding process.
Figure 6 provides a transparent view into every iteration of the code’s execution, exposing all the crucial particulars. It displays the participants, referred to as users or agents, together with their rank and bid for that particular round. The rank signifies their hierarchical position at that particular moment, depending on elements such as the bid amount or other criteria established by the code. The bid represents the valuation or proposition that each user/agent presents. The figure provides a comprehensive timeline of the full execution by showing this information for each round. This allows us to observe the evolution of ranks and bids, leading to a more profound comprehension of the code’s behavior.
The repeated victories achieved by agent 4 as shown in
Figure 7 during a single code execution suggest an imbalance that may be attributed to the initial minimum and maximum price settings.
These prices may be advantageous for agent 4’s bidding approach, as it thrives on low first bids within an artificially high minimum threshold. This result highlights the importance of the initial price setup in guaranteeing fairness and efficiency. Through the analysis of how these limitations affect the rates of success in numerous iterations, the system administrator can identify and modify them in order to obtain a desirable configuration. This process of fine-tuning promotes a fair competition in which all participants compete based on their plans, rather than predetermined price restrictions, in contrast to Stackelberg games, where bids can exhibit significant divergence across rounds, as shown in
Figure 8, and are more difficult to fine-tune in order to fit every scenario.
Furthermore, our methodology creates an ecosystem that incentivizes consumers to engage in the B-RAN by leveraging their equipment to aid in network offloading and call rerouting. This participation allows users to connect to the network even when they are outside their original MNO’s coverage area. In addition, temporary MNOs might generate financial gains by providing their resources to the original MNO. The fair nature of our approach becomes evident by our experimentation process as we make no distinction between agents that represent MNOs and agents that represent users.
This way, we remain true to our main objective and try to establish a monetary system that is both democratic and equitable. This approach guarantees that temporary MNOs have the chance to provide services to end users who have legally entered into contracts with other MNOs. The values of democracy and justice are crucial to our strategy, as they serve as safeguards against a situation where only the most inexpensive providers monopolize the market. This scenario would not be viable, as it would decrease the motivation for small or individual operators and MNOs to take part, resulting in a decrease in network coverage and overall competition. Decreased competition may lead to lower pricing, but it can also result in the adoption of inefficient methods that are not cost-effective. Given the lack of empirical evidence for this specific network structure, we make the assumption that there is no limit to the number of prospective bidders. During our trials, the execution time remained under one second, even when we used an extremely high number of 1000 bidders (agents), which is unlikely to occur in real-world scenarios. The swift execution time of our model suggests that it may be seamlessly included in the smart contract, enabling us to concentrate on enhancing other aspects of the model.
After careful analysis, we have concluded that the reverse auction theory is the most appropriate framework for our ecosystem. This theory is highly compatible with the system we strive to promote, as it places great emphasis on the principles of fairness and the expansion of networks. Despite extensive research in the literature, Stackelberg games excel in situations where cost considerations hold paramount significance. Stackelberg games are commonly used in situations when there are just a few dominant players in an industry, known as oligopolies. These players tend to focus on minimizing costs rather than promoting fairness and expanding their networks. On the other hand, our ecosystem is advantageous with the reverse auction method as it promotes involvement from a wider array of participants, including smaller and individual MNOs. This inclusiveness promotes a more egalitarian and equitable distribution of network resources. Additionally, it promotes the development of a broader and stronger network by encouraging a wide range of participants, thereby preventing the drawbacks of an oligopoly where a small number of major firms could exert control. The reverse auction hypothesis promotes sustainability and competition by prioritizing fairness and network expansion, which matches our long-term goals.
Furthermore, we prioritize particular aspects in the code that may be readily adjusted to correspond with the philosophical requirements of the network. The discount factor and termination criteria are customizable characteristics that are meant to easily adapt to different network requirements. Administrators can effectively adjust and expand the network as required due to its versatility. By implementing these modifications, we provide network managers with the capacity to adapt effectively to evolving circumstances and requirements, thereby guaranteeing the highest level of performance and long-term viability. The emphasis on adjustable parameters not only increases the adaptability of our system, but also promotes the expandability of the network. Administrators have the ability to modify these settings in order to align with certain operational objectives, such as optimizing efficiency, increasing coverage, or achieving a balance between cost-effectiveness and fairness. Consequently, our ecosystem can sustain its strength and flexibility, being able to adapt to new challenges and opportunities while upholding its fundamental principles of democracy and equality.
6. Conclusions and Future Works
The paper presents a novel financial incentive scheme, known as the SPP module, which aims to incentivize users to act as temporary MNOs. The objective of this initiative is to enhance communication and data transfer for users in areas where their main service providers have inadequate coverage. The research shows, via thorough experimentation and algorithmic improvement, that DRL is more scalable and adaptable than classic game theory approaches in this specific setting. By incorporating dynamic programming into a reverse auction architecture based on DRL, system administrators can customize settings to fulfill either democratic or limited criteria in different contexts. Moreover, the code’s low level of complexity and its ability to easily adapt to different scales make it very suitable for integration as a smart contract within a blockchain. This integration allows for the utilization of the benefits provided by blockchain B-RAN technology. This integration guarantees that the system maintains its strength, versatility, and ability to adjust to changing network requirements. Currently, we are incorporating additional variables into our model, such as the resources available to each MNO. In addition, we are evaluating the duration of execution and the equitable distribution of resources, examining how these variables affect the intricacy of the code and, consequently, the functioning of the blockchain. The ongoing endeavor is to improve the system’s performance and maintain its fairness and efficiency as it expands.
Author Contributions
Conceptualization, K.K. and A.D.; methodology, K.K.; validation, K.K., I.G., E.K., A.D. and C.S.; formal analysis, K.K.; investigation, K.K.; resources, K.K.; data curation, K.K.; writing—original draft preparation, K.K and A.D.; writing—review and editing, A.D., C.S., I.G. and E.K.; visualization, K.K.; supervision, C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was in part funded by the EU Horizon Europe NANCY project (An Artificial Intelligent Aided Unified Network for Secure Beyond 5G Long Term Evolution) under Grant number 101096456.
Data Availability Statement
Data is available upon request.
Acknowledgments
The authors would like to acknowledge all the partners in the project for their support.
Conflicts of Interest
All authors were employed by the company Eight Bells Ltd. The remaining authors declare that the research was conducted in the absence of any commercial financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | artificial intelligence |
| B-RAN | blockchain-radio access network |
| DRL | deep reinforcement learning |
| MNO | mobile network operator |
| RL | reinforcement learning |
| SLA | Service Level Agreement |
| SPP | Smart Pricing Policies |
| UE | User Equipment |
References
- Azariah, W.; Bimo, F.A.; Lin, C.W.; Cheng, R.G.; Nikaein, N.; Jana, R. A Survey on Open Radio Access Networks: Challenges, Research Directions, and Open Source Approaches. Sensors 2024, 24, 1038. [Google Scholar] [CrossRef] [PubMed]
- Perera, L.; Ranaweera, P.; Kusaladharma, S.; Wang, S.; Liyanage, M. A Survey on Blockchain for Dynamic Spectrum Sharing. IEEE Open J. Commun. Soc. 2024, 5, 1753–1802. [Google Scholar] [CrossRef]
- Dekhandji, F.Z.; Recioui, A. An Investigation into Pricing Policies in Smart Grids. Eng. Proc. 2022, 14, 4015. [Google Scholar] [CrossRef]
- Salazar, E.J.; Jurado, M.; Samper, M.E. Reinforcement Learning-Based Pricing and Incentive Strategy for Demand Response in Smart Grids. Energies 2023, 16, 1466. [Google Scholar] [CrossRef]
- Millea, A. Deep Reinforcement Learning for Trading—A Critical Survey. Data 2021, 6, 119. [Google Scholar] [CrossRef]
- Hurtado Sánchez, J.A.; Casilimas, K.; Caicedo Rendon, O.M. Deep Reinforcement Learning for Resource Management on Network Slicing: A Survey. Sensors 2022, 22, 3031. [Google Scholar] [CrossRef] [PubMed]
- Onopa, S.; Kotulski, Z. State-of-the-Art and New Challenges in 5G Networks with Blockchain Technology. Electronics 2024, 13, 974. [Google Scholar] [CrossRef]
- Yaga, D.; Mell, P.; Roby, N.; Scarfone, K. Blockchain Technology Overview; Technical Report NIST IR 8202; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar] [CrossRef]
- Giupponi, L.; Wilhelmi, F. Blockchain-Enabled Network Sharing for O-RAN in 5G and Beyond. IEEE Netw. 2022, 36, 218–225. [Google Scholar] [CrossRef]
- Xu, H.; Liu, X.; Zeng, Q.; Li, Q.; Ge, S.; Zhou, G.; Forbes, R. DecentRAN: Decentralized Radio Access Network for 5.5G and Beyond. In Proceedings of the 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 28 May–1 June 2023; pp. 556–561. [Google Scholar] [CrossRef]
- Velliangiri, S.; Manoharan, R.; Ramachandran, S.; Rajasekar, V. Blockchain Based Privacy Preserving Framework for Emerging 6G Wireless Communications. IEEE Trans. Ind. Inform. 2022, 18, 4868–4874. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Li, R. Reinforcement learning based bilevel real-time pricing strategy for a smart grid with distributed energy resources. Appl. Soft Comput. 2024, 155, 111474. [Google Scholar] [CrossRef]
- Li, Y. Deep Reinforcement Learning: An Overview. arXiv 2018, arXiv:1701.07274. [Google Scholar]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert Syst. Appl. 2023, 231, 120495. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Jin, J.; Guo, Z.; Bai, W.; Wu, B.; Liu, X.; Wu, W. Congestion-aware Stackelberg pricing game in urban Internet-of-Things networks: A case study. Comput. Netw. 2024, 246, 110405. [Google Scholar] [CrossRef]
- Kim, S. Hierarchical aerial offload computing algorithm based on the Stackelberg-evolutionary game model. Comput. Netw. 2024, 245, 110348. [Google Scholar] [CrossRef]
- Islam, S.N. A Review of Peer-to-Peer Energy Trading Markets: Enabling Models and Technologies. Energies 2024, 17, 1702. [Google Scholar] [CrossRef]
- Cintuglu, M.H.; Martin, H.; Mohammed, O.A. Real-Time Implementation of Multiagent-Based Game Theory Reverse Auction Model for Microgrid Market Operation. IEEE Trans. Smart Grid 2015, 6, 1064–1072. [Google Scholar] [CrossRef]
- Huck, S.; Normann, H.T.; Oechssler, J. Learning in Cournot Oligopoly—An Experiment. Econ. J. 1999, 109, 80–95. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, J. Differential effects of social influence sources on self-reported music piracy. Decis. Support Syst. 2015, 69, 70–81. [Google Scholar] [CrossRef]
- Zhang, J.; Da, Q.; Wang, Y. The dynamics of Bertrand model with bounded rationality. Chaos Solitons Fractals 2009, 39, 2048–2055. [Google Scholar] [CrossRef]
- Sharkey, W.W.; Sibley, D.S. A Bertrand model of pricing and entry. Econ. Lett. 1993, 41, 199–206. [Google Scholar] [CrossRef]
- Flamini, M.; Naldi, M. Optimal Pricing in a Rented 5G Infrastructure Scenario with Sticky Customers. Future Internet 2023, 15, 82. [Google Scholar] [CrossRef]
- Kim, D.H.; Ndikumana, A.; Kazmi, S.A.; Kim, K.; Munir, M.S.; Saad, W.; Hong, C.S. Pricing Mechanism for Virtualized Heterogeneous Resources in Wireless Network Virtualization. In Proceedings of the 2020 International Conference on Information Networking (ICOIN), Barcelona, Spain, 7–10 January 2020; pp. 366–371. [Google Scholar] [CrossRef]
- Kumar, S.K.A.; Crawford, D.; Stewart, R. Pricing Models for 5G Multi-Tenancy using Game Theory Framework. IEEE Commun. Mag. 2024, 62, 66–72. [Google Scholar] [CrossRef]
- Zhang, K.; Gui, X.; Ren, D.; Du, T.; He, X. Optimal pricing-based computation offloading and resource allocation for blockchain-enabled beyond 5G networks. Comput. Netw. 2022, 203, 108674. [Google Scholar] [CrossRef]
- Liu, K.; Qiu, X.; Chen, W.; Chen, X.; Zheng, Z. Optimal Pricing Mechanism for Data Market in Blockchain-Enhanced Internet of Things. IEEE Internet Things J. 2019, 6, 9748–9761. [Google Scholar] [CrossRef]
- Datar, M.; Altman, E.; Cadre, H.L. Strategic Resource Pricing and Allocation in a 5G Network Slicing Stackelberg Game. IEEE Trans. Netw. Serv. Manag. 2023, 20, 502–520. [Google Scholar] [CrossRef]
- Luong, N.C.; Wang, P.; Niyato, D.; Liang, Y.C.; Han, Z.; Hou, F. Applications of Economic and Pricing Models for Resource Management in 5G Wireless Networks: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 3298–3339. [Google Scholar] [CrossRef]
- Flamini, M.; Naldi, M. Cournot Equilibrium in an Owner-Renter Model for 5G Networks under Flat-Rate Pricing. In Proceedings of the 2020 43rd International Conference on Telecommunications and Signal Processing (TSP), Milan, Italy, 7–9 July 2020; pp. 158–161. [Google Scholar] [CrossRef]
- Assila, B.; Kobbane, A.; El Koutbi, M. A Cournot Economic Pricing Model for Caching Resource Management in 5G Wireless Networks. In Proceedings of the 2018 14th International Wireless Communications & Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018; pp. 1345–1350. [Google Scholar] [CrossRef]
- Nouruzi, A.; Mokari, N.; Azmi, P.; Jorswieck, E.A.; Erol-Kantarci, M. Smart Dynamic Pricing and Cooperative Resource Management for Mobility-Aware and Multi-Tier Slice-Enabled 5G and Beyond Networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 2044–2063. [Google Scholar] [CrossRef]
- Jiao, Y.; Wang, P.; Niyato, D.; Suankaewmanee, K. Auction Mechanisms in Cloud/Fog Computing Resource Allocation for Public Blockchain Networks. IEEE Trans. Parallel Distrib. Syst. 2019, 30, 1975–1989. [Google Scholar] [CrossRef]
- Matsuda, T.; Inada, T.; Ishihara, S. Communication Method Using Cellular and D2D Communication for Reverse Auction-Based Mobile Crowdsensing. Appl. Sci. 2022, 12, 11753. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).