Readout Circuit Design for RRAM Array-Based Computing in Memory Architecture
Abstract
1. Introduction
2. SAR ADC Design for Traditional ADC Readout Circuits
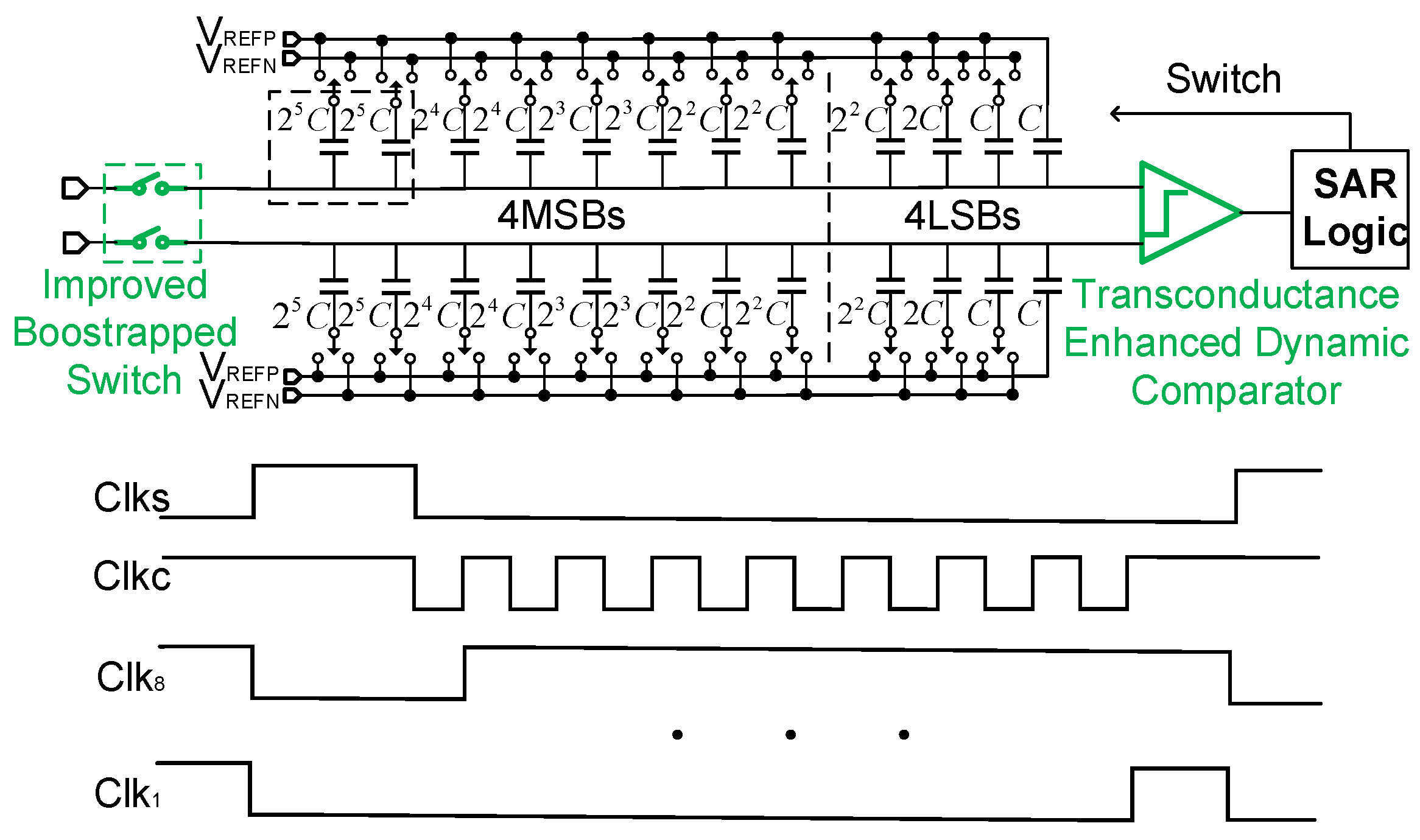
- Improved Bootstrapped Switch: From the hold to the sampling phase, the linearity is enhanced by reducing the charge leakage related to Vin through the addition of a MOS transistor;
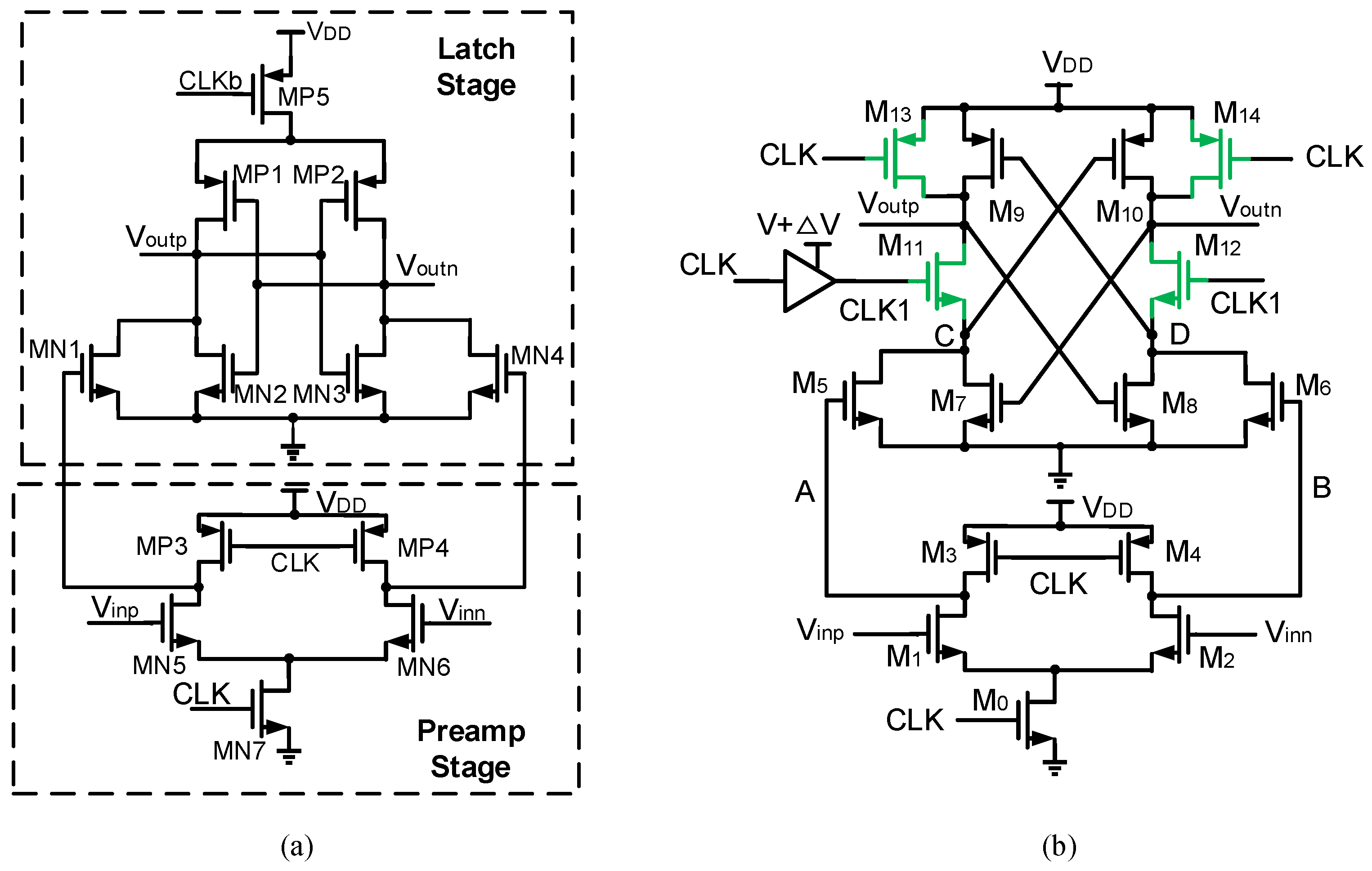
- Upgraded Dynamic Comparator: During the latching phase, the comparative speed is elevated via increase in the equivalent transconductance (gm);
- CDAC Capacitor Array: Employing a “sandwich” three-layer capacitor structure augmented with a dummy structure, this element features a minimal area and high matching precision;
- Switching Strategy: For the top four bits, a splitting capacitor scheme is used to secure the common-mode voltage at 1/2 . The lower four bits employ a monotonic switching strategy to avoid excessive capacitor mismatches caused by excessively small unit capacitors;
- SAR Logic: To enhance the overall comparison efficiency, we adopt an asynchronous timing scheme in SAR logic [9].
2.1. Linearity-Improved Bootstrapped Switch
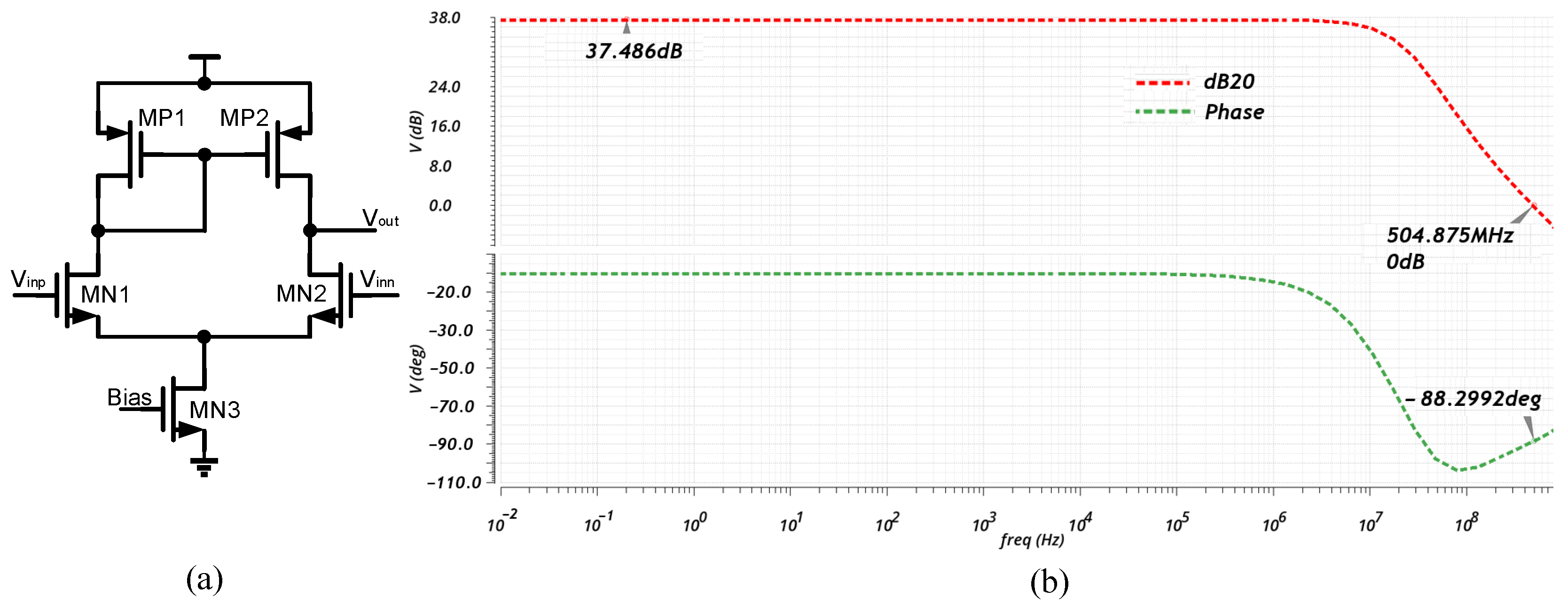
2.2. Transconductance-Enhanced Dynamic Comparator
2.3. CDAC Switching Scheme and Unit Capacitor
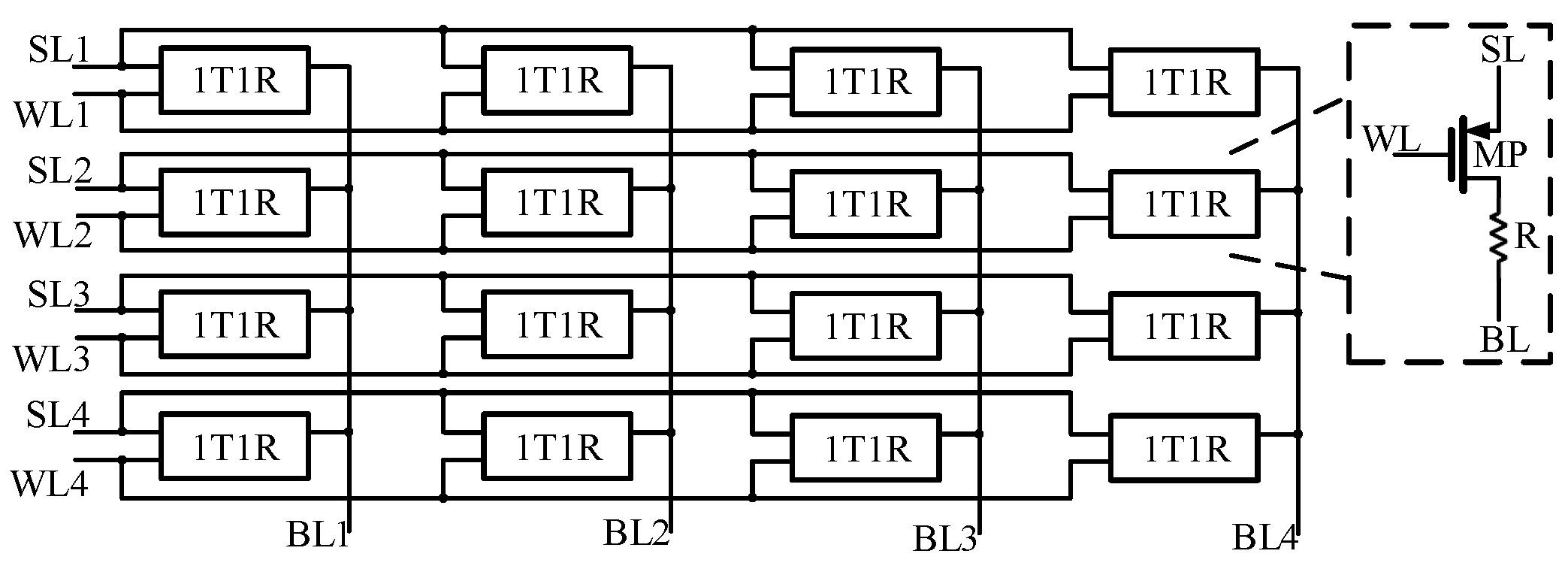
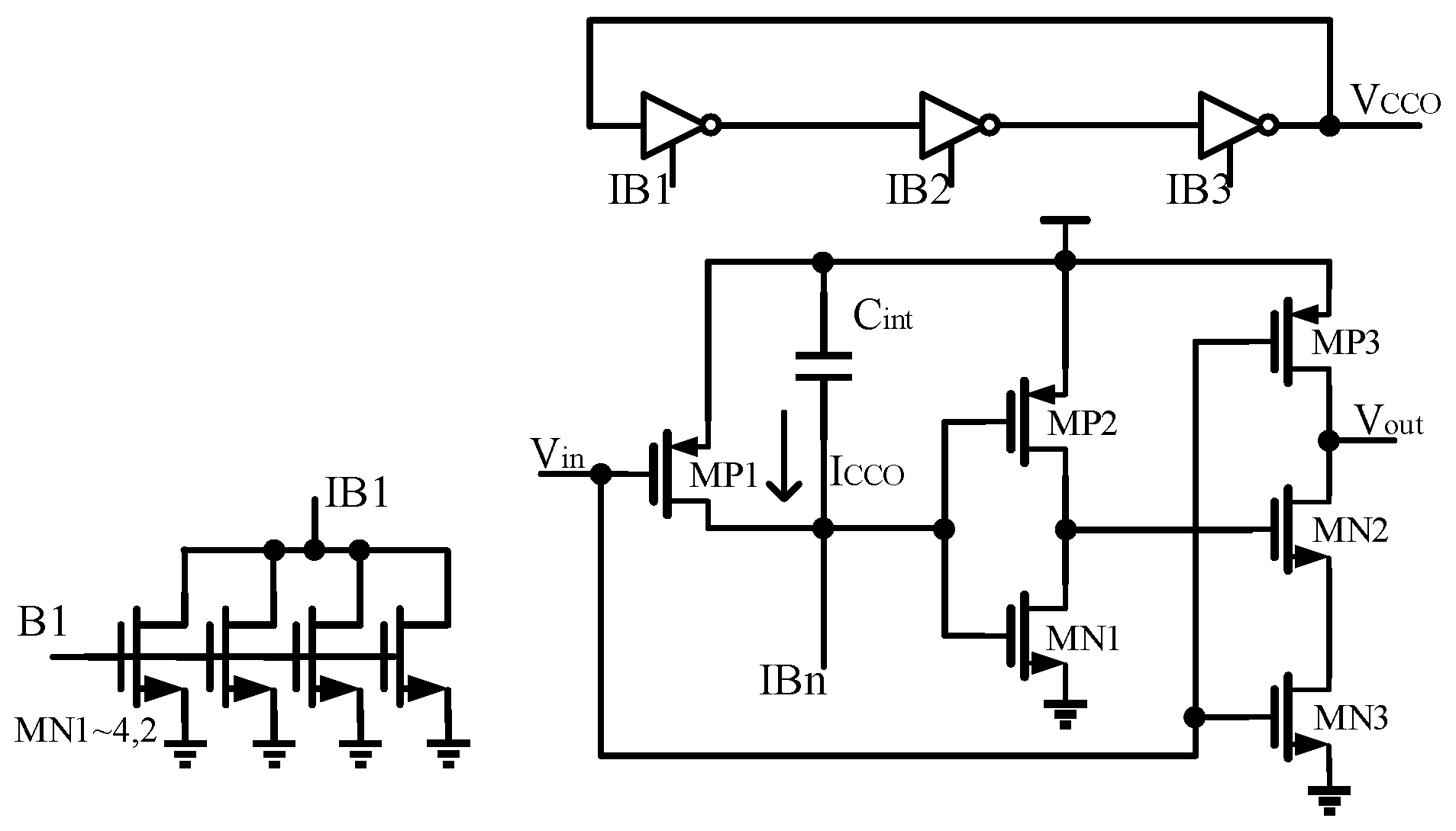
3. CCO-Type Readout Circuit
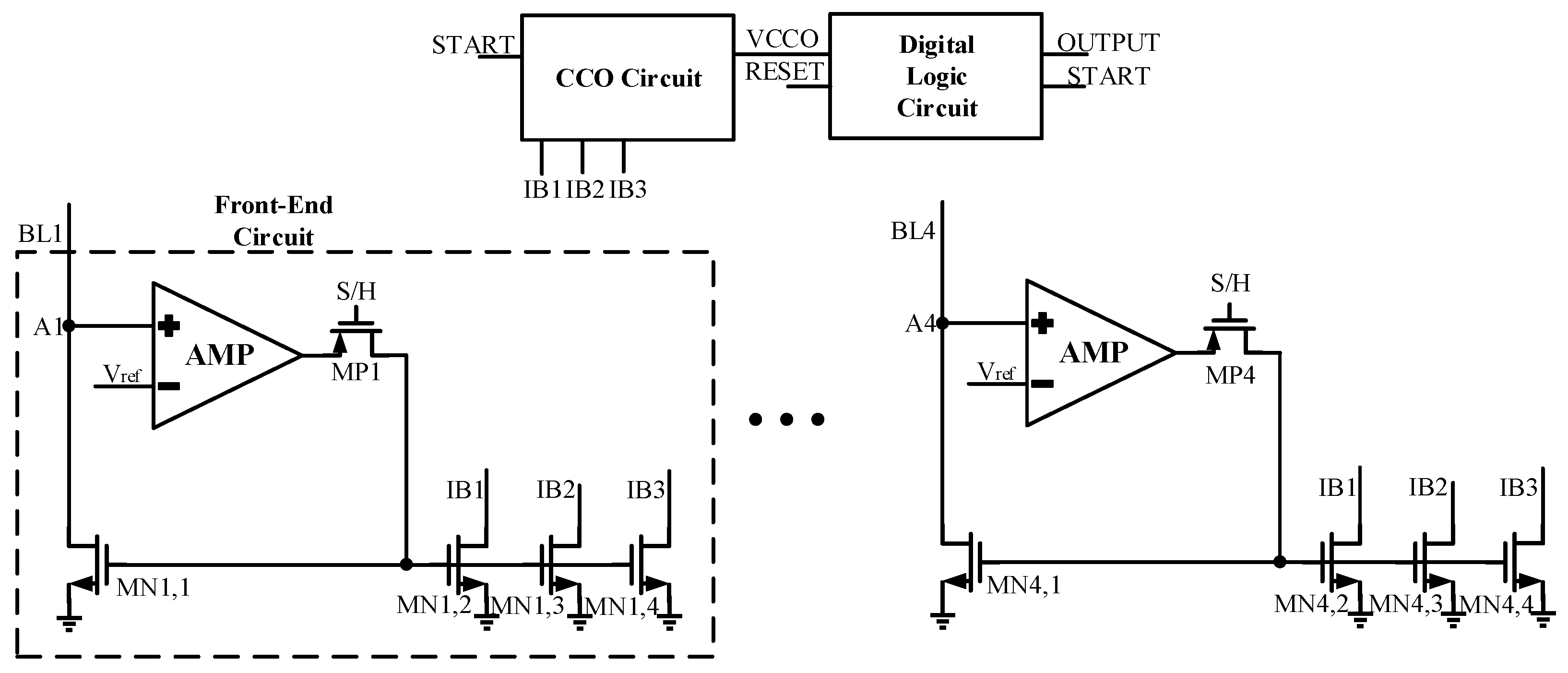
- Clamp voltageThe current within an RRAM array is computed as . Consequently, variations in column output voltage within the CIM array induce changes in the column’s current, thus impacting accuracy. The CCO-type readout circuit designed in this paper leverages a clamping action generated by a negative feedback circuit, constructed from an operational amplifier and a current mirror, to clamp the voltage at Point A (A1–A4) to . This maintains a constant voltage difference across the array, thereby enhancing the linearity of the CIM storage compute array’s output current.
- Selection of size in current mirrorGiven the order of magnitude variation in column current within the CIM array, careful consideration should be given to sizing MN1,1–MN4,1: these NMOS transistors must remain in the saturation region during column current changes. Therefore, prudent selection of the dimensions for these four NMOS transistors is critical during the design process. Considering the mA level current in the CIM array columns, direct replication of current via a current mirror results in prohibitive power consumption. Hence, scaling of the current is performed using (MN1,2, MN1,3, MN1,4); moreover, different proportions of (MN1,2, MN1,3, MN1,4) to (MN4,2, MN4,3, MN4,4) facilitate the assignment of varied weights to different columns within the CIM.
- Design of CCOThis study uses a design for a CCO characterized by low process-sensitivity, thereby eliminating the need for an additional reference voltage. Additionally, leveraging the complementary nature of technology-induced variations in capacitance and voltage, the design’s sensitivity to manufacturing process variations is mitigated [16].
3.1. Front-End Circuit Design
3.2. Design of CCO
3.3. Digital Logic Circuit
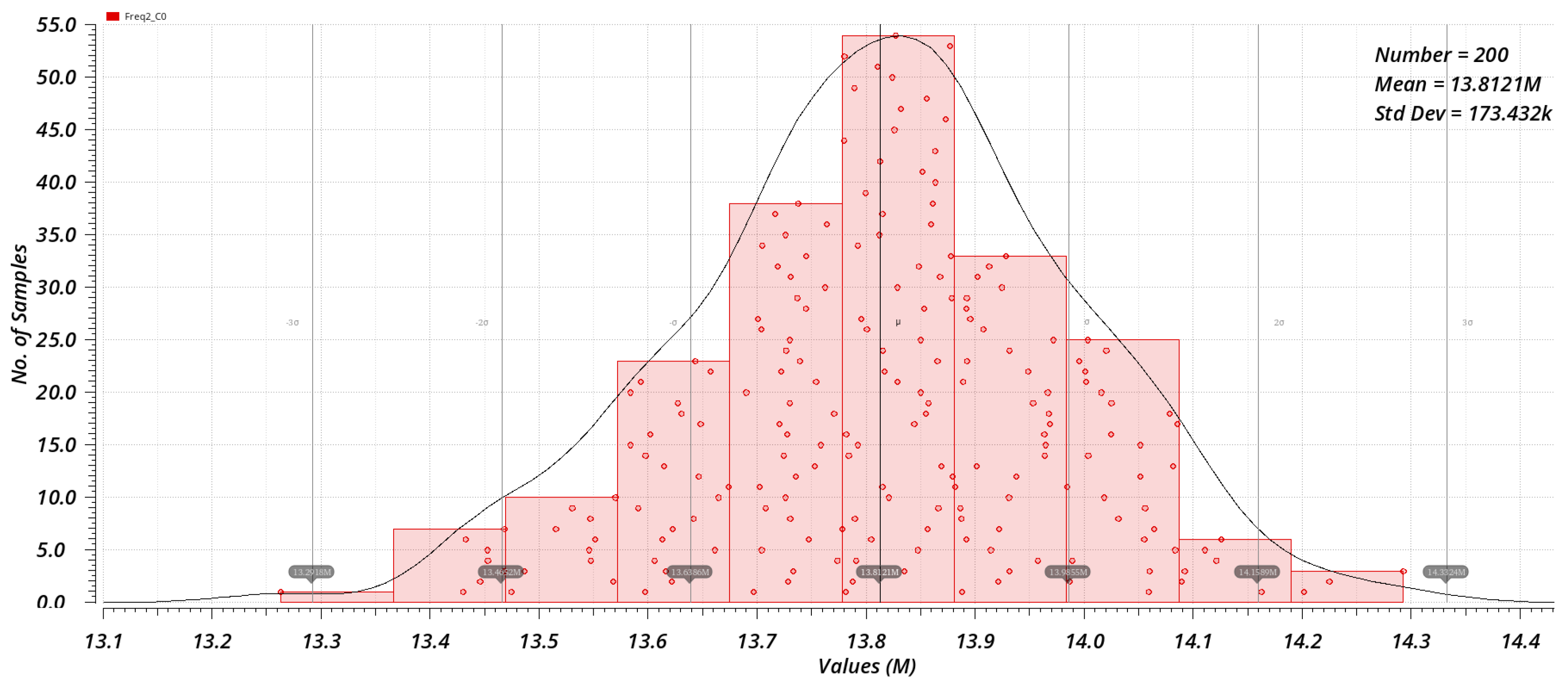
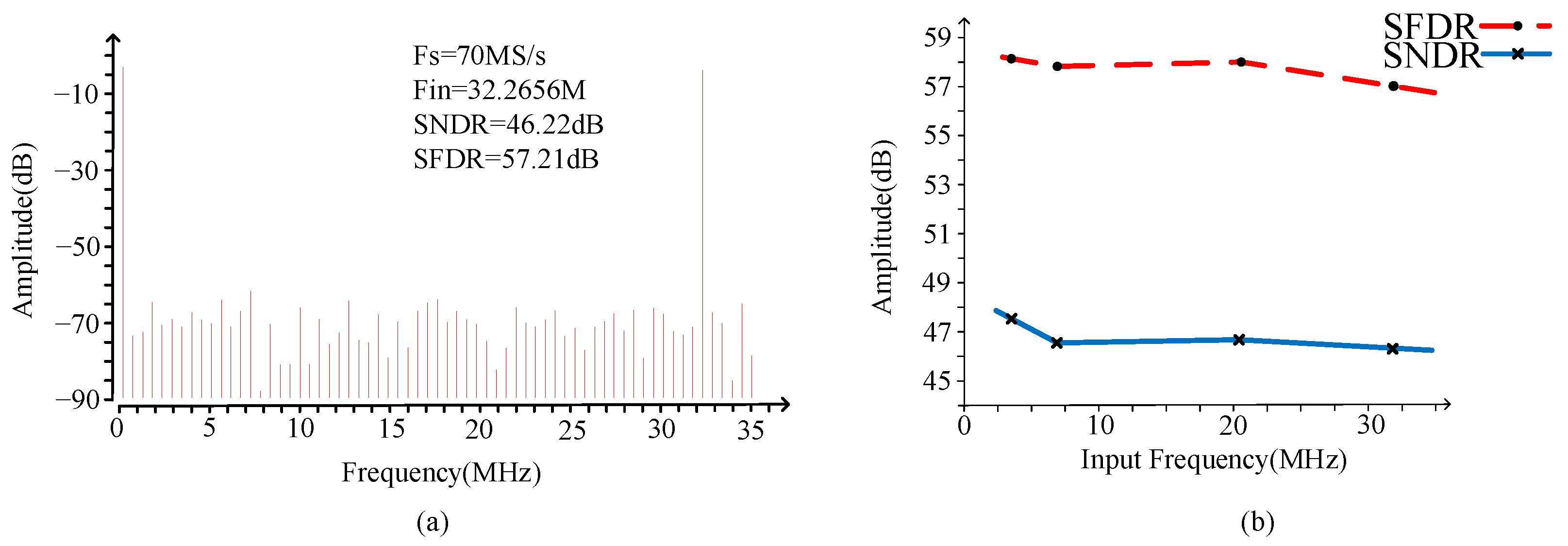
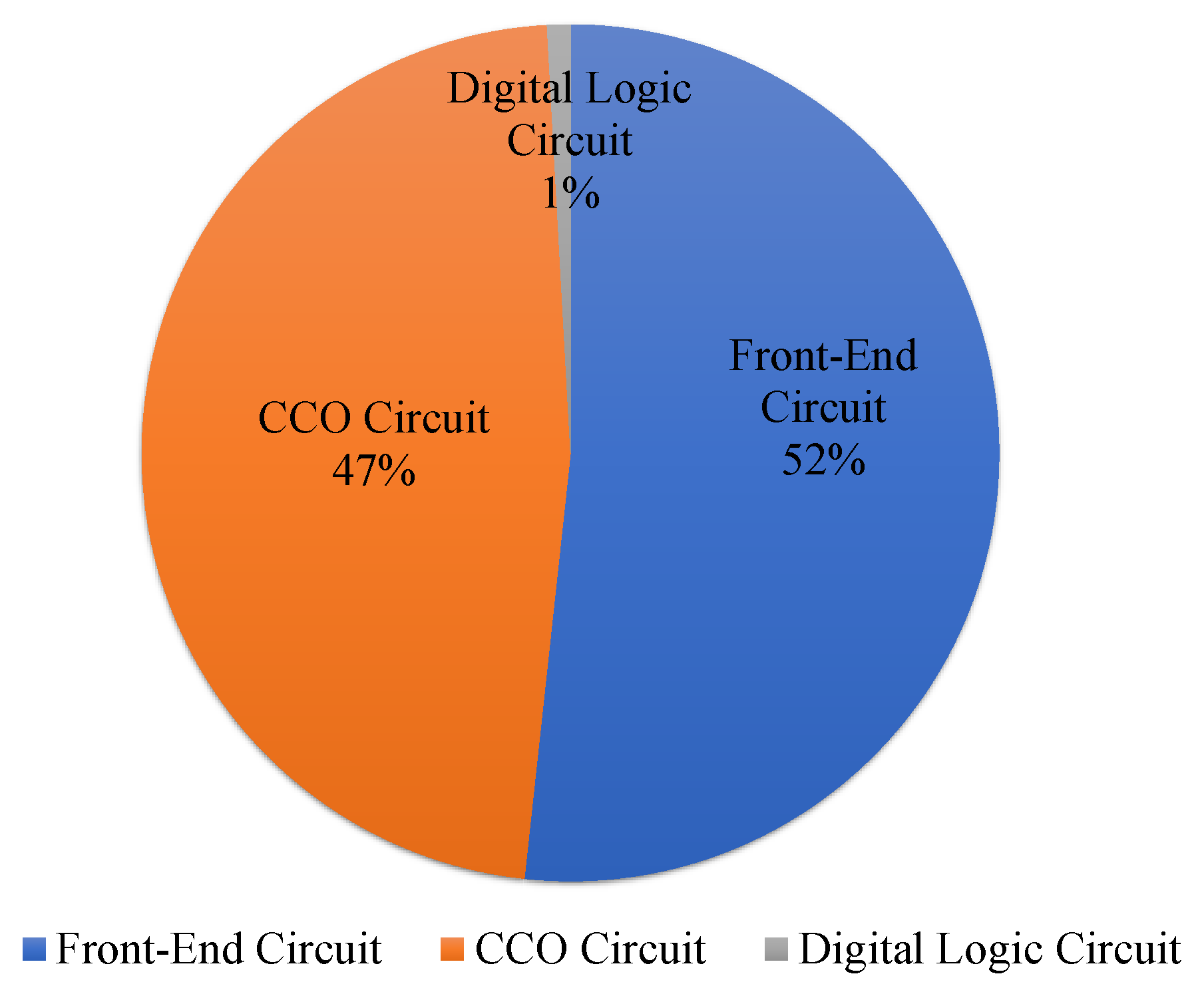
4. Simulation Results
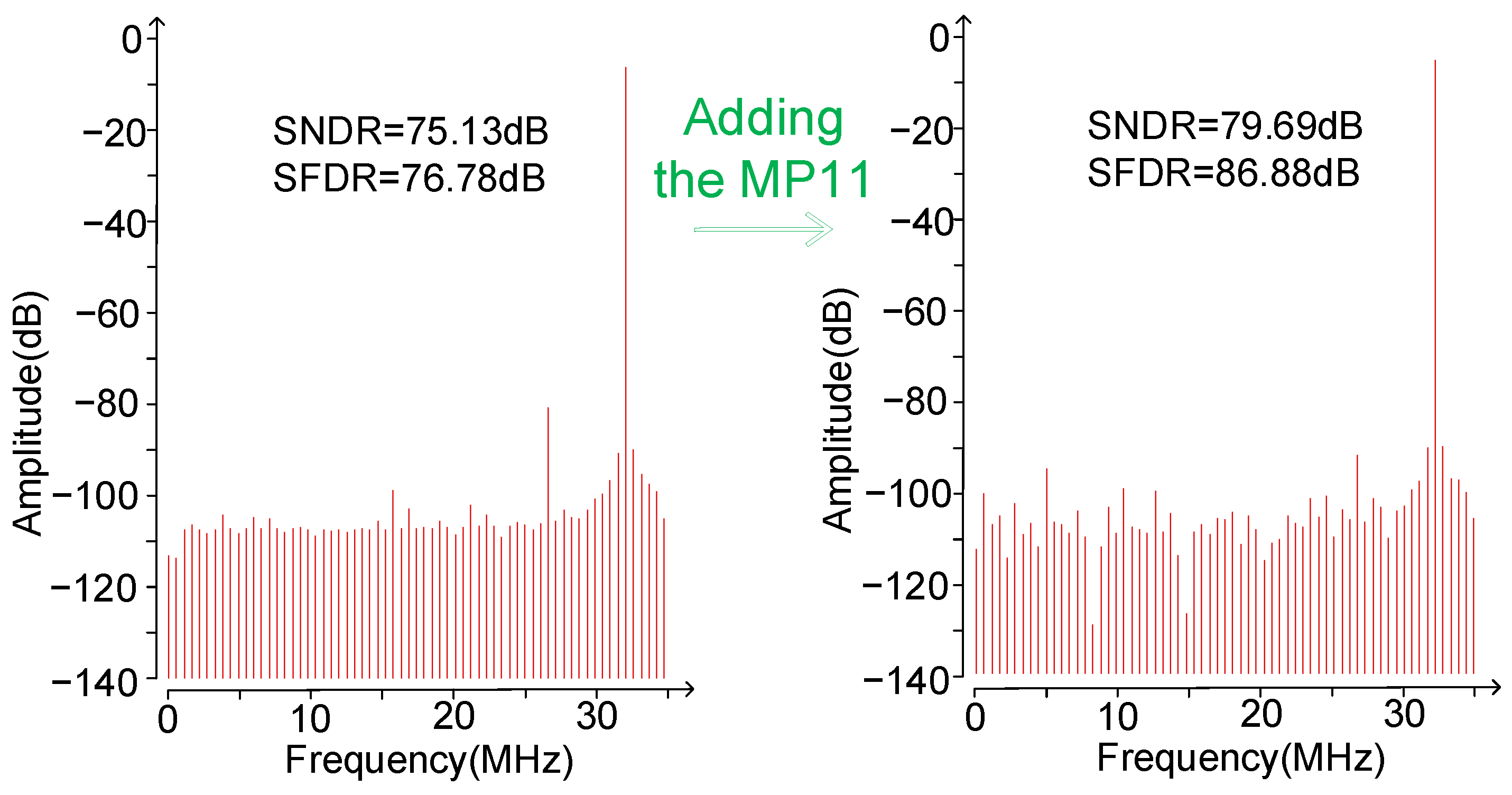
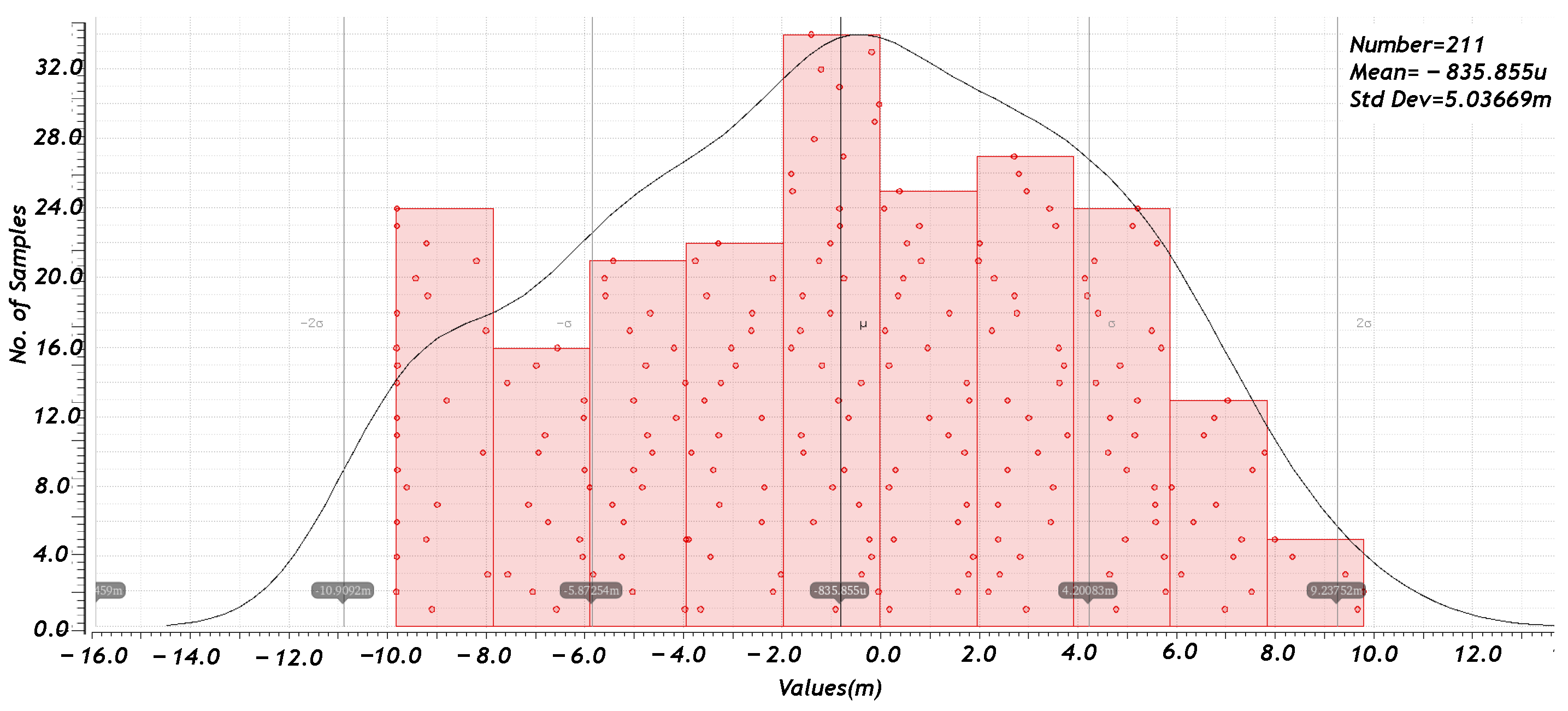
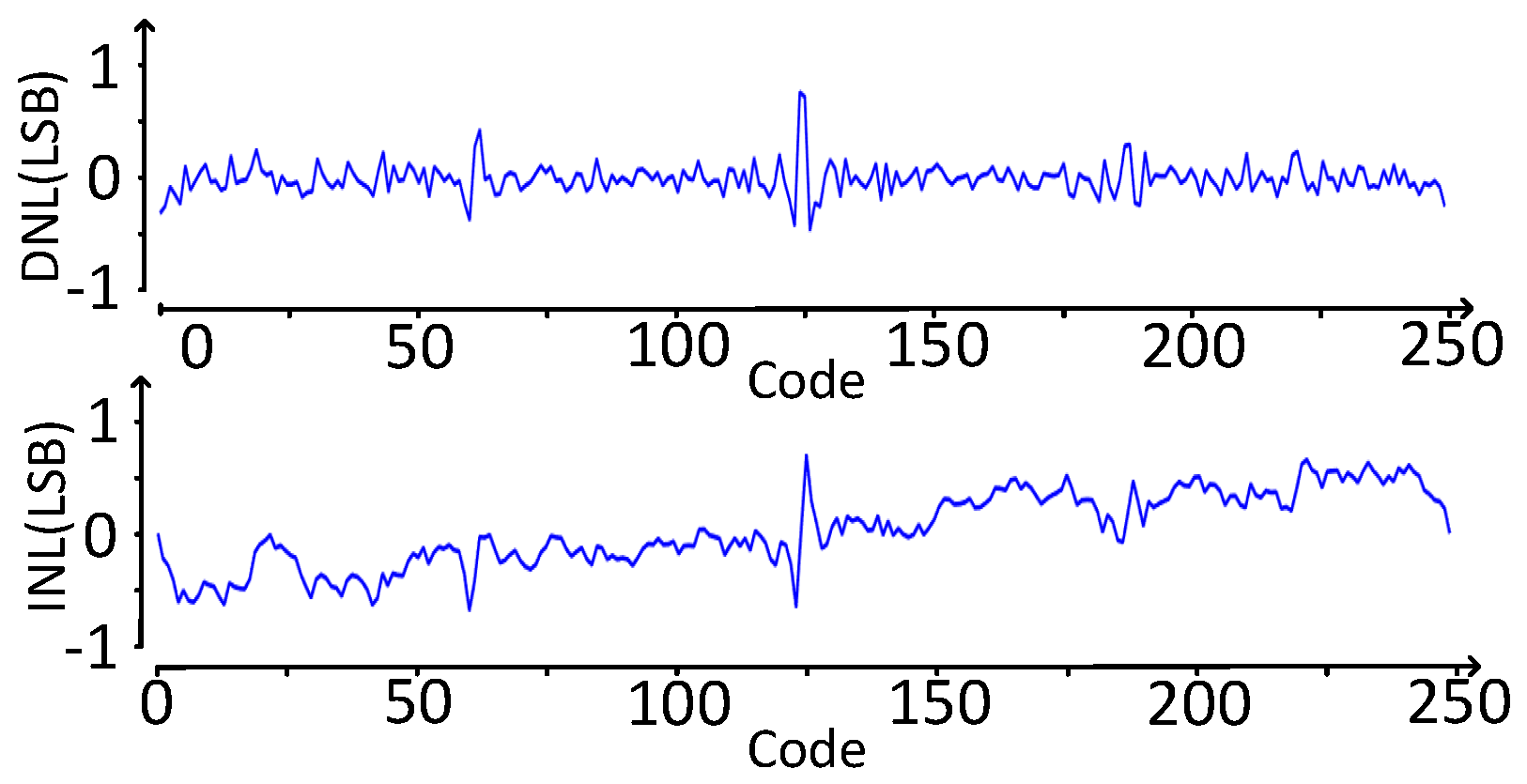
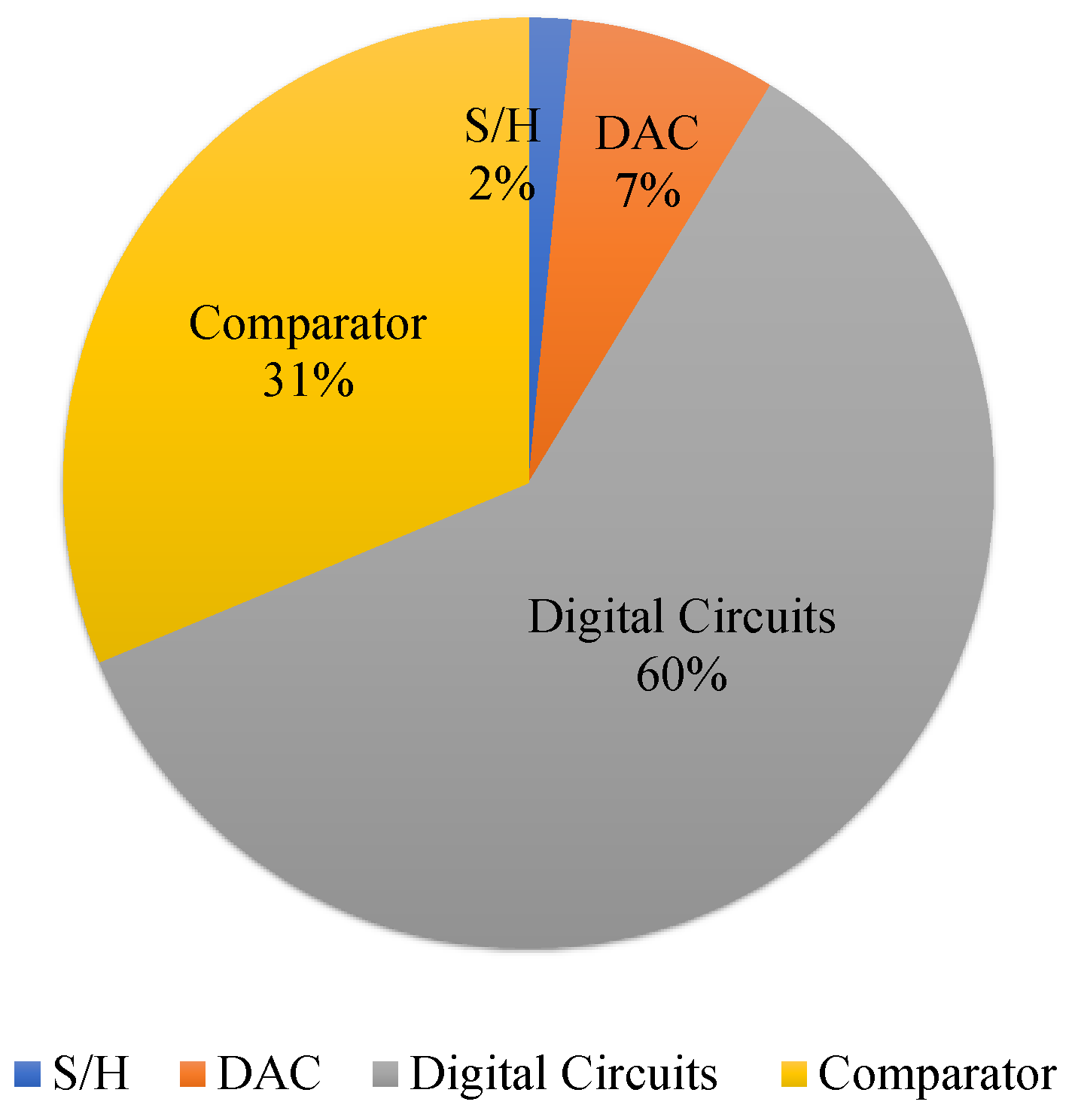
4.1. SAR ADC Readout Circuit Layout and Post-Simitation Results
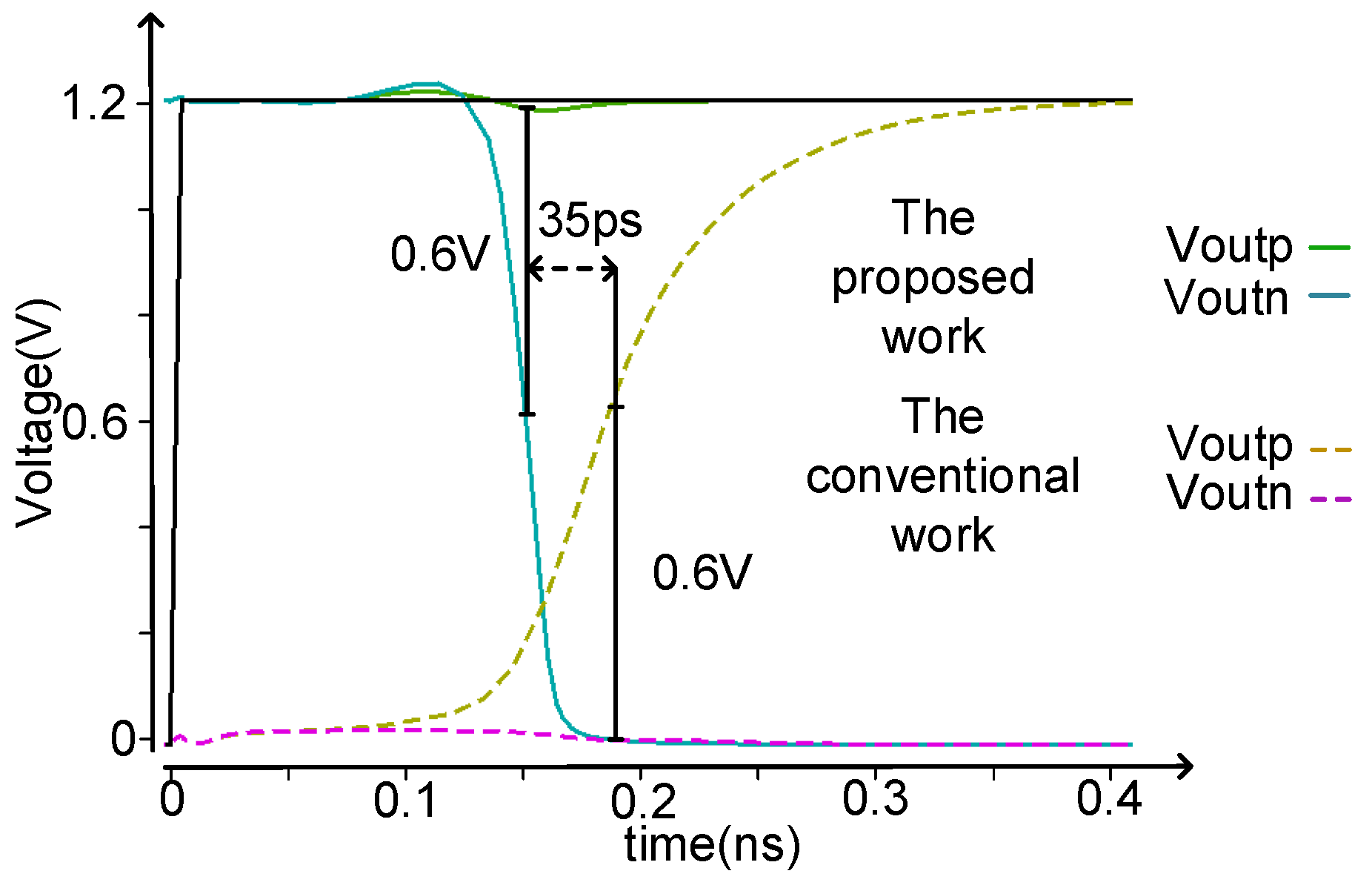
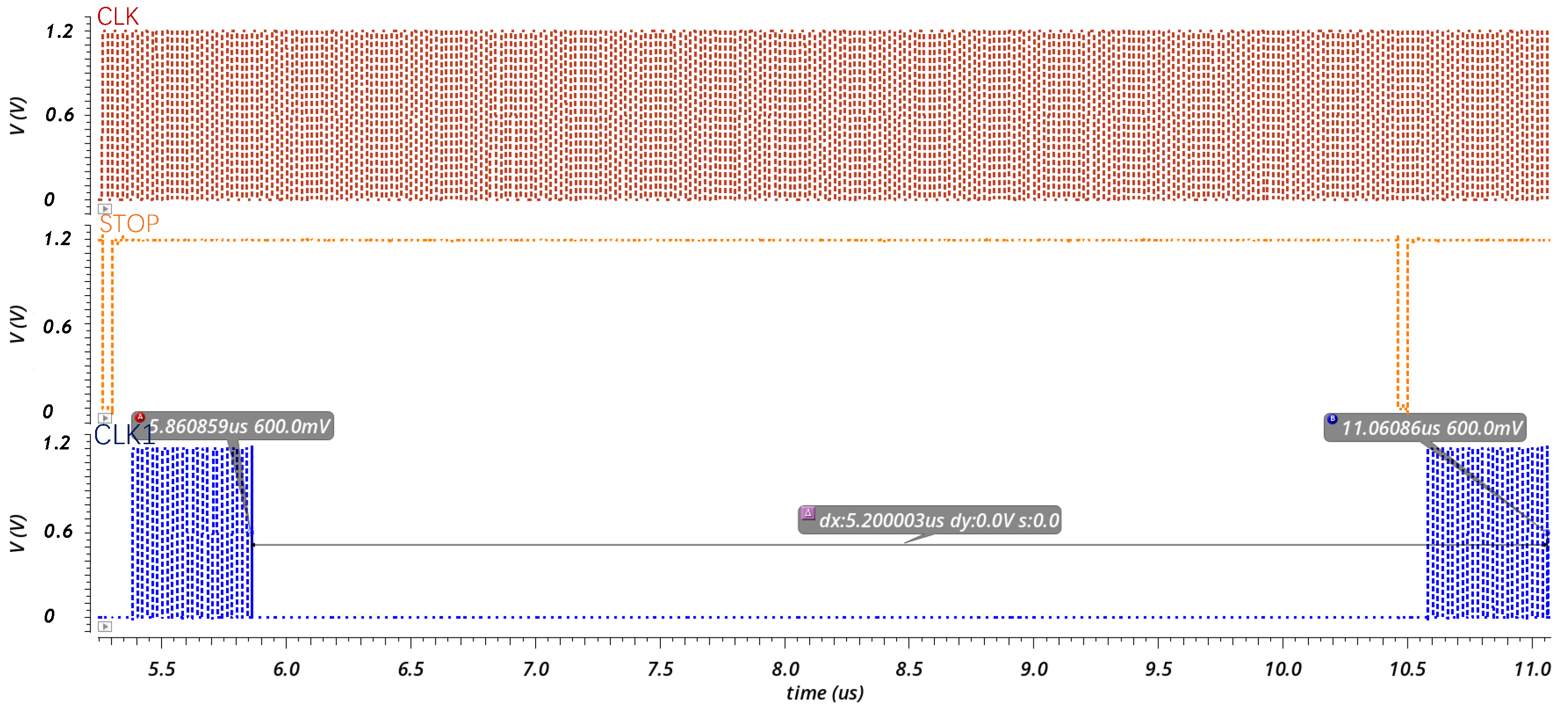
4.2. Simulation of Current-Controlled Oscillator-Type Readout Circuit
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meng, F.H.; Lu, W.D. Compute-in-Memory Technologies for Deep Learning Acceleration. IEEE Nanotechnol. Mag. 2024, 18, 44–52. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, B.; Yao, P.; Wu, D.; Chen, J.; Pang, Y.; Zhang, W.; Liao, Y.; Xue, C.X.; Chen, W.H.; et al. 33.2 A fully integrated analog ReRAM based 78.4 TOPS/W compute-in-memory chip with fully parallel MAC computing. In Proceedings of the 2020 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 500–502. [Google Scholar]
- Lee, K.; Cheon, S.; Jo, J.; Choi, W.; Park, J. A charge-sharing based 8t sram in-memory computing for edge dnn acceleration. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 739–744. [Google Scholar]
- Xiao, K.; Cui, X.; Qiao, X.; Song, J.; Luo, H.; Wang, X.; Wang, Y. A 28nm 32Kb SRAM computing-in-memory macro with hierarchical capacity attenuator and input sparsity-optimized ADC for 4b MAC operation. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 1816–1820. [Google Scholar] [CrossRef]
- Chou, T.; Tang, W.; Botimer, J.; Zhang, Z. Cascade: Connecting rrams to extend analog dataflow in an end-to-end in-memory processing paradigm. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture, Columbus, OH, USA, 12–16 October 2019; pp. 114–125. [Google Scholar]
- Liu, H.; Qian, Z.; Wu, W.; Ren, H.; Liu, Z.; Ni, L. AFPR-CIM: An Analog-Domain Floating-Point RRAM-based Compute-In-Memory Architecture with Dynamic Range Adaptive FP-ADC. arXiv 2024, arXiv:2402.13798. [Google Scholar]
- Mayahinia, M.; Singh, A.; Bengel, C.; Wiefels, S.; Lebdeh, M.A.; Menzel, S.; Wouters, D.J.; Gebregiorgis, A.; Bishnoi, R.; Joshi, R.; et al. A voltage-controlled, oscillation-based adc design for computation-in-memory architectures using emerging rerams. ACM J. Emerg. Technol. Comput. Syst. 2022, 18, 1–25. [Google Scholar] [CrossRef]
- Singh, A.; Lebdeh, M.A.; Gebregiorgis, A.; Bishnoi, R.; Joshi, R.V.; Hamdioui, S. Srif: Scalable and reliable integrate and fire circuit adc for memristor-based cim architectures. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 1917–1930. [Google Scholar] [CrossRef]
- Harpe, P.; Zhou, C.; Wang, X.; Dolmans, G.; de Groot, H. A 30fJ/conversion-step 8b 0-to-10MS/s asynchronous SAR ADC in 90 nm CMOS. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 7–11 February 2010; pp. 388–389. [Google Scholar]
- Chen, H.; He, L.; Deng, H.; Yin, Y.; Lin, F. A high-performance bootstrap switch for low voltage switched-capacitor circuits. In Proceedings of the 2014 IEEE International Symposium on Radio-Frequency Integration Technology, Hefei, China, 27–30 August 2014; pp. 1–3. [Google Scholar]
- Xu, X.; Shui, Y.; Wang, A. A 0.0025 mm 2 8-bit 70MS/s SAR ADC with a Linearity-Improved Bootstrapped Switch for Computation in Memory. In Proceedings of the 2023 8th International Conference on Integrated Circuits and Microsystems (ICICM), Nanjing, China, 20–23 October 2023; pp. 412–416. [Google Scholar]
- Khorami, A.; Dastjerdi, M.B.; Ahmadi, A.F. A low-power high-speed comparator for analog to digital converters. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 2010–2013. [Google Scholar]
- Ginsburg, B.P.; Chandrakasan, A.P. An energy-efficient charge recycling approach for a SAR converter with capacitive DAC. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005; pp. 184–187. [Google Scholar]
- Wang, A.; Shi, C.J.R. A 10-bit 50-MS/s SAR ADC with 1 fJ/conversion in 14 nm SOI FinFET CMOS. Integration 2018, 62, 246–257. [Google Scholar] [CrossRef]
- Jiang, Z.; Wong, H.S.P. Stanford University resistive-switching random access memory (RRAM) Verilog-A model. nanoHUB 2014. [Google Scholar]
- Shui, Y.; Wang, A. A 14.17 pJ·K2 FoM CMOS Temperature Sensor with 173 μm2 Sensing Core for Remote Sensing in 65 nm CMOS. IEEE Sens. J. 2023, 23, 27059–27067. [Google Scholar] [CrossRef]
- Yoon, Y.G.; Park, S.H.; Cho, S. A time-based noise shaping analog-to-digital converter using a gated-ring oscillator. In Proceedings of the 2011 IEEE MTT-S International Microwave Workshop Series on Intelligent Radio for Future Personal Terminals, Daejeon, Republic of Korea, 24–25 August 2011; pp. 1–4. [Google Scholar]
- Liu, S.; Rabuske, T.; Paramesh, J.; Pileggi, L.; Fernandes, J. Analysis and background self-calibration of comparator offset in loop-unrolled SAR ADCs. IEEE Trans. Circuits Syst. Regul. Pap. 2017, 65, 458–470. [Google Scholar] [CrossRef]
- Tang, F.; Ma, Q.; Shu, Z.; Zheng, Y.; Bermak, A. A 28 nm cmos 10 bit 100 ms/s asynchronous sar adc with low-power switching procedure and timing-protection scheme. Electronics 2021, 10, 2856. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, Z.; Hou, X. A 10-bit 50-ms/s asynchronous sar adc in 65nm cmos. In Proceedings of the 2022 IEEE 14th International Conference on Advanced Infocomm Technology (ICAIT), Chongqing, China, 8–11 July 2022; pp. 225–229. [Google Scholar]
- Huang, Y.; Luo, C.; Guo, G. A cryogenic 8-bit 32 ms/s sar adc operating down to 4.2 k. Electronics 2023, 12, 1420. [Google Scholar] [CrossRef]
- Liu, C.; Yan, B.; Yang, C.; Song, L.; Li, Z.; Liu, B.; Chen, Y.; Li, H.; Wu, Q.; Jiang, H. A spiking neuromorphic design with resistive crossbar. In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 7–11 June 2015; pp. 1–6. [Google Scholar]






| MOS | MN1,1–MN4,1 | MN1,2–MN1,4 | MN2,2–MN2,4 | MN3,2–MN3,4 | MN4,2–MN4,4 |
|---|---|---|---|---|---|
| W/L | 20/600n | 120n/600n | 240n/600n | 480n/600n | 960n/600n |
| MOS | MN1 | MN2 | MN3 | MP1 | MP2 | MP3 |
|---|---|---|---|---|---|---|
| W/L | 600n/200n | 120n/60n | 120n/60n | 3/60n | 1/200n | 240n/60n |
| [18] * | [19] * | [20] + | [21] + | This Work + | |
|---|---|---|---|---|---|
| Technology (nm) | 130 | 28 | 65 | 180 | 110 |
| Active Area (mm2) | 0.048 | 0.026 | 0.105 | 0.253 | 0.00255 |
| Resolution (bits) | 8 | 10 | 10 | 8 | 8 |
| Supply (V) | 1.2 | 0.9 | 1.2 | 1.8 | 1.2 |
| Sampling Rate (MS/s) | 150 | 100 | 50 | 32 | 70 |
| SNDR (dB) | 42.9 | 51.54 | 52.09 | 47.7 | 46.2 |
| ENOB (bits) | 6.83 | 8.27 | 8.36 | 7.63 | 7.4 |
| Power (W) | 640 | 1.1 m | 2.79 m | 2.4 m | 553 |
| FOM (fJ/Conv.-step) | 37.5 | 35.6 | 169 | 378 | 47.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Wang, A.; Shui, Y. Readout Circuit Design for RRAM Array-Based Computing in Memory Architecture. Electronics 2024, 13, 2478. https://doi.org/10.3390/electronics13132478
Xu X, Wang A, Shui Y. Readout Circuit Design for RRAM Array-Based Computing in Memory Architecture. Electronics. 2024; 13(13):2478. https://doi.org/10.3390/electronics13132478
Chicago/Turabian StyleXu, Xingjie, Aili Wang, and Yuhang Shui. 2024. "Readout Circuit Design for RRAM Array-Based Computing in Memory Architecture" Electronics 13, no. 13: 2478. https://doi.org/10.3390/electronics13132478
APA StyleXu, X., Wang, A., & Shui, Y. (2024). Readout Circuit Design for RRAM Array-Based Computing in Memory Architecture. Electronics, 13(13), 2478. https://doi.org/10.3390/electronics13132478






