Global Regulation by Integral Feedback for Lower-Triangular Nonlinear Systems with Actuator Failures and Limited Delays
Abstract
1. Introduction
2. Preliminaries
3. Main Results
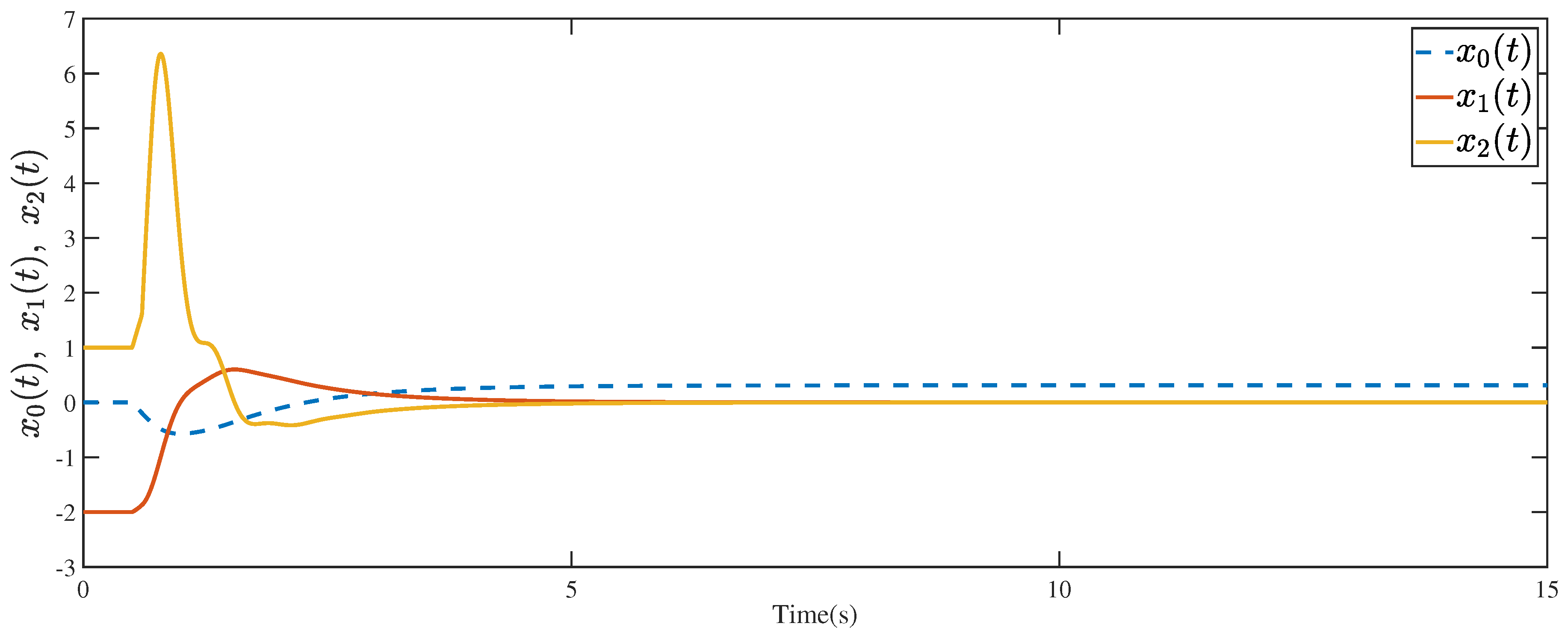
4. A Simulation Example
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khalil, H. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Sepulchre, R.; Jankovic, M.; Kokotovic, P.V. Constructive Nonlinear Control; Springer: New York, NY, USA, 1997. [Google Scholar]
- Lin, W.; Wei, W. Semiglobal asymptotic stabilization of lower triangular systems by digital output feedback. IEEE Trans. Autom. Control 2018, 64, 2135–2141. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, P.; Jiang, Z. Event-triggered input-to-state stabilization of nonlinear systems subject to disturbances and dynamic uncertainties. Automatica 2019, 108, 108488. [Google Scholar] [CrossRef]
- Qian, C.; Lin, W. A continuous feedback approach to global strong stabilization of nonlinear systems. IEEE Trans. Autom. Control 2001, 46, 1061–1079. [Google Scholar] [CrossRef]
- Liu, Y. Global asymptotic regulation via time-varying output feedback for a class of uncertain nonlinear systems. SIAM J. Control. Optim. 2013, 51, 4318–4342. [Google Scholar] [CrossRef]
- Yang, J.; Ding, Z. Global output regulation for a class of lower triangular nonlinear systems: A feedback domination approach. Automatica 2017, 76, 65–69. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H. Adaptive asymptotic tracking using barrier functions. Automatica 2018, 98, 239–246. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, Y.; Wu, Y. Global robust output tracking control for a class of uncertain cascaded nonlinear systems. Automatica 2018, 93, 274–281. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Y. A new approach to global asymptotic tracking for a class of low-triangular nonlinear systems via output feedback. IEEE Trans. Autom. Control 2012, 57, 3192–3196. [Google Scholar] [CrossRef]
- Li, K.; Hua, C.; You, X.; Guan, X. Output feedback-based consensus control for nonlinear time delay multiagent systems. Automatica 2020, 111, 108669. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Feng, G. Leader-follower consensus of time-varying nonlinear multi-agent systems. Automatica 2015, 52, 8–14. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, Y.; Su, H.; Lin, C. Event-driven guaranteed cost control design for nonlinear systems with actuator faults via reinforcement learning algorithm. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4135–4150. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C. Adaptive Backstepping Control of Uncertain Systems: Nonsmooth Nonlinearities, Interactions or Time-Variations; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Benosman, M.; Lum, K. Application of passivity and cascade structure to robust control against loss of actuator effectiveness. Int. J. Robust Nonlinear Control 2010, 20, 673–693. [Google Scholar] [CrossRef]
- Vemuri, A.T.; Polycarpou, M.M. Robust nonlinear fault diagnosis in input-output systems. Int. J. Control 1997, 68, 343–360. [Google Scholar] [CrossRef]
- Gao, Z.; Antsaklis, P. Stability of the pseudo-inverse method for reconfigurable control systems. Int. J. Control 1991, 53, 717–729. [Google Scholar] [CrossRef]
- Corradini, M.; Orlando, G. Actuator failure identification and compensation through sliding modes. IEEE Trans. Control. Syst. Technol. 2007, 15, 184–190. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C. Adaptive compensation for infinite number of actuator failures or faults. Automatica 2011, 47, 2197–2210. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Adaptive compensation for actuator failures with event-triggered input. Automatica 2017, 85, 129–136. [Google Scholar] [CrossRef]
- Karafyllis, I.; Krstic, M. Nonlinear stabilization under sampled and delayed measurements, and with inputs subject to delay and zero-order hold. IEEE Trans. Autom. Control 2012, 57, 1141–1154. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, X.; Li, H. Global regulation for feedforward systems with both discrete delaysand distributed delays. Automatica 2020, 113, 108753. [Google Scholar] [CrossRef]
- Zhou, B.; Luo, W. Improved Razumikhin and Krasovskii stability criteria for time-varying stochastic time-delay systems. Automatica 2018, 89, 382–391. [Google Scholar] [CrossRef]
- Richard, J. Time-delay systems: An overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- Mazenc, F.; Niculescu, S.; Bekaik, M. Backstepping for nonlinear systems with delay in the input revisited. SIAM J. Control. Optim. 2011, 49, 2263–2278. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, W.; Lin, Y. Nonsmooth feedback control of time-delay nonlinear systems: A dynamic gain based approach. IEEE Trans. Autom. Control 2017, 62, 438–444. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C.; Cheng, Z. Asymptotic stabilization via output feedback for nonlinear systems with delayed output. Int. J. Syst. Sci. 2006, 37, 599–607. [Google Scholar] [CrossRef]
- Zhao, C.; Lin, W. Global stabilization by memoryless feedback for nonlinear systems with a limited input delay and large state delays. IEEE Trans. Autom. Control 2021, 66, 3702–3709. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Chang, Y. Sampled-data integral control of nonholonomic systems with unknown constant disturbances. IEEE Trans. Circuits Syst. Ii: Express Briefs 2022, 69, 2792–2796. [Google Scholar] [CrossRef]
- Gu, S.; Qian, C.; Zhang, N. Finite-time integral control for a class of nonlinear planar systems with non-vanishing uncertainties. Automatica 2022, 136, 110036. [Google Scholar] [CrossRef]
- Tsinias, J. A theorem on global stabilization of nonlinear systems by linear feedback. Syst. Control Lett. 1991, 17, 357–362. [Google Scholar] [CrossRef]
- Chen, C.; Qian, C.; Sun, S.; Liang, Y. Global output feedback stabilization of a class of nonlinear systems with unknown measurement sensitivity. IEEE Trans. Autom. Control 2017, 63, 2212–2217. [Google Scholar] [CrossRef]
- Qian, C.; Du, H. Global output feedback stabilization of a class of nonlinear systems via linear sampled-data control. IEEE Trans. Autom. Control 2012, 57, 2934–2939. [Google Scholar] [CrossRef]
- Qian, C.; Lin, W. Output feedback control of a class of nonlinear systems: A nonseparation principle paradigm. IEEE Trans. Autom. Control 2002, 47, 1710–1715. [Google Scholar] [CrossRef]
- Zhu, J.; Qian, C. A necessary and sufficient condition for local asymptotic stability of a class of nonlinear systems in the critical case. Automatica 2018, 96, 234–239. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, Y. Practical tracking via adaptive event-triggered feedback for uncertain nonlinear systems. IEEE Trans. Autom. Control 2019, 64, 3920–3927. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wei, D.; Zhang, G.; Li, J. Global Regulation by Integral Feedback for Lower-Triangular Nonlinear Systems with Actuator Failures and Limited Delays. Electronics 2023, 12, 1127. https://doi.org/10.3390/electronics12051127
Chen X, Wei D, Zhang G, Li J. Global Regulation by Integral Feedback for Lower-Triangular Nonlinear Systems with Actuator Failures and Limited Delays. Electronics. 2023; 12(5):1127. https://doi.org/10.3390/electronics12051127
Chicago/Turabian StyleChen, Xiandong, Dajun Wei, Guoteng Zhang, and Jinbao Li. 2023. "Global Regulation by Integral Feedback for Lower-Triangular Nonlinear Systems with Actuator Failures and Limited Delays" Electronics 12, no. 5: 1127. https://doi.org/10.3390/electronics12051127
APA StyleChen, X., Wei, D., Zhang, G., & Li, J. (2023). Global Regulation by Integral Feedback for Lower-Triangular Nonlinear Systems with Actuator Failures and Limited Delays. Electronics, 12(5), 1127. https://doi.org/10.3390/electronics12051127





