Research on Rolling Bearing Fault Diagnosis Based on Variational Modal Decomposition Parameter Optimization and an Improved Support Vector Machine
Abstract
:1. Introduction
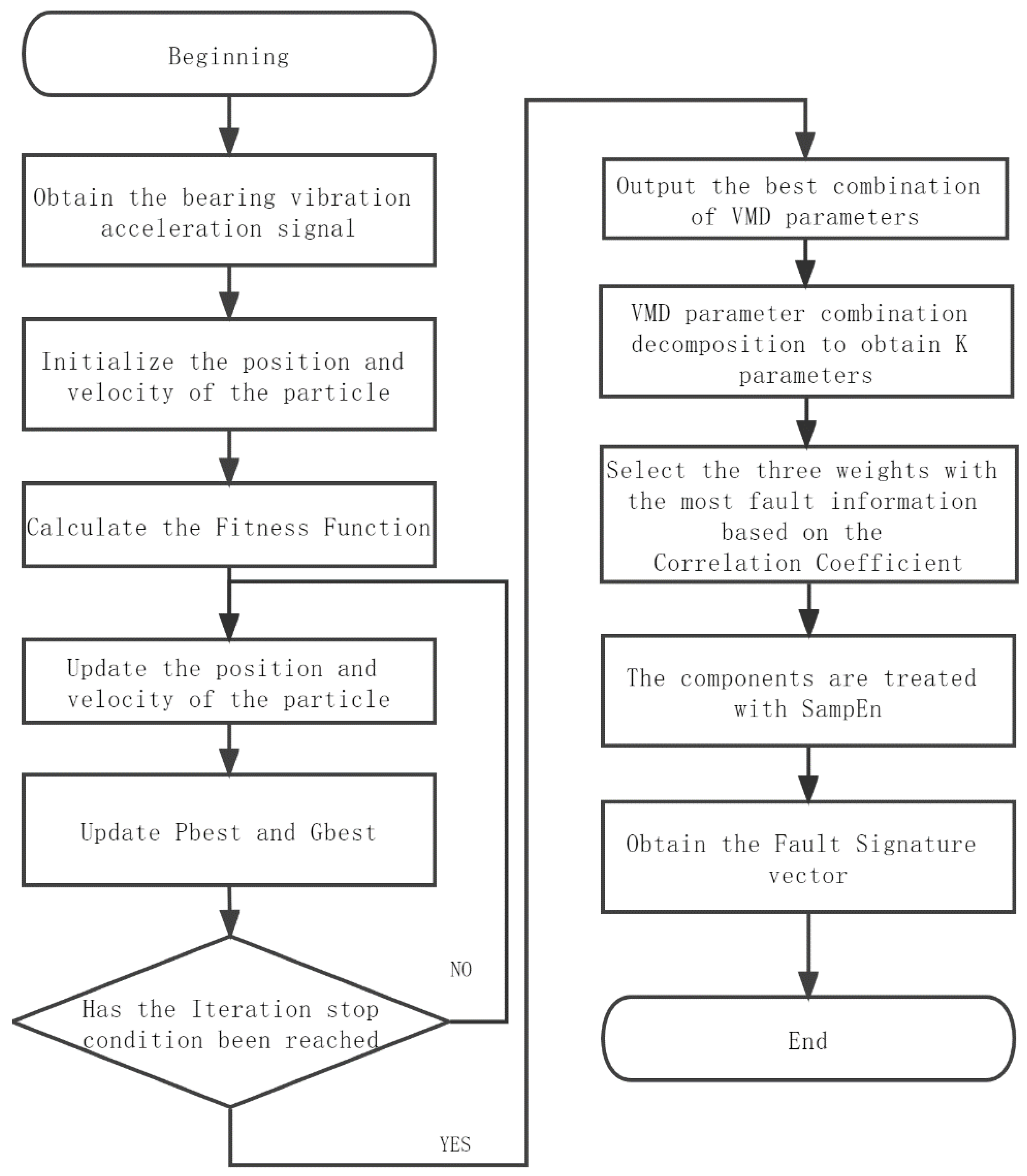
2. Fault Feature Extraction Algorithm for Rolling Bearings Based on IPSO-VMD
2.1. Principle of Variational Modal Decomposition
2.2. Improved Particle Swarm Optimization Algorithm
- (1)
- Set the inertia weight coefficient based on the random strategy
- (2)
- Setting learning factors based on linearly varying policies
2.3. Fitness Function
2.4. Fault Feature Extraction and Testing
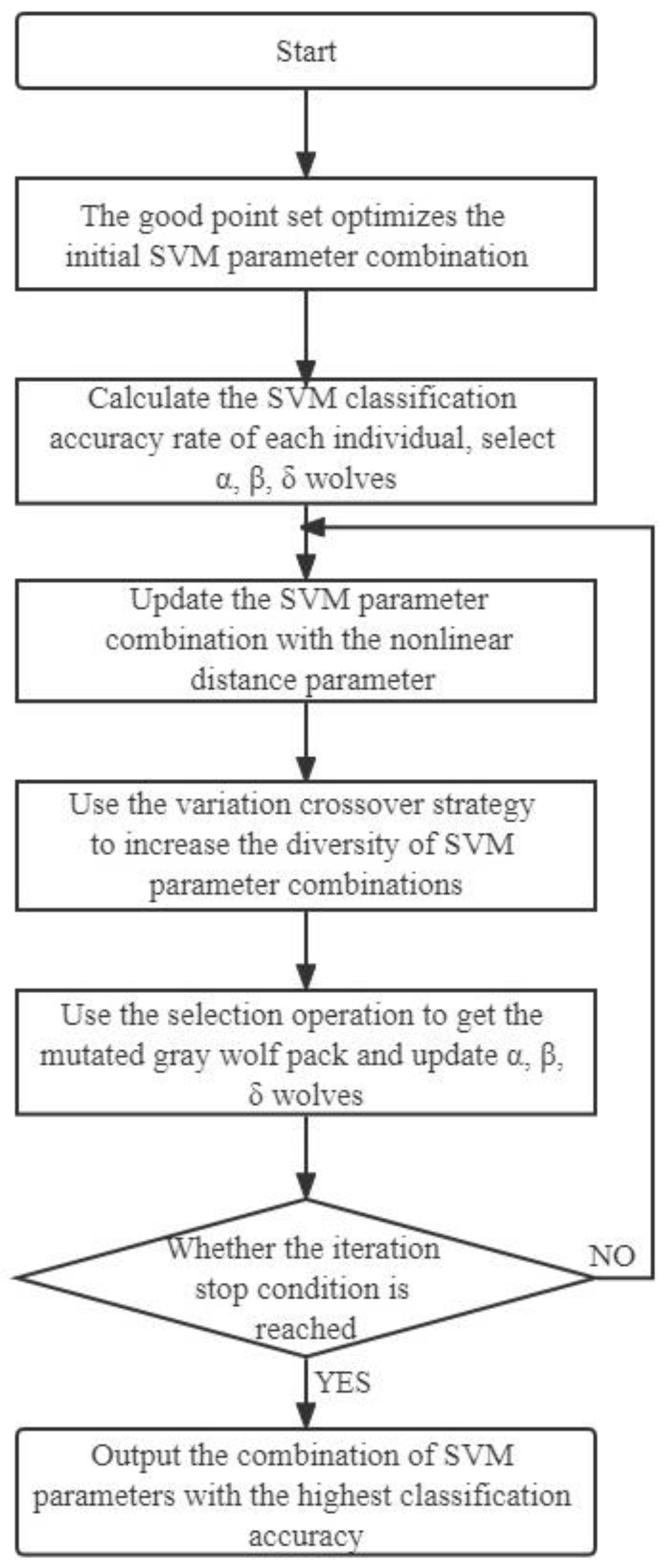
3. Bearing Fault Diagnosis Based on IGWO-SVM
3.1. Principle of Support Vector Machine
3.2. Improved Gray Wolf Algorithm
- (1)
- Distance parameter strategy based on nonlinear control
- (2)
- Population initialization strategy based on the good-point set theory
- (3)
- Population diversification strategy based on mutation crossover
3.3. Improved Gray Wolf Algorithm Optimization Support Vector Machine
4. Rolling Bearing Fault Diagnosis Experiment
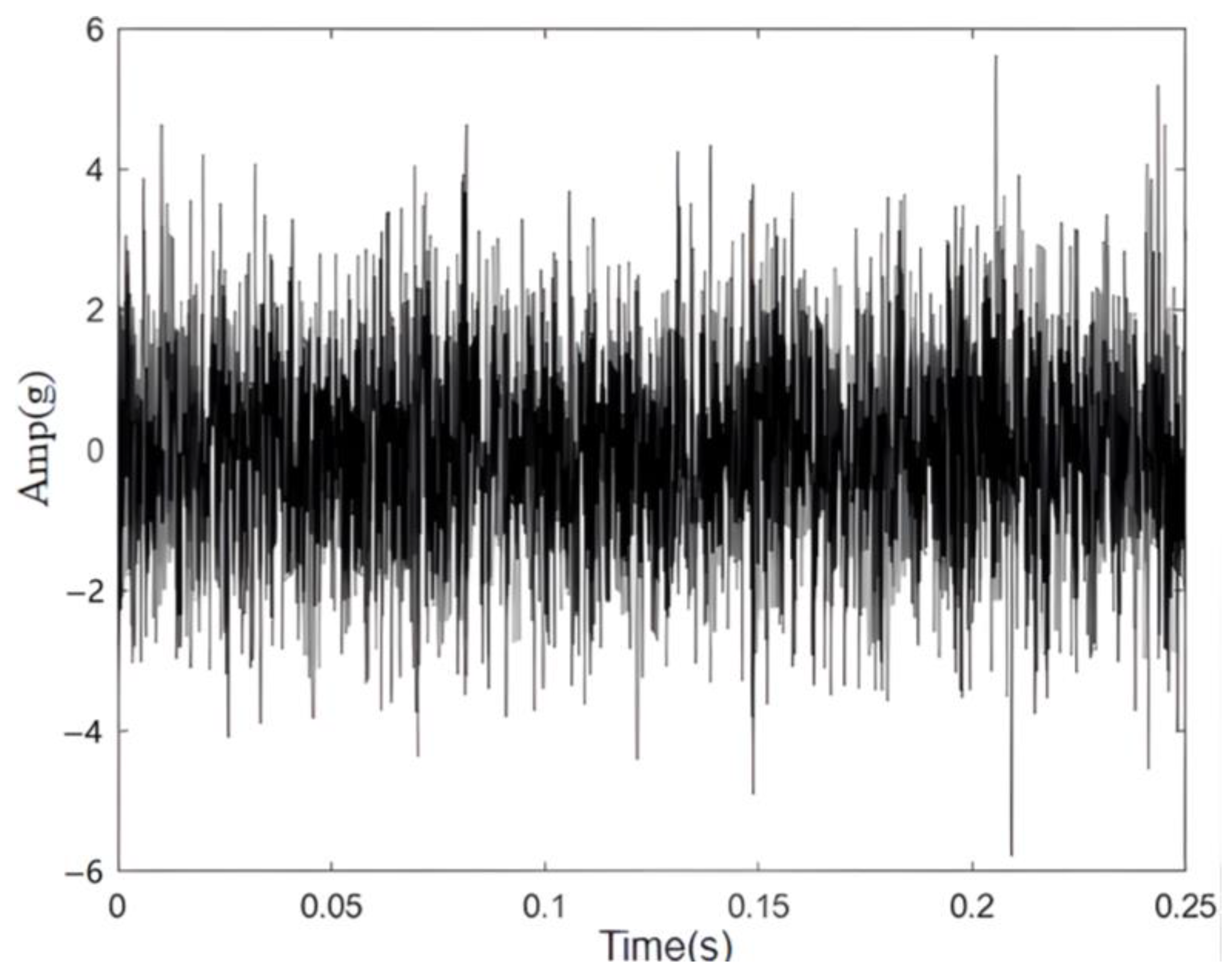
4.1. Experimental Data Collection
4.2. Fault Feature Extraction of Signals
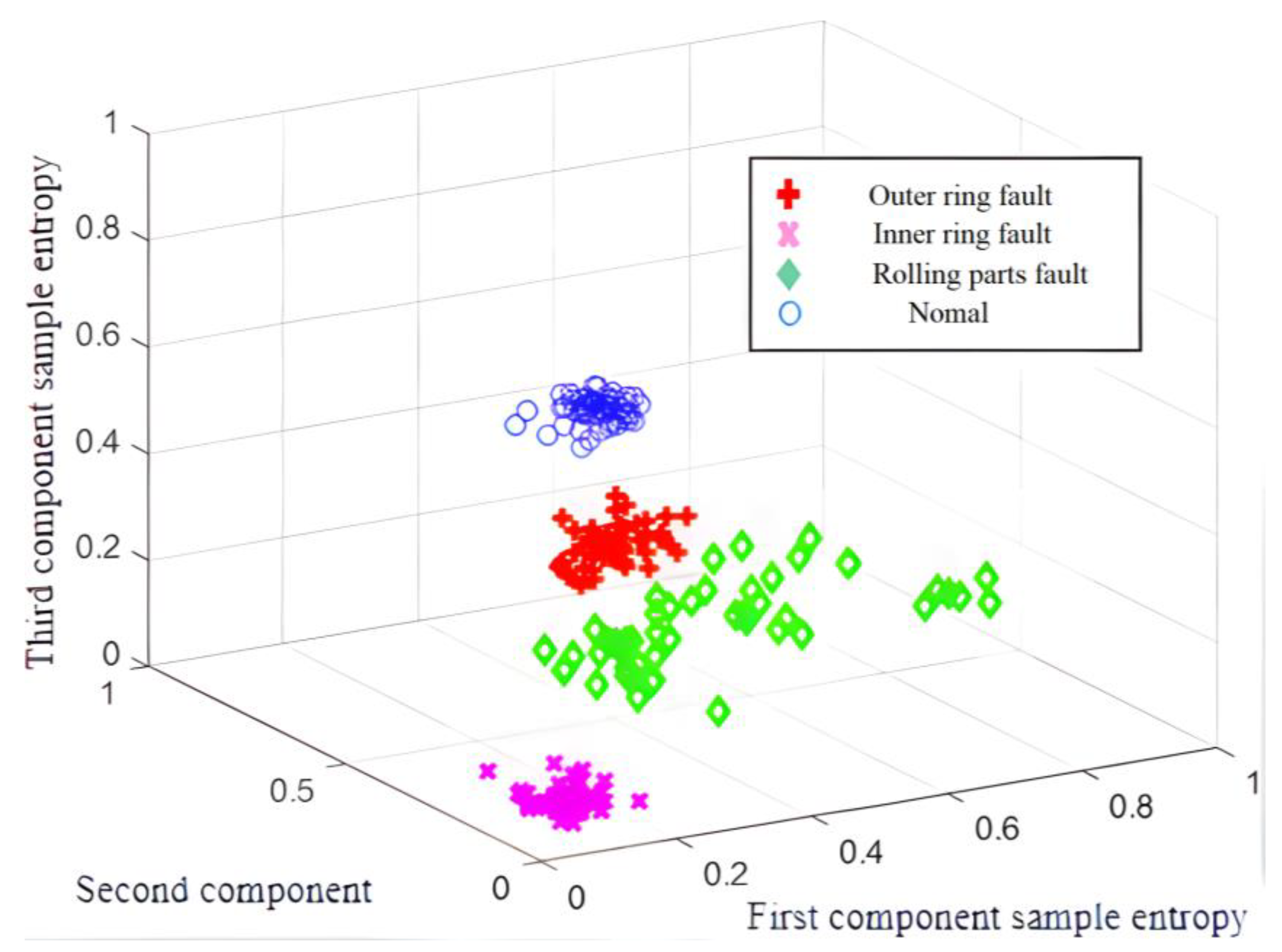
4.3. Analysis of Fault Diagnosis Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Q.; Dai, S.; Bi, X. Fault Diagnosis of Rolling Bearings based on EEMD. Comput. Simul. 2021, 38, 361–364, 369. [Google Scholar]
- Wu, F.; Ding, J.; Liu, S.; Lu, X. Fault Diagnosis of Transmission Shaft System of Automobile based on VMD and PSO-SVM. Mech. Transm. 2019, 43, 120–124, 149. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-assisted Data Analysis Method. Adv. Adapt. Data Anal. 2005, 8, 12–22. [Google Scholar] [CrossRef]
- Xu, G.; Dai, H. Suspension Fault Diagnosis of Metro Series with EEHD Decomposition and Multi-feature Combination. Mach. Manuf. Autom. 2021, 50, 191–195. [Google Scholar]
- Konstantin, D.; Dominique, Z. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar]
- Liu, C.; Wu, Y.; Zhen, C. Rolling Bearings Fault Diagnosis based on Variational Mode Decomposition and Fuzzy C Means Clustering. Proc. CSEE 2015, 35, 3358–3365. [Google Scholar]
- Wang, F.; Liu, C.; Zhang, T.; Guo, B.; Han, Q.; Li, H. Fault Diagnosis Method of Rolling Bearing based on k-value Optimization VMD. J. Vib. Test. Diagn. 2018, 38, 540–547. [Google Scholar]
- Li, H.; Wu, X.; Liu, T. Fault Feature Extraction of Rolling Bearing based on Information Entropy Optimization Variational Mode Decomposition. J. Vib. Shock. 2018, 37, 219–225. [Google Scholar]
- Zhang, J.; Ji, J.; Xu, T. A Bearing Fault Diagnosis Method based on Variational Mode Decomposition Parameter Optimization. Sci. Technol. Eng. 2021, 21, 3601–3605. [Google Scholar]
- Chang, Y.; Bao, G.; Cheng, S.; He, T.; Yang, Q. Improved VMD-KFCM Algorithm for the Fault Diagnosis of Rolling Bearing Vibration Signals. IET Signal Process. 2021, 15, 238–250. [Google Scholar] [CrossRef]
- Zhu, S.; Xia, H.; Peng, B.; Zio, E.; Wang, Z.; Jiang, Y. Feature Extraction for Early Fault Detection in Rotating Machinery of Nuclear Power Plants based on Adaptive VMD and Teager Energy Operator. Ann. Nucl. Energy 2021, 160, 1083–1092. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, S.; Fan, Z.P. Bearing Fault Diagnosis based on Improved Particle Swarm Optimized VMD and SVM models. Adv. Mech. Eng. 2021, 13, 1–12. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, S.; Wu, W. Research on Bearing Vibration Signal Analysis Method Combined with CNN. Mech. Sci. Technol. 2022, 41, 1943–1949. [Google Scholar] [CrossRef]
- Deng, H.; Zhang, W.X.; Liang, Z.F. Application of BP Neural Network and Convolutional Neural Network (CNN) in Bearing Fault Diagnosis. Mater. Sci. Eng. 2021, 1043, 42–46. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, J.; Guo, X.; Tan, L. A self-Adaptive CNN with PSO for Bearing Fault Diagnosis. Syst. Sci. Control. Eng. 2020, 9, 11–22. [Google Scholar] [CrossRef]
- Pinedo-Sanchez, L.A.; Mercado-Ravell, D.A.; Carballo-Monsivais, C.A. Vibration Analysis in Bearings for Failure Prevention using CNN. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 628–644. [Google Scholar] [CrossRef]
- Song, L.; Sun, L. Study on Fault Diagnosis Method of EEMD-GSSA-SVM Rolling Bearing. Transducer Microsyst. 2022, 41, 56–59. [Google Scholar]
- Meng, F.; Du, W.; Gong, X.Y. Fault Identification of Rolling Bearings based on Particle Swarm Optimization Least Squares Support Vector Machine. Bearings 2020, 12, 43–50. [Google Scholar]
- Chen, Q.; Chen, Z.Y.; Fu, Y. Bearing Fault Diagnosis of Chaotic Bat Algorithm Optimization Correlation Vector Machine. Sens. Microsyst. 2021, 40, 142–145. [Google Scholar]
- Ma, C.P.; Li, M.H.; Gong, Q.L. Fault Diagnosis of Rolling Bearings of Optimized Support Vector Machine based on Sparrow Search Algorithm. Sci. Technol. Eng. 2021, 21, 4025–4029. [Google Scholar]
- Zhou, J.; Huang, S.; Wang, M.; Qiu, Y. Performance Evaluation of Hybrid GA–SVM and GWO–SVM Models to Predict Earthquake-Induced Liquefaction Potential of Oil: A Mul-dataset Investigation. Eng. Comput. 2022, 38, 4197–4215. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, N.; Cui, X. Fault Diagnosis Method of Aircraft Anti-skid Brake System Base on GWO-PNN. In Proceedings of the 2021 33rd Chinese Control and Decision Conference, Kunming, China, 22–24 May 2021; pp. 5402–5406. [Google Scholar]
- Sharma, S.; Kapoor, A. An Efficient Routing Algorithm for IoT Using GWO Approach. Int. J. Appl. Metaheuristic Comput. 2021, 12, 67–84. [Google Scholar] [CrossRef]
- Gul, F.; Rahiman, W.; Alhady, S.S.N.; Ali, A.; Mir, I.; Jalil, A. Meta-Heuristic Approach for Solving Multi-Objective Path Planning for Autonomous Guided Robot using PSO–GWO Optimization Algorithm with Evolutionary Programming. J. Ambient. Intell. Humaniz. Comput. 2020, 12, 7873–7890. [Google Scholar] [CrossRef]
- Ma, R.; Karimzadeh, M.; Ghabussi, A.; Zandi, Y.; Baharom, S.; Selmi, A.; Maureira-Carsalade, N. Assessment of Composite Beam Performance using GWO–ELM Metaheuristic Algorithm. Eng. Comput. 2022, 38, 2083–2099. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, S.Y.; Bai, G.Z. Improved Particle Swarm Optimization based on Nonlinear Decreasing Inertial Weights. J. Chongqing Technol. Bus. Univ. (Nat. Sci. Ed.) 2021, 38, 1–9. [Google Scholar]
- Yang, B.; Qian, W. Review of Inertia Weight Improvement Strategies in Particle Swarm Optimization Algorithm. J. Bohai Univ. (Nat. Sci. Ed.) 2019, 40, 274–288. [Google Scholar]
- Li, L. Application of CEEMDAN method in fault feature extraction and pattern recognition of rolling bearing. J. Lanzhou Jiaotong Univ. 2021, 1, 36–40. [Google Scholar]
- Li, H.R.; Peng, J. Particle Swarm Optimization Algorithm with Nonlinear Inertial Weights and Cauchy Variation. Comput. Digit. Eng. 2021, 49, 1325–1329, 1362. [Google Scholar]
- Huang, J.; Guan, Y.N. SVM Parameter Optimization Method based on Good Point Set Particle Swarm Algorithm. J. Packag. 2019, 11, 74–80. [Google Scholar]









| Signal Type | Signal-to-Noise Ratio (SNR) | Mean Square Error (MSE) |
|---|---|---|
| Noisy Signal | −8 | 2.0394 |
| EMD | −7.6971 | 1.8701 |
| Fixed parameter VMD | −5.8897 | 1.4549 |
| IPSO-VMD | 1.0934 | 0.2471 |
| Method of Fault Feature Extraction | Methods of Fault Diagnosis | Correct Diagnosis of Outer Rings | Correct Diagnosis of Inner Rings | Correct Diagnosis of Rolling Element | Normal State Classification Accuracy Rate | Correct Rate of Overall Diagnosis |
|---|---|---|---|---|---|---|
| IPSO-VMD | SVM | 75 | 100 | 92.5 | 100 | 91.88 |
| GWO-SVM | 85 | 100 | 92.5 | 100 | 94.38 | |
| IGWO-SVM | 92.5 | 100 | 100 | 100 | 98.13 |
| Type | Inner Diameter | Outer Diameter | Rolling Element Diameter | The Number of Rolling Bodies | Contact Angle |
|---|---|---|---|---|---|
| N205/NJ205 | 25 mm | 52 mm | 8 mm | 12 | 0 |
| Bearing Type | Fault Site | Bearing Speed | Each Set of Sample Points | Number of Collected Groups |
|---|---|---|---|---|
| Cylindrical roller bearings | Raceway surface of the outer ring | 540 r/min | 4096 | 50 |
| Cylindrical roller bearings | Raceway surface of the inner ring | 540 r/min | 4096 | 50 |
| Cylindrical roller bearings | Rolling element surface | 540 r/min | 4096 | 50 |
| Cylindrical roller bearings | No faults | 540 r/min | 4096 | 50 |
| Bearing Type | The First Component Sample Entropy | The Second Component Sample Entropy | The Third Component Sample Entropy | Labels |
|---|---|---|---|---|
| Outer ring fault bearing | 0.2641 | 0.2844 | 0.4301 | 1 |
| 0.2837 | 0.2919 | 0.4384 | 1 | |
| 0.2435 | 0.2613 | 0.4247 | 1 | |
| Inner ring fault bearing | 0.0926 | 0.0849 | 0.0798 | 2 |
| 0.0583 | 0.2358 | 0.0699 | 2 | |
| 0.0710 | 0.0970 | 0.0629 | 2 | |
| Rolling element fault bearing | 0.2259 | 0.2335 | 0.3222 | 3 |
| 0.2532 | 0.2195 | 0.2974 | 3 | |
| 0.3060 | 0.3314 | 0.3152 | 3 | |
| Normal bearing | 0.4643 | 0.6269 | 0.5380 | 4 |
| 0.4174 | 0.6428 | 0.5523 | 4 | |
| 0.4015 | 0.5876 | 0.4765 | 4 |
| Accuracy of Outer Rings Diagnosis | Accuracy of Inner Rings Diagnosis | Accuracy of Rolling Element Diagnosis | Accuracy of Rolling Normal State Classification | Accuracy of Rolling Overall Diagnosis | |
|---|---|---|---|---|---|
| First experiment | 97.5 | 100 | 100 | 100 | 99.375 |
| Second experiment | 92.5 | 100 | 97.5 | 100 | 97.5 |
| Third experiment | 97.5 | 100 | 100 | 100 | 99.375 |
| Forth experiment | 100 | 100 | 100 | 100 | 100 |
| Fifth experiment | 97.5 | 100 | 95 | 100 | 98.125 |
| Average accuracy | 97 | 100 | 98.5 | 100 | 98.875 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Meng, W.; Liu, X.; Fei, J. Research on Rolling Bearing Fault Diagnosis Based on Variational Modal Decomposition Parameter Optimization and an Improved Support Vector Machine. Electronics 2023, 12, 1290. https://doi.org/10.3390/electronics12061290
Li L, Meng W, Liu X, Fei J. Research on Rolling Bearing Fault Diagnosis Based on Variational Modal Decomposition Parameter Optimization and an Improved Support Vector Machine. Electronics. 2023; 12(6):1290. https://doi.org/10.3390/electronics12061290
Chicago/Turabian StyleLi, Lin, Weilun Meng, Xiaodong Liu, and Jiyou Fei. 2023. "Research on Rolling Bearing Fault Diagnosis Based on Variational Modal Decomposition Parameter Optimization and an Improved Support Vector Machine" Electronics 12, no. 6: 1290. https://doi.org/10.3390/electronics12061290
APA StyleLi, L., Meng, W., Liu, X., & Fei, J. (2023). Research on Rolling Bearing Fault Diagnosis Based on Variational Modal Decomposition Parameter Optimization and an Improved Support Vector Machine. Electronics, 12(6), 1290. https://doi.org/10.3390/electronics12061290





