Abstract
Rural mobility has a lack of innovative proposals in contrast with its urban counterpart. This research aims to bring solutions that ease the implementation of reliable and flexible rural transportation. Demand-responsive transportation is chosen to develop a public transportation service providing interurban trips among several rural settlements. Given the characteristics of rural displacement demand, a novel approach is introduced to optimize the service’s economic costs: the dynamic transfer point allocation. The problem is fully formulated and an architecture is introduced describing the workflow of the whole system. Data from an interurban bus transportation service are used to build a case study of a rural area of Valencia, Spain, and develop several examples illustrating the benefits of the proposed approach. The results reveal that the dynamic creation of transfer points can simplify the transportation fleet’s itineraries and boost the amount of served travel requests. Finally, a discussion of the benefits and dangers of flexible features in rural transportation is developed, underscoring the need to achieve a balance between dynamic operation and service quality.
1. Introduction
Historically, better transportation services have been implemented in urban areas than in their rural counterparts. Cities contain more potential customers and steadier demand, making the economic viability of their transportation services easier to achieve. Nevertheless, rural inhabitants have crucial displacement needs, such as commuting, school transportation, and even trips to the nearest health center. In general, rural settlements count on traditional public transportation options that provide no adaptability or flexibility for their users’ experience. Because of the characteristics of rural areas, with a low and scarce transportation demand, we aim for demand-responsive transportation (DRT) systems as a potential service to provide flexible and user-tailored transportation. However, demand-responsive services have shown a high failure rate in the past. With that in mind, our research aims to determine how demand-responsive transportation can be effectively implemented in rural areas. To answer such an inquiry, we introduce the notion of dynamic transfer point allocation.
The problem of dynamic transfer point allocation in the field of rural demand-responsive mobility revolves around the task of effectively designating transfer points to optimize the operational efficiency of DRT services in rural settlements. Within this context, transfer points denote specific locations where passengers have the opportunity to switch between distinct fleet vehicles, such as buses or vans, en route to their ultimate destinations. Conventionally, transportation systems establish fixed transfer points. Nevertheless, such an approach may prove inadequate for accommodating the diverse needs of rural passengers. This issue arises from the inherent variability in transportation demand within rural areas, wherein demand levels can exhibit significant fluctuations across different times of day, days of the week, or even seasons of the year [1]. The proposal of activation and deactivation of transfer points according to real-time demand comprises a novel approach to DRT optimization that avoids the issues that static transfer locations raise.
Viable solutions to address this challenge can be derived from the application of data-driven methodologies, which leverage real-time data to enact adaptive changes in response to prevailing demand patterns [2]. For instance, a transportation provider could harness real-time data concerning passenger requests and travel behaviors to identify regions experiencing heightened demand. Subsequently, based on this data-driven insight, the provider could strategically allocate additional transfer points to facilitate efficient passenger transit and ensure that travelers can reach their intended destinations expeditiously. This data-driven approach holds the potential to enhance the effectiveness and responsiveness of rural demand-responsive mobility services.
The exploration of these intelligent techniques in the context of rural DRT optimization, however, remains relatively limited. Several factors contribute to this, including the scarcity of relevant data and, to some extent, the lower socioeconomic incentive for developing concrete solutions for rural mobility challenges [3].
In alignment with the aforementioned research gap, our research aims at the development of artificial intelligence techniques to optimize flexible rural mobility. We believe that the introduction of dynamic features in rural transportation has the potential to alleviate the challenges derived from its demand shape. Continuously assessing passenger requests, traffic conditions, and other relevant factors, these algorithms enable the dynamic reconfiguration of the transportation layout to enhance service efficiency and adapt to changing conditions. From the many dynamic features, the current research focuses on the real-time activation of transfer points, putting forth the following research question: How does the creation of transfer points impact a demand-responsive service?
Our paper contributes to the topic at hand with an architecture proposal that integrates a demand-responsive scheduling service together with a dynamic transfer point allocation system. The data that such an architecture requires are explained, in addition to its workflow. Then, a case study is developed, deploying a DRT service over a real rural area. The different examples of transfer point allocation developed illustrate how this method operates and its beneficial impact on the transportation service’s benefits. Finally, we provide a discussion assessing our results and going over crucial challenges of rural transportation, such as the necessary trade-off between operational cost optimization and service quality in transportation services, as well as the adoption rate of flexible transportation, which is generally harder on rural settlements.
This work is an extended version of the paper “Dynamic transfer point allocation for rural demand-responsive mobility” [4], presented at the Sustainable Smart Cities and Territories International Conference (SSCt 2023). The rest of the paper is structured as follows: Section 2 presents previous related work; Section 3 formalizes the problem of transfer point allocation for rural demand-responsive mobility; then, Section 4 illustrates the optimization of rural DRT services through the development of a real-world-inspired case study. Section 5 assesses the results of the case study, discussing the challenges that flexible transportation systems face when implemented in a rural area; finally, Section 6 sums up the work and presents future contributions.
2. Literature Review
The analysis of prior research in this paper unfolds along three distinct aspects. First, it revisits articles containing artificial intelligence techniques that could aid in the implementation of our proposal. Second, it delves into publications encompassing transfer point or hub allocation, independently of the domain in which they are situated. Finally, the analysis also scrutinizes works that are intrinsically linked to the domain of demand-responsive systems operating within rural environments.
2.1. Artificial Intelligence for Transfer Point Allocation
Artificial intelligence (AI) introduces a multifaceted approach to address the dynamic transfer point allocation challenge in rural transportation, as detailed in recent research [5]. Regarding DRT optimization, one fundamental approach involves the development of AI models capable of predicting demand for transportation services in rural regions [6]. These models take into account a multitude of factors, including temporal aspects such as time of day, day of the week, and seasonality, as well as external influences like weather conditions and special events. By leveraging these predictive models, transportation providers can proactively allocate transfer points in response to anticipated fluctuations in demand, ensuring efficient service delivery.
Additionally, AI plays a pivotal role in route optimization for vehicles operating in rural areas [7]. Real-time data on demand patterns and road conditions are harnessed to guide the efficient deployment of vehicles, enabling them to traverse the most direct and timely routes. This not only enhances operational efficiency but also ensures that passengers reach their destinations swiftly and efficiently.
Regarding the explored problem, there are specific AI techniques that could be employed for the implementation of dynamic transfer point allocation. Genetic algorithms [8], for instance, offer a powerful approach wherein they generate an initial set of potential transfer point locations and subsequently refine them through iterative evolution guided by real-time demand patterns. These algorithms adaptively optimize the locations of transfer points to align with evolving passenger needs. Moreover, decision trees can be employed to analyze real-time demand patterns and make informed decisions regarding optimal transfer point locations based on predefined criteria. This structured approach enables the system to select transfer points that maximize efficiency and align with specific operational objectives. Finally, neural networks can be leveraged to analyze real-time demand patterns and forecast the most efficient locations for transfer points. By processing complex data and identifying subtle patterns, neural networks can provide valuable insights into transfer point optimization.
The problem of transfer point allocation is closely related to vehicle routing. The routes of vehicles have to be taken into account to dynamically choose positions within the transportation network where transfers may occur. In addition, once a transfer point is implemented, vehicle rerouting may be necessary to get the most out of transfers. There are several AI techniques used as a base in the development of innovative routing techniques. The authors in [9] employ genetic algorithms, a metaheuristic technique, to solve the dynamic routing of shipping containers in a fuzzy environment, which brings a more realistic approach to the problem. Similarly, the work in [10] addresses the multiple traveling salesman problem, arguably a routing problem, through a novel metaheuristic optimization algorithm referred to as penguin search. Finally, the problem modeling employed in the research in [11], which is also interesting, deals with a multi-depot vehicle routing problem. These proposals illustrate the potential that AI techniques have to aid in transportation decision making and many of its specific problems.
2.2. Hub Allocation across Different Domains
In the topic of hub allocation, various research works have been conducted across diverse domains. One notable approach involves the strategic distribution of hubs and the allocation of non-hub nodes to these hub locations, with the objective of minimizing the maximum travel time or distance between any origin–destination pair. This problem is referred to as the p-hub center allocation problem. To address this challenge, researchers have employed integer programming solutions, as demonstrated in notable studies such as [12]. This work introduces a novel model for assessing the influence of fixed costs in the design of transportation hub networks. This model affords the flexibility for diverse network types to emerge, contingent upon the inherent cost structure. By integrating environmental hub location modeling methodologies with a three-index formulation, the authors elucidate how a more intricate cost model can give rise to a range of network configurations, each contingent on the relative magnitudes of the constituent cost elements.
Hub allocation is also important for the domains of the aviation and telecommunication industry. In the study [13], researchers introduce an innovative solution to efficiently address larger instances of hub allocation problems. Their novel DBLSA (Diversity-Based Large-Scale Algorithm) offers a promising avenue for tackling these complex challenges effectively. By showcasing the efficacy of the DBLSA algorithm, this study paves the way for further exploration of advanced metaheuristic methodologies that incorporate learning mechanisms. Hailing from a distinct domain, the study presented in [14] introduces an innovative approach centered on genetic algorithms to address the challenge of locating hubs within an agricultural product transportation network. The primary objective is to curtail transportation expenses while guaranteeing the punctual delivery of agricultural goods. The authors conducted extensive testing utilizing data encompassing 48 states of the United States to validate their approach. The results unveiled a notable achievement, showcasing a remarkable 16.73% reduction in total transportation costs when compared to the conventional approach of direct routing.
Hub identification within bus networks has garnered research attention as well. In this endeavor, the study detailed in [15] proposes a node failure model to discern hub stations and crucial lines within bus networks. The innovation extends to the introduction of fresh evaluation indicators, specifically the neighborhood degree ratio and transfer index, designed to assess station significance and line accessibility. The model is validated utilizing the Xiamen bus network in China, demonstrating the effectiveness of the newly introduced indicators in comparison to conventional complex network indicators.
Expanding on the same field, the study outlined in [16] introduces an innovative bi-objective multi-modal hub location problem. This problem is devised to address the complexities associated with the design of urban public transportation networks in the presence of uncertainty. The model takes into account multiple assignment and capacity options and uses a fuzzy multi-objective programming approach for small-sized problems and a metaheuristic algorithm for medium and large-sized problems. The aim is the maximization of transportation benefits and the minimization of transportation time. The research conducts practical demonstrations on a real-world case study related to the monorail project in the holy city of Qom, Iran. Furthermore, sensitivity analyses are performed to validate the model and the proposed approaches.
Within the domain of hub location literature, a particular and specialized challenge emerges in the form of the allocation of transfer points. This unique problem is delineated in the work presented in [17], where the authors introduce the transfer point location problem, identifying the optimal location for a helicopter pad, serving as a transfer point, to cater to a set of demand points necessitating emergency services originating from a central facility, such as a hospital. The paper focuses its attention on a specific scenario in which the location of the central facility is already known, being the primary objective to determine the most strategic location for a single transfer point, delving into both the “minisum” and “minimax” variants of the model, scrutinizing these approaches to ascertain the most suitable configuration.
2.3. Rural Demand-Responsive Systems
On the other hand, previous research in the field of demand-responsive mobility also addresses the challenge of optimizing service delivery, often with consideration of the concept of transfer points.
The work in [18] introduces a methodology geared towards aiding decision makers in making informed choices between two distinct operating policies, demand-responsive and fixed-route, for establishing connectivity between a residential area and a major transit network. The concept of transfer points takes center stage as pivotal locations where passengers can seamlessly transition between a demand-responsive transit service and a fixed-route transit service, thereby bridging the residential area with the broader transit network. In addition, the study identifies the most suitable policy that not only aligns with the specific transportation needs of the residential area but also maximizes the overall quality of service delivery.
Similarly, the authors in [19] delve into the implementation of a demand-responsive connector designed to facilitate the transportation of commuters from their residential addresses to transit hubs through a shuttle service. Their study also explores various strategies for implementing the associated vehicle scheduling problems. In this regard, the research offers a mixed integer linear programming formulation as well as a heuristic method to address these challenges. An intriguing finding is that a more flexible transportation system, as exemplified by demand-responsive connectors, can yield cost advantages, especially in scenarios where transit services are frequent or transit hubs are situated nearby, without significantly compromising passenger convenience.
In summary, the review of related work presented in this paper shows the notable diversity in domains and solution types that have been explored within the context of the transfer point allocation. However, it becomes evident that there is a compelling need to formulate the problem from a broader and more generalized perspective. Our particular interest is to tackle the challenges encountered in rural environments, characterized by their unique and often demanding conditions, as well as limited access to essential resources and infrastructure. In essence, this comprehensive approach represents a pivotal step toward addressing the challenges of rural transportation. By leveraging methodologies from a wide array of disciplines and domains, we can develop impactful solutions that bridge the gap between rural and urban mobility, fostering progress and well-being in underserved communities across the globe.
3. Problem Formulation
This section provides a brief overview of DRT systems and outlines their optimization through the dynamic allocation of transfer points. Then, it proceeds by formulating the problem and introducing an architectural framework that illustrates the intended operation of the entire system. Finally, it highlights the constraints that must be taken into account when implementing a solution in this context.
3.1. Optimizing DRT Systems through Dynamic Transfer Point Allocation
A dynamic DRT system offers displacement services to its users without a fixed schedule. Instead, vehicles depart on demand, according to the passengers’ necessities. Passengers issue travel requests (or bookings) with a particular lead time indicating their origin, destination, and the trip’s time window [20]. Such a window indicates the earliest possible pick-up time and the latest possible arrival time of the passenger. The system uses the flexibility given by these time intervals to allocate a passenger to a specific vehicle.
Once a booking is issued, the system assigns the issuing passenger to a vehicle. This assignment will depend on the number of deployed vehicles and their location, capacity, current route, and schedule. The assignment of a new passenger may involve a detour of the current route and a change in the vehicle’s schedule. A passenger can be assigned to a vehicle provided that the changes resulting from their inclusion do not breach the time windows of other scheduled passengers. As can be deduced, demand-responsive systems require allocation, routing, and scheduling algorithms able to return optimized solutions in real time.
Consider a set of settlements in a specific rural area. A dynamic DRT system serves those settlements providing transportation between them. In addition, trips between the nearest city and any of the settlements are also provided.
Given the distinctive characteristics of transportation demand in rural regions, it is anticipated that demand levels will be relatively low and scarce. With the primary objective of optimizing service efficiency and cost-effectiveness, the transportation provider aims to explore the concept of creating dynamic transfer points. These transfer points are intended to consolidate passengers originating from various locations into a single vehicle, effectively maximizing vehicle occupancy. Importantly, the creation of these transfer points will be dynamic and responsive to real-time demand patterns, with their formation contingent on the actual demand revealed through the issuance of trip requests within a specified timeframe.
A transfer point can be allocated by identifying a set of viable locations within the road network that connects the rural settlements and the nearby city. Ideally, the introduction of these transfer points should lead to a reduction in the total distance traveled by the vehicles in the fleet. In certain scenarios, it may even obviate the necessity to deploy an additional vehicle. However, it is essential to recognize that not all situations warrant the inclusion of transfer points. For a particular demand, the incorporation of a transfer point may not yield any discernible cost reductions. In such cases, it is deemed more efficient to operate the fleet without any transfers.
The main argument in favor of the implementation of DRT with dynamic transfer point allocation comes from the poor investment in quality transportation that rural areas are subjected to. The implementation of the proposed method, as described, will enable us to simulate DRT services in different rural areas, study their demand, and find out if they would benefit from dynamic transfer point allocation. Given the difficulty of successful implementation of DRT services, having the infrastructure to simulate and adjust them is of the utmost importance.
3.2. Formulation
The dynamic transfer point allocation problem has a series of elements that must be formalized to describe a solution. The DRT system provides services to various users in need of displacement, each of them represented by their booking, an explicit request for displacement. Such a need is fulfilled by a fleet of vehicles, each of them serving the bookings it has assigned. In addition to the DRT elements, we must characterize a transfer, the action of dropping off a passenger at a particular location within an established time window and their subsequent pick-up by a different vehicle to complete their journey. A transfer takes place in a concrete transfer point, a location dynamically selected by the system to act as a transfer hub for the vehicle fleet during a certain period of the DRT operation. In the following, we further describe each of the aforementioned elements.
Bookings. A passenger’s booking b has the following associated elements:
- Origin : location at which the passenger will be picked up.
- Destination : location at which the passenger will be dropped off.
- Earliest pick-up time : time at which the passenger will be at their origin and ready to be picked up.
- Latest arrival time : time at which the passenger needs to be at their destination.
- Set of vehicle transfers : an initially empty set of transfer operations. Once a booking is allocated to a vehicle, the DRT system computes the necessary transfers, if any, that the passenger will perform during their trip.
Vehicles. A vehicle v has the following elements related to it:
- Capacity : number of passengers the vehicle can carry simultaneously.
- Schedule : an ordered finite list of tuples of (location , time ) indicating the order in which the vehicle will visit its route’s stops and the time it will arrive at each one of them.Each tuple must be associated with at least one of the assigned bookings of the vehicle.
- Route : Physical route that connects every stop in the vehicle’s schedule. Represented in the system as a set of geographic coordinates.
Transfer operations. A transfer operation is represented by:
- Associated booking : booking whose issuing passenger(s) is going to be transferred.
- Transfer point : location at which the passenger will be dropped off and subsequently picked up.
- Drop-off vehicle : vehicle from which the passenger will be dropped off.
- Pick-up vehicle : following vehicle the passenger will ride in after being picked up from the transfer point.
- Earliest pick-up time : time at which the passenger will be at the transfer point and ready to be picked up.
- Latest drop-off time : time at which the passenger needs to be at the transfer point to ensure the completion of a trip within its time window.
Workflow. The procedure to dynamically allocate a transfer point operates as follows. Figure 1 shows the system’s architecture and helps describe the workflow. The system-wide objective function, for this work, is set to the minimization of the operational costs of the DRT service, although other approaches could be configured. The system receives as input a snapshot of the DRT service, describing its current state (Figure 1, Input data). This includes:
- Vehicle location, capacity, and scheduled route for the whole fleet.
- Demand, in terms of customer bookings.
- A set of locations that describe possible transfer points.
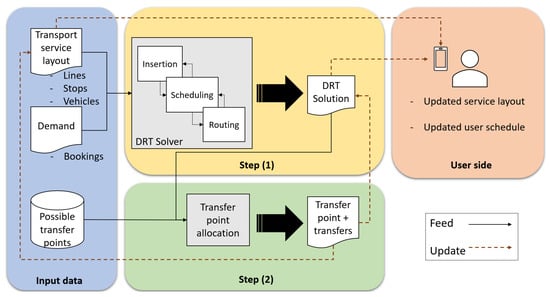
Figure 1.
Architecture and workflow of the dynamic transfer point allocation system.
The first step is to obtain a DRT solution (Figure 1, Step (1)). We say a DRT service is solved when all of the known demand has been processed; that is, all passengers are assigned to a vehicle so that their trip is guaranteed completion. Therefore, the DRT solution describes the insertion of the maximum number of bookings to the schedules of any fleet vehicle so that the time constraints of all customers (both new and those already assigned to a vehicle) are preserved. The insertion of a booking to a vehicle schedule causes it to update its route. In some cases, deploying an additional vehicle may be necessary to serve a particular booking. The solved scenario incurs a series of operational costs, among which the vehicle traveled kilometers (VTK) as well as their operational time stand out.
The second step aims to reduce the operational costs derived from the obtained DRT solution (Figure 1, Step (2)). The algorithm analyzes whether creating a transfer point can achieve such a reduction. A transfer point introduces the possibility of transferring passengers among vehicles. An operational cost reduction would then be achieved by simplifying vehicle schedules and routes due to introducing one or many passenger transfers. In addition, this could allow other vehicles to absorb the demand initially assigned to a particular vehicle, leaving the latter available sooner or even avoiding the need to deploy it. Since the activation of the transfer point must be performed dynamically, it is crucial to consider the current position of each of the fleet’s vehicles as well as the relationship between their schedule and the trip that customer bookings demand. The location of the transfer point will determine how much the operational costs can be reduced. The algorithm analyzes the activation of all possible transfer points of the input set and keeps those locations whose activation supposes a cost reduction while preserving all system constraints.
The output of the process is the location of the transfer point and the updates to vehicle schedules that its introduction brings. The DRT solution is updated to include the computed passenger transfers. Such changes are broadcast to the fleet and, in turn, to every customer whose planned trip may have changed due to the inclusion of a transfer (Figure 1, User side).
3.3. Modeling Constraints and Limitations
DRT requires several restrictions on the trip to be configured for each traveler. These constraints are mainly associated with the capacity of the fleet vehicles and the time window described by each passenger booking. Firstly, the number of passengers in a vehicle cannot exceed the vehicle’s capacity. For that, the DRT solver must take into account the number of passengers the vehicle will carry at any point of their schedule, knowing how many passengers get off and get on the vehicle at each station. Secondly, each passenger must be picked up at such a time that they are waiting in their origin location. Finally, a passenger’s destination must be reached before the end of their time window. These constraints guide the assignment of passengers to vehicles or, in other words, the insertion of a passenger booking into a vehicle’s schedule.
For the implementation of a transfer, we must define similar constraints. In general, a transfer can only be performed if:
- The drop-off of passengers at the transfer point does not violate other vehicle passengers’ time constraints.
- There is at least one vehicle with enough capacity to pick up the transferring passengers without violating other vehicle passengers’ time constraints.
- The transferring passenger’s time constraints are preserved.
Besides this, transfer points do not have a capacity limit, nor is there a limit on the number of transfers occurring simultaneously in the same transfer point.
Finally, it is worth mentioning that additional service quality-related constraints may be introduced. Examples of these may be establishing upper bounds for passenger waiting (to be picked up) time, passenger on-board (traveling in a vehicle) time, and passenger (waiting for a) transfer time. Limiting these times also limits the capacity of the system to optimize the operation and the percentage of accepted bookings. However, it improves the general passenger experience.
The presented architecture has two main technical challenges. On the one hand, it requires updated information on the state of the transportation service, including its layout and location of vehicles and passengers. This, in turn, requires all infrastructure to be reliably connected. On the other hand, the algorithms that implement the different modules need to run with fairly low computational costs to assess real-time data and output modifications over the service layout and operations. Both these challenges are sensitive to the scale of the system and thus shall be taken into account for its implementation.
Framing the proposal in a real transportation system, the real-time creation of physical spaces for transfer operations is a major challenge in itself. Firstly, the eligible locations have to ensure the safety of passengers and drivers during the vehicle transfers. Secondly, the dynamic introduction of transfer operations may cause real-time updates of already planned passenger trips. This feature may entail problems that we will elaborate on in the discussion.
4. Case Study
To further illustrate the functioning of the proposed architecture, this section describes a trace of the two main optimization mechanisms proposed: the DRT solver and the transfer point allocation process. Such a trace is developed using the public interurban bus transportation data (https://dadesobertes.gva.es/va/dataset/gtfs-itineraris-horaris-transport-public-interurba-autobus-comunitat-valenciana, accessed on 3 November 2023) from the Comunitat Valenciana, Spain, as a base to define a rural DRT service and its stops.
4.1. Application Domain
An interurban DRT service is formulated over a slice of the main territory of the Comunitat Valenciana, a region of Spain. A dataset is employed to allocate the stops for the service and define its routes. Specifically, the data describe all the itineraries carried out by the different interurban public transport services by bus concessioned by the regional government. The dataset defined 341 stops within the selected area; for the algorithmic trace, and taking into account the focus on interurban mobility, a single stop per town is kept.
The following example is centered in the area shown by Figure 2, which includes the city of Valencia and several towns located to the south of it. The chosen area contains many medium-to-small towns, which are mainly surrounded by crop fields. Historically, the main economic activity of the area was centered on the primary sector, specifically agriculture. As the country modernized, relatively small factories appeared which complemented the economic activity. Today, the surviving factories continue to employ a large part of the population of these villages. In addition, they all have small businesses run by residents that are the backbone of the local economy. Finally, it is worth noting that those towns that are closer to Valencia, the capital of the region, also serve as dormitory towns for workers from Valencia, as they offer much more affordable rents and home purchase prices than in the capital. This fact raises the importance of fluid transportation between the towns and the main city. When it comes to the population, rural settlements in this area show an older population, on average, than bigger cities of the country.
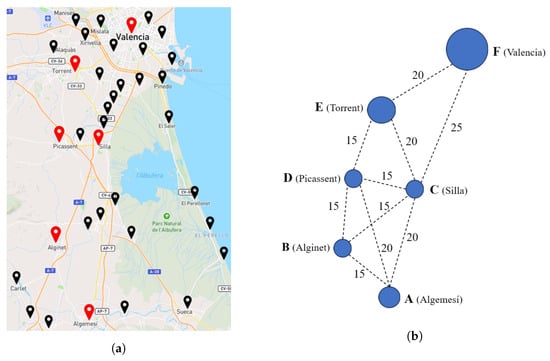
Figure 2.
Demand-responsive transportation service layout developed for the case study. (a) Area of the Comunitat Valenciana chosen for the deployment of the service. A single stop per settlement has been kept. Stops used in the example are highlighted in red. (b) Detail of the service layout. Stops are represented as a blue circle. Connections among stops are labeled by the average car travel time in min.
The DRT service contains the elements described in the problem formulation (see Section 3). For the sake of the example, the service runs fully dynamically without any predefined service area, line, or route preassigned to any vehicle. Instead, vehicles build their itineraries according to their assigned customer bookings. Customers send bookings defining their origin and destination stops and a simplified time window containing only their earliest pick-up time. The DRT solver allocates bookings iteratively to the vehicle’s itinerary, ensuring the lowest possible operational cost increase. With their booking allocated, the customer is informed of their expected pick-up and arrival times, as well as the itinerary their assigned vehicle is following, in real time, and is expected to follow after their pick-up.
4.2. Dynamic Transfer Point Allocation Trace
To develop a trace of the operation of the proposed architecture, a subset of the stops, those highlighted in red in Figure 2a, is selected. This reduced scenario presents six stops compressed within Valencia (F) and Algemesí (A), the northern and southern ends of the service, respectively. Figure 2b shows a simplified graphic of the transportation service layout, including the time, in min, that it takes to travel between those connected stops.
4.2.1. Initial Scenario
The initial scenario defines a travel demand as well as the location and initial itineraries of each fleet vehicle, and can be visualized in Figure 3a. The fleet comprises vehicles and , allocated in stops A and B, respectively, at the beginning of their shift, time . Their itineraries () contain just their current stop, and their routes () are empty. Passenger demand comprises four bookings (, , , and ), each characterized by their origin and destination stops and earliest pick-up time () in min. Table 1 depicts the initial scenario according to the problem formulation.
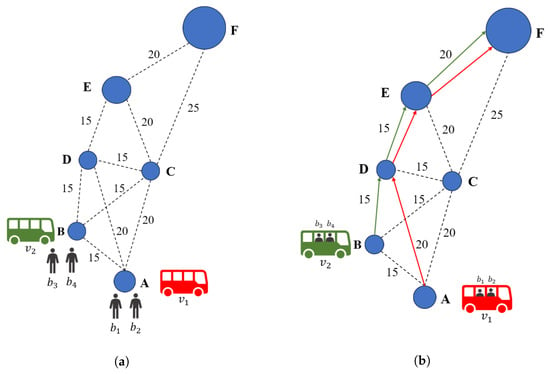
Figure 3.
DRT service layout evolution from the initial scenario to the solution computed by the DRT solver. Human icons represent bookings, whereas bus icons with different colors depict vehicles. (a) Initial scenario of the DRT service. At this point, vehicle schedules are empty and the demand has not been allocated. (b) Solved scenario with passenger booking assignments and planned route for each vehicle. Vehicle ’s route is depicted by red arrows, whereas ’s route is depicted by green arrows.

Table 1.
Initial scenario data, including customer bookings and vehicle locations.
For the sake of the example, a few problem constraints are redefined. All demand is known by the system scheduler beforehand. In addition, bookings do not define the constraint of the latest arrival time. The time taken by passengers getting on or off the vehicle is disregarded. The routing of vehicles is guided by traveling through the shortest path. Finally, the system optimization function is the minimization of the service’s operational costs, which is the metric that will guide the assignment of a booking to a particular vehicle. These costs include the vehicle’s traveled distance and operational time. In the developed example, however, the reduction in operational costs will also imply the optimization of passengers’ time (waiting and traveling).
4.2.2. Step 1: DRT Solver
The DRT solver (see Figure 1, Step (1)) assigns each booking to a vehicle, updating its schedule iteratively. The algorithm checks all feasible assignments and implements the one that minimizes passenger time, thus favoring service quality. Because of the combinatorial nature of the problem, for the development of this example, we have chosen to show only the most relevant assignment considerations, neglecting to mention those that the system would discard explicitly.
Booking is initially selected and its assignment to both and is explored. The assignment of a booking b to a vehicle v will be denoted as . Equation (1) shows the effect on each of the vehicle’s schedules and routes of assigning booking to them, following the notation defined in Section 3.
The assignment would add to ’s schedule a stop in E at time , and modify its route to go from A to D and finally reach E (’s destination stop). As can be seen, the passenger of booking would get to their destination at time . provides the clear advantage of already being at the stop where the trip defined by originates. On the other hand, assignment would incur a 15 min waiting time for the passenger of , as would need to move from stop B to A to pick them up. This, in turn, would delay their arrival time at E to . The system assigns to , as indicated in bold in Equation (1).
Following, is considered for assignment, as Equation (2) reflects.
Following the reasoning developed for the assignment of , the system assigns to as well, updating its schedule and route as shown above.
Regarding bookings and , it can be observed in Figure 3a that vehicle is located at the same stop where the trip defined by each of the bookings starts. In addition, at this point in the DRT solver process, has an empty schedule. It is easy to understand that the best option is to assign both of the bookings to . Table 2 shows the DRT solver’s output: all bookings have been assigned to a vehicle, which in turn has consistent itineraries and defined routes. Figure 3b shows a graphic representation of such a solution, including the planned routes of each vehicle.

Table 2.
Solution of the DRT initial scenario. For each fleet vehicle, its assigned bookings, schedule, and route are presented. Regarding passengers, the waiting, traveling, and total time of their trips are shown in min.
At this point, we have illustrated how the DRT solver computes the passenger–vehicle assignments taking into account a system-wide optimization function. The computed solution ensures the shortest possible trip for each passenger, considering the service’s limitations. However, observing the planned routes of the vehicles, a potential concern arises: Both and travel in parallel towards the northern side of the service area and finish their trip at stop E. Future demand that may originate on the southeastern side of the system may be left unattended as all fleet vehicles are too far away.
4.2.3. Step 2: Transfer Point Allocation
Once the DRT solver has obtained a solution, such a solution is fed to the transfer point allocation system (see Figure 1, Step (2)). The transfer point allocation considers passenger transfers as a method to further optimize the DRT solutions. The set of eligible transfer points is composed of the stops of the service, although it would also be possible to include locations that would not be stops normally.
Once again, the combinatorial nature of the problem forces us to restrict the transfer point search to a concrete example to illustrate its optimization potential. Specifically, stop C is chosen for the activation of a transfer point and the subsequent optimization. All feasible transfers of passengers from all vehicles occurring at stop C would be explored. For this example, we directly present those transfers that will be implemented.
If one observes the shape of the demand, bookings can be grouped according to their destination stop. This allows for the implementation of passenger transfers that simplify the vehicle routes and, in turn, may bring overall improvements to service quality. Specifically, transfers shown in Equation (3) are computed and implemented.
The transfer operation indicates, according to the problem formulation, that the passenger of booking will be dropped off at stop C by and picked up by at time at the earliest. Analogously, describes the transfer of from to , which can happen at the earliest at . The main achievement of the operations described above is the grouping of and , whose destination stop is E, in , and that of and , with destination stop F, in .
The implementation of transfer operations may modify the schedule of the involved vehicles. The DRT solution, presented in Table 2, defines the schedule and route of every vehicle. As can be observed, none of the vehicles have planned to go through stop C, which will now be necessary to perform the transfers. The implementation of and brings the subsequent schedule changes, which are reflected on Equation (4), where the schedule and route are presented for each vehicle, and Table 3. Passenger traveling time is now divided into two periods. The transfer column indicates the time the passenger waited to transfer vehicles. In turn, the standby column indicates time spent by passengers inside a stopped vehicle. Finally, Figure 4 shows the evolution of the DRT solution with transfers.

Table 3.
Solution of the DRT initial scenario considering stop C as a transfer point. Time is expressed in min. Trips are now split into two travel periods. In addition, the time waiting for a transfer is also considered under the “Transfer” column.
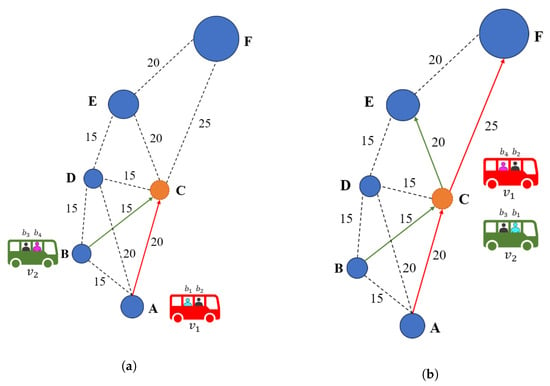
Figure 4.
Evolution of the DRT service from the initial scenario to the final solution, now considering stop C as a transfer point, represented by the orange color. Vehicle ’s route is depicted by red arrows, whereas ’s route is depicted by green arrows. (a) Initial passenger–vehicle assignments are preserved. Vehicles now move first towards the transfer point as it is their first stop. (b) Vehicles exchange passengers and and continue their journey, which now differs in the destination stop.
If we compare the solution obtained by the DRT solver (Table 2) with that obtained after the transfer point allocation process (Table 3), the vehicles now go from their origins to stop C, perform the transfer as soon as possible, and then continue on to their destination stop (F for , E for ). Such a change in schedule brings several improvements:
- The overall vehicle operational time is reduced. reaches the end of its schedule at , whereas does it at . On the first solution, both vehicles finished at . The sooner a vehicle is free, the better the service can deal with unexpected travel requests.
- A better distribution of fleet vehicles is achieved. The routes and final stops of and are now different. This allows for a better allocation of future travel requests.
- From a service quality perspective, there is a compromise in the experience of the different passengers. Both passengers traveling to stop F now reach it at time , whereas the initial solution scheduled their arrival at . Such a time gain is partially reflected in the other couple of passengers, who, instead of reaching stop E at , now do so 5 min later, at . The overall total time of all passengers, however, is reduced by 10 min, from 180 (35 + 55 + 35 + 55) to 170 (40 + 45 + 40 + 45).
4.2.4. Extended Example: Allocating On-Line Bookings
The dynamic activation of transfer points has the potential to bring yet another optimization to the DRT service optimization. In the following, we extend the example above to include previously unknown demand and show how counting with transfer operations can boost service quality in a service with limited infrastructure. For the sake of this example, we keep the previous bookings , , , and , and add one more: .
Following the last example, at time , the situation is the one depicted by Figure 5a. is located at stop C, carrying and . is 5 min away from stop C, carrying and . A transfer among passengers and is expected to happen at in stop C. just appeared in the system.
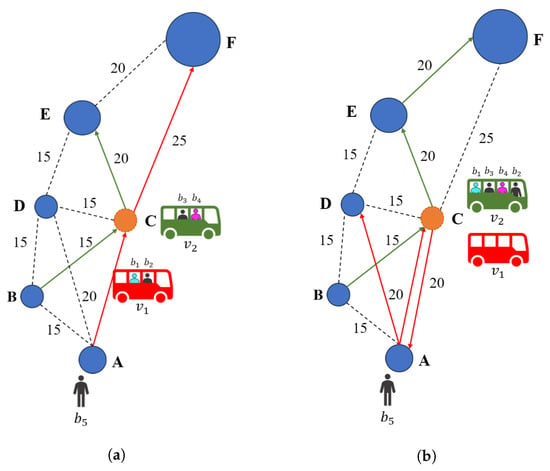
Figure 5.
Graphical representation of changes in the DRT solution that allow the system to serve booking . Stop C acts as a transfer point, as represented by its orange color. New transfer operations and vehicle schedules are computed. Vehicle ’s route is depicted by red arrows, whereas ’s route is depicted by green arrows. (a) DRT service snapshot at time . (b) System solved to serve at time .
The current schedules of both fleet vehicles define routes that go progressively further away from stop A, where is waiting to be picked up. The DRT solver, on its own, would assign to , as it is the first vehicle that will be free at time , once and reach stop E. Still, there is at least a 30 min trip from stop E to A. The earliest time could be picked up is at after a 55 min wait. Such a long wait would generally cause users to refrain from using the service and look for an alternative displacement option. The option to deploy a new vehicle to serve would not be uncommon for DRT services. However, the current work focuses on solutions that optimize modest services with a limited budget for infrastructure. Consequently, the deployment of an additional vehicle is disregarded.
The dynamic transfer point allocation process, and specifically its ability to consider transfer operations, is able to find a different solution to serve within a reasonable time. The transfer operations defined in Equation (5) are applied.
These operations aim to accumulate all trips with destinations on the northern side of the service in a single vehicle, thus leaving the other one free to serve and other possible bookings originating in the southern area. These transfers would replace the previously presented transfer operations and thus cause a recalculation of vehicle schedules. The final solution is presented in Equation (6), where the schedule and route are presented for each vehicle, Table 4, and depicted in Figure 5b.

Table 4.
Solution of the DRT initial scenario considering stop C as a transfer point and the issuance of previously unknown booking at time . Time is expressed in min.
If we compare the last solution (Table 4) with the initial transfer point solution (Table 3), in the current configuration, is left available as soon as possible to serve , whose expected waiting time falls from 55 to 25 min. This, however, comes at the cost of heavily impacting the trip of those passengers whose final destination is F, whose expected total time increased from 45 to 60 min. In this last example, the total times for passengers to are even longer than in the DRT solution without transfers (Table 2).
With the introduction of previously unknown demand, we have been able to illustrate how the proposed dynamic transfer point allocation process enables rural DRT services with limited infrastructure to provide better service quality. In this last example, the choice of serving one more customer, instead of potentially losing them as a client, has been made, causing a negative impact on other passengers’ traveling experience. In reality, such a decision would be taken according to the priorities of the service operator and whether they consider that serving one more customer compensates for the negative impact on the already scheduled trips. In terms of the optimization algorithm, the operator’s priorities would be encoded in the objective function, ensuring that the trip scheduling and dynamic activation of transfer points are performed following them.
5. Discussion
With the development of a case study in Section 4, the effect that dynamic transfer point allocation has over the operation of a DRT service has been quantified. Following, the current section discusses relevant issues that derive from the results of the aforementioned case study. The impact that operational cost optimization may have on service quality is assessed. Moreover, the discussion focuses on the potential effects on the system’s adoption rate and proposes techniques to improve the number of potential users.
5.1. Case Study Assessment
As has been exposed in Section 4.2, the inclusion of transfer points and transfer operations has the potential to improve the operation of rural DRT services. This improvement, however, depends on the specific situation of the service at a determined point in time, including the vehicle’s location, capacity, and known demand. Because of that, the dynamic activation and deactivation of transfer points is justified, as it allows temporary modifications of the service layout that deal with a distinct troublesome situation.
The developed example has been designed to illustrate the usefulness of the proposed optimization method. Nevertheless, two contrasting solutions have arisen. On the one hand, the initial solution is optimized through passenger transfers in such a way that the total time is improved for half of the passengers while causing a slight increase in the time for the other half. In this case, however, the solution is objectively better from a global perspective. On the other hand, the extended example shows how transfer operations facilitate serving more customers, although such a benefit comes at the expense of the previous time improvement in the trip of all other passengers, which is no longer in place.
From the service provider’s perspective, the latter situation may be acceptable and even desirable, as it increases the monetary profit of the service as well as the client base. However, the passenger’s perspective may instead be negative, as they do not have a global overview of the situation and thus will be concerned mainly about their own trip and experience. This issue cannot be ignored by the transportation provider, and thus several questions arise. Shall we allow the optimization process to worsen a customer’s trip? And, if so, in what situations shall we allow it? Finally, taking into account that a worsening of service quality may be necessary for a globally optimized operation, what techniques could we apply to increase and maintain the number of customers in our service? The following sections address these questions and discuss their possible answers, providing an analysis that complements our proposal.
5.2. The Effect of Operational Cost Optimization on Passenger Experience
The enhancement of cost-efficiency within a transportation system typically involves the streamlining of resource allocation by the transportation provider. The optimization strategy proposed in this study centers on the dynamic establishment of transfer points. The motivation for this optimization stems from the suboptimal investment of resources in the domain of adaptable transportation services, particularly in rural settlements, where transportation demand is notably scarce. However, it is worth noting that the introduction of one or multiple vehicle transfers during a passenger’s journey may be perceived as less than favorable in terms of the passenger experience. Thus, the successful implementation of our proposed strategy necessitates the attainment of a harmonious balance between enhancing operational efficiency and preserving passenger satisfaction.
The delineated system encompasses a set of configurable parameters that allow for the customization of various degrees of optimization concerning passenger experience. In the following, we assess the values of these parameters and their corresponding impact on service quality.
5.2.1. Flexibility in the Update of a Passenger’s Schedule
Upon the allocation of a passenger booking to a vehicle, the passenger is apprised of their personalized itinerary, which includes precise information regarding the location and estimated time of pick-up, the planned route to be traversed by the vehicle, including designated stops during the passenger’s journey, and lastly, the location and projected time of arrival at the drop-off point. Additionally, it is pertinent to note that the passenger’s journey, as defined by their booking, will already be in progress if the passenger is currently aboard a vehicle. The dynamic activation of a transfer point has the potential to introduce variability into a vehicle’s schedule, consequently affecting the passenger’s schedule and, as a result, their entire trip.
Consider the example developed in Section 4.2. After the first step, the DRT solver obtains a feasible solution to the transportation, described in Table 2. This, in turn, would trigger the notification of the passengers, including all the aforementioned data. The passengers associated with bookings and would receive an estimated time of arrival to their destination at time , whereas those pertinent to bookings and contemplate an arrival time of . At this point, all passengers are fully aware of their planned trip.
The transfer point allocation is then run, and a new solution, presented in Table 3, brings changes in all passenger’s schedules. Passengers from bookings and now experience a transfer. In addition, the expected arrival time of every passenger has been modified, positively in some cases, and slightly negatively in others. All of these changes would be communicated to the customers as soon as the new itineraries were fixed. Finally, including the last extended example, in which the solution, as shown by Table 4, is modified again to serve a new remotely located booking , the passengers would receive a third update in their schedule, this time bringing a significant time increment to two of them.
With such a dynamic example, we have also managed to illustrate how the optimization of the service can be perceived by its users. Passengers could have received three different itineraries from the application, with the latter being communicated once the journey of all passengers had already started. This raises two concerns. First, the excess of dynamicity in the passenger schedules implies a lack of consistency, which may favor the loss of customer confidence in the service, as it is perceived as less reliable. Second, passengers may understand changes in their schedule as a way in which the system disregards service quality in order to boost benefits. This is especially relevant for schedule modifications that significantly worsen a passenger’s trip. Considering these issues, it is worth exploring the flexibility of the proposed optimization methods to determine when passenger schedule modifications are reasonable.
Under the system’s flexibility, we encounter the following scenarios:
- In a fully flexible configuration, the system permits adjustments to the schedules of passengers whose journeys are already underway. These passengers receive timely notification regarding the modification of their originally planned route, including transfer information. Passengers must be informed of these alterations with adequate advance notice prior to reaching the designated transfer point.
- In a semi-flexible context, it is permitted to adjust the schedules of passengers whose trips have been assigned but have not yet commenced. In this context, passengers have already received an initial itinerary for their journey, although they have not yet boarded their designated vehicle. In the event of schedule modifications, passengers will be duly informed, which may entail changes such as a reassignment to a different vehicle and the addition of transfer points to their route.
- In the static variant, transfer points are exclusively incorporated to optimize service for bookings that are already issued but have not yet been assigned. Passengers falling within this category will be provided with a single schedule that encompasses all vehicle transfers, if any, as part of their journey itinerary, and will not be modified.
A more elevated degree of flexibility increases the likelihood of optimizing the service operation through passenger transfers. However, flexibility also foments a more pronounced impact on service quality, both for the better and for the worse. Passengers may experience a sense of insecurity, and as a consequence, their trust in the transportation system may diminish if the extent of schedule alterations becomes overly aggressive.
5.2.2. Maximum Number of Vehicle Transfers
The developed case study featured a single transfer point activation. In situations where multiple transfer points are activated, it becomes conceivable that a passenger’s itinerary may encompass more than one vehicle transfer. The transportation provider retains the flexibility to regulate the maximum permissible count of vehicle transfers scheduled for a specific passenger. An elevated maximum transfer threshold increases the potential for the system to achieve substantial reductions in operational costs. Nevertheless, it is crucial to acknowledge that a higher threshold also corresponds to a less favorable passenger experience, as it introduces the likelihood of a more convoluted journey with multiple transfers. Thus, the optimization of this parameter requires a balance between operational cost reduction and the preservation of an optimal passenger experience.
5.3. Adoption Rate in Flexible Transportation Systems
A prevalent problem in rural areas is the lack of acceptance of digitization of everyday tasks, which is more pronounced than in its urban counterparts [21,22]. In this line, flexible transportation systems, particularly in rural areas, face the challenge of their adoption rate. Utilizing a DRT service can be arguably more intricate for its users when compared to traditional transportation systems featuring fixed routes and schedules. The degree of flexibility inherent in such services imposes greater demands on users, requiring explicit bookings, selection of pick-up times, and the specification of precise locations, among other factors. Consequently, the greater the demand placed on users, the more challenging it becomes for individuals accustomed to traditional transportation to adapt to the novel mobility service.
In the context of rural settlements, where the population tends to skew older on average compared to urban areas, the necessity for smartphone applications to interact with the transportation system may constitute a formidable barrier to adoption [23]. The lesson derived from these observations emphasizes the importance of achieving a balance in the design of flexible transportation systems. Such systems must be tailored to cater to the distinct needs of their potential user base. Consequently, one should exercise prudence when incorporating levels of flexibility that lack substantial justification [24].
Alternative approaches to augmenting the adoption rate and potentially further optimizing a transportation system encompass the utilization of persuasion and gamification techniques.
Persuasion techniques, when integrated into a system, aim to stimulate specific behaviors among its user base. These techniques are primarily leveraged to encourage favorable behaviors, analogous to their application in motivating physical activity [25]. When adapted to a transportation application, these techniques aspire to motivate users to acquire knowledge and exercise more responsible resource utilization within the fleet. However, the ethical considerations of influencing individuals’ behaviors must always be conscientiously contemplated when implementing persuasion strategies [26].
On the other hand, the gamification approach introduces a reward system within the application, thereby incentivizing users who exhibit improved utilization of the system. This mechanism serves as a catalyst for enhancing the performance of all users collectively. Gamification has found relevance in addressing transportation challenges [27,28]. A common application involves influencing users to distribute transportation demand uniformly, with the overarching goal of averting system congestion. Achieving this objective can manifest through a variety of strategies, contingent on the complexity of the situation. For instance, straightforward tactics like conveying positive messages or offering modest incentives, such as complimentary rides, may suffice for certain users. Conversely, in scenarios necessitating broad user engagement, more intricate strategies, including dynamic pricing policies, may be employed to reduce trip costs during low-demand periods [29].
Numerous techniques hold promise for enhancing the adoption rate of a flexible transportation system. Nevertheless, it is imperative to exercise caution when implementing strategies involving dynamic alterations to system usage, particularly pricing adjustments. Thorough research and meticulous application are essential in order to prevent users from perceiving these changes as exploitative or deceptive, which could lead to the development of adverse sentiments towards the application. Building and maintaining user trust should remain a paramount consideration in the deployment of such dynamic approaches.
6. Conclusions
This paper has undertaken an evaluation of the optimization possibilities within rural DRT systems through the implementation of dynamic transfer point allocation. The proposed method comprises a novel approach that abandons the use of fixed locations in favor of dynamic locations calculated according to the demand for specific time periods. The incorporation of transfer points introduces an opportunity to reduce the expense to operational resources by simplifying vehicle schedules via the introduction of passenger transfers. The paper presents a comprehensive system architecture and describes the procedural workflow for dynamic transfer point allocation. A formal problem formulation is developed, delineating all pertinent elements of the proposed infrastructure.
A case study is developed to provide a trace of the operation of the proposed architecture. With the creation of an initial rural DRT scenario and its subsequent optimization, the benefits of service optimization through transfer operations are visualized. Moreover, the impact that such an optimization method may have on aspects of the transportation service, such as service quality, is also assessed.
Departing from the results of the case study, a discussion is formulated, underscoring the significance of striving for an equilibrium between optimization flexibility and service quality within flexible transportation systems. Such systems must remain attuned to the needs of their prospective user base, with the ultimate objective of augmenting the rate of adoption by effectively catering to their requirements.
The implementation of the proposed method through AI techniques brings several benefits. On a technical level, a complex combinatorial task such as the transfer point allocation could be solved in real time with a feasible computational cost. Regarding DRT-specific benefits, the technique has the ability to cut costs and improve economic viability. The examples reflect, in addition, a potential to better divide fleet vehicles among the service layout, facilitating the acceptance of isolated travel requests. This, in turn, translates into an increment in the number of users of the service. Finally, concerning social benefits, we achieve more affordable prices for flexible rural transportation and promote the use of innovative techniques in provincial areas.
Future Work
The present study offers an initial attempt of the development of an artificial intelligence algorithm designed to facilitate the optimization of rural DRT systems. By formulating the problem formally and outlining the architectural framework, this research has successfully delineated the prerequisites for an upcoming solution. Regarding the conclusions presented about the case study, we must underscore that these are drawn from predefined examples and thus their scope may be limited. Nevertheless, our results illustrate the improvement potential of the dynamic transfer point allocation process.
On the technical side, subsequent efforts will be centered on the actual implementation of distinct modules within the proposed architecture, with particular emphasis on the DRT solver and its associated transfer point allocation algorithm. The implementation step will give us the chance to try different allocation, scheduling, and routing algorithms with the aim of finding those that best fit the architecture’s requirements. Furthermore, ongoing work also involves the procurement of relevant input data necessary for testing our system, a task that presents nontrivial challenges, particularly in the context of rural transportation scenarios.
Regarding research work, once the system is implemented, we plan to conduct extensive experimentation through simulation. This implies reproducing a real-world rural area over which to deploy a DRT service operated with our architecture. The initial experimentation will focus on assessing operational changes with and without transfer points. Then, we will set up specific scenarios to test the limits of the operational cost optimizations discussed in Section 5.2, such as the system’s flexibility and the maximum number of vehicle transfers. Finally, we would like to include strategic agents that represent customers with different tolerances towards traveling time and transfer operations, thus improving our customer satisfaction assessment in the results.
Finally, we would also like to comment on potential areas where our contribution could be applied. In this paper, we have orchestrated a rural public transportation service based on demand-responsive mobility. Nevertheless, our architecture could also manage distinct instances of rural transportation, such as school transport, medical and emergency transport, and even interurban delivery services, such as those provided in cities by enterprises like Uber Eats (https://www.ubereats.com/, accessed on 3 November 2023) or Glovo. (https://glovoapp.com/, accessed on 3 November 2023) Besides the transportation domain, there are other fields where the proposed system could be adapted to fit, as exemplified by the literature cited in Section 2.2. Areas dealing with the flow of communication over a network could benefit from the allocation of nodes where information exchange may occur. The algorithms we will develop to implement our architecture could be adapted to different domains to provide optimized solutions.
Author Contributions
Conceptualization, P.M., J.J. and F.D.l.P.; Investigation, P.M.; Methodology, V.J.; Project administration, F.D.l.P.; Supervision, V.J.; Validation, J.J. and V.J.; Visualization, P.M.; Writing—original draft, P.M.; Writing—review and editing, J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported with grant PID2021-123673OB-C31 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. Pasqual Martí is supported by grant ACIF/2021/259 funded by the “Conselleria de Innovación, Universidades, Ciencia y Sociedad Digital de la Generalitat Valenciana”. Jaume Jordán is supported by grant IJC2020-045683-I funded by MCIN/AEI/10.13039/501100011033 and by “European Union NextGenerationEU/PRTR”.
Data Availability Statement
Publicly available datasets were employed in this study. This data can be found here: https://dadesobertes.gva.es/va/dataset/gtfs-itineraris-horaris-transport-public-interurba-autobus-comunitat-valenciana.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schasché, S.E.; Sposato, R.G.; Hampl, N. The dilemma of demand-responsive transport services in rural areas: Conflicting expectations and weak user acceptance. Transp. Policy 2022, 126, 43–54. [Google Scholar] [CrossRef]
- Li, X. Data-Driven Optimization Models for Shared Mobility-on-Demand Systems. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2022. [Google Scholar]
- Moseley, M. Accessibility: The Rural Challenge; Routledge Revivals, Taylor & Francis: Abingdon, UK, 2023. [Google Scholar]
- Martí, P.; Jordán, J.; de la Prieta, F.; Julian, V. Dynamic Transfer Point Allocation for Rural Demand-Responsive Mobility. In Trends in Sustainable Smart Cities and Territories; Castillo Ossa, L.F., Isaza, G., Cardona, Ó., Castrillón, O.D., Corchado Rodriguez, J.M., De la Prieta Pintado, F., Eds.; Springer: Cham, Switzerland, 2023; pp. 453–464. [Google Scholar]
- Martí, P.; Jordán, J.; Julian, V. Demand-Responsive Mobility for Rural Areas: A Review. In Proceedings of the Highlights in Practical Applications of Agents, Multi-Agent Systems, and Complex Systems Simulation. The PAAMS Collection: International Workshops of PAAMS 2022, L’Aquila, Italy, 13–15 July 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 129–140. [Google Scholar]
- Aghayari Hir, M.; Zaheri, M.; Rahimzadeh, N. Prediction of Rural Travel Demand by Spatial Regression and Artificial Neural Network Methods (Tabriz County). J. Transp. Res. 2022, 20, 367–386. [Google Scholar] [CrossRef]
- Porru, S.; Misso, F.E.; Pani, F.E.; Repetto, C. Smart mobility and public transport: Opportunities and challenges in rural and urban areas. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 88–97. [Google Scholar] [CrossRef]
- Homayouni, S.M.; Fontes, D.B.; Gonçalves, J.F. A multistart biased random key genetic algorithm for the flexible job shop scheduling problem with transportation. Int. Trans. Oper. Res. 2023, 30, 688–716. [Google Scholar] [CrossRef]
- Das, M.; Roy, A.; Maity, S.; Kar, S.; Sengupta, S. Solving fuzzy dynamic ship routing and scheduling problem through new genetic algorithm. Decis. Mak. Appl. Manag. Eng. 2022, 5, 329–361. [Google Scholar] [CrossRef]
- Mzili, I.; Mzili, T.; Riffi, M.E. Efficient routing optimization with discrete penguins search algorithm for MTSP. Decis. Mak. Appl. Manag. Eng. 2023, 6, 730–743. [Google Scholar] [CrossRef]
- Khodashenas, M.; Najafi, S.E.; Kazemipoor, H.; Sobhani, M. Providing an integrated multi-depot vehicle routing problem model with simultaneous pickup and delivery and package layout under uncertainty with fuzzy-robust box optimization method. Decis. Mak. Appl. Manag. Eng. 2023, 6, 372–403. [Google Scholar] [CrossRef]
- O’Kelly, M.E.; Campbell, J.F.; de Camargo, R.S.; de Miranda, G., Jr. Multiple allocation hub location model with fixed arc costs. Geogr. Anal. 2015, 47, 73–96. [Google Scholar] [CrossRef]
- Rathore, H.; Nandi, S.; Pandey, P.; Singh, S.P. Diversification-based learning simulated annealing algorithm for hub location problems. Benchmarking Int. J. 2019, 26, 1995–2016. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, Q.; Huang, J.; Cheng, G. Research on optimal hub location of agricultural product transportation network based on hierarchical hub-and-spoke network model. Phys. Stat. Mech. Apps. 2021, 566, 125412. [Google Scholar] [CrossRef]
- Zhang, H.; Zhuge, C.; Yu, X. Identifying hub stations and important lines of bus networks: A case study in Xiamen, China. Phys. A Stat. Mech. Appl. 2018, 502, 394–402. [Google Scholar] [CrossRef]
- Kaveh, F.; Tavakkoli-Moghaddam, R.; Triki, C.; Rahimi, Y.; Jamili, A. A new bi-objective model of the urban public transportation hub network design under uncertainty. Ann. Oper. Res. 2021, 296, 131–162. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, Z.; Wesolowsky, G.O. The transfer point location problem. Eur. J. Oper. Res. 2007, 179, 978–989. [Google Scholar] [CrossRef]
- Li, X.; Quadrifoglio, L. Feeder transit services: Choosing between fixed and demand responsive policy. Transp. Res. Part C Emerg. Technol. 2010, 18, 770–780. [Google Scholar] [CrossRef]
- Lee, A.; Savelsbergh, M. An extended demand responsive connector. EURO J. Transp. Logist. 2017, 6, 25–50. [Google Scholar] [CrossRef]
- Zigrand, L.; Wolfler Calvo, R.; Traversi, E.; Alizadeh, P. Optimization-driven Demand Prediction Framework for Suburban Dynamic Demand-Responsive Transport Systems. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-23, Macao, China, 19–25 August 2023; Elkind, E., Ed.; International Joint Conferences on Artificial Intelligence Organization: New York, NY, USA, 2023; Volume 8, pp. 6335–6342. [Google Scholar] [CrossRef]
- Hasebrook, J.P.; Michalak, L.; Kohnen, D.; Metelmann, B.; Metelmann, C.; Brinkrolf, P.; Flessa, S.; Hahnenkamp, K. Digital transition in rural emergency medicine: Impact of job satisfaction and workload on communication and technology acceptance. PLoS ONE 2023, 18, e0280956. [Google Scholar] [CrossRef]
- Daduna, J.R. Evolution of public transport in rural areas-new technologies and digitization. In Proceedings of the Design, User Experience, and Usability. Case Studies in Public and Personal Interactive Systems: 9th International Conference, DUXU 2020, Held as Part of the 22nd HCI International Conference, HCII 2020, Copenhagen, Denmark, 19–24 July 2020; Proceedings, Part III 22. Springer: Berlin/Heidelberg, Germany, 2020; pp. 82–99. [Google Scholar]
- König, A.; Grippenkoven, J. The actual demand behind demand-responsive transport: Assessing behavioral intention to use DRT systems in two rural areas in Germany. Case Stud. Transp. Policy 2020, 8, 954–962. [Google Scholar] [CrossRef]
- Sörensen, L.; Bossert, A.; Jokinen, J.P.; Schlüter, J. How much flexibility does rural public transport need? – Implications from a fully flexible DRT system. Transp. Policy 2021, 100, 5–20. [Google Scholar] [CrossRef]
- Schooley, B.; Akgun, D.; Duhoon, P.; Hikmet, N. Persuasive AI Voice-Assisted Technologies to Motivate and Encourage Physical Activity. In Proceedings from IPCV’20, HIMS’20, BIOCOMP’20, and BIOENG’20; Springer: Berlin/Heidelberg, Germany, 2021; pp. 363–384. [Google Scholar]
- Ferreyra, N.; Aïmeur, E.; Hage, H.; Heisel, M.; van Hoogstraten, C. Persuasion Meets AI: Ethical Considerations for the Design of Social Engineering Countermeasures. In Proceedings of the 12th Int. Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management, SCITEPRESS, Budapest, Hungary, 2–4 November 2020. [Google Scholar]
- Drakoulis, R.; Bellotti, F.; Bakas, I.; Berta, R.; Paranthaman, P.K.; Dange, G.R.; Lytrivis, P.; Pagle, K.; De Gloria, A.; Amditis, A. A gamified flexible transportation service for on-demand public transport. IEEE Trans. Intell. Transp. Syst. 2018, 19, 921–933. [Google Scholar] [CrossRef]
- Kazhamiakin, R.; Loria, E.; Marconi, A.; Scanagatta, M. A Gamification Platform to Analyze and Influence Citizens’ Daily Transportation Choices. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2153–2167. [Google Scholar] [CrossRef]
- Wang, W.; Gan, H.; Wang, X.; Lu, H.; Huang, Y. Initiatives and challenges in using gamification in transportation: A systematic mapping. Eur. Transp. Res. Rev. 2022, 14, 41. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).