EEG-Based Functional Connectivity Analysis for Cognitive Impairment Classification

Abstract

Understanding how mild cognitive impairment affects global neural networks may explain changes in brain electrophysiology. Using graph theory and the visual oddball paradigm, we evaluated the functional connectivity of neuronal networks in brain lobes. The study involved 30 participants: 14 with mild cognitive impairment (MCI) and 16 healthy control (HC) participants. We conducted an examination using the visual oddball paradigm, focusing on electroencephalography signals with targeted stimuli. Our analysis employed functional connectivity utilizing the change point detection method. Additionally, we implemented training for linear discriminant analysis, K-nearest neighbor, and decision tree techniques to classify brain activity, distinguishing between subjects with mild cognitive impairment and those in the healthy control group. Our results demonstrate the efficacy of combining functional connectivity measurements derived from electroencephalography with machine learning for cognitive impairment classification. This research opens avenues for further exploration, including the potential for real-time detection of cognitive decline in complex real-world scenarios.

1. Introduction

Early cognitive impairment is commonly viewed as a preclinical phase of Alzheimer’s disease (AD) and other forms of dementia [1]. MCI represents a significant challenge for affected individuals and healthcare professionals striving to effectively understand and address this condition [2]. MCI occupies a unique position on the spectrum of cognitive aging, serving as an intermediate stage between normal aging and more severe forms of cognitive decline, such as AD [3,4]. According to statistics provided by the World Health Organization, the global tally of individuals living with various forms of dementia has surpassed 55 million [5]. Due to global demographic changes in aging, detection techniques used to explore and understand MCI have evolved to become more effective and accurate [6]. MCI frequently correlates with disruptions in synaptic function. Synapses themselves serve as the central information-processing modules in the brain and performance a pivotal role in numerous cognitive functions throughout development and adulthood and during aging [7].

Neuronal activity changes in response to sensory or motor stimuli; thus, paradigms are used to assess cognitive function [8], which can be seen when using electroencephalography (EEG), a technique with high temporal resolution that allows the assessment of brain oscillations within detailed rhythms that could reflect the biophysical properties of local interactions [9]. Consequently, EEG can noninvasively study functional interactions between cortical processes [10], which makes EEG a practical tool for estimating functional connectivity [11].

EEG functional connectivity has been estimated based on correlation and coherence [12]; however, these estimates do not eliminate conduction volume [13,14], which refers to underlying connections between brain regions. More precisely, volumetric conduction concerns the propagation of electric fields originating from a cortical source as they cross through biological tissues towards the recording electrodes [15,16]. Calculating accuracy estimates, it is necessary to employ measures like Phase Lag Index (PLI), weighted (w)PLI, and direct (d)PLI. These tools rely on analyzing phase differences between the electrodes rather than depending on the absolute phase of the EEG signal [17]. This approach ensures lower sensitivity to fluctuations in the signal caused by conduction volume and, consequently, provides a more accurate measure of functional connectivity between brain regions [18]. Imperatori et al. [8] demonstrated that measures based on the phase index exhibit different sensitivity to distinct functional connectivity dynamics and may thus offer complementary information.

Several methods of functional connectivity have been applied to assess mild cognitive impairment. Adebisi and Veluvolu [19] provided a comprehensive overview of the recent advancements in electrophysiology signals, specifically EEG and magnetoencephalography (MEG), for the analysis of functional and practical brain networks in dementia-related disorders. The review highlights various connectivity measures and graph theory metrics employed in the field, discusses the challenges associated with threshold selection for network construction, and emphasizes the need to automatically apply machine learning techniques to discriminate dementia-related disorders.

Yan and Zhao et al. [20] introduced wPLI as a novel measurement of phase synchronization in patients with AD; the elevated power spectral density within the Theta band was compared between MCI and healthy control (HC) patient groups, which was linked to disruptions in directional, computational, and delayed memory capacity.

Developing novel experimental methods to quantify brain functions remains crucial; therefore, detecting abrupt time-domain changes in the EEG signal is a prerequisite for implementing functional connectivity analysis, overcoming non-stationarity, which is complemented by other works that have demonstrated the need to carry out dynamic connectivity analysis due to the problems involved in conducting studies based on a fixed window to evaluate an EEG time series [4].

Our study aims to apply change point detection methods to identify abrupt signal changes and assess changes in functional connectivity [4], which is fundamental to understanding the dynamics of the brain network and its alterations in conditions such as MCI. The automatic analysis of subjects with MCI through functional connectivity is still an ongoing problem; however, our results show a significant data contribution from subjects over 70 years of age [21].

In addition to enhancing our ability to interpret data, our approach is further enriched by incorporating machine learning techniques for classification. We utilize graph-based metrics as informative features [21]. The creation of an adjacency matrix, which reveals the structural connections among different EEG channels, facilitates the operation of this application [22]. Machine learning algorithms have shown that EEG graph measurements can effectively differentiate between individuals with amnesic Mild Cognitive Impairment (MCI) and those with non-amnesic MCI, suggesting that these measurements may serve as predictive markers for the progression to Alzheimer’s Disease-related dementia in MCI patients [23].

We applied this analytical approach in a simplified context by investigating connectivity patterns in the oddball paradigm among both MCI and healthy control (HC) subjects. In this research, our focus was on preserving the interpretability of neural activity in MCI subjects, which we analyzed through functional connectivity (FC) and processed using machine learning across different brainwave frequencies. Through statistical analysis and cross-validation, we achieved performance results approaching 99%. We employed connectivity matrices as adjacency matrices to construct graphs, which were subsequently used as features for established machine learning models. This demonstrates that this methodology should be considered as a valuable tool for characterizing brain activity in individuals with MCI while maintaining physiological interpretability.

2. Materials and Methods

2.1. Participants

Thirty subjects—fourteen subjects diagnosed with MCI and sixteen HC subjects (nineteen females; 70.63 ± 9 years old, eleven males; 70.36 ± 11 years old)—were recruited by the Universidad Autónoma de Manizales (Laboratorio de Nuerofisiología), Caldas (Colombia). Written informed consent was obtained from all participants, and the study was carried out after prior institutional ethical approval was received.

The task was divided as follows: 30 min for the placement of electrodes and EEG calibration, followed by 6 min of visual stimulus. The neurophysiology laboratory is a comfortable environment for older adults, and snacks were provided for the participants.

2.1.1. Survey Participant Inclusion and Exclusion Criteria

Inclusion Criteria: Research subjects without neurological disorders (except those relevant to the study) or sensory impairments, with written consent and authorization (informed consent).

Exclusion Criteria: Subjects experiencing seizures, a history of neurological or psychiatric disorders (except those relevant to the study), any upper limb motor impairments, and the presence of visual or auditory difficulties.

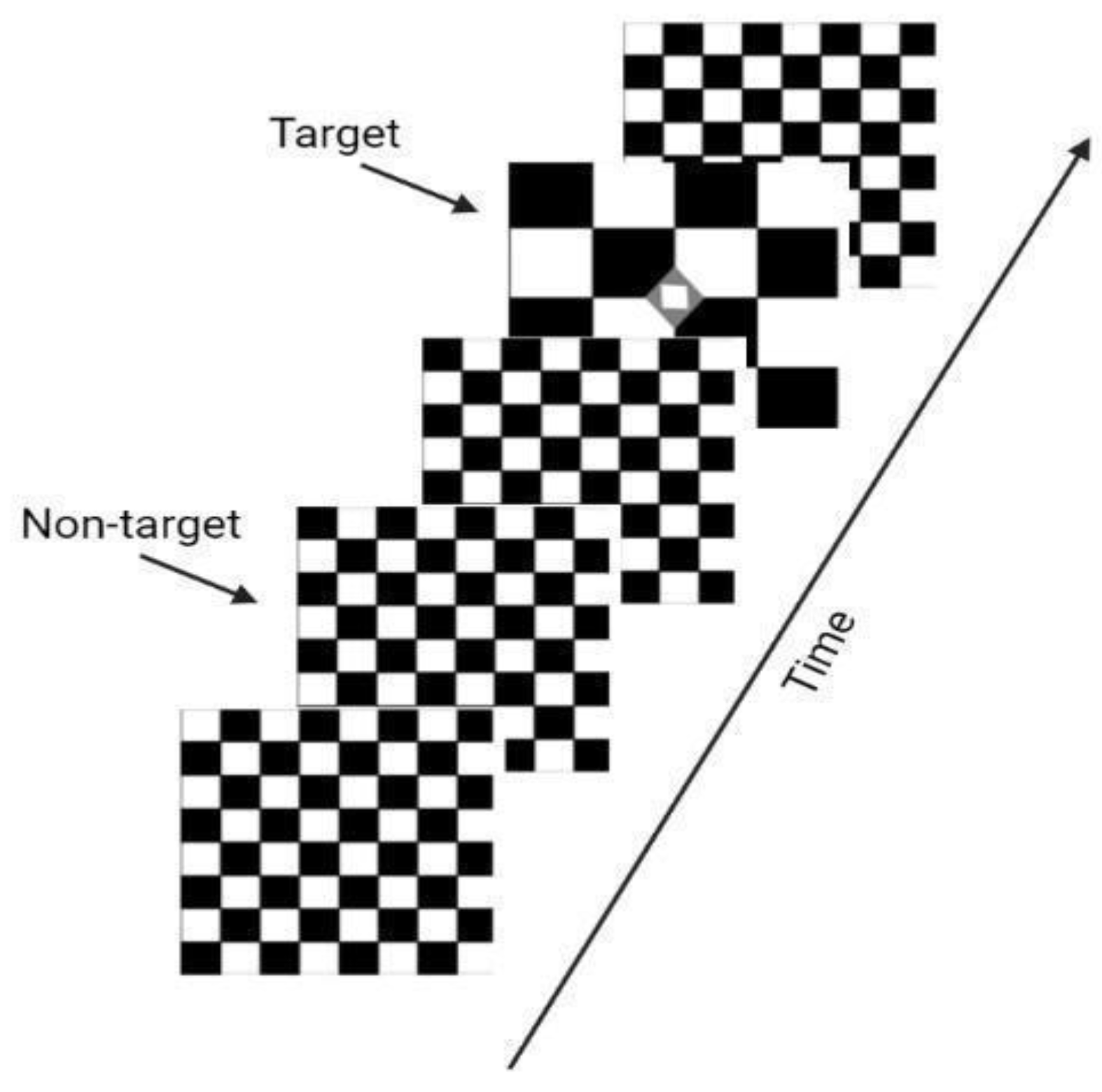
2.1.2. Attention Protocol

Signals were acquired using a Cadwell-brand electroencephalography device and visual stimulation through a protocol designed for attention:

The subject was situated in an isolated room in a comfortable position, facing a 22-inch screen positioned at eye level one meter away.

The EEG signal was acquired using surface electrodes arranged in a cup configuration at twenty-three defined locations based on the 10/20 system with a common reference A1–A2 (Linked-Mastoid montage) (Figure 1). To ensure accurate data capture, electrode impedance was maintained below 5 kΩ, and a Cadwell Easy III^® device was employed.

Stimuli were presented using Presentation^® software 2.4 (https://www.neurobs.com/) on a screen in front of the research subject. An internal synchronization between Presentation^® and the EEG amplifier was established via DC ports, where the analog signal was digitized (rendered as square pulses). These pulses were recorded using the data collection equipment, from which both the signal obtained from Presentation^® and the EEG were then extracted.

2.1.3. Recording and Equipment

Laboratory assistants in a neighboring room used video monitoring to evaluate participants, ensuring their adherence to instructions and checking for signs of drowsiness or sleep onset throughout the recording session. Participants were seated at a distance of approximately 1 m from the screen. The experimental task was an oddball visual paradigm involving three visual stimuli placed in a checkerboard pattern (Figure 2). The first visual stimulus contained 8 × 8 monochromatic squares (black and white), each 1 cm by 1 cm, and was used as the non-target stimulus. The second visual stimulus was designed with the same characteristics but with the colors interspersed with the first image. Finally, the third visual stimulus represented the target stimulus, containing 4 × 4 monochromatic images with 2 cm amplitude squares (Figure 3), in which a gray rhombus is located in the center of the image with a white square inside. This paradigm is a task that is widely used to measure cognitive functions. In addition, this paradigm considers the length and distance of the stimulus, the forms of representation, and the use of colors for visual stimuli [21].

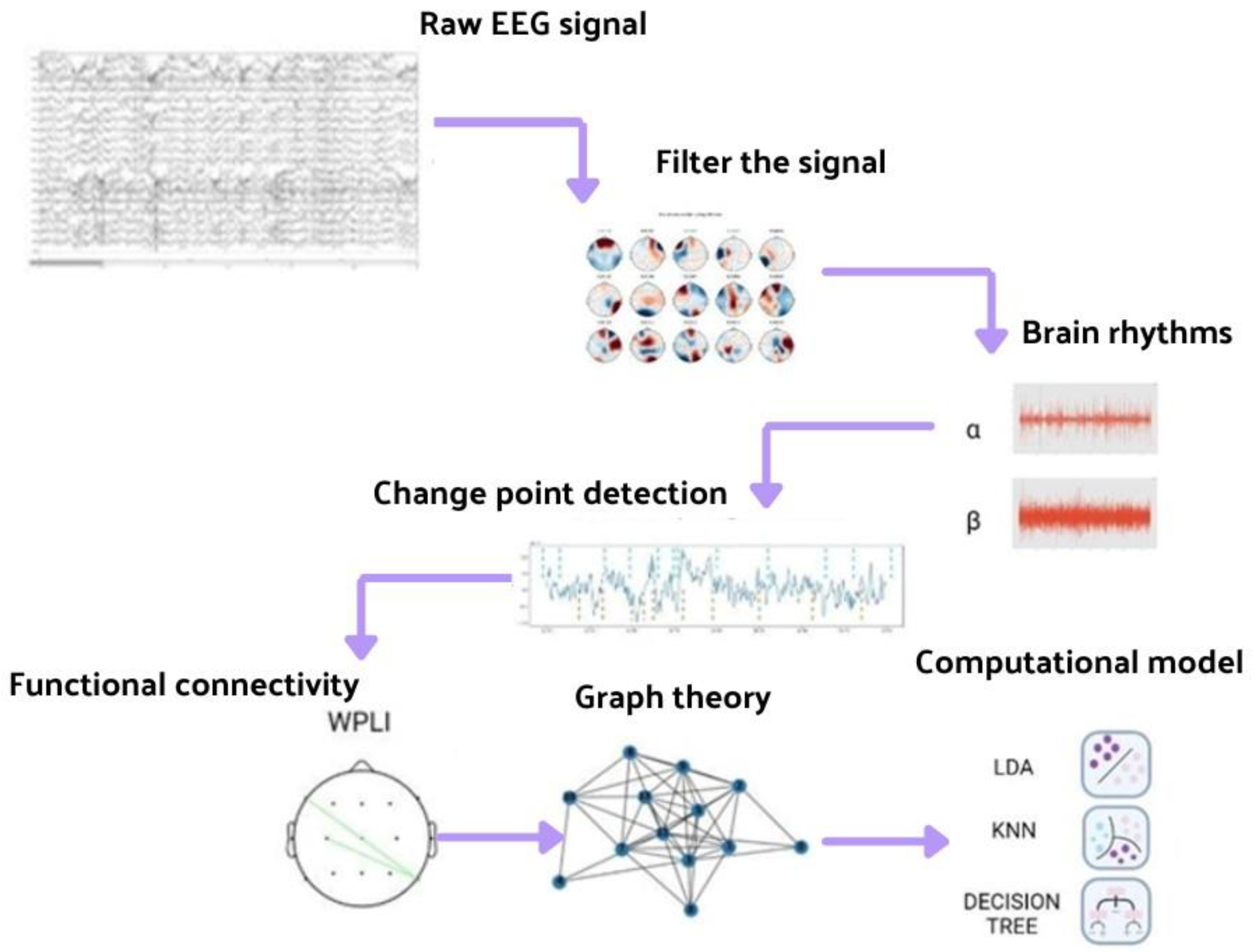
2.2. EEG Preprocessing

Analysis was conducted with Python 3 using the MNE 0.23 package after obtaining raw EEG data [22]. The raw signal was filtered with a digital band-pass filter [22] (Figure 1). The signal was split into each brain rhythm of interest: Delta (0.5–4 Hz), Theta (4–8 Hz), Alpha (8–12 Hz), Beta (12–35 Hz), and Gamma (35–100 Hz) [18,19,20]; though, in accordance with the observation and analysis of the spectrogram derived from the raw signal, the analysis centered on Alpha and Beta rhythms (Figure 4).

Additionally, Independent Component Analysis (ICA) was employed to linearly separate independent sources that were mixed across multiple sensors based on their statistical independence. Additionally, ICA was utilized for artifact removal and to eliminate ocular noise through the process of projection [23]. The Infomax algorithm is an independent component analysis method that reduces the remaining pairwise mutual information versus the percentage of dipolar components.

2.3. Change Point Detection

Change point detection, an essential analytical technique, facilitates the identification of significant shifts within sequential data. This study presents a methodological approach employing the “ruptures” library in Python to discern crucial transition points within time series data. By elucidating these shifts, this method contributes to a deeper understanding of underlying temporal dynamics in various domains, such as electrophysiological signals. The foundation of methodology rests on the meticulous preparation of time series data, denoted as $x=\left\{x_1,x_2,\dots , x_n\right\}$, where $n$ represents the temporal dimension of the sequence under analysis [24].

The “ruptures” library encapsulates advanced algorithms tailored for change point detection. This study adopts the pruned exact linear time (PELT) algorithm, known for its computational efficiency of $O(n\log n)$ in guaranteeing optimal change point detection [25]. At its core, the PELT algorithm is grounded in minimizing a comprehensive cost function, represented as:

$$cost\left(t,\tau \right)=cost\left(\tau \right)+penalty\left(t-\tau \right)$$

(1)

where $t$ denotes the current time point, $\tau$ signifies a potential change point, $cost\left(\tau \right)$ captures the cost of the segment spanning from the last change point to $\tau$, and $penalty\left(t-\tau \right)$ accounts for the penalty associated with introducing a new change point at $\tau$ based on a designated penalty term.

The iterative nature of the algorithm involves the computation of the cost function for each prospective $\tau$, ultimately selecting the point that minimizes cost. This optimal selection designates the preferred location for the ensuing change point. The iterative process is systematically repeated until the conclusion of the temporal sequence.

For the signal segmentations, the lengths of the sections were tested according to the augmented Dickey–Fuller test and the non-stationary Kolmogorov–Smirnov (KS) test [26,27].

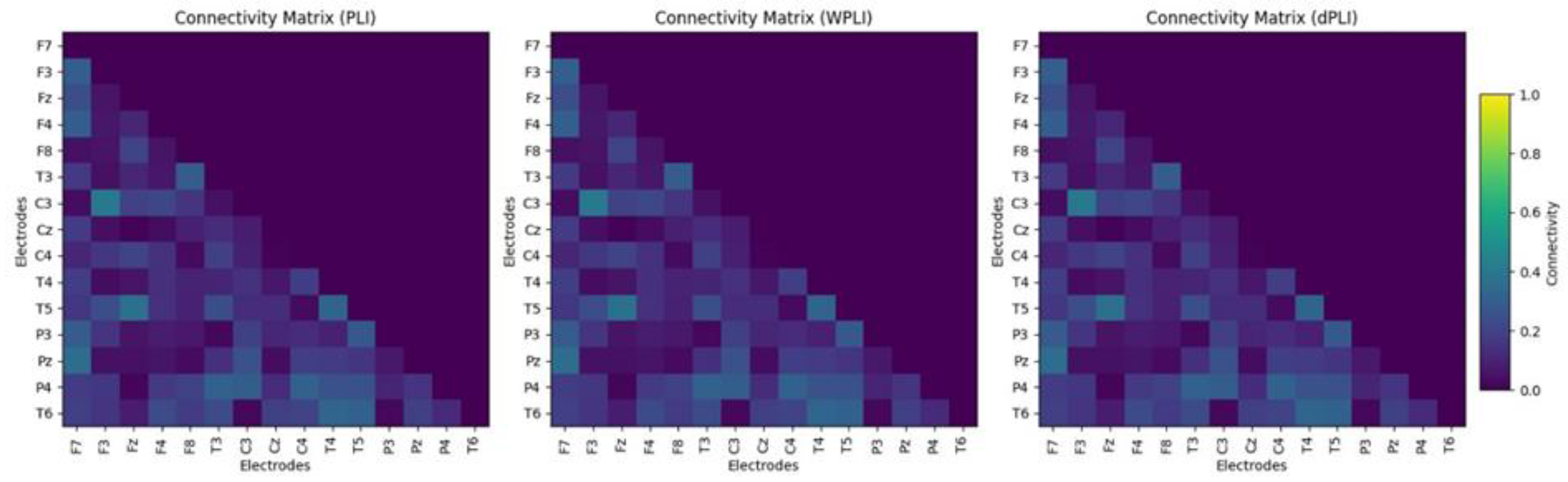
2.4. Functional Connectivity

The WPLI analyzes the synchronization of phases among distinct brain regions in studies of functional connectivity [18] and provides insight into the coherence of oscillatory brain activity between regions, which can reveal patterns of communication and coordination within the brain.

$$WPLI=\frac{\left|E\left\{Im\left({\overline{C}}_{ij}\left(t\right)\right)\right\}\right|}{E\{\left|Im\left({\overline{C}}_{ij}\left(t\right)\right)\right|},$$

(2)

where

• $Im\left(x\right)$ Represents the imaginary part of $x$.
• ${\overline{C}}_{ij}\left(t\right)$ Is the cross-spectral density of the signals from regions $i$ and $j$ at time $t$.
• $E\left\{.\right\}$ Denotes the expected value or ensemble average over time.

WPLI reduces the influence of cross-talk and artifacts caused by volume conduction, allowing the extraction of more accurate insights into the underlying neural interactions and network dynamics [28].

2.5. Graph Theory

Threshold

In graph theory, it is imperative to acknowledge that not all connections necessitate explicit calculation. A threshold method is expected to be applied in the analysis of weighted graphs; however, this methodology encounters difficulties when precisely selecting the threshold value. This challenge emerges from the recognition that adopting a higher threshold could potentially inhibit the successful construction of a brain network; in comparison, a lower threshold may lead to connectivity measures that lack substantive meaning.

This concern was addressed using a method of relevance analysis on the connectivity vector. This approach employed proportional thresholding from a 70% to 30% ratio, thus retaining the most pertinent connectivity while eliminating weaker signals. In vivo and in vitro human and animal data estimations informed this criterion. The level of consistency for this thresholding procedure was determined to ensure the retention of 30% of the most robust connections [29].

For each graph, three segregation metrics were calculated: Clustering coefficient (CC), Modularity (Q), and Transitivity (T). Two integration metrics were calculated: Characteristic Path Length and Betweenness Centrality (BC).

The Clustering Coefficient (CC) is a network metric that quantifies the extent to which nodes within a graph exhibit clustering tendencies, forming densely interconnected groups. This metric reflects the likelihood that the neighbors of a given node are also connected. A high CC value indicates a higher level of local connectivity within a network. This metric is valuable when it comes to assessing how nodes form distinct clusters or communities within a more extensive network structure [29].

Modularity (Q) is a measure used to evaluate the degree of segregation or division of a network into distinct communities or modules. This measure quantifies how well network nodes group into separate clusters, with a higher Q value indicating a more robust network division into distinct groups. Community detection algorithms often employ Q to uncover connectivity patterns within complex networks [29].

Transitivity (T) is a network metric that assesses the likelihood that if node A is linked to node B and node B is linked to node C, there exists a high probability of a connection between nodes A and C. In other words, this metric assesses the tendency of triangles to form within a network. T provides insight into the level of transitive relationships in a network, indicating to what extent nodes form interconnected loops or cycles [29].

Characteristic Path Length is a network metric that calculates the mean shortest path length between every possible pair of nodes within a graph. This metric denotes the average count of edges that need to be crossed to connect one node with another. A shorter characteristic path length indicates more efficient communication and shorter routes between nodes, implying better overall network integration and information flow [29].

Betweenness Centrality (BC) is a measure that identifies the importance of a node in facilitating communication between other nodes in a network. This measure assesses the extent to which a particular node lies on the shortest paths between pairs of nodes. Nodes with high BC values significantly influence information flow within a network, as they function as crucial bridges or connectors between different network parts. This metric represents a valuable means of understanding which nodes play a pivotal role in maintaining efficient communication and connection throughout a network [29].

2.6. Computational Modeling

Linear Discriminant Analysis (LDA): Linear Discriminant Analysis (LDA) is primarily used to classify patterns into two categories, although it can be extended to handle multiple categories. LDA operates under the assumption that all categories are linearly separable. To achieve this, it creates a multiple linear discriminant function, which essentially defines several hyperplanes in the feature space to distinguish between the categories. In the case of two categories, LDA constructs a hyperplane that optimally projects the data, maximizing the separation between the two classes. The creation of this hyperplane is based on two concurrent criteria: maximizing the distance between the means of the two classes and minimizing the variance within each category [30]. Supposing that for the two features of the dataset, the possibilities for feature 1 and feature 2 are p₁ and p₂; the class means, and generally mean are μ₁, μ₂, and μ; and the variances of the features are cov1 and cov2, correspondingly [31].

$$\mu =p_{1}X{\mu }_1+p_{2}X{\mu }_2$$

(3)

The criteria essential for distinguishing between features are determined by the dispersion within each class and the dispersion between classes. In the context of a multi-class scenario, the measures of dispersion are computed as follows [32]:

$$S_w={{\displaystyle \sum }}_{j=1}^C{p}_j\times co{v}_j$$

(4)

In which C denotes the quantity of classes, and

$$co{v}_j=\left(x_j-{\mu }_j\right){\left(x_j-{\mu }_j\right)}^{\tau }$$

(5)

The computation of inter-class dispersion is as follows:

$$S_b=\frac{1}{C}{{\displaystyle \sum }}_{j=1}^C\left(x_j-{\mu }_j\right){\left(x_j-{\mu }_j\right)}^{\tau }$$

(6)

Thus, the goal is to discover a discriminant plane that optimizes the ratio between inter-class and intra-class dispersions:

$$J_{LDA=\frac{W S_{b{W}^{\tau }}}{W{S}_w{W}^{\tau }}}$$

(7)

K-Nearest Neighbor (KNN): K-nearest neighbor (KNN) is a relatively straightforward, entirely non-parametric classification method. When presented with a point x₀ that needs to be classified into one of K groups, the algorithm identifies the K observed data points closest to x₀. The classification rule assigns x₀ to the group with the largest number of observed data points among these K nearest neighbors. If there is no majority, the unclassified point is randomly assigned to one of the majority groups [32]. The benefit of employing K-nearest neighbors (KNN) classification lies in its simplicity, requiring the user to make just two decisions: the choice of the number of neighbors, denoted as “k”, and the selection of a distance metric. Commonly used distance metrics include Euclidean distance, Mahalanobis distance, and city-block distance, often referred to as Manhattan distance. The optimal number of neighbors is typically determined through methods such as cross-validation or by assessing the classifier’s performance on an independent test dataset [33].

$$dist\left(\left(x,y\right),\left(a,b\right)\right)=\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2}$$

(8)

$$P(y=j|X=x)=\frac{1}{K}{{\displaystyle \sum }}_{i\in A}I{(y)}^{\left(i\right)}=j$$

(9)

Decision Tree: Decision tree learning is a supervised machine learning method that generates a decision tree using a set of training data. This decision tree, which can serve as a classification or regression model, acts as a predictive tool, mapping observations about an item to conclusions regarding the target values. In the structure of decision trees, terminal nodes, often referred to as leaves, correspond to the assigned classifications or labels. Nodes that are not terminal leaves represent specific features, while the branches symbolize the conjunctions of features that ultimately lead to those classifications [34]. This algorithm consists of split nodes $N^{split}$ and leaf nodes $N^{leaf}$, each split node $s\in N^{split}$ achieves a split decision and the dataset to either the left child node cl(s) or the right child node cr(s). When using aligned axis separate decisions, the splitting rule is based on a single splitting feature f(s) and an onset value $\theta \left(s\right)$ [33].

$$x\in cl\left(s\right)\iff X_{f\left(s\right)}<\theta \left(s\right)x\in cl\left(s\right)\iff X_{f\left(s\right)}<\theta \left(s\right)$$

(10)

$$x\in cr\left(s\right)\iff X_{f\left(s\right)}\ge \theta \left(s\right)x\in cr\left(s\right)\iff X_{f\left(s\right)}\ge \theta \left(s\right)$$

(11)

3. Results

3.1. Functional Connectivity

Among the advantages of this strategy, WPLI accounts for the phase lag in neural communication, which improves the accuracy of the results [34]. Additionally, volume conduction and familiar sources have less influence on WPLI. This criterion holds substantial relevance within our research—it explicitly mitigates erroneous associations, which can represent a problem/limitation for other methods. Overall, WPLI provides more reliable and informative results when studying functional connectivity in the brain (Figure 5).

WPLI was designed to address the bias introduced by the volume conduction effect, which can lead to spurious connectivity measures in traditional phase-based connectivity measures like the PLI. DPLI provides additional information regarding whether one signal leads or lags concerning the other; this may not always be necessary, depending on the specific analysis requirements. Therefore, researchers use wPLI in many cases due to its sensitivity to signal strength, robustness to noise, and utility in functional connectivity and graph analysis [35,36].

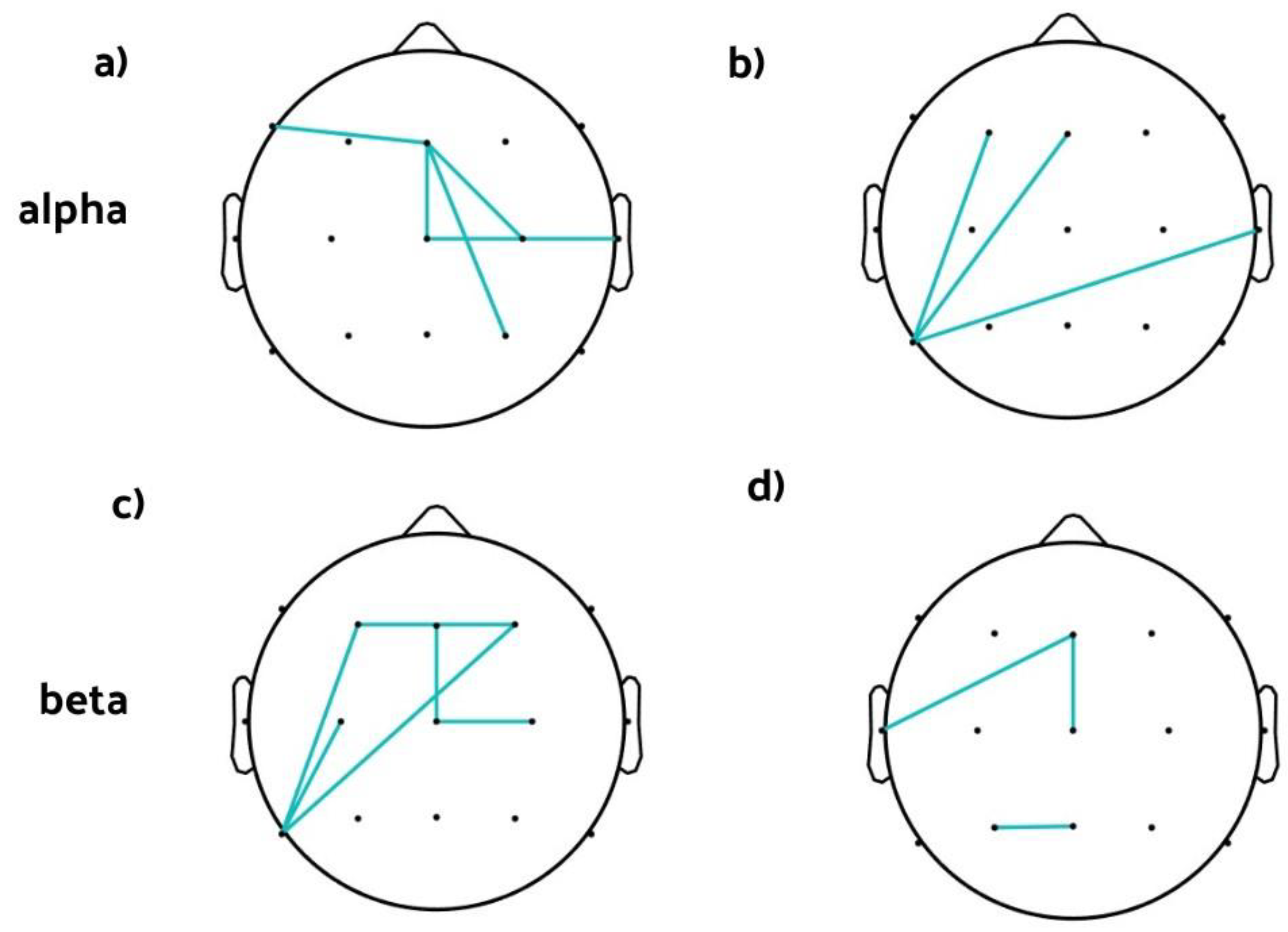
3.2. Interpretability from Functional Connectivity–WPLI According to the Task Paradigm

To establish a physiological foundation for MCI, we conducted a comprehensive analysis of neural responses in the brain elicited by oddball paradigms. This analysis involved the examination of functional connectivity patterns derived from wPLI [37]. As previously outlined, we computed the functional connectivity graph that carries the highest significance in distinguishing tasks related to MCI, specifically the target task. This selection encompasses electrode links that fall within the 70th percentile of normalized relevance weight calculations. We used the tool described in [38] to make the pictures.

As demonstrated in Figure 6, each group of individual skills elicits distinct sets of connections involving different nodes and relevant links. These variations can potentially induce specific alterations in network integration and segregation [39]. In accordance with our findings, the connectivity graphs estimated for MCI subjects (Figure 6c) in the Alpha rhythm activity reveal connections spanning from left frontal electrodes to right and left parietal electrodes, ultimately connecting with the right temporal region. In contrast, Figure 6a illustrates that HC subjects exhibit more intricate connections than MCI subjects in the frontal–temporal–frontal areas, which we presume to be correlated with cognitive activities. Furthermore, when examining Beta rhythm (Figure 6b–d), HC subjects exhibit more robust connections across all lobes than MCI subjects.

Figure 7 focuses on the brain connectivity of MCI and HC subjects. We observed a significant difference between both subjects. Regarding the Alpha band with the target stimulus in the HC subject (Figure 7a), we observed connections at electrodes Fz and Pz, with Fz related to reasoning functions and the parietal lobe associated with attention, perception, and stimulus processing [39,40]. MCI subjects did not exhibit attention-related connections; the three connections from F3, Fz, and T4 directly connected to T5.

As for the Beta band, which is associated with intense brain activity, active thinking, and focus [41], the connections in the frontal and cognitive electrodes provided insight into the attention the HC subject had during the target stimulus, which we did not observe in the MCI subject (Figure 7c,d).

3.3. Classification Model Selection

We examined the connectivity matrices of both healthy control (HC) and mild cognitive impairment (MCI) subjects, utilizing the weighted Phase Lag Index (wPLI). These distinctive graph matrices were integrated into the text classification process, and we applied three distinct models: Linear Discriminant Analysis (LDA), k-Nearest Neighbors (KNN), and Decision Tree. After evaluating the performance of each model during the training phase, we selected the classification model that exhibited the most favorable outcomes. We then gathered accuracy rates, recall rates, and precision values for each model in association with various questions. (

Table 1. Classification performance comparison for each model with WPLI.

Model	Accuracy	Recall	Precision
Linear Discriminant Analysis (LDA)	99.702%	0.993	0.989
K-Nearest Neighbors (KNN)	99.652%	0.9995	0.985
Decision Tree	99.92%	0.9997	0.997

).

In accordance with KNN, we use three neighbors. Selecting this small value reduces the model’s bias, which tends to adapt to the data for pattern detection and makes them more robust. Moreover, as the number of neighbors increases, the calculation time required for making predictions increases. We used CART (Classification and Regression Trees) for the decision tree algorithm. We chose this type of model for its ease of interpretation. This becomes indispensable in applications in which gaining insight into decision-making is paramount. In LDA, we use Singular Value Decomposition (SVD), which is the most suitable option for most cases. We have extracted all available linear discriminant components [41].

We employed the area under the receiver operating characteristic curve (ROC-AUC) to evaluate the three models using K-fold cross-validation. Although neural networks have demonstrated impressive performance, we opted for straightforward classification methods. Our primary aim was to ensure that the model’s physiological information remains interpretable while maintaining the highest possible reliability. This approach ensures that neurologists, psychologists, or any domain professionals can readily interpret the diagnostic results, which aligns with the central focus of our research.

The size of our dataset primarily drove the choice of k in K-fold cross-validation. In machine learning, selecting an appropriate value for k ensures the reliability of model performance evaluation [42]. In our case, we carefully considered the dataset size and its implications for model validation. Our dataset, while representative of the problem we were addressing, fell into the category of a relatively small dataset. Given the limited data available, we chose a smaller value of k. Specifically, we decided to use k = 5 for our K-fold cross-validation.

By selecting k = 5, we aimed to obtain reliable estimates of our model’s performance while ensuring that the training and testing subsets within each fold were substantial enough to support meaningful learning and evaluation. This choice allowed us to make the most efficient use of our dataset’s size while maintaining the integrity of our cross-validation process.

We opted to utilize simplistic models characterized by their minimal parameter count and ease of application. This deliberate choice is rooted in our primary research objective, which centers on the comprehensive examination of neuronal connectivity and the construction of graph-based representations. Notably, the machine learning models employed in our study have been meticulously configured, with parameter settings aligned with established best practices and state-of-the-art methodologies.

Our methodological approach encompassed the partitioning of the dataset, the implementation of rigorous validation techniques, and a meticulous statistical adjustment process. This methodological rigor ensured our findings’ validity and reliability and adhered to recognized data analysis and machine learning standards.

3.4. Statistical Analysis

Segregation properties did not differ significantly between MCI and HC subjects in the Alpha and Beta bands (

Table 2. Comparison between segregation and integration properties in Alpha band.

Parameters	Mean Control	Mean MCI	p-Value
Clustering Coefficient (CC)	0.919165	0.970967	7.39 × 10−8
Modularity (Q)	0.898720	0.975127	1.1732 × 10−7
Transitivity	0.916208	0.969849	3.139 × 10−8
Betweenness Centrality (BC)	0.0062881	0.0026251	0.0000357
Path Length	0.999635	0.9562682	0.0000139

and

Table 3. Comparison between segregation and integration properties in Beta band.

Parameters	Mean Control	Mean MCI	p-Value
Clustering Coefficient (CC)	0.724474	0.825242	7.4745 × 10−8
Modularity (Q)	0.641988	0.743990	0.00001185
Transitivity	0.707032	0.79985	2.0935 × 10−8
Betweenness Centrality (BC)	0.027314	0.01923	0.012501
Path Length	1.25492	1.1338126	4.6909 × 10−8

).

A distinct pattern emerged when interpreting the properties of the Alpha band (Table 2). The BC parameter surfaced as a pivotal differentiator between MCI and HC subjects. We found a significantly lower mean BC value for MCI (0.0026251) than HC subjects (0.0062881), signifying a marked discrepancy with potential diagnostic implications. Analysis of the CC parameter revealed a value of 0.970967 in MCI and 0.919165 in HC subjects; the p-value of 7.39 × 10⁻⁸ underlines the robust statistical significance, highlighting a potentially heightened tendency for local clustering within HC subjects. Analysis of the Q parameter revealed a value of 0.975127 for MCI and 0.898720 for HC subjects; the p-value of 1.1732 × 10⁻⁷ reveals a highly significant difference, implying a more pronounced division into distinct modules within MCI subjects. Our analysis also uncovered intriguing insights into Transitivity. MCI subjects exhibited a mean value of 0.969849, and HC subjects of 0.916208; the p-value of 3.139 × 10⁻⁸ indicated a highly significant difference and a heightened likelihood of interconnectedness between nodes in the MCI group. Finally, examining Path Length revealed additional noteworthy findings. MCI subjects exhibited a mean path length of 0.9562682 and HC subjects of 0.999635; the p-value of 0.00001395 implies a significant difference and a more streamlined and efficient communication pattern within MCI subjects.

Substantial disparities also emerged between MCI and HC subjects when analyzing Beta band properties (Table 3); these variations underscore distinctive features across multiple parameters associated with segregation and integration within the Beta band. Analysis of the CC parameter revealed a mean value of 0.825242 for MCI and 0.724474 for HC subjects; the p-value of 7.4745 × 10⁻⁸ implies a highly significant difference and suggests enhanced local clustering within MCI subjects compared to HC subjects. Analysis of the Q parameter revealed a mean value of 0.743990 for MCI and 0.641988 for HC subjects; the p-value of 0.00001185 indicates a significant difference and suggests that MCI subjects exhibited more pronounced separation into modules than HC subjects. Analysis of T values revealed a mean value of 0.79985 for MCI and 0.707032 for HC subjects; the p-value of 2.0935 × 10⁻⁸ implies a highly significant difference and interconnectedness between nodes within MCI subjects. Finally, analysis of the BC parameter revealed a mean value of 0.01923 for MCI and 0.027314 for HC subjects; the p-value of 0.012501 indicates a significant difference and suggests that MCI subjects’ nodes played a less central role in communication maintenance than in HC subjects.

In this study, our primary objective revolved around maintaining the interpretability of neural activity patterns within the context of MCI subjects. We accomplished this by achieving FC analysis, and our approach was further complemented with machine learning techniques applied across various brainwave frequencies. The outcome of this research, following extensive statistical analysis and rigorous cross-validation, resulted in performance metrics that approached 99% accuracy.

To understand neuronal interactions in the brain, we used connectivity matrices, which we subsequently transformed into adjacency matrices to construct graphs. These graphs have physiological significance and are used as features for well-established machine learning models.

The implications of our findings emphasize the potential of this methodology as a tool for characterizing brain activity in individuals diagnosed with MCI.

4. Discussion

We investigated the effects of functional connectivity change assessment on the brain using EEG in MCI and HC subject analysis. Firstly, we observed activity in the signal spectrum within the Theta band associated with MCI. Spectral variations in our study, and those observed by Marlats et al. [43], recorded this spectral shift. Cerebral activity in the Alpha and Beta bands reflected the paradigm applied to the subjects. The results of the change point detection algorithm revealed abrupt changes in these rhythms, which could support the diagnosis of neurodegeneration. Similar analyses have been employed in other EEG signal studies [19,25].

Regarding frequency bands, our findings align with the contributions of functional connectivity analysis [44], as both studies demonstrated significantly reduced functional connectivity in the Alpha band. However, concerning the Beta frequency band, our study did not encounter significant differences in this frequency band in MCI compared to HC subjects. As for graph metrics, BC decreased in MCI subjects compared to HC subjects in the Alpha and Beta bands in both studies [44]. In the context of cognitive impairment, we used graph theory to study how neuronal network changes affect information flow, leading to symptoms such as memory loss or difficulty with decision-making [45]. Previous studies have shown that subjects with AD and MCI have decreased BC in specific brain regions [41], suggesting that these channels (respective regions) may play a role in the disease and that changes in their connectivity could contribute to cognitive impairment; however, more research is required to understand the relationship between graph theory, centrality measures, and cognitive impairment.

In this study, our primary objective was to evaluate the performance of the visual oddball paradigm in individuals with MCI, specifically focusing on the development of a workload classifier. To achieve this goal, we employed EEG due to its well-known high temporal resolution and suitability for capturing real-time brain activity. Our methodology centered on functional connectivity, a technique known for its efficiency and relevance to cognitive regulation under varying levels of mental effort.

To classify cognitive effort into two distinct categories, MCI and HC, we turned to machine learning techniques. This classification approach aimed to provide valuable predictions that could aid medical decision-making processes [42]. Within our study, we generated functional connectivity networks, elucidating the interactions between different brain regions using the WPLI. Subsequently, we utilized the connectivity matrix to derive essential graph metrics, which served as inputs for our classification models, enabling the differentiation of various workload levels.

Remarkably, our study yielded state-of-the-art multi-class workload classification accuracy using EEG, functional connectivity, and graph metrics. These findings underscore the potential of EEG-based model-free functional connectivity and graph measurements when coupled with machine learning. This combination offers an accurate, reliable, and expeditious approach to assessing MCI. However, it is essential to note that a more comprehensive comparative analysis of different connectivity measures would necessitate a future study, one that includes a larger participant pool and explores diverse permutations and combinations of brain regions. This future work will undoubtedly enhance our understanding of the effectiveness of these methodologies in the context of cognitive assessment.

5. Limitations

The limited dataset used in our study represented a significant constraint; however, this limitation is a common factor in studies on illness classifications [43]. Despite this limitation, our system performed well, demonstrating that HC and MCI comparisons provided evidence of alterations in brain structure. Furthermore, using a 22-channel EEG system inherently constrains our ability to achieve an extensive spatial resolution of cerebral regions.

6. Future Work

Our study has shed light on the intricate relationship between mild cognitive impairment and functional connectivity, offering a promising avenue for future research in the realm of neurodegenerative disorders and brain function assessment. Here, we outline potential directions that can build upon our work and further our understanding in these domains.

While our study primarily focused on MCI, it is crucial to extend our investigations to encompass a wider range of neurodegenerative conditions, such as AD, Parkinson’s disease, and other forms of dementia. This expansion can help uncover commonalities and distinctions in functional connectivity patterns across various disorders, offering valuable insights into their underlying mechanisms. We are currently initiating related research in the field of mental health.

Moreover, we would like to integrate other neuroimaging modalities like functional magnetic resonance imaging (fMRI) and magnetoencephalography (MEG) with EEG to provide a more comprehensive view of brain function and connectivity. Future studies could explore the synergistic benefits of combining multiple modalities to enhance diagnostic accuracy.

7. Conclusions

Our study contributes to the growing body of research on functional connectivity and dementia-related disorders. Notably, we apply change point detection methods to identify abrupt signal changes, a novel approach in this domain. This is a critical step in understanding the dynamics of the brain network and its alterations in conditions like MCI. We enhance our interpretative capabilities and diagnostic accuracy by integrating machine-learning techniques and graph-based metrics. We construct an adjacency matrix to operationalize this approach to represent structural relationships among EEG channels. Our findings indicate that EEG graph measures hold promise as predictive markers for disease progression in MCI subjects. Our research, which focuses on the connectivity analysis of EEG oddball paradigms in MCI and HC subjects, offers valuable insights into this burgeoning field, and highlights the potential for early detection and intervention in neurodegenerative disorders.