Efficient Hardware Implementation of Elliptic-Curve Diffie–Hellman Ephemeral on Curve25519

Abstract

Hardware architecture optimized for implementing the elliptic-curve Diffie–Hellman ephemeral (ECDHE) on 256-bit Montgomery elliptic curves presents unique challenges, particularly for resource-constrained IoT and mobile devices. This work aims to provide an efficient hardware implementation of ECDHE on Curve25519, including a dedicated finite state machine (FSM) designed to handle point multiplication and ECDHE operations, utilizing constant-time algorithms and a unified memory block for resource management. Additionally, we introduce an optimized modular computation unit that covers modular addition, subtraction, multiplication, and inversion. Our proposed hardware architecture enhances the efficiency of ECDHE operations while maintaining low resource utilization, considerably reduced latency, and low power consumption. Synthesized on the Xilinx Artix-7 platform, our design boasts 64,000 Slices and a clock speed of 102 MHz, and it computes an ECDHE scalar multiplication operation in 1.1 ms, consuming 117 mW. The proposed hardware design can be applied to various platforms, including mobile devices and IoT systems.

1. Introduction

The Internet is much more encrypted now than it was in the past. Information is much more secure with the widespread application and usage of Internet security protocols, such as elliptic curve cryptography (ECC) in Transport Layer Security (TLS) [1,2]. The standard requires many devices, including personal computers, smartphones, and Internet of Things (IoT) devices, to compute cryptography encryption and decryption whenever they communicate over the World Wide Web.

While practical ECC computations are crucial in safeguarding user data privacy on mobile and IoT devices, the primary bottlenecks are the limited processing power and energy resources of these devices. Hardware implementation is designed to increase computational speed and reduce energy consumption through paralleling techniques used on low-power microcontrollers or mobile phones.

Many methods for calculating and processing ECC on hardware differ in performance, area, occupied memory, power consumption, and security level. We focus on putting our design onto a field-programmable gate array (FPGA). Research by Izu et al. [3] shows a method that applies simple algorithms and utilizes the FPGA structure to achieve high efficiency, which is a trade-off with the area. The above study also builds on the original work of Aoki et al. [4]. One of the initial adoptions of digital signal processors (DSPs) for modular operation is from [5]. While using a DSP has the advantage of fast computational speed, it requires the DSP resource to be available and consume more power. To enhance a modular addition, Rogawski et al. suggested using fast carry chain adders [6] based on a parallel prefix network [7]. The result is better speed in modular adding and subtracting operations, with a trade-off with latency of pipeline stages. For modular multiplication, the choice is between a high-radix multiplier [8] or high-density karatsuba with NLP multiplication [9]. A high radix level increases the complexity of the design, and it is better to compensate for the low radix level with better hardware adders. Redundant binary representation is another notable method for modular multipliers [10]. P. Kocher et al. pointed out that the vulnerability to power analysis attacks is notable in the hardware design for cryptography processing in FPGAs [11]. Fischer et al. also gave an example structure against energy analysis [12].

In the case of Curve25519, Sasdrich et al. presented the first Curve25519 hardware design [13]. Kopperman et al. presented two Curve25519 hardware implementations that could process ECDHE scalar multiplication under 100 $\mathsf{\mu }$s [14,15]. Interleaved modular multipliers were used in research [16] to reduce power consumption. Niasar et al. [17] presented three designs with low resource requirements, area–time efficiency, and high performance. Research [18] showed a hardware–software hybrid design for resource-constrained devices. Research [19] showed scalable point multiplication for Curve25519. Kudithi et al. [20] implemented their design with a radix-2 multiplier, using mixed Jacobian coordinates on different FPGA platforms and application-specific integrated circuits (ASIC). With different parameters, Kieu et al. [21] supported multiple curves on their FPGA and ASIC designs.

Our research is to create a hardware design that handles cryptography operation for the TLS curve Curve25519 [22]. The ECC operation includes elliptic-curve Diffie–Hellman ephemeral (ECDHE) key generation and computation.

The main contribution of this paper includes creating a hardware design structure that can do the following:

• Generate the public key for ECDHE and compute the shared key according to IEEE P1363 [23] with support for the TLS 256-bit elliptic curve Curve25519 [2].
• Employ a fast elliptic computation unit optimized for modular addition, subtraction, multiplication, and inversion.
• Comprise a specialized finite state machine (FSM) that executes point multiplication and ECDHE operations, utilizing a constant-time algorithm and relying on a single consolidated memory block to optimize resource utilization.

The remaining sections of this paper are structured as follows. Section 2 provides an overview of the mathematical backgrounds and parameters of Curve25519. Section 3 is the proposed hardware design for implementing Curve25519 elliptic-curve Diffie–Hellman ephemeral (ECDHE) processes. Our findings and results are elaborated upon in Section 4. Section 5 discusses our design, including comparisons with relevant references. Section 6 concludes and summarizes this paper.

2. Backgrounds

2.1. Elliptic Curve Cryptography Mathematics

ECC is based on a finite field in the form of an integer mod p, where p is prime. A field F is a set of elements with addition and multiplication operators. For every element a in field F, except 0, there exists an element ${\mathrm{a}}^{-1}\in F$ so that $a\ast a^{-1}=1$.

In a finite field of order p (prime field), for a prime number p, a finite field of degree p, $GF\left(p\right)$, is defined as the set $Z_p=0,1,\dots ,p-1$, with the algebraic operations modulo p. Each element in $Z_p$ (except 0) has a modular inverse (i.e., there exists z, $w\in Z_p$ such that $\mathrm{wz}=1\mathrm{mod}\left(\mathrm{p}\right)\mathrm{or}\mathrm{z}={\mathrm{w}}^{-1}\mathrm{mod}\left(\mathrm{p}\right)$).

2.2. Curve25519 Parameters

The curve presented in this paper is Curve25519 (Montgomery curve).

Table 1. Curve25519 parameters.

Parameter	Value
p	$2^{255}-19$
a	486662
u(S)	09
v(S)	1478161944758954479102059356840998688726460613
	4606134616475288964881837755586237401
n	$2^{252}$ + 0x14def9dea2f79cd65812631a5cf5d3ed
h	08

presents the parameters and corresponding values of Curve25519 from standards [24,25,26]. These are the values used in the hardware design proposed in the paper. The curve is defined in a prime field with the prime p close to a power of 2 to optimize the efficiency of modulo computations.

2.3. Computation on Montgomery Curve

A Montgomery curve on the field $F_p$ is in the following form:

$$B{y}^2=x^3+A{x}^2+x(A,B\in F_p,B\ne 0,A^2\ne 4)$$

(1)

On the projective coordinate system, with $\mathrm{x}=\frac{\mathrm{X}}{\mathrm{Z}}$ and $y=\frac{Y}{Z}$, the form is presented in the function below. Notice that Y is no longer needed. $\mathrm{P}\left(\mathrm{x}:\mathrm{y}\right)$ is now $P(X:Z)$ with $Z\ne 0$. There are two special points $\mathrm{O}=\left(0:1:0\right)$ and $T=(0:0:1)$ that are converted to $\mathrm{O}=\left(1:0\right)$ and $\mathrm{T}=(0:0)$.

This form allows us to use the Montgomery powering ladder algorithm to compute scalar multiplication on the Montgomery curve. A modified version of this algorithm is preferred because of the side-channel attack prevention [27].

2.4. Elliptic-Curve Diffie–Hellman Ephemeral (ECDHE)

ECDHE is the method used during the key exchange between the server and the client so that the result is a pre-master secret known to both parties. During the handshake, after the server and client have agreed on which cipher suite and curve to use, both of them know the parameter domain, including the following values:

• p: prime number p defined for the field $F_p$
• a: parameters of the curve equation
• $S(u,v)$: coordinates of base point (generator)
• n: order of S, defined as the smallest integer for which $nS=0$
• h: the cofactor

The pre-master secret agreement process is as follows:

• The server chooses a random number $k<(0<k<n)$. Then, the server calculates $kS$ and sends it to the client.
• The client chooses a random number $k^{\prime } (0<k^{\prime }<n)$. The client calculates $k^{\prime }S$ and sends it to the server.
• Server and client, after obtaining the ephemeral data k or $k^{\prime }$ of the other end, can calculate the pre-master secret $P=k{k}^{\prime }S=k^{\prime }kS$

3. Hardware Design

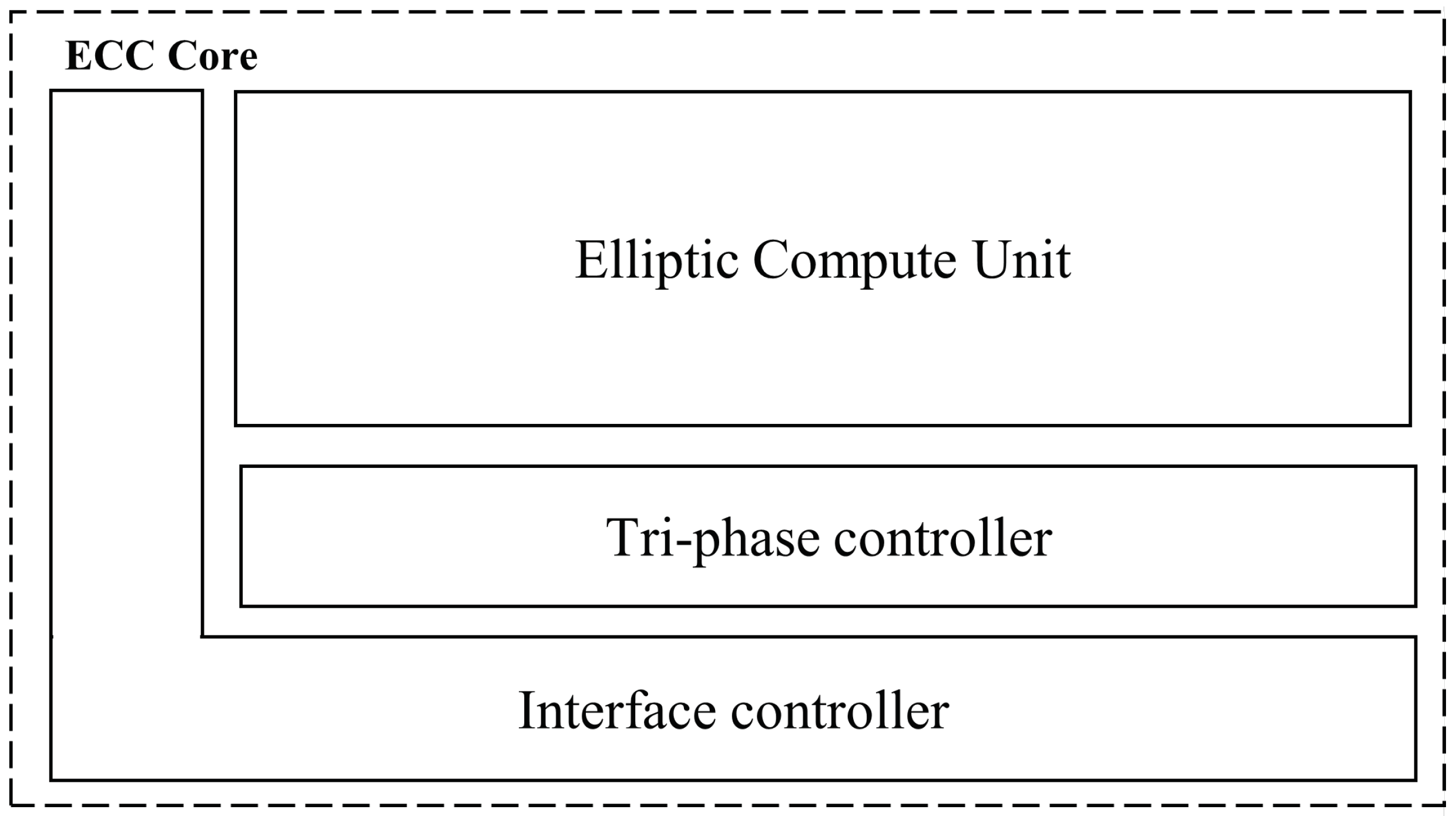
The ECC Core is the proposed hardware structure for implementing elliptic curve cryptography over Curve25519. The ECC Core features a data input bus and start signal along with a mode input for choosing between modes of operation. The calculation status is updated to the output, and the result follows.

The design method is implemented as intuitive, easy-to-modify hardware modules that can work individually with their tasks. The ECU handles modular addition, subtraction, multiplication, and inversion. The Figure 1 presents the structure of the ECC Core. It includes an interface controller, a tri-phase controller, and an ECU.

The interface controller handles data output and input, mode selection, and testing purposes. The tri-phase controller (TPC) is the finite state machine (FSM) for scalar multiplication, random number generation, memory interface, etc., to serve the ECDHE key generation and computation process. The ECU processes modular arithmetic tasks given by the TPC.

3.1. Interface Controller

The interface controller connects the system’s primary input and output interfaces to the TPC. It also does random number generation and error checking for invalid values during computation. Figure 2 shows the general structure of the interface controller with dedicated FSMs for receiving the input and processing ECDHE key generation and computation. The input received is 512-bit in parallel for ease of computation. We synthesized our design with another serial-to-parallel interface to eliminate the pin issue. The I/O interface has 32-bit input and output controlled with ready, acknowledge, and a busy flag to receive or output data from the memory in 32-bit chunks. We designed the FSMs so that the state transitions depend only on the current state and mode input, minimizing complex logic. This simplistic FSM architecture provides low-latency performance while minimizing the attack surfaces side-channel leaking and improving security [28].

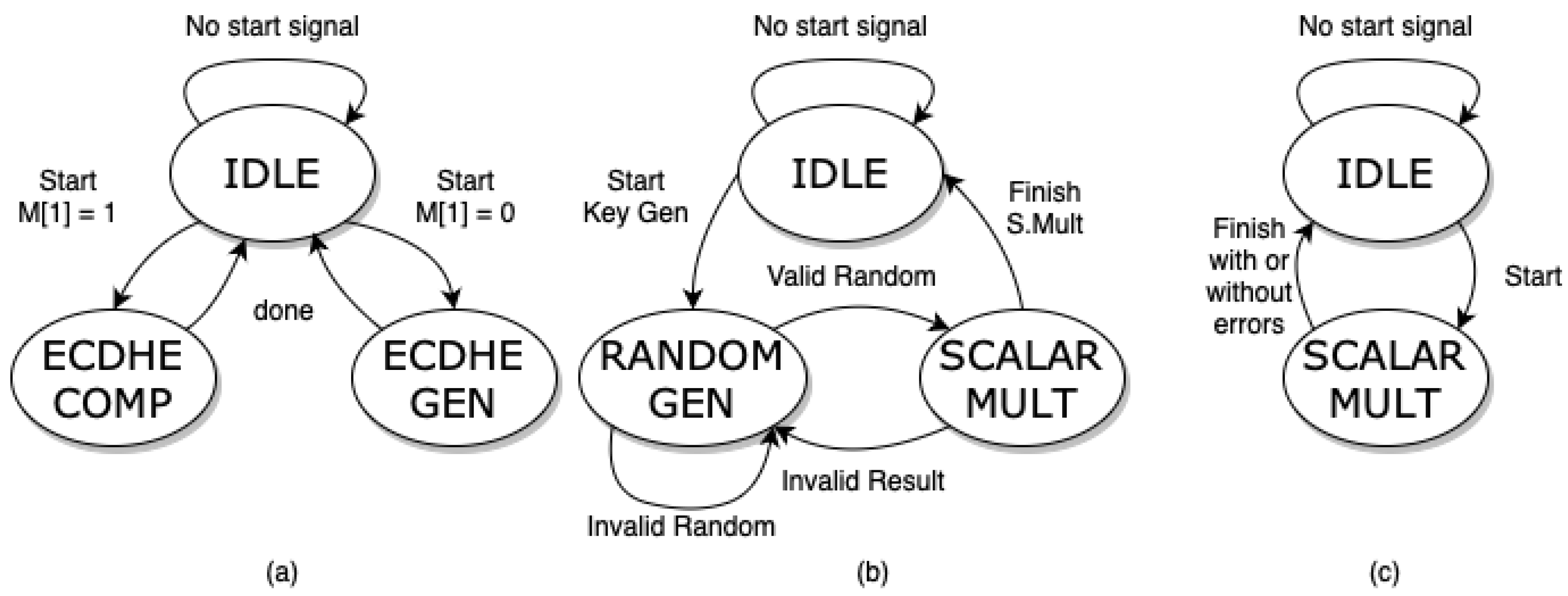
For ECDHE key generation and computation, the first 256-bit of the input is u, and the latest 256-bit is k. Figure 3 shows the three FSMs. Figure 3a is the interface controller FSM that interacts with the ECDHE generation FSM (Figure 3b) and ECDHE computation FSM (Figure 3c).

The interface controller FSM (a) waits for the start signal and reads the mode input M[1] from the I/O interface to choose between the ECDHE key generation operation or ECDHE key computation. The ECDHE key generation FSM (b) starts with the random generation of k. If k is non-zero, we start the scalar multiplication operation with P from the curve parameter Table 1. If the result returns an invalid point (point at infinity or zero), the random generation process starts again to obtain another random k for calculation. The ECDHE computation FSM (c) instructs the tri-phase controller to obtain the data from memory and start the scalar multiplication process.

The ECDHE generation procedure starts with choosing a random k (and repeating if k is not valid), computing scalar multiplication, and checking for validation (Q is not point zero) according to Section 2.4. The ECDHE computation procedure receives data from the input and computes the scalar multiplication. Then, it checks for validation (P is not point zero).

3.2. Tri-Phase Controller

The tri-phase controller interacts with the interface controller and the ECU and controls its internal memory block. We use a BRAM as the internal memory block where values are generated between each operation in the memory. The memory size used is 32 × 256-bit, enough for operations on 256-bit operands of ECDHE key generation and computation. Figure 4 presents the structural diagram of the tri-phase controller.

3.2.1. Internal Memory Access

We use 32 × 256-bit random access memory with a synchronous read-and-write clock. We use 23 addresses as storage for global variables and 9 as temporary variables. The number is to accommodate the modified scalar multiplication for Montgomery curves.

Table 2. Memory addresses and descriptions for the 32 × 256-bit memory.

Name	Value	Description
X_G	0	X-coordinate of point G
Y_G	1	Y-coordinate of point G
X_3G	2	X-coordinate of point 3G
Y_3G	3	Y-coordinate of point 3G
Z_3G	4	Z-coordinate of point 3G
X_5G	5	X-coordinate of point 5G
Y_5G	6	Y-coordinate of point 5G
Z_5G	7	Z-coordinate of point 5G
X_7G	8	X-coordinate of point 7G
Y_7G	9	Y-coordinate of point 7G
Z_7G	10	Z-coordinate of point 7G
X_KG	15	X-coordinate of point KG
PKEY	17	Public key
ZRRAM	18	All zero value
ONERAM	19	All one value
TEMP	20–28	Temporary value
BLNK	31	Blank value

shows how we named each address. The names correspond to the variables in Algorithm 1.

Algorithm 1 Modified scalar multiplication for Montgomery curves.

1: $x_1=u,x_2=1,z_2=0,x_3=u,z_3=1,swap=0,a24=$ 121,665 2: for ($t=bits-1$ down to 0) do 3:      $swap=swa{p}^{k\left[t\right]}$ 4:      $(x_2,x_3)=SWAP(swap,x_2,x_3)$ 5:      $(z_2,z_3)=SWAP(swap,z_2,z_3)$ 6:      $swap=k\left[t\right]$ 7:      $A=x_2+z_2$ 8:      $AA=A^2$ 9:      $B=x_2-z_2$ 10:    $BB=B^2$ 11:    $E=AA-BB$ 12:    $C=x_3+z_3$ 13:    $D=x_3-z_3$ 14:    $DA=D\ast A$ 15:    $CB=C\ast B$ 16:    $x_3={(DA+CB)}^2$ 17:    $z_3=x_1\ast {(DA-CB)}^2$ 18:    $x_2=AA\ast BB$ 19:    $z_2=E\ast (AA+a24\ast E)$ 20: end for 21: $(x_2,x_3)=SWAP(0,x_2,x_3)$ 22: $(z_2,z_3)=SWAP(0,z_2,z_3)$ 23: return  $x_2\ast \left(MONTINV\left(z_2\right)\right)$

3.2.2. Tri-Phase Scalar Multiplication for Montgomery Curves

The algorithm used in the design to perform scalar multiplication for Montgomery elliptic curves (here, we use curve X25519) is S.Turner’s algorithm [24,27]. This algorithm ensures the constant-time characteristic for all input values.

Because the original algorithm is written in Python for software, we made some changes to the algorithm to make it suitable for hardware. The modified algorithm is shown in Algorithm 1. The constant $a24$ is $(\mathrm{486,662}-2)/4=\mathrm{121,665}$ for curve25519/X25519. Specifically, the following process is performed:

• Remove the k shift and switch to indexing.
• Drop the swap value on the last two swaps because the last 3 bits of k are always zero after correctly decoding in RFC 7748 [24].
• Remove the last exponent. Montgomery exponential can be performed on hardware, but it takes too much time; instead, Montgomery inverse gives the same result, which is proved below:
  We can quickly prove that the Montgomery exponential step is the Montgomery inverse.
  Given $t=a^{-1}modp$ and $t=a^{p-2}modp$
  $\iff a\ast tmodp=1modp$
  $\iff a\ast a^{p-2}modp=1modp$
  $\iff a^{p-1}modp=1modp$
  This is Fermat’s little theorem [29].

Montgomery scalar multiplier is divided into three parts. The structural diagram for the multiplier is presented in the tri-phase scalar multiplication FSM in Figure 4.

• Initialization phase (init)

  -

  Initialize values in the memory block.

  -

  Decode the input scalar value in the form $2^{254}+8\ast random(0,2^{255}-1)$ and convert it from Little-Endian to an integer.

  -

  Decode the input point coordinate value, convert little-endian to an integer, and give the mask to bit 256.

• Calculation phase (comp)

  -

  Perform the loop of swapping, multiplying, and adding points 255 times.

  -

  Interact with ECU’s internal memory from 45-state FSM.

• Final phase

  -

  Perform the final calculation with one Montgomery inverse and one Montgomery multiplication.

  -

  Normalize and save the result in the internal memory.

Appendix A shows the operations we execute in each step of the finite state machine for each phase in the tri-phase controller. The operation accesses the corresponding address in the internal memory to store or load necessary values for computation.

3.3. Random Number Generator

We utilize a pseudo-random number generator (PRNG) to generate random numbers. Generally, we adopt a linear feedback shift register design, as outlined in [30], with adjustments to accommodate a 256-bit format. Feedback is incorporated at specific positions: 256, 254, 251, and 246. PRNGs are straightforward and primarily employed for simulation and testing. The structure of the Galois 256-bit LFSR is visually represented in Figure 5.

3.4. Elliptic Compute Unit

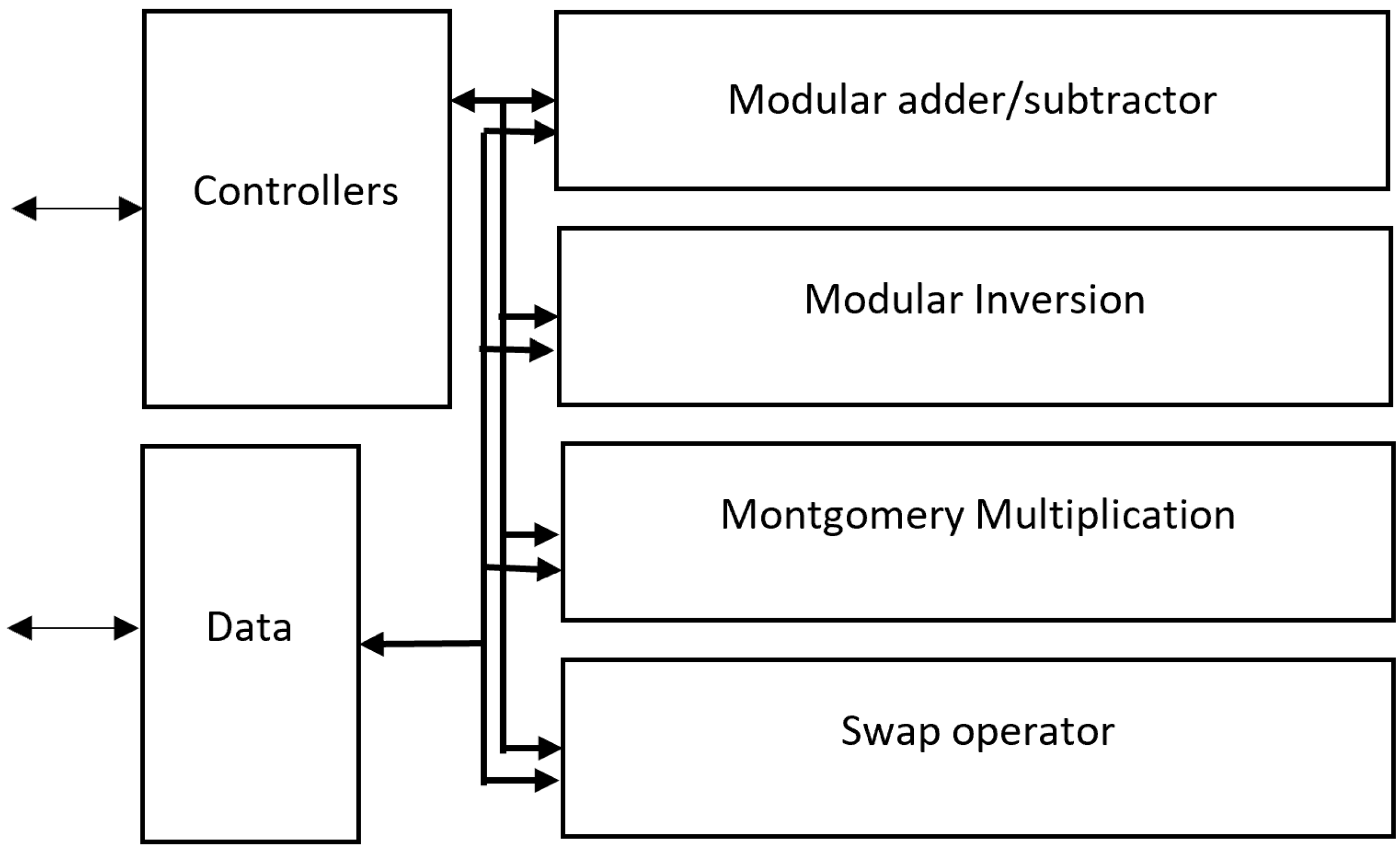
The elliptic compute unit (ECU) receives data and control signals from the tri-phase controller. It consists of four modules for four operations: modular addition, Montgomery multiplication, Montgomery inversion, and swap operator.

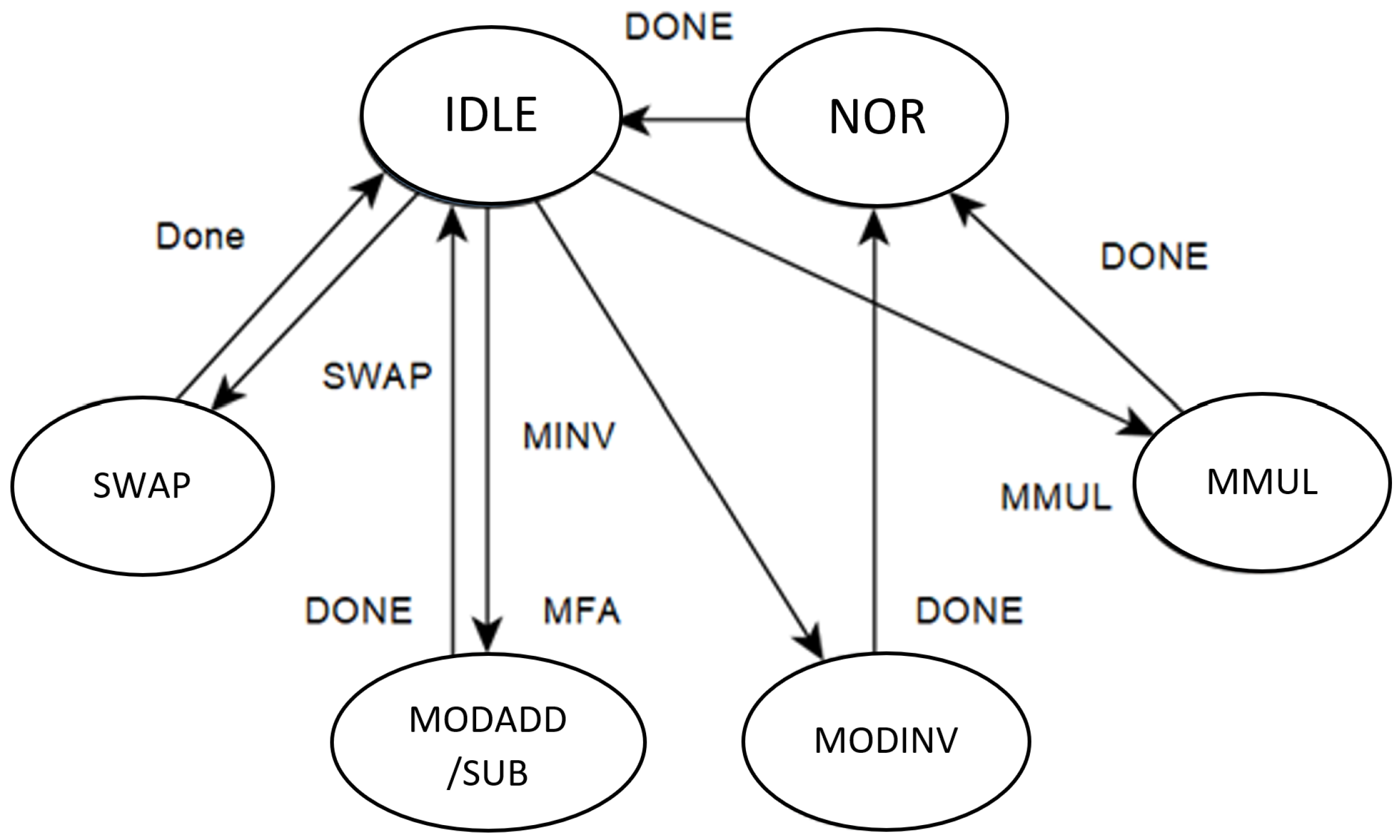
Figure 6 shows the structural diagram of the ECU, and Figure 7 presents the controller state machine of the ECU. For modular addition, subtraction, and swap state, the state machine starts the corresponding operation based on the mode selection signal and returns when the module finishes. A normalized (NOR) state is needed for modular inverse and multiplication before returning the result. The normalized state removes the excess $R^{-2}$ from Montgomery multiplication and inversion. Because the ECU affects the critical path of the design heavily, we try to optimize our design on each operation unit of the ECU carefully. Every operation of the ECU is for 256-bit operands and uses a constant-time algorithm to prevent side-channel attacks.

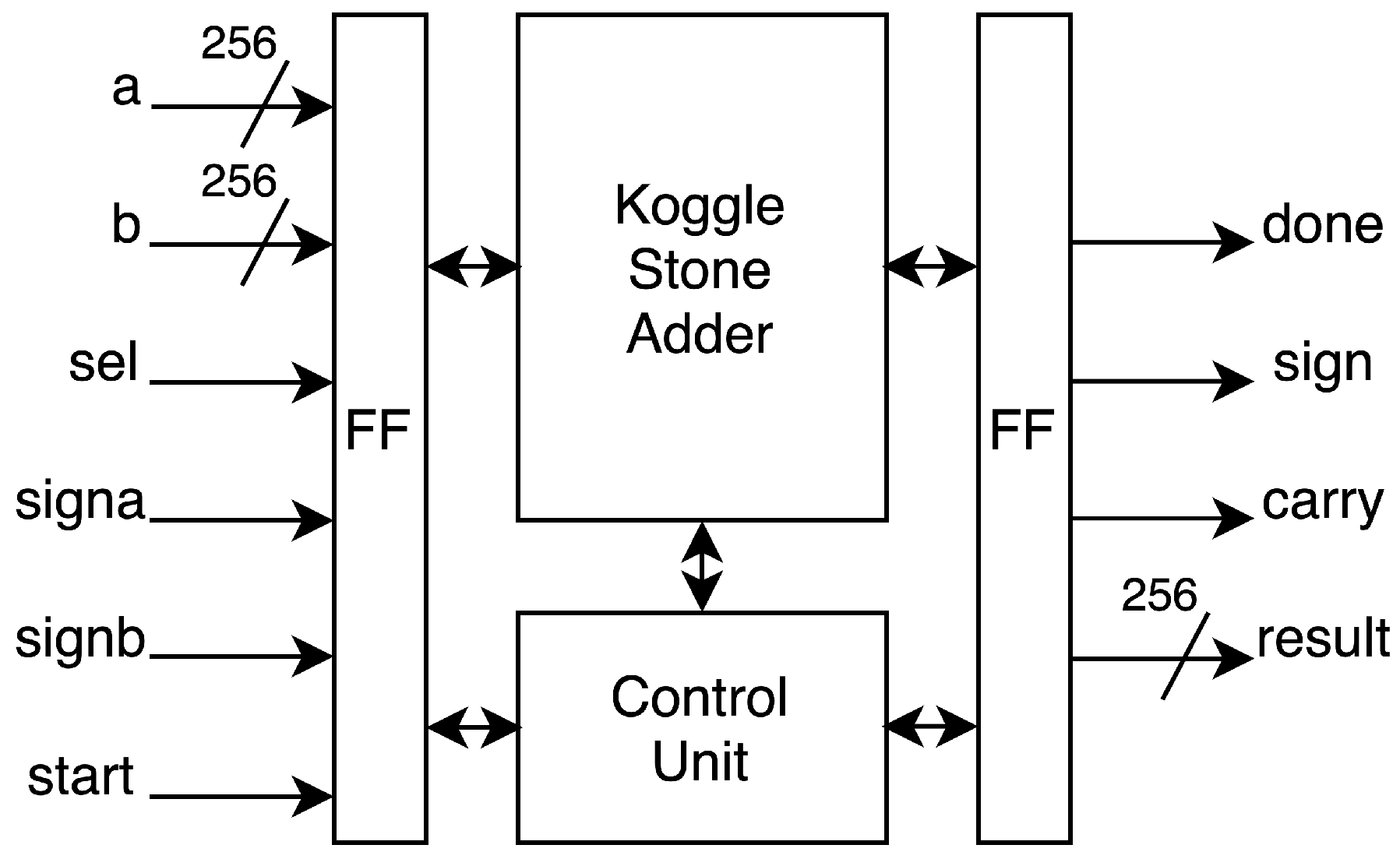
3.5. Modular Adder and Subtractor

To optimize timing for the 256-bit modular adder and subtractor, we use a Kogge–Stone adder (KSA) structure. We designed the dual-purpose modular addition and subtraction unit based on the high-radix parallel prefix network modular adder/subtractor proposed by Rogawski et al. [6]. This Koggle–Stone parallel prefix network adder/subtractor (KSA) is appropriate for optimizing operating frequency and pipeline.

The adder receives 256-bit input a and b with two MSBs processed by the controller. The low 256-bit section is the input for KSA. The controller also processes the $sig{n}_a,sig{n}_b,c_1$ and determines the result’s $sig{n}_o$ and $c_o$. Signal $sel$ selects the mode between subtraction and addition. The design has 2 clock latencies. Figure 8 provides the dual-purpose structure packed with a micro finite state machine.

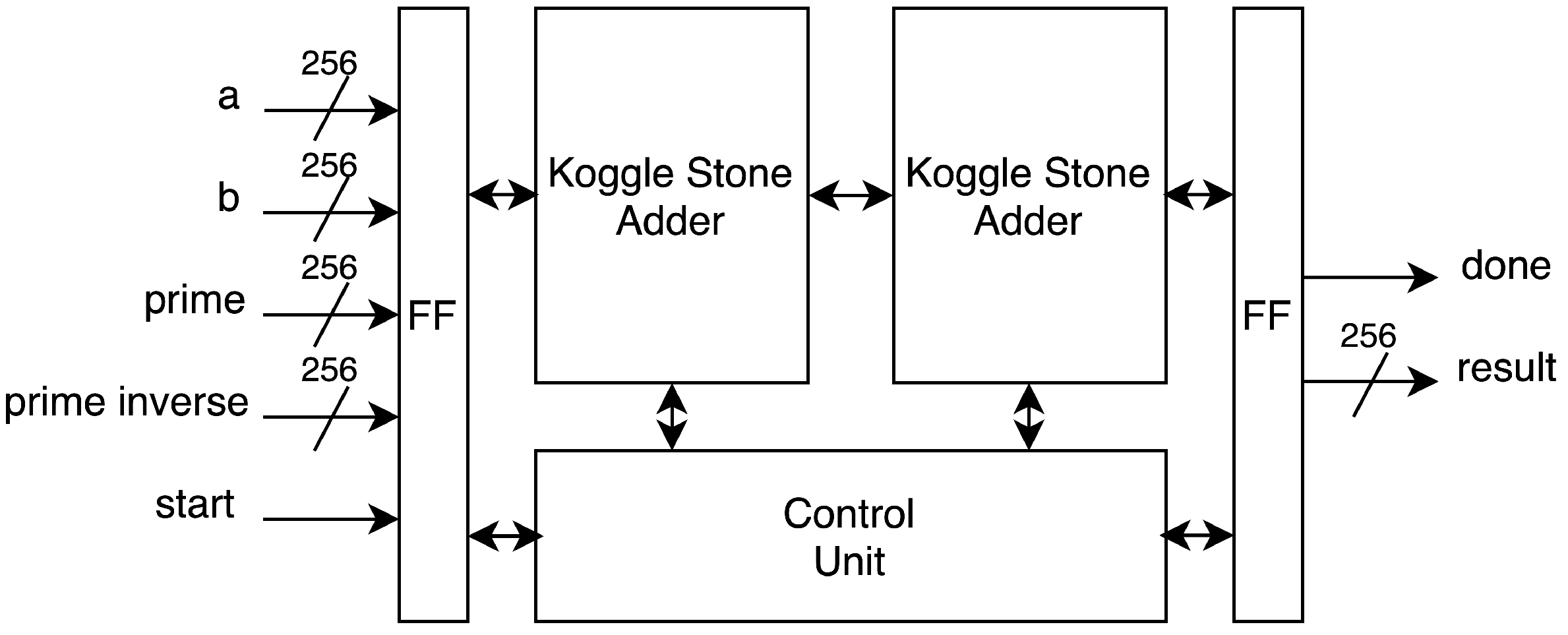
3.6. Montgomery Multiplication

For modular multiplication, we utilize radix-2 Montgomery modular multiplication, as proposed by Xiao et al. [8], but modified with KSAs instead of 256-bit regular adders for high performance. Algorithm 2 shows the Montgomery modular multiplication used in the proposed design.

The hardware design for the Montgomery multiplication architecture uses the referenced algorithm with $uk=1,u=k=1$, which uses the mux and carry load adder and the shift register to compute the values of S through each loop. $S_{ij}$ computation uses 16-bit adders. $R=2^{256}$ is a constant. It has a 256-bit input port for the Multiplicand and Multiplier a and b and the prime and pre-calculated inverse prime number. The start signal starts the operation. It completes the multiplication after 256 loops and outputs the 256-bit result and a done signal. Figure 9 shows the structural diagram.

Algorithm 2 Montgomery modular multiplication

1: Input: $A={\sum }_{i=0}^{i=k-1}{a}_i{2}^i$, $B={\sum }_{i=0}^{i=k-1}{b}_i{2}^i$, $M={\sum }_{i=0}^{i=k-1}{m}_i{2}^i$, $M^{\prime }=inverse(M,2^k)$ 2: Output:  $AB{R}^{-1}modMwithR=2^k$ 3: $S=0$ 4: for ($i=0$ to $n-1$) do 5:    $S=S+b\left[i\right]\ast A$ 6:    $q_i=(\left(Smod2\right)\ast M’)mod2;$ 7:    $S=(S+q_i\ast N)/2;$ 8: end for 9: return  S

3.7. Montgomery Inversion

We design the modular inversion block based on the constant-time binary extended Euclidean algorithm proposed by Savacs [31], with modifications including Koggle–Stone adders and optimized control logic. It consists of three consecutive Koggle–Stone adder blocks (DELTA_UV, DELTA_RS, and SIGMA) performing arithmetic operations. An INV_CONTROL finite state machine controls the sequencing and operations of the DELTA_UV, DELTA_RS, and SIGMA blocks.

The algorithm computes the modular inversion result within 512 iterations, with the calculation time depending on the length of our prime value.

Figure 10 shows the structural diagram of the Montgomery inversion unit. It uses a 256-bit data input. The start signal starts the unit and resets the count from the controller to 512 loops, with $u=v=r=s=0$. We check for stage jumping between the second and eighth computation steps at each iteration. At each computationstep, delta_uv, delta_rs, and sigma are calculated sequentially. After one iteration, the value is stored and looped back until the counter reaches 0. The output is a 256-bit result and done signal.

4. Results

We used Python on Google Colab with RFC 7748 [24] and High-Assurance Cryptographic Library (HACL) [32] to build the testing environment for our design. Testing was performed with Known Answer Test (KAT) from the mentioned standards. The design was tested in the simulation environment. The simulation results show that it ran correctly for the cases outlined in the KAT of the standard ECDHE with Curve25519 from [24].

We synthesized our design on Vivado and implemented it on Xilinx Artix-7. Our design achieved a speed of 102 MHz, computing ECDHE key generation and computation in 110 thousand clock cycles. The resource utilization report shows 6409 Slice usage, zero digital signal processors (DSPs), and four block random access memories (BRAMs). Additional information regarding the resource utilization of key internal modules is provided in

Table 3. Resource consumption of internal modules.

Module	Slice LUTs	Slice Registers	Slice	Block RAM Tile
ECC Core	18,427	21,710	6409	4
Interface controller	34	52	20	0
Tri-phase controller	2136	1555	832	4
Elliptic compute unit	16,257	20,100	5794	0
Modular adder and subtractor	2324	4086	1144	0
Montgomery multiplication	3778	4814	1573	0
Montgomery inversion	10,155	11,200	3253	0

. Xilinx Power Estimator estimated the design power consumption at $117\mathrm{m}\mathrm{W}$. After 1.1 $\mathrm{m}\mathrm{s}$, the design finished the scalar multiplication operation. The value was calculated from the number of cycles it took to complete the operation times the speed of the design.

5. Discussion

To comprehensively evaluate the efficiency of our proposed hardware architecture designed for elliptic-curve Diffie–Hellman ephemeral (ECDHE) operations on the 256-bit Montgomery Curve25519, we present a comparative analysis to relevant prior works, as summarized in

Table 4. Comparison of resource utilization and latency with related works.

	Slices	DSP	BRAM	Frequency (MHz)	Latency (ms)	Power (mW)	$\mathit{A}\times \mathit{T}$
[16]	12.9 K	0	0	137.5	0.28	236 1	3.6 2
[14]	21 K	260	0	115	0.12	789 1	21.8 2
[15]	17.9 K	175	0	115	0.12	709 1	15.2 2
[20] [a]	7.4 K	0	0	122.8	2.44	-	18.0 2
[20] [b]	5.5 K	0	0	122.8	2.44	-	13.42 2
[20] [c]	6.6 K	0	0	105.9	2.83	-	18.7 2
[20] [d]	8.7 K	0	0	76.31	3.93	-	34.2 2
[21]	3 K	0	0	78	2.81 3	-	8.43 2
This work	6.4 K	0	4	102	1.1	117 1	7.04 2

Note: ¹ Estimated with Xillinx Power Estimator. ² DSP is estimated as 619 Slices [20]. BRAM resources are ignored. ³ Estimated from Throughputs. [a] Kudithi et al.’s implementation on Kintex-7 FPGA. [b] Kudithi et al.’s implementation on Virtex-7 FPGA. [c] Kudithi et al.’s implementation on Virtex-6 FPGA. [d] Kudithi et al.’s implementation on Virtex-5 FPGA.

. The table shows resource utilization (in Slice(s), DSP(s), BRAM(s), latency, and power consumption. To better compare to the previous result, we use a figure of merit called $A\times T$, or area × time, where the area is in kSlices and time is the latency in $\mathrm{m}\mathrm{s}$, as shown in Equation (2), which is normalized to our proposed design.

$$A\times T=Area\left(kSlice\right)\ast Time\left(Latencyin\mathrm{m}\mathrm{s}\right)$$

(2)

Our architecture has advantages in terms of resource utilization and power efficiency. With a reduced utilization of 6414 slices and four Block RAMs (BRAM), we achieved a clock frequency of 102 MHz. The latency of 1100 $\mathsf{\mu }$s is competitive among the listed works, even though it may be slightly higher than some implementations. The problem with using only BRAM to store data and temporary values is that it increases the latency with each ECU read-and-write operation.

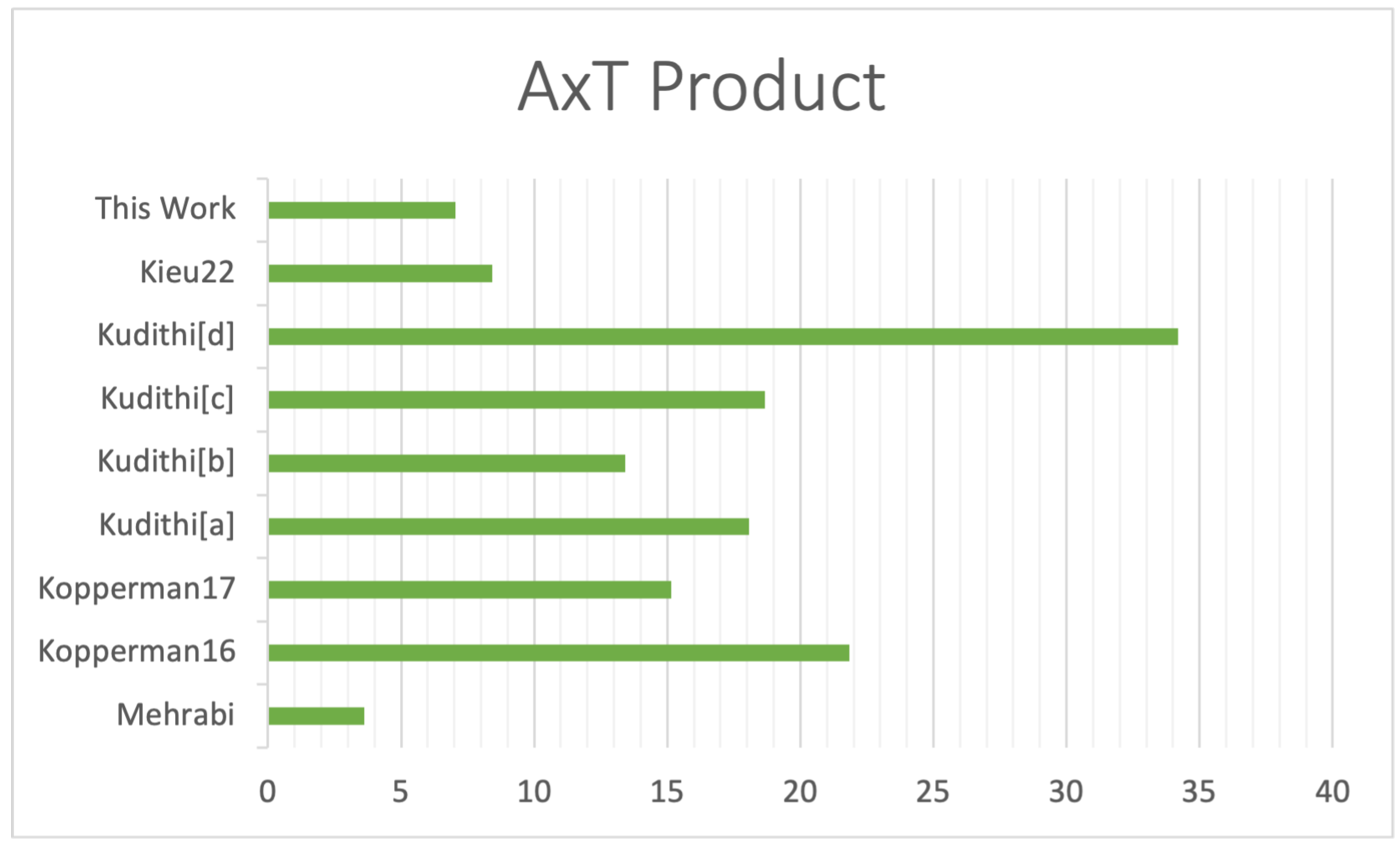
Figure 11 shows the $A\times T$ products of our work and other implementations. Mehrabi et al. [16] presented a multiple multipliers implementation that commanded a higher allocation of resources and higher power usage compared to our design. However, their design did not use any BRAM, achieving a better latency and a higher $A\times T$ product than ours. However, in terms of power consumption, our design consumes only half of the power estimation. Our work’s $A\times T$ product is better than the other designs. Koppermann et al. [14,15] provided high-performance implementation with heavy DSP usage to improve their latency compared to our design, so their area factor is higher when comparing $A\times T$ values. Different implementations of [20] use the radix-2 multiplier for modular operation, achieving a good area utilization result but slower latency than ours. The design in [21] is the smallest hardware implementation in terms of area that supports Curve25519; however, they used the multiple carry saves adder to perform arithmetic operations, so their design speed was considerably slow.

While a higher clock frequency was employed in some prior works to achieve lower latencies, our approach strives for a balance between performance and energy consumption. Our architecture demonstrates efficient resource usage, making it well-suited for scenarios that prioritize secure communication and cryptographic key exchange without sacrificing substantial power resources. Our design proves to be better suited when considering lightweight FPGA and ASIC configurations devoid of DSP blocks.

The security of IoT devices is an important consideration when implementing system designs. As Di Matteo et al. [33] and Zulberti et al. [34] discussed, side-channel attacks, such as simple power analysis (SPA) and differential power analysis (DPA), on cryptographic hardware pose a significant threat. While side-channel attack countermeasures are crucial for comprehensive IoT security, an in-depth examination is beyond the scope of this paper. Our implementation focuses instead on core functionality and performance, with security considerations noted as crucial future work.

6. Conclusions

This paper introduces an efficient hardware architecture for the execution of elliptic-curve Diffie–Hellman ephemeral (ECDHE) on the 256-bit Montgomery elliptic curves, Curve25519. We introduce optimized FSMs and a structured approach to modular computation units in the design to enhance performance and resource utilization. Compared to related works, our design offers a compelling solution that balances computational power proficiency and optimized resource allocation. In future research, the latency of our design can be further improved by reducing the finite state machine overhead, implementing a register-based approach, and accessing RAM only when necessary. This approach has the potential to significantly reduce the existing latency, making our design more competitive compared to other reference implementations.