Design of Generalized Enhanced Static Segment Multiplier with Minimum Mean Square Error for Uniform and Nonuniform Input Distributions
Abstract
1. Introduction
2. Static Segment Method
2.1. Static Segment Multiplier and Correction Technique
2.2. Enhanced SSM Multiplier
3. Proposed Generalized ESSM Multiplier
3.1. Hardware Implementation
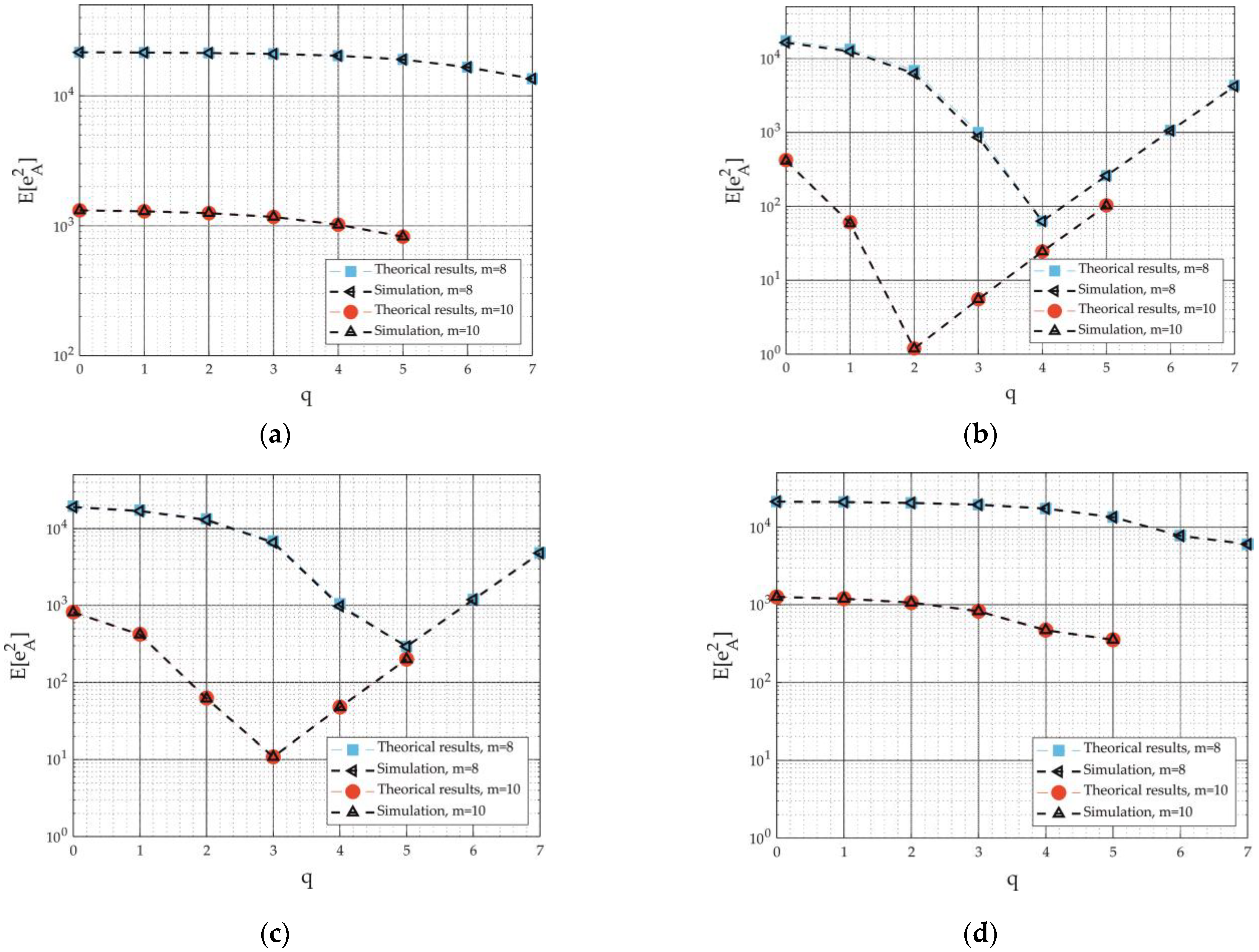
3.2. Minimization of the Mean Square Approximation Error
4. Results
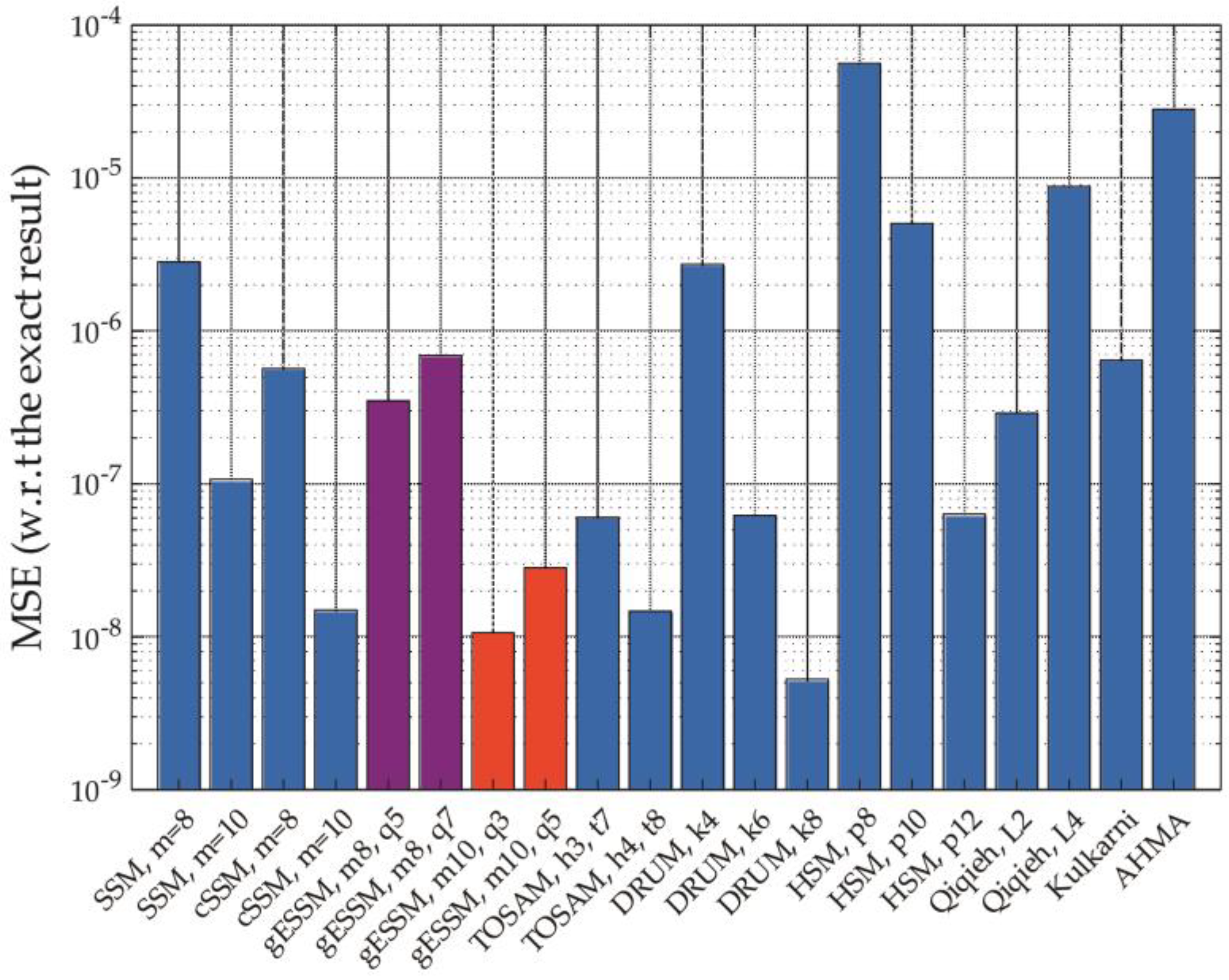
4.1. Assessment of Accuracy
4.2. Hardware Implementation Results
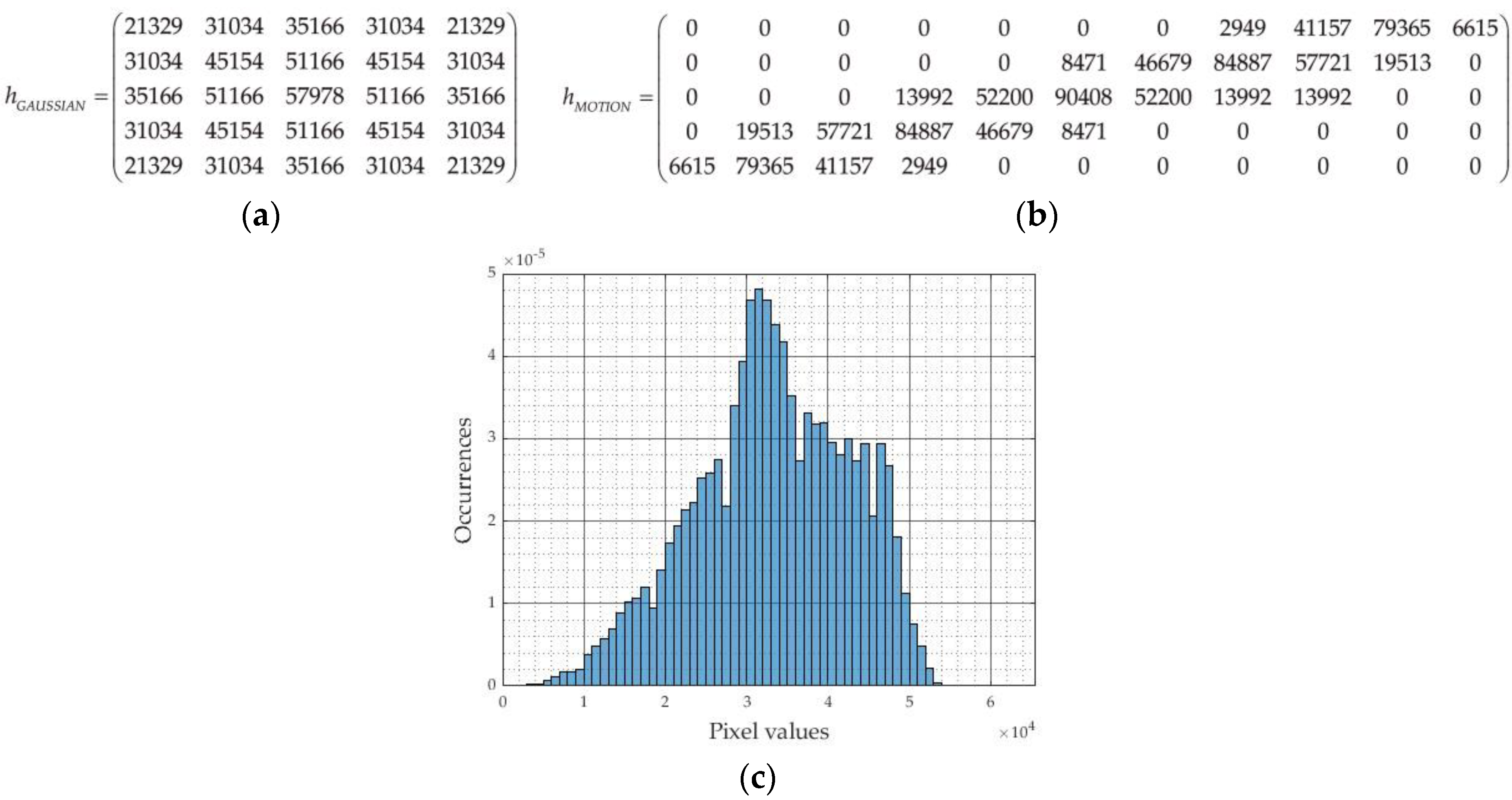
4.3. Image Processing Application
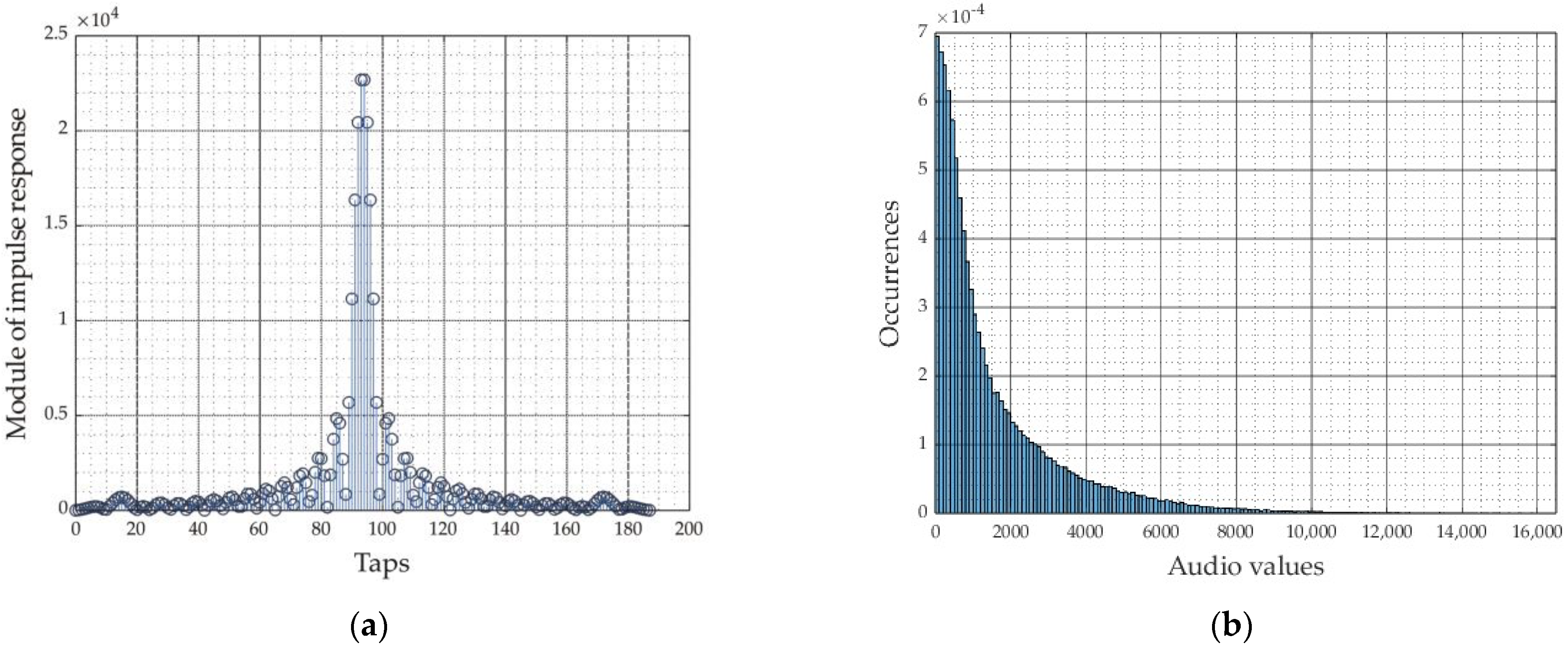
4.4. Audio Application
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Spagnolo, F.; Perri, S.; Corsonello, P. Approximate Down-Sampling Strategy for Power-Constrained Intelligent Systems. IEEE Access 2022, 10, 7073–7081. [Google Scholar] [CrossRef]
- Vaverka, F.; Mrazek, V.; Vasicek, Z.; Sekanina, L. TFApprox: Towards a Fast Emulation of DNN Approximate Hardware Accelerators on GPU. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 294–297. [Google Scholar] [CrossRef]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Adam, H.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2704–2713. [Google Scholar] [CrossRef]
- Montanari, D.; Castellano, G.; Kargaran, E.; Pini, G.; Tijani, S.; De Caro, D.; Strollo, A.G.M.; Manstretta, D.; Castello, R. An FDD Wireless Diversity Receiver With Transmitter Leakage Cancellation in Transmit and Receive Bands. IEEE J. Solid State Circuits 2018, 53, 1945–1959. [Google Scholar] [CrossRef]
- Kiayani, A.; Waheed, M.Z.; Antilla, L.; Abdelaziz, M.; Korpi, D.; Syrjala, V.; Kosunen, M.; Stadius, K.; Ryynamen, J.; Valkama, M. Adaptive Nonlinear RF Cancellation for Improved Isolation in Simultaneous Transmit–Receive Systems. IEEE Trans. Microw. Theory Tech. 2018, 66, 2299–2312. [Google Scholar] [CrossRef]
- Zhang, T.; Su, C.; Najafi, A.; Rudell, J.C. Wideband Dual-Injection Path Self-Interference Cancellation Architecture for Full-Duplex Transceivers. IEEE J. Solid State Circuits 2018, 53, 1563–1576. [Google Scholar] [CrossRef]
- Di Meo, G.; De Caro, D.; Saggese, G.; Napoli, E.; Petra, N.; Strollo, A.G.M. A Novel Module-Sign Low-Power Implementation for the DLMS Adaptive Filter With Low Steady-State Error. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 297–308. [Google Scholar] [CrossRef]
- Meher, P.K.; Park, S.Y. Critical-Path Analysis and Low-Complexity Implementation of the LMS Adaptive Algorithm. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 778–788. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, L.; Jonker, P.P.; Elliott, D.G.; Lombardi, F.; Han, J. A High-Performance and Energy-Efficient FIR Adaptive Filter Using Approximate Distributed Arithmetic Circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 313–326. [Google Scholar] [CrossRef]
- Esposito, D.; Di Meo, G.; De Caro, D.; Strollo, A.G.M.; Napoli, E. Quality-Scalable Approximate LMS Filter. In Proceedings of the 2018 25th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Bordeaux, France, 9–12 December 2018; pp. 849–852. [Google Scholar] [CrossRef]
- Di Meo, G.; De Caro, D.; Petra, N.; Strollo, A.G.M. A Novel Low-Power High-Precision Implementation for Sign–Magnitude DLMS Adaptive Filters. Electronics 2022, 11, 1007. [Google Scholar] [CrossRef]
- Bruschi, V.; Nobili, S.; Terenzi, A.; Cecchi, S. A Low-Complexity Linear-Phase Graphic Audio Equalizer Based on IFIR Filters. IEEE Signal Process. Lett. 2021, 28, 429–433. [Google Scholar] [CrossRef]
- Kulkarni, P.; Gupta, P.; Ercegovac, M. Trading Accuracy for Power with an Underdesigned Multiplier Architecture. In Proceedings of the 2011 24th Internatioal Conference on VLSI Design, Chennai, India, 2–7 January 2011; pp. 346–351. [Google Scholar] [CrossRef]
- Zervakis, G.; Tsoumanis, K.; Xydis, S.; Soudris, D.; Pekmestzi, K. Design-Efficient Approximate Multiplication Circuits Through Partial Product Perforation. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 3105–3117. [Google Scholar] [CrossRef]
- Zacharelos, E.; Nunziata, I.; Saggese, G.; Strollo, A.G.M.; Napoli, E. Approximate Recursive Multipliers Using Low Power Building Blocks. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1315–1330. [Google Scholar] [CrossRef]
- Qiqieh, I.; Shafik, R.; Tarawneh, G.; Sokolov, D.; Yakovlev, A. Energy-efficient approximate multiplier design using bit significance-driven logic compression. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 7–12. [Google Scholar] [CrossRef]
- Esposito, D.; Strollo, A.G.M.; Alioto, M. Low-power approximate MAC unit. In Proceedings of the 2017 13th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Giardini Naxos-Taormina, Italy, 12–15 June 2017; pp. 81–84. [Google Scholar] [CrossRef]
- Fritz, C.; Fam, A.T. Fast Binary Counters Based on Symmetric Stacking. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 2971–2975. [Google Scholar] [CrossRef]
- Ahmadinejad, M.; Moaiyeri, M.H.; Sabetzadeh, F. Energy and area efficient imprecise compressors for approximate multiplication at nanoscale. Int. J. Electron. Commun. 2019, 110, 152859. [Google Scholar] [CrossRef]
- Yang, Z.; Han, J.; Lombardi, F. Approximate compressors for error-resilient multiplier design. In Proceedings of the 2015 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFTS), Amherst, MA, USA, 12–14 October 2015; pp. 183–186. [Google Scholar] [CrossRef]
- Ha, M.; Lee, S. Multipliers With Approximate 4–2 Compressors and Error Recovery Modules. IEEE Embed. Syst. Lett. 2018, 10, 6–9. [Google Scholar] [CrossRef]
- Strollo, A.G.M.; Napoli, E.; De Caro, D.; Petra, N.; Meo, G.D. Comparison and Extension of Approximate 4-2 Compressors for Low-Power Approximate Multipliers. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3021–3034. [Google Scholar] [CrossRef]
- Park, G.; Kung, J.; Lee, Y. Design and Analysis of Approximate Compressors for Balanced Error Accumulation in MAC Operator. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2950–2961. [Google Scholar] [CrossRef]
- Kong, T.; Li, S. Design and Analysis of Approximate 4–2 Compressors for High-Accuracy Multipliers. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 1771–1781. [Google Scholar] [CrossRef]
- Jou, J.M.; Kuang, S.R.; Chen, R.D. Design of low-error fixed-width multipliers for DSP applications. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1999, 46, 836–842. [Google Scholar] [CrossRef]
- Petra, N.; De Caro, D.; Garofalo, V.; Napoli, E.; Strollo, A.G.M. Design of Fixed-Width Multipliers With Linear Compensation Function. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 947–960. [Google Scholar] [CrossRef]
- Hashemi, S.; Bahar, R.I.; Reda, S. DRUM: A Dynamic Range Unbiased Multiplier for approximate applications. In Proceedings of the 2015 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Austin, TX, USA, 2–6 November 2015; pp. 418–425. [Google Scholar] [CrossRef]
- Vahdat, S.; Kamal, M.; Afzali-Kusha, A.; Pedram, M. TOSAM: An Energy-Efficient Truncation- and Rounding-Based Scalable Approximate Multiplier. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 1161–1173. [Google Scholar] [CrossRef]
- Narayanamoorthy, S.; Moghaddam, H.A.; Liu, Z.; Park, T.; Kim, N.S. Energy-Efficient Approximate Multiplication for Digital Signal Processing and Classification Applications. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 1180–1184. [Google Scholar] [CrossRef]
- Strollo, A.G.M.; Napoli, E.; De Caro, D.; Petra, N.; Saggese, G.; Di Meo, G. Approximate Multipliers Using Static Segmentation: Error Analysis and Improvements. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 2449–2462. [Google Scholar] [CrossRef]
- Li, L.; Hammad, I.; El-Sankary, K. Dual segmentation approximate multiplier. Electron. Lett. 2021, 57, 718–720. [Google Scholar] [CrossRef]
- GitHub. Available online: https://github.com/scale-lab/DRUM (accessed on 18 April 2020).
- GitHub. Available online: https://github.com/astrollo/SSM (accessed on 16 February 2020).
- DataShare. Available online: https://datashare.ed.ac.uk/handle/10283/2791 (accessed on 21 August 2017).

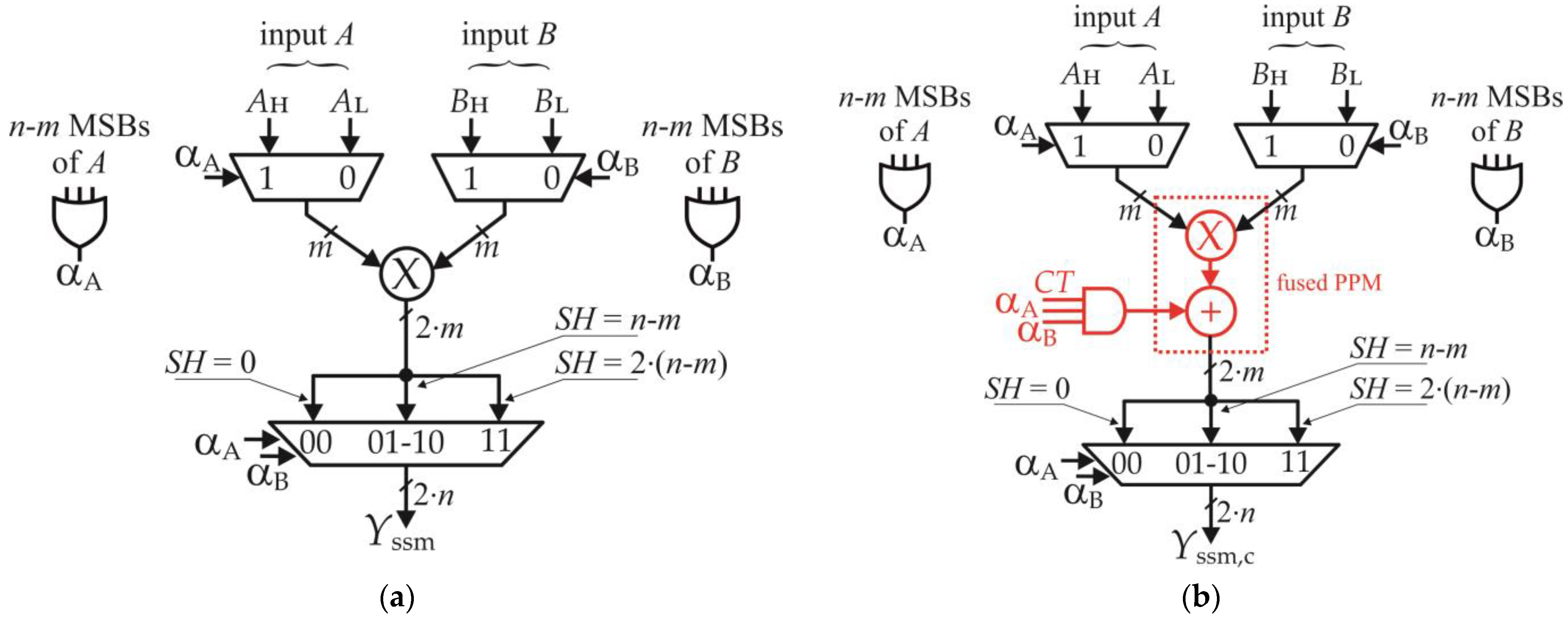
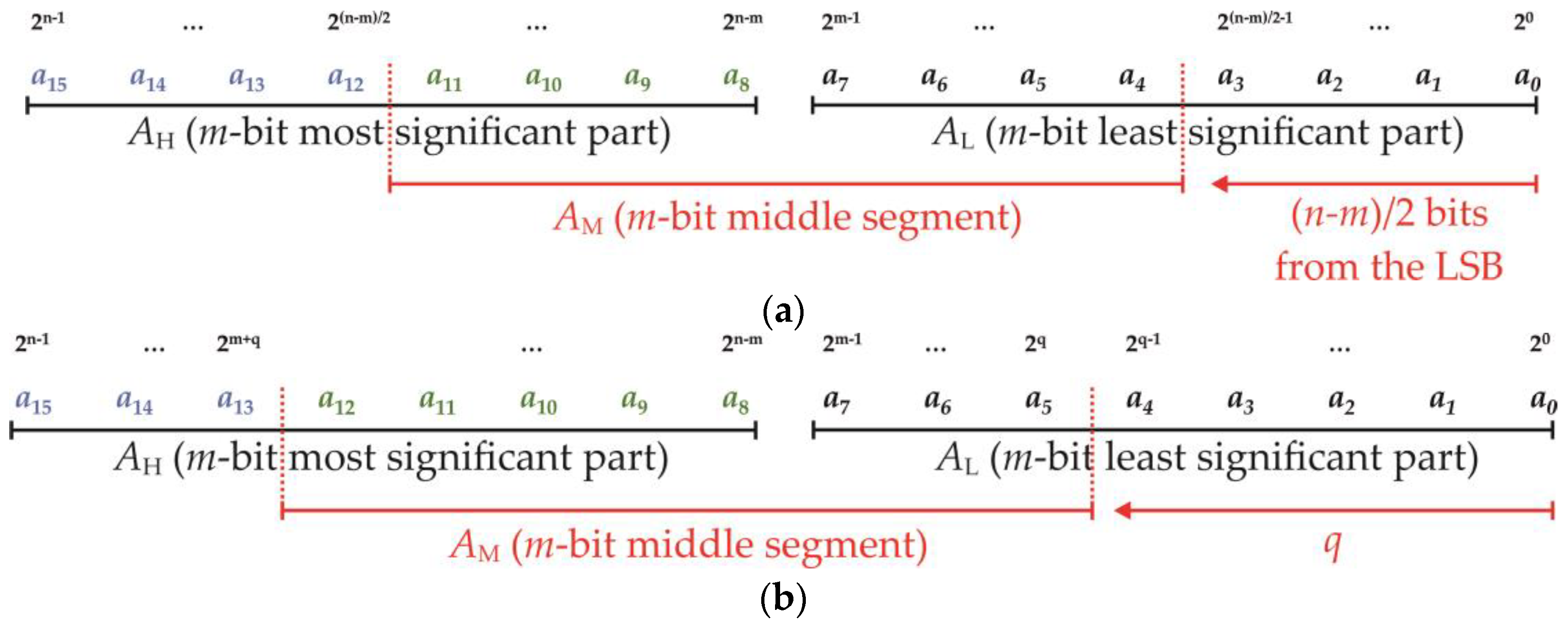
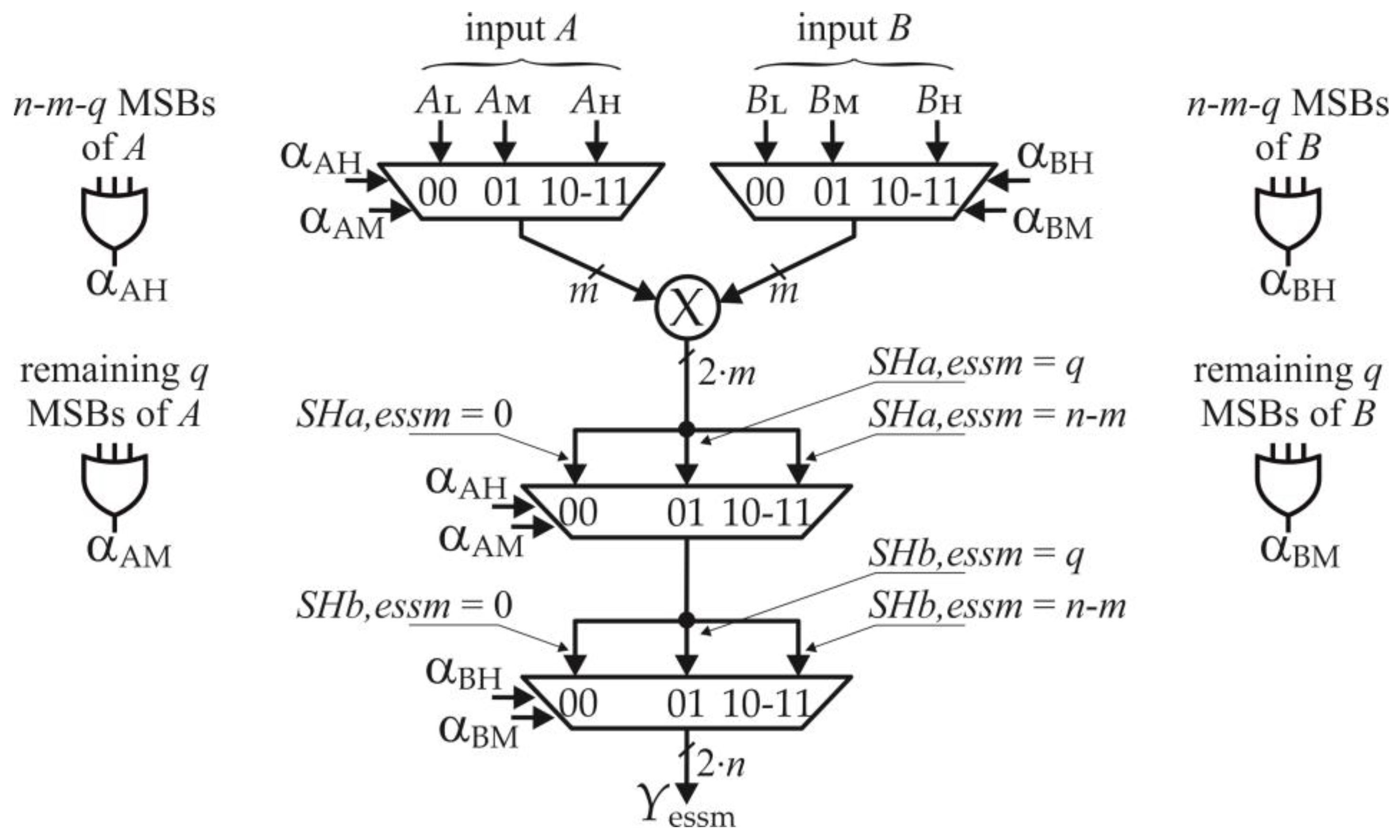



| αAH, αAM, αBH, αBM | SHessm |
|---|---|
| (0000) | 0 |
| (0001), (0100) | (n − m)/2 |
| (0010), (0011), (0101), (1000), (1100) | n − m |
| (0110), (0111), (1001), (1101) | (3/2)·(n − m) |
| (1010), (1011), (1110), (1111) | 2·(n –m) |
| αAH, αAM, αBH, αBM | SHessm |
| (0000) | 0 |
| (0001), (0100) | q |
| (0101) | 2·q |
| (0010), (0011), (1000), (1100) | n − m |
| (0110), (0111), (1001), (1101) | n − m + q |
| (1010), (1011), (1110), (1111) | 2·(n − m) |
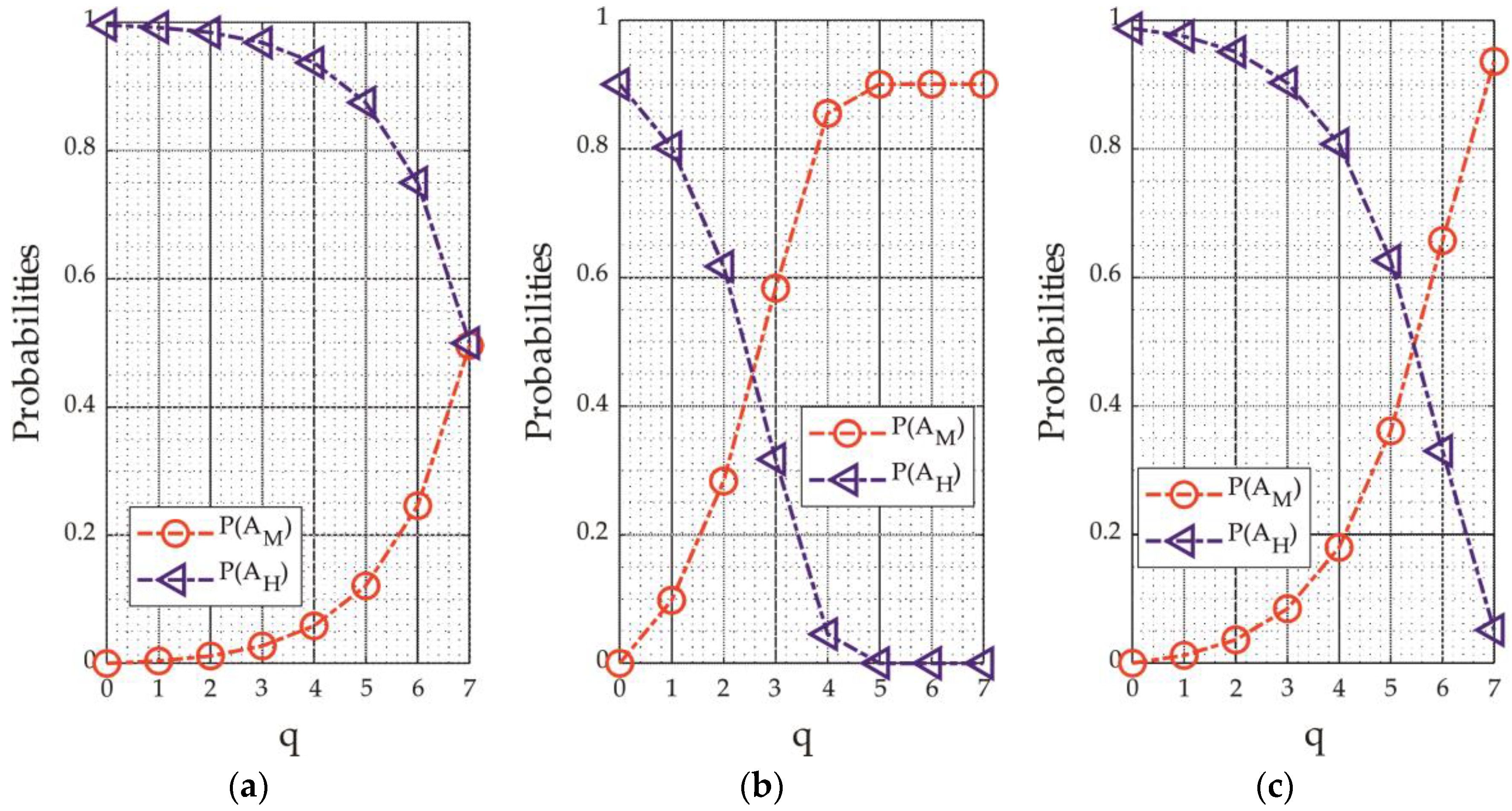
| Input Stochastic Distribution | P(AM) | P(AH) |
|---|---|---|
| Uniform | ||
| Half-normal |
| Multiplier | Uniform Distribution | Half-Normal Distribution (σ = 2048) | |||||
|---|---|---|---|---|---|---|---|
| NMED | MRED | NoEB | NMED | MRED | NoEB | ||
| SSM [29] | m = 8 | 1.93 ×·10−3 | 2.08 × 10−2 | 8.8 | 8.29 × 10−5 | 1.87 × 10−1 | 13.1 |
| m = 10 | 4.73 × 10−4 | 3.99 × 10−3 | 10.8 | 1.46 × 10−5 | 1.96 × 10−2 | 15.3 | |
| cSSM [30] | m = 8 | 6.70 × 10−4 | 9.49 × 10−3 | 10.2 | 8.28 × 10−5 | 1.87 × 10−1 | 13.1 |
| m = 10 | 1.63 × 10−4 | 1.73 × 10−3 | 12.2 | 1.46 × 10−5 | 1.96 × 10−2 | 15.3 | |
| TOSAM [28] | h = 3 | 2.69 × 10−3 | 1.05 × 10−2 | 7.8 | 6.24 × 10−6 | 9.98 × 10−3 | 16.4 |
| h = 4 | 1.34 × 10−3 | 5.27 × 10−3 | 8.8 | 3.13 × 10−6 | 5.02 × 10−3 | 17.3 | |
| DRUM [27] | k = 4 | 1.41 × 10−2 | 5.89 × 10−2 | 5.5 | 3.85 × 10−5 | 6.20 × 10−2 | 13.7 |
| k = 6 | 3.51 × 10−3 | 1.46 × 10−2 | 7.5 | 9.53 × 10−6 | 1.52 × 10−2 | 15.7 | |
| k = 8 | 8.82 × 10−4 | 3.66 × 10−3 | 9.5 | 2.39 × 10−6 | 3.68 × 10−3 | 17.7 | |
| HSM [31] | p = 8 | 1.47 × 10−2 | 1.03 × 10−1 | 5.5 | 3.53 × 10−4 | 7.05 × 10−1 | 11.0 |
| p = 10 | 7.15 × 10−3 | 3.72 × 10−2 | 6.5 | 1.02 × 10−4 | 1.70 × 10−1 | 12.3 | |
| p = 12 | 3.51 × 10−3 | 1.56 × 10−2 | 7.5 | 9.76 × 10−6 | 3.92 × 10−2 | 15.7 | |
| Qiqieh [16] | L = 2 | 2.43 × 10−4 | 2.88 × 10−3 | 11.0 | 1.90 × 10−5 | 3.27 × 10−2 | 14.0 |
| L = 4 | 1.12 × 10−2 | 5.90 × 10−2 | 5.7 | 5.78 × 10−5 | 8.35 × 10−2 | 12.8 | |
| Kulkarni [13] | 1.39 × 10−2 | 3.32 × 10−2 | 4.7 | 1.28 × 10−5 | 1.74 × 10−2 | 14.1 | |
| AHMA [19] | 2.14 × 10−2 | 1.18 × 10−1 | 4.9 | 1.65 × 10−4 | 2.42 × 10−1 | 11.3 | |
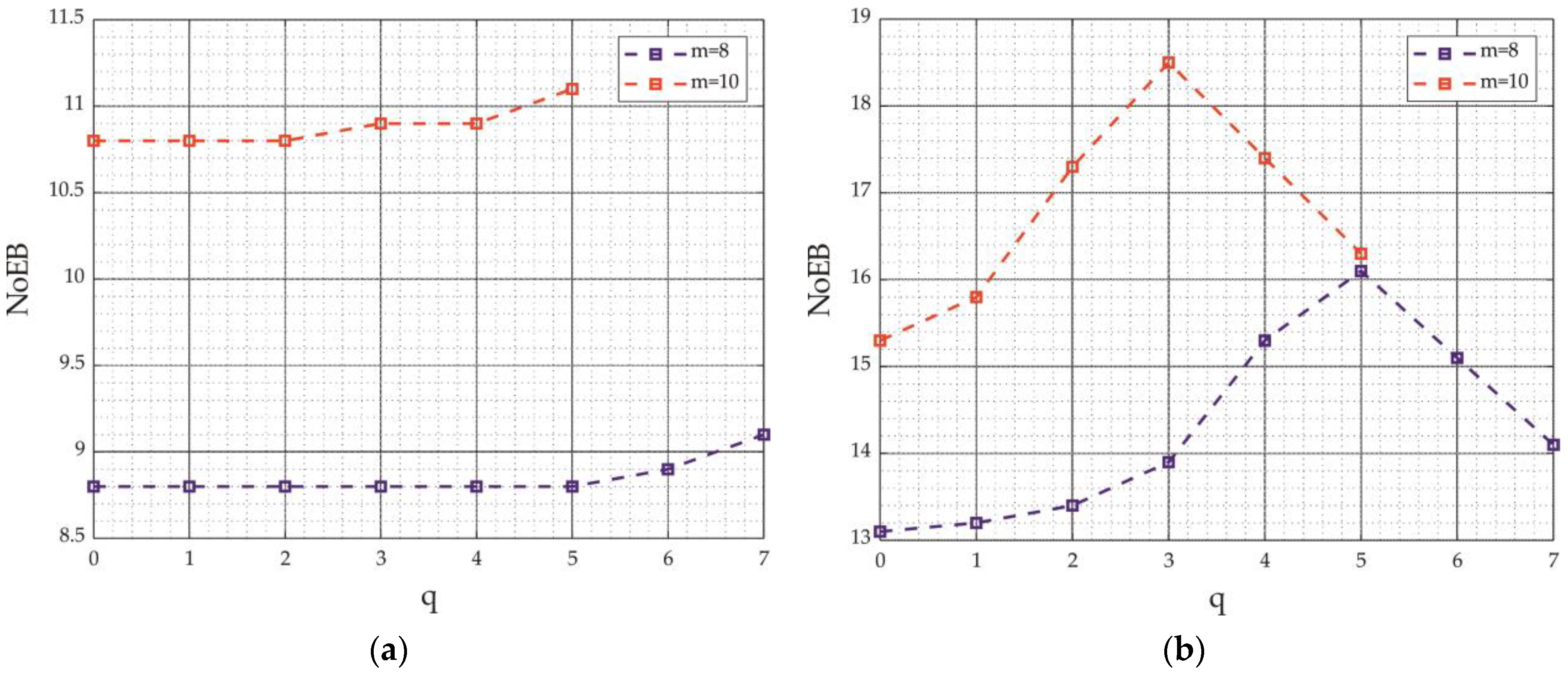
| gESSM | m = 8, q = 5 | 1.73 × 10−3 | 9.68 × 10−3 | 8.8 | 1.06 × 10−5 | 2.55 × 10−2 | 16.1 |
| m = 8, q = 7 | 1.45 × 10−3 | 1.19 × 10−2 | 9.1 | 4.24 × 10−5 | 9.93 × 10−2 | 14.1 | |
| m = 10, q = 3 | 4.26 × 10−4 | 2.22 × 10−3 | 10.9 | 1.64 × 10−6 | 2.21 × 10−3 | 18.5 | |
| m = 10, q = 5 | 3.55 × 10−4 | 2.30 × 10−3 | 11.1 | 7.24 × 10−6 | 9.73 × 10−3 | 16.3 | |
| Multiplier | Minimum Delay [ps] | Area [µm2] | Equivalent NAND Count | Power @1GHz (Uniform Input) | Power @1GHz (Half-Normal Input) | |
|---|---|---|---|---|---|---|
| Exact | 336 | 791.3 | 1256 | 1300.3 | 721.8 | |
| SSM [29] | m = 8 | 272 (−19.0%) | 190.1 (−76.0%) | 302 | 201.4 (−84.5%) | 77.6 (−89.2%) |
| m = 10 | 313 (−6.8%) | 308.6 (−61.0%) | 490 | 346.8 (−73.3%) | 281.8 (−61.0%) | |
| cSSM [30] | m = 8 | 272 (−19.0%) | 197.4 (−75.0%) | 313 | 214.7 (−83.5%) | 85.6 (−88.1%) |
| m = 10 | 313 (−6.8%) | 352.3 (−55.5) | 559 | 395.0 (−69.6%) | 358.6 (−50.3%) | |
| TOSAM [28] | h = 3 | 311 (−7.4%) | 341.2 (−56.9%) | 542 | 367.1 (−71.8%) | 394.5 (−45.3%) |
| h = 4 | 335 (−0.3%) | 494.9 (−37.4%) | 786 | 582.4 (−55.2%) | 613.5 (−15.0%) | |
| DRUM [27] | k = 4 | 257 (−23.5%) | 126.5 (−84.0%) | 201 | 155.9 (−88.0%) | 171.8 (−76.2%) |
| k = 6 | 357 (+6.3%) | 241.9 (−69.4%) | 384 | 389.1 (−70.1%) | 377.4 (−47.7%) | |
| k = 8 | 365 (+8.6%) | 414.3 (−47.6%) | 658 | 691.1 (−46.9%) | 656.2 (−9.1%) | |
| HSM [31] | p = 8 | 251 (−25.3%) | 112.9 (−85.7%) | 179 | 137.3 (−89.4%) | 115.7 (−84.0%) |
| p = 10 | 354 (+5.4%) | 204.8 (−74.1%) | 325 | 306.3 (−76.4%) | 339.6 (−53.0%) | |
| p = 12 | 364 (+8.3%) | 347.1 (−56.1%) | 551 | 538.2 (−58.6%) | 582.8 (−19.3%) | |
| Qiqieh [16] | L = 2 | 262 (−22.0%) | 440.8 (−44.3%) | 700 | 578.6 (−55.5%) | 330.9 (−54.2%) |
| L = 4 | 218 (−35.1%) | 271.9 (−65.6%) | 432 | 385.8 (−70.3%) | 241.6 (−66.5%) | |
| Kulkarni [13] | 289 (−14.0%) | 508.9 (−35.7%) | 808 | 620.4 (−52.3%) | 364.7 (−49.5%) | |
| AHMA [19] | 208 (−38.1%) | 282.4 (−64.3%) | 448 | 327.5 (−74.8%) | 252.1 (−65.1%) | |
| gESSM | m = 8, q = 5 | 312 (−7.1%) | 235.6 (−70.2%) | 347 | 289.9 (−77.7%) | 210.63 (−70.8%) |
| m = 8, q = 7 | 293 (−12.8%) | 226.0 (−71.4%) | 359 | 284.4 (−78.1%) | 122.20 (−83.1%) | |
| m = 10, q = 3 | 327 (−2.7%) | 393.4 (−50.3%) | 624 | 510.9 (−60.7%) | 524.8 (−27.3%) | |
| m = 10, q = 5 | 329 (−2.1%) | 420.2 (−46.9%) | 667 | 602.0 (−53.7%) | 494.6 (−31.5%) |
| Multiplier | Gaussian Filter | Motion Filter | Average | ||||
|---|---|---|---|---|---|---|---|
| SSIM | PSNR (dB) | SSIM | PSNR (dB) | SSIM | PSNR (dB) | ||
| SSM [29] | m = 8 | 1.000 | 42.6 | 1.000 | 42.7 | 1.000 | 42.6 |
| m = 10 | 1.000 | 53.4 | 1.000 | 55.2 | 1.000 | 54.3 | |
| cSSM [30] | m = 8 | 1.000 | 58.4 | 1.000 | 54.7 | 1.000 | 56.5 |
| m = 10 | 1.000 | 68.5 | 1.000 | 67.6 | 1.000 | 68.0 | |
| TOSAM [28] | h = 3 | 1.000 | 48.8 | 0.999 | 54.8 | 0.999 | 51.8 |
| h = 4 | 1.000 | 63.9 | 1.000 | 63.4 | 1.000 | 63.7 | |
| DRUM [27] | k = 4 | 0.984 | 35.7 | 0.980 | 37.9 | 0.982 | 36.8 |
| k = 6 | 0.999 | 51.7 | 0.999 | 48.9 | 0.999 | 50.3 | |
| k = 8 | 1.000 | 64.8 | 1.000 | 62.8 | 1.000 | 63.8 | |
| HSM [31] | p = 8 | 0.982 | 35.7 | 0.978 | 36.0 | 0.980 | 35.8 |
| p = 10 | 0.996 | 45.2 | 0.994 | 45.7 | 0.995 | 45.5 | |
| p = 12 | 0.999 | 51.7 | 0.999 | 48.9 | 0.999 | 50.3 | |
| Qiqieh [16] | L = 2 | 1.000 | 63.9 | 1.000 | 65.0 | 1.000 | 64.5 |
| L = 4 | 0.982 | 32.0 | 0.981 | 31.2 | 0.981 | 31.6 | |
| Kulkarni [13] | 0.993 | 39.2 | 0.997 | 42.6 | 0.995 | 40.9 | |
| AHMA [19] | 0.950 | 25.3 | 0.948 | 25.4 | 0.949 | 25.4 | |
| gESSM | m = 8, q = 5 | 1.000 | 44.4 | 1.000 | 45.5 | 1.000 | 45.0 |
| m = 8, q = 7 | 1.000 | 47.1 | 1.000 | 46.3 | 1.000 | 46.7 | |
| m = 10, q = 3 | 1.000 | 53.7 | 1.000 | 57.4 | 1.000 | 55.5 | |
| m = 10, q = 5 | 1.000 | 60.0 | 1.000 | 60.4 | 1.000 | 60.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Meo, G.; Saggese, G.; Strollo, A.G.M.; De Caro, D. Design of Generalized Enhanced Static Segment Multiplier with Minimum Mean Square Error for Uniform and Nonuniform Input Distributions. Electronics 2023, 12, 446. https://doi.org/10.3390/electronics12020446
Di Meo G, Saggese G, Strollo AGM, De Caro D. Design of Generalized Enhanced Static Segment Multiplier with Minimum Mean Square Error for Uniform and Nonuniform Input Distributions. Electronics. 2023; 12(2):446. https://doi.org/10.3390/electronics12020446
Chicago/Turabian StyleDi Meo, Gennaro, Gerardo Saggese, Antonio G. M. Strollo, and Davide De Caro. 2023. "Design of Generalized Enhanced Static Segment Multiplier with Minimum Mean Square Error for Uniform and Nonuniform Input Distributions" Electronics 12, no. 2: 446. https://doi.org/10.3390/electronics12020446
APA StyleDi Meo, G., Saggese, G., Strollo, A. G. M., & De Caro, D. (2023). Design of Generalized Enhanced Static Segment Multiplier with Minimum Mean Square Error for Uniform and Nonuniform Input Distributions. Electronics, 12(2), 446. https://doi.org/10.3390/electronics12020446







