Joint Dispatching and Cooperative Trajectory Planning for Multiple Autonomous Forklifts in a Warehouse: A Search-and-Learning-Based Approach
Abstract
:1. Introduction
1.1. Related Work
1.1.1. Dispatching Methods for Multiple Forklifts
1.1.2. Cooperative Trajectory Planning Methods for Multiple Forklifts
1.1.3. Joint Dispatching and Planning Methods for Multiple Forklifts
1.2. Motivations
1.3. Contributions
1.4. Organization
2. Problem Statement
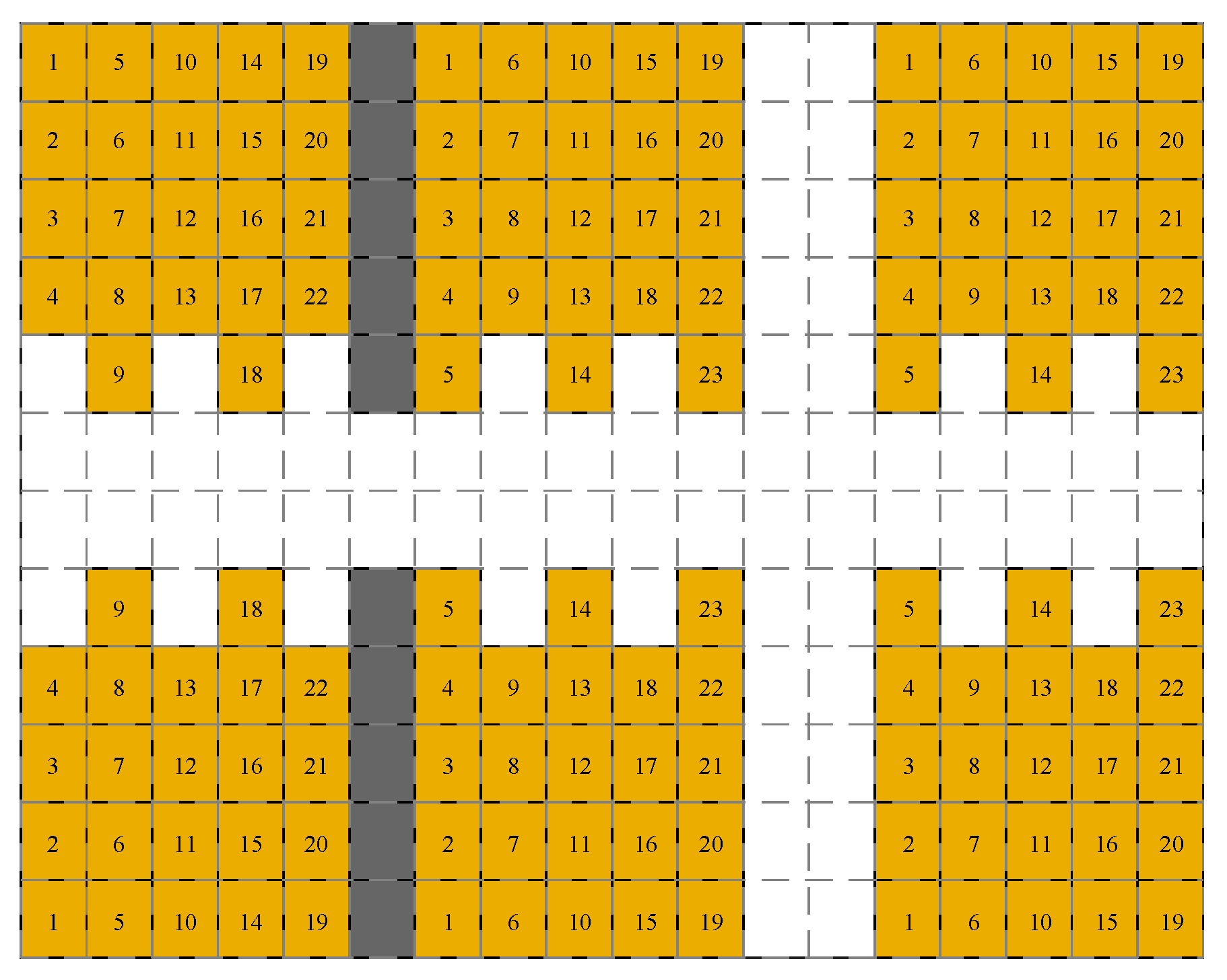
2.1. Warehouse Layout
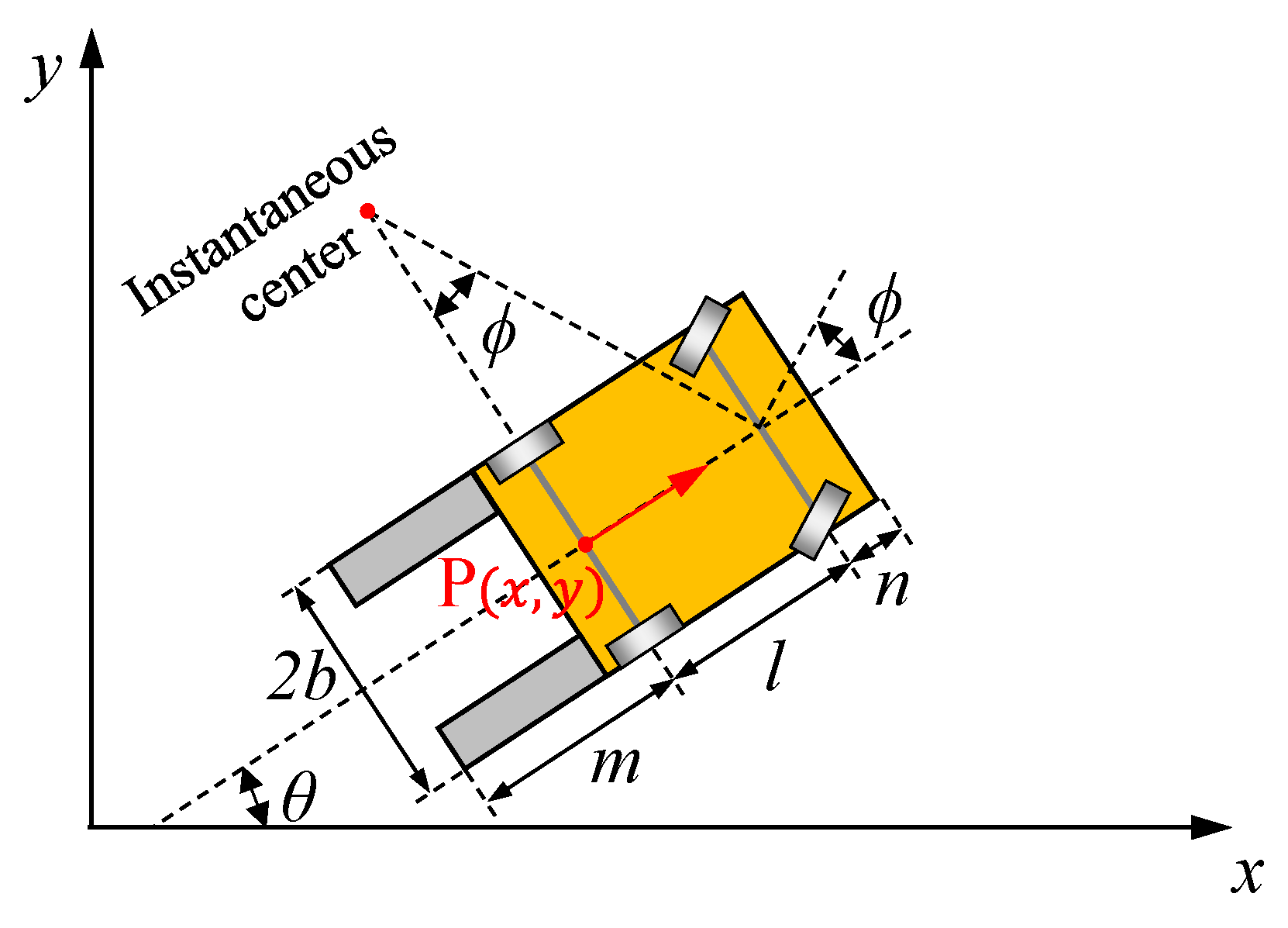
2.2. Kinematics of a Forklift Vehicle
3. ANN-Combined Score-Based Dispatching Approach
| Algorithm 1: ANN combined score-based dispatching algorithm |
|
3.1. Vehicle Selection and Initial Pose of a New Subtask
3.2. Scoring System
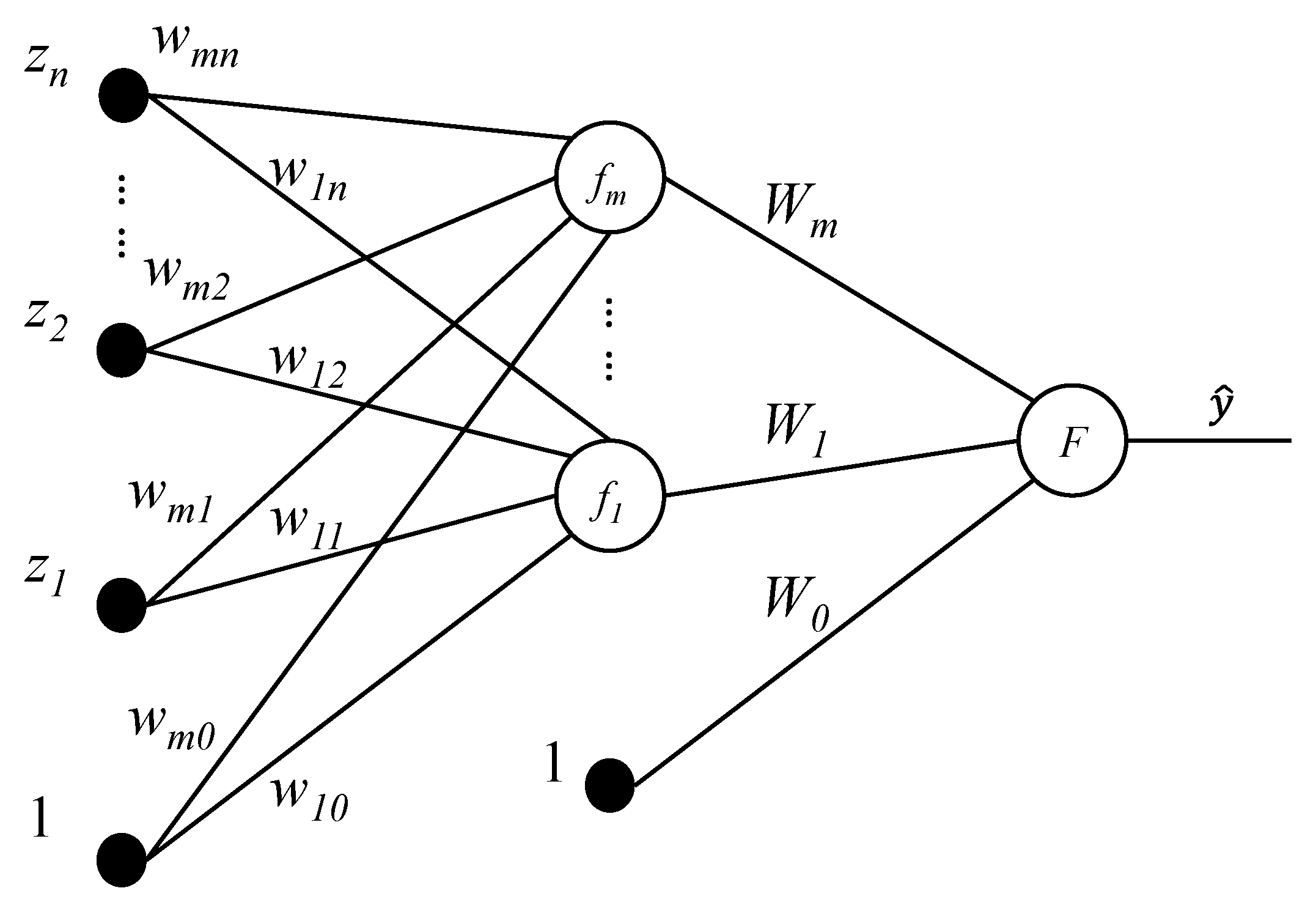
3.3. ANN Correction Method
3.4. Final Pose Selection
4. Improved Hybrid A* Search Algorithm
| Algorithm 2: Improved hybrid A* search algorithm |
|
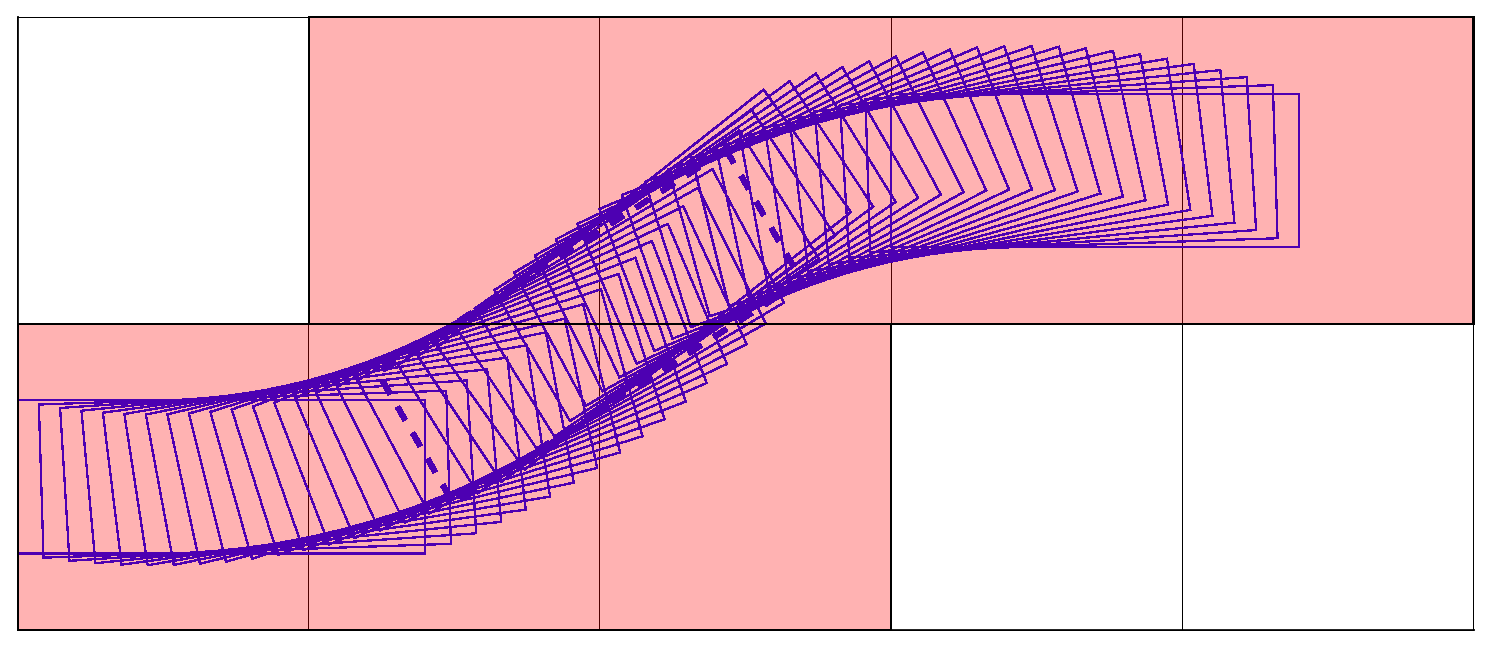
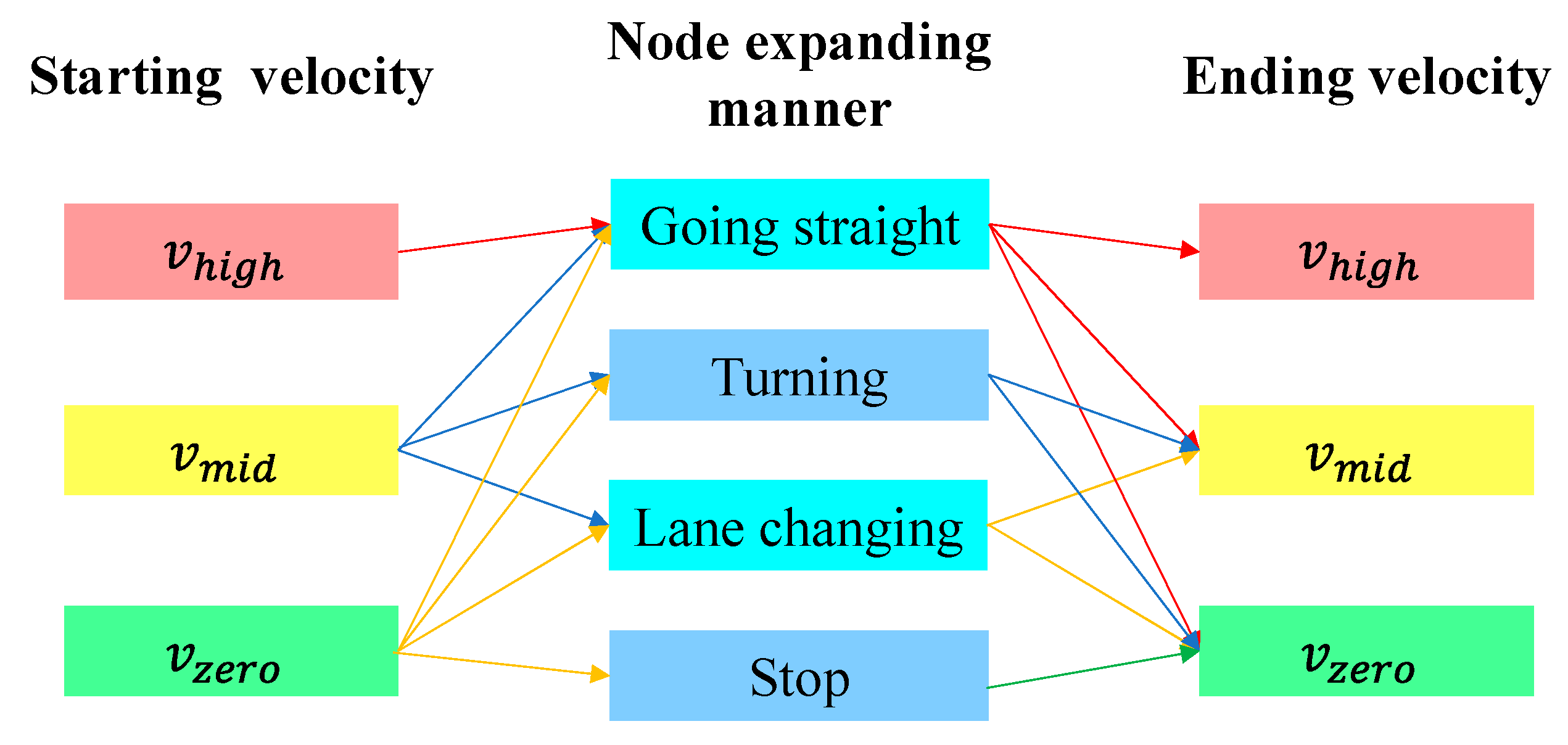
4.1. Node Expansion Method
4.2. Velocity Planner
4.3. Collision Detection Strategy
| Algorithm 3: Collision detection algorithm |
|
4.4. Trajectory Cost Function
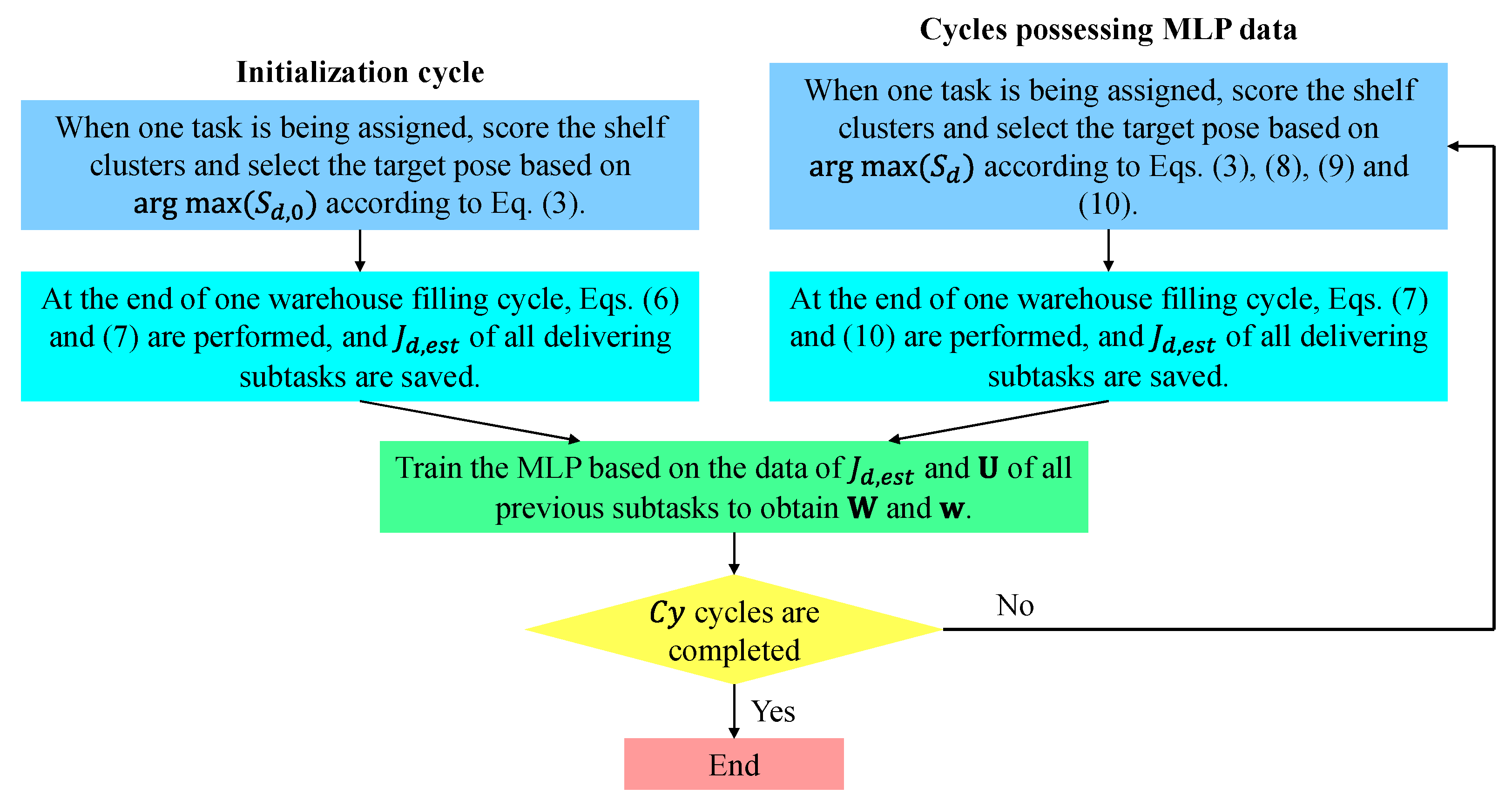
5. Joint Dispatching and Cooperative Trajectory Planning Framework
| Algorithm 4: Cooperative operation algorithm |
|
6. Numerical Experiments
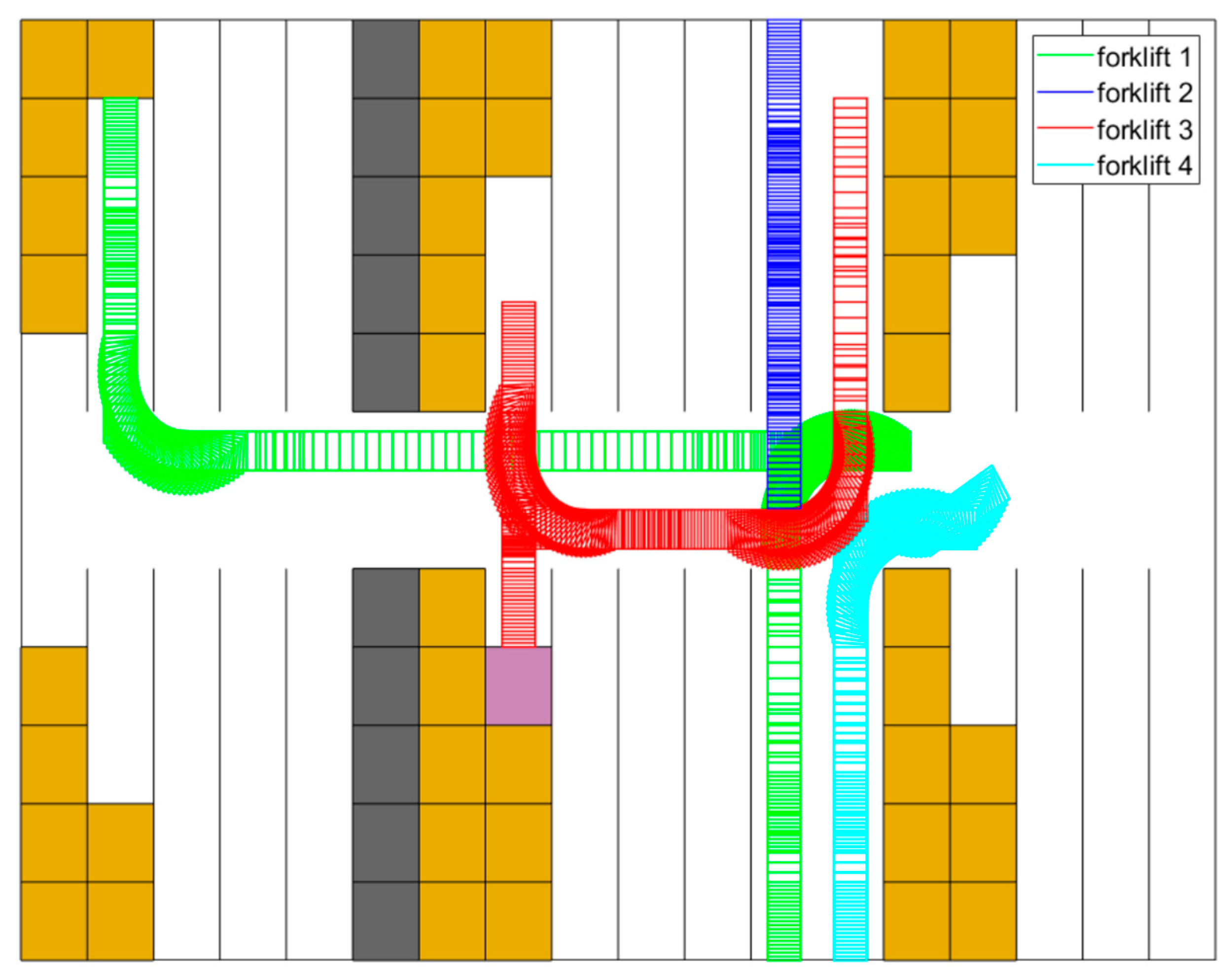
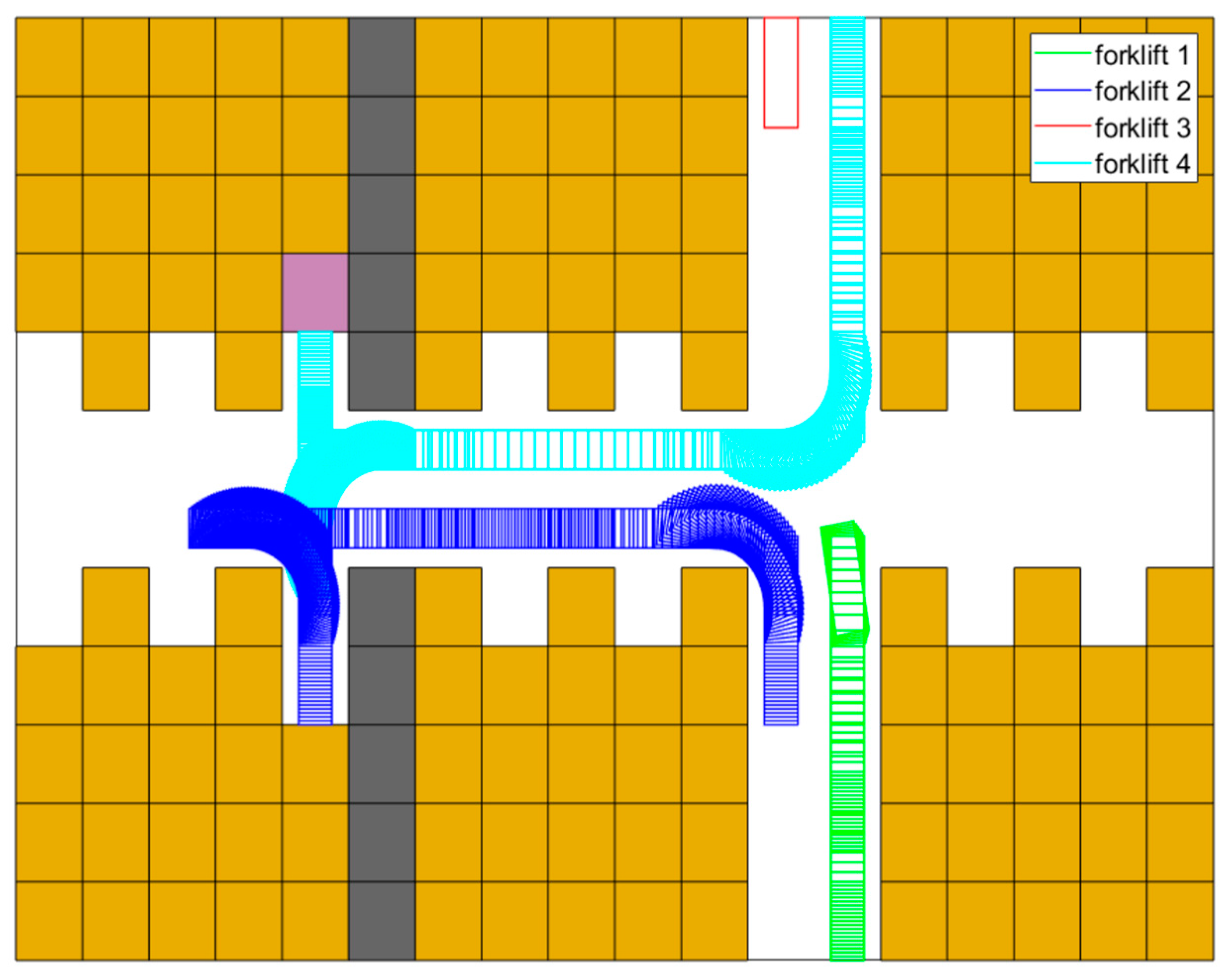
6.1. On the Performance of the Trajectory Planning Technique
6.2. On the Performance of Dispatching Strategies
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bozek, P.; Karavaev, Y.L.; Ardentov, A.A.; Yefremov, K.S. Neural network control of a wheeled mobile robot based on optimal trajectories. Int. J. Adv. Robot. Syst. 2020, 17, 2. [Google Scholar] [CrossRef]
- Blatnický, M.; Dižo, J.; Sága, M.; Gerlici, J.; Kuba, E. Design of a Mechanical Part of an Automated Platform for Oblique Manipulation. Appl. Sci. 2020, 10, 8467. [Google Scholar] [CrossRef]
- Yang, Q.; Lian, Y.; Xie, W. Hierarchical planning for multiple AGVs in warehouse based on global vision. Simul. Model. Pract. Theory 2020, 104, 102124. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Yang, J.; Wang, B. A new method to design fuzzy controller for unmanned autonomous forklift. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 946–951. [Google Scholar] [CrossRef]
- Zhong, Z.; Wan, M.; Pei, Z.; Qin, X. Spatial and temporal optimization for smart warehouses with fast turnover. Comput. Oper. Res. 2021, 125, 105091. [Google Scholar] [CrossRef]
- Weidinger, F.; Boysen, N.; Briskorn, D. Storage assignment with rack moving mobile robots in KIVA warehouses. Transp. Sci. 2018, 52, 1297–1588. [Google Scholar] [CrossRef]
- Yu, W.; Wang, S.; Wang, R.; Tan, M. Generation of temporal-spatial Bezier curve for simultaneous arrival of multiple unmanned vehicles. Inf. Sci. 2017, 418–419, 34–45. [Google Scholar] [CrossRef]
- Ouyang, Y.; Li, B.; Zhang, Y.; Acarman, T.; Guo, Y.; Zhang, T. Fast and optimal trajectory planning for multiple vehicles in a nonconvex and cluttered environment: Benchmarks, methodology, and experiments. In Proceedings of the 2022 IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 10746–10752. [Google Scholar]
- Chen, B.M. On the trends of autonomous unmanned systems research. Engineering 2022, 12, 20–23. [Google Scholar] [CrossRef]
- Miyamoto, T.; Inoue, K. Local and random searches for dispatch and conflict-free routing problem of capacitated AGV systems. Comput. Ind. Eng. 2016, 91, 1–9. [Google Scholar] [CrossRef]
- Stutzle, T.; Ruiz, R. Iterated Local Search. In Handbook of Heuristics; Marti, R., Pardalos, P., Resende, M., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Zhang, X.; Sang, H.; Li, J.; Han, Y.; Duan, P. An effective multi-AGVs dispatching method applied to matrix manufacturing workshop. Comput. Ind. Eng. 2022, 163, 107791. [Google Scholar] [CrossRef]
- Lin, L.; Shinn, S.W.; Gen, M.; Hwang, H. Network model and effective evolutionary approach for AGV dispatching in manufacturing system. J. Intell. Manuf. 2006, 17, 465–477. [Google Scholar] [CrossRef]
- Bao, Y.; Jiao, G.; Huang, M. Cooperative optimization of pod repositioning and AGV task allocation in Robotic Mobile Fulfillment Systems. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 2597–2601. [Google Scholar] [CrossRef]
- Lee, I.G.; Chung, S.H.; Yoon, S.W. Two-stage storage assignment to minimize travel time and congestion for warehouse order picking operations. Comput. Ind. Eng. 2020, 139, 106129. [Google Scholar] [CrossRef]
- Fragapane, G.; de Koster, R.; Sgarbossa, F.; Strandhagen, J.O. Planning and control of autonomous mobile robots for intralogistics: Literature review and research agenda. Eur. J. Oper. Res. 2021, 294, 405–426. [Google Scholar] [CrossRef]
- Hu, H.; Jia, X.; He, Q.; Fu, S.; Liu, K. Deep reinforcement learning based AGVs real-time scheduling with mixed rule for flexible shop floor in industry 4.0. Comput. Ind. Eng. 2020, 149, 106749. [Google Scholar] [CrossRef]
- Zhou, T.; Tang, D.; Zhu, H.; Zhang, Z. Multi-agent reinforcement learning for online scheduling in smart factories. Robot. Comput.-Integr. Manuf. 2021, 72, 102202. [Google Scholar] [CrossRef]
- Lian, Y.; Yang, Q.; Liu, Y.; Xie, W. A spatio-temporal constrained hierarchical scheduling strategy for multiple warehouse mobile robots under industrial cyber-physical system. Adv. Eng. Inform. 2022, 52, 101572. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.; Dou, S.; Peng, L.; Su, X. Research summary of intelligent optimization algorithm for warehouse AGV path planning. In Lecture Notes in Operations Research; Shi, X., Bohács, G., Ma, Y., Gong, D., Shang, X., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, H.; Xie, Y.; Guo, M. Path planning for multiple mobile robots under double-warehouse. Inf. Sci. 2014, 278, 357–379. [Google Scholar] [CrossRef]
- Xidias, E.K. A decision algorithm for motion planning of car-like robots in dynamic environments. Cybern. Syst. 2021, 52, 1909844. [Google Scholar] [CrossRef]
- Li, B.; Acarman, T.; Zhang, Y.; Ouyang, Y.; Yaman, C.; Kong, Q.; Zhong, X.; Peng, X. Optimization-based trajectory planning for autonomous parking with irregularly placed obstacles: A lightweight iterative framework. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11970–11981. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Feng, Y.; Zhang, Y.; Ge, Y.; Shao, Z. Balancing computation speed and quality: A decentralized motion planning method for cooperative lane changes of connected and automated vehicles. IEEE Trans. Intell. Veh. 2018, 3, 340–350. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, N. Airport AGV path optimization model based on ant colony algorithm to optimize Dijkstra algorithm in urban systems. Sustain. Comput. Inform. Syst. 2022, 35, 100716. [Google Scholar] [CrossRef]
- Zacharia, P.T.; Xidias, E.K. AGV routing and motion planning in a flexible manufacturing system using a fuzzy-based genetic algorithm. Int. J. Adv. Manuf. Technol. 2020, 109, 1801–1813. [Google Scholar] [CrossRef]
- Kneissl, M.; Madhusudhanan, A.K.; Molin, A.; Esen, H.; Hirche, S. A multi-vehicle control framework with application to automated valet parking. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5697–5707. [Google Scholar] [CrossRef]
- Dresner, K.; Stone, P. Multiagent traffic management: A reservation-based intersection control mechanism. In Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems, New York, NY, USA, 23 July 2004; pp. 530–537. [Google Scholar]
- Guney, M.A.; Raptis, I.A. Dynamic prioritized motion coordination of multi-AGV systems. Robot. Auton. Syst. 2021, 139, 103534. [Google Scholar] [CrossRef]
- Digani, V.; Caramaschi, F.; Sabattini, L.; Secchi, C.; Fantuzzi, C. Obstacle avoidance for industrial AGVs. In Proceedings of the 2014 IEEE 10th International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 4–6 September 2014; pp. 227–232. [Google Scholar] [CrossRef]
- Stern, R. Multi-Agent Path Finding—An Overview. In Artificial Intelligence. Lecture Notes in Computer Science; Osipov, G., Panov, A., Yakovlev, K., Eds.; Springer: Cham, Switzerland, 2019; Volume 11866. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Li, L.; Li, Y.; Dong, H. A bi-level cooperative operation approach for AGV based automated valet parking. Transp. Res. Part C 2021, 128, 103140. [Google Scholar] [CrossRef]
- Meng, Y.; Li, L.; Wang, F.; Li, K.; Li, Z. Analysis of cooperative driving strategies for nonsignalized intersections. IEEE Trans. Veh. Technol. 2018, 67, 2900–2911. [Google Scholar] [CrossRef]
- Lee, C.K.M.; Lin, B.; Ng, K.K.H.; Lv, Y.; Tai, W.C. Smart robotic mobile fulfillment system with dynamic conflict-free strategies considering cyber-physical integration. Adv. Eng. Inform. 2019, 42, 100998. [Google Scholar] [CrossRef]
- Rochel, P.; Rios, H.; Mera, M.; Dzul, A. Trajectory tracking for uncertain Unicycle Mobile Robots: A Super-Twisting approach. Control Eng. Pract. 2022, 122, 105078. [Google Scholar] [CrossRef]
- Zhang, T. An estimation method of the fuel mass injected in large injections in Common-Rail diesel engines based on system identification using artificial neural network. Fuel 2022, 310, 122404. [Google Scholar] [CrossRef]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path planning for autonomous vehicles in unknown semi-structured environment. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- Li, B.; Shao, Z. A unified motion planning method for parking an autonomous vehicle in the presence of irregularly placed obstacles. Knowl. Based Syst. 2015, 86, 11–20. [Google Scholar] [CrossRef]









| Abbreviation | Description |
|---|---|
| Current Maneuver | ||
|---|---|---|
| Stop | - | |
| Going straight | , then else | |
| Turning | ||
| Lane changing |
| Parameter | Description | Setting |
|---|---|---|
| Forklift front overhang length | 0.3 m | |
| Forklift rear overhang length | 1 m | |
| Forklift wheelbase | 1.5 m | |
| Forklift width | 1 m | |
| Horizontal boundaries of map | m | |
| Vertical boundaries of map | m | |
| Node resolution for search algorithms | 2 m | |
| Maximum iteration in the time dimension involved A* search | 500 | |
| Maximum iteration of redispatching | 10 | |
| Maximum iteration in the improved A* search | 5000 | |
| Calibration parameters | ||
| Modeled time lengths of maneuvers | s | |
| Penalty for turning maneuver | 4 | |
| Penalty for lane changing maneuver | 6 | |
| Penalty for speed inverse maneuver | 6 | |
| Time postponed when one trajectory planning is failed | 10 s | |
| in Equation (3) | 20 s | |
| Time length after the virtual vehicle entering the rack passage to evaluate | 20 s | |
| Time period for picking goods and unloading goods | s |
| Strategy Name | Filling | Emptying | ||
|---|---|---|---|---|
| Decision Failure Times | End Time (s) | Decision Failure Times | End Time (s) | |
| ANN combined strategy | 38 | 2388.25 | 27 | 2597.25 |
| Comprehensive strategy | 38 | 2441.00 | 21 | 2658.25 |
| Greedy strategy | 135 | 2768.75 | 75 | 3419.00 |
| Traffic jam removing strategy | 120 | 2709.00 | 51 | 3117.75 |
| Balance strategy | 55 | 2557.75 | 35 | 2660.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Li, H.; Fang, Y.; Luo, M.; Cao, K. Joint Dispatching and Cooperative Trajectory Planning for Multiple Autonomous Forklifts in a Warehouse: A Search-and-Learning-Based Approach. Electronics 2023, 12, 3820. https://doi.org/10.3390/electronics12183820
Zhang T, Li H, Fang Y, Luo M, Cao K. Joint Dispatching and Cooperative Trajectory Planning for Multiple Autonomous Forklifts in a Warehouse: A Search-and-Learning-Based Approach. Electronics. 2023; 12(18):3820. https://doi.org/10.3390/electronics12183820
Chicago/Turabian StyleZhang, Tantan, Hu Li, Yong Fang, Man Luo, and Kai Cao. 2023. "Joint Dispatching and Cooperative Trajectory Planning for Multiple Autonomous Forklifts in a Warehouse: A Search-and-Learning-Based Approach" Electronics 12, no. 18: 3820. https://doi.org/10.3390/electronics12183820
APA StyleZhang, T., Li, H., Fang, Y., Luo, M., & Cao, K. (2023). Joint Dispatching and Cooperative Trajectory Planning for Multiple Autonomous Forklifts in a Warehouse: A Search-and-Learning-Based Approach. Electronics, 12(18), 3820. https://doi.org/10.3390/electronics12183820







