Power Function Algorithms Implemented in Microcontrollers and FPGAs

Abstract

The exponential function $a^x$ is widespread in many fields of science. Its calculation is a complicated issue for Central Processing Units (CPUs) and Graphics Processing Units (GPUs), as well as for specialised Digital Signal Processing (DSP) processors, such as Intelligent Processor Units (IPUs), for the needs of neural networks. This article presents some simple and accurate exponential function calculation algorithms in half, single, and double precision that can be prototyped in Field-Programmable Gate Arrays (FPGAs). It should be noted that, for the approximation, the use of effective polynomials of the first degree was proposed in most cases. The characteristic feature of such algorithms is that they only contain fast ‘bithack’ operations (‘bit manipulation technique’) and Floating-Point (FP) addition, multiplication, and (if necessary) Fused Multiply-Add (FMA) operations. We published an article on algorithms for this class of function recently, but the focus was on the use of approximations of second-degree polynomials and higher, requiring two multiplications and two additions or more, which poses some complications in FPGA implementation. This article considers algorithms based on piecewise linear approximation, with one multiplication and one addition. Such algorithms of low complexity provide decent accuracy and speed, sufficient for practical applications such as accelerators for neural networks, power electronics, machine learning, computer vision, and intelligent robotic systems. These are FP-oriented algorithms; therefore, we briefly describe the characteristic parameters of such numbers.

1. Introduction

The available literature in this field addresses the need to develop newer and newer methods of calculating exponential and power functions [1,2,3,4,5,6,7,8,9,10,11]. Numerical methods are needed for scientific calculations with increased accuracy and for the implementation of neural networks in hardware. The implementation of advanced applications in FPGAs and Application Specific Integrated Circuits (ASIC) requires high algorithm speeds and a reduction of hardware resources and power consumption [2,12]. The starting points of the improvements in the algorithms described in the literature are:

-

Piecewise Linear Approximation Computation (PLAC) [2,4,9,12,13,14,15,16]

-

Look-Up Table methods (LUT) [1,2,5,6,12,16]

-

Taylor’s methods [1,6]

-

partitioning method of 32-bit format for computations into four eight-bit numbers, which are used in LUT multiplications [1]

-

CORDIC methods [4,17].

Refs. [4,13] concern the method of PLAC. The PLAC algorithm runs in two stages. The first stage is optimisation by a segmenter, to find the minimum number of segments within a software-predefined Maximum Absolute Error (MAE). The second stage is quantisation. The hardware architecture has also been improved, simplifying the indexing logic and leading to a reduction in hardware redundancy. Ref. [4] takes into account the number of segments needed in a piecewise linear approximation, depending on the interval and the desired approximation error.

The initial solution presented in [13] had more flaws, such as reusing the endpoints of recorded segments; the search order was wrong, the indexing logic in the index generator was redundant; only the MAEsoft was controlled in the segmenter; and the quantisation of the circuit was not solved before hardware implementation.

Ref. [1] concerns the approximation of the exponential function by Taylor series expansion. The ‘divide and conquer’ technique was applied to the mantissa area. The accuracy, number of operations, and LUT size were taken into consideration. Here, the mantissa range was divided into several regions, and cases from one to eight ranges were analysed. For a larger number of ranges, the number of terms in the Taylor expansion was clearly reduced while maintaining the assumed accuracy. The number of terms in the Taylor expansion is closely related to the number of mathematical operations. For example, an eight-term Taylor expansion requires ten multiplications and additions/subtractions. The expansion coefficients are stored in the LUT in advance. This requires a large amount of LUT memory. For example, storing the coefficients for four-range splitting required a four-word LUT.

Refs. [16,18] presented an FPGA implementation of single-precision FP arithmetic based on an indirect method that transforms x^y into a chain of operations involving logarithm, multiplication, exponential function, and dedicated logic for the negative e base case. Speed is increased by systematically introducing pipeline steps into the data path of exponential and logarithmic units and their subunits. In [16], an innovative method of linear piecewise approximation (PWL) was proposed for the approximate representation of non-linear logarithmic and antilogarithmic functions ($lo{g}_2\left(x\right)$, $2^x$).

A slightly different solution was presented in [6], concerning the implementation of the double-precision exponential function in an FPGA. The most significant 27 bits of the input fractional part x are computed using LUT-based methods. The rest of the least significant bits are computed using the Taylor-Maclaurin expansion because the LUT approach is inefficient for the least significant bits. The relative error is approximately $2^{-55}$.

Refs. [2,12] analysed the problem of cost-effective inference for non-linear operations in Deep Neural Networks (DNN). The focus was on the exponential function ‘exp’ in the Softmax layer of the DNN for object detection. The goal here was to minimise hardware resources and reduce power consumption without losing application accuracy.

Similarly, as in [16], the Piecewise Linear Function (PLF) was applied to approximate exp. In this case, the number of elements required to maintain detection accuracy was reduced, and then the PLF was constrained to a smaller domain in order to minimise the bit width of the segments in the LUT, resulting in lower energy and resource costs. The calculation costs of each element were stored in the LUT. Then, based on the values in the LUTs of these segments, a decision was made as to which segment was selected for the calculation of the approximate value of the affine function. DNNs were trained with Softmax and exp was replaced in the Softmax layer by PLF in the inference phase. The way in which the size of the LUT depends on the number of segments was analysed, affecting the accuracy of the application in the context of detecting objects using DNN.

Ref. [5] focused on the issue of computing execution time for exponential functions in neural networks. This function is used to compute most of the activation functions and probability distributions used in neural network models. There is a need to develop algorithms faster than those from mathematical libraries. A method of approximating the exponential function by manipulating the components of the standard (IEEE-754) FP representation is presented. The exponential function is modelled as a LUT with linear interpolation in many software packages. The basis of the innovation here is that the components of the FP representation, according to the IEEE-754 standard, can be manipulated by accessing the same memory location [5].

On average, the integer EXP macro was 6 nanoseconds faster than the integer-to-float conversion that takes place in the control program. An additional trick is applied, namely, if the input argument is an integer, the EXP macro does not perform any FP operations. The implementation of this macro depends on the byte order of the machine. The use of a global static variable is problematic in multi-threaded environments because each thread must have a private copy of the eco data structure. There is no overflow or error handling. The user must ensure that the argument is in the valid range (approximately −700 to 700). This only approximates the exponential function. Some numerical methods may amplify the approximation error; each algorithm that uses EXP should therefore be tested against the original version first.

Ref. [17] presented a fixed-point architecture. Very High-Speed Integrated Circuit Hardware Description Language (VHDL) source code is provided for power function computations. A fully customised architecture was based on the extensive CORDIC hyperbolic algorithm. Each stage utilised two-barrel shifters, a LUT, and multiplexers. The master stage required five adders, and the slave stage required three adders. The state machine controlled the iteration counter for the add/sub inputs of the adders. The customised hyperbolic CORDIC architecture allowed the user to modify the design parameters: the number of bits (B), number of fractional bits (FW), number of positive iterations (N), and number of negative iterations (M + 1).

The use of fixed-point arithmetic optimised resource usage. It was not possible to use the entire algorithm’s input domain because the numerical range is limited. For each function, 13 × 9 = 117 different hardware profiles were generated. The application of fixed-point arithmetic optimised the use of resources.

CORDIC and the digital recursive method do not meet the hard real-time constraints, taking into consideration the fact that both operations are clock-based and require many clock cycles to compute the results. Up to 824 iterations may be required for the calculation. The output register of each stage requires two additional cycles.

Traditional activation functions of convolutional neural networks face problems such as gradient decay, neuron death, and output offset. To overcome these problems, a new activation function, the Fast Exponentially Linear Unit (FELU), was proposed in [9] to accelerate exponential linear computations and reduce network uptime. FELU has the advantages of a Rectified Linear Unit (RELU) and Exponential Linear Unit (ELU). The contribution of FELU is the usage of a fast exponential function that approximates the calculation of the natural gradient in the negative part, which can speed up the calculations and reduce network uptime by speeding up the calculation of the exponent. Simple bitwise displacement and integer algebraic operations were applied to achieve a fast exponential approximation based on the IEEE-754 representation of FP calculations.

The remainder of this paper is organised as follows: Section 2 describes the Schraudolph algorithm and provides its numerical evaluation. The formulas for approximating the indicator function are also presented. Section 3 is devoted to testing the execution time of FP indicator functions on STM32 microcontrollers. Section 4 presents the implementation of the exponential functions on FPGAs. Finally, conclusions are drawn in Section 5.

2. Floating-Point Numbers

Assume the FP argument is presented as:

$$x={(-1)}^{S_x}{M}_x\cdot 2^{w_x-bias}={(-1)}^{S_x}\left(1+m_x\right)\cdot 2^{w_x-bias},$$

(1)

where:

• $S_x$—sign and $S_x$ = {0, 1}, 0—for positive numbers, 1—for negative numbers;
• $w_x=E_x+bias$—shifted exponent;
• $E_x$—exponent calculated according to the equation:

$$E_x=\lfloor {\log }_2\left(\left|x\right|\right)\rfloor =\mathrm{floor}\left({\log }_2\left(\left|x\right|\right)\right),$$

• $M_x$—the mantissa, calculated as:

$$M_x=\frac{\left|x\right|}{2^{E_x}},$$

(2)

and is within the range $M_x\in \left[1,2\right)$. It is given in the form $M_x=1+m_x$, where $m_x\in \left[0,1\right)$ is the fractional part of the mantissa.

2.1. Scheme of the Algorithm for Approximating the Function $a^x$

1.

We use a familiar approach—calculating $a^x$ by the functions $2^z$. In this case we will write [5,15]:

$$a^x=2^z=2^{z_i+z_f}=2^{z_i}·2^{z_f},$$

(3)

$$z=x·{\log }_2\left(a\right)=x\frac{\ln \left(a\right)}{\ln \left(2\right)}=z_i+z_f$$

(4)

2.

Now we need to calculate two functions: $2^{z_i}$ and $2^{z_f}$. For FP numbers, we calculate the value of variable z according to the formula:

$$int z=\left(x·{\log }_2\left(a\right)+bias\right)·N_m,$$

(5)

where: bias = 15, 127, and 1023 (for half, single, and double precision formats, respectively);

• $N_{m }=2^{10}$—for half precision,
• $N_m=2^{23}$—for single precision, and
• $N_m=2^{52}$—for double precision.

Here the type conversion takes place: all calculations in (5) are carried out in FP (half, single, double), and the result is given as an integer. We convert float-integer types according to the bit manipulation technique.

If we need to calculate a function $a^{-x}$ then Equation (5) should have the form

$$int z=\left(bias-x·{\log }_2\left(a\right)\right)·N_m.$$

(6)

3.

We divide the variable int z into $z_i$ i $z_f$ using exponential and mantissa masks.

4.

We divide the mantissa $z_f\in \left[0,1\right)$ into equal 2^j parts, where j = 1, 2, 4, 8, 16, 32, ... We approximate functions $2^{z_f}$ on each part by piecewise linear approximation $2^{z_f}$≅$bet{a}_i+alph{a}_i{z}_f-1, i=1,2,3,\dots$ $2^j$.

5.

Using the bitwise OR operator, we combine the exponent and the linearised mantissa back together.

6.

We convert this number from an integer to a float. It should be noted that all the algorithms described in this paper work in the full range of normalised numbers. For single precision, these are numbers from $\pm 1.18·{10}^{-38}$ to $\pm 3.39·{10}^{38}$.

2.2. The General Approach of N. Schraudolph, Applied to Calculating the Function $a^x$

It is known that N. Schraudolph proposed a very simple approach to calculation error reduction of the $e^x$ function with the approximation $2^{z_f}$ by the formula: $2^{z_f}$ ≅ (1 +$z_f$) [5,15]. This technique can also be applied to functions of the form $a^x$. In this case, from the number int z, obtained from Equation (5), the constant c should be subtracted, which is determined by the formula: $c=\mathrm{floor}\left(\gamma /\ln (2\right)·N_m).$ The number c is utilised to reduce the relative error. The coefficient γ is calculated according to the equation $\gamma =\ln \left(\ln \left(2\right)+2/\exp \left(1\right)\right)-\ln \left(2\right)-\ln \left(\ln \left(2\right)\right)$. In this case, (5) will look like this:

$$int z=\left(x·{\log }_2\left(a\right)+bias-c\right)·N_m=\left(x·{\log }_2\left(a\right))·N_m+(bias-c\right)·N_m.$$

(7)

Next, inverse processing z (integer) → y (float) was performed. As an example, the code for calculating the function ${10}^x$ for single precision is presented below, where $N_m=2^{23}, c=0.04367749$, ${\log }_2\left(10\right)·N_m\cong 27866353=0\mathrm{x}01\mathrm{a}934\mathrm{f}1$, $\left(bias-c\right)·N_m\cong 1064986823=0\mathrm{x}3\mathrm{f}7\mathrm{a}68\mathrm{c}7$:

       float a10_x(float x)
                { int z = x * 0x01a934f1 + 0x3f7a68c7;
           float y = *(float*)&z;
      return y;
}

Note that the accuracy of the algorithm only constitutes $\left|{\delta }_{max}\left|=\right|2.98·{10}^{-2}\right|$ or $-{\log }_2\left(\left|{\delta }_{max}\right|\right)=5.06$ correct bits. Here, ${\delta }_{max}$ is the maximum value of the relative error.

$$\delta =\frac{y}{{10}^x}-1.$$

2.3. New Piecewise Linear Approximation Algorithms

To increase accuracy, we first use the method described in the scheme above, but with one feature (as described below).

We use the following equations to calculate alpha[] and beta[] coefficients for functions $2^{z_f}$ on the interval [a,b):

$$alph{a}_i=-\frac{-2^a+2^b}{-b+a};bet{a}_i=\frac{\left(a\ast 2^b-2^{ab}\right)}{-b+a}.$$

As an example, we present the code of the algorithm to calculate the following function $e^x$, for $j=2$:

               const float alpha[2] = {0.8284271247f,
      1.171572875f};
              const int beta[2] = {0, −1439258};
         float exp_12f(float x)
   {float y;
     int j;
                  int z = x*0xb8aa3b + 0x3f800000;
             int zii = z&0x7f800000;
             int zif = z&0x007fffff;
        j = zif >> 22;
                 zif = (int)(zif*alpha[j] + beta[j]);
       zii |= zif;
           y = *(float*)&zii;
               y* = 0.9925613f; //Figure 1.
       return y;
}

A very important detail of all the codes should be noted, in that the tables of alpha[] and beta[] coefficients are filled with the same ones for any type of function $a^x$, only the operators corresponding to the implementation of Equation (5) (marked in green) change. Note that, instead of pointers in the code, one can use the type union. A characteristic feature of this type of algorithm is the presence of the additional FP multiplication at the output of the algorithm, which gives a uniformly distributed relative error (see Figure 1). Black lines represent the exp_12f code without row y* = 0.9925613f, and red lines represent the whole exp_12f function.

The accuracy of the algorithm is only $\left|{\delta }_{max}\right|=7.44·{10}^{-3}$, or 7.07 correct bits. The presence of the FP multiplication at the output is a defect, which complicates its hardware implementation. Therefore, we continue with a simplified approach without using this multiplication.

To reduce errors, we use the following technique: in the first part, we set the linear approximation coefficients so that at point 0, the approximation is linear and the function $2^{z\_f}$ has the same values (i.e., equal to 1). The maxima of the relative errors are at point b, and within the subinterval, they would be located symmetrically about zero. At the same time, the linear approximation coefficients for z_f ∈ [0,b) are calculated according to the formula:

$$\begin{array}{l}alph{a}_i\\ =\ln \left(2\right)\\ \ast \left(4^a-2^{\left(1+a+b\right)}\right)\\ /(-LambertW\left(\frac{\exp \left(\frac{\ln \left(2\right)\ast a\ast 2^a-2^a+2^{\left(1+b\right)}-2^{\left(1+b\right)}\ast \ln \left(2\right)\ast b}{2^a-2^{\left(1+b\right)}}\right)}{2^a-2^{\left(1+b\right)}-2^{\left(1+b\right)}}\right)\ast 2^a\\ +2^{\left(1+b\right)}\\ \ast LambertW(\exp (\left(\ln \left(2\right)\ast \mathrm{a}\ast 2^a-2^a+2^{\left(1+b\right)}-2^{\left(1+b\right)}\ast \ln \left(2\right)\ast \frac{\mathrm{b}}{2^a-2^{\left(1+b\right)}}\right)\\ -\ln \left(2\right)\ast \mathrm{b}\ast 2^a+\ln \left(2\right)\ast \mathrm{a}\ast 2^a);\end{array}$$

$$\begin{array}{l}bet{a}_i\\ =(\ln \left(2\right)a\ast \left(2^{\left(1+a+b\right)}\right)\\ -LambertW\left(\frac{\exp \left(\frac{\ln \left(2\right)\ast a\ast 2^a-2^a+2^{\left(1+b\right)}-2^{\left(1+b\right)}\ast \ln \left(2\right)\ast b}{2^a-2^{\left(1+b\right)}}\right)}{2^a-2^{\left(1+b\right)}}\right)\ast 4^a\\ +2^{\left(1+a+b\right)}\\ \ast LambertW\left(\frac{\exp \left(\frac{\ln \left(2\right)\ast a\ast 2^a-2^a+2^{\left(1+b\right)}-2^{\left(1+b\right)}\ast \ln \left(2\right)\ast b}{2^a-2^{\left(1+b\right)}}\right)}{2^a-2^{\left(1+b\right)}}\right)\\ -\ln \left(2\right)b\\ \ast 4^a)/(-\mathrm{LambertW}\left(\frac{\exp \left(\frac{\ln \left(2\right)\ast a\ast 2^a+2^{\left(1+b\right)}-2^{\left(1+b\right)}\ast \ln \left(2\right)\ast b}{2^a-2^{\left(1+b\right)}}\right)}{2^a-2^{\left(1+b\right)}}\right)\ast 2^a\\ +2^{\left(1+b\right)}\ast LambertW\left(\frac{\exp \left(\frac{\ln \left(2\right)\ast a\ast 2^a+2^{\left(1+b\right)}-2^{\left(1+b\right)}\ast \ln \left(2\right)\ast b}{2^a-2^{\left(1+b\right)}}\right)}{2^a-2^{\left(1+b\right)}}\right)\\ -\ln \left(2\right)b\ast 2^a+\ln \left(2\right)\mathrm{a}\ast 2^a);\end{array}$$

and on all other subintervals $i=2,3,\dots 2^j$:

$$\begin{array}{ll}alph{a}_i& =-(4\ln \left(2\right)\ast e^{\left(\frac{2^b}{2^b-2^a}\right) }(2^{\left(\frac{2^{b}a\ast 2^{a}b+a\ast 2^a-2^b+2^a+b{2}^b}{2^b-2^a}\right)}\\ & -2^{\left(-\frac{-2^{\left(1+b\right)}\ast a\ast 2^b-2^a}{2^b-2^a}\right)}))/(\left(-2^{\left( \frac{a{2}^{\left(a\right)}+b{2}^b}{2^b-2^a}\right)}\right)\ast \left(e^{\left(\frac{2^a}{2^b-2^a}\right)}\right)\\ & +\left(2^{\left( \frac{2^{b}a+2^{a}b}{2^b-2^a}\right)}\right)\ast \left(e^{\left(\frac{2^a}{2^b-2^a}\right) }\right)+\ln \left(2\right)a\ast \left(e^{\left(\frac{2^b}{2^b-2^a}\right) }\right)\\ & \ast \left(2^{\left( \frac{a(2^{\left(a\right)}+2^b)}{2^b-2^a}\right)}\right)-\ln \left(2\right)b\ast \left(e^{\left(\frac{2^b}{2^b-2^a}\right) }\right)\\ & \ast (2^{\left( \frac{a(2^{\left(a\right)}+2^b)}{2^b-2^a}\right)}))\end{array}$$

$$\begin{array}{ll}bet{a}_i=(4\ln \left(2\right)& \ast e^{\left(\frac{2^b}{2^b-2^a}\right) }(2^{\left(\frac{2^{b}a\ast 2^{a}b+a\ast 2^a-2^b+2^a+b{2}^b}{2^b-2^a}\right)}\ast a-2^{\left(-\frac{-2^{\left(1+b\right)}\ast a\ast 2^b-2^a}{2^b-2^a}\right)}\\ & \ast b))/(\left(-2^{\left( \frac{a{2}^{\left(a\right)}+b{2}^b}{2^b-2^a}\right)}\right)\ast \left(e^{\left(\frac{2^a}{2^b-2^a}\right) }\right)+\left(2^{\left( \frac{2^{b}a+2^{a}b}{2^b-2^a}\right)}\right)\ast \left(e^{\left(\frac{2^a}{2^b-2^a}\right) }\right)\\ & +\ln \left(2\right)a\ast \left(e^{\left(\frac{2^b}{2^b-2^a}\right) }\right)\ast \left(2^{\left( \frac{a(2^{\left(a\right)}+2^b)}{2^b-2^a}\right)}\right)-\ln \left(2\right)b\ast \left(e^{\left(\frac{2^b}{2^b-2^a}\right)}\right)\\ & \ast (2^{\left( \frac{a(2^{\left(a\right)}+2^b)}{2^b-2^a}\right)}))\end{array}$$

An example of the code of such an algorithm, for calculating the function $e^x$ for j = 2, is given below.

              const int alpha[2] = {6714081,
     9754211};
              const int beta[2] = {0, −1491339};
          float exp_12int(float x)
{
      float y;
     int j;
                  int z = x*0xb8aa3b + 0x3f800000;
             int zii = z&0x7f800000;
             int zif = z&0x007fffff;
        j = zif >> 22;
                    zif = (int)((zif*(int64_t) alpha[j]) >> 23) + beta[j];
       zii |= zif;
                y = *(float*)&zii; //Figure 2.
       return y;
}

Here we use a linear approximation with minimal relative error in each section except the first one. In the first section, we use a linear approximation with a slightly larger relative error to stay within the value of the zi range. It should be noted that, in this code, except for the row int z = x*0xb8aa3b + 0x3f800000 (multiplication of the float type), only integer type operations are used. The accuracy of the algorithm is ${\delta }_{max}=9.92$·10⁻³, or 6.65 correct bits.

The relative error is shown in Figure 2. For another number of mantissa parts, the test results of the algorithms are collected in

Table 1. Maximal relative error.

j	Max Relative Error	Correct Bits
2	9.92·10−3	6.65
4	2.53·10−3	8.62
8	6.43·10−4	10.65
16	1.65·10−4	12.56
32	4.02·10−5	14.60

. The code structure of such algorithms is invariant, except for the size of the coefficients: array alpha[j], beta[j] and number of right shift bits j = zif >> (23 − j), where the number of parts of the mantissa is $2^j$.

We have also developed algorithms for calculating function computation with different numbers of mantissa division intervals (see

Table 2. Time of execution of expf(x) and powf(2,x) functions on STM32H747.

Function	T [ns]	Processor Cycles No.
EXP_P1_2p	11.59	5
EXP_P1_2pM	12.87	5
EXP_P1_4pM	12.87	5
EXP_P1_16p_wM_int	9.85	4
pow2_P1_8p_wM_int	8.60	4
pow2_16p_int	8.33	4
pow2_P1_32p_wM_int	8.64	4
powf(2,x) from math.h	50.00	-
expf(x) from math.h	25.40	-

). As can be seen from the comparison of Table 1 and Table 2, the maximum errors are the same, which confirms the validity of the previously formulated theory.

3. Execution Time Testing of Floating-Point Functions expf(x) and powf(2,x) on Micro Controllers of the STM32 Family

The goal of the next experiment was to compare the execution time of the novel exponential and the power of the two invented functions.

Our case study in the field of microcontrollers focused on the STM32F746, STM32H747, and STM32H750 models using the Discovery evaluation platforms. For our research, we utilized the Keil uVision software environment (version 5.3). The microcontroller was connected via the basic USB/ST-Link debugging interface.

The results are depicted in Table 2,

Table 3. Time of execution expf(x) and powf(2,x) functions on STM32H750.

Function	T [ns]	Processor Cycles No.
EXP_P1_2p	12.76	6
EXP_P1_2pM	9.63	5
EXP_P1_4pM	9.63	5
EXP_P1_16p_wM_int	8.43	4
pow2_P1_8p_wM_int	8.43	4
pow2_16p_int	8.02	4
pow2_P1_32p_wM_int	8.64	4
powf(2,x) from math.h	43.80	21
expf(x) from math.h	22.65	11

and

Table 4. Time of execution expf(x) and powf(2,x) functions on STM32F746.

Function	T [ns]	Processor Cycles No.
EXP_P1_2p	39.87	155
EXP_P1_2pM	43.72	170
EXP_P1_4pM	44.24	172
EXP_P1_16p_wM_int	37.55	146
pow2_P1_8p_wM_int	38.58	150
pow2_16p_int	42.18	164
pow2_P1_32p_wM_int	38.58	150
powf(2,x) from math.h	12.99	3
expf(x) from math.h	28.25	6

, for three different microcontrollers. We also measured the execution times of the FP powf(2,x) and floating expf(x) functions from the math.h library. An interesting observation is that these times are equal to 50.0 ns and 25.4 when executed on the STM32H747 at a main clock speed of 400 MHz and measured by the same method. Thus, for every case, the execution time of our latest functions, expf(x) and powf(2,x) is much shorter than those functions from the ‘math.h’ library. The fastest power function was the FP pow2_16p_int (time 8.33 ns). The fastest sixteen parts without multiplication P1_16p_wM_int exponential function required 9.85 ns. Examples of our function’s designations are given in Table 2, Table 3, Table 4,

Table 5. Memory usage in STM32H750 by expf(x) and powf(2,x) functions.

Function	Function Code Size [No. Words]
EXP_P1_2p	136
EXP_P1_2pM	144
EXP_P1_4pM	160
EXP_P1_16p_wM_int	112
pow2_P1_8p_wM_int	170
pow2_16p_int	234
pow2_P1_32p_wM_int	116
powf(2,x) from math.h	1852
expf(x) from math.h	624

,

Table 6. Memory usage in STM32H747 by expf(x) and powf(2,x) functions.

Function	Function Code Size [No. Words]
EXP_P1_2p	140
EXP_P1_2pM	148
EXP_P1_4pM	164
EXP_P1_16p_wM_int	236
pow2_P1_8p_wM_int	170
pow2_16p_int	234
pow2_P1_32p_wM_int	114
powf(2,x) from math.h	1848
expf(x) from math.h	624

,

Table 7. Memory usage in STM32F746 by expf(x) and powf(2,x) functions.

Function	Function Code Size [No. Words]
EXP_P1_2p	414
EXP_P1_2pM	424
EXP_P1_4pM	424
EXP_P1_16p_wM_int	390
pow2_P1_8p_wM_int	386
pow2_16p_int	506
pow2_P1_32p_wM_int	388
powf(2,x) from math.h	1848
expf(x) from math.h	624

,

Table 8. Results of the implementation in Artix 7 FPGA.

Function	T [ns]	No. Cycles	No. DSP	% DSP	No. LUT	% LUT	No. FFs	% FFs
EXP_P1_2p	230	23	5	6.25	1835	12.50	552	1.9
EXP_P1_2pM	270	27	5	6.25	1857	12.70	588	2.0
EXP_P1_4pM	270	27	5	6.25	1945	13.30	590	2.0
EXP_P1_16p_wM_int	120	12	6	7.50	1126	7.70	582	2.0
pow2_P1_8p_wM_int	120	12	6	7.50	1120	7.67	582	2.0
pow2_16p_int	120	12	6	7.50	1126	7.70	582	2.0
pow2_P1_32p_wM_int	120	12	6	7.50	1138	7.80	582	2.0

and

Table 9. Results of the implementation in Kintex 7 FPGA.

Function	T [ns]	No. Cycles	No. DSP	% DSP	No. LUT	% LUT	No. FFs	% FFs
EXP_P1_2p	180	18	5	2.1	1837	4.5	502	6.1
EXP_P1_2pM	210	21	5	2.1	1858	4.5	537	6.5
EXP_P1_4pM	210	21	5	2.1	1946	4.7	542	6.6
EXP_P1_16p_wM_int	80	8	6	2.5	1135	2.8	506	6.2
pow2_P1_8p_wM_int	80	8	6	2.5	1129	2.8	506	6.2
pow2_16p_int	80	8	6	2.5	1135	2.8	506	6.2
pow2_P1_32p_wM_int	80	8	6	2.5	1147	4.7	506	6.2

: EXP_P1_16p_wM_int exponential function, 16 parts, without Multiplication, integer approximation, EXP_P1_4pM—exponential function 4 parts, with Multiplication.

Table 3 presents the execution times of the same functions on the microcontroller STM32H750 with the main clock of 480 MHz.

The fastest power function was the float pow2_16p_int (time 8.02 ns). The fastest exponential functions performed on this microcontroller turned out to be EXP_P1_16p_wM_int (time 8.43 ns).

Table 4 collects the execution time results of the same functions on the microcontroller STM32F746 with the main clock at 216 MHz. The fastest exponent functions were the float EXP_P1_16p_wM_int and float exp_18p_wM_int (time 37.55 ns). The fastest power functions executed on this microcontroller turned out to be float pow2_P1_32p_wM_int and pow2_18int (time 38.58 ns).

From the console of the Keil uVision tool, we extracted the memory occupancy data for each microcontroller within the STM32 families, which were utilized in the experiments. Table 5, Table 6 and Table 7 compile the memory usage information for all functions presented in the paper.

In the cases of the STM32H750 and STM32H474 microcontrollers (Table 5 and Table 6), it is clearly visible that the ‘powf’ function from the ‘math.h’ library consumes at least eight times more memory than our functions. Similarly, for the ‘expf’ function, this ratio is approximately 2.6 in favor of our exponential functions.

In the case of the STM32F746 microcontroller (Table 7), it is clearly visible that the ‘powf’ function from the ‘math.h’ library consumes at least 3.6 times more memory than our functions. Conversely, the ‘expf’ function from the ‘math.h’ library occupies 50% more memory than our exponential functions.

4. FPGA Implementation of expf(x) and pow2f(x) Functions

All of the above functions were implemented on a few selected families of FPGAs. For this purpose, the Vitis automatic synthesis tool was applied. This tool generated Verilog code at the RTL level. In this way, the project was implemented by utilising ready-made IP blocks (by Xilinx) as FP operators (FP7.1), a DSP with a certain quantity of LUT-based logic, etc. The Xilinx IP FP7.1 implements basic FP operations inside our functions; as “+”, “−”, DSP blocks execute possible multiplications. The C functions presented in this paper are easily implementable on FPGAs and occupy a small amount of FPGA resources.

The FPGA 7 Series from Xilinx is optimised for low-power applications requiring serial transceivers and high DSP and logic throughput. They provide the lowest total material costs for high-throughput, cost-sensitive applications. They represent High-Performance, Low-power (HPL) (28 nm), High-K Metal Gate (HKMG) process technology. The logic is based on real 6-input LUT technology, configurable as distributed memory. DSP slices are constructed with a 25 × 18 multiplier, 48-bit accumulator, and a pre-adder for high-performance filtering, including optimised symmetric coefficient filtering.

DSP applications use many binary multipliers and accumulators, which are best implemented in dedicated DSP slices. All 7 series FPGAs have many dedicated, full custom, low-power DSP slices, combining high speed with small size, while retaining system design flexibility. Each DSP slice fundamentally consists of a dedicated 25 × 18 bit two’s complement multiplier and a 48-bit accumulator, both capable of operating up to 741 MHz. The multiplier can be dynamically bypassed and two 48-bit inputs can feed a Single-Instruction-Multiple-Data (SIMD) arithmetic unit (dual 24-bit add/subtract/accumulate or quad 12-bit add/subtract/accumulate), or a logic unit that can generate any one of ten different logic functions of the two operands. The DSP includes an additional pre-adder, typically used in symmetrical filters. This pre-adder improves performance in densely packed designs and reduces the DSP slice count by up to 50%. The DSP also includes a 48-bit-wide Pattern Detector that can be used for convergent or symmetric rounding. The pattern detector is also capable of implementing 96-bit-wide logic functions when used in conjunction with the logic unit. The DSP slice provides extensive pipelining and extension capabilities that enhance the speed and efficiency of many applications beyond DSP, such as wide dynamic bus shifters, memory address generators, wide bus multiplexers, and memory-mapped I/O register files. The accumulator can also be used as a synchronous up/down counter. Powerful Clock Management Tiles (CMT), combining Phase-Locked Loop (PLL) and mixed mode clock manager (MMCM) blocks for high precision and low jitter (Xilinx 7 Series Data Sheet, v2.6.1, Sept’20).

The Artix 7 family includes up to 215 k Logic Cells, 13 Mb Block Ram, and 740 DSP slices. The eore sophisticated families, Kintex 7 and Virtex 7, include the following: Kintex 7—up to 478 k Logic Cells, 34 Mb Block Ram, and 1920 DSP slices; Virtex 7—up to 1955 k Logic Cells, 68 Mb Block Ram, and 3600 DSP slices.

For the first case study, one of the widespread FPGA Artix 7 chips was chosen. The clock frequency was set to a default value 100 MHz, because most widespread FPGAs can operate with this clock. This makes it easier to compare the achievements of FPGAs from different families. The execution times and resources used for Artix 7 are presented in Table 8. The fastest exponential function turned out to be exp(x) P1 16 parts, which required 12 clock cycles to complete it (120 ns). All of the powf(2,x) were executed in the same timespan of 12 clock cycles (120 ns). Passing local or global variables to functions has no effect on the execution speed of those functions, unlike STM32 microcontrollers. The implementation of individual functions slightly differs in terms of the amount of FPGA logical resources used.

The implementation of our innovative functions in the smallest chip of the Artix family (xc7a25t-csg325-3) required between 6.25 and 7.50% of built-in DSP blocks. The first three exponential functions only used 5 DSP blocks, whereas only P1 16 parts without multiplication functions were built with 6 DSPs. All the power functions required 6 DSPs. Exponential functions occupied from 7.7% (P1 16 parts without multiplication) up to 13.3% for the P1 4 parts multiplication function. All of our functions occupied no more than 2% of available flip-flops inside the chip. All of the results obtained with the Xilinx Vitis Automated Synthesis Tool are shown in Table 8.

We also investigated the performance of the expf(x) function realised by Xilinx FP7.1. It requires 7 clock cycles i to complete it and occupies 7 DSP blocks, 943 LUTs, and 332 flip-flops. There are 8.8% of available DSPs, 6.5% of LUTs, and 1.1% of flip-flops. The powf(2,x) does not exist in the set of functions realised by the FP7.1 operator. Hence, our functions can complement the implementation of high-precision functions, which easily utilise resources of FP7.1 and DSPs.

FPGA Kintex^®-7 was then tested. This family is optimised for best price-performance with a two times improvement, compared to previous generations, enabling a new class of FPGAs. All the powf(2,x) functions were performed in the same time of 8 clock cycles (80 ns). The fastest exponential function, similar to the case of Artix 7, turned out to be P1 16 parts without multiplication and it was executed in 8 clock cycles (80 ns).

Implementation of our innovative functions in the smallest chip of the Kintex family (xc7k70t-fbv676-3) required between 2.1 and 2.5% of built-in DSP blocks. The first three exponential functions collected in Table 9, used 5 DSP blocks; whereas, only P1 16 parts without multiplication function were built with 6 DSPs. All the power functions required 6 DSPs. This is the same as the Artix 7 case. Exponential functions occupied from 2.8% (P1 16 parts without multiplication) up to 4.7% (for the P1 4 parts multiplication function). Each of our functions occupied less than 7% of available flips-flops inside the FPGA. All the results obtained with the Xilinx Vitis Automated Synthesis Tool are shown in Table 9 below.

The achievements and required FPGA resources for the function expf(x) implemented by the FP 7.1 operator have also been checked. It requires 5 clock cycles to complete, uses 7 DSP blocks, 912 LUTs and 201 flip-flops. It requires 8.8% of available DSPs, 2.2% LUTs, and 0.25% of flip-flops.

The Virtex^®-7 Family is optimised for the highest system performance and capacity with a two times improvement in system performance. The highest capability devices are enabled by stacked silicon interconnect (SSI) technology. The xqvu37p-fsqh2892-2-e chip chosen by us is characterised by rich resources and top performances in the Virtex family.

The fastest exponential function, as in the cases of Artix 7 and Kintex 7, revealed P1 16 parts without multiplication and it was completed in 6 clock cycles (60 ns). All of the powf(2,x) functions were executed in the same time of 6 clock cycles (60 ns). Implementation of our innovative functions in this chip only required between 0.05 and 0.08% of built in DSP blocks. The first three exponential functions used 5 DSP blocks, and only P1 16 parts without multiplication function was built with 7 DSPs. All the power functions required 7 DSPs. Exponential functions occupied from 0.09% (P1 16 parts without multiplication) up to 0.14% (for the P1 2 parts and P1 4 parts multiplication functions). All our functions only occupied about 0.02% of available flip-flops inside the chip. All the results are given in

Table 10. Results of the implementation in Virtexuplus FPGA.

Function	T [ns]	No. Cycles	No. DSP	% DSP	No. LUT	% LUT	No. FFs	% FFs
EXP_P1_2p	120	12	5	0.05	1753	0.13	457	0.02
EXP_P1_2pM	130	13	5	0.05	1765	0.14	460	0.02
EXP_P1_4pM	130	13	5	0.05	1853	0.14	462	0.02
EXP_P1_16p_wM_int	60	6	7	0.08	1141	0.09	471	0.02
pow2_P1_8p_wM_int	60	6	7	0.08	1141	0.09	471	0.02
pow2_16p_int	60	6	7	0.08	1141	0.09	471	0.02
pow2_P1_32p_wM_int	60	6	7	0.08	1141	0.09	471	0.02

. The achievements and required FPGA resources for function expf(x) implemented by the FP7.1 operator for the VirtexUltraPlus are as follows. It requires 3 clock cycles to complete, uses 7 DSP blocks, 760 LUTs and 144 flip-flops. It requires 8.8% of available DSPs and insignificant numbers of LUTs (0.0058%), and flip-flops (0.0052%).

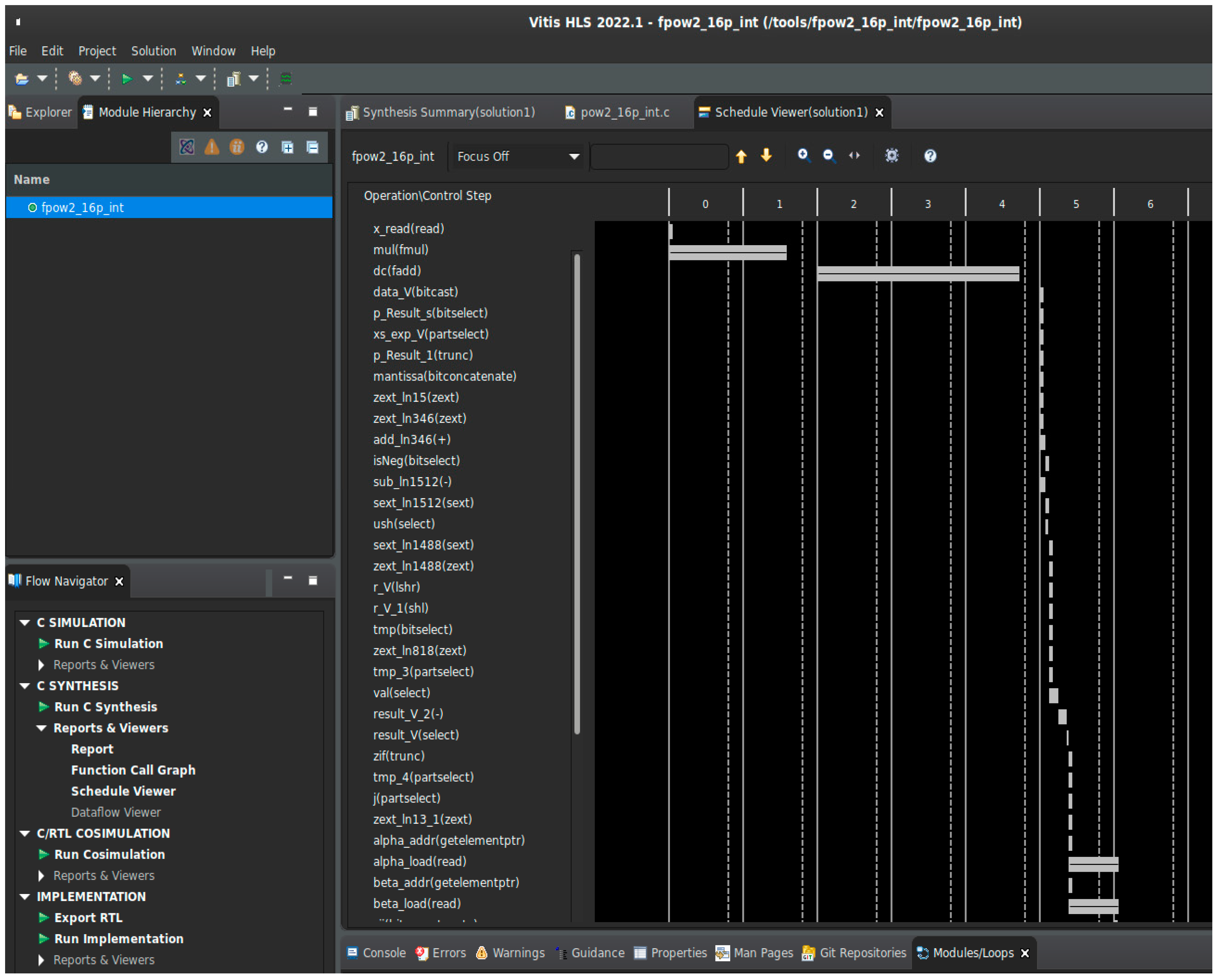
Figure 3 below presents a screenshot excerpt from the Xilinx Vitis tool, showing the report of the ‘pow2_16p_int’ function implementation on the Virtex Ultra Plus FPGA. The latency and required FPGA resources are visible in this figure.

Figure 4 reveals a decomposition example of pow2_16p_int function into individual instructions and their execution time.

Figures for all functions presented in the tables are available on GitHub within projects under the ‘scheduler’ tab for each individual function.

Finally, we implemented our innovative algorithms in one of Xilinx’s most technologically advanced families—Versal.

Versal^® devices are the industry’s first adaptive computer acceleration platform (ACAP), combining adaptable processing and acceleration engines with programmable logic and configurable connectivity to enable customised, heterogeneous hardware solutions for a wide variety of applications in Data Center, Automotive, 5G Wireless, Wired, and Defense. Versal ACAPs feature transformational features like an integrated silicon host interconnect shell and Intelligent Engines (AI and DSP), Adaptable Engines, and Scalar Engines, providing superior performance/watts over conventional FPGAs, CPUs, and GPUs. Versal ACAPs are built around an integrated shell, composed of a programmable Network on a Chip (NoC), which enables seamless memory-mapped access to the full height and width of the device. ACAPs comprise a multicore scalar processing system, an integrated block for PCIe^® with DMA and Cache Coherent Interconnect Designs (CPM), SIMD VLIW AI Engine accelerators (for artificial intelligence and complex signal processing), and Adaptable Engines in the Programmable Logic (PL).

The fastest exponential functions, unlike the case in all previous experiments, turned out to be functions occupying the first three positions in

Table 11. Results of the implementation in Versal FPGA.

Function	T [ns]	No. Cycles	No. DSP	% DSP	No. LUT	% LUT	No. FFs	% FFs
EXP_P1_2p	20	2	1	0.05	1472	0.16	67	0.004
EXP_P1_2pM	20	2	2	0.10	1472	0.16	67	0.004
EXP_P1_4pM	20	2	2	0.10	1535	0.17	69	0.004
EXP_P1_16p_wM_int	40	4	2	0.10	736	0.08	123	0.007
pow2_P1_8p_wM_int	40	4	2	0.10	736	0.08	123	0.007
pow2_16p_int	40	4	2	0.10	736	0.08	123	0.007
pow2_P1_32p_wM_int	40	4	2	0.10	736	0.08	123	0.007

These functions were only executed in 2 clock cycles (20 ns). The execution of P1 16 parts without multiplication function needs 4 clock cycles (20 ns).

All of the powf(2,x) functions were executed in the same time of 4 clock cycles (40 ns). Implementation of our innovative functions in this chip only required between 1 and 2 built-in DSP blocks. This chip possesses up to 1968 such blocks. The first exponential function in Table 11 only used 1 DSP block. An exclusively P1 16 parts without multiplication function was built with 7 DSPs. All remaining exponential and powf(2,x) functions required 2 DSP blocks.

Exponential functions occupied from 0.08% as an example function P1 16 parts without multiplication and all the powf(2,x) functions up to 0.17% of available in the chip LUTs for P1 4 parts multiplication function. The functions in the first two positions in the table occupied 0.16% of LUTs. The first three exponential functions only occupied about 0.004% of available flips-flops inside the chip. The function P1 16 parts without multiplication and all powf(2,x) functions only occupied 0.007% of available flip-flops in the chip. All of the results achieved using the Versal chip are presented in Table 11.

For comparison, the achievements and FPGA resources required for function expf(x), implemented by the FP 7.1 operator inside the Versal chip, were checked the Vitis implementation reports. The expf(x) function requires 2 clock cycles to complete and uses 1 DSP block, 930 LUTs and 99 flip-flops. There are insignificant numbers of LUTs (0.001%) and flip-flops (0.0055%).

Our research reveals that the functions proposed by us are well-suited for implementation in the newest FPGA families. They occupy a negligible amount of resources and effectively use the solutions and resources available in these chips. With reference to the available literature in the field, we implemented our pow2f(x) functions in the same FPGA Zynq7000 chip under the same timing condition (clock frequency 125 MHz) as in [17]. The time performances of our functions observed in

Table 12. Achievements of pow2f(x) functions on Zynq7000.

Function	T [ns]	No. Cycles	No. DSP	No. LUT	No. FFs
pow2_P1_8p_wM_int	104	13	6	1512	607
pow2_16p_int	104	13	6	1518	607
pow2_P1_32p_wM_int	104	13	6	1530	607

are better than those presented in [17] in every case, see

Table 13. Execution time(ns) for ex/ln(x), xy on Zynq7000.

Function	N (Number of Positive Iterations), M = 5
	8	12	16	20	24	32	36	40
$e^x/\ln \left(x\right)$	136	168	208	240	272	336	368	408
$x^y$	280	344	424	488	552	680	744	824

.

All C codes and FPGA projects are available on: https://github.com/pawelgepner/Power_Function/tree/main (accessed on 6 August 2023).

5. Conclusions

In this article, algorithms for the exponential and power function calculation for FP numbers (half, single, and double precision) were developed. Our contribution to the field can be formulated as follows:

• To increase the accuracy, we proposed the modification of the Schraudolph method, applied to calculating the function $a^x$;
• Our novel algorithms are based on piecewise linear approximation, float to integer and inverse type conversion, and bit manipulations technics;
• To achieve the speedup of algorithms and the ease of hardware implementation, we were focused and influenced by their architecture, based on one multiplication and one addition.

Such algorithms, with low complexity, provide decent accuracy and speed, sufficient for practical applications as accelerators for neural networks, power electronics, machine learning, computer vision, and intelligent robotic systems.

Our innovative algorithms are executed in a very short time on microcontrollers of the STM32H7 family. This family has extensive DSP blocks. Moreover, they are easily executable on older families of microcontrollers (STM32F).

Our research reveals that the functions proposed by us are well suited for implementation in the newest FPGA families too. They occupy a negligible amount of resources and effectively use the solutions and resources available in these chips.