Wideband DOA Estimation Utilizing a Hierarchical Prior Based on Variational Bayesian Inference
Abstract
1. Introduction
2. Signal Model
3. Proposed Approach
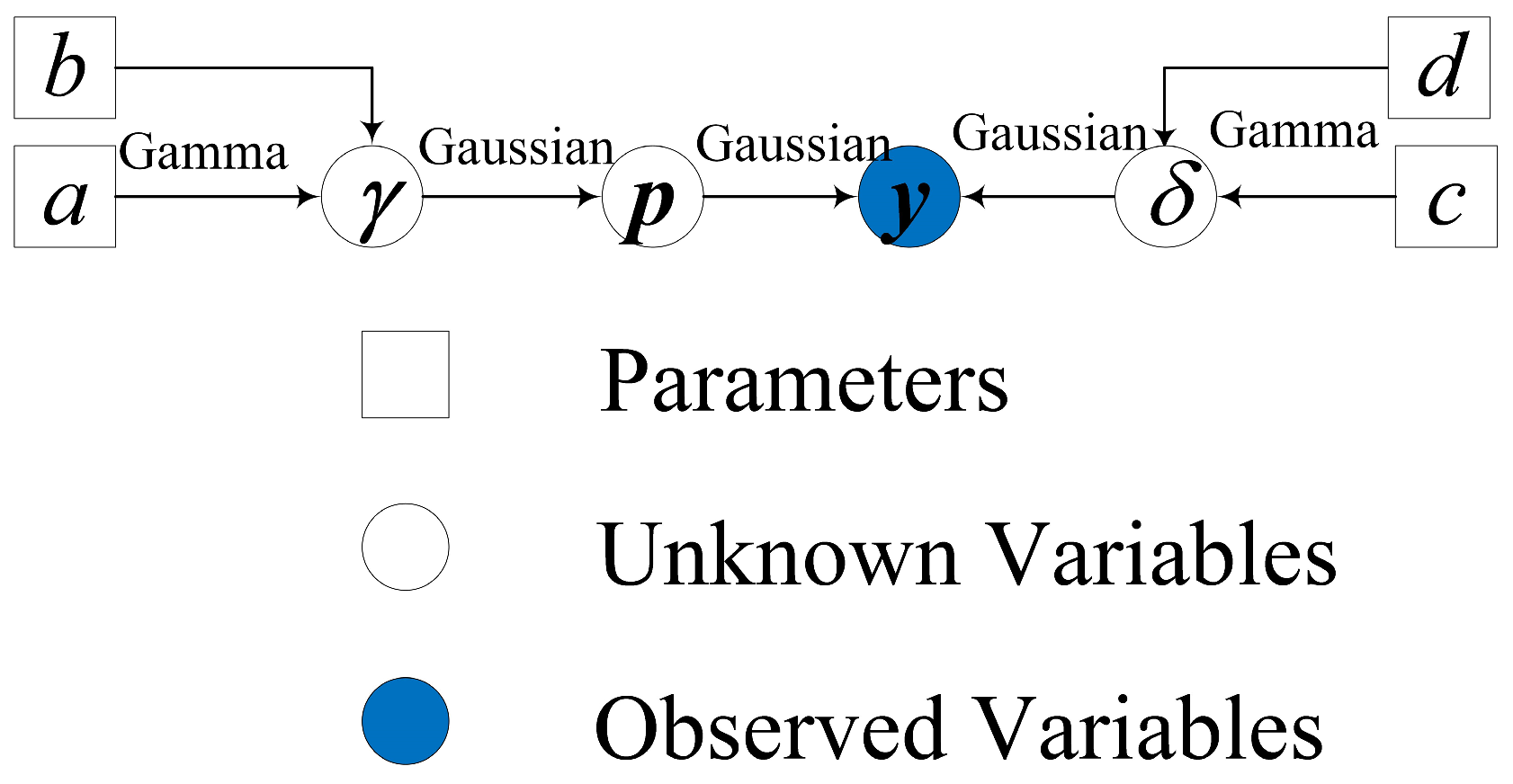
3.1. Bayesian Model
3.2. Variational Bayesian Inference
- (1)
- Initialization. Set the first iterative number , (ensure uninformative distribution), and . Preset error tolerance and maximal iterative number .
- (2)
- Repetition. Input , and .While ( or ) do:{Compute and according to (15) and (16), respectively;Compute and according to (20) and (24), respectively;Update ;Regard as .}End while
- (3)
- Output. Obtain final and calculate the corresponding DOA.
3.3. Computational Complexity
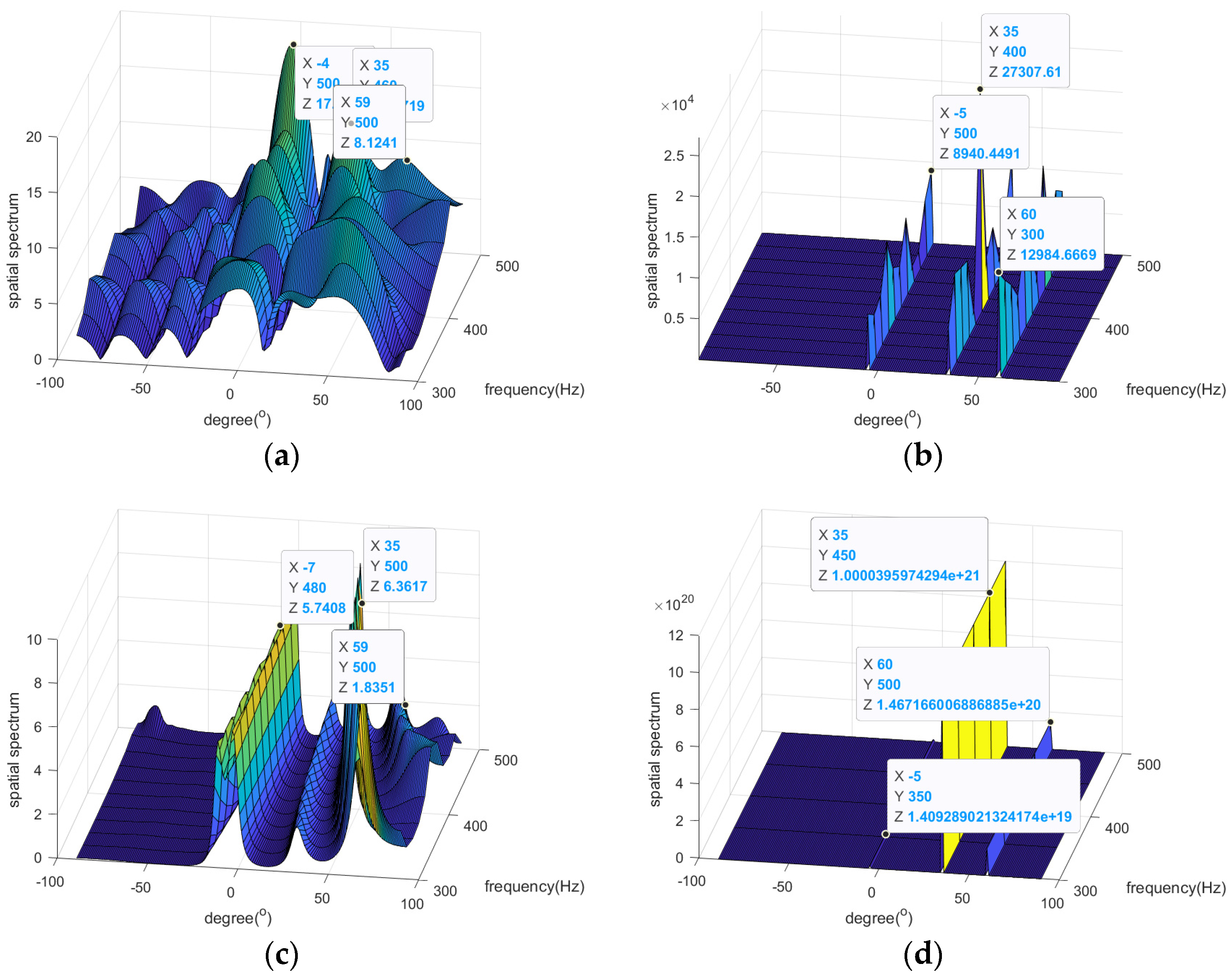
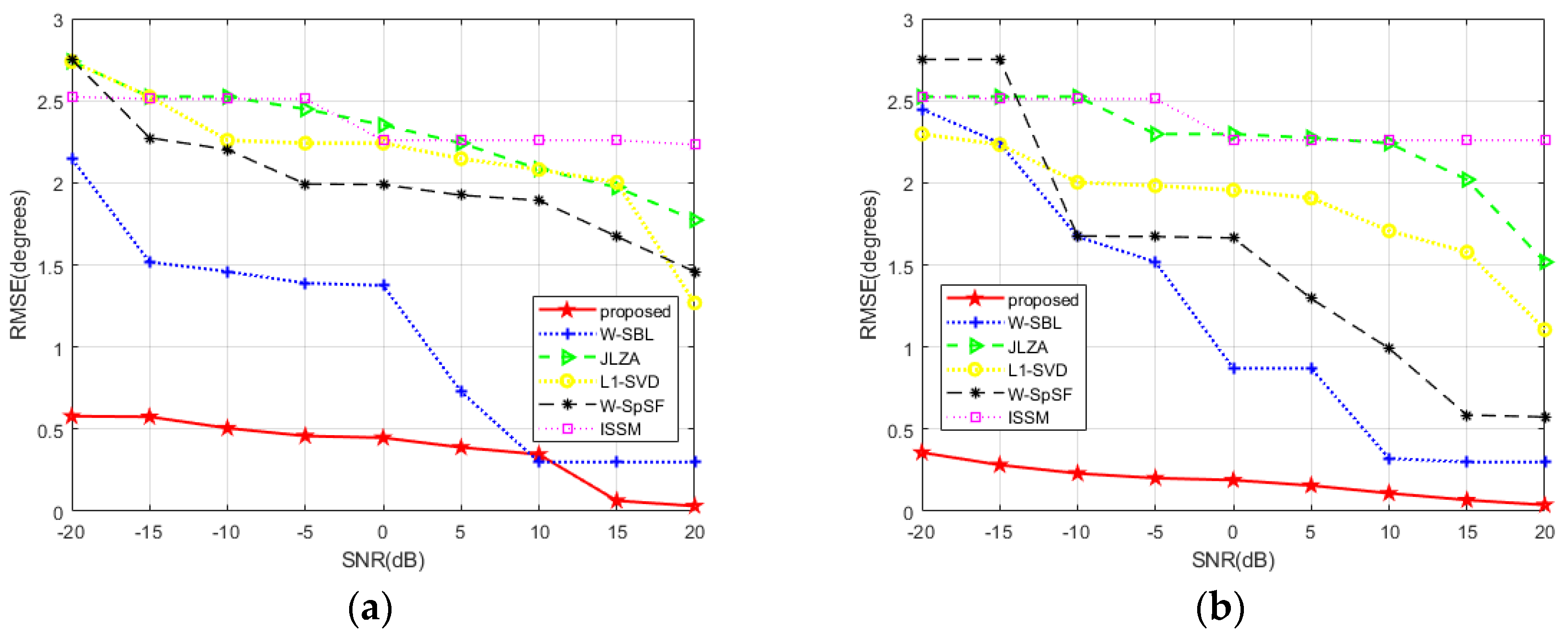
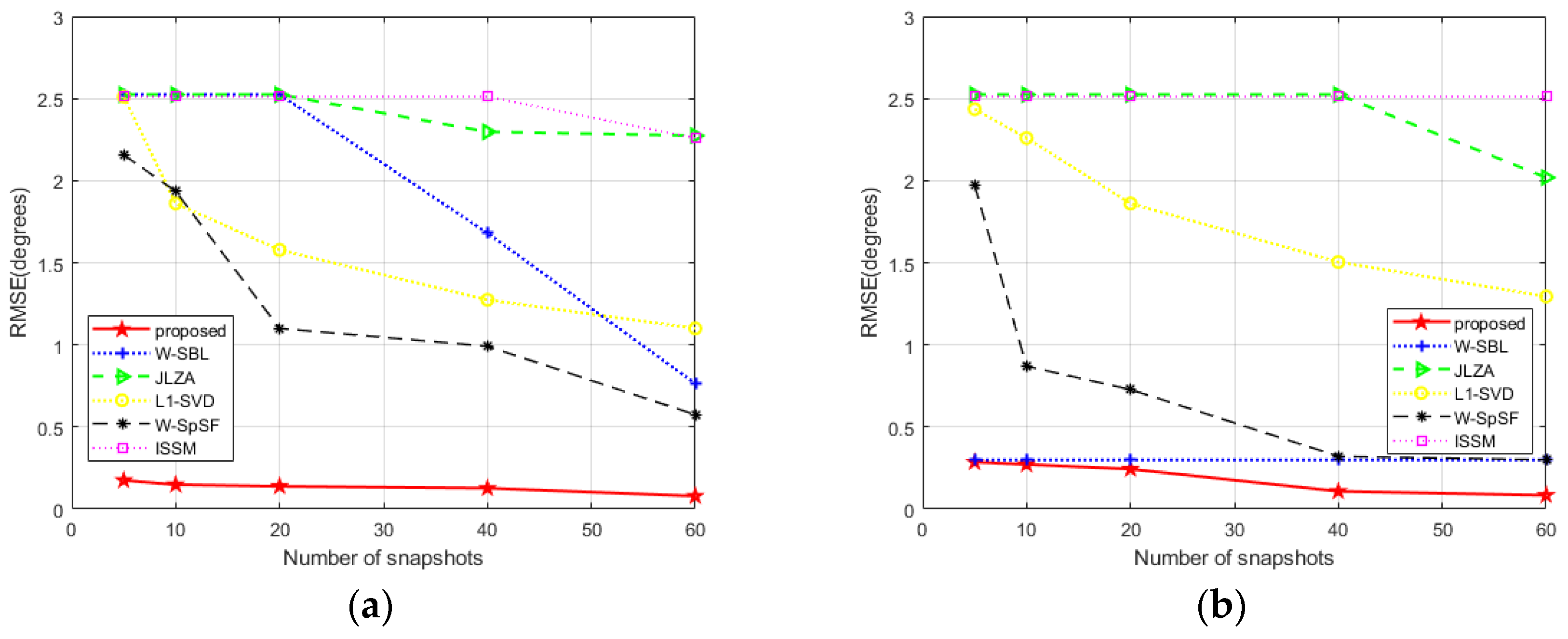
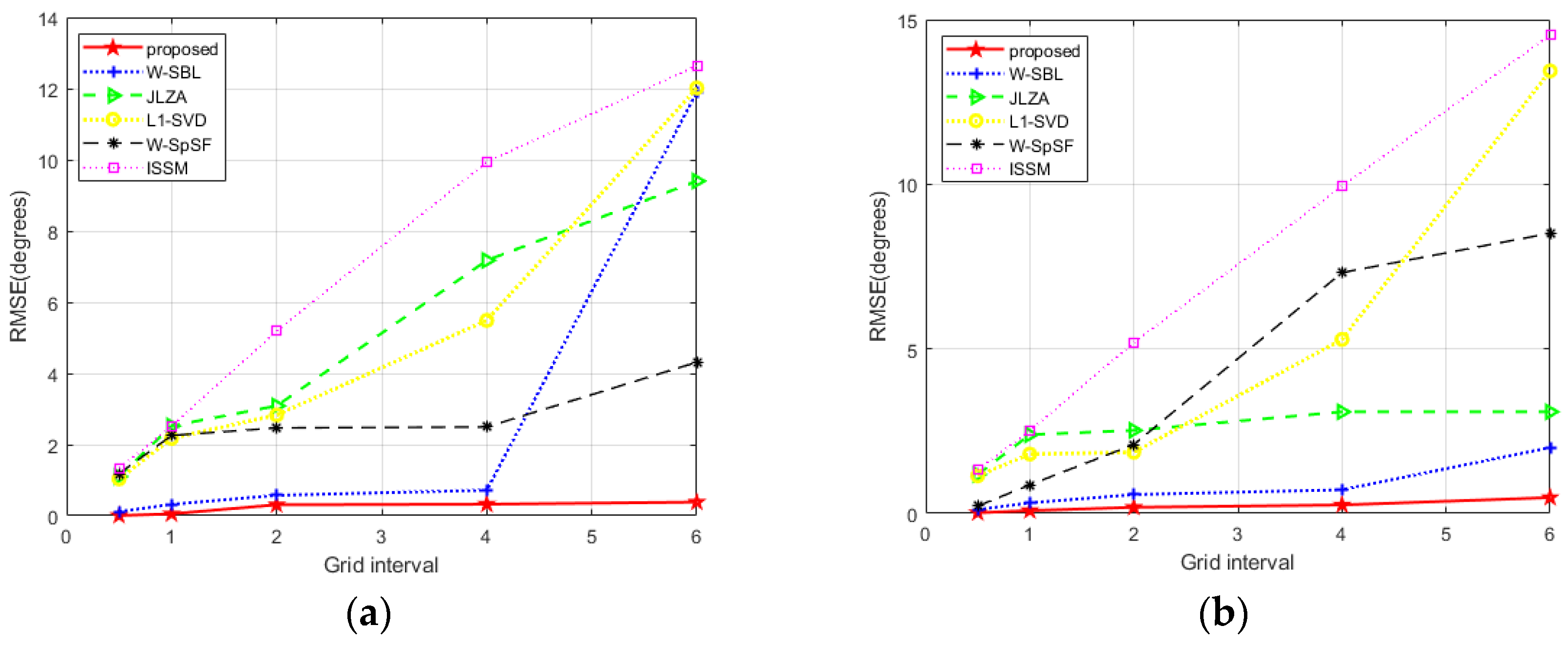
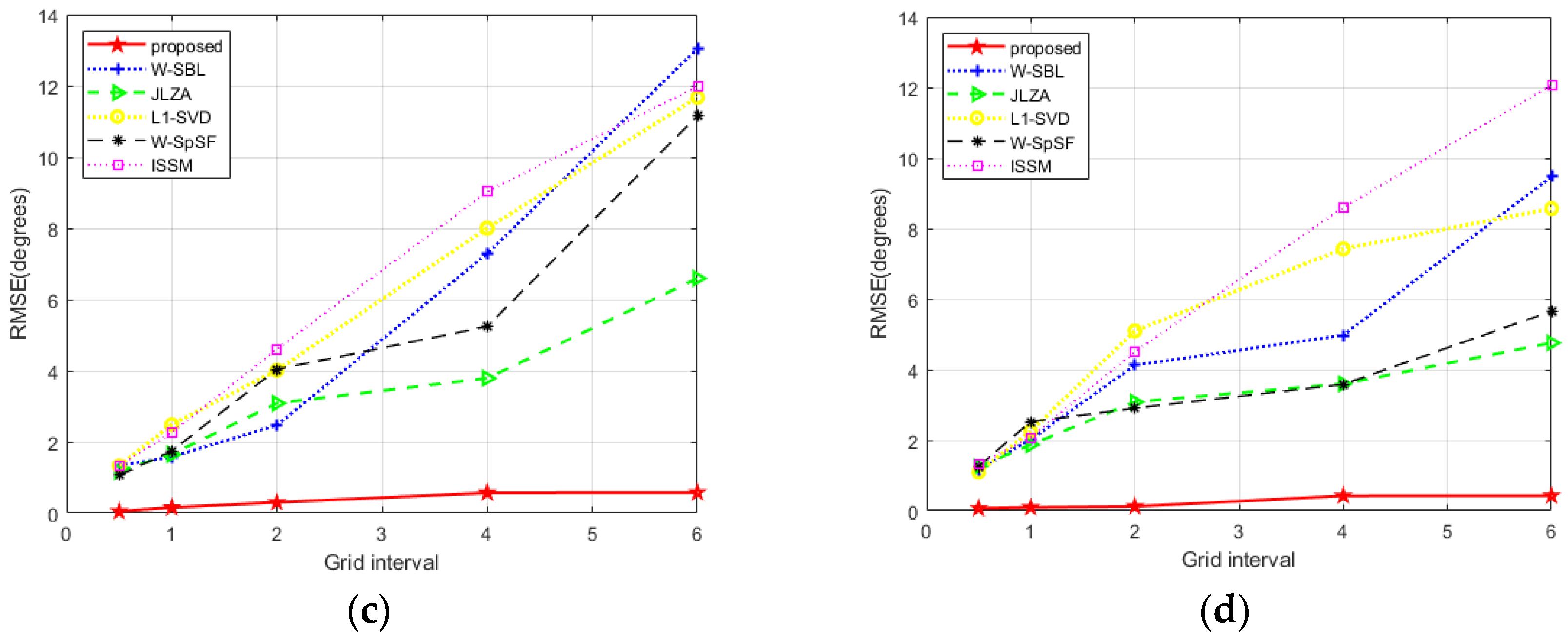
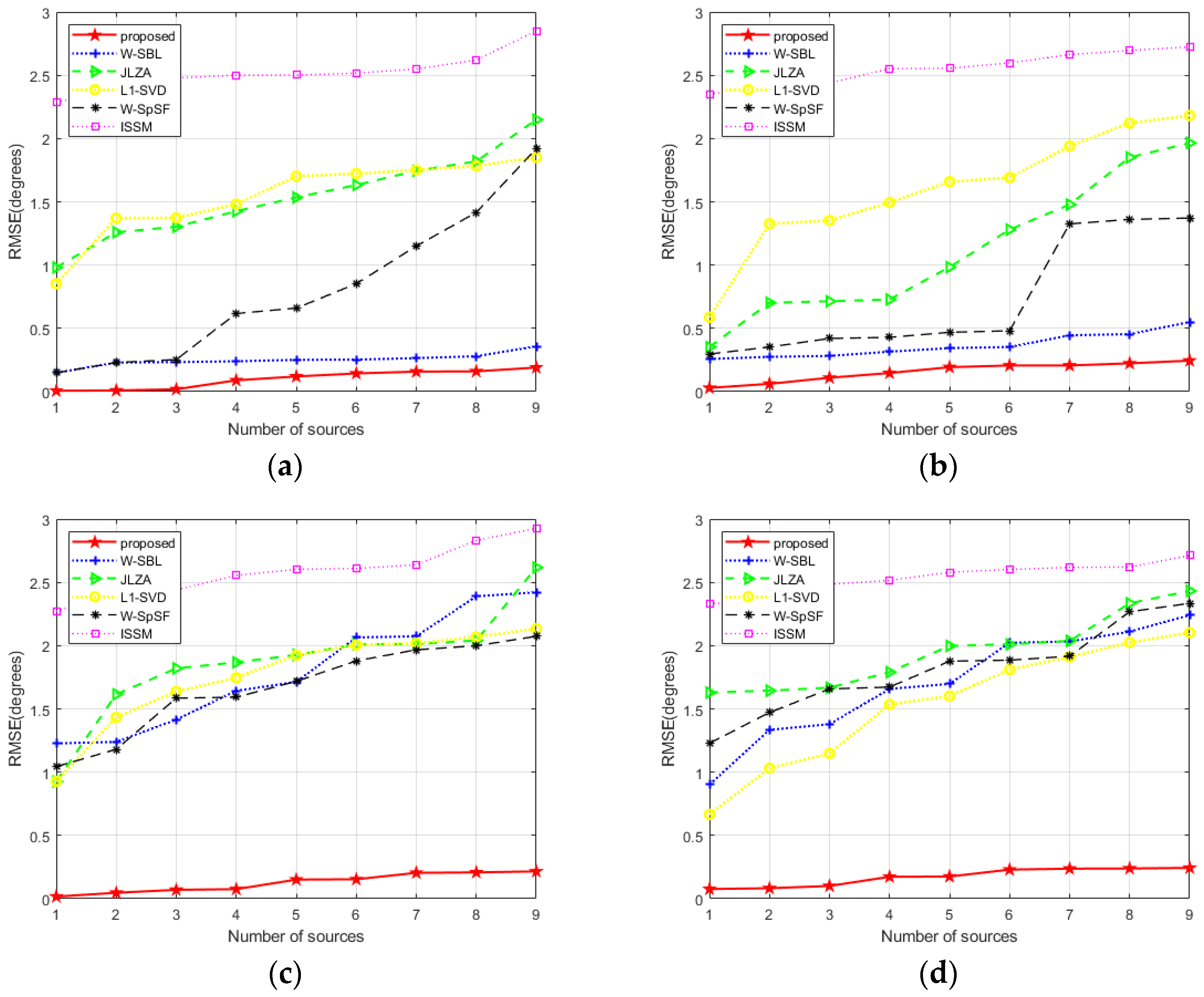
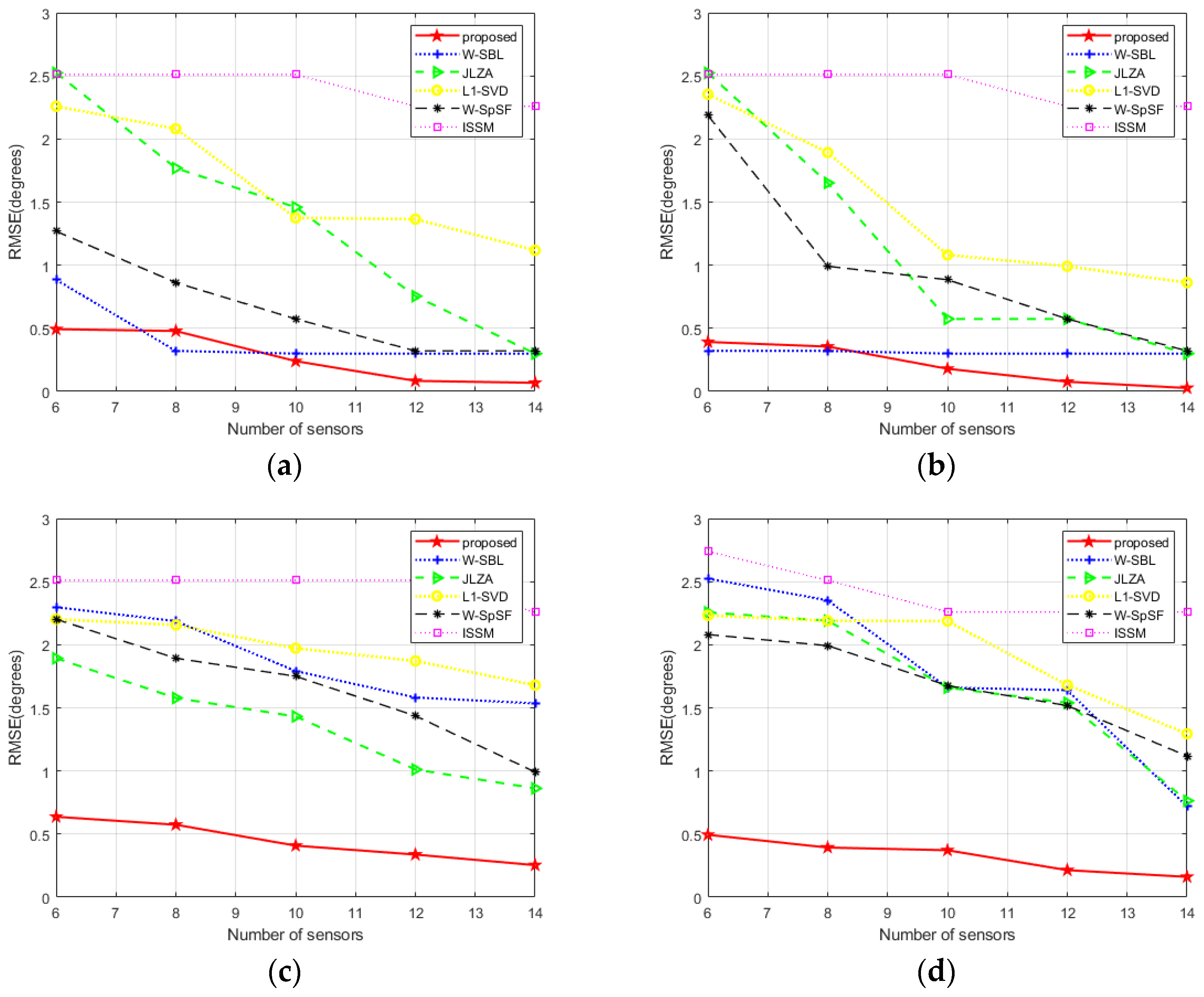
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Proc. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Liu, C.; Zakharov, Y.V.; Chen, T. Broadband underwater localization of multiple sources using basis pursuit de-noising. IEEE Trans. Signal Process. 2011, 60, 1708–1717. [Google Scholar] [CrossRef]
- Liu, Z.M.; Huang, Z.T.; Zhou, Y.Y. An efficient maximum likelihood method for direction-of-arrival estimation via sparse Bayesian learning. IEEE Trans. Wirel. Commun. 2012, 11, 1–11. [Google Scholar] [CrossRef]
- Su, G.; Morf, M. The signal subspace approach for multiple wide-band emitter location. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 1502–1522. [Google Scholar]
- Allam, M.; Moghaddamjoo, A. Two-dimensional DFT projection for wideband direction-of-arrival estimation. IEEE Trans. Signal Process. 1995, 43, 1728–1732. [Google Scholar] [CrossRef]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Hung, H.; Kaveh, M. Focussing matrices for coherent signal-subspace processing. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1272–1281. [Google Scholar] [CrossRef]
- El-Keyi, A.; Kirubarajan, T. Adaptive beamspace focusing for direction of arrival estimation of wideband signals. Signal Process. 2008, 88, 2063–2077. [Google Scholar] [CrossRef]
- Tang, Z.; Blacquiere, G.; Leus, G. Aliasing-free wideband beamforming using sparse signal representation. IEEE Trans. Signal Process. 2011, 59, 3464–3469. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, W.; Cui, W.; Wu, S. Underdetermined DOA estimation under the compressive sensing framework: A review. IEEE Access 2016, 4, 8865–8878. [Google Scholar] [CrossRef]
- Gan, L.; Wang, X. DOA estimation of wideband signals based on slice-sparse representation. EURASIP J. Adv. Signal Process. 2013, 2013, 18. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, Y.; Liu, J.; Yu, Z. Underdetermined wideband DOA estimation for off-grid sources with coprime array using sparse Bayesian learning. Sensors 2018, 18, 253. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Feng, W.; Feng, C.; Ma, T.; Zou, B. Deep Unfolded Gridless DOA Estimation Networks Based on Atomic Norm Minimization. Remote Sens. 2022, 15, 13. [Google Scholar] [CrossRef]
- Hyder, M.M.; Mahata, K. Direction-of-Arrival Estimation Using a Mixed l2,0 Norm Approximation. IEEE Trans. Signal Process. 2010, 58, 4646–4655. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- He, Z.Q.; Shi, Z.P.; Huang, L.; So, H.C. Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting. IEEE Signal Process. Lett. 2014, 22, 435–439. [Google Scholar] [CrossRef]
- Hu, N.; Sun, B.; Zhang, Y.; Dai, J.; Wang, J.; Chang, C. Underdetermined DOA estimation method for wideband signals using joint nonnegative sparse Bayesian learning. IEEE Signal Process. Lett. 2017, 24, 535–539. [Google Scholar] [CrossRef]
- Zhao, L.; Li, X.; Wang, L.; Bi, G. Computationally efficient wide-band DOA estimation methods based on sparse Bayesian framework. IEEE Trans. Veh. Technol. 2017, 66, 11108–11121. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. Sparse Bayesian learning for basis selection. IEEE Trans. Signal Process. 2004, 52, 2153–2164. [Google Scholar] [CrossRef]
- Wipf, D.P.; Rao, B.D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem. IEEE Trans. Signal Process. 2007, 55, 3704–3716. [Google Scholar] [CrossRef]
- Zhang, Z.; Rao, B.D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning. IEEE J. Sel. Top. Signal Process. 2011, 5, 912–926. [Google Scholar] [CrossRef]
- Tzikas, D.G.; Likas, A.C.; Galatsanos, N.P. The variational approximation for Bayesian inference. IEEE Signal Process. Mag. 2008, 25, 131–146. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| Real Gaussian distribution with mean and covariance | |
| Complex Gaussian distribution with mean and covariance | |
| Kronecker product | |
| Hadamard product | |
| Khatri–Rao product | |
| identity matrix | |
| Constant | |
| i.i.d | Independent and identically distributed |
| Conditional probability density distribution of variable with respect to variable | |
| Probability density distribution of variable with respect to variable | |
| Probability density distribution | |
| Expectation with respect to | |
| Transforming matrix into vector diagonally or transforming vector into matrix diagonally | |
| Obtain the norm after finding the norm for each row of a matrix |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Zhang, X.; Zong, B.; Lv, F.; Xu, J.; Wang, Z. Wideband DOA Estimation Utilizing a Hierarchical Prior Based on Variational Bayesian Inference. Electronics 2023, 12, 3074. https://doi.org/10.3390/electronics12143074
Li N, Zhang X, Zong B, Lv F, Xu J, Wang Z. Wideband DOA Estimation Utilizing a Hierarchical Prior Based on Variational Bayesian Inference. Electronics. 2023; 12(14):3074. https://doi.org/10.3390/electronics12143074
Chicago/Turabian StyleLi, Ninghui, Xiaokuan Zhang, Binfeng Zong, Fan Lv, Jiahua Xu, and Zhaolong Wang. 2023. "Wideband DOA Estimation Utilizing a Hierarchical Prior Based on Variational Bayesian Inference" Electronics 12, no. 14: 3074. https://doi.org/10.3390/electronics12143074
APA StyleLi, N., Zhang, X., Zong, B., Lv, F., Xu, J., & Wang, Z. (2023). Wideband DOA Estimation Utilizing a Hierarchical Prior Based on Variational Bayesian Inference. Electronics, 12(14), 3074. https://doi.org/10.3390/electronics12143074






