Emergent Cooperation and Strategy Adaptation in Multi-Agent Systems: An Extended Coevolutionary Theory with LLMs

Abstract

The increasing complexity of Multi-Agent Systems (MASs), coupled with the emergence of Artificial Intelligence (AI) and Large Language Models (LLMs), have highlighted significant gaps in our understanding of the behavior and interactions of diverse entities within dynamic environments. Traditional game theory approaches have often been employed in this context, but their utility is limited by the static and homogenous nature of their models. With the transformative influence of AI and LLMs on business and society, a more dynamic and nuanced theoretical framework is necessary to guide the design and management of MASs. In response to this pressing need, we propose an Extended Coevolutionary (EC) Theory in this paper. This alternative framework incorporates key aspects of coevolutionary dynamics, adaptive learning, and LLM-based strategy recommendations to model and analyze the strategic interactions among heterogeneous agents in MASs. It goes beyond game theory by acknowledging and addressing the diverse interactions (economic transactions, social relationships, information exchange) and the variability in risk aversion, social preferences, and learning capabilities among entities. To validate the effectiveness of the EC framework, we developed a simulation environment that enabled us to explore the emergence of cooperation and defection patterns in MASs. The results demonstrated the potential of our framework to promote cooperative behavior and maintain robustness in the face of disruptions. The dynamics and evolution of the Multi-Agent System over time were also visualized using advanced techniques. Our findings underscore the potential of harnessing LLMs to facilitate cooperation, enhance social welfare, and promote resilient strategies in multi-agent environments. Moreover, the proposed EC framework offers valuable insights into the interplay between strategic decision making, adaptive learning, and LLM-informed guidance in complex, evolving systems. This research not only responds to the current challenges faced in modeling MASs, but also paves the way for future research in this rapidly developing field.

1. Introduction

The modern world is increasingly characterized by complex systems and interactions. These systems often involve a multitude of diverse entities, ranging from individuals and organizations to autonomous agents in Artificial Intelligence (AI)-driven environments. At the heart of understanding these complex interactions is strategic decision making, which is a vital aspect in economics, sociology, biology, and, more recently, in AI.

The study of strategic decision making has long been an essential aspect of understanding interactions among diverse entities in various domains, such as economics, sociology, and biology. Classical game theory, which was pioneered by John von Neumann and further developed by John Nash [1,2], has provided a foundational framework for analyzing these interactions and predicting the outcomes of strategic choices. However, with the rapid advancements in AI and the emergence of Large Language Models (LLMs), there is a growing need to develop new theoretical frameworks that can better capture the dynamics of Multi-Agent Systems (MASs) in the presence of these disruptive forces [3,4,5,6].

One of the key challenges in modeling strategic interactions is the inherent complexity of the environments and agents involved. In real-world scenarios, entities often have diverse characteristics, such as different risk aversions, social preferences, and learning capabilities, that can significantly influence their decision-making processes [7]. Moreover, these entities interact through various channels, including economic transactions, social relationships, and information exchange, which can further complicate the analysis of their strategic behaviors [8].

Human–Computer Interaction (HCI) is a multidisciplinary field that focuses on the design, implementation, and evaluation of interactions between humans and computers. It encompasses a wide range of topics, including the joint performance of tasks by humans and computers; the structure of communication between humans and computers; human capabilities to use computers; algorithms and programming of the interface itself; engineering concerns that arise in designing and building interfaces; the process of specification, design, and implementation of interfaces; and design trade offs.

Multi-Agent Systems (MASs) represent a paradigm in AI that models complex systems as a collection of autonomous agents that are each capable of reactive, proactive, and social behavior. These agents, which can be software programs or physical entities, interact with one another and their environment to achieve individual or shared objectives. Key concepts in MASs include coordination and control; reasoning and planning; and learning and adaptation.

In this study, we explored the intersection of HCI and MASs by integrating the EC framework with Large Language Models (LLMs) [9,10] to model and simulate the dynamics of cooperation and defection in MASs. The EC framework combines elements from game theory, coevolutionary algorithms, and MASs to analyze and predict the behavior of agents in various interaction scenarios. By incorporating LLMs as AI agents that can provide strategic recommendations and influence human decision making, we aim to create a more comprehensive model of HCI in the context of MASs.

The core of our proposal lies in the use of intelligent sensors and sensor networks as a means to facilitate the communication and cooperation between human and intelligent agents. These sensors enable the collection of valuable data and allow for real-time adaptation and learning in response to changing environmental conditions or agent interactions. By integrating MASs and HCI, we hope to develop novel technologies and solutions centered around the use of intelligent sensors in various applications, thereby ultimately enhancing the effectiveness and efficiency of MASs in diverse HCI contexts.

HCI plays a critical role in understanding and facilitating effective cooperation between humans and intelligent agents within MASs. While HCI encompasses a wide range of topics, in this paper, we emphasize the societal and economic perspectives of interactions between humans and AI-driven entities, such as LLMs. These perspectives involve the exchange of information, the joint performance of tasks, and the influence of AI-based strategic recommendations on human decision-making processes. By integrating HCI and MASs, we aim to create a comprehensive model that captures the evolving nature of interactions in complex systems, thereby ultimately offering insights into promoting cooperation, enhancing social welfare, and building resilience in multi-agent environments.

At the core of our proposal, we regard LLMs as intelligent sensors or AI agents that interact with human counterparts within MASs. These LLMs, which can be conceived as advanced AI-driven entities or even embodied as robots, provide strategic recommendations, process information, and influence human decision-making processes. By integrating LLMs as intelligent sensors within MASs, we facilitate the collection of valuable data that enables real-time adaptation and learning in response to changing environmental conditions or agent interactions. Our approach aims to develop novel technologies and solutions that center on the use of intelligent sensors and robots in various applications, thereby ultimately enhancing the effectiveness and efficiency of MASs across diverse HCI contexts.

Traditional approaches have largely relied on game theory. However, as the digital era progresses, disruptive forces such as AI and LLMs are transforming the landscape of strategic decision making. These advancements underline the pressing need for new theoretical frameworks that are capable of capturing the nuanced dynamics of MASs amidst this transformative wave.

To this end, we introduce an Extended Coevolutionary (EC) Theory as an alternative to traditional game theory approaches for modeling and analyzing strategic interactions among heterogeneous agents. Our EC framework aims to capture the evolving nature of MASs and incorporate the potentially disruptive influence of LLMs on business and society. The main contributions of this study are:

• The development of a comprehensive theoretical framework that integrates coevolutionary dynamics, adaptive learning, and LLM-based strategy recommendations for understanding the emergence of cooperation and defection patterns in MASs.
• The design of a simulation environment that allows for the exploration of the EC framework, thus incorporating heterogeneous agents and multi-layer networks to model diverse interactions among entities.
• The evaluation of the effectiveness of the EC framework in promoting cooperative behavior and robustness in the face of disruptions by using various performance metrics and advanced visualization techniques.

By achieving these objectives, we hope to provide valuable insights into the interplay between strategic decision making, adaptive learning, and LLM-informed guidance in complex, evolving systems. Our findings have the potential to inform the development of novel strategies and interventions for harnessing the power of AI and LLMs in promoting cooperation, enhancing social welfare, and building resilience in multi-agent environments.

The remainder of this paper is organized as follows: In Section 2, we provide a comprehensive review of the related work that covers topics such as game theory and NASH equilibrium, coevolutionary algorithms, MASs, and AI. Section 3 presents the EC framework and discusses its key components, such as coevolutionary dynamics, adaptive learning, and the role of LLMs in strategy formation. Section 3.4 introduces the concept of LLMs in the EC framework and explains how they can be used to generate strategy recommendations and influence agent interactions. In Section 4, we present the methodology, which provides proofs of the EC framework to establish its mathematical foundations. Section 5 details the simulation environment used in our experiments, including implementation details, performance metrics, and visualization techniques. Section 6 presents the results and analysis of our experiments by examining the emergence of cooperation and defection patterns, the influence of LLM-based strategy recommendations, and the overall system robustness and resilience. Section 7 discusses the broader implications of our findings for business and society, as well as the limitations of our current framework and potential avenues for future work. Finally, Section 8 concludes the paper by summarizing our key findings and contributions to the field of MASs and HCI.

2. Related Work and Theoretical Context

Game theory is a mathematical framework for studying strategic interactions among rational agents [11]. A central concept in game theory is the NASH equilibrium, which is a state in which no player can improve their utility by unilaterally changing their strategy, given the strategies of the other players [1]. The concept of NASH equilibrium has been widely applied to model and analyze a variety of strategic situations, including economic transactions, social dilemmas, and political negotiations [12]. Recent research has explored the extensions of classical game theory to incorporate more realistic assumptions about agent behavior and the dynamics of strategic interactions, such as bounded rationality, learning, and adaptation [13,14]. These extensions have led to the development of new solution concepts and methods for predicting and influencing the outcomes of strategic interactions in complex, evolving environments.

Coevolutionary algorithms are a class of evolutionary algorithms that model the adaptive processes of learning and optimization in populations of interacting agents [15]. In coevolutionary algorithms, agents adapt their strategies over time in response to the strategies of other agents in the population, thereby leading to the emergence of complex patterns of cooperation, competition, and specialization [16,17,18]. These algorithms have been used to study a wide range of problems in AI, optimization, and MASs, including the evolution of cooperation in social dilemmas [19,20,21], the development of efficient algorithms for hard optimization problems [22,23], and the emergence of communication and coordination in MASs [24,25].

MASs [26] are part of a subfield of AI that focuses on the development of computational models and algorithms for simulating and controlling the interactions among multiple autonomous agents [27,28,29]. MAS research aims to understand the underlying principles that govern the behavior of complex, distributed systems, and to develop methods for coordinating the actions of individual agents to achieve global objectives [30,31].

Recent advances in AI, particularly in the areas of machine learning and Large Language Models (LLMs) [32,33,34], have opened up new possibilities for modeling and analyzing strategic interactions in MASs [35]. While there is limited research on the direct integration of LLMs in this specific setting, our work aims to bridge this gap and explore the potential impacts of AI on the dynamics of cooperation, competition, and social welfare in evolving multi-agent environments. The infusion of LLM-based advice into agent decision making opens up promising avenues for investigation, particularly regarding the potential benefits and challenges posed by AI-driven guidance in MASs. Notably, LLMs, such as GPT-3.5-turbo, are capable of generating human-like natural language text, thereby allowing them to provide strategic guidance and recommendations to agents in a Multi-Agent System [36]. By incorporating LLM-based advice into the decision-making processes of agents, researchers have begun investigating the potential benefits and challenges that may arise from AI-driven guidance in MASs.

For instance, recent studies have shown that LLMs can enhance the performance of agents in various tasks, such as negotiation [37] and coordination [38], by providing real-time strategic recommendations based on the current state of the environment and agent interactions. These initial findings suggest that LLMs can play a significant role in shaping the dynamics of multi-agent systems and, ultimately, the outcomes of strategic interactions.

In summary, while the direct integration of LLMs in the context of strategic interactions and MASs is still an emerging area of research, our work aims to contribute to the understanding of the potential benefits and challenges associated with incorporating AI-driven guidance in complex, evolving environments. By extending existing theories and methodologies, such as coevolutionary algorithms and game theory, our proposed Extended Coevolutionary (EC) framework seeks to capture the unique characteristics of LLMs and their potential impact on the dynamics of cooperation, competition, and social welfare in Multi-Agent Systems.

3. EC Theory

In this section, we present the Extended Coevolutionary (EC) Theory framework, which is the main contribution of our work. Our EC framework integrates concepts from game theory, coevolutionary algorithms, and AI to study the emergence and evolution of cooperation and defection in Multi-Agent Systems (MASs). Specifically, the EC framework extends classical game-theoretic models [17,39] by incorporating adaptive learning, heterogeneous agents, and multi-layer network structures. Moreover, we introduce the use of LLMs, such as GPT-3.5-turbo, to assist agents in forming their strategies, thereby enabling a more comprehensive understanding of the dynamics of strategic interactions in complex environments. In the following subsections, we detail the key components and theoretical tools used in the development of the EC framework.

3.1. Coevolutionary Dynamics and Adaptive Learning

Coevolutionary dynamics are central to our proposed EC framework, as they capture the process by which agents adapt their strategies in response to the strategies of others in the population. The EC framework employs adaptive learning mechanisms in which agents update their strategies based on the utilities they receive from interacting with other agents.

Let $s_z$ denote the strategy of agent z, and let $U_z(s_z,s_{-z})$ represent the utility of agent z given its own strategy $s_z$ and the strategies of all other agents $s_{-z}$. The adaptive learning process can be described by the following update rule:

$$s_z(t+1)=s_z\left(t\right)+\alpha \nabla U_z(s_z\left(t\right),s_{-z}\left(t\right)),$$

(1)

where $\alpha$ is the learning rate, and $\nabla U_z$ is the gradient of the utility function with respect to the strategy $s_z$. This update rule captures the process by which agents adjust their strategies to maximize their utilities based on the current state of the population.

3.2. Large Language Models in Strategy Formation

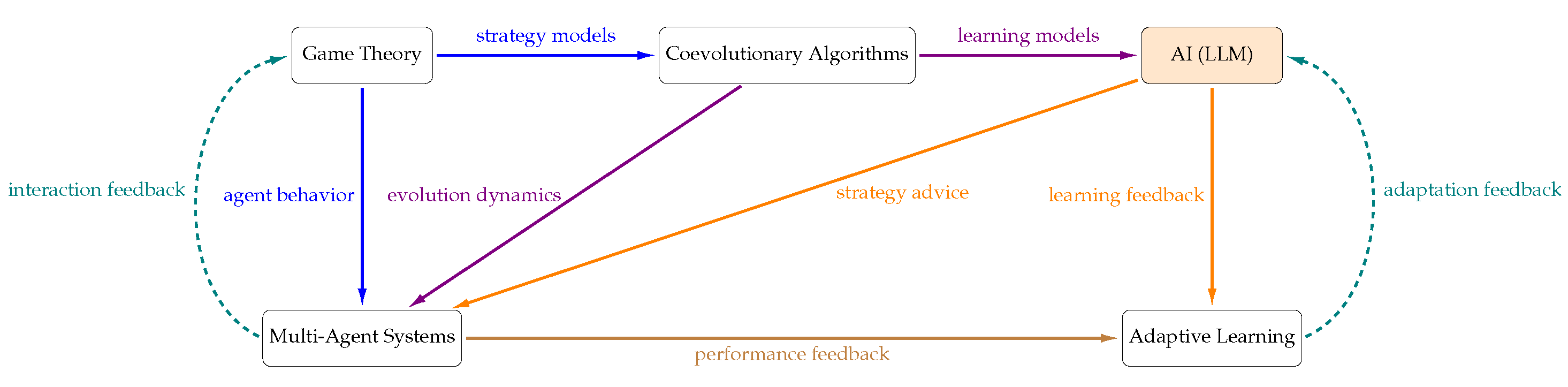
In our EC framework, we also incorporated the use of LLMs, such as GPT-3.5-turbo, to assist agents in forming their strategies. These AI agents can provide valuable insights and recommendations based on the current state of the game and the strategies of neighboring agents. By integrating LLMs into the adaptive learning process, we can explore how the introduction of AI agents influences the dynamics of cooperation and defection in MASs; an illustrative diagram can be seen in Figure 1.

Indeed, the feedback process in adaptive learning extends beyond modifying interaction strategies. Adaptive learning involves an iterative process of adjusting the model parameters based on the feedback received, thereby continuously improving the performance of the model. In our EC framework, adaptive learning not only informs the strategies adopted by agents, but also refines the underlying models that drive agent behavior. Specifically, the “learning feedback” from the LLM to the adaptive learning component of the system captures this process of continuous improvement. When the LLM provides strategic advice to the agents, it includes not only immediate actions, but also feedback on the current strategies. This feedback is then used to adjust the models that inform agent behavior, thereby enabling them to learn and adapt over time. Moreover, the “adaptation feedback” from the adaptive learning component back to the LLM signifies the updates in model parameters based on the performance and interaction feedback. This continuous feedback loop ensures that the LLM, and, thus, the strategies it recommends, evolves over time to better support agent interactions.

3.3. Heterogeneous Agents and Multi-Layer Network Model

The EC framework acknowledges the importance of agent heterogeneity and complex network structures in shaping the dynamics of strategic interactions. We modeled agents with varying characteristics, such as different levels of risk aversion, social preferences, and learning capabilities. Furthermore, we introduced a multi-layer network model that captures multiple types of interactions between agents, such as economic transactions, social relationships, and information exchange.

The multi-layer network is represented by a tuple $G=(V,E_1,E_2,\dots ,E_k)$, where V is the set of nodes (agents), and $E_z$ is the set of edges (interactions) in layer z. The multi-layer network allows us to study the interdependencies between different types of interactions and their effects on cooperation and defection dynamics in the population.

3.4. Large Language Models in EC

LLMs, such as GPT-3.5-turbo, play a significant role in the EC framework, especially in the context of strategic formation and adaptive learning. These AI agents can analyze the current state of the game, the strategies employed by neighboring agents, and can provide valuable insights and recommendations for the agents’ next actions. The incorporation of LLMs within the EC framework enables a deeper understanding of the dynamics of cooperation and defection, as well as the influence of AI agents on the overall system.

3.4.1. LLM-Based Adaptive Learning

In the EC framework, LLMs are used to support agents during the adaptive learning process. At certain intervals, agents consult the LLM for advice on their next strategic move while considering the strategies of their neighbors. To formalize this interaction, let $Q_{z,t}$ be the LLM’s recommendation for agent z at time t. We can express the recommendation as a function of the neighboring agents’ strategies $s_{-z}\left(t\right)$:

$$Q_{z,t}=f\left(s_{-z}\left(t\right)\right),$$

(2)

where $f(·)$ is the function representing the LLM’s recommendation process.

In the context of real-time applications, the function $f(·)$ needs to be efficient and robust. Efficiency is required to ensure that the recommendation process does not introduce significant latency into the system, which is especially critical in real-time applications where timely response is often necessary. Robustness, on the other hand, is needed to ensure that the recommendation process can handle a wide range of possible inputs and still produce meaningful outputs. This is crucial in a dynamic Multi-Agent System where the strategies of neighboring agents can vary significantly over time. In the context of LLMs, the function $f(·)$ is implemented by the LLM’s underlying ML model. The model is trained on a large corpus of data and is capable of generating strategic recommendations based on the input it receives. The specifics of this process depend on the architecture and training of the LLM. In the case of GPT-3.5-turbo, for example, the model takes the current context, including the strategies of neighboring agents, and generates a recommendation based on patterns it has learned during its training.

The agent’s strategy update can then be modeled as a combination of its original adaptive learning process and the LLM’s recommendation:

$$s_z(t+1)=(1-\beta )\left(s_z\left(t\right)+\alpha \nabla U_z(s_z\left(t\right),s_{-z}\left(t\right))\right)+\beta Q_{z,t},$$

(3)

where $\beta \in [0,1]$ represents the influence rate of the LLM on the agent’s strategy. When $\beta =0$, the agent relies solely on its original adaptive learning process; when $\beta =1$, the agent fully adopts the LLM’s recommendation.

3.4.2. Incorporating LLM Uncertainty

Given the probabilistic nature of LLM-generated recommendations, it is essential to consider the uncertainty associated with the LLM’s advice. One way to account for this uncertainty is to introduce a confidence measure $c_{z,t}$ that is associated with the LLM’s recommendation:

$$c_{z,t}=g\left(Q_{z,t}\right),$$

(4)

where $g(·)$ is a function that maps the LLM’s recommendation to a confidence value in the range $[0,1]$.

By incorporating the confidence measure, we can adjust the agent’s strategy update rule as follows:

$$s_z(t+1)=(1-\beta c_{z,t})\left(s_z\left(t\right)+\alpha \nabla U_z(s_z\left(t\right),s_{-z}\left(t\right))\right)+\beta c_{z,t}{Q}_{z,t}.$$

(5)

This modified update rule allows agents to weigh the LLM’s advice based on the confidence associated with the recommendation, thereby leading to a more nuanced adaptive learning process.

In summary, our EC Theory framework provides a powerful and flexible approach for studying the emergence and evolution of cooperation and defection in MASs. By incorporating adaptive learning, heterogeneous agents, multi-layer network structures, and LLMs, the EC framework can offer novel insights into the complex dynamics of strategic interactions in diverse settings. Futhermore, the integration of LLMs within the EC framework provides a novel perspective on the dynamics of cooperation and defection in MASs. The LLM-assisted adaptive learning process, along with the consideration of LLM uncertainty, contributes to a more comprehensive understanding of the complex strategic interactions in diverse settings.

4. Methodology

Let us assume that our EC framework can be reduced to a simple two-player game with finite strategy sets and that the utility functions incorporate only the immediate payoffs without the adaptive learning mechanisms or LLM-based strategy recommendations. The proof below demonstrates the existence of a NASH equilibrium for this simplified game using Brouwer’s fixed-point theorem.

Theorem 1. 

Given a two-player game in the EC framework with each player having a finite set of strategies and where the utility functions are based only on immediate payoffs, without any adaptive learning mechanisms or Large Language Model (LLM) based strategy recommendations, there exists a NASH equilibrium.

Proof. 

Let us consider a two-player game represented by the EC framework, with each player o having a finite set of strategies $S_o$, where $o\in \{1,2\}$. Let $\mathbf{s}=(s_1,s_2)$ denote a strategy profile, where $s_o\in S_o$ for both players.

• Define the utility functions $u_o\left(\mathbf{s}\right)$ for each player o as the immediate payoffs from the chosen strategy profile $\mathbf{s}$.
• Define the best response correspondence $B_o:S_{-o}\to S_o$ for each player o, which maps a strategy of the opponent to the set of best responses for player o. Since $S_o$ is finite, the best response correspondence is nonempty and upper hemicontinuous.
• Define the correspondence $G:S_1\times S_2\to S_1\times S_2$ as $G(s_1,s_2)=(B_1\left(s_2\right),B_2\left(s_1\right))$. This maps a strategy profile $\mathbf{s}$ to the set of best response profiles for both players. Since $B_o$ is nonempty and upper hemicontinuous for both players, G is also nonempty and upper hemicontinuous.
• Define the strategy space $S=S_1\times S_2$ and assume it is a compact and convex set. Compactness follows from the finiteness of the strategy sets, and convexity follows, since we can treat the strategies as probability distributions over the pure strategies.
• Apply Brouwer’s fixed-point theorem, which states that every continuous function from a compact, convex set to itself has a fixed point. Since G is nonempty, upper hemicontinuous, and maps S to itself, it has a fixed point ${\mathbf{s}}^{*}=(s_1^{*},s_2^{*})\in S$.
• At this fixed point ${\mathbf{s}}^{*}$, we have $s_1^{*}\in B_1\left(s_2^{*}\right)$ and $s_2^{*}\in B_2\left(s_1^{*}\right)$. This means that, given the strategy of the opponent, each player is choosing their best response, thus making ${\mathbf{s}}^{*}$ a NASH equilibrium.

By following these steps and applying Brouwer’s fixed-point theorem, we have proven the existence of a NASH equilibrium for a simplified two-player game within the EC framework. □

An interesting point to note here is that the convex combination in (4) is proposed under the assumption that the weightings of the adaptive learning mechanism and the LLM’s recommendation sum to one, which is often a mathematical convenience that helps to maintain the strategy within a defined strategy space. This is particularly important when strategies are represented as probability distributions over a finite set of pure strategies, where the sum of probabilities must equal to one. A convex combination ensures that the resulting strategy is a valid probability distribution. However, considering an affine combination could also bring an interesting perspective. An affine combination could potentially allow for a greater range of weightings and, thus, may offer more flexibility. It could provide a richer representation of how the agent might incorporate the advice from the LLM or the learning mechanism in its decision-making process. But it is important to note that using an affine combination could lead to situations where the strategy might fall outside the original strategy space, especially if the strategies are represented as probability distributions. We could indeed modify the model to allow for affine combinations of the adaptive learning mechanism and the LLM’s recommendation, provided that we adjust the strategy space and the interpretation of the strategies accordingly. We could also explore different mechanisms to determine the relative weightings of the two components, beyond a simple fixed weight. For instance, the weightings could depend on the agent’s confidence in the LLM’s recommendation or on the performance of the adaptive learning mechanism.

Another important issue to consider is that the existing formulation does not characterize the LLM-related uncertainty and seems to be more related to the sensitivity of the agents’ strategies to the LLM’s recommendations. To address this point, we could propose to revise the model to explicitly consider the uncertainty in the LLM’s recommendation. The LLM’s recommendation $Q_{z,t}$ could be modeled as a random variable instead of a deterministic function of the neighboring agents’ strategies $s_{-z}\left(t\right)$. This could better represent the inherent uncertainty of AI systems. We could also explore ways to quantify this uncertainty. For instance, we could explore this by incorporating a measure of the variance or entropy associated with the LLM’s recommendation. We might also consider modifying the utility functions to reflect the agents’ risk attitudes towards the LLM-related uncertainty. For example, risk-averse agents might prefer strategies that minimize the potential negative impact of an inaccurate LLM recommendation, while risk-neutral agents might be indifferent to this uncertainty. However, it is important to note that introducing uncertainty into the model may complicate the analysis. The existence of a NASH equilibrium, as demonstrated in the proof using Brouwer’s fixed-point theorem, may no longer be guaranteed. This is because the fixed-point theorem assumes that the function (in this case, the correspondence G) is deterministic, whereas introducing uncertainty into the LLM’s recommendation might render G stochastic.

Given the complexity of LLMs and the inherent difficulties in mathematically formalizing their properties, proving a specific aspect of the EC framework that incorporates LLM-based strategy recommendations is challenging. However, we can attempt to provide a simple proof that demonstrates the potential improvement in utility for an agent following LLM-based strategy recommendations.

The assumptions and simplifications include the following:

• Consider a two-player game represented by the EC framework, with each player o having a finite set of strategies $S_o$, where $o\in \{1,2\}$.
• Assume that the LLM provides strategy recommendations for player 1.
• Let the true utility functions $u_o\left(\mathbf{s}\right)$ for each player o be known and fixed.
• Assume that the LLM’s recommendations are based on the true utility functions of both players and that the LLM generates recommendations that maximize player 1’s expected utility, given player 2’s strategy.

The proof indeed builds on several strong assumptions and simplifications, especially the third one, where we assume that the true utility functions are known and fixed. This is, of course, an oversimplification; in real-world scenarios, utility functions might be unknown or dynamically changing. This assumption is made primarily to make the proof tractable, thereby providing a simplified demonstration of the potential benefits of incorporating LLM-based strategy recommendations. The third assumption can be interpreted as a “perfect information” assumption. We are assuming that the LLM is omniscient and has complete information about the utility functions of both players.

Theorem 2. 

Consider a two-player game represented by the EC framework, where each player o has a finite set of strategies $S_o$ ($o\in \{1,2\}$), and the true utility functions $u_o\left(\mathbf{s}\right)$ for each player o are known and fixed. Assume that the LLM provides strategy recommendations for player 1 and that these recommendations are based on the true utility functions of both players. If the LLM’s recommendations aim to maximize player 1’s expected utility given player 2’s strategy, then player 1’s expected utility following the LLM’s recommendations will be at least as high as when choosing any other strategy from their strategy set.

Proof. 

Let $\mathbf{s}=(s_1,s_2)$ denote a strategy profile, where $s_o\in S_o$ for both players. Define $s_1^R$ as the strategy recommendation provided by the LLM for player 1, given player 2’s strategy $s_2$.

1.

Define the expected utility for player 1 when following the LLM’s recommendation as $E\left[u_1(s_1^R,s_2)\right]$.

2.

Since the LLM generates recommendations based on the true utility functions of both players and aims to maximize player 1’s expected utility, we have $E\left[u_1(s_1^R,s_2)\right]\ge E\left[u_1(s_1,s_2)\right]$ for any $s_1\in S_1$.

3.

If player 1 chooses to follow the LLM’s strategy recommendation $s_1^R$, their expected utility will be at least as high as when choosing any other strategy from their strategy set.

□

In this simplified proof, we have shown that following LLM-based strategy recommendations can potentially improve the expected utility for player 1. However, it is important to note that this proof is built on several assumptions and simplifications that may not hold in more complex scenarios or when considering adaptive learning mechanisms and heterogeneous agents.

These proofs provide a strong foundation for understanding the theoretical aspects of the EC framework and the potential benefits of incorporating LLM-based strategy recommendations in Multi-Agent Systems.

5. Simulation Environment

The EC framework was implemented as a simulation environment to explore the interactions between heterogeneous agents in a multi-layer network. The simulation consists of a discrete-time system with the following steps:

• Initialization: Create a set of N heterogeneous agents with varying characteristics such as risk aversion, social preferences, and learning capabilities. Generate a multi-layer network representing various types of interactions between agents, such as economic transactions, social relationships, and information exchange.
• Iteration: For each time step $t\in \{1,2,\dots ,T\}$, where T is the total number of simulation rounds:

  (a)

  Simulate interactions between agents based on their current strategies and update their utilities.

  (b)

  Apply adaptive learning to update the agents’ strategies, with LLM consultations at specified intervals.

  (c)

  Update the network structure based on the evolving strategies and utilities of agents.

• Analysis: Evaluate the system’s performance using various metrics and visualize the network’s evolution to gain insights into the dynamics of cooperation and defection.

The multi-layer network structure we use in the simulation is not only a complex system composed of three interconnected layers—economic’, social’, and ‘information’—but it is also a reflection of real-world multi-agent systems. Each layer represents a distinct type of interaction among the agents. These interactions are not isolated; instead, they collectively influence the decision-making process of the agents in a holistic manner. For example, an agent’s economic decisions may be influenced by their social interactions and the information they receive. Moreover, these interactions and their consequences can feedback into each layer, thereby causing changes that can further influence the decision-making process. In addition to interacting within and across layers, the agents themselves are characterized by their strategies and attributes that were previously presented. For instance, the strategies formulated in the context of the EC framework are implemented by the agents as they interact within and across the layers of the multi-layer network.

Formally, the multi-layer network can be defined as a tuple $G=(V,E_1,E_2,E_3)$, where:

• V is the set of nodes (entities) in the network, each characterized by a strategy, risk aversion, social preference, learning capability, and utility.
• $E_1$ represents the set of edges in the ‘economic’ layer indicating economic interactions between the entities.
• $E_2$ represents the set of edges in the ‘social’ layer indicating social interactions between the entities.
• $E_3$ represents the set of edges in the ‘information’ layer indicating information exchange between the entities.

The multi-layer network was constructed as a multi-graph in order to allow for multiple edges between a pair of nodes that are each associated with a different layer. The edges within each layer were generated using a random graph model with a specified edge probability. This model ensured that the network structure exhibited a random distribution of edges, thus capturing the inherent uncertainty and complexity of real-world interaction patterns among agents. The multi-layer network structure served as a robust and versatile framework for simulating the interplay of various interaction types among agents, thereby facilitating a comprehensive understanding of the system’s dynamics and evolution.

While this multi-layer network structure was used here for simulation purposes, its design is representative of the type of complex multi-agent systems seen in real-world situations. By using such a structure, we can capture and study the interplay of various interaction types among agents, which is crucial for understanding the dynamics and evolution of Multi-Agent Systems.

5.1. Performance Metrics

To measure the effectiveness of the EC framework, several performance metrics were introduced, including overall social welfare, the prevalence of cooperation, and the robustness of the system to shocks or disruptions. The selection of these metrics was motivated by their ubiquity in Multi-Agent Systems literature and their relevance to the specific aspects we aimed to enhance through the EC framework.

• Overall social welfare: The sum of all agents’ utilities at time t. This metric is traditionally used in economics and game theory to measure the total benefit accrued by all members of a system, thus providing an aggregate measure of system performance. Higher social welfare indicates that more agents are achieving higher utility, which aligns with the goal of our EC framework to improve individual and collective outcomes.

  $$W\left(t\right)=\sum _{z=1}^N{U}_z\left(t\right).$$

  (6)
• Prevalence of cooperation: The proportion of agents employing a cooperative strategy at time t. This metric is particularly relevant for Multi-Agent Systems where cooperative behavior can lead to mutual benefit or improved social welfare. As the EC framework aims to encourage cooperative behavior, monitoring the prevalence of cooperation provides a direct measure of this aspect of the system’s performance.

  $$P_c\left(t\right)=\frac{{\sum }_{z=1}^{N}I[s_z\left(t\right)=\mathrm{cooperate}]}{N},$$

  (7)

  where $I[·]$ is the indicator function, which equals 1 if the condition inside the brackets is true and equals 0 otherwise.
• Robustness: The ability of the system to maintain cooperation levels in the face of shocks or disruptions. In Multi-Agent Systems literature, the robustness of a system is often a critical measure of performance, and it indicates how well the system can adapt to changes or uncertainties. Given that real-world Multi-Agent Systems often face dynamic environments and perturbations, we incorporated this metric to evaluate how well the EC framework could maintain performance under such conditions.

  $$R\left(t\right)=\frac{P_c\left(t\right)-P_c(t-1)}{P_c(t-1)}.$$

  (8)

5.2. Visualization Techniques

Effective visualization techniques are essential for understanding the complex dynamics of the EC framework. Several approaches can be employed to illustrate the evolution of the system, including:

• Time-lapse network visualization: Display the network’s evolution over time in an animation in order to highlight changes in network structure, agent strategies, and cooperation levels. This visualization can be created using libraries such as NetworkX or Gephi, where nodes represent agents, and edges represent relationships. The nodes’ colors and sizes can be adjusted based on the cooperation levels, thereby allowing observers to track the development of cooperation and defection strategies over time.
• Interactive visualizations: Develop interactive visualizations that allow users to explore the relationships between agents, their strategies, and the various types of interactions in the multi-layer network. This can be achieved using web-based visualization libraries such as D3.js or Plotly, which enable the creation of dynamic, responsive visualizations. For example, users could filter agents based on certain attributes, adjust time scales, or zoom into specific areas of the network to investigate local dynamics. Tooltips can also be added to display additional information about individual agents and their strategies by hovering or clicking.
• Heatmaps: Generate heatmaps to visualize the spatial distribution of cooperation and defection strategies, thus providing insights into the emergence of clusters or patterns within the network. This can be done using Python libraries such as Matplotlib or Seaborn, where the X-axis represents rounds, the Y-axis represents agents, and the color intensity indicates the cooperation level of each agent. Such heatmaps can help identify regions of high cooperation or defection, as well as detect sudden shifts in strategies or the formation of stable cooperation clusters over time.

These visualization techniques, along with the performance metrics, provide valuable tools for analyzing the behavior of agents and the overall dynamics of cooperation and defection within the EC framework.

6. Results and Analysis

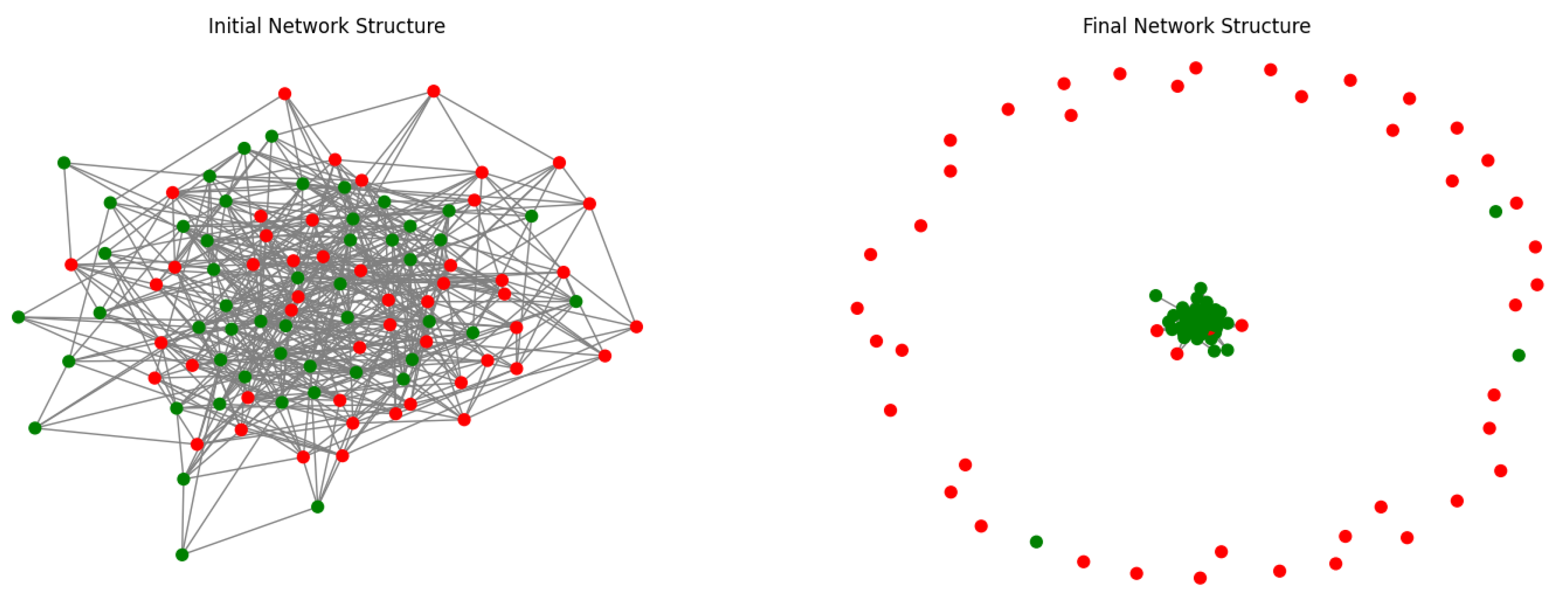
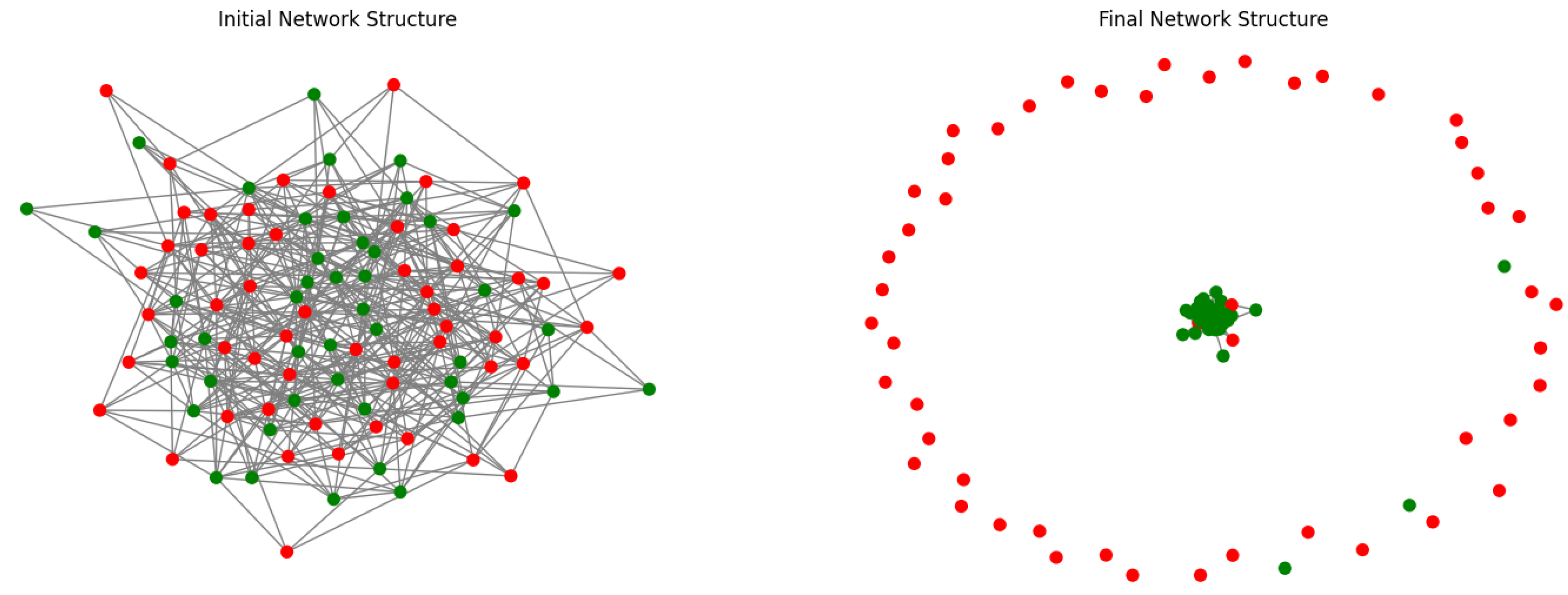
In this section, we present the results and analysis of our experiments with the EC framework, with a focus on the emergence of cooperation and defection patterns among heterogeneous agents in the Multi-Agent System. We investigated the role of adaptive learning and the impact of LLM-based strategy recommendations on these patterns, as well as the network’s overall robustness and resilience. The network’s initial and final structures, as shown in Figure 2 and Figure 3, provide a visual representation of the evolution of these patterns over time.

The experiments conducted in this study were executed using a custom-built Multi-Agent System simulator, which was designed specifically to study the emergence of cooperation and defection patterns in complex networks. This simulator allows for the creation and manipulation of heterogeneous agents by implementing adaptive learning processes and incorporating LLM-based strategy recommendations. It is capable of simulating dynamic, evolving multi-layer networks while tracking and visualizing changes in the system over time. The simulator provides a comprehensive platform for observing and analyzing the effects of various hyperparameters and network structures on agent behavior and overall system performance. The visualizations generated by the simulator facilitate a deeper understanding of the complex dynamics at play within the Multi-Agent System, thereby enabling researchers to fine-tune the EC framework and optimize its potential for fostering cooperation in diverse real-world applications.

Through the implementation of the EC framework, we observed the emergence of cooperation and defection patterns within the Multi-Agent System. The adaptive learning process, combined with the varying characteristics of heterogeneous agents, led to the formation of clusters of cooperators and defectors within the network. These clusters evolved dynamically over time, having been influenced by the agents’ strategies and interactions with their neighbors. Next, we will delve deeper into the factors contributing to these patterns and their significance in the context of the EC framework.

In the simulations conducted, a set of hyperparameters was used to determine the behavior of the agents and the network. The total number of agents, or entities, in the network was set to 100. The simulation was run over 500 rounds to observe the evolution of agent strategies and network properties. The initial cooperation factor was set to $0.5$, meaning that 50% of the agents started with a cooperative strategy. The learning rate was set at $0.1$, which determined the probability of agents adapting their strategies based on their neighbors’ performance. To model the addition of new connections between agents, an edge addition probability of $0.05$ was used, thereby allowing the network to evolve over time. Finally, a cooperation threshold of $0.6$ was implemented, which represented the minimum proportion of cooperative neighbors needed for an agent to switch to a cooperative strategy. These hyperparameters guided the simulation and influenced the outcomes of social welfare and cooperation prevalence within the network.

The prevalence of cooperation increased when agents were able to learn from their neighbors’ strategies, particularly in the presence of high levels of trust and reciprocity. Conversely, when agents were more risk-averse or selfish, defection patterns emerged, leading to suboptimal outcomes for both the individual agents and the system as a whole.

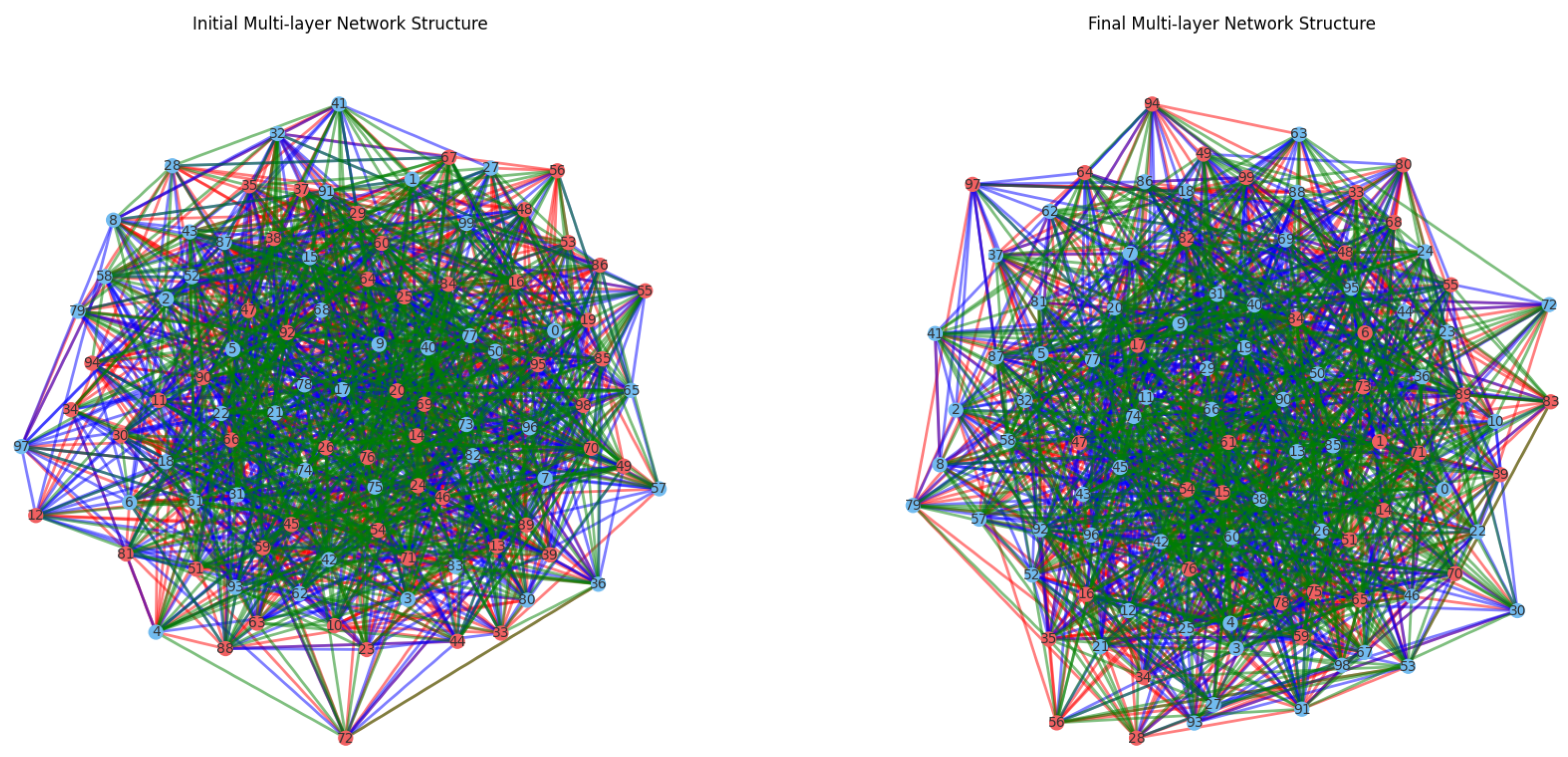
The incorporation of LLMs into the EC framework significantly impacted the adaptive learning process and the formation of cooperation and defection patterns, as shown in Figure 2, Figure 3, Figure 4 and Figure 5. The LLM consult interval served as an effective mechanism to analyze their influence on the system. By consulting the LLMs at specific intervals, we could observe the impact of their recommendations on the agents’ decision making, as well as the resulting cooperation and defection patterns over time.

When agents consulted LLMs for strategy recommendations, they were more likely to make informed decisions based on the broader context of their neighbors’ strategies and the network structure. The LLM-based recommendations promoted cooperation, especially when the majority of neighbors were already cooperating, as agents sought to maximize their utilities through mutual cooperation.

The choice of using an LLM consult interval, rather than a direct comparison of the system with and without LLMs, allowed us to better understand the dynamic interplay between LLM-guided decision making and the agents’ autonomous adaptive learning. This approach offers insights into the complex, evolving relationships between agents, their strategies, and the network structure, which might be obscured in a direct comparison scenario.

Moreover, LLMs helped agents to adapt more quickly to changes in their environment, such as the emergence of defectors or fluctuations in the levels of trust and reciprocity within the network. This increased adaptability allowed the agents to maintain cooperation levels and achieve higher overall social welfare. For instance, Figure 4 illustrates the multi-layer network structures before and after the simulation, where they achieved an overall social welfare of 2442.3 and a prevalence of cooperation of 63.00%, with an LLM consult interval of 15,000 rounds.

The EC framework demonstrated robustness and resilience in the face of shocks and disruptions, such as the introduction of defectors or changes in the network structure. The adaptive learning process, along with the influence of LLM-based strategy recommendations, allowed agents to swiftly adjust their strategies in response to these perturbations.

The system’s robustness was further enhanced by the multi-layer network model, which captured different types of interactions between agents. This multi-layer structure allowed agents to maintain cooperation levels in one layer, even when facing disruptions in another layer. For instance, in the multi-layer system studied in Figure 4, the EC achieved a change in social welfare after a shock of 1819 and a change in cooperation prevalence after the shock of 5.00%, with an LLM consult interval of $\mathrm{30,000}$ rounds. Overall, the EC framework proved to be a resilient approach to modeling and promoting cooperation in complex MASs.

The visualizations generated during the simulation provided valuable insights into the dynamics of the EC framework. Time-lapse network visualizations revealed the emergence of cooperation and defection patterns, as well as the evolution of the network structure over time. Interactive visualizations allowed for the exploration of agent strategies, network layers, and the relationships between agents in greater detail.

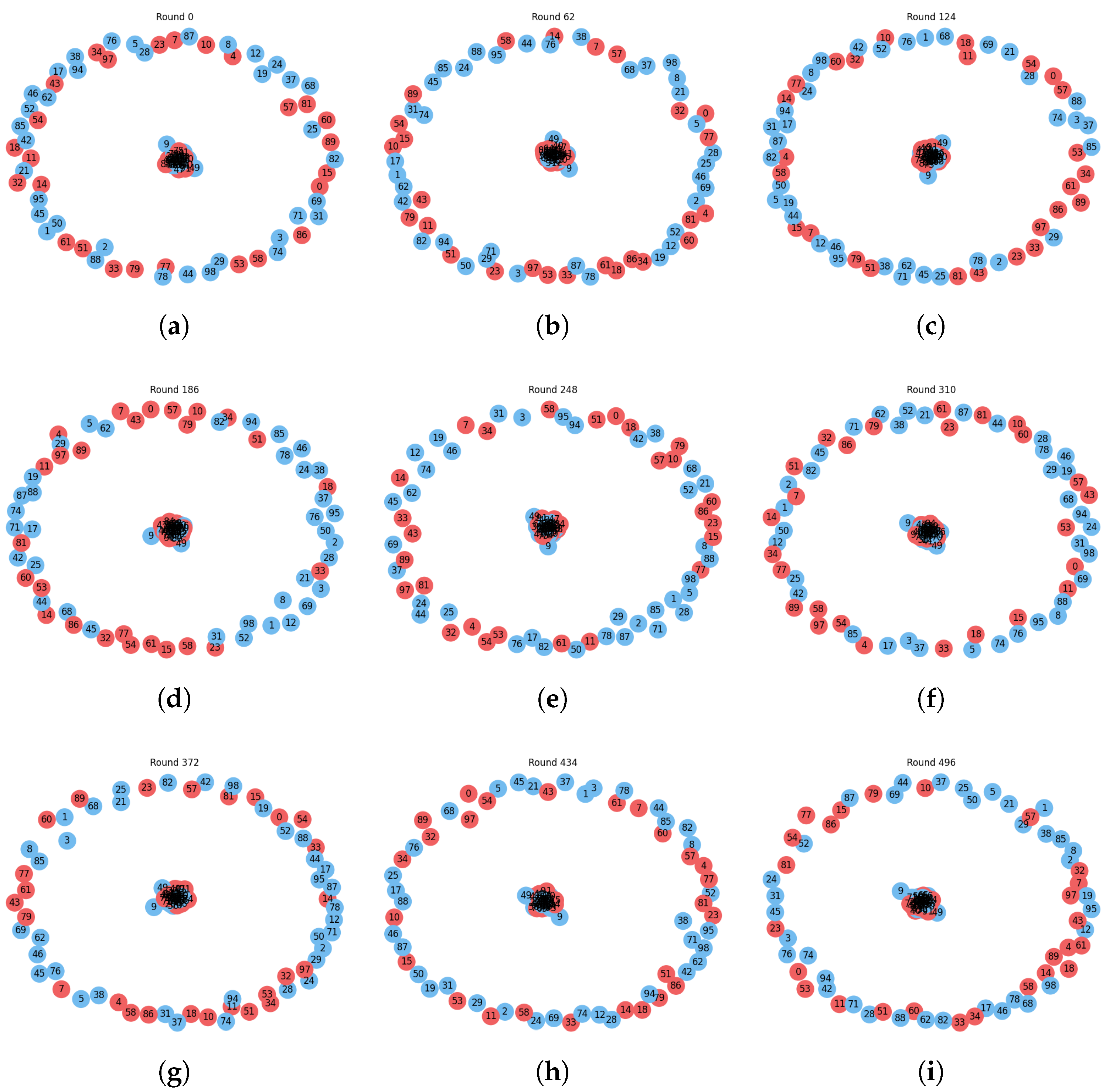
As shown in Figure 5, the evolution of cooperation in the multi-layer network is illustrated across representative rounds. Each plot presents the state of the network at different points in time, with blue nodes representing cooperative entities and red nodes symbolizing defecting entities. Node numbers represent the unique identifiers for each agent. The cooperative prevalence values, indicated in the subcaptions, provide insights into the percentage of cooperative agents within the network at each round.

Over the course of the simulation, we can observe shifts in the prevalence of cooperation and defection within the network, as well as the formation of clusters of cooperative and defecting agents. These changes can be attributed to the adaptive learning processes, the interactions between entities across multiple layers, and the influence of LLM-based strategy recommendations. The figure provides valuable insights into the dynamics of cooperation in complex multi-layer networks and highlights the significance of considering multiple dimensions of interaction when studying the evolution of cooperation.

We would like to emphasize that, while the EC framework has been demonstrated via a simplified simulation, we believe that the principles and mechanisms it encapsulates, such as adaptive learning, multi-layered interactions, and the use of LLM-based strategy recommendations, bear significant relevance to complex real-world scenarios. The ability of our framework to model and promote cooperation among diverse and adaptive agents provides a powerful tool to address various challenges in different contexts.

7. Implications for Business and Society

The EC framework, as demonstrated by our simulation, has far-reaching implications for both businesses and society as a whole. By promoting cooperation and fostering positive interactions between agents, the EC framework can be applied to a variety of real-world scenarios to optimize social welfare and enhance cooperation.

In the context of businesses, the EC framework can be used to model and improve cooperative behavior between employees, teams, or departments, potentially leading to increased productivity and efficiency within organizations. Moreover, the insights gained from the LLM-based strategy recommendations can inform decision-making processes and help organizations adapt to changing environments.

From a societal perspective, the EC framework can be applied to model and address pressing issues such as climate change, public health, and economic inequality. By encouraging cooperative behavior among individuals, communities, and nations, the EC framework can facilitate the development of sustainable solutions to these complex challenges.

Despite the promising results obtained from the EC framework, several limitations should be acknowledged. First, the simulation environment used in this study is a simplified representation of real-world systems. The assumptions made about agent behavior, network structure, and interactions may not fully capture the complexity of real-world situations. Additionally, the choice of LLMs and their implementation within the EC framework may also influence the outcomes observed in the simulation.

8. Conclusions

In this paper, we have presented a comprehensive framework that integrates EC Theory, MASs, and LLMs to simulate and analyze the dynamics of cooperation and defection in complex environments. By incorporating heterogeneous agents, adaptive learning mechanisms, and LLM-based strategy recommendations, our framework provides a more realistic and flexible representation of HCI in MASs.

We have also discussed the implementation details of our simulation environment, including performance metrics, visualization techniques, and the use of intelligent sensors for data collection and real-time adaptation. Through the analysis of various simulation results, we have demonstrated the emergence of cooperation and defection patterns, the influence of LLM-based strategy recommendations, the robustness and resilience of the system under different conditions, and the utility of our visualization techniques for understanding multi-agent system dynamics.

Furthermore, we have discussed the broader implications of our findings for business and society, thereby highlighting the potential benefits and challenges associated with the integration of LLMs and MASs in various domains. We have also acknowledged the limitations of our current framework, including the incorporation of additional layers of interaction, more advanced LLM-based strategy formation mechanisms, and the development of more sophisticated visualization and analysis tools.

In our proposed framework, we extended the concept of HCI to encompass the interaction between human agents and AI-driven agents, such as LLMs, in complex Multi-Agent Systems. This extended interpretation of HCI aims to capture the intricate dynamics of cooperation and defection that arise when humans and AI collaborate, compete, or coexist in various domains. By integrating LLMs as a form of human–computer interface, we created a more adaptive and flexible representation of these interactions, where the LLM modifies the beliefs and strategies of human agents based on the information provided. This approach allows for a deeper understanding of the potential benefits and challenges associated with human–AI collaboration in complex environments and contributes to the development of more effective and efficient Human–Computer Interaction strategies in diverse real-world applications.

In conclusion, our study represents a significant step towards a deeper understanding of the interplay between humans and computers in cooperative and competitive settings. By integrating advanced AI technologies, such as LLMs, with well-established theories from game theory and MASs, we aim to pave the way for more effective and efficient Human–Computer Interaction and unlock the potential of intelligent agents to address a wide range of complex problems in various domains.

Future work should focus on refining the EC framework by incorporating more realistic models of agent behavior, interaction mechanisms, and network structures. This can be achieved through the integration of empirical data, as well as the application of advanced modeling techniques. Furthermore, the performance of different LLMs and their suitability for various contexts should be explored.

Additional areas of future work include the investigation of alternative learning processes, the development of more sophisticated visualization techniques, and the study of the EC framework’s applicability to a broader range of real-world scenarios. By addressing these limitations and expanding upon the current work, the EC framework has the potential to significantly contribute to our understanding of cooperation and defection in MASs.