Economic Optimization Scheduling Based on Load Demand in Microgrids Considering Source Network Load Storage
Abstract
:1. Introduction
- The economic scheduling model considering the load demand for microgrid systems under the mechanism of a peak-valley tariff is established comprehensively;
- An improved WSO algorithm which introduces the dynamic weight factor of soldier ranking and the time sequence iteration update strategy of weak soldiers is used to solve the economic scheduling model under three scenarios.
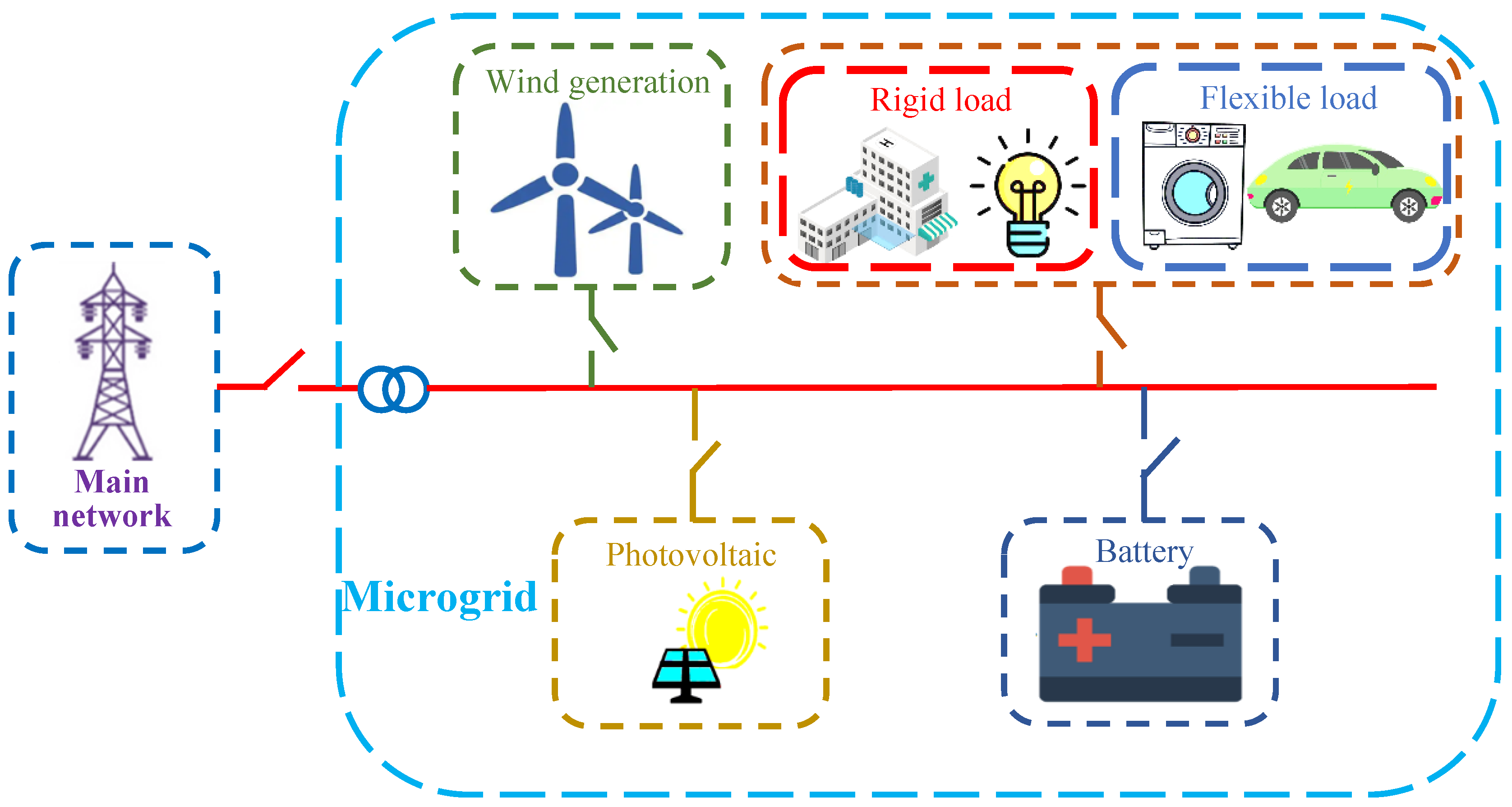
2. Microgrid Structure and Mathematical Model
2.1. Microgrid Structure
2.2. Mathematical Model of Microgrid
2.2.1. Photovoltaic Generation Model
2.2.2. Wind Generation Model
2.2.3. Battery Model
2.2.4. Power Exchange Model
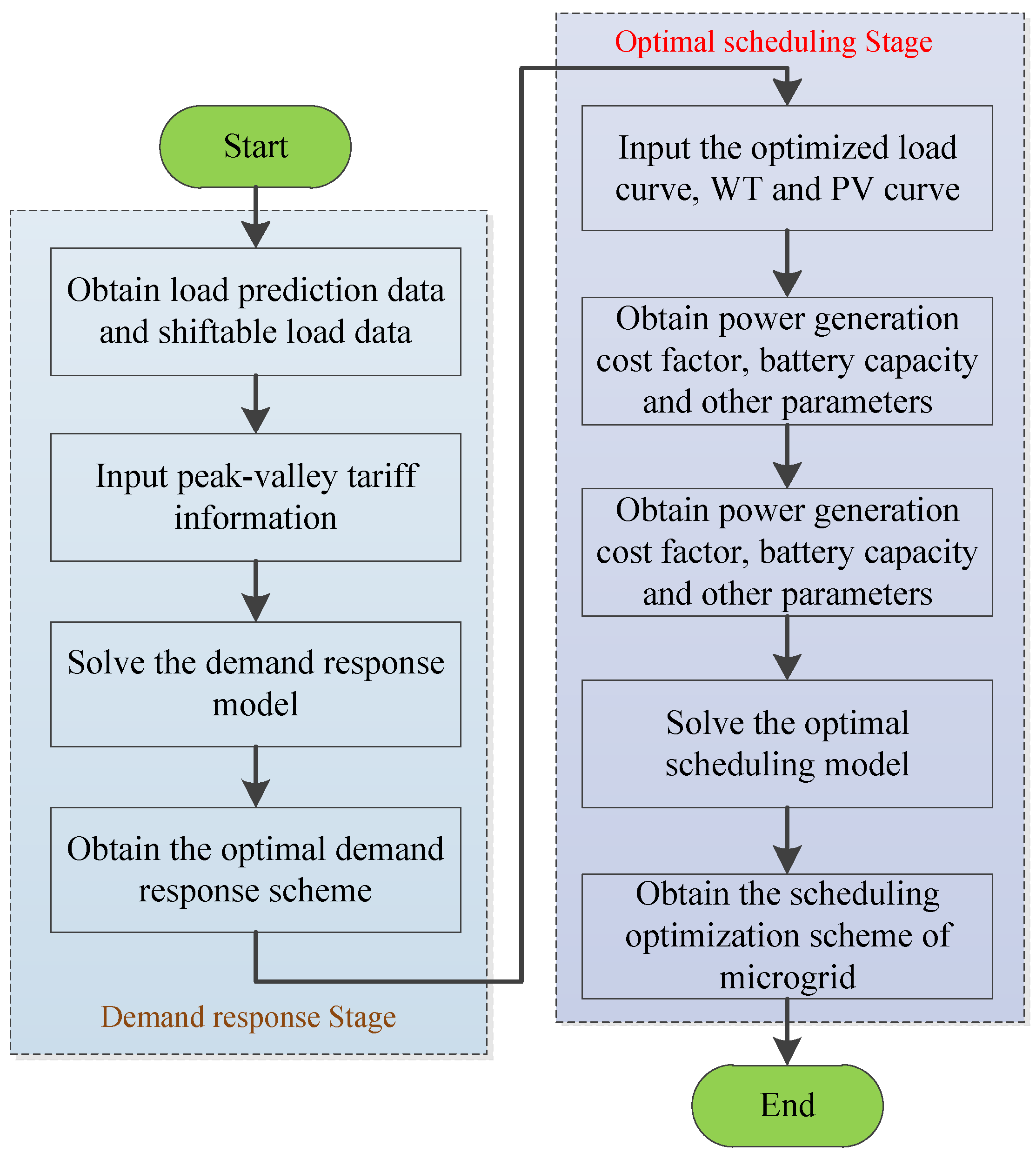
2.3. Demand Response and Optimal Scheduling Model
2.3.1. Demand Response Model
- (a)
- Demand response strategy
- (b)
- Objective function
- (c)
- Constraint condition.
2.3.2. Optimal Scheduling Model of Microgrid
- (a)
- Objective Function
- (b)
- Constraint condition
- Distributed generation constraint
- Power exchange constraints
- Battery constraints.
3. Improved War Strategy Optimization Algorithm
3.1. War Strategy Optimization Algorithm
- Attack strategy
- Rank and weight updating
- Defense strategy
- Replacement/Relocation of weak soldiers
3.2. Improved WSO Algorithm
- Improved rank and weight updating
- Improved replacement/relocation of weak soldiers
3.3. Parameter Selection
4. Results and Discussion
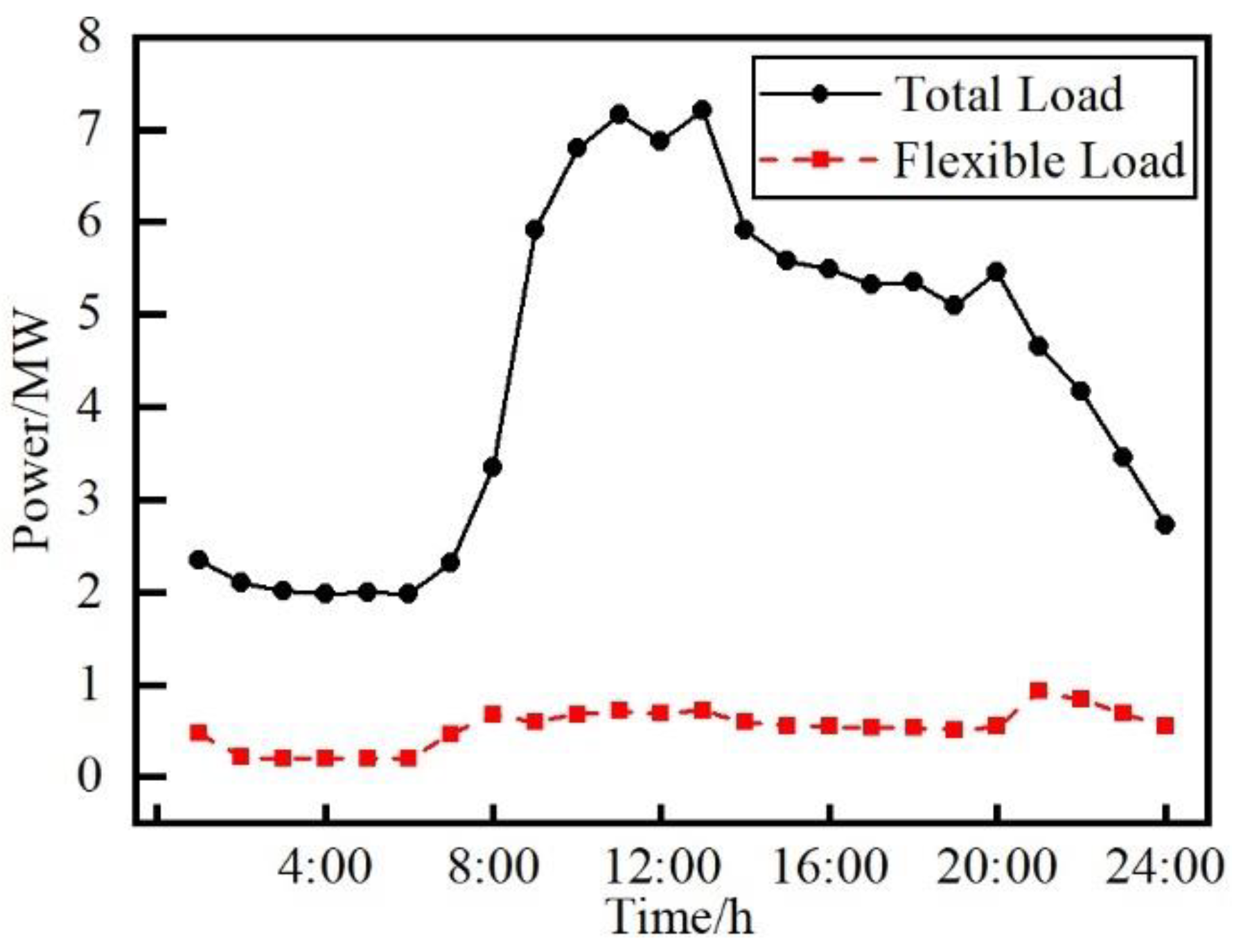
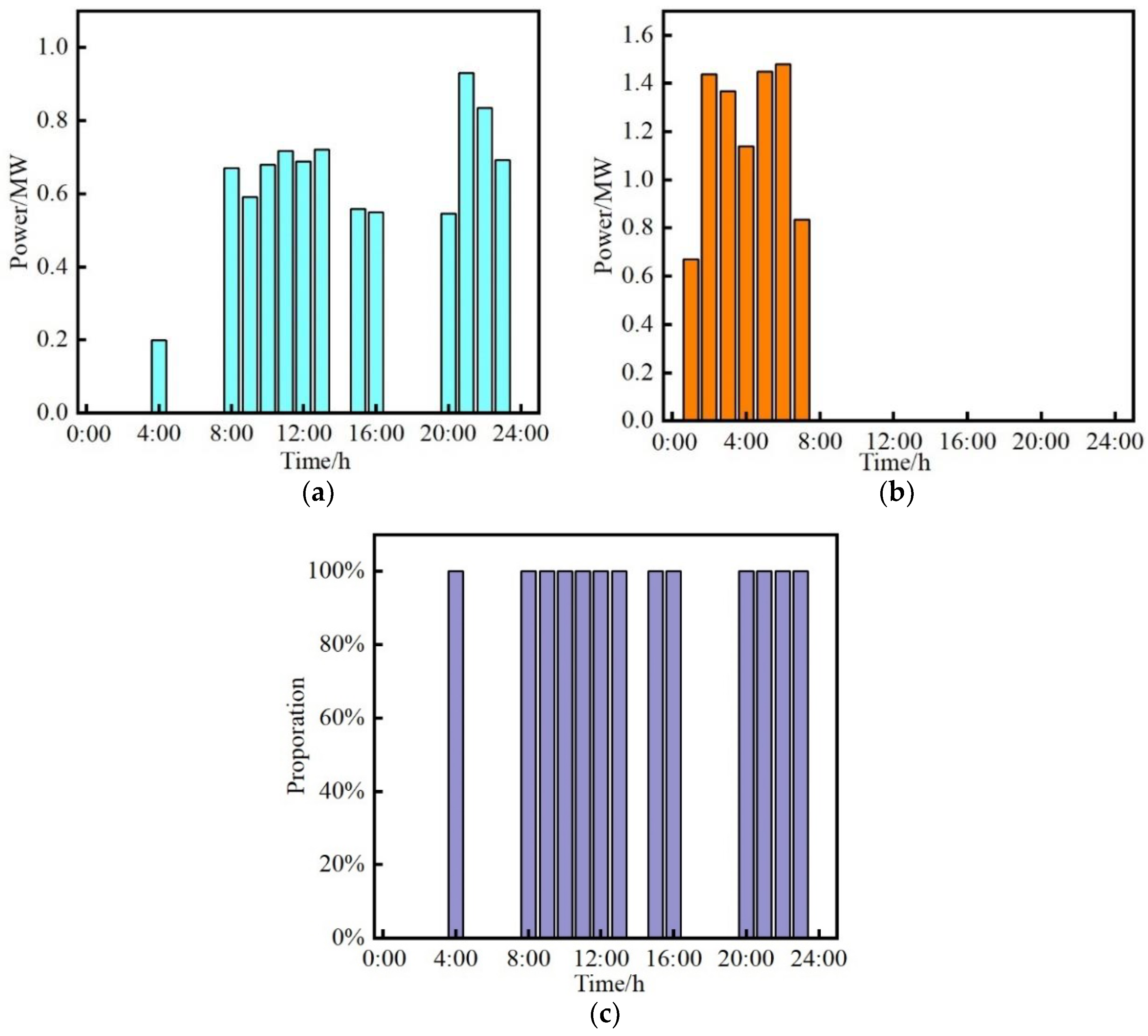
4.1. Demand Response
4.2. Optimal Scheduling of Microgrid
- Scenario 1: Microgrid operates without batteries
- Scenario 2: Microgrid operates with batteries
- Scenario 3: Microgrid operates with batteries and demand response
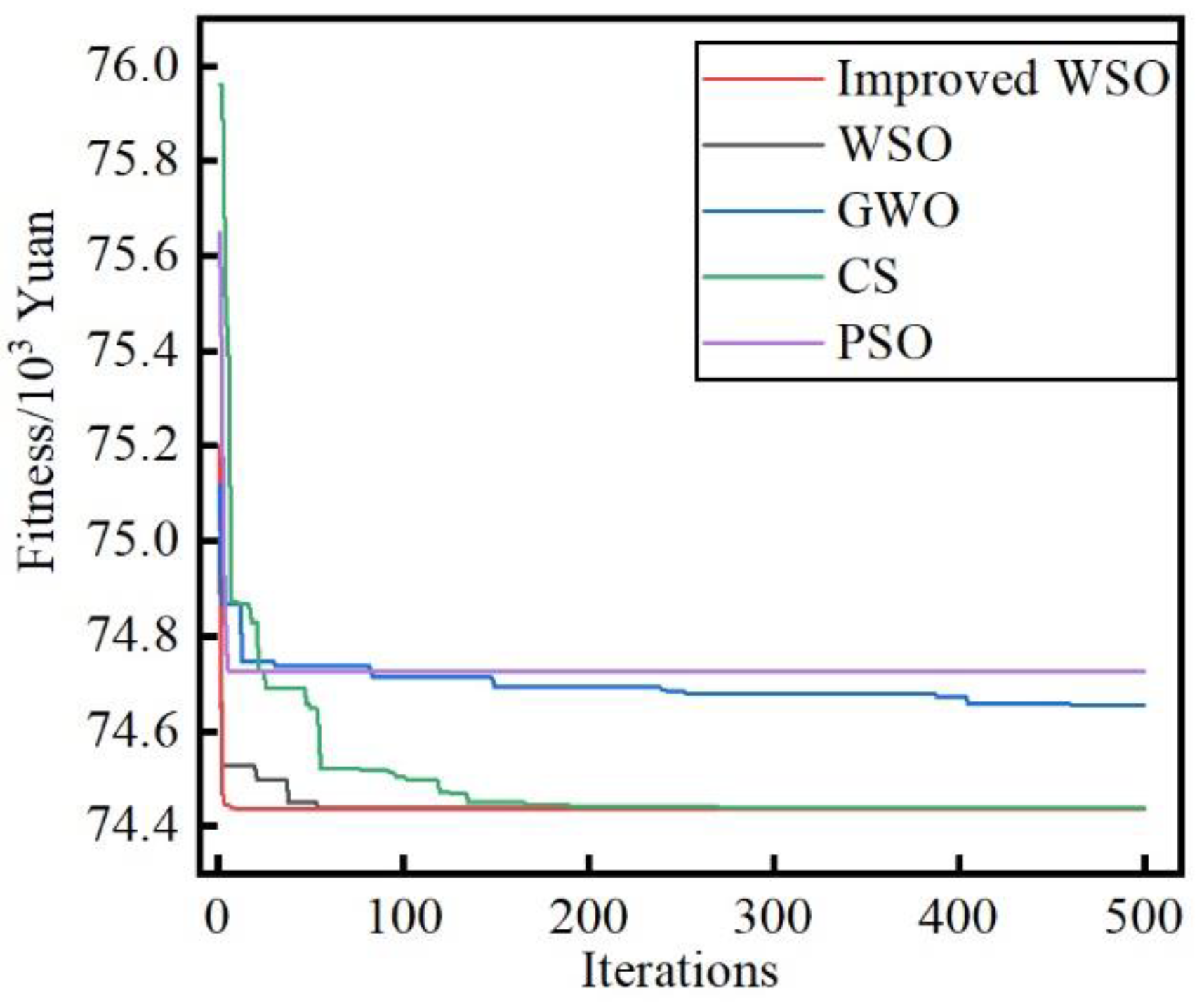
4.3. Algorithm Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Acronyms and Abbreviations
| WSO | War Strategy Optimization |
| PSO | Particle Swarm Optimization |
| CS | Cuckoo Search |
| GWO | Grey Wolf Optimization |
| WT | Wind Turbine |
| PV | Photovoltaic |
| DR | Demand Response |
| AC | Alternating Current |
References
- Zhang, J.; Chen, Z. The Impact of AMI on the Future Power System. Autom. Electr. Power Syst. 2010, 34, 10–14+23. [Google Scholar]
- Gang, W.Q.; Cun, Y.M.; Zhao, Z.Y.; Jie, Z.Y.; Hong, L.J.; Tao, G. Review on Evaluation Methods of Combined Heating, Power and Biogas System Coupled With Renewable Energy. Power Syst. Technol. 2021, 45, 937–950. [Google Scholar]
- Strategy for revolution in energy production and consumption (2016–2030). Electr. Appl. Ind. 2017, 5, 39–47.
- Caineng, Z.; Dongbo, H.; Chengye, J.; Bo, X.; Qun, Z.; Songqi, P. Connotation and pathway of world energy transition and its significance for carbon neutral. Acta Pet. Sin. 2021, 42, 233–247. [Google Scholar]
- Alasseri, R.; Tripathi, A.; Rao, T.J.; Sreekanth, K.J. A review on implementation strategies for demand side management (DSM) in Kuwait through incentive-based demand response programs. Renew. Sustain. Energy Rev. 2017, 77, 617–635. [Google Scholar] [CrossRef]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A survey on demand response programs in smart grids: Pricing methods and optimization algorithms. IEEE Commun. Surv. Tutor. 2014, 17, 152–178. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Mu, Y.; Zhao, D.; Chen, C.; Shen, B. Optimal scheduling of isolated microgrid with an electric vehicle battery swapping station in multi-stakeholder scenarios: A bi-level programming approach via real-time pricing. Appl. Energy 2018, 232, 54–68. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhong, H.; Lai, X.; Xia, Q.; Shu, C.; Kang, C. Distributed real-time demand response based on Lagrangian multiplier optimal selection approach. Appl. Energy 2017, 190, 949–959. [Google Scholar] [CrossRef]
- Navin, N.K.; Sharma, R. A fuzzy reinforcement learning approach to thermal unit commitment problem. Neural Comput. Appl. 2019, 31, 737–750. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H. Incentive-based demand response for smart grid with reinforcement learning and deep neural network. Appl. Energy 2019, 236, 937–949. [Google Scholar] [CrossRef]
- Wei, C.; Shen, Z.; Xiao, D.; Wang, L.; Bai, X.; Chen, H. An optimal scheduling in interconnected microgrids based on RO and Nash strategy for peer-to-peer trading bargaining. Appl. Energy 2021, 295, 117024. [Google Scholar] [CrossRef]
- Shuai, H.; Fang, J.; Ai, X.; Tang, Y.; Wen, J.; He, H. Stochastic Optimization of Economic Dispatch for Microgrid Based on Approximate Dynamic Programming. IEEE Trans. Smart Grid 2019, 10, 2440–2452. [Google Scholar] [CrossRef] [Green Version]
- Gong, Y.; Yang, X.; Xu, J.; Chen, C.; Zhao, T.; Liu, S.; Lin, Z.; Yang, L.; Qian, H.; Ke, C. Optimal operation of integrated energy system considering virtual heating energy storage. Energy Rep. 2021, 7, 419–425. [Google Scholar] [CrossRef]
- Wang, Y. Coordinated Heat and Power Scheduling of Micro-Energy Grid Considering Heat Balance Model of Building and Indoor Comfort Demand. Master’s Thesis, Tianjin University, Tianjin, China, 2018. [Google Scholar]
- Khalili, T.; Nojavan, S.; Zare, K. Optimal performance of microgrid in the presence of demand response exchange: A stochastic mufti-objective model. Comput. Electr. Eng. 2019, 74, 429–450. [Google Scholar] [CrossRef]
- Yang, H.; Shi, B.; Huang, W.; Ding, Y.; Wang, J.; Yu, W.; Zhu, Z. Day-Ahead Optimized Operation of Micro Energy Grid Considering Integrated Demand Response. Electr. Power Constr. 2021, 42, 75–82. [Google Scholar]
- Zhang, Y.; Lin, X.; Xu, Z.; Chen, Z. Dispatching Method of Micro-energy Grid Based on Light Robust Optimization. Autom. Electr. Power Syst. 2018, 42, 75–82. [Google Scholar]
- Ma, T.; Wu, J.; Hao, L. Energy Flow Modeling and Optimal Operation Analysis of Micro Energy Grid Based on Energy Hub. Power Syst. Technol. 2018, 42, 75–82. [Google Scholar] [CrossRef]
- Chen, F.; Deng, H.; Shao, Z. Distributed robust synergistic scheduling of electricity, natural gas; heating and cooling systems via alternating direction method of multipliers. Int. J. Energy Res. 2021, 45, 8456–8473. [Google Scholar] [CrossRef]
- Wang, J.; Shi, J.; Wen, F.; Li, J.; Zhang, L. Optimal Operation of CHP Microgrid with Concentrating Solar Power Plants Considering Demand Response. Autom. Electr. Power Syst. 2019, 43, 176–185. [Google Scholar]
- Zhang, H.; Cheng, Z.; Jia, R.; Zhou, C.; Li, M. Economic Optimization of Electric-gas Integrated Energy System Considering Dynamic Characteristics of Natural Gas. Power Syst. Technol. 2021, 45, 1304–1311. [Google Scholar]
- Chedid, R.; Sawwas, A.; Fares, D. Optimal design of a university campus micro-grid operating under unreliable grid considering PV and battery storage. Energy 2020, 200, 117510. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Abdussami, M.R.; Adham, M.I. Optimal planning of nuclear-renewable micro-hybrid energy system by particle swarm optimization. IEEE Access 2020, 8, 181049–181073. [Google Scholar] [CrossRef]
- Xingshen, L.I.; Jing, Z.; Yu, H.E.; Ying, Z.; Ying, L.; Kaifeng, Y. Multi-objective Optimization Dispatching of Microgrid Based on Improved Particle Swarm Algorithm. Electr. Power Sci. Eng. 2021, 37, 1. [Google Scholar]
- Zhang, L.; Guo, H.; Yao, L. Research on Microgrid Optimization Based on Improved Bat Algorithm. Power Syst. Clean Energy 2021, 37, 122–126. [Google Scholar]
- Wang, P.-Y.; Gao, M.-H.; Li, G.-L.; Wang, Y.-T. Multiple Objective Optimization of Microgrid Based on Distributed Neural Dynamics Algorithm. Sci. Technol. Eng. 2021, 21, 4063–4070. [Google Scholar]
- Liu, Y.; Zhang, H. Optimization of Units’ Restoration Sequence Based on Minimizing Risk of Electrical Energy Loss. Autom. Electr. Power Syst. 2015, 39, 30–36+53. [Google Scholar]
- Kim, H.-J.; Kim, M.-K.; Lee, J.-W. A two-stage stochastic p-robust optimal energy trading management in microgrid operation considering uncertainty with hybrid demand response. Int. J. Electr. Power Energy Syst. 2021, 124, 106422. [Google Scholar] [CrossRef]
- Imchen, S.; Das, D.K. Scheduling of distributed generators in an isolated microgrid using opposition based Kho-Kho optimization technique. Expert Syst. Appl. 2023, 229, 0957–4174. [Google Scholar] [CrossRef]
- Basak, S.; Bhattacharyya, B. Optimal scheduling in demand-side management based grid-connected microgrid system by hybrid optimization approach considering diverse wind profiles. ISA Trans. 2023, 19–578. [Google Scholar] [CrossRef]
- Premadasa, P.N.D.; Silva, C.M.M.R.S.; Chandima, D.P.; Karunadasa, J.P. A multi-objective optimization model for sizing an off-grid hybrid energy microgrid with optimal dispatching of a diesel generator. J. Energy Storage 2023, 68, 107621. [Google Scholar] [CrossRef]
- Haowu, C.; Shenghong, L.; Jianquan, Z. Bi-level Optimization of Microgrid Economic Dispatch Considering Demand-side Response. Power Syst. Auromation 2023, 45, 79–84. [Google Scholar]
- Ayyarao, T.S.; Ramakrishna, N.S.S.; Elavarasan, R.M.; Polumahanthi, N.; Rambabu, M.; Saini, G.; Khan, B.; Alatas, B. War Strategy Optimization Algorithm: A New Effective Metaheuristic Algorithm for Global Optimization. IEEE Access 2022, 10, 25073–25105. [Google Scholar] [CrossRef]
- Manbachi, M.; Ordonez, M. Intelligent Agent-Based Energy Management System for Islanded AC–DC Microgrids. IEEE Trans. Ind. Inform. 2020, 16, 4603–4614. [Google Scholar] [CrossRef]
- Yavuz, A.; Celik, N.; Chen, C.-H. A Sequential Sampling-based Particle Swarm Optimization to Control Droop Coefficients of Distributed Generation Units in Microgrid Clusters. Electr. Power Syst. Res. 2023, 216, 109074. [Google Scholar] [CrossRef]
- Rodriguez, M.; Arcos, D.; Martinez, W. Fuzzy logic-based energy management for isolated microgrid using meta-heuristic optimization algorithms. Appl. Energy 2023, 335, 120771. [Google Scholar] [CrossRef]
- Wu, Z.; Luo, Y.; Hu, S. Optimization of jamming formation of USV offboard active decoy clusters based on an improved PSO algorithm. Def. Technol. 2023, 2214–9147. [Google Scholar] [CrossRef]
- Singh, P.; Anwer, N.J.S.; Lather, J.S. Energy management and control for direct current microgrid with composite energy storage system using combined cuckoo search algorithm and neural network. J. Energy Storage 2022, 55, 105689. [Google Scholar] [CrossRef]
- Naserbegi, A.; Aghaie, M.; Zolfaghari, A. Implementation of Grey Wolf Optimization (GWO) algorithm to multi-objective loading pattern optimization of a PWR reactor. Ann. Nucl. Energy 2020, 148, 107703. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Installed capacity of PV | 5 MW |
| Installed capacity of WT | 10 MW |
| Wb | 8 MW |
| γ | 0.78 CNY/(KW·h) |
| δ | 0.63 CNY/(KW·h) |
| λ | 0.2 CNY/(KW·h) |
| Price Type | Time Period/t | Purchase Price/(CNY/(kW·h)) | Selling Price/(CNY/(kW·h)) |
|---|---|---|---|
| Valley | 1~7, 22~24 | 0.25 | 0.22 |
| Normal | 8~10, 16~19 | 0.53 | 0.42 |
| Peak | 11~15, 20~21 | 0.82 | 0.65 |
| Electricity Cost before Demand Response/(CNY) | Electricity Cost after Demand Response/(CNY) | |
|---|---|---|
| Valley | 6277.24 | 7939.4 |
| Normal | 19,778.57 | 18,458.84 |
| Peak | 35,136.06 | 31,726.01 |
| Total | 61,191.87 | 58,124.25 |
| Cost of Electricity Purchasing | Income from Electricity Sales | Maintenance Cost of Wind Turbine | Maintenance Cost of Photovoltaic Module | Total Cost | |
|---|---|---|---|---|---|
| Cost/CNY | 9583.40 | 14,828.22 | 39,562.51 | 43,475.8 | 77,793.49 |
| Cost of Electricity Purchasing | Income from Electricity Sales | Maintenance Cost of Wind Turbine | Maintenance Cost of Photovoltaic Module | Maintenance Cost of Battery | Total Cost | |
|---|---|---|---|---|---|---|
| Cost/CNY | 6211.37 | 14,596.22 | 39,562.51 | 43,475.8 | 2399.99 | 77,053.45 |
| Cost of Electricity Purchasing | Income from Electricity Sales | Maintenance Cost of Wind Turbine | Maintenance Cost of Photovoltaic Module | Maintenance Cost of Battery | Total Cost | |
|---|---|---|---|---|---|---|
| Cost/CNY | 5180.86 | 16,181.11 | 39,562.5 | 43,475.8 | 2399.99 | 74,438.04 |
| Algorithm | Parameter | Value |
|---|---|---|
| PSO | Pop Size | p = 1000 |
| Number of iterations | G = 500 | |
| Learning factor | c1 = c2 = 1.49445 | |
| Inertia weight | wmax = 0.8, wmin = 0.4 | |
| Flight speed | Vmax = 1, Vmin = −1 | |
| CS | Number of nests | N = 1000 |
| Number of iterations | G = 500 | |
| Discovery probability | Pa = 0.25 | |
| Step size scaling factor | α = 1 | |
| GWO | Pop Size | p = 1000 |
| Number of iterations | G = 500 | |
| Convergence factor | decreases linearly from 2 to 0 | |
| WSO | Number of soldiers | p = 1000 |
| Number of iterations | G = 500 | |
| Guide factor | ρr = 0.8 | |
| Improved WSO | Number of soldiers | p = 1000 |
| Number of iterations | G = 500 | |
| Guide factor | ρr = 0.8 |
| Algorithm | Cost/CNY | Iterations | Computation Time/s |
|---|---|---|---|
| PSO | 74,726.13 | 500 | 7.344387 |
| CS | 74,438.17 | 500 | 15.42264 |
| GWO | 74,654.15 | 500 | 4.549247 |
| WSO | 74,438.08 | 500 | 1.952064 |
| Improved WSO | 74,438.04 | 500 | 1.895227 |
| PSO | CS | GWO | WSO | Improved WSO | |
|---|---|---|---|---|---|
| Wind | 39,562.5 | 39,562.5 | 39,562.5 | 39,562.5 | 39,562.5 |
| Photovoltaic | 43,475.8 | 43,475.8 | 43,475.8 | 43,475.8 | 43,475.8 |
| Battery | 2879.99 | 2400.26 | 2160.165 | 2400 | 2399.99 |
| Purchase | 6028.88 | 5181.31 | 5637.17 | 5180.88 | 5180.86 |
| Sell | 17,221.04 | 16,181.69 | 16,181.5 | 16,181.11 | 16,181.11 |
| Total cost | 74,726.13 | 74,438.17 | 74,654.15 | 74,438.08 | 74,438.04 |
| Computational time/s | 7.344387 | 15.42264 | 4.549247 | 1.952064 | 1.895227 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Wu, X.; Sun, K.; Du, X.; Wang, H.; Zhao, J. Economic Optimization Scheduling Based on Load Demand in Microgrids Considering Source Network Load Storage. Electronics 2023, 12, 2721. https://doi.org/10.3390/electronics12122721
He Y, Wu X, Sun K, Du X, Wang H, Zhao J. Economic Optimization Scheduling Based on Load Demand in Microgrids Considering Source Network Load Storage. Electronics. 2023; 12(12):2721. https://doi.org/10.3390/electronics12122721
Chicago/Turabian StyleHe, Yuling, Xuewei Wu, Kai Sun, Xiaodong Du, Haipeng Wang, and Jianli Zhao. 2023. "Economic Optimization Scheduling Based on Load Demand in Microgrids Considering Source Network Load Storage" Electronics 12, no. 12: 2721. https://doi.org/10.3390/electronics12122721
APA StyleHe, Y., Wu, X., Sun, K., Du, X., Wang, H., & Zhao, J. (2023). Economic Optimization Scheduling Based on Load Demand in Microgrids Considering Source Network Load Storage. Electronics, 12(12), 2721. https://doi.org/10.3390/electronics12122721







