Abstract
This article presents an efficient crypto processor architecture for point multiplication acceleration of side-channel secured Binary Huff Curves (BHC) on FPGA (field-programmable gate array) over . We have implemented six finite field polynomial multiplication architectures, i.e., (1) schoolbook, (2) hybrid Karatsuba, (3) 2-way-karatsuba, (4) 3-way-toom-cook, (5) 4-way-toom-cook and (6) digit-parallel-least-significant. For performance evaluation, each implemented polynomial multiplier is integrated with the proposed BHC architecture. Verilog HDL is used for the implementation of all the polynomial multipliers. Moreover, the Xilinx ISE design suite tool is employed as an underlying simulation platform. The implementation results are presented on Xilinx Virtex-6 FPGA devices. The achieved results show that the integration of a hybrid Karatsuba multiplier with the proposed BHC architecture results in lower hardware resources. Similarly, the use of a least-significant-digit-parallel multiplier in the proposed design results in high-speed (in terms of both clock frequency and latency). Consequently, the proposed BHC architecture, integrated with a least-significant-digit-parallel multiplier, is 1.42 times faster and utilizes 1.80 times lower FPGA slices when compared to the most recent BHC accelerator architectures.
1. Introduction
The rapid increase in the development of technological devices causes security threats. Amongst several others, cryptography is one of the choices that offer different security services such as data encryption/decryption, signature generation/verification, etc. [1]. It has two types, i.e., symmetric and asymmetric. The symmetric cryptography requires a singular key, named as a private key, to execute encryption and decryption operations. On the other hand, two distinct keys are needed to operate asymmetric algorithms. Out of these two keys, the first one is a private key while the other is a public key. Encryption operation is executed using a private key while decryption is performed with a public key. Moreover, asymmetric algorithms are becoming more prevalent as these offer secured cryptographic services [2,3].
The typical examples of asymmetric algorithms are Diffie Hellman (DH) [4], ECC (Elliptic Curve Cryptography) and RSA (Rivest–Shamir–Adleman) [5,6,7]. The DH is a key exchange protocol that was initially proposed to share the public keys between the sender and recipient to initiate communication. To perform data encryption and decryption, the RSA and ECC algorithms were proposed [5,6,7]. Comparatively, the former takes larger key lengths, more channel bandwidths, higher hardware resources, and higher computational cost [2]. For instance, to achieve a 128-bit security level, RSA and DH require 3072-bits while for identical security levels, ECC requires only 256-bits [8]. Consequently, ECC is an attractive choice for its counterpart algorithm (i.e., RSA).
The ECC involves several models for implementations such as, (1) Weierstrass [9], (2) Binary Edward Curves (BEC) [10], (3) Hessian Curves (HC) [11], and (4) Binary Huff Curves (BHC) [12]. Comparatively, the Weierstrass model is vulnerable to side-channel attacks (SCA). The reason is that it requires different mathematical operations for point doubling (PD) and addition (PA) computations. The PA and PD are second layer operations of ECC and are needed to perform the point multiplication (PM) [9] (third layer operation of ECC). To resist side-channel attacks, one of the solutions is the employment of unified point addition and doubling operations. Therefore, BHC, BEC, and HC models of ECC provide unified mathematical operations for point addition and doubling executions [10,11,12]. On the other hand, the HC and BEC models are comparatively better for achieving a higher throughput. Similarly, to achieve a higher security level, BHC model is more preferable [13,14]. Therefore, this work intends to describe the hardware implementation of the most secured BHC model of ECC as it inherently provides resistance against side-channel attacks.
1.1. Algorithmic Evolution of BHC Model of ECC and the Corresponding Hardware Accelerators
In the context of elliptic curves, the BHC model was first proposed in [12]. The initial mathematical operations/formulations for the unified addition law of BHC were proposed in 2011 [15]. In 2013, the PA and PD law of the BHC model was revisited [14]. Recently, in 2018, the unified PD and PA formulations of the BHC model of 2013 were re-evaluated and a new vulnerability against SCA attacks has been identified [16]. Additionally, the revised mathematical formulations for the unified addition law of BHC have also been presented. Two different approaches, i.e., software, or hardware, are available in the literature to implement the various models of cryptosystems related to ECC. The benefits of software implementations are a comfort to use and upgrade, low development cost, flexibility and portability. In addition to these benefits, the corresponding drawbacks include an inferior performance and vulnerability against the protection of private keys compared to fabricated hardware [1]. These drawbacks have urged many researchers/investigators to analyze the hardware demonstrations of various ECC models. Subsequently, the existing hardware accelerators of the BHC model of ECC are described in [13,14,17,18,19,20]. Their architectural details are provided in the following.
Hardware accelerator based on unified addition law of 2011 [13]: On Xilinx Virtex-4 FPGA, a dedicated BHC architecture over is presented in [13]. Along with numerous routing multiplexers, finite field adders and squarer modules, the arithmetic unit of their design incorporates Itoh-Tsujii inversion algorithm and hybrid Karatsuba multiplier. The term hybrid stands for the combination of general and simple Karatsuba multiplier. The general Karatsuba multiplier is used mainly because over smaller bits, it is more suitable to efficiently utilize the look-up tables, whereas, over longer bits, simple Karatsuba multipliers aids towards minimizing the gate counts. Based on these architectural characteristics, they achieve an operational clock frequency of 81 MHz. Moreover, the area cost of their design in terms of FPGA slices is 20,437. The latency (time to operate one PM operation) of their architecture is 73 s.
Designs concerning the unified addition law of 2013 [14,17,18,19]: The architecture described in [14], achieves an operational clock frequency of 183 MHz over on Xilinx Virtex-7 FPGA, utilizing FPGA slices of 6032 while the computational time for one PM is 40 s. Moreover, their design takes 7370 clock cycles for one PM calculation. A two-stage pipelined design over for PM computation is presented in [17]. Their architecture utilizes 7681 and 6342 slices on Xilinx Virtex-6 and Virtex-7 FPGA devices, achieving the clock frequency of 296 and 369. The time needed for one PM execution is 39 and 32 s. Another FPGA implementation, of both Weierstrass and BHC curves over and is implemented in [18] using a digit-parallel multiplier with digit length of 32-bits for the computation of PM. Their design utilizes 4520 and 8866 slices over and , respectively, on Xilinx Virtex-7 FPGA. Moreover, they achieved the frequency of 280 and 271 MHz for key lengths of 163 and 233, respectively.
To accomplish an improved throughput over area ratio, a 4-stage pipelined design over is shown in [19]. They reviewed the mathematical illustration of BHC with an objective to lessen the hardware resources and consequently, they acquired a 43% decrease. To work on the throughput, two techniques they have utilized: (i) critical path reduction with the use of pipeline registers and (ii) reduction in the clock cycles by the scheduling of mathematical operations of unified addition law.
Architectures supporting the unified addition law of 2018 [20]: In [20], the first hardware accelerator for a recently proposed unified addition law of BHC is presented, which is a four-staged pipelined architecture utilizing a total of 7123 FPGA slices on Virtex-7 target device. For the computation of one PM. Their design takes a total of 15,495 clock cycles. Moreover, after post-place-and-route-level, a maximum clock frequency of 188 MHz is achieved. The time needed to operate one PM is 82.4 s.
1.2. Limitations in the Existing Architectures
Section 1.1 demonstrates the state-of-the-art hardware architectures proposed for PM computation of BHC [13,14,17,18,19]. These designs are constructed on elder unified addition formulations, published in 2011 [15] and 2013 [14]. A hardware implementation of the most recently proposed unified addition law (published in 2018 and is constructed in [16]) of BHC utilizes a higher hardware area and takes more computational time [20]. It is important to note that security is always a critical demand in almost all cryptographic applications, e.g., RFID (radio-frequency-identification-networks), WSN (wireless sensor networks), IoT (internet-of-things) [21], etc. These applications require minimum hardware resources for cryptographic computations in a reasonable time. Therefore, there is a real need for the area-optimized implementations of side-channel resistant cryptographic algorithms for area-constrained applications.
1.3. Novelty and Contributions
To address the limitations, described in Section 1.2, the novelty of this work includes: (1) a novel PM architecture, (2) implementation and integration of several polynomial multipliers into our novel PM architecture, and (3) a comprehensive description of the implementation of our novel PM design and evaluation results along with a comparison to state-of-the-art. To achieve this, our contributions are as follows:
- Crypto processor architecture: We have presented an area-optimized FPGA-based crypto processor architecture responsible for accelerating the PM of the BHC model of ECC over .
- Design trade-offs for various multipliers: For performance and area trade-offs of polynomial multipliers, we have implemented six different multiplication architectures: (1) schoolbook, (2) hybrid Karatsuba, (3) 2-way-karatsuba, (4) 3-way-toom-cook, (5) 4-way-toom-cook and (6) digit-parallel-least-significant, in a Verilog HDL.
- Design trade-offs for BHC model of ECC: We have integrated each polynomial multiplication architecture in our novel BHC processor architecture for design trade-offs (or performance evaluations), concerning hardware resource utilization, clock frequency, latency (time for execution of one PM) and consumed power.
- Finally, a dedicated controller is utilized for the management and coordination of various processing tasks.
The polynomial multipliers and the proposed PM architecture over are implemented in Verilog HDL and tested on Xilinx FPGA devices. The implementation results show that the integration of hybrid Karatsuba multiplier with the proposed BHC architecture results in minimum hardware resources (8498 slices, 3999 LUTs and 5209 FFs). Similarly, the least-significant-digit-parallel multiplier, integrated with the proposed BHC design, results in high-speed (in terms of both clock frequency (164 MHz) and latency (80 s)). To summarize, the proposed BHC architecture, integrated with a least-significant-digit-parallel multiplier, is 1.42 times faster. Moreover, the hardware resource (FPGA slices) utilization is 1.80 times less than the most recent BHC accelerator, published in [20].
The remainder of this work is structured as follows: Section 2 provides the related background about the BHC model of ECC. Our proposed crypto processor architecture for BHC model of ECC is described in Section 3. The implementation results and various design trade-offs are discussed in Section 4. Finally, Section 5 concludes the findings of this work.
2. Related Background
Generally, ECC includes four layers of model for implementations [3,9]. The lowermost layer contains the finite field addition, multiplication, squaring, inversion and subtraction. Moreover, the layer two operations are PA and PD, which are giverned by layer one operations. The third layer operation of ECC and its execution depends on the calculations of PA and PD operations. Finally, the highest layer is known as protocol and is used for the execution of encryption and decryption operations. Consequently, to implement the four-layer model of ECC, there are several choices for the designers to choose different settings according to the cryptographic applications. These choices are described in the text that follows:
Basis representation: To implement ECC, two kinds of representations are available as state-of-the-art, i.e., polynomial, and normal [3,19]. The prior is significant where frequent finite field multiplications are needed to compute while the latter is more convenient where frequent finite field squares are essential to perform [18]. Therefore, the BHC model of ECC requires frequent multiplications (will be described later in this paper), so we have used polynomial basis representations in this work.
Coordinate systems: Two coordinates system representations are commonly available, i.e., affine coordinates and the Projective coordinates [1,9,19]. The general affine coordinate representation requires finite field inversion during the calculation of each PA and PD computation while the projective coordinates are helpful to decrease the related inversion cost. In addition, the projective coordinates are more beneficial to increase the speed or throughput of the designed cryptosystem. There are various projective coordinates for the implementation of different models of ECC [9]. However, the most frequently used are (1) Standard, (2) Jacobian, and (3) the Lopez Dahab. These projective coordinate systems have their pros and cons. To understand complete comparison over these projective coordinate systems, we refer interested readers to [9]. Therefore, to reduce the inversion cost a Lopez Dahab projective coordinate system has been used in this work.
Finite fields: A field contains a set F with multiplication, denoted by (.), and addition, represented by (+), operations. Moreover, a field is supposed to be limited if the set F is limited. In ECC, prime , and binary fields are most frequently used [9,17,19,20]. The primary fields are more appropriate for software implementations, whereas for hardware implementations, use of binary fields is a preferable choice. Therefore, we have selected field for computations as we are dealing with hardware implementations.
2.1. Bhc over
A non-singular elliptic curve over in general affine coordinate system is defined by using Equation (1):
In Equation (1), a and b are the elliptic curve parameters while . The variables x and y are the base point coordinates. Finally, is the irreducible polynomial. The Huff model for elliptic curves (as introduced in Section 1), using Equation (1) was presented in [12] in 2010. Therefore, the Equation (2) defines the BHC model of ECC over a binary field in a Lopez Dahab projective coordinates. For complete mathematical formulations, we turn readers to [12].
In Equation (2), the curve parameters a and b belong to when . Moreover, X, Y and Z are the projective Lopez Dahab points.
2.2. Point Multiplication
For PM computation, (1) an initial point P on the curve and (2) an integer k whose size is equal to the size of the field which is under consideration [22] are required. Then, the PM is performed by adding the k copies of point P, i.e., . A variety of PM algorithms are available as state-of-the-art. However, a descriptive comparison over various PM algorithms is provided in [1]. We notifying that the HC, BEC and BHC curves have more computational complexity when compared to the Weierstrass ECC curve. Therefore, the following Algorithm 1 is more frequently utilized for PM computation in HC, BEC and BHC curves of ECC and is (also) used in our work.
| Algorithm 1: Double and Add PM Algorithm [17,19,20] |
Input: with , Output: 1 , , , , 2 for(i from m-1 down to 0)do 3 , 4 if , then 5 , 6 end 7 end if 8 end for 9 end 10 |
There are three main steps in Algorithm 1: (1) affine to projective conversions (see operations given in line 1 of Algorithm 1), (2) PM computation in projective coordinates (see operations given in lines 2 to 9 of Algorithm 1) and (3) reconversions to affine coordinates (see operations given in line 10 of Algorithm 1). As shown in Algorithm 1), the PM is depending on the unified addition law. If the bit of k in Algorithm 1 becomes one, then only the PA operation (see line 5) is performed. Similarly, if the bit of k becomes zero, then PA followed with PD is required to compute (see lines 3 and 5).
2.3. Unified Addition Law () of BHC
The first formal construction of unified PA law of Huff model over field was presented in [15]. The vulnerabilities against unified addition law of [15] were presented in [14] and a new mathematical formulation was constructed. The unified law of [14] has been re-evaluated in [16] and provided some new vulnerabilities. Consequently, the unified addition law of BHC model of ECC, presented in 2011, 2013 and 2018, is shown in columns two to four of Table 1.

Table 1.
Unified addition laws (UAL) of BHC model of ECC over .
In Table 1, the , , and are the initial projective points, , , and are new computed points and , , and are the final Lopez Dahab projective points. While computing unified PA law the temporary storage elements ( to ) are responsible to keep the intermediate results. The curve constants, ( and ) can be computed as, and . It is important here to mention that this work utilizes pre-computed and values as used in [13,14,17,18,19,20]. Additionally, we have incorporated mathematical formulations for computation of from column three of Table 1.
It is important to highlight that the unified addition laws of column two, three and four of Table 1, inherently offers resistance to side-channel attacks. Consequently, we have considered side-channel prevention at the algorithmic level instead of the design in our work.
3. Proposed Architecture
The proposed architecture for the unified BHC model of ECC is shown in Figure 1. The proposed architecture contains a memory unit, two routing multiplexers ( and ), an arithmetic and logic unit (ALU), and a finite state machine (FSM)-based control unit. The ALU is responsible for performing arithmetic operation (addition, multiplication and squaring). The memory unit stores the intermediate results of PM while implementing the Algorithm 1. Inside the memory unit, two multiplexers and a demultiplexer have been used to perform data read and write back. The FSM-based dedicated control unit governs the overall functions of the proposed hardware architecture of BHC.
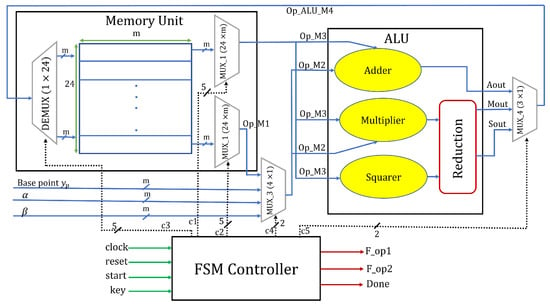
Figure 1.
Proposed hardware architecture of BHC for PM computation.
3.1. Memory Unit (MU)
For the storage of intermediate and final results of Algorithm 1, we first have to identify the required memory size. Concerning this, we have rewritten the unified addition law of column three of Table 1 in Table 2. Column one in Table 2 provides the number of instructions while the list of instructions is shown in column two. The last column in Table 2 provides the additional details for the number of instructions needed for polynomial addition, multiplication and squaring operations.

Table 2.
Unified addition law of 2018 (shown in column three of Table 1) according to singular adder, multiplier and squarer.
As shown in Table 2, it has been analyzed that there are 37 instructions in the unified addition law of BHC when considered as a singular operator form for implementation. Based on these instructions we brought the idea for the required memory unit size. Consequently, we have used a register array of size to store the intermediate and the final results for PM computation of BHC. Here, the value for m represents the size of each memory address and is equivalent to the size of field under consideration (i.e., 233-bits). To read data from the memory unit, two multiplexers have been used in the proposed architecture, as shown in Figure 1. Similarly, a single demultiplexer is employed for updating the contents of each particular register, as shown in Figure 1. The corresponding control signals, i.e., C1, C2, and C3—shown in Figure 1, required for read/write operations are with size 5-bits.
3.2. Routing Multiplexers
As presented in Figure 1, two routing multiplexers have been used in the proposed hardware architecture. The two inputs to are initial curve parameters with third input coming as an operand from the register array of a memory unit. The output of is first input to the ALU, as shown in Figure 1. Another multiplexer, i.e., , is incorporated outside the ALU to select an appropriate result after polynomial addition, multiplication and squarer unit for writeback over memory unit using the demultiplexer. C4 and C5 are the corresponding control signals, as shown in Figure 1.
3.3. Arithmetic and Logic Unit
The ALU comprises of an adder unit, a multiplier unit, and a squarer unit, as shown in Figure 1. Two inputs to ALU are from, (1) the routing multiplexer Mux_3, and (2) the register array of a memory unit. There are three outputs, i.e., one from the polynomial adder unit, second from the multiplier unit, and last from the squarer unit, from ALU to routing multiplexer Mux_4. Implementation of these arithmetic operators (adder, multiplier, and squarer) is further described in the next subsequent sections:
3.3.1. Adder and Squarer Units
An array of a bitwise exclusive-(OR) gates is used to perform polynomial addition, as implemented in solutions [14,17,18,19,20]. The length of two inputs and an output is m-bit. Following [18,20], polynomial squaring is performed by inserting a 0 after each input data bit. The input to squaring unit is an m-bit polynomial and the size of output is bits.
3.3.2. Multiplier Unit
The performance of the entire model of ECC mainly depends on the utilized multiplier. As shown in column three of Table 2, 17 out of 37 instructions are required for multiplication operation while the remaining instructions are for addition and squaring. However, to evaluate the performance of the recently proposed unified BHC model of ECC, described in [16], six different multipliers have been incorporated in the datapath of our proposed architecture. Therefore, the employed multipliers are: (1) schoolbook, (2) hybrid Karatsuba, (3) 2-way-karatsuba, (4) 3-way-toom-cook, (5) 4-way-toom-cook and (6) least-significant-digit-parallel. All these multipliers takes two polynomials as input each with size m-bit resulting in an output of bit polynomial. A descriptive implementation trends for schoolbook, 2-way-karatsuba, 3-way-toom-cook and 4-way-toom-cook multipliers are presented in [23,24]. It is important to mention that these multipliers are not shown in Figure 1; however, the implementation details of these multipliers are described in the text that follows:
- Schoolbook multiplier: The multiplication using the schoolbook method is executed by generating simple partial products. After generating partial products, shift and add operations are used yielding a result of size bits. A total of clock cycles are needed to perform one multiplication for input operands length of m-bits. Moreover, a schoolbook multiplication method is more convenient to save hardware resources without considering the clock cycles [23].
- Hybrid Karatsuba multiplier: The Karatsuba multiplication method uses the divide and conquer approach for the multiplication of two polynomials each of size m-bits. The divide and conquer approach is performed in chronological order, i.e., polynomial multiplications starting from lower to higher bits. Moreover, the hybrid approach is attained by implementing the simple and general Karatsuba multipliers as used in [13]. A simple Karatsuba multiplier is utilized to perform multiplication over smaller bits, whereas the general Karatsuba multiplier is employed to perform multiplication over longer bits. The objective of using a simple Karatsuba multiplier is the reduction of logic delays, whereas for minimizing the overall gate counts the general Karatsuba multiplier is used. It requires only a single clock cycle for one polynomial multiplication and is more suitable to reduce the latency of the PM operation.
- 2-way-karatsuba multiplier: Two m-bit input polynomials are divided into two sub-polynomials to perform multiplication. The sub-polynomials can then multiplied either by using simple Karatsuba, general Karatsuba, or the schoolbook multiplication method [25]. However, in this work, a schoolbook multiplication method is incorporated to compute the inner products (required to compute in the 2-way-karatsuba). Finally, it requires clock cycles [23,24], when m is the length of the input polynomial or the underlying field.
- 3-way-toom-cook multiplier: In this multiplier, two m-bit input polynomials are divided into three sub-polynomials. The sub-polynomials are then multiplied by using a schoolbook multiplication method to compute the inner products (required to compute in the 3-way-toom-cook). Finally, it requires clock cycles [23], when m is the length of the input polynomials.
- 4-way-toom-cook multiplier: Similar to other multipliers, i.e., 2-way-karatsuba, and 3-way-toom-cook, two m-bit input polynomials are divided into four sub-polynomials to perform multiplication. The sub-polynomials are then multiplied by using a schoolbook multiplication method to compute the inner products (required to compute in the 4-way-toom-cook). Subsequently, it requires clock cycles [24], when m is the length of the input polynomials.
- Least-significant-digit-parallel multiplier: Two input polynomials ( and ) each having size of m-bits, are multiplied by creating digits of polynomial (with size of each digit 32-bits). The input polynomial is multiplied with each created digit of size 32 bits, to produce the resulting polynomials of size bits, where d is the size of a created digit. By using the addition and shifting of polynomials of size bits, the final polynomial generated having a size of bits. Similar to the hybrid Karatsuba multiplier, the digit parallel multiplier takes one clock cycle for computation.
3.3.3. Reduction Unit
The resulting bit size after every squaring and multiplication is double i.e., bits for an m bit input. Therefore, a polynomial reduction operation is needed after each finite field multiplication and squaring operation [13,18,21]. Therefore, to perform a polynomial reduction, in this work, we used the NIST (National Institute of Standards and Technology) recommended reduction algorithm (see Algorithm 2.42 of [9]). It takes one clock cycle for computation because it can easily be implemented using numerous wires in Verilog HDL.
3.3.4. Polynomial Inversion Computation
The polynomial inversion computation is not shown in Figure 1. However, to compute polynomial inversion, the square Itoh-Tsujii algorithm (originally described in [26]) is implemented in this work. It requires only field squaring’s and multiplications. For with bit key length, inversion is computed by using squarer operations followed with 10 field multiplications [3]. The implemented addition chain for inversion computations is 1, 1, 3, 1, 7, 14, 1, 29, 58 and 116. The computational cost of inversion depends on the used multiplier. In this work, we employed six multipliers, so the computational cost for inversion is also different. For our various units of the proposed architecture, clock cycles information will be provided in the next subsequent section.
3.4. Control Unit
An FSM-based dedicated control unit is used for governing the functionalities of proposed processor design. The controller is responsible for generating the corresponding control signals for reading/writing (C1, C2 and C3) and routing multiplexers (C4 and C5), respectively. In order to implement Algorithm 1, the proposed architecture consists of 100 states (State 0 to 99), as shown in Figure 2. The corresponding details for these states are as follows.
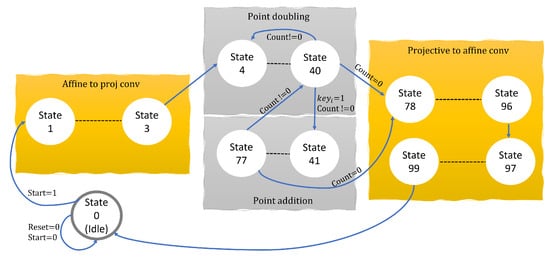
Figure 2.
Dedicated control unit of proposed hardware architecture.
- Affine to Lopez Dahab projective conversions (States 1 to 3): State 0 is an idle state where none of the operations is performed. From, state 1 to 3, the arithmetic operations involved in line 1 of Algorithm 1 is performed.
- Point doubling states (States 4 to 40): The states from 4 to 40 generates control signals for the computation of point doubling (using a list of instructions shown in column two of Table 2). Moreover, state 40 is responsible to check each bit of k, i.e., (the signal is shown in Figure 2). Once the value for then the next state will be 41, otherwise, the next state will be 4. Additionally, state 40 is also in charge of checking the signal (shown in Figure 2) for counting the number of points on the defined BHC curve. Initially, the value for is set to . Once the value for then the next state will state 78 otherwise the next state will be 4.
- Lopez Dahab to affine coordinate system (States 78 to 99): The states from 78 to 99 generates control signals for the computation of Lopez Dahab to a general affine coordinate system. As shown in line 10 of Algorithm 1, an associated inversion operation is required to perform. Therefore, 78 to 96 states are responsible to perform an inversion operation using the square version of the Itoh-Tsujii algorithm. Furthermore, additional operations of line 10 of Algorithm 1 are implemented from 97 to 99 states.
Clock Cycles Calculation
For our proposed hardware architecture, Equation (3) can be used to determine the total number of clock cycles.
- Affine to Lopez Dahab projective conversions: As shown in Equation (3), conversions from affine to Lopez Dahab projective coordinate system takes a total of 3 clock cycles.
- Point doubling: The PD requires clock cycles, where determines the clock cycles for 17 multiplication instructions in the of BHC while n presents the clock cycle for one finite field multiplication. Additional 20 clock cycles are needed for the computation of addition and squaring instructions. The value for m presents the key length.
- Point addition: Similarly, the PA requires clock cycles, where determines the clock cycles for the computation of 17 multiplication instructions in the of BHC while n determines the clock cycle for one multiplication. Additional 20 cycles are needed to compute addition and squaring instructions. The value for m shows the key length.
- Lopez Dahab to affine coordinate system: Finally, clock cycles are needed for conversion from Lopez Dahab to affine coordinates. A total of clock cycles are needed for each finite field inversion. In this work, the inversion is computed using a square Itoh-Tsujii inversion algorithm. For the remaining operations in Lopez Dahab to affine coordinate conversions, additional clock cycles are needed.
Consequently, the total number of calculated clock cycles for our proposed hardware architecture are given in Table 3. Column one provides the name of the employed multiplier in the datapath of our proposed BHC architecture. Column two provides the clock cycles (n) for one finite field multiplication. Columns three to five presents the clock cycles for various steps of Algorithm 1. Affine to Lopez Dahab conversion is step-1. PA and PD computations for PM operation determine step-2. The reconversions from Lopez Dahab to affine conversions is step-3. Finally, the total clock cycles (TCCs) are shown in the last column of Table 3.

Table 3.
Clock cycles for proposed hardware architecture using various finite field multipliers over .
For operand lengths of m-bit polynomials, Table 3 show that the hybrid Karatsuba and least-significant-digit-parallel multipliers demand the minimum clock cycles for computation of the BHC model of ECC as compared to schoolbook, 2-way-karatsuba, 3-way-toom-cook and 4-way-toom-cook multipliers.
4. Implementation Results and Comparisons
The implementation results and comparison to state-of-the-art are described in Section 4.1 and Section 4.2, respectively.
4.1. Results
Our results for various polynomial multipliers are shown in Section 4.1.1. Similarly, the results for BHC model of ECC are given in Section 4.1.2.
4.1.1. Implementations of Polynomial Multipliers
For each implemented finite field multiplier, i.e., schoolbook, 2-way-karatsuba, 3-way-toom-cook, 4-way-toom-cook, hybrid Karatsuba and least-significant-digit-parallel, an RTL model has been written in Verilog (HDL) with underlying simulation platform of Xilinx ISE (14.2). The implementations over Xilinx Virtex-6 (xc6vlx550t-2ff1760) FPGA device after post-place-and-route-level are provided in Table 4. As shown in Table 4, column one provides the name of the implemented multiplier while column two to column four provides the area information in terms of flip flops (FFs), slices and look-up-tables (LUTs). The column five in Table 4 presents the operational clock frequency. Finally, the last column shows the performance of the finite field multipliers in terms of a ratio of throughput over area (slices). The throughput is calculated by the ratio of clock cycles (given in column two of Table 3) over operational frequency.

Table 4.
Implementation results of the multipliers over .
Area comparison: The schoolbook multiplier utilizes lower hardware resources as compared to other multipliers, shown in columns two to four in Table 4. When comparing the hybrid Karatsuba multiplier, it utilizes 6.90 times higher hardware resources (FPGA slices) when compared with the schoolbook multiplier. Similarly, the hardware resource utilization of the 2-way-karatsuba, 3-way-toom-cook and 4-way-toom-cook multipliers is 2.42, 2.62 and 3.71 times higher when compared with the bit-serial schoolbook multiplier. The least-significant-digit-parallel multiplier utilizes only 1.43 times more FPGA slices than the schoolbook multiplier.
Frequency comparison. As shown in the last column of Table 4, the maximum frequency (436 MHz) over Virtex 6 FPGA device is achieved for a 4-way-toom-cook multiplier. It is important to note that the least-significant-digit-parallel multiplier achieves comparable clock frequency (416 MHz) to the 4-way-toom-cook multiplier and it utilizes 1.43 times lower hardware resources (794 FPGA slices). Therefore, there is always a trade-off between clock frequency (throughput) and the utilized area.
Latency comparison. Latency determines the time needed to perform one polynomial multiplication. It can be calculated using the ratio of clock cycles over frequency. The clock cycles for the multipliers we implement in this paper, are shown in column two of Table 3. The latency values for multipliers are not given in Table 4; however, the calculated values are presented here. Therefore, the latency values for schoolbook, 2-way-karatsuba, 3-way-toom-cook, 4-way-toom-cook, hybrid Karatsuba and least-significant-digit-parallel multipliers are 2.40 s, 1.34 s, 0.82 s, 0.13 s, 1.00 s and 0.56. These values show that the 4-way-toom-cook and least-significant-digit-parallel multipliers are convenient for high-speed cryptographic applications because these require minimum time for execution of one polynomial multiplication.
Throughput/Slices comparison. Higher is the ratio of throughput over slices, higher will be the performance. The calculated throughput/area values for schoolbook, 2-way-karatsuba, 3-way-toom-cook, 4-way-toom-cook, hybrid Karatsuba and least-significant-digit-parallel multipliers are 753.4, 556.5, 850.8, 3748.6, 60,496.0 and 52,6315.7. This demonstrates that the highest values are calculated for bit-parallel, i.e., hybrid Karatsuba and least-significant-digit-parallel, multipliers as these require one clock cycle for one finite field multiplication. Therefore, these multipliers are more suitable for high-speed applications. The schoolbook, 2-way-karatsuba and 3-way-toom-cook multipliers are appropriate for applications that need low hardware resource utilization. The implementation of our 4-way-toom-cook multiplier is useful for applications that demand both throughput and area simultaneously.
4.1.2. Results for Point Multiplication of BHC
Similar to our multiplier implementations, the RTL model for the computation of PM of our BHC model of ECC has been written in Verilog (HDL) with Xilinx ISE (14.2) design suite tool as an underlying simulation platform. Thereafter, each implemented multiplier, i.e., schoolbook, 2-way-karatsuba, 3-way-toom-cook, 4-way-toom-cook, hybrid Karatsuba and least-significant-digit-parallel, is integrated with the proposed PM architecture to evaluate the performance of the recently proposed unified addition law of BHC. The input parameters are selected from NIST recommended document [27]. Therefore, the implementation results over Xilinx Virtex-6 (xc6vlx550t-2ff1760) FPGA device after post-place-and-route-level are shown in Table 5. Column one in Table 5 provides the specification of our implemented design in terms of the used polynomial multiplier. The area information in terms of slices, LUTs and FFs is provided in column two to column four. The design’s timing information in terms of clock cycles (CCs), clock frequency (MHz) and the time required for the computation of one PM (i.e., latency) is provided in column five to seven. Finally, the total consumed power is illustrated in the last column, i.e., column eight.

Table 5.
Implementation results of the BHC model of ECC, constructed in 2018, over .
The term latency can be defined as the ratio of required clock cycles to the operational clock frequency (in MHz), and is defined in Equation (4):
As compared to other multipliers (schoolbook, 2-way-karatsuba, 3-way-toom-cook, 4-way-toom-cook and hybrid Karatsuba), the unified addition law of BHC results in lower latency (i.e., 80.0 s) when considering the least-significant-digit-parallel multiplier in the data path, as depicted in the last column of Table 5. Moreover, the overall hardware resource utilization in terms of slices, LUTs and FFs for the hybrid Karatsuba multiplier is lower (i.e., 8498 slices, 3999 LUTs and 5209 FFs) when compared to other multipliers configurations in the data path of our proposed hardware architecture, as shown in columns two to four of Table 5, respectively. Rather than the hardware resources and computational time, the lower clock cycles are acquired when hybrid Karatsuba and least-significant-digit-parallel multipliers are integrated into our PM architecture. When concerning only the clock frequency for comparison, the use of 4-way-toom-cook and least-significant-digit-parallel multipliers seem more beneficial as these achieve an operational frequency of more than 100 MHz while other multipliers result in the range from 50 to 100 MHz. The results presented above show that there is always exist some sort of trade-off between various design parameters (i.e., clock frequency, area, latency, etc.).
As for as the power consumption of our PM architecture is concerned for comparison, integration of a bit-serial multiplier, i.e., schoolbook, results in the least value of 1.46 mW, as compared to 2-way-karatsuba, 3-way-toom-cook, 4-way-toom-cook, hybrid Karatsuba and least-significant-digit-parallel multipliers where the corresponding power consumption is 1.83, 2.57, 2.92, 3.31 and 3.16 mW. Moreover, we have analyzed that the use of hybrid Karatsuba results in higher power consumption (3.31 mW) because its critical path results in higher delays when compared to the critical paths of other multipliers. If we compare the power consumption of bit-parallel multipliers, i.e., hybrid Karatsuba, and least-significant-digit-parallel, the latter is less power-hunger (3.16 mW) as compared to the former.
Selection of singular implementation for state-of-the-art comparison: We clarify that it is not possible to compare all state-of-the-art implementations from Table 5. Hence, we have selected only one design for comparison to the state-of-the-art in Section 4.2. In this regard, we have defined a design metric in terms of , and is calculated using Equation (5). The higher value of throughput over area ratio higher will be the performance of the design.
Figure 3 shows that the highest ratio of throughput over slices value is achieved for our design named with ThisWork. Consequently, we have selected the proposed architecture integrated with a least-significant-digit-parallel multiplier for state-of-the-art comparison.
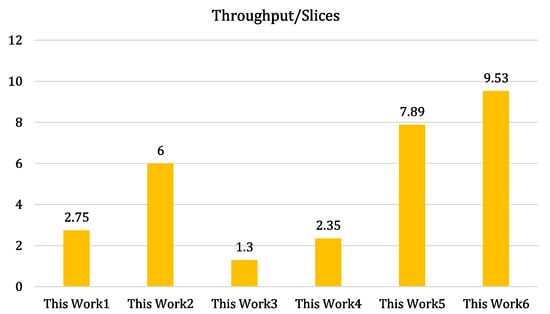
Figure 3.
Design metric ().
4.2. State-of-the-Art Implementations Comparison
The created RTL model for proposed hardware architecture (This work6) has been synthesized for FPGA devices that are used as state-of-the-art implementations, as presented in Table 6. Therefore, we use xc4vfx100 device for Xilinx Virtex-4 and 7vx690tffg1930 for Virtex-7 FPGA. It is important to note that although we have several hardware accelerators for various models of ECC (Weierstrass, BEC, HC and BHC), a realistic comparison to all these is not possible to provide as these differ in their mathematical formulations for PA and PD computations. Therefore, for a reasonable comparison, we have compared our results only with the hardware accelerators for the BHC model of ECC. In Table 6, the column one provides the name of the reference design while the implemented mathematical model for the unified addition law of BHC is presented in column two. Column three provides the implementation device. The area information in terms of slices, LUTs and FFs is provided in column four to column six. Similarly, column seven to column nine provides the timing information in terms of clock cycles, clock frequency (MHz) and the time required for the computation of one PM (latency).

Table 6.
Comparisons to state-of-the-art implementations over .
4.2.1. Comparison to of 2011
As shown in Table 6, the architecture described in [13] is implemented on Virtex-4 device. Comparatively, the hardware architecture proposed in this paper is 1.52 times slower in terms of computational time (latency). The reason is that the unified addition law of the BHC model of ECC (presented in 2011) requires fewer mathematical formulations (we refer readers to Table 1) as compared to the mathematical model constructed in 2018 (we used this and interested readers can consult Table 2). On the other hand, the hardware resource utilization (slices) of our proposed architecture is 1.49 times lesser. The reason for the use of lower hardware resources is the employment of a least-significant-digit-parallel multiplier instead of combined general and simple Karatsuba multipliers, used in [13]. Additionally, we achieved a higher operational frequency of 118 MHz (shown in column eight of Table 6) that is comparatively 1.45 times higher.
4.2.2. Comparison to of 2013
For Virtex-4 FPGA, in terms of latency, our proposed architecture is 1.44 (ratio of 111 with 77) times slower than the architecture proposed in [17]. On the other hand, the hardware resource (slices) utilization of our proposed architecture is 1.27 times lower than the [17].
The latency of the designs presented in [14,17,18,19] for the computation of one PM on Virtex-7 FPGA devices (last column of Table 6), is lower as compared to our design. This is due to the requirement of a larger number of instructions (total = 37) in the unified addition law of BHC that was recently proposed in 2018, shown in Table 2. The number of instructions involved in the unified addition law of BHC, provided in 2013, is 31. Therefore, there are seven additional instructions in the unified addition law of BHC (proposed in 2018) that result in higher computational cost (latency) when compared with the BHC model proposed in 2013. Instead of latency, the use of a least-significant-digit-parallel multiplier in our work results in lesser hardware resource utilization (slices) when compared with BHC designs, reported in [14,17,18,19].
4.2.3. Comparison to of 2018
The most interesting architecture is described in [20] where two-stage and four-stage pipelined designs are presented, including the without scheduling and their proposed scheduling of instructions for unified addition law. On a similar Virtex-7 FPGA device, our architecture utilizes 1.80 (ratio of 7123 with 3948) times lower slices as compared to their most optimized 4-stage pipelined design. The reason is the use of multiple arithmetic operators in the datapath of [20] while we used only single adder, multiplier, squarer and reduction operators. Moreover, our design requires 1.18 (ratio of 15,495 with 13,124) times lower clock cycles because the use of pipelining incurs structural hazards in [20] which results in an increase in the cycles. Additionally, our non-pipelined architecture results in 1.23 (ratio of 223 with 188) times higher operational frequency. Despite the other parameters, i.e., area, frequency, and clock cycles, our architecture is 1.42 (ratio of 82.4 with 58) times faster in terms of latency.
5. Conclusions
This article has presented design trade-offs for side-channel resistant Binary Huff Curves on FPGA. In this regard, we have presented an efficient crypto processor architecture for PM acceleration of the BHC model of ECC over . Moreover, we have implemented six finite field polynomial multiplication architectures, i.e., schoolbook, hybrid Karatsuba, 2-way-karatsuba, 3-way-toom-cook, 4-way-toom-cook and digit-parallel-least-significant. Then for the evaluation of design trade-offs, we have integrated each implemented polynomial multiplier with our proposed BHC architecture. The selected polynomial multipliers and BHC model of ECC are implemented in a Verilog HDL using the Xilinx ISE design suite tool. The implementation results are given on Xilinx Virtex-6 FPGA. The achieved results show that the integration of hybrid Karatsuba multiplier with our proposed BHC architecture results in the least hardware resources (8498 slices, 3999 LUTs and 5209 FFs). The least-significant-digit-parallel multiplier integrated with our proposed BHC design results in high-speed (in terms of both clock frequency (164 MHz) and latency (80 s)). The proposed BHC architecture integrated with a least-significant-digit-parallel multiplier is 1.42 times faster and utilizes 1.80 times lower FPGA slices as compared to the most recent BHC accelerator.
Author Contributions
Conceptualization, A.R.J., H.K. and A.A.; data extraction, U.U. and M.R.; results compilation, M.R. and U.U.; validation, M.R. and A.R.A.; writing—original draft preparation, U.U.; critical review, M.R., A.R.J., A.R.A. and A.A.; draft optimization, U.U.; supervision, A.R.J. and M.R.; funding acquisition, H.K., A.R.A. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
We are thankful to the support of Deanship of Scientific Research at King Khalid University, Abha, Saudi Arabia for funding this work under grant number R.G.P.2/132/42.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rashid, M.; Imran, M.; Jafri, A.R.; Al-Somani, T.F. Flexible architectures for cryptographic algorithms—A systematic literature review. J. Circuits Syst. Comput. 2019, 28, 1930003. [Google Scholar] [CrossRef]
- Li, J.; Zhong, S.; Li, Z.; Cao, S.; Zhang, J.; Wang, W. Speed-Oriented Architecture for Binary Field Point Multiplication on Elliptic Curves. IEEE Access 2019, 7, 32048–32060. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M.; Jafri, A.R.; Kashif, M. Throughput/area optimised pipelined architecture for elliptic curve crypto processor. IET Comput. Digit. Tech. 2019, 13, 361–368. [Google Scholar] [CrossRef] [Green Version]
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Rivest, R.L.; Shamir, A.; Adleman, L.M. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Advances in Cryptology—CRYPTO ’85 Proceedings; Williams, H.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 417–426. [Google Scholar]
- Imran, M.; Shehzad, F. FPGA Based Crypto Processor for Elliptic Curve Point Multiplication (ECPM) over GF (2233). Int. J. Inf. Secur. Res. 2017, 7, 706–713. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography 2004. pp. 1–311. Available online: https://link.springer.com/book/10.1007/b97644 (accessed on 6 March 2022).
- Bernstein, D.J.; Lange, T.; Rezaeian Farashahi, R. Binary edwards curves. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 244–265. [Google Scholar]
- Farashahi, R.R.; Joye, M. Efficient Arithmetic on Hessian Curves. In Public Key Cryptography—PKC 2010; Nguyen, P.Q., Pointcheval, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 243–260. [Google Scholar]
- Joye, M.; Tibouchi, M.; Vergnaud, D. Huffs model for elliptic curves. In International Algorithmic Number Theory Symposium; Springer: Berlin/Heidelberg, Germany, 2010; pp. 234–250. [Google Scholar]
- Chatterjee, A.; Sengupta, I. High-speed unified elliptic curve cryptosystem on FPGAs using binary huff curves. In Progress in VLSI Design and Test; Springer: Berlin/Heidelberg, Germany, 2012; pp. 243–251. [Google Scholar]
- Ghosh, S.; Kumar, A.; Das, A.; Verbauwhede, I. On the implementation of unified arithmetic on binary huff curves. In International Conference on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 349–364. [Google Scholar]
- Devigne, J.; Joye, M. Binary huff curves. In ‘Cryptographers’ Track at the RSA Conference; Springer: Berlin/Heidelberg, Germany, 2011; pp. 340–355. [Google Scholar]
- Cho, S.M.; Jin, S.; Kim, H. Side-channel vulnerabilities of unified point addition on binary huff curve and its countermeasure. Appl. Sci. 2018, 8, 2002. [Google Scholar] [CrossRef] [Green Version]
- Jafri, A.R.; ul Islam, M.N.; Imran, M.; Rashid, M. Towards an optimized architecture for unified binary huff curves. J. Circuits Syst. Comput. 2017, 26, 1750178. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M.; Jafri, A.R.; Najam-ul Islam, M. ACryp-Proc: Flexible asymmetric crypto processor for point multiplication. IEEE Access 2018, 6, 22778–22793. [Google Scholar] [CrossRef]
- Rashid, M.; Imran, M.; Jafri, A.R.; Mehmood, Z. A 4-stage pipelined architecture for point multiplication of binary huff curves. J. Circuits Syst. Comput. 2020, 29, 2050179. [Google Scholar] [CrossRef]
- Rashid, M.; Imran, M.; Kashif, M.; Sajid, A. An Optimized Architecture for Binary Huff Curves With Improved Security. IEEE Access 2021, 9, 88498–88511. [Google Scholar] [CrossRef]
- Yeh, L.Y.; Chen, P.J.; Pai, C.C.; Liu, T.T. An Energy-Efficient Dual-Field Elliptic Curve Cryptography Processor for Internet of Things Applications. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1614–1618. [Google Scholar] [CrossRef]
- Rashid, M.; Hazzazi, M.M.; Khan, S.Z.; Alharbi, A.R.; Sajid, A.; Aljaedi, A. A Novel Low-Area Point Multiplication Architecture for Elliptic-Curve Cryptography. Electronics 2021, 10, 2698. [Google Scholar] [CrossRef]
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Open-source Library of Large Integer Polynomial Multipliers. In Proceedings of the 2021 24th International Symposium on Design and Diagnostics of Electronic Circuits Systems (DDECS), Vienna, Austria, 7–9 April 2021; pp. 145–150. [Google Scholar] [CrossRef]
- Imran, M.; Abideen, Z.U.; Pagliarini, S. An Experimental Study of Building Blocks of Lattice-Based NIST Post-Quantum Cryptographic Algorithms. Electronics 2020, 9, 1953. [Google Scholar] [CrossRef]
- Kashif, M.; Cicek, I.; Imran, M. A Hardware Efficient Elliptic Curve Accelerator for FPGA Based Cryptographic Applications. In Proceedings of the 2019 11th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2019; pp. 362–366. [Google Scholar] [CrossRef]
- Itoh, T.; Tsujii, S. A fast algorithm for computing multiplicative inverses in GF (2m) using normal bases. Inf. Comput. 1988, 78, 171–177. [Google Scholar] [CrossRef] [Green Version]
- NIST. Recommended Elliptic Curves for Federal Government Use. 1999. Available online: https://csrc.nist.gov/csrc/media/publications/fips/186/2/archive/2000-01-27/documents/fips186-2.pdf (accessed on 6 March 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).