An Analysis of Hardware Design of MLWE-Based Public-Key Encryption and Key-Establishment Algorithms

Abstract

This paper presents a review of module ring learning with errors-based (MLWE-based) public-key encryption and key-establishment algorithms. In particular, we introduce the preliminaries of public key cryptography, MLWE-based algorithms, and arithmetic operations in post-quantum cryptography. We then focus on analyzing the state-of-the-art hardware architecture designs of CRYSTALS-Kyber at different security levels, including hardware architectures for Kyber-512, Kyber-768, and Kyber-1024. This analysis is dedicated to providing complete guidelines for selecting the most suitable CRYSTALS-Kyber hardware architecture to apply in post-quantum cryptography-based security systems in reality, with different requirements of security levels and hardware efficiency.

1. Introduction

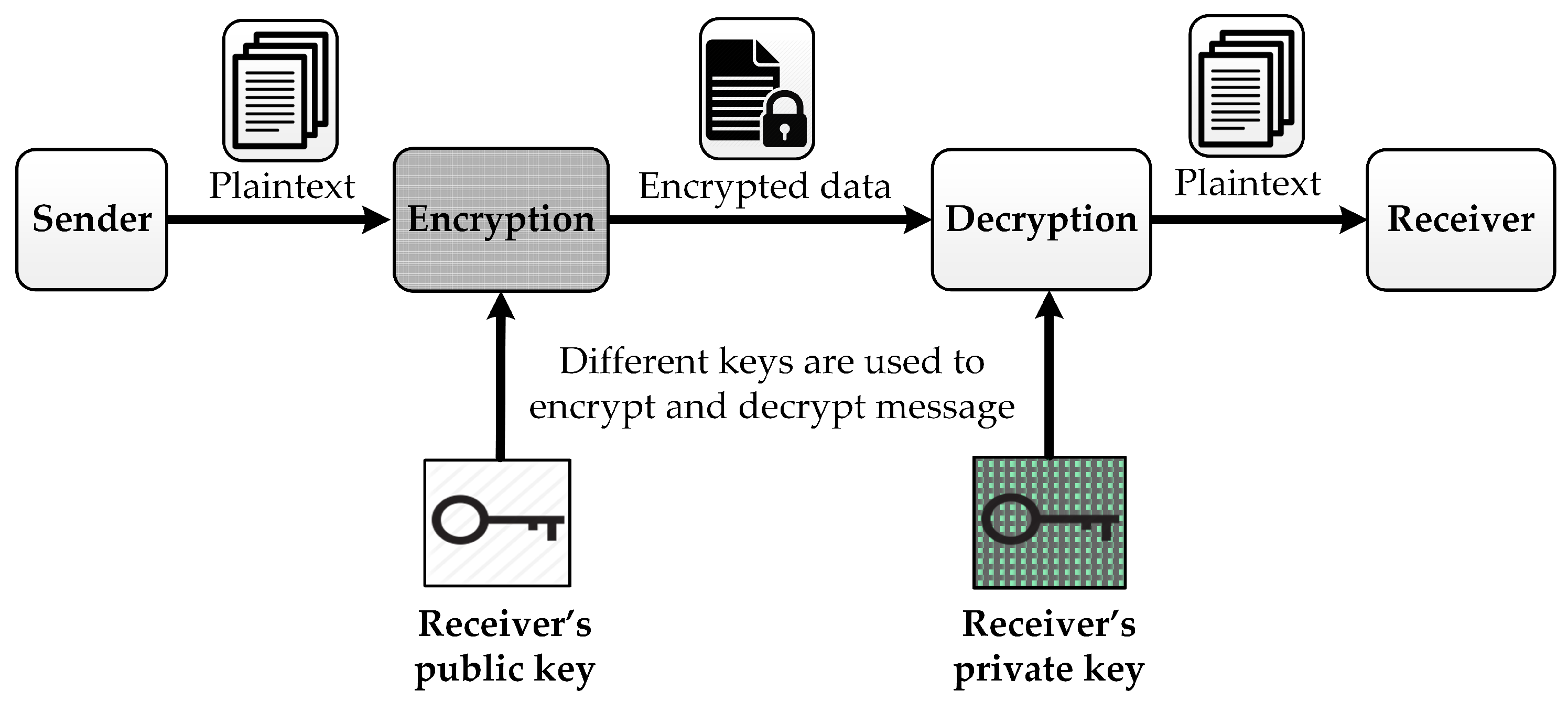
Cryptography is broadly categorized into symmetric key cryptography and asymmetric key cryptography (or public key cryptography). In symmetric key cryptography, a single key is used between a sender and a receiver to enable secure communication, and the key is kept confidential from anyone else. Public key cryptography utilizes a public key in encryption and a private key in decryption, as demonstrated in Figure 1. While the private key is kept secret to use in the decryption operation, the public key is published to everyone and used in the encryption operation. The encryption process generates the encrypted message (ciphertext) from the input message (plaintext) and the public key. The ciphertext can be decrypted using the private key. One of the most well-known asymmetric cryptographic algorithms was developed by Rivest–Shamir–Adleman (RSA) [1,2,3,4]. The RSA algorithm is the earliest public key cryptographic algorithm developed and published for commercial use. It is widespread and has been integrated in both Netscape Web and Microsoft browsers to provide security solutions for e-commerce applications. The patented RSA encryption algorithm has, in fact, become a standard for public-use encryption applications. Elliptic curve cryptography (ECC) [5,6,7,8,9] is another widely used public key cryptography algorithm. The ECC encryption and decryption operations rely on an elliptic curve and arithmetic operations over a Galois field, either GF(p) or GF($2^m$). In the key-generation operation, the recipient selects a base point $P_S$ on the elliptic curve and a random number as its private key $k_S$ to calculate ECC point multiplication $Q_S=k_S\times P_S$. The public key is stored publicly so that the sender can use the receiver’s public key to encrypt the input data before sending the data over the network. At the receiver side, the data sent by the transmitter can be retrieved using ECC point multiplication operations and the private key of the receiver.

With the rapid growth of quantum computers, the existing public key schemes can be basically broken in the next few years. In 2016, National Institute of Standard and Technology (NIST) launched the post-quantum cryptography (PQC) project to discover PQC candidates for future standardization  [10]. The goal of the PQC project is to develop cryptographic systems that are secure against both classical and quantum computers, and that can be compatible with existing communications protocols and networks. Round 3 finalists include (1) four candidates for public-key encryption (PKE) and key-establishment (KEM) algorithms (Classic McEliece, CRYSTALS-Kyber, NTRU, Saber), (2) three candidates for digital signature algorithms (CRYSTALS-Dilithium, Falcon, Rainbow), and (3) alternate candidates. Among the PKE and KEM algorithms in the round 3 finalists, the CRYSTALS-Kyber algorithm is a promising candidate.

Learning with errors (LWE) problems are lattice-based problems attracting a lot of attention from research communities in recent years. In LWE problems, given a finite field ${\mathbb{Z}}_q$ with modulus q, two matrices A and p, and a small noise e, it is a challenge to find the secret key s from the equation $A·s+e=p$. Many proposals using standard LWE [11] and the structured ring-LWE [12,13,14,15,16,17] have been conducted. The typical advantage of standard LWE is easy scalability. However, it introduces a significant decrease in efficiency. The structured LWE offers better efficiency in terms of speed and key and ciphertext sizes. Nevertheless, there is a tradeoff between efficiency and security because of the additional structure [18]. Module-LWE can balance these two extremes. In [18], the authors of the CRYSTALS-Kyber algorithm mentioned that Kyber helps to reduce structure and offers much better scalability compared to ring-LWE. The performance of Kyber is very similar to the ring-LWE-based schemes, using 256 bits to encrypt messages [19].

The implementations of CRYSTALS-Kyber include software design [18,20], software and hardware codesign [20], and pure hardware design [20,21,22,23,24]. In [18], the authors showed the implementation results on Intel Haswell CPUs and ARM Cortex-M4 CPUs. The authors in [20] described the software implementation of post-quantum cryptography schemes including CRYSTALS-Kyber using C language on ARM Cotex-A53. In order to accelerate the operations of Kyber, the authors in [25] introduced massively parallel algorithms implemented on a GPU. The authors in [20] also presented a software and hardware codesign of Kyber. The software and hardware codesign offers a remarkable improvement in encapsulation time and decapsulation time compared with pure software implementation results. The pure hardware implementations in [20,21,22,23,24] introduce different approaches, with a focus on reducing hardware complexity and speeding up the processing time.

In this paper, we summarize the CRYSTALS-Kyber public-key encryption and key-establishment algorithms. We then present an analysis of the state-of-the-art implementations of CRYSTALS-Kyber in pure software, software and hardware codesign, and pure hardware. From the existing implementation results, we recommend the most suitable Kyber hardware architecture for various systems which have different requirements of hardware resources and latency.

The rest of this paper is structured as follows. Section 2 gives background information about CRYSTALS-Kyber. Section 3 presents an analysis of the implementation of the state-of-the-art designs. We discuss some potential solutions to improve the existing works in Section 4. Finally, conclusions are drawn in Section 5.

2. Background

In this section, we introduce CRYSTALS-Kyber, an MLWE-based public-key encryption and key-establishment algorithms that entered round 3 of the PQC standardization. Kyber has first been introduced in [26], which includes three parameter sets, as reported in

Table 1. Kyber parameter sets  [18].

Algorithm	NIST Security Level	Parameters
		$\mathit{n}$	$\mathit{k}$	$\mathit{q}$	(${\mathbf{\eta }}_{\mathbf{1}}$, ${\mathbf{\eta }}_{\mathbf{2}}$)	(${\mathit{d}}_{\mathit{u}}$, ${\mathit{d}}_{\mathit{v}}$)
Kyber-512	1	256	2	3329	(3, 2)	(10, 4)
Kyber-768	3	256	3	3329	(2, 2)	(10, 4)
Kyber-1024	5	256	4	3329	(2, 2)	(11, 5)

, corresponding to three security levels of NIST. Polynomials are of the same degree $n=256$, and the polynomial coefficients are members of the prime field $Z_q$, where q = 3329 for all security levels. However, for each security level, different numbers of polynomials are required. These polynomials are considered as a vector whose size is specified by a parameter k. The values of k are 2, 3, and 4, corresponding to the security levels 1, 3, and 5, respectively. The remaining parameters ${\eta }_1$, ${\eta }_1$, $d_u$, and $d_v$ are chosen to balance between security, ciphertext size, and failure probability. A detailed explanation of parameter selection can be found in [18]. Centered binomial distribution (CBD) is used to generate secret noise polynomials. In this paper, the same notation presented in [18] is used. For example, regular font letters represent elements in R or $R_q$, bold lower-case letters denote vectors with coefficients in R or $R_q$, bold upper-case letters are matrices. For bytes and byte arrays, ${\mathcal{B}}^k$ is the set of byte arrays of length k, and $a\left|\right|b$ is the concatenation of two byte arrays a and b. More details about notation can be found in [18].

2.1. Public-Key Encryption Algorithm

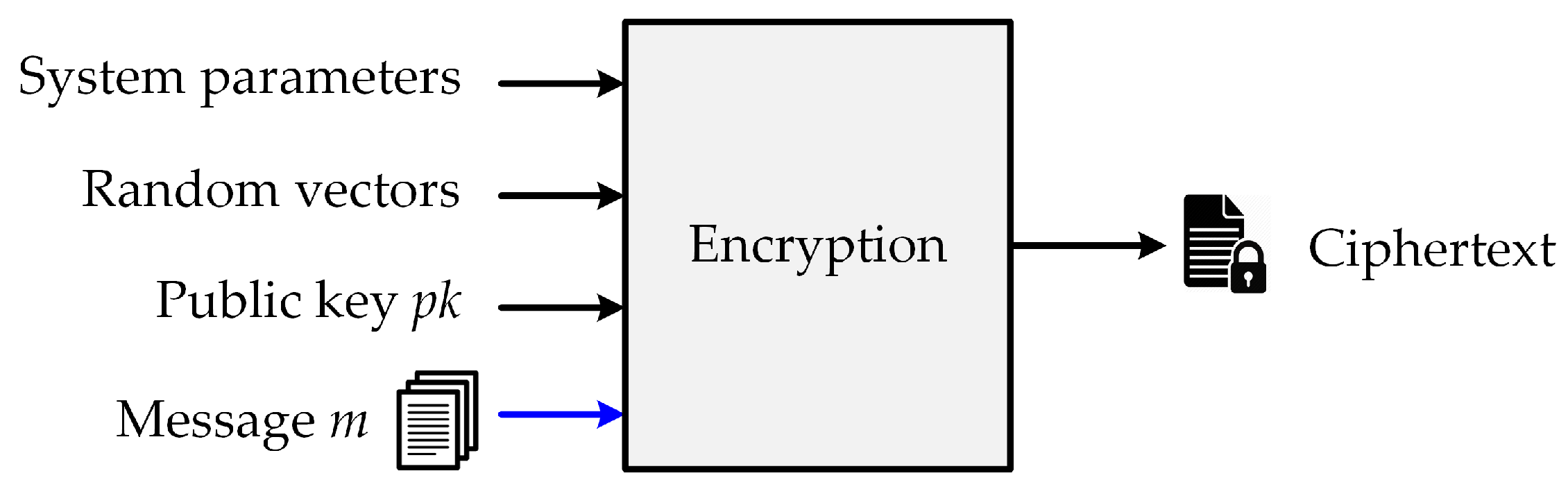
Operations in the PKE algorithm includes key generation, encryption, and decryption. The key-generation function generates a public key $pk$ and a private key $sk$, which are then used in encryption and decryption operations, respectively. Particularly, the public key participates in the encryption process to generate a ciphertext c from the input message m and the public key $pk$. The public-key encryption process is illustrated in Figure 2.

The decryption function restores the original message m from the ciphertext c and the private key $sk$, as described in Figure 3.

The functions of the Kyber chosen-plaintext attack public-key encryption (Kyber.CPAPKE) are defined as follows:

• Kyber.CPAPKE key-generation function

The Kyber.CPAPKE key-generation function generates a public key $pk$ used for the encryption process and a secret key $sk$ used for the decryption process. Noise vectors s and e are sampled from a CBD. The public matrix $\hat{\mathbf{A}}$ is generated from a rejection sampler. The public key $pk$ and private key $sk$ are computed as $pk=(\rho ,\hat{\mathbf{t}})$, and $sk=\hat{\mathbf{s}}$, in which $\hat{\mathbf{t}}=\hat{\mathbf{A}}\circ \hat{\mathbf{s}}+\hat{\mathbf{e}}$. The details of the Kyber.CPAPKE key-generation function are described in Algorithm 1. In this algorithm, XOF is an extendable output function instantiated with SHAKE-128. A parse function returns the NTT-representation of the input byte stream. G is a hash function G: ${\mathcal{B}}^{*}\to {\mathcal{B}}^{32}\times {\mathcal{B}}^{32}$. PRF and NTT represent a pseudo-random function and the number theoretic transform, respectively.

Algorithm 1: Kyber PKE key-generation algorithm (Kyber.CPAPKE.KeyGen) [18].

Output: Public key $pk\in {\mathcal{B}}^{12·k·n/8+32}$,

Secret key $sk\in {\mathcal{B}}^{12·k·n/8}$

1   $d\leftarrow \in {\mathcal{B}}^{32}$

2   $(\rho ,\sigma ):=\mathrm{G}\left(d\right)$

3   $N:=0$

4   for i from 0 to $k-1$ do

5     for j from 0 to $k-1$ do

6         $\hat{\mathbf{A}}\left[i\right]\left[j\right]:=\mathrm{Parse}\left(\mathrm{XOF}(\rho ,j,i)\right)$

7     end for

8   end for

9   for i from 0 to $k-1$ do

10      $\mathbf{s}\left[i\right]:={\mathrm{CBD}}_{{\eta }_1}\left(\mathrm{PRF}(\sigma ,N)\right)$

11      $N:=N+1$

12   end for

13   for i from 0 to $k-1$ do

14      $\mathbf{e}\left[i\right]:={\mathrm{CBD}}_{{\eta }_1}\left(\mathrm{PRF}(\sigma ,N)\right)$

15      $N:=N+1$

16   end for

17   $\hat{\mathbf{s}}:=\mathrm{NTT}(\mathrm{s})$

18   $\hat{\mathbf{e}}:=\mathrm{NTT}(\mathrm{s})$

19   $\hat{\mathbf{t}}:=\hat{\mathbf{A}}\circ \hat{\mathbf{s}}+\hat{\mathbf{e}}$

20   $pk:={\mathrm{Encode}}_{12}\left(\hat{\mathbf{t}}{\mathrm{mod}}^{+}q\right)\left|\right|\rho$

21   $sk:={\mathrm{Encode}}_{12}\left(\hat{\mathbf{s}}{\mathrm{mod}}^{+}q\right)$

22   return $(pk,sk)$

• Kyber.CPAPKE encryption function

The Kyber.CPAPKE encryption function constructs ciphertext $c=(c_1,c_2)$ from input message m, random coins $r\in {\mathcal{B}}^{32}$, and the public key $pk$, as presented in Algorithm 2. As described in Algorithm 2, ${\hat{\mathbf{A}}}^T$ is generated from a uniform distribution, and r, e${}_1$, and $e_2$ are sampled from a binomial sampler. The ciphertext c is constructed as $c=({\mathrm{Compress}}_q(\mathbf{u},d_u),$${\mathrm{Compress}}_v(v,d_v))$, where $\mathbf{u}={\mathrm{NTT}}^{-1}({\hat{\mathbf{A}}}^T\circ \hat{\mathbf{r}})+{\mathbf{e}}_1$ and $v={\mathrm{NTT}}^{-1}({\hat{\mathbf{t}}}^T\circ \hat{\mathbf{r}})+e_2+m$. NTT${}^{-1}$ is the inverse number theoretic transform.

Algorithm 2: Kyber PKE encryption algorithm (Kyber.CPAPKE.Enc($pk,m,r$)) [18].

Input: Message $m\in {\mathcal{B}}^{32}$,

Public key $pk\in {\mathcal{B}}^{12·k·n/8+32}$,

Random coins $r\in {\mathcal{B}}^{32}$

Output: Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$

1   $N:=0$

2   $\hat{\mathbf{t}}:={\mathrm{Decode}}_{12}\left(pk\right)$

3   $\rho :=pk+12·k·n/8$

4   for i from 0 to $k-1$ do

5     for j from 0 to $k-1$ do

6         ${\hat{\mathbf{A}}}^T\left[i\right]\left[j\right]:=\mathrm{Parse}\left(\mathrm{XOF}(\rho ,i,j)\right)$

7     end for

8   end for

9   for i from 0 to $k-1$ do

10      $\mathbf{r}\left[i\right]:={\mathrm{CBD}}_{{\eta }_1}\left(\mathrm{PRF}(r,N)\right)$

11      $N:=N+1$

12   end for

13   for i from 0 to $k-1$ do

14      ${\mathbf{e}}_1\left[i\right]:={\mathrm{CBD}}_{{\eta }_2}\left(\mathrm{PRF}(r,N)\right)$

15      $N:=N+1$

16   end for

17   $e_2:={\mathrm{CBD}}_{{\eta }_2}\left(\mathrm{PRF}(r,N)\right)$

18   $\hat{\mathbf{r}}:=\mathrm{NTT}(\mathrm{r})$

19   $\mathbf{u}:={\mathrm{NTT}}^{-1}({\hat{\mathbf{A}}}^T\circ \hat{\mathbf{r}})+{\mathbf{e}}_1$

20   $v:={\mathrm{NTT}}^{-1}({\hat{\mathbf{t}}}^T\circ \hat{\mathbf{r}})+e_2+{\mathrm{Decompress}}_q({\mathrm{Decode}}_1\left(m\right),1)$

21   $c_1:={\mathrm{Encode}}_{d_u}\left({\mathrm{Compress}}_q(\mathbf{u},d_u)\right)$

22   $c_2:={\mathrm{Encode}}_{d_v}\left({\mathrm{Compress}}_q(v,d_v)\right)$

23   return $c=(c_1,c_2)$

• Kyber.CPAPKE decryption function

The Kyber.CPAPKE decryption function shown in Algorithm 3 recovers the original message m from the ciphertext c using a secret key $sk$. The value of m is calculated as $m=\mathrm{Compress}(v-{\mathrm{NTT}}^{-1}({\hat{\mathbf{s}}}^T\circ \hat{\mathbf{u}})$, where u and v are extracted from c.   

Algorithm 3: Kyber PKE decryption algorithm (Kyber.CPAPKE.Dec) [18].

Input:  Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$,

Secret key $sk\in {\mathcal{B}}^{12·k·n/8}$

Output:  Message $m\in {\mathcal{B}}^{32}$

1   $\mathbf{u}:={\mathrm{Decompress}}_q({\mathrm{Decode}}_{d_u}\left(c\right),d_u)$

2   $v:={\mathrm{Decompress}}_q({\mathrm{Decode}}_{d_v}(c+d_u·k·n/8),d_v)$

3   $c_1:={\mathrm{Encode}}_{d_u}\left({\mathrm{Compress}}_q(\mathbf{u},d_u)\right)$

4   $c_2:={\mathrm{Encode}}_{d_v}\left({\mathrm{Compress}}_q(v,d_v)\right)$

5   $\hat{\mathbf{s}}:={\mathrm{Decode}}_{12}\left(sk\right)$

6   $m:={\mathrm{Encode}}_1\left({\mathrm{Compress}}_q(v-{\mathrm{NTT}}^{-1}({\hat{\mathbf{s}}}^T\circ \mathrm{NTT}\left(\mathbf{u}\right)),1)\right)$

7   return m

2.2. Key-Establishment Algorithm

The Kyber key-establishment algorithm (Kyber.CCAKEM) includes key generation, encapsulation, and decapsulation. Kyber.CCAKEM is constructed from the CPA-secure public-key encryption described in Algorithms 1–3. The encapsulation operation constructs ciphertext c and a shared key K from the input message m, public key $pk$, and random vectors, as illustrated in Figure 4. Figure 5 describes the decapsulation operation, which recovers the shared key K from ciphertext c and private key $sk$.

The following algorithms describe the key generation, encapsulation, and decapsulation of Kyber.CCAKEM in detail.

• Kyber.CCAKEM key generation algorithm

The Kyber.CCAKEM key-generation algorithm generating public key $pk\in {\mathcal{B}}^{12·k·n/8+32}$ and secret key $sk\in {\mathcal{B}}^{12·k·n/8+96}$ is presented in Algorithm 4. Initially, $pk$ and $s{k}^{\prime }$ are constructed by the Kyber.CPAPKE.KeyGen() algorithm presented in Algorithm 1. The value of the secret key $sk$ is then calculated using the formula $sk:=\left(s{k}^{\prime }\right|\left|pk\right|\left|\mathrm{H}\left(pk\right)\right|\left|z\right)$, where z is a value in ${\mathcal{B}}^{32}$. H is a hash function, H: ${\mathcal{B}}^{*}\to {\mathcal{B}}^{32}$.

Algorithm 4: Kyber KEM key-generation algorithm (Kyber.CCAKEM.KeyGen) [18].

Output:  Public key $pk\in {\mathcal{B}}^{12·k·n/8+32}$,

Secret key $sk\in {\mathcal{B}}^{12·k·n/8+96}$

1   $z\leftarrow {\mathcal{B}}^{32}$

2   $(pk,s{k}^{\prime }):=\mathrm{Kyber}.\mathrm{CPAPKE}.\mathrm{KeyGen}\left(\right)$

3   $sk:=\left(s{k}^{\prime }\right|\left|pk\right|\left|\mathrm{H}\left(pk\right)\right|\left|z\right)$

4   return $(pk,sk)$

• Kyber.CCAKEM encapsulation algorithm

The Kyber.CCAKEM encapsulation algorithm returns the ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$ and shared key $K\in {\mathcal{B}}^{*}$ from input public key $pk$ that was generated from Algorithm 5. Specifically, the ciphertext c is constructed by the Kyber.CPAPKE encryption function in Algorithm 2, and the shared key K is generated using the SHA3-256, SHA3-512, and SHAKE-256 algorithms from the input message m and ciphertext c. More details about the functions used to generate K can be found in [18].    

Algorithm 5: Kyber.CCAKEM.Enc($pk$) [18].

Input:  Public key $pk\in {\mathcal{B}}^{12·k·n/8+32}$

Output:  Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$,

Shared key $K\in {\mathcal{B}}^{*}$

1   $m\leftarrow {\mathcal{B}}^{32}$

2   $m\leftarrow \mathrm{H}\left(m\right)$

3   $(\overline{K},r)\leftarrow \mathrm{G}\left(m\right||\mathrm{H}\left(pk\right))$

4   $c:=\mathrm{Kyber}.\mathrm{CPAPKE}.\mathrm{Enc}(pk,m,r)$

5   $K:=\mathrm{KDF}\left(\overline{K}\right|\left|\mathrm{H}\left(c\right)\right)$

6   return $(c,K)$

• Kyber.CCAKEM decapsulation algorithm

The Kyber.CCAKEM decapsulation algorithm restores the shared key K from the input ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$ and secret key $sk\in {\mathcal{B}}^{12·k·n/8+96}$, as described in Algorithm 6.  

Algorithm 6: Kyber.CCAKEM.Dec($c,sk$) [18].

Input:  Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$,

Secret key $sk\in {\mathcal{B}}^{12·k·n/8+96}$

Output:  Shared key $K\in {\mathcal{B}}^{*}$

1   $pk:=sk+12·k·n/8$

2   $h:=sk+24·k·n/8+32\in {\mathcal{B}}^{32}$

3   $z:=sk+24·k·n/8+64$

4   $m^{\prime }:=\mathrm{Kyber}.\mathrm{CPAPKE}.\mathrm{Dec}(\mathbf{s},(\mathbf{u},v))$

5   $(\overline{K},r^{\prime }):=\mathrm{G}(m^{\prime }\left|\right|h)$

6   $c^{\prime }:=\mathrm{Kyber}.\mathrm{CPAPKE}.\mathrm{Enc}(pk,m^{\prime },r^{\prime })$

7   $\mathbf{if}c=c^{\prime }\mathbf{then}$

8      $\mathbf{return}K=\mathbf{KDF}\left(\overline{K^{\prime }}\right|\left|\mathrm{H}\left(c\right)\right)$

9   else

10      $\mathbf{return}K=\mathbf{KDF}\left(z\right|\left|\mathrm{H}\right(c\left)\right)$

11   endif

12   return K

The Kyber PKE enrcryption/decryption and Kyber KEM encapsulation/decapsulation algorithms are summarized in

Table 2. Comparison of Kyber PKE encryption/decryption and Kyber KEM encapsulation/decapsulation algorithms.

Algorithm	Input	Output
PKE encryption	Input message $m\in {\mathcal{B}}^{32}$ Public key $pk\in {\mathcal{B}}^{12·k·n/8+32}$ Random coins $r\in {\mathcal{B}}^{32}$	Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$
KEM encapsulation	Public key $pk\in {\mathcal{B}}^{12·k·n/8+32}$	Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$ Shared key $K\in {\mathcal{B}}^{*}$
PKE decryption	Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$ Secret key $sk\in {\mathcal{B}}^{12·k·n/8}$	Original message $m\in {\mathcal{B}}^{32}$
KEM decapsulation	Ciphertext $c\in {\mathcal{B}}^{d_u·k·n/8+d_v·n/8}$ Secret key $sk\in {\mathcal{B}}^{12·k·n/8+96}$	Shared key $K\in {\mathcal{B}}^{*}$

.

2.3. Arithmetic Operations in CRYSTALS-Kyber

In this section, we introduce the typical arithmetic operations in CRYSTALS-Kyber, which include number theoretic transform (NTT), modular reduction, and sampling.

• Number Theoretic Transform

Polynomial multiplication in $R_q$ using NTT offers multiple advantages [18]: simple code space, high speed, and no additional memory is required. NTT is a form of the well-known fast Fourier transform (FFT) [27,28], with all arithmetic operations performed in a finite field. NTT uses the n-th primitive root of unity ${\omega }_n$ in the ring ${\mathbb{Z}}_q$. Given a polynomial a in $R_q$:

$$a\left(x\right)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{255}{x}^{255}.$$

(1)

NTT(a) is expressed as:

$$\hat{a}\left(x\right)={\hat{a}}_0+{\hat{a}}_{1}X+{\hat{a}}_2{X}^2+\cdots ++{\hat{a}}_{255}{X}^{255}.$$

(2)

Since NTT plays a crucial role in the hardware architecture design of post-quantum cryptography, improving NTT performance has received great attention. In [29], the authors proposed the algorithmic and hardware optimizations to design the NTT-based polynomial multiplication architecture. In [30], the authors introduced a fast modular multiplication method and a memory access scheme using doubled bandwidth ping-pong; the polynomial multiplication can be accelerated using the significantly fewer hardware resources.

• Modular reduction algorithm

Modular reduction for Kyber is specified in [18] as follows: define $r^{\prime }=r{\mathrm{mod}}^{\pm }\alpha$ as the unique element $r^{\prime }$ in $-\frac{\alpha }{2}<r^{\prime }\le \frac{\alpha }{2}$ such that $r^{\prime }=r\mathrm{mod}\alpha$ for an even positive integer $\alpha$. For an odd positive integer $\alpha$, the rank becomes $-\frac{\alpha -1}{2}\le r^{\prime }\le \frac{\alpha -1}{2}$. Define $r^{\prime }=r{\mathrm{mod}}^{+}\alpha$ as the unique element $r^{\prime }$ in $0\le r^{\prime }<\alpha$ such that $r^{\prime }=r\mathrm{mod}\alpha$. Generally, modular reduction can be simplified as $r\mathrm{mod}\alpha$.

In hardware design, the modular reduction operation in multiplication can be executed using Barrett’s reduction [31] or Montgomery’s reduction [32]. Montgomery’s reduction algorithm requires converting numbers into and out of Montgomery form [33]. For Barrett’s modular reduction, the SAM2 technique is utilized to accelerate its operation in hardware. Barrett’s modular reduction requires a large number of shift blocks, adders, subtractors, and may be subject to timing attacks [33].

• Sampling

The Kyber design is based on the module ring learning with errors encryption scheme, which typically considers LWE with either a rounded Gaussian [34] or a discrete Gaussian [35]. The authors of Kyber use centered binomial noise, which relies on LWE, in the design of Kyber.

In uniform sampling, Kyber uses a deterministic approach to sample elements in $R_q$, where $q=3329$. These elements are statistically close to a uniform distribution [18]. Specifically, a byte stream $B=b_0,b_1,b_2,\dots$ is the input of a $\mathrm{parse}\mathrm{function}:\mathcal{B}\to R_q$, to compute the number theoretic transform of $a\in R_q$. The details of the parse function can be found in [18]. The output of the parse function is as follows:

$$\hat{a}\left(x\right)={\hat{a}}_0+{\hat{a}}_{1}X+\cdots ++{\hat{a}}_{n-1}{X}^{n-1}.$$

(3)

Centered binomial distribution ${\mathcal{B}}_{\eta }$ is used to sample noise in Kyber, where $\eta =2$ or $\eta =3$. The centered binomial distribution is described in Algorithm 7.   

Algorithm 7:${\mathrm{CBD}}_{\eta }:{\mathcal{B}}^{64\eta }\to R_q$ [18].

Input:  Byte array $B=(b_0,b_1,b_2,\dots ,b_{64\eta -1})\in {\mathcal{B}}^{64\eta }$

Output:  Polynomial $f\in R_q$

1   $({\beta }_0,\dots ,{\beta }_{512\eta -1}):=\mathrm{BytesToBits}\left(B\right)$

2    $\mathbf{for}i\mathrm{from}0\mathrm{to}255\mathbf{do}$

3       $a:={\sum }_{j=0}^{\eta -1}{\beta }_{2i\eta +j}$

4       $b:={\sum }_{j=0}^{\eta -1}{\beta }_{2i\eta +\eta +j}$

5       $f_i:=a-b$

6    end for

7   return $f_0+f_{1}X+f_2{X}^2+\cdots +f_{255}{X}^{255}$

3. Implementation of CRYSTALS-Kyber

In this section, we introduce existing implementation results of CRYSTALS-Kyber in pure software, software/hardware codesign, and pure hardware. We then analyze these results with a focus on hardware architecture design, and recommend suitable Kyber hardware architectures among the state-of-the-art designs for specific design goals.

The pure software implementation results of Kyber on Intel Haswell CPUs and ARM Cortex-M4 CPUs are reported in

Table 3. Results of Kyber pure software design on Intel Haswell CPUs and ARM Cortex-M4 CPUs [18].

Algorithm	Function	Time (Clock Cycles)
		Intel Haswell CPUs	ARM Cortex-M4 CPUs
Kyber-512	Encapsulation	154,524	561,518
	Decapsulation	187,960	519,237
Kyber-768	Encapsulation	235,260	915,676
	Decapsulation	274,900	853,001
Kyber-1024	Encapsulation	346,648	1,407,769
	Decapsulation	396,584	1,326,409

. Cycle counts are obtained on one core of a CPU and the results on an Intel Haswell CPU are the C-reference implementation results. As can be seen from Table 3, the software implementation on Intel Haswell CPUs offers a better performance, in terms of number of clock cyles, than the implementation on ARM Cortex-M4 CPUs, for both encapsulation and decapsulation processes at all security levels.

Table 4. Existing pure software design and software/hardware codesign results of Kyber [36].

Algorithm	Function	Time ($\mathsf{\mu }\mathrm{s}$)
		Pure Software Design	Software/Hardware Codesign
Kyber-512	Encapsulation	332.0	15.2
	Decapsulation	433.0	17.1
Kyber-768	Encapsulation	536.7	17.8
	Decapsulation	670.1	20.1
Kyber-1024	Encapsulation	787.5	22.0
	Decapsulation	953.7	24.7

shows the processing time in microseconds of the Kyber encapsulation and decapsulation operations in both software design and software/hardware codesign. As can be seen, the Kyber encapsulation and decapsulation operations implemented in the software/hardware codesign are much faster than those on pure software design. Specifically, with Kyber-1024, the encapsulation time and decapsulation time in software/hardware codesign are accelerated by up to 35.8 times and 38.6 times, compared with those in pure software design, respectively.

The pure hardware implementation results of Kyber-512, Kyber-768, and Kyber-1024 are presented in

Table 5. Comparison of the existing Kyber-512 hardware architectures.

Parameter	[37]	[23]	[24]	[36]	[29]	[21]
Device	Virtex-7	Artix-7	Artix-7	Artix-7	Artix-7	Artix-7
LUTs	1978 K	89 K	7 K	12 K	11 K	18 K
FFs	194 K	NA	5 K	10 K	10 K	5 K
Slices	NA	NA	2 K	4 K	4 K	5 K
DSPs	0	354	2	8	8	6
BRAMs	0	202	3	15	13	15
Frequency (MHz)	67	155	161	210	200	115
Total time ($\mathsf{\mu }$s)	1169	761	72	35	31	148
Area × Time (LUTs × s)	2312.28	67.73	0.50	0.42	0.34	2.66

,

Table 6. Comparison of the state-of-the-art Kyber-768 hardware architectures.

Parameter	[23]	[24]	[36]	[29]	[21]
Device	Artix-7	Artix-7	Artix-7	Artix-7	Artix-7
LUTs	167 K	7 K	12 K	12 K	16 K
FFs	NA	5 K	10 K	10 K	6 K
Slices	NA	2 K	4 K	4 K	4 K
DSPs	292	2	8	12	9
BRAMs	202	3	15	14	16
Frequency (MHz)	155	161	210	200	115
Total time ($\mathsf{\mu }$s)	1155	111	46	40	209
Area × Time (LUTs × s)	192.89	0.78	0.55	0.48	3.34

and

Table 7. Comparison of the state-of-the-art Kyber-1024 hardware architectures.

Parameter	[23]	[24]	[36]	[29]	[21]
Device	Artix-7	Artix-7	Artix-7	Artix-7	Virtex-7
LUTs	133 K	7 K	12 K	13 K	16 K
FFs	NA	5 K	12 K	12 K	6 K
Slices	NA	2 K	5 K	54 K	5 K
DSPs	548	2	8	16	12
BRAMs	202	3	15	16	17
Frequency (MHz)	192	161	210	185	156
Total time ($\mathsf{\mu }$s)	1260	154	63	56	205
Area × Time (LUTs × s)	167.58	1.08	0.76	0.72	3.28

, respectively. As can be seen in Table 5, among the Kyber-512 architectures, the design in [37] requires the highest hardware resources. In addition, the architecture in [37] introduces the longest latency compared with other works. The architecture in [23] helps reduce the hardware complexity, in terms of LUTs, and the processing time, compared with [37]. However, the area-to-time ratio of the architecture in [23] is still large. The architectures in [21,24,29,36] offer better values of hardware complexity and latency. Therefore, these architectures are suitable for the systems which require high speed and low complexity. Among the Kyber-512 architectures in Table 5, the design in [21] offers the best value of area-to-time ratio, and the design in [24] requires the lowest hardware resources to execute the Kyber-512 functions.

Among the Kyber-768 architectures in Table 6, the proposal in [29] obtains the best value of area-to-time ratio compared with other designs, followed by the architecture in [36]. Therefore, the design in [29] is the best candidate for systems which strictly consider the balance between hardware resource and latency. In addition, the design in [24] offers a reasonable area–time efficiency on the lowest hardware resources. Therefore, the work in [24] is an ideal candidate to deploy Kyber-768 on low hardware resource systems.

At NIST security level 5, the Kyber-1024 architecture in [29] is still the best work in terms of area–time ratio. For the resource-constraint systems, the architecture in [24] is the best choice. The design in [36] can be implemented on low hardware resources and offers an acceptable value of area–time ratio.

4. Discussion

From the analysis results, the architecture in [29] requires the lowest latency to perform Kyber encapsulation and decapsulation at different security levels. In addition, this architecture can offer the best value of area–time ratio at three security levels of CRYSTALS-Kyber. The architecture in [24] requires the lowest hardware resources. The performance of the existing CRYSTALS-Kyber architectures can be improved by deploying novel solutions to accelerating polynomial multiplication, such as integrating a novel parallel polynomial multiplication into the architecture in [24]. Discovering an efficient method for scheduling arithmetic operations is another technique to reduce hardware consumption and improve the area–time ratio.

5. Conclusions

In this paper, we introduced CRYSTALS-Kyber, a public key cryptography algorithm that entered round 3 of the NIST PQC standardization. We briefly described the background information of Kyber and introduced the key-encryption and key-establishment algorithms in detail. Furthermore, we analyzed the existing implementations of the pure software design, software and hardware codesign, and pure hardware design of Kyber, with a focus on pure hardware design. From the analysis results, we recommended the most suitable candidates at three security levels for different systems which have specific requirements of hardware resources, latency, and area-to-time balancing.