Abstract
As vital equipment in high-speed train power supply systems, the failure of onboard traction transformers affect the safe and stable operation of the trains. To diagnose faults in onboard traction transformers, this paper proposes a hybrid optimization method based on quickly and accurately using support vector machines (SVMs) as fault diagnosis systems for onboard traction transformers, which can accurately locate and analyze faults. Considering the limitations of traditional transformers for identifying faults, this study used kernel principal component analysis (KPCA) to analyze the feature quantity of dissolved gas analysis (DGA) data, electrical test data, and oil quality test data. The improved seagull optimization algorithm (ISOA) was used to optimize the SVM, and a Henon chaotic map was introduced to initialize the population. Combined with differential evolution (DE) based on the adaptive formula, the foraging formula of the seagull optimization algorithm (SOA) was improved to increase the diversity of the algorithm and enhance its ability to find the optimal parameters of SVM, which made the simulation results more accurate. Finally, the KPCA–ADESOA–SVM model was constructed and applied to fault diagnosis for the traction transformer. The example analysis compared the diagnosis results of the proposed diagnosis model with those of the traditional diagnosis model, showing further optimization of the feature quantity and improvements in the diagnosis accuracy. This proves that the proposed diagnosis model has high generalization performance and can effectively increase the fault diagnosis accuracy and speed of traction transformers.
1. Introduction
With the rapid development of railway systems, ensuring the safe and stable operation of trains has become a top priority. As important equipment in train power supply systems, onboard traction transformer fault diagnosis in time is the key to ensure the safe operation of the train [1,2,3,4]. The onboard traction transformer is different from an ordinary power transformer; its operating conditions and working environment are relatively poor, and accumulated faults from long-term work on trains can result in incalculable losses. For example, on 19 May 2014, a subway train in Junpu City, Gyeonggi-do, South Korea, exploded due to a traction transformer failure on the top of the car, resulting in 11 injuries. On 25 January 2018, a serious electrical equipment malfunction occurred on a G281 train, which was stopped at Dingyuan station, Anhui Province, China. The traction transformer installed on the bottom of the No. 2 train failed, causing the No. 2 car to catch fire. Therefore, the timely fault diagnosis of traction transformers and accurate identification of the fault type can avoid irreversible damage to transformers and train and greatly protect the safety of passengers and property.
The faults of onboard traction transformers can be mainly divided into internal faults and external faults [5]. Internal faults are mainly due to the winding phase, short circuit, grounding short circuit, turn-to turn-short circuit, core burning, etc.; external faults are due to single-phase grounding short circuit and phase-to-phase short circuit between outgoing lines. This paper analyzes, processes, and diagnoses the internal faults of traction transformers. The traditional fault diagnosis of traction transformers is similar to that of power transformers, which are mainly diagnosed by the DGA method [6]. Examples include the Duval triangle method, the three-ratio method, Rogers’ method, and others [7,8]. Although these methods are early research methods in the field of transformer fault diagnosis, they still have many shortcomings, which are that the coding is incomplete, the boundary is too absolute, and the coding is beyond the boundary. When a transformer fails, its internal gas capacity will also change, so the DGA method can better identify the fault. However, using DGA data on its own for fault diagnosis for traction transformers results in errors. With the development of artificial intelligence algorithms, an increasing number of algorithms have arisen that can be applied to transformer fault diagnosis, and in which the DGA data are analyzed and processed to obtain fault results, such as artificial neural networks [9,10,11,12], support vector machines [13,14,15,16], and fuzzy theory [17,18].
The performance of artificial neural networks is excellent, although its model is complex and needs a lot of data to support the model; fuzzy theory is suitable for nonlinear, time-varying and incomplete systems, but its system stability needs to be improved.
In this paper, DGA data, electrical test data, and oil quality test data are combined to form the fault data of a traction transformer. At the same time, to carry out a more accurate fault diagnosis, a support vector machine suitable for the small sample and nonlinear data is selected as the basic algorithm [6].
In recent years, many scholars at home and abroad have put forward their views in the field of traction transformer fault diagnosis. Xiao [19] used a Bayesian network to build a traction transformer fault diagnosis model with traction load characteristics and carried out a large number of experimental tests that achieved good research results, but the Bayesian network itself has the shortcomings of classification error. There is still room for improvement, and the author’s analysis of the follow-up results is not sufficient. Fu [20] established and studied the HPSO-WNN diagnosis model for the traction transformer algorithm, and proposed using chromatographic data and electrical test data to diagnose onboard transformer faults. The simulation results reached 96%, but the complexity of the fault data was high, and the author did not study it to improve the diagnosis efficiency. Dai [21] proposed KPCA with random forest to construct a diagnosis model for traction transformers. KPCA was used to process the DGA data and random forest (RF) was used for fault diagnosis. The diagnosis effect of the combination of the two methods was greatly improved, but the DGA data could not accurately diagnose the fault of the traction transformer. Moreover, random forest has a poor classification effect for noisy data processing; it is easy to produce an overfitting phenomenon, and the calculation time is longer than in other algorithms. Zhou [22] used a genetic programming (GP) algorithm to carry out hotspot temperature prediction and thermal capacity estimation for traction transformers and carried out a simulation experiment by combining physical data acquisition with the traction transformer mechanism. The simulation results showed that the innovation and practicability of this paper were strong, but it is well known that the measurement results of temperature are related to many characteristic quantities. The author did not perform an in-depth analysis of this aspect, and the GP algorithm still has a significant room for improvement to increase the accuracy of the diagnosis.
This paper proposes a fault diagnosis model for the traction transformer based on a KPCA- and ISOA-optimized SVM. Because there are many features of traction transformer fault data, KPCA is proposed to process the traction transformer data, to reduce the dimension of features and the complexity of data, and to reduce the speed of fault diagnosis and improve the accuracy of the diagnosis results. To address the fact that the parameters of SVMs are difficult to determine, SOA is used to optimize the parameters of the SVM. To overcome the defects of SOA, this paper proposes the Henon chaos initialization method to overcome the defects of SOA population initialization, and innovatively proposes an improved method combining ADE and SOA for the defects that SOA easily determines, which greatly improves the algorithm optimization’s accuracy and speed. The simulation results are compared with those of ISOA-SVM, SOA-SVM, and PSO-SVM. The simulation results show that the proposed model greatly increases the diagnosis accuracy and speed of the traction transformer fault diagnosis model.
Significantly, the improved meta-heuristic algorithm was used to optimize the SVM to establish the transformer fault diagnosis model, which has a good effect in the current field, but, in line with the “no free lunch” theory mentioned in [23], the actual performance of the model proposed in this paper in other engineering fields remains to be discussed; the actual performance of the algorithm needs to be further improved and analyzed according to object-oriented characteristics.
The first and second sections of this paper introduce the basic theory of KPCA and SVMs. The third section introduces the seagull optimization algorithm and its improved method in detail. In the fourth section, the fault diagnosis model of traction transformers is established based on KPCA-ISOA-SVM. In the fifth section, the use of the benchmark function to test the ISOA optimization algorithm to verify its performance is discussed. In the sixth section, a simulation test of the fault model is carried out, and the superior diagnosis accuracy and speed of the proposed model are verified by a comparison with the three models. The seventh section summarizes and prospects the article, and puts forward its shortcomings.
2. KPCA
KPCA is a kernel function improvement based on the PCA. KPCA overcomes the disadvantages of PCA, which can process linear data, and combines the kernel function to process nonlinear features, allowing it to deeply mine the features of nonlinear data [24,25]. The main steps of feature mining are as follows:
- (1)
- Sample data matrix Xk for input fault characteristic quantity of traction transformer. Through kernel function, data samples are mapped to φ(Xk), The nuclear moment matrix, K, is calculated first, followed by the matrix K′.
The data samples are mapped to φ(Xk), and then to the matrix K′:
where A is a N × N matrix, whose matrix elements are all 1/N.
- (2)
- The eigenvalue of matrix K′/l is λi (i = 1,2,…,l) and the eigenvector is vi (i = 1,2,…,l)
- (3)
- The m eigenvalues in λi and their corresponding eigenvector vm are extracted according to a cumulative contribution rate of 90%. Finally, the dimension reduction matrix Y is obtained.
where .
3. Basic Theory of SVM
The purpose of support vector machines [26,27,28] is to solve the problem of linear binary classification. Their principle is to find the optimal hyperplane that can classify two types of sample in two-dimensional space. Its discrimination model is:
In Equation (3): ω is the weight vector and b is the deviation. Based on the complexity of the data in this paper, nonlinear processing is required, so the relaxation factor ξi is introduced, constructing a soft interval classifier:
In Equation (4), C is the penalty factor. At the same time, Lagrange multiplier λi is introduced.
Next, according to KKT conditions:
It can be seen from (6) that there is a partial λi ≠ 0, so the best values of λ and b are obtained through (7):
By taking ω* in (7) into (1), one can obtain the classification decision function:
In Equation (8), K(xi,xj) = φΤ(xi) φ(xj) is the kernel function. The radial basis function (RBF) has only one parameter, σ, which has strong anti-interference ability, small sample processing performance, and excellent generalization ability. The specific formula is as follows:
where σ is the hyperparameters of the RBF kernel functions.
For SVM, the optimal classification result can be achieved only by finding the kernel function parameter, σ, and the best penalty factor, C but both C and σ need to be set manually, and the effect is poor. Therefore, it is particularly important to use the optimization algorithm to optimize the two SVM parameters.
4. ISOA
Aiming at a solution to the defect that it is difficult to set the optimization parameters in SVM, this paper proposes an improved SOA to optimize C and σ. This section will introduce the seagull optimization algorithm and the basic theory of its improved method in detail.
4.1. SOA
SOA is a new meta-heuristic algorithm, proposed by Gaurav Dhiman and Vijay Kumar in 2018 [29,30,31]. The principle of SOA is based on the migration and foraging behavior of seagulls. The migration behavior is that the seagull population flies from uninhabitable areas to livable areas, and this, therefore, affects the global search for seagull populations. Foraging behavior, also known as aggressive behavior, describes the foraging behavior of the seagull population in inhabited areas, and therefore mainly affects the local search for populations. Figure 1 shows the specific optimization flow chart of the SOA.
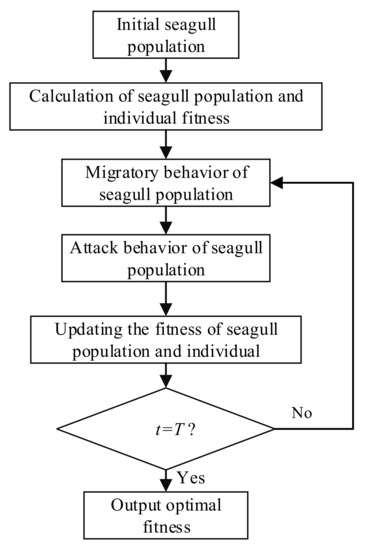
Figure 1.
SOA optimization process.
- (1)
- Migratory Behavior
The migration behavior of seagulls is mainly the movement of the seagull population from one location to another. This behavior should meet three conditions, as follows.
- Avoiding collisions
To avoid collisions with surrounding seagulls, SOA uses variable A to adjust the position of each seagull.
where represents the position of the seagull, which does not collide with other seagulls; represents the current position of seagulls; t indicates the current iteration; A represents the migration behavior of the seagulls in each search space; and the size of a is through fc control.
where the value of fc is 2, and T is the maximum number of iterations. The value of A decays linearly from the beginning of the iteration to the end of the iteration and decays from 2 to 0.
- The direction of movement towards the best neighbor
After ensuring that individual seagulls will not collide, move all seagulls towards the seagull in the best position.
indicates the moving direction of the individual seagull towards the best individual.
B is a random number between 0 and 8.
- The direction of movement towards the best neighbor
After calculating the convergence direction of each seagull, the individual seagull begins to move towards this position.
is the new position for each seagull after moving.
- (2)
- Foraging Behavior
Foraging behavior mainly uses the experience of migration behavior. During the migration process, seagulls can constantly change their attack angle and speed. When they hunt, they move in the air spirally. The specific formula is as follows:
k is a random number between 0 and 2π and r is the radius of the helix, which is controlled by the u and v parameters. Finally, combined with the new position of the seagull, the formula of the overall updated seagull position is obtained as follows:
is the best position of the seagull population, and the other seagull positions are updated. In the seagull optimization algorithm, variable A decays linearly from 2 to 0, and variable B is responsible for stable optimization in the process of migration to foraging.
4.2. Henon Mapping
The population generated by SOA population initialization has the disadvantages of low ergodicity and randomness. This paper uses a Henon map to initialize the SOA population. The Henon map has high ergodicity and is suitable for the initialization of the SOA population [32]. Henon’s specific formula is as follows:
where a and b are the system control parameters, x and y are the input parameter, and n is number of iterations. Figure 2 is the Henon bifurcation diagram. When b is set to 0.3, a = 1.4, and Henon is in a chaotic state.
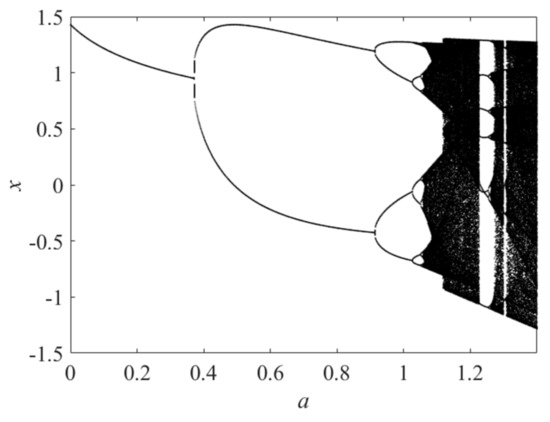
Figure 2.
Bifurcation diagram of Henon chaotic map.
To better reflect the advantages of the Henon map, this paper compares it with the traditional logistic map, as shown in Figure 3.
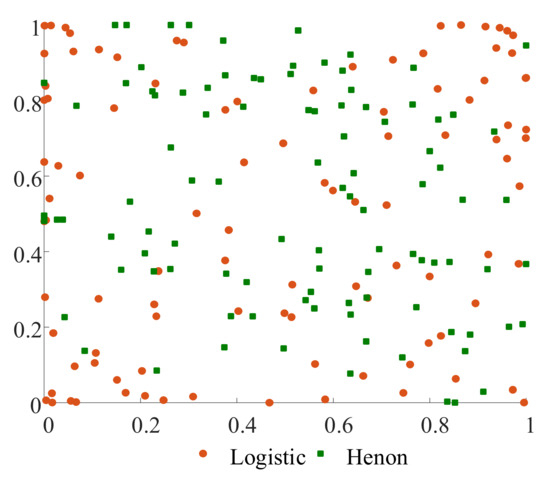
Figure 3.
Initialization comparison diagram.
As can be seen from Figure 3, compared with logistic mapping, the population generated by the Henon map has higher randomness, which can enable the algorithm to effectively conduct global optimization at the beginning of the iteration.
4.3. Differential Evolution Algorithm
DE is a metaheuristic algorithm based on group search. Its form is similar to the genetic algorithm (GA). It is based on three steps: mutation, crossover, and selection. However, the difference is that the mutation step of DE is based on a different strategy. The algorithm has high performance and can effectively jump out of local optimization [33,34,35].
- Variation
The mutation is the most important step to distinguish DE from the genetic algorithm. The main part is the difference vector, composed of the vector difference of two different random vectors, which is then superimposed with a separate vector to obtain a new vector with volatility. The specific formula is as follows:
In Equation (18), , , and show three different individuals in the population and F represents the variation factor. The usual value range is 0–2, which controls the size of the difference vector.
- Crossover
Cross-operation on the population can maintain the diversity of the algorithm population. The specific formula is as follows:
In Equation (19), rand() represents a random number between 0 and 1; rand(0, n) represents a random integer between 0 and n; and CR represents the crossover factor, which is generally between 0 and 1. The value of CR affects the optimization of the algorithm. When the CR value is large, the crossover probability of the algorithm is large, the globality is strong, and the diversity of the population is maintained. When the CR value is small, the crossover probability of the algorithm is small, which makes it easy for the algorithm to fall into local optimization.
- Choice
The selection operation of the DE algorithm is completed based on the greedy algorithm. By comparing the fitness of initialized individuals with that of mutation and crossover individuals, the optimal individual is selected to enter the next iteration. The implementation method is as follows:
4.4. Adaptive DE Algorithm
A greedy algorithm reduces the population diversity of DE and makes the algorithm easy to process. Therefore, this paper uses an adaptive formula to improve the DE mutation factor to enhance the population diversity [36]. For the mutation operator, the most common mutation method, DE/rand/1, which has the characteristics of maintaining population diversity, was selected. The specific formula of improved mutation factor F is as follows:
Equation (21) causes the variation factor to decay in a cosine manner as the number of iterations decreases.
Considering the characteristics of variation factor F, this paper makes F perform cosine attenuation. Through the simulation test, it was found that the effect of selecting a 0.4–0.8 interval for F was the best option. As shown in Figure 4, F can perform cosine attenuation with the increase in the iteration times in the iterative process, which can give appropriate disturbance to the variation step without causing the algorithm to fall into local optimization in the middle of the iteration. The mutation step is carried out more smoothly to avoid the shortcomings of slow convergence speed or easily falling into local optimization in the iterative process caused by the difficult setting of F.
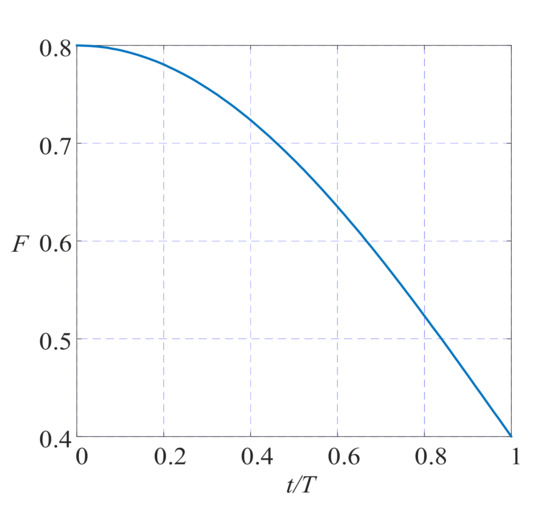
Figure 4.
The adaptive curve of F.
4.5. ADE SOA
When the seagull population is attacking, performing the mutation, crossover, and selection operations in ADE can help SOA jump out of local optimization in time. Specific optimization methods are introduced below. We select three seagulls in SOA for the mutation operation. The three seagulls are α, β, and δ.
The variation value obtained from Equation (22) is cross-processed with the position of contemporary seagulls through the cross mechanism:
Finally, the seagull position is compared with the position obtained by crossing according to the selection mechanism to obtain the contemporary optimal value:
Combining ADE with the attack formula of SOA can avoid the premature phenomenon of WOA and greatly increase the population diversity of SOA.
4.6. Introduction to Optimization Process of ISOA
Based on the above, improved method, the ISOA optimization model is established. The pseudo-code of ISOA is shown in Algorithm 1.
- 1.
- Firstly, Henon chaos initialization is used to replace the original population initialization.
- 2.
- Secondly, the combination of ADE and SOA is used to improve the attack formula of SOA.
- 3.
- Finally, the ISOA optimization model is established to optimize the parameters of the SVM.
As reported in Section 4, this study used the benchmark function to test the performance of ISOA, PSO, GWO, and SOA to verify the performance of the optimization model proposed in this paper.
| Algorithm 1 ISOA pseudo-code | |
| Input: seagull population | |
| Output: seagull optimal position | |
| 1: | Initialize population size M, dimension D, the maximum number of iterations Tmax; |
| Initialize , u, v, k, A, B; | |
| 3: | Randomly generate M seagulls in the space by Equation (17); |
| 4: | Calculate the population fitness and find the optimal individual |
| 5: | while do |
| 6: | Calculate new seagull position by Equations (10), (12) and (14); |
| 7: | Compute using Equation (15); |
| 8: | Calculate by Equation (16); |
| 9: | Initialize variation factor F by Equation (21); |
| 10: | Combined differential evolution by Equations (22)–(24) and get the next generation of seagull population; |
| 11: | Update seagull optimal position ; |
| 12: | ; |
| 13: | end while |
| 14: | Return . |
5. Improved Seagull Optimization Algorithm
To verify the effectiveness of the SOA improvement methods, we used six test functions and four CEC benchmark test functions in CEC-2017 to simulate ISOA in MATLAB and compared the test results with the test results of SOA, GWO, WOA, and PSO.
The parameters of the four algorithms were set as follows: the population number m was set to 50 and the number of iterations Tmax = 500; in PSO, c1 = c2 = 1.5, Vmax = 6, ωmax = 1, ωmin = 0.2, and GWO had no parameters. The u and v of SOA and ISOA were 1 and fc was 2; CR in ISOA was set to 0.5. Twenty simulation tests were conducted for all the test functions and the results were recorded, compared, and analyzed to find the optimal value, average value, and variance in the simulation results of the traditional benchmark functions, and then analyzed and compared with the optimal value of the CEC-2017 test function. Four kinds of benchmark test function are shown in Table 1, six kinds of test function of CEC-2017 are shown in Table 2, and the three-dimensional image of the function is shown in Figure 5.

Table 1.
Benchmark function.

Table 2.
CEC-2017 Function.
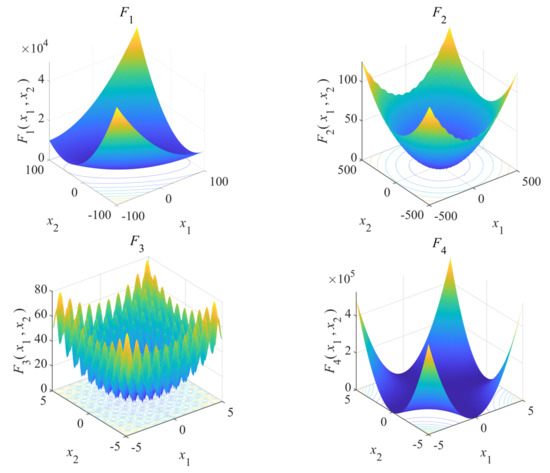
Figure 5.
Three-dimensional diagram of benchmark function.
Figure 6 and Table 3 show the simulation results of four benchmark functions. From the simulation results, we can see that in the test results of unimodal function F1 of the four algorithms, the average value, variance, and optimal value of ISOA were better than SOA, GWO, WOA, and PSO to a certain extent. From the simulation image, it can be seen that ISOA found the minimum value of the function when it was optimized to about 250 generations. From the simulation results of multimodal functions F2 and F3, it can be seen that ISOA can find better values than the other three algorithms, with faster convergence speed and stronger stability, and the result of WOA was the same as that of ISOA, but the convergence speed of ISOA was significantly faster. In the fixed-dimension multimodal benchmark function F4, ISOA still found a better algorithm than the other four algorithms, with remarkable optimization ability and improved convergence speed compared with SOA.
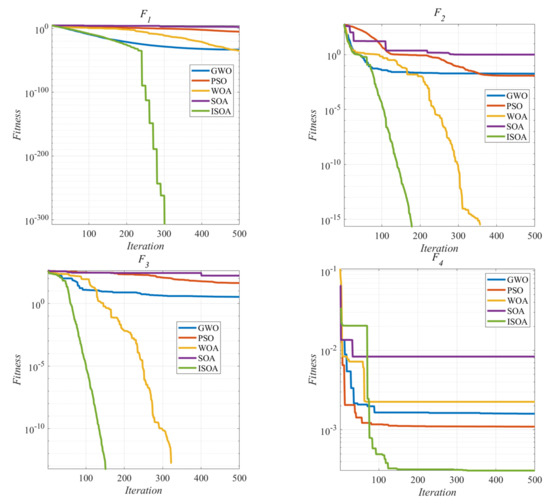
Figure 6.
Benchmark function test results.

Table 3.
Benchmark function results.
Six CEC-2017 test functions were selected for the simulation test. It is obvious from Table 4 that the simulation results of ISOA in the six CEC test functions were the best compared with the other four algorithms. Among the CEC-6 simulation results, the simulation accuracy of ISOA was nearly two orders of magnitude higher than that of the other optimization algorithms, and all the optimization results of ISOA almost reached the minimum value. Combined with the above analysis, it can be concluded that ISOA greatly improved the optimization accuracy and convergence speed, and the improvement effect was remarkable.

Table 4.
CEC-2017 function test results.
6. Establishment of Traction Transformer Fault Diagnosis Model Based on KPCA-ISOA-SVM
This section introduces the traction transformer fault diagnosis model based on KPCA-ISOA-SVM in detail. The specific flow chart is shown in Appendix A.
6.1. Data Preprocessing
In this paper, 135 sets of data of 12 feature quantities extracted through experiments combined with DGA data, oil quality test data, and electrical test data collected from KDZ7 series EMUs were used for fault diagnosis: H2, CH4, C2H6, C2H4, C2H2, furfural content in oil, electrical strength, no-load loss change, insulation oil conductivity, and winding DC resistance change. The fault types corresponding to the fault data were divided into six types: normal, inter-turn short circuit, interlayer short circuit, interstream short circuit, winding partial discharge, and winding deformation. The fault classification is shown in Table 5.

Table 5.
Fault classification number.
Considering the complexity and great difference between the fault data in the mixed data set, it was necessary to normalize all the fault data. The processed data were within the range of 0 to 1 for the simulation test. The specific processing formula is as follows:
In Equation (25): i = 1, 2, …, 5; x′i is the fault data after sample normalization, xi is the original fault data and xmax and xmin are the xi maximum and minimum values in I, respectively.
6.2. Fault Data Processing Based on KPCA
Considering the complexity of the data and the difficulty of the calculation, KPCA was used to process the fault data of the traction transformer. The cumulative contribution rate of the principal component variance is shown in Figure 7, in which the variance contribution rate of the first principal component is shown to have reaches 41.53% and the cumulative contribution rate of the first five principal components reached 94.16%. Therefore, the first five-dimensional principal components were selected as the diagnostic data.
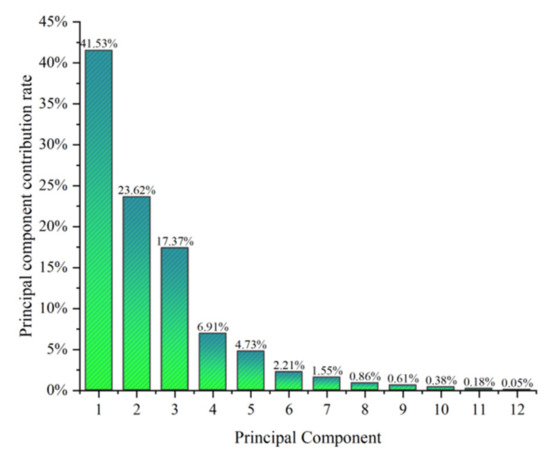
Figure 7.
The cumulative contribution rate of the principal component variance.
6.3. Established Optimization Model
The SVM parameters were optimized based on KPCA-ISOA to obtain the optimal coefficient C and kernel function parameter σ. The SVM fault diagnosis model was established according to the obtained optimal parameters. The specific operation process of ISOA is as follows:
- step 1.
- The fault data are divided into the training set and verification set, and the fault data are processed by the KPCA principal component.
- step 2.
- Initialize SOA parameters. Initialize the population size and set parameters such as iteration times, dimension, and parameter optimization boundary.
- step 3.
- Population initialization. The population is initialized by Henon chaotic map, and the population fitness value, x, is calculated.
- step 4.
- Migration behavior. The seagull optimization algorithm performs migration according to Equations (10)–(14), and the seagull population performs global optimization.
- step 5.
- Aggressive behavior. The seagull optimization algorithm carries out the attack behavior according to Equation (16) to obtain the current best individual position of the seagull.
- step 6.
- Update the intermediate population. According to Equations (18) and (19), the original seagull population is mutated and crossed to obtain the position of the individual of the intermediate population.
- step 7.
- Population selection. The selection operation is carried out through Equation (24), and the next-generation seagull population is selected and updated from the populations obtained in step 5 and step 6.
- step 8.
- Judge the termination conditions. If the termination conditions are met, input the obtained optimal parameters C and σ to SVM; Otherwise, go to step 3.
6.4. Fault Diagnosis
The established KPCA-ISOA-SVM fault diagnosis model was used to diagnose the traction transformer fault data processed by KPCA through the MATLAB simulation tool. After the diagnosis, the diagnosis results were output. The diagnosis results included the γ and σ optimal values, test accuracy, training accuracy, and simulation time.
7. Fault Diagnosis of Traction Transformer Based on KPCA-ISOA-SVM
The KPCA-ISOA-SVM fault diagnosis model was used to simulate and test the fault data of the traction transformer, and the simulation results were compared with the diagnosis results of ISOA, SOA-SVM, and GWO-SVM. The diagnostic results were mainly judged according to two aspects: diagnosis accuracy and diagnosis time. The number of iterations was 200, the population number of the four algorithm models was 50, the u and v of SOA and ISOA were 1, fc was 2, and CR in ISOA was 0.5. In this paper, the fault data were divided into the training set and the verification set. The training set was used to train the traction transformer fault diagnosis model, and the verification set simulate and verified the trained model. In this paper, the data imported by the training model were allocated at a ratio of 2:1, so the training set was 90 groups of data and the verification set was 45 groups of data. The specific classification is shown in Table 6.

Table 6.
Fault classification number.
GWO-SVM, SOA-SVM, and ISOA-SVM were used to simulate the fault diagnosis of the data. The diagnosis accuracy is shown in Figure 8.
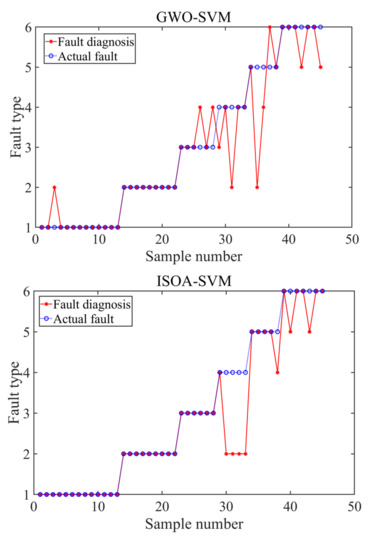
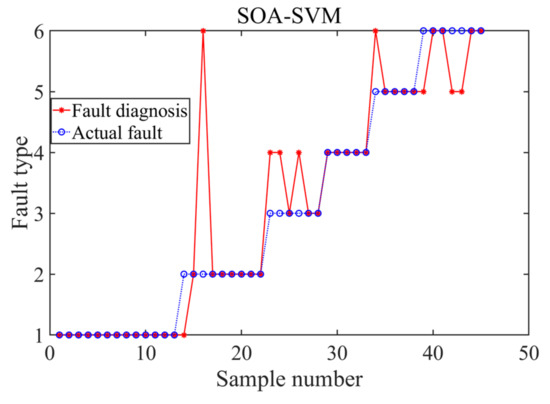
Figure 8.
Diagnosis results.
In Figure 8, the diagnosis result of GWO-SOA was the worst; the number of misjudgments was 10 and the diagnosis accuracy was 77.78%. SOA-SVM was second, with nine misjudgments, and a diagnosis accuracy of 80%. The diagnosis accuracy of the ISOA was slightly improved; there were seven misjudgments, and the diagnosis accuracy was 84.44%. The diagnosis accuracy of the ISOA-SVM model was improved compared with SOA-SVM and was much higher than the GWO-SVM model. For the ISOA-SVM model, a fault diagnosis was carried out after the KPCA processing of the data. Figure 9 shows the diagnosis results.
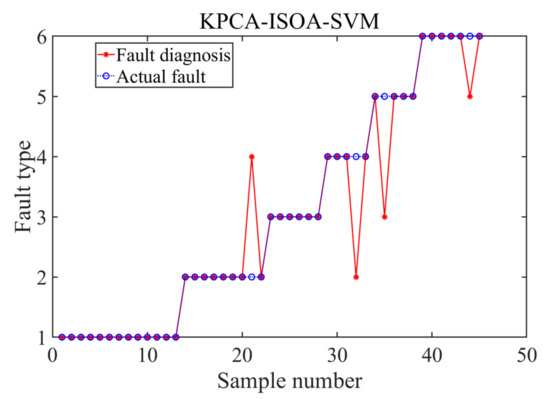
Figure 9.
Diagnosis results.
As shown in Figure 9, the diagnosis results obtained by the same fault diagnosis simulation of the data processed by KPCA and the data not processed were quite different. There were only four misjudgments in the simulation results of the KPCA-ISOA-SVM, and the fault diagnosis accuracy was 91.11%. Compared with the traditional SOA-SVM model, it showed a great improvement and was much higher than the diagnosis accuracy of the GWO-SVM. To better show the advantages of the model in this paper, the diagnosis speeds of the four diagnosis models are given in Table 7.

Table 7.
Fault model diagnosis speed.
As shown in Table 7, the diagnosis speed of ISOA-SVM was 87 s, which is a certain improvement compared with SOA-SVM and GWO-SVM, which proves the effectiveness of the improved method in this paper. The KPCA-ISOA-SVM only takes 41 s. The data processed by KPCA greatly reduced the data complexity and greatly improved the fault diagnosis speed. To more clearly compare the simulation results of the four models, Table 8 lists the fault diagnosis accuracy and the correct judgment number of the four models.

Table 8.
Fault model diagnosis results.
By analyzing the above simulation results in combination with Table 8, compared with SOA-SVM, the KPCA- ISOA-SVM improved the fault diagnosis accuracy by 11.11% and reduced the number of misjudgments by five, while the diagnosis time was increased by 63 s, which greatly reduced the fault diagnosis time and improved the diagnosis efficiency. The above results also made it possible to clearly and intuitively compare the four diagnostic models. According to this comparison, the model in this study has a higher diagnosis accuracy and a faster diagnosis speed. The results also fully reflect that the model in this paper had the strongest diagnostic performance, the highest reliability, and highest practical application value.
8. Conclusions
Aiming to address the shortcomings of the traditional traction transformer fault diagnosis model, the KPCA-ISOA-SVM fault diagnosis model is proposed. Firstly, a principal component analysis was carried out for the traction transformer fault data, and then the diagnosis model based on the SOA-SVM was established. To improve the performance of the model, Henon chaotic mapping was used and ADE was combined with SOA. The improved method effectively improved the ergodicity, randomness, and diversity of the SOA initialization population, and could better find the best parameters of the SVM. The KPCA-ISOA-SVM traction transformer fault diagnosis model was established by combining the above methods, and the simulation experiment was carried out combined with the fault data. Finally, the following conclusions were obtained:
- 1.
- Compared with the ISOA-SVM, GWO-SVM, SOA-SVM, and KPCA-ISOA-SVM greatly improved the diagnosis accuracy and speed, which effectively proves that the traction transformer fault data processed by KPCA is more suitable for fault diagnosis.
- 2.
- ISOA, SOA, GWO, and PSO tests were carried out. It was seen that ISOA greatly improved the optimization performance and convergence speed, which reflects the effectiveness of the improvement of ISOA.
- 3.
- Due to the special working environment of the traction transformer, there may be a little deviation in the fault state diagnosed only for the fault data. The combination of the fault diagnosis with more parameters can achieve better results.
This paper establishes a traction transformer fault diagnosis model based on KPCA-ISOA-SVM, which can diagnose the traction transformer fault quickly and accurately, has strong generalization ability, and has a certain practical significance. However, there are still some deficiencies to be further studied in the follow-up research, with the ultimate goal of establishing an accurate and effective fault diagnosis model.
Author Contributions
Data curation, Y.L.; formal analysis, J.Z.; funding acquisition, H.D.; investigation, S.L.; project administration, S.L.; resources, H.D.; validation, H.D.; writing—original draft, J.Z.; writing—review and editing, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Tianyou Youth Talent Lift Program of Lanzhou Jiaotong University, in part by the University Innovation Fund Project of Gansu Provincial Department of Education (no. 2020A-036), and in part by the Youth Science Fund Project of Lanzhou Jiaotong University (no. 2019029).
Conflicts of Interest
There is no conflict of interest in this manuscript.
Appendix A
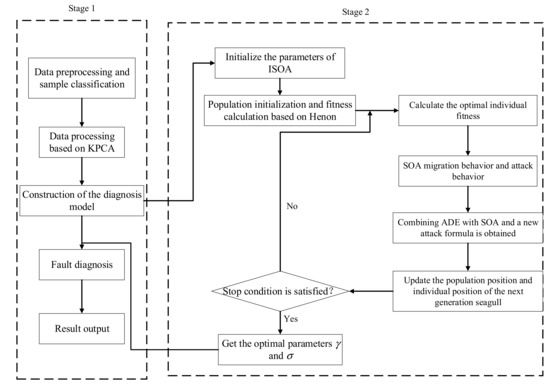
Figure A1.
Flow chart.
References
- Wu, G.; Li, X.; Yang, Y.; Hu, G.; Gao, B.; Zhang, W.; Wang, Z. Research Progress of Fault Prediction and Health Management for Onboard Traction Transformers. High Volt. Eng. 2020, 46, 145–158. [Google Scholar]
- Liu, J.; Fan, X.; Zheng, H.; Zhang, Y.; Zhang, C.; Lai, B.; Wang, J.; Ren, G.; Zhang, E. Aging condition assessment of transformer oil-immersed cellulosic insulation based upon the average activation energy method. Cellulose 2019, 26, 3891–3908. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, J.; Li, W.; Wu, Z.; Gao, S.; Guo, L.; Liu, H. FRA modelling for diagnosing axial displacement of windings in traction transformers. IET Electr. Power Appl. 2019, 13, 2121–2127. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, H.; Zhang, Y.; Zhou, T.; Zhao, J.; Li, J.; Liu, J.; Li, J. Comparative Investigation on the Performance of Modified System Poles and Traditional System Poles Obtained from PDC Data for Diagnosing the Ageing Condition of Transformer Polymer Insulation Materials. Polymers 2018, 10, 191. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Chen, T.; Fu, Q. New research on intelligent fault diagnosis technology of onboard traction transformer. Comput. Eng. Appl. 2012, 48, 27–31. [Google Scholar]
- Zeng, B.; Guo, J.; Zhu, W.; Xiao, Z.; Yuan, F.; Huang, S. A Transformer Fault Diagnosis Model Based on Hybrid Grey Wolf Optimizer and LS-SVM. Energies 2019, 12, 4170. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Sun, X.; Zhang, Y.; Zhong, X.; Cheng, L. A Power Transformer Fault Diagnosis Method-Based Hybrid Improved Seagull Optimization Algorithm and Support Vector Machine. IEEE Access 2021, 10, 17268–17286. [Google Scholar] [CrossRef]
- Guo, C.; Wang, B.; Wu, Z.; Ren, M.; He, Y.; Albarracín, R.; Dong, M. Transformer Failure Diagnosis Using Fuzzy Association Rule Mining Combined with Case-Based Reasoning. IET Gener. Transm. Distrib. 2020, 14, 2202–2208. [Google Scholar] [CrossRef]
- Fei, X.; Zhijiang, L.; Hao, Z.; Daogang, P.; Qian, Z.; Yiwen, T. Application of mixed neural network in transformer fault diagnosis. J. Electron. Meas. Instrum. 2017, 31, 118. [Google Scholar]
- Illias, H.A.; Chai, X.R.; Bakar, A.H.A. Hybrid modified evolutionary particle swarm optimization-time varying acceleration coefficient-artificial neural network for power transformer fault diagnosis. Measurement 2016, 90, 94–102. [Google Scholar] [CrossRef]
- Li, A.; Yang, X.; Xie, Z.; Yang, C. An optimized GRNN-enabled approach for power transformer fault diagnosis. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1181–1188. [Google Scholar] [CrossRef]
- Teng, W.; Fan, S.; Gong, Z.; Jiang, W.; Gong, M. Fault diagnosis of transformer based on fuzzy clustering and the optimized wavelet neural network. Syst. Sci. Control Eng. 2018, 6, 359–363. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, X.; Zheng, H.; Yao, H.; Liu, J.; Zhang, C.; Peng, H.; Jiao, J. A Fault Diagnosis Model of Power Transformers Based on Dissolved Gas Analysis Features Selection and Improved Krill Herd Algorithm Optimized Support Vector Machine. IEEE Access 2019, 7, 102803–102811. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, X.; Dai, B.; Yang, P.; Wang, Z. A transformer fault diagnosis methodbased on hybrid improved grey wolf optimization andleast squares-support vector machine. IET Gener. Transm. Distrib. 2022, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, H.; Liao, R.; Wang, Y.; Yang, L.; Yan, C. A New Support Vector Machine Model Based on Improved Imperialist Competitive Algorithm for Fault Diagnosis of Oil-immersed Transformers. J. Electr. Eng. Technol. 2017, 12, 830–839. [Google Scholar] [CrossRef] [Green Version]
- Kari, T.; Gao, W.; Zhao, D.; Abiderexiti, K.; Mo, W.; Wang, Y.; Luan, L. Hybrid feature selection approach for power transformer fault diagnosis based on support vector machine and genetic algorithm. IET Gener. Transm. Distrib. 2018, 12, 5672–5680. [Google Scholar] [CrossRef]
- Zhang, J.J.; Liang, Y.S.; Yin, Y.J.; Guo, C.X. Transformers fault diagnosis based on fuzzy theory and support vector machine. J. Electr. Power Sci. Technol. 2011, 26, 61–66. [Google Scholar]
- Mani, G.; Jerome, J. Intuitionistic Fuzzy Expert System based Fault Diagnosis using Dissolved Gas Analysis for Power Transformer. J. Electr. Eng. Technol. 2014, 9, 2058–2064. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.; Pan, W.; Guo, X.; Bi, S.; Feng, D.; Lin, S. Fault Diagnosis of Traction Transformer Based on Bayesian Network. Energies 2020, 13, 4966. [Google Scholar] [CrossRef]
- Fu, Q.; Chen, T.F.; Zhu, J.J. Research on Traction Transformer Faults Diagnosis Algorithm Based on HPSO-WNN. J. China Railw. Soc. 2012, 34, 26–32. [Google Scholar]
- Dai, C.; Liu, Z.; Hu, K.; Huang, K. Fault diagnosis approach of traction transformers in high-speed railway combining kernel principal component analysis with random forest. IET Electr. Syst. Transp. 2016, 6, 202–206. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, J.; Wang, L.; Yuan, S.; Huang, L.; Wang, D.; Guo, L. A Method for Hot-Spot Temperature Prediction and Thermal Capacity Estimation for Traction Transformers in High-Speed Railway Based on Genetic Programming. IEEE Trans. Transp. Electrif. 2019, 5, 1319–1328. [Google Scholar] [CrossRef]
- Orosz, T.; Rassõlkin, A.; Kallaste, A.; Arsénio, P.; Pánek, D.; Kaska, J.; Karban, P. Robust Design Optimization and Emerging Technologies for Electrical Machines: Challenges and Open Problems. Appl. Sci. 2020, 10, 6653. [Google Scholar] [CrossRef]
- Liang, Y.; Gao, Z.; Gao, J.; Xu, G.; Wang, R. The instrument fault detection and identification based on kernel principal component analysis and coupling analysis in process industry. Trans. Inst. Meas. Control 2021, 43, 1531–1544. [Google Scholar] [CrossRef]
- Chen, B.; Huang, D.; Zhang, F. The Modeling Method of a Vibrating Screen Efficiency Prediction Based on KPCA and LS-SVM. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1950009. [Google Scholar] [CrossRef]
- Pan, M.; Li, C.; Gao, R.; Huang, Y.; You, H.; Gu, T.; Qin, F. Photovoltaic power forecasting based on a support vector machine with improved ant colony optimization. J. Clean. Prod. 2020, 277, 123948. [Google Scholar] [CrossRef]
- Fan, J.; Wang, F.; Sun, Q.; Bin, F.; Liang, F.; Xiao, X. Hybrid RVM-ANFIS algorithm for transformer fault diagnosis. IET Gener. Transm. Distrib. 2017, 11, 3637–3643. [Google Scholar] [CrossRef]
- Dudzik, W.; Nalepa, J.; Kawulok, M. Evolving data-adaptive support vector machines for binary classification. Knowl. Based Syst. 2021, 227, 107221. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl. Based Syst. 2018, 165, 169–196. [Google Scholar] [CrossRef]
- Ehteram, M.; Banadkooki, F.B.; Fai, C.M.; Moslemzadeh, M.; Sapitang, M.; Ahmed, A.N.; Irwan, D.; El-Shafie, A. Optimal operation of multi-reservoir systems for increasing power generation using a seagull optimization algorithm and heading policy. Energy Rep. 2021, 7, 3703–3725. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Zhang, Y.; Ye, X.; Xiong, X.; Zhang, F. A Novel Hybrid Model Based on an Improved Seagull Optimization Algorithm for Short-Term Wind Speed Forecasting. Processes 2021, 9, 387. [Google Scholar] [CrossRef]
- Zhuo, X.; Bi, M.; Hu, Z.; Li, H.; Wang, X.; Yang, X. Secure scheme for OFDM-PON system using TR based on modified Henon chaos. Opt. Commun. 2020, 462, 125304. [Google Scholar] [CrossRef]
- Karaboğa, D.; Ökdem, S. A Simple and Global Optimization Algorithm for Engineering Problems: Differential Evolution Algorithm. Turk. J. Electr. Eng. Comput. Sci. 2004, 12, 53–60. [Google Scholar]
- Zeng, Z.; Zhang, M.; Chen, T.; Hong, Z. A new selection operator for differential evolution algorithm. Knowl. Based Syst. 2021, 226, 107150. [Google Scholar] [CrossRef]
- Dixit, A.; Mani, A.; Bansal, R. An adaptive mutation strategy for differential evolution algorithm based on particle swarm optimization. Evol. Intell. 2021, 1–15. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, S.; Yang, H.; Lei, Z. SCJADE: Yet Another State-of-the-Art Differential Evolution Algorithm. IEEJ Trans. Electr. Electron. Eng. 2021, 16, 644–646. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).