Optimal Selection and Integration of Batteries and Renewable Generators in DC Distribution Systems through a Mixed-Integer Convex Formulation
Abstract
1. Introduction
- i.
- The simultaneous integration of BESS and dispersed generators in monopolar DC networks, since this problem is typically addressed independently by integrating only one of these devices into the DC grid, or both in a sequential fashion, i.e., in the first stage, the dispersed sources are assigned, and batteries are integrated in the second stage.
- ii.
- The reformulation of the exact MINLP model that represents the optimal placement and sizing of BESS and DG into a mixed-integer convex (MIC) formulation via the application of McCormick envelopes to approximate the product between two continuous variables through a linear equivalent restriction.
2. Mathematical Representation
2.1. Objective Function
| Value of the objective function regarding the cost of the daily energy losses (COP$/day). | |
| Average energy cost of the energy in the electricity market (COP$/Wh-day). | |
| Voltage value at node i for each period of time t (V). | |
| Voltage value at node j for each period of time t (V). | |
| Conductive effect that relates nodes i and j (S). | |
| Variation of the period of time where electrical variables are assumed as constants (h). | |
| Set that contains all the number of periods of study. | |
| Set that contains all the nodes of the monopolar DC network. |
2.2. Mathematical Formulation for including Batteries
| Power generation in the slack source connected at node i in the period of time t (W). | |
| Power generation in the distributed generator connected at node i in the period of time t (W). | |
| Power generation/absorption in the BESS connected at node i in the period of time t (W). | |
| Power demand at node i in the period of time t (W). | |
| State of charge of the BESS at node i in the period of time t (%). | |
| Battery charge/discharge coefficient (%/Wh). | |
| Binary variable that defines whether a BESS is connected at node i or not. | |
| Initial state of charge of the BESS at node i (%). | |
| Final state of charge of the BESS at node i (%). | |
| Minimum power generation in the slack source connected at node i in the period of time t (W). | |
| Maximum power generation in the slack source connected at node i in the period of time t (W). | |
| Minimum power generation in the distributed generator connected at node i in the period of time t (W). | |
| Maximum power generation in the distributed generator connected at node i in the period of time t (W). | |
| Minimum power bound allowed for the BESS system at node i in the period of time t (W). | |
| Maximum power bound allowed for the BESS system at node i in the period of time t (W). | |
| Minimum voltage regulation limit allowed for all the nodes in the network (V). | |
| Maximum voltage regulation limit allowed for all the nodes in the network (V). | |
| Lower state-of-charge bound for the BESS connected at node i (%). | |
| Upper state-of-charge bound for the BESS connected at node i (%). | |
| Maximum number of BESS available for integration in a monopolar DC network. | |
| Set that contains all the BESS technologies available. |
2.3. Formulation for the Optimal Placement of Renewable Energy Sources
| Binary variable that defines whether a PV source is connected at node i or not. | |
| Binary variable that defines whether a wind source is connected at node i or not. | |
| Power generation in the PV source connected at node i in the period of time t (W). | |
| Power generation in the wind source connected at node i in the period of time t (W). | |
| Minimum power generation in the PV source connected at node i in the period of time t (W). | |
| Maximum power generation in the PV source connected at node i in the period of time t (W). | |
| Minimum power generation in the wind source connected at node i in the period of time t (W). | |
| Maximum power generation in the wind source connected at node i in the period of time t (W). | |
| Maximum number of PV sources available for integration in a monopolar DC network. | |
| Maximum number of wind sources available for integration in a monopolar DC network. |
2.4. Interpretation of the Optimization Models
2.4.1. BESS Model Interpretation
2.4.2. Renewable Energy Model Interpretation
3. Proposed MIC Reformulation
| General nonlinear function of two variables. | |
| Auxiliary variable number 1. | |
| Auxiliary variable number 2. | |
| Initial value of the auxiliary variable number 1. | |
| Initial value of the auxiliary variable number 2. | |
| High-order terms of the Taylor series expansion for a general nonlinear function. | |
| Initial voltage value at node i for each period of time t (V). | |
| Initial voltage value at node j for each period of time t (V). |
- i.
- ii.
4. Solution Methodology
| Algorithm 1 Simultaneous allocation of BESS and renewable energy sources in monopolar DC networks using MIC models and recursive programming. |
 |
5. Monopolar DC Network under Study
6. Numerical Implementation and Results
- Case 2: This simulation case employs the proposed MIC model to find the optimal location of the BESS. These locations are set in the exact MINLP model in order to determine the exact value of the objective function.
- Case 3: This simulation case employs the proposed MIC model to optimally allocate the renewable energy resources. These locations are set in the exact MINLP model in order to determine the exact value of the objective function.
- Case 4: The simultaneous location of the BESS and the renewable energy sources is found via the recursive implementation in Algorithm 1. These locations are set in the exact MINLP model in order to determine the exact value of the objective function.
6.1. Numerical Results for Case 1
6.2. Numerical Results for Case 2
6.3. Numerical Results for Case 3
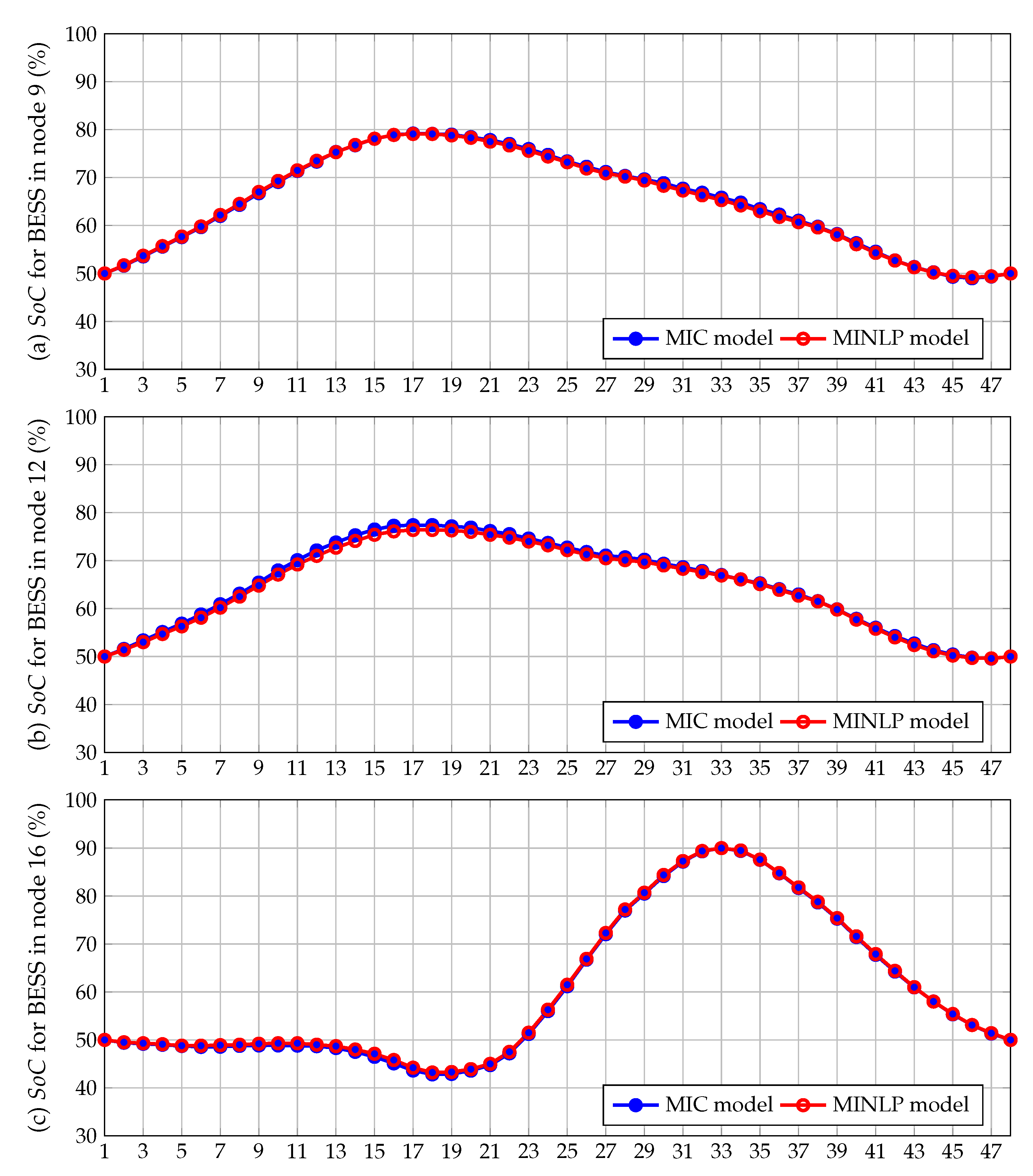
6.4. Numerical Results for Case 4
6.5. Summary of the Methodology
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nandini, K.; Jayalakshmi, N.; Jadoun, V.K. An overview of DC Microgrid with DC distribution system for DC loads. Mater. Today Proc. 2022, 51, 635–639. [Google Scholar] [CrossRef]
- Stieneker, M.; Doncker, R.W.D. Medium-voltage DC distribution grids in urban areas. In Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Montoya, O.D.; Serra, F.M.; Angelo, C.H.D. On the Efficiency in Electrical Networks with AC and DC Operation Technologies: A Comparative Study at the Distribution Stage. Electronics 2020, 9, 1352. [Google Scholar] [CrossRef]
- Elattar, E.E.; Elsayed, S.K. Optimal Location and Sizing of Distributed Generators Based on Renewable Energy Sources Using Modified Moth Flame Optimization Technique. IEEE Access 2020, 8, 109625–109638. [Google Scholar] [CrossRef]
- Paul, S.; Dey, T.; Saha, P.; Dey, S.; Sen, R. Review on the development scenario of renewable energy in different country. In Proceedings of the 2021 Innovations in Energy Management and Renewable Resources (52042), Kolkata, India, 5–7 February 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- kumar Nath, U.; Sen, R. A Comparative Review on Renewable Energy Application, Difficulties and Future Prospect. In Proceedings of the 2021 Innovations in Energy Management and Renewable Resources (52042), Kolkata, India, 5–7 February 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. The increasing impact of weather on electricity supply and demand. Energy 2018, 145, 65–78. [Google Scholar] [CrossRef]
- Dostál, Z.; Ladányi, L. Demands on energy storage for renewable power sources. J. Energy Storage 2018, 18, 250–255. [Google Scholar] [CrossRef]
- Guerrero, J.; Blaabjerg, F.; Zhelev, T.; Hemmes, K.; Monmasson, E.; Jemei, S.; Comech, M.; Granadino, R.; Frau, J. Distributed Generation: Toward a New Energy Paradigm. IEEE Ind. Electron. Mag. 2010, 4, 52–64. [Google Scholar] [CrossRef]
- Sibtain, D.; Murtaza, A.F.; Ahmed, N.; Sher, H.A.; Gulzar, M.M. Multi control adaptive fractional order PID control approach for PV/wind connected grid system. Int. Trans. Electr. Energy Syst. 2021, 31, e12809. [Google Scholar] [CrossRef]
- Magaldi, G.L.; Serra, F.M.; de Angelo, C.H.; Montoya, O.D.; Giral-Ramírez, D.A. Voltage Regulation of an Isolated DC Microgrid with a Constant Power Load: A Passivity-Based Control Design. Electronics 2021, 10, 2085. [Google Scholar] [CrossRef]
- Grisales, L.F.; Grajales, A.; Montoya, O.D.; Hincapie, R.A.; Granada, M.; Castro, C.A. Optimal location, sizing and operation of energy storage in distribution systems using multi-objective approach. IEEE Lat. Am. Trans. 2017, 15, 1084–1090. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Grisales-Noreña, L.F.; Cruz-Peragón, F.; Alcalá, G. Economic Dispatch of Renewable Generators and BESS in DC Microgrids Using Second-Order Cone Optimization. Energies 2020, 13, 1703. [Google Scholar] [CrossRef]
- Akinyele, D.; Rayudu, R. Review of energy storage technologies for sustainable power networks. Sustain. Energy Technol. Assess. 2014, 8, 74–91. [Google Scholar] [CrossRef]
- Shaqsi, A.Z.A.; Sopian, K.; Al-Hinai, A. Review of energy storage services, applications, limitations, and benefits. Energy Rep. 2020, 6, 288–306. [Google Scholar] [CrossRef]
- Olabi, A.; Onumaegbu, C.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.A.; Alami, A.H.A. Critical review of energy storage systems. Energy 2021, 214, 118987. [Google Scholar] [CrossRef]
- Karanja, J.M.; Hinga, P.K.; Ngoo, L.M.; Muriithi, C.M. Optimal Battery Location for Minimizing the Total Cost of Generation in a Power System. In Proceedings of the 2020 IEEE PES/IAS PowerAfrica, Nairobi, Kenya, 25–28 August 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Serra, F.M.; Montoya, O.D.; Alvarado-Barrios, L.; Álvarez-Arroyo, C.; Chamorro, H.R. On the Optimal Selection and Integration of Batteries in DC Grids through a Mixed-Integer Quadratic Convex Formulation. Electronics 2021, 10, 2339. [Google Scholar] [CrossRef]
- Montoya, O.D. A convex OPF approximation for selecting the best candidate nodes for optimal location of power sources on DC resistive networks. Eng. Sci. Technol. Int. J. 2020, 23, 527–533. [Google Scholar] [CrossRef]
- Wong, L.A.; Ramachandaramurthy, V.K. Optimal Allocation of Battery Energy Storage System Using Whale Optimization Algorithm. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, Mauritius, 7–8 October 2021. [Google Scholar]
- Home-Ortiz, J.M.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Mantovani, J.R.S. Optimal location-allocation of storage devices and renewable-based DG in distribution systems. Electr. Power Syst. Res. 2019, 172, 11–21. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.; Montoya, O.D.; Ramos-Paja, C.A. An energy management system for optimal operation of BSS in DC distributed generation environments based on a parallel PSO algorithm. J. Energy Storage 2020, 29, 101488. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Holguín, E.; Garces, A.; Grisales-Noreña, L.F. Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model. J. Energy Storage 2019, 21, 1–8. [Google Scholar] [CrossRef]
- Kerdphol, T.; Tripathi, R.N.; Hanamoto, T.; Qudaih, Y.; Mitani, Y. ANN based optimized battery energy storage system size and loss analysis for distributed energy storage location in PV-microgrid. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Wang, Z.; Low, S.H.; Mei, S. Optimal Power Flow in Stand-Alone DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5496–5506. [Google Scholar] [CrossRef]
- Ploskas, N.; Sahinidis, N.V. Review and comparison of algorithms and software for mixed-integer derivative-free optimization. J. Glob. Optim. 2021, 82, 433–462. [Google Scholar] [CrossRef]
- Torres, J.J.; Li, C.; Apap, R.M.; Grossmann, I.E. A Review on the Performance of Linear and Mixed Integer Two-Stage Stochastic Programming Software. Algorithms 2022, 15, 103. [Google Scholar] [CrossRef]
- Garcés, A. On the Convergence of Newton’s Method in Power Flow Studies for DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5770–5777. [Google Scholar] [CrossRef]
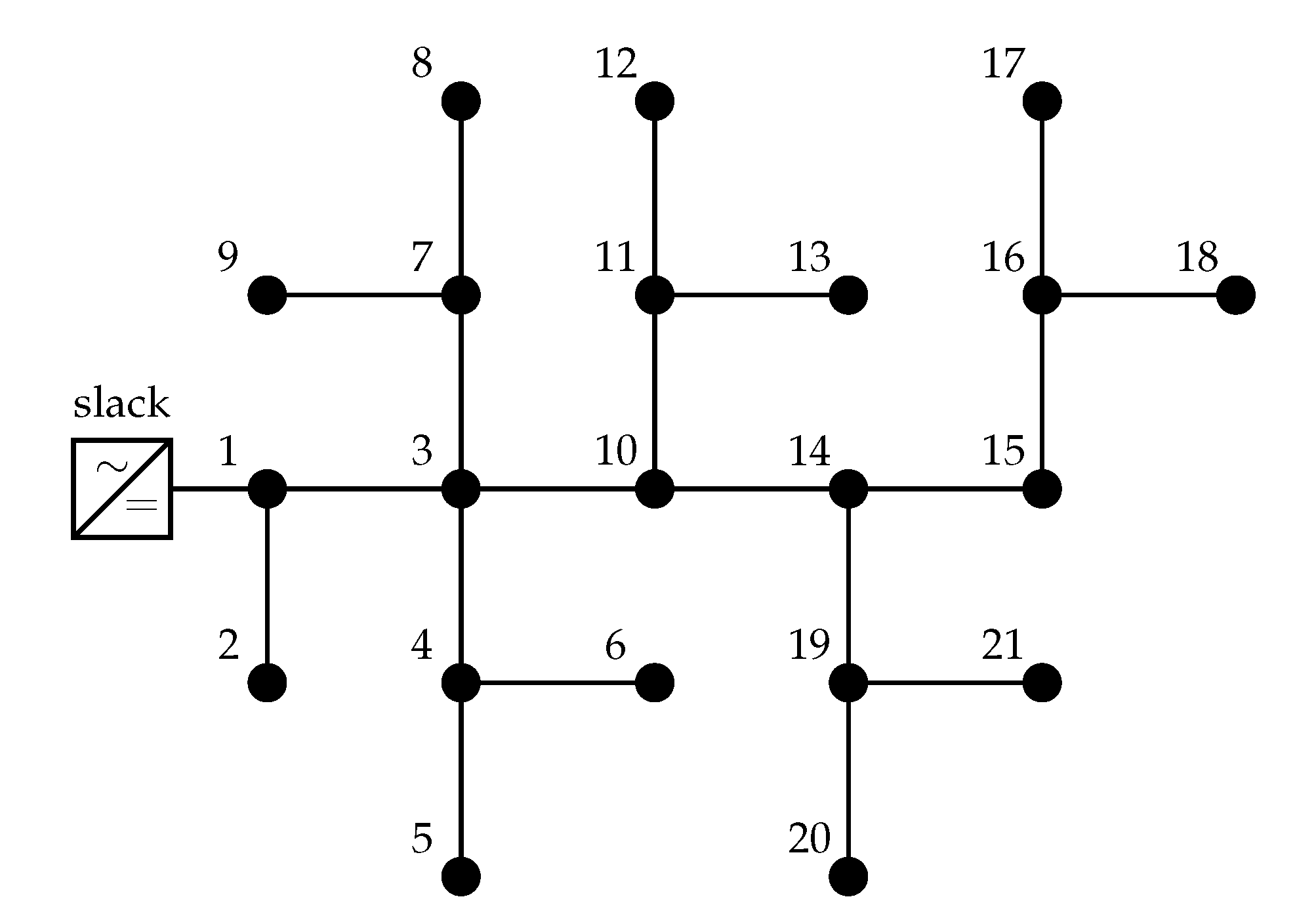


| Node i | Node j | (pu) | (pu) | Node i | Node j | (pu) | (pu) |
|---|---|---|---|---|---|---|---|
| 1 (slack) | 2 | 0.0053 | 0.70 | 11 | 12 | 0.0079 | 0.68 |
| 1 | 3 | 0.0054 | 0.00 | 11 | 13 | 0.0078 | 0.10 |
| 3 | 4 | 0.0054 | 0.36 | 10 | 14 | 0.0083 | 0.00 |
| 4 | 5 | 0.0063 | 0.04 | 14 | 15 | 0.0065 | 0.20 |
| 4 | 6 | 0.0051 | 0.036 | 15 | 16 | 0.0064 | 0.23 |
| 3 | 7 | 0.0037 | 0.00 | 16 | 17 | 0.0074 | 0.43 |
| 7 | 8 | 0.0079 | 0.32 | 16 | 18 | 0.0081 | 0.34 |
| 7 | 9 | 0.0072 | 0.80 | 14 | 19 | 0.0078 | 0.09 |
| 3 | 10 | 0.0053 | 0.00 | 19 | 20 | 0.0084 | 0.21 |
| 10 | 11 | 0.0038 | 0.45 | 19 | 21 | 0.0081 | 0.21 |
| Time (h) | (pu) | Dem. (%) | Time (h) | (pu) | Dem. (%) | Time (h) | (pu) | Dem. (%) |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.8105 | 34 | 8.5 | 0.9263 | 62 | 16.5 | 0.9737 | 90 |
| 1.0 | 0.7789 | 28 | 9.0 | 0.9421 | 68 | 17.0 | 1 | 90 |
| 1.5 | 0.7474 | 22 | 9.5 | 0.9579 | 72 | 17.5 | 0.9947 | 90 |
| 2.0 | 0.7368 | 22 | 10.0 | 0.9579 | 78 | 18.0 | 0.9895 | 90 |
| 2.5 | 0.7263 | 22 | 10.5 | 0.9579 | 84 | 18.5 | 0.9737 | 86 |
| 3.0 | 0.7316 | 20 | 11.0 | 0.9579 | 86 | 19.0 | 0.9579 | 84 |
| 3.5 | 0.7368 | 18 | 11.5 | 0.9579 | 90 | 19.5 | 0.9526 | 92 |
| 4.0 | 0.7474 | 18 | 12.0 | 0.9526 | 92 | 20.0 | 0.9474 | 100 |
| 4.5 | 0.7579 | 18 | 12.5 | 0.9474 | 94 | 20.5 | 0.9211 | 98 |
| 5.0 | 0.8000 | 20 | 13.0 | 0.9474 | 94 | 21.0 | 0.8947 | 94 |
| 5.5 | 0.8421 | 22 | 13.5 | 0.9421 | 90 | 21.5 | 0.8684 | 90 |
| 6.0 | 0.8789 | 26 | 14.0 | 0.9368 | 84 | 22.0 | 0.8421 | 84 |
| 6.5 | 0.9158 | 28 | 14.5 | 0.9421 | 86 | 22.5 | 0.7947 | 76 |
| 7.0 | 0.9368 | 34 | 15.0 | 0.9474 | 90 | 23.0 | 0.7474 | 68 |
| 7.5 | 0.9579 | 40 | 15.5 | 0.9474 | 90 | 23.5 | 0.7211 | 58 |
| 8.0 | 0.9421 | 50 | 16.0 | 0.9474 | 90 | 24.0 | 0.6947 | 50 |
| Node | Type | |||
|---|---|---|---|---|
| 7 | A | 0.0625 | 4 | −3.2 |
| 10 | B | 0.0813 | 3.2 | −2.4616 |
| 15 | B | 0.0813 | 3.2 | −2.4616 |
| Node | Type | (pu) | (pu) |
|---|---|---|---|
| 12 | Wind | 2.2152 | 0 |
| 21 | Photovoltaic | 2.8158 | 0 |
| Period (h) | (pu) | (pu) | Period (h) | (pu) | (pu) | Period (h) | (pu) | (pu) |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.6303 | 0 | 8.5 | 0.8271 | 0.0403 | 16.5 | 0.9892 | 0.4193 |
| 1.0 | 0.6194 | 0 | 9.0 | 0.8523 | 0.1344 | 17.0 | 0.9652 | 0.2784 |
| 1.5 | 0.6098 | 0 | 9.5 | 0.8788 | 0.2710 | 17.5 | 0.9244 | 0.1373 |
| 2.0 | 0.6050 | 0 | 10.0 | 0.9064 | 0.3673 | 18.0 | 0.8607 | 0.0374 |
| 2.5 | 0.6122 | 0 | 10.5 | 0.9328 | 0.4584 | 18.5 | 0.7743 | 0.0007 |
| 3.0 | 0.6411 | 0 | 11.0 | 0.9520 | 0.6125 | 19.0 | 0.7251 | 0 |
| 3.5 | 0.6927 | 0 | 11.5 | 0.9640 | 0.8134 | 19.5 | 0.7167 | 0 |
| 4.0 | 0.7395 | 0 | 12.0 | 0.9700 | 0.9122 | 20.0 | 0.7167 | 0 |
| 4.5 | 0.7779 | 0 | 12.5 | 0.9748 | 0.9633 | 20.5 | 0.7251 | 0 |
| 5.0 | 0.7887 | 0 | 13.0 | 0.9784 | 1.0000 | 21.0 | 0.7263 | 0 |
| 5.5 | 0.7671 | 0 | 13.5 | 0.9832 | 0.9582 | 21.5 | 0.7179 | 0 |
| 6.0 | 0.7479 | 0 | 14.0 | 0.9880 | 0.8791 | 22.0 | 0.7095 | 0 |
| 6.5 | 0.7287 | 0 | 14.5 | 0.9940 | 0.7308 | 22.5 | 0.6987 | 0 |
| 7.0 | 0.7371 | 0 | 15.0 | 0.9988 | 0.7645 | 23.0 | 0.6915 | 0 |
| 7.5 | 0.7731 | 0 | 15.5 | 1.0000 | 0.6866 | 23.5 | 0.6867 | 0 |
| 8.0 | 0.8031 | 0.0016 | 16.0 | 0.9964 | 0.5893 | 24.0 | 0.6831 | 0 |
| Model | BESS’ Location | Generators’ Location | Costs (COP$/Day) | Error (%) |
|---|---|---|---|---|
| MINLP | 7 (A), 10 (B), 15 (B) | 12 (Wind), 21 (PV) | 52,957.92 | 0 |
| MIC | 7 (A), 10 (B), 15 (B) | 12 (Wind), 21 (PV) | 50,890.10 | 3.90 |
| Model | BESS’ Location | Generators’ Location | Costs (COP$/Day) | Error (%) |
|---|---|---|---|---|
| MINLP | 21 (A), 9 (B), 16 (B) | 12 (Wind), 21 (PV) | 41,847.61 | 0 |
| MIC | 21 (A), 9 (B), 16 (B) | 12 (Wind), 21 (PV) | 40,202.20 | 3.93 |
| Model | BESS’ Location | Generators’ Location | Costs (COP$/Day) | Error (%) |
|---|---|---|---|---|
| MINLP | 7 (A), 10 (B), 15 (B) | 10 (Wind), 15 (PV) | 29,697.73 | 0 |
| MIC | 7 (A), 10 (B), 15 (B) | 10 (Wind), 15 (PV) | 28,693.60 | 3.38 |
| Iteration | Gen. Location | BESS’ Location | Costs (COP$/Day) | Gen. Model | BESS’ Model |
|---|---|---|---|---|---|
| 1 | Wind:12, PV:21 | A:21, B:9, B:16 | 40,202.2 | ✓ | |
| 2 | Wind:11, PV:16 | A:21, B:9, B:16 | 25,075.0 | ✓ | |
| 3 | Wind:11, PV:16 | A:16, B:9, B:12 | 24,438.5 | ✓ | |
| 4 | Wind:10, PV:16 | A:16, B:9, B:12 | 23,993.2 | ✓ | |
| 5 | Wind:10, PV:16 | A:16, B:9, B:12 | 23,987.3 | ✓ |
| Model | BESS’ Location | Generators’ location | Costs (COP$/Day) | Error (%) |
|---|---|---|---|---|
| MINLP | 16 (A), 9 (B), 12 (B)) | 10 (PW), 16 (PV) | 24,734.98 | 0 |
| MIC | 16 (A), 9 (B), 12 (B) | 10 (PW), 16 (PV) | 23,987.30 | 3.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basto-Gil, J.D.; Maldonado-Cardenas, A.D.; Montoya, O.D. Optimal Selection and Integration of Batteries and Renewable Generators in DC Distribution Systems through a Mixed-Integer Convex Formulation. Electronics 2022, 11, 3139. https://doi.org/10.3390/electronics11193139
Basto-Gil JD, Maldonado-Cardenas AD, Montoya OD. Optimal Selection and Integration of Batteries and Renewable Generators in DC Distribution Systems through a Mixed-Integer Convex Formulation. Electronics. 2022; 11(19):3139. https://doi.org/10.3390/electronics11193139
Chicago/Turabian StyleBasto-Gil, Jerson Daniel, Angel David Maldonado-Cardenas, and Oscar Danilo Montoya. 2022. "Optimal Selection and Integration of Batteries and Renewable Generators in DC Distribution Systems through a Mixed-Integer Convex Formulation" Electronics 11, no. 19: 3139. https://doi.org/10.3390/electronics11193139
APA StyleBasto-Gil, J. D., Maldonado-Cardenas, A. D., & Montoya, O. D. (2022). Optimal Selection and Integration of Batteries and Renewable Generators in DC Distribution Systems through a Mixed-Integer Convex Formulation. Electronics, 11(19), 3139. https://doi.org/10.3390/electronics11193139







