Digital Image Blending Using Inaccurate Addition
Abstract
:1. Introduction
2. Acronyms and Expansions
- LOA [21]: Lower-part OR adder
- M-HEAA: Modified HEAA [25]
- OLOCA [26]: Optimized LOA with a constant 1 assigned for (K–2) sum bits of the imprecise part, where K is the size of the imprecise part of an N-bit OLOCA
- HOERAA [27]: Hardware optimized and error reduced approximate adder
- HOAANED: Hardware optimized approximate adder with a near-normal error distribution [28]
- HERLOA: Hybrid error reduction LOA [29]
- M-HERLOA: Modified HERLOA [30]
- ERCPAA: Error reduced carry prediction approximate adder [31]
- COREA: Carry OR error reduced adder [32]
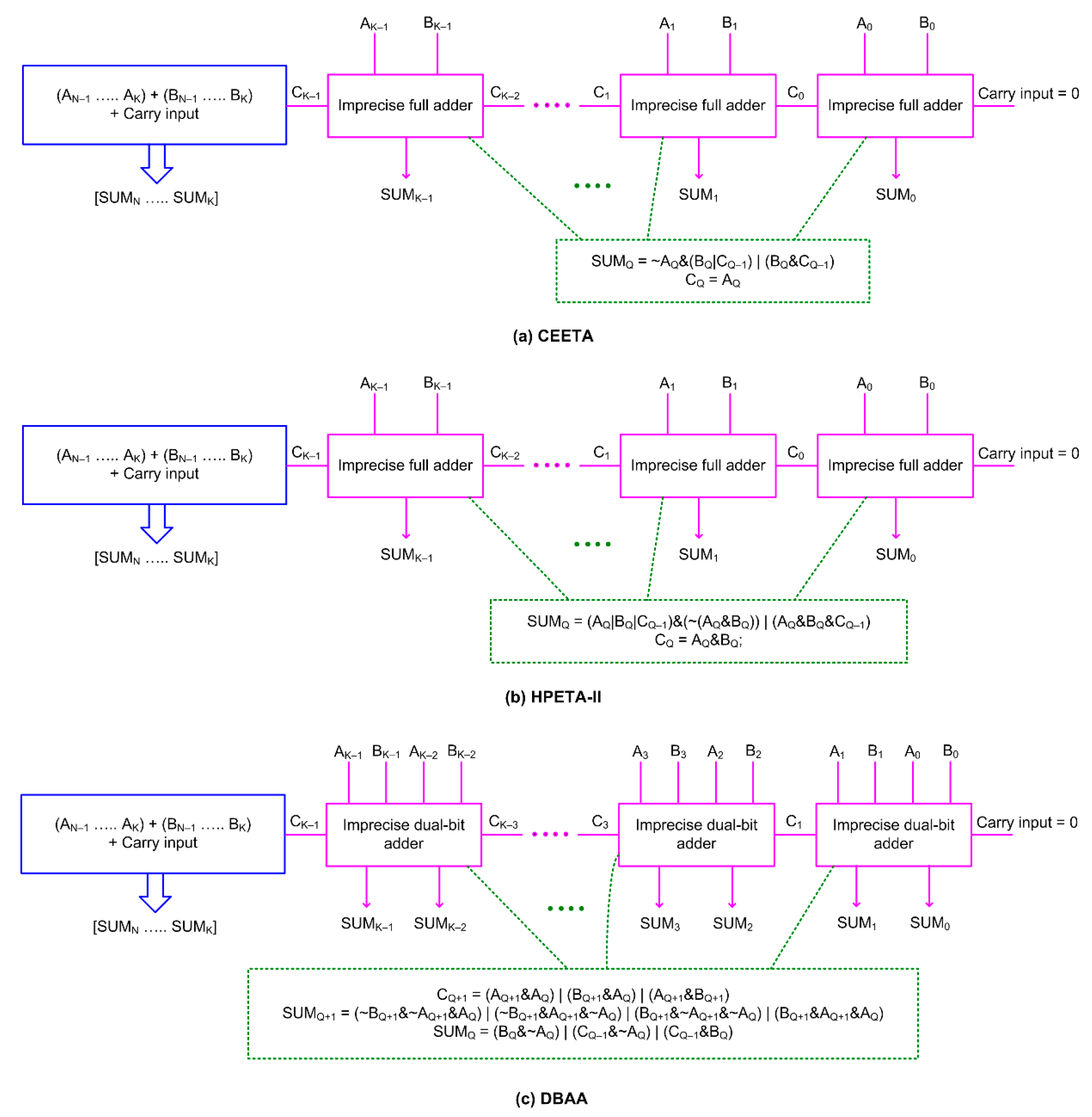
- CEETA: Compact energy efficient error tolerant adder [33]
- HPETA-II: High performance error tolerant adder II, as shown in Figure 12 of [34]
- DBAA: Double bit (adder based) approximate adder [35], labeled as DBAA here
- SAAR: Segmented approximate adder [36]
3. Architectures of Inaccurate Adders
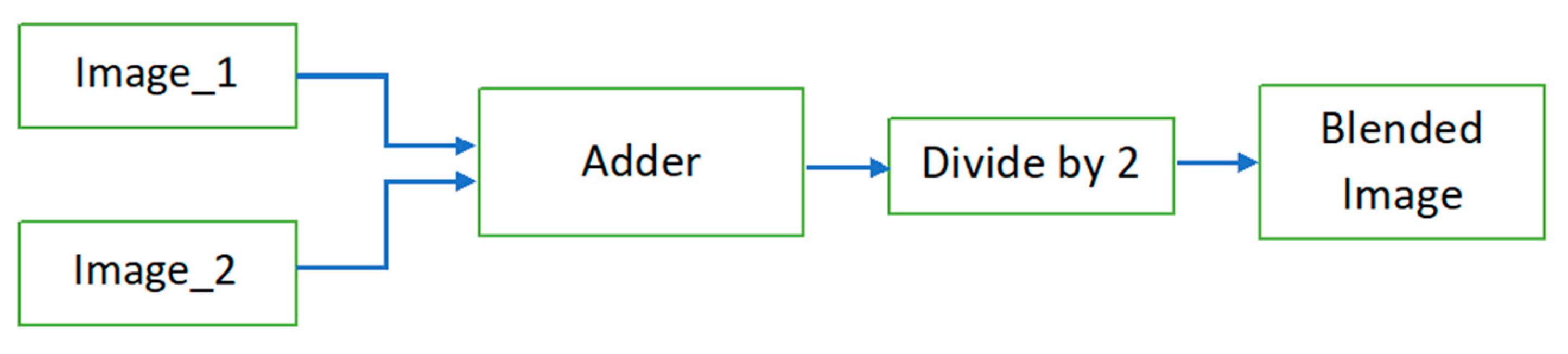
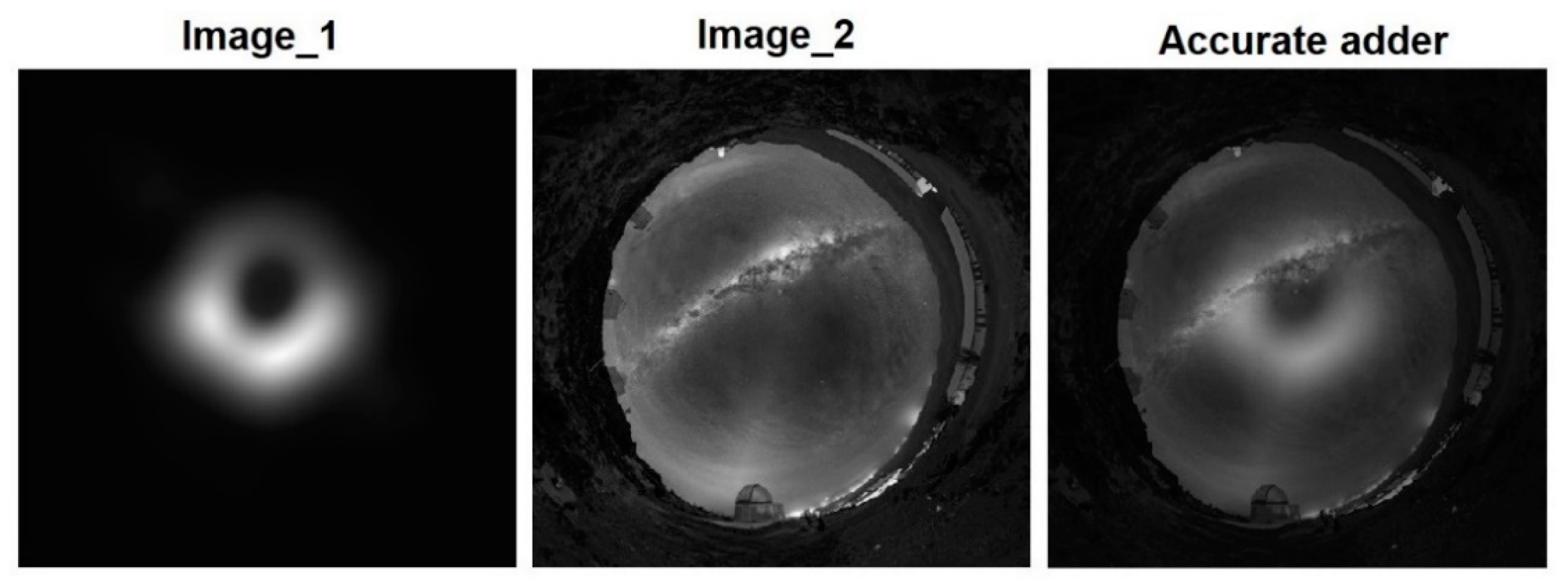
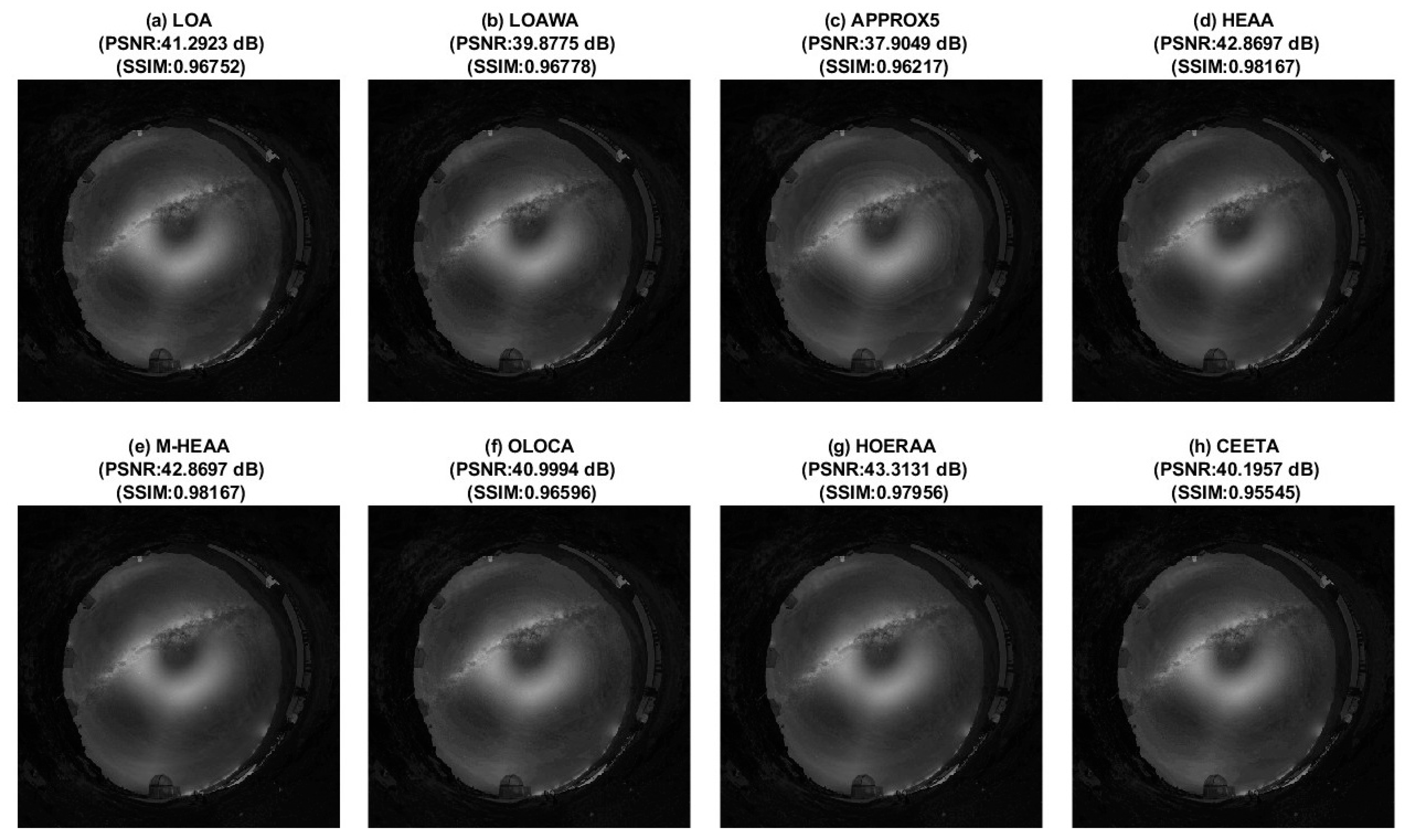
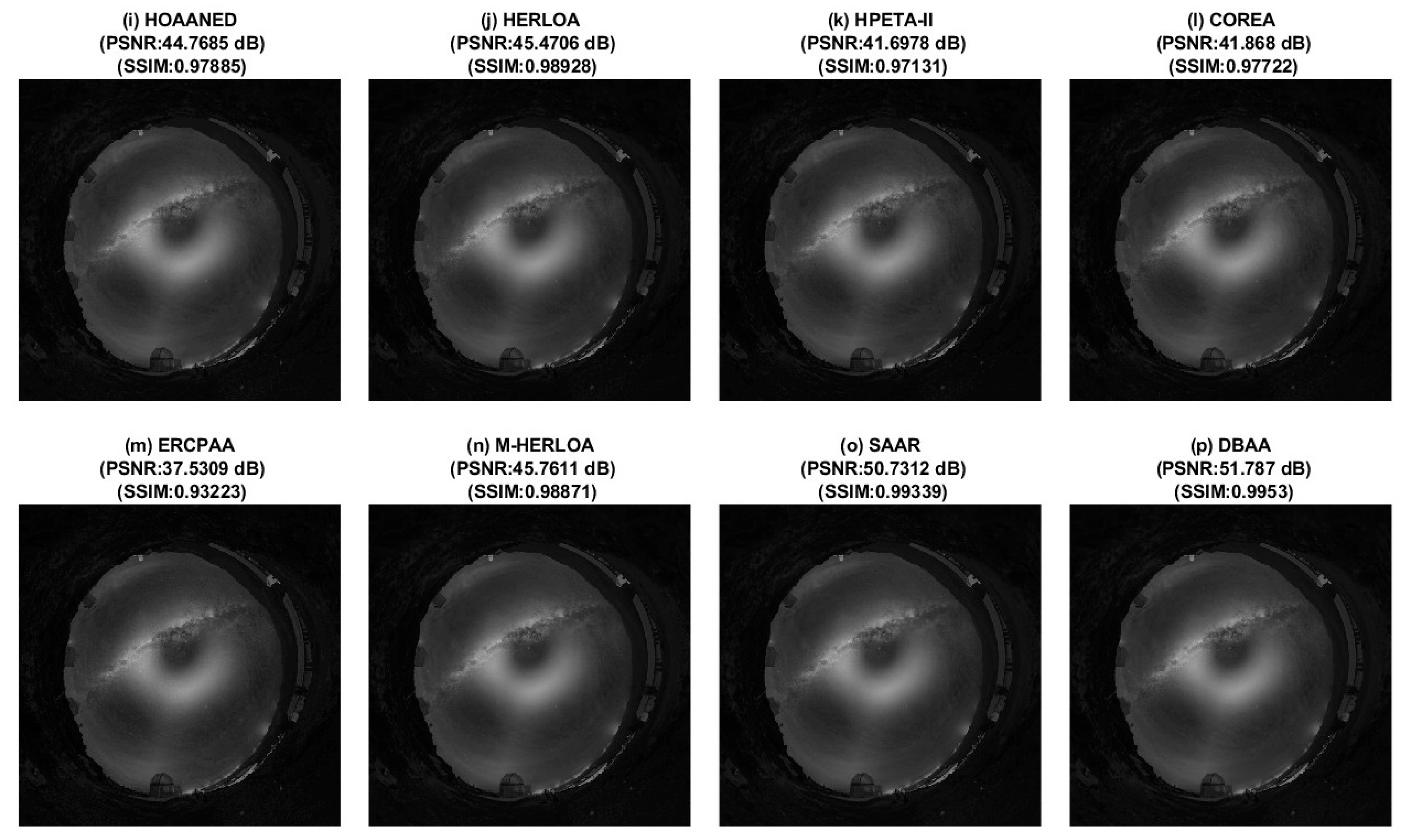
4. Image Blending
5. Error Characteristics and Error Metrics of Inaccurate Adders
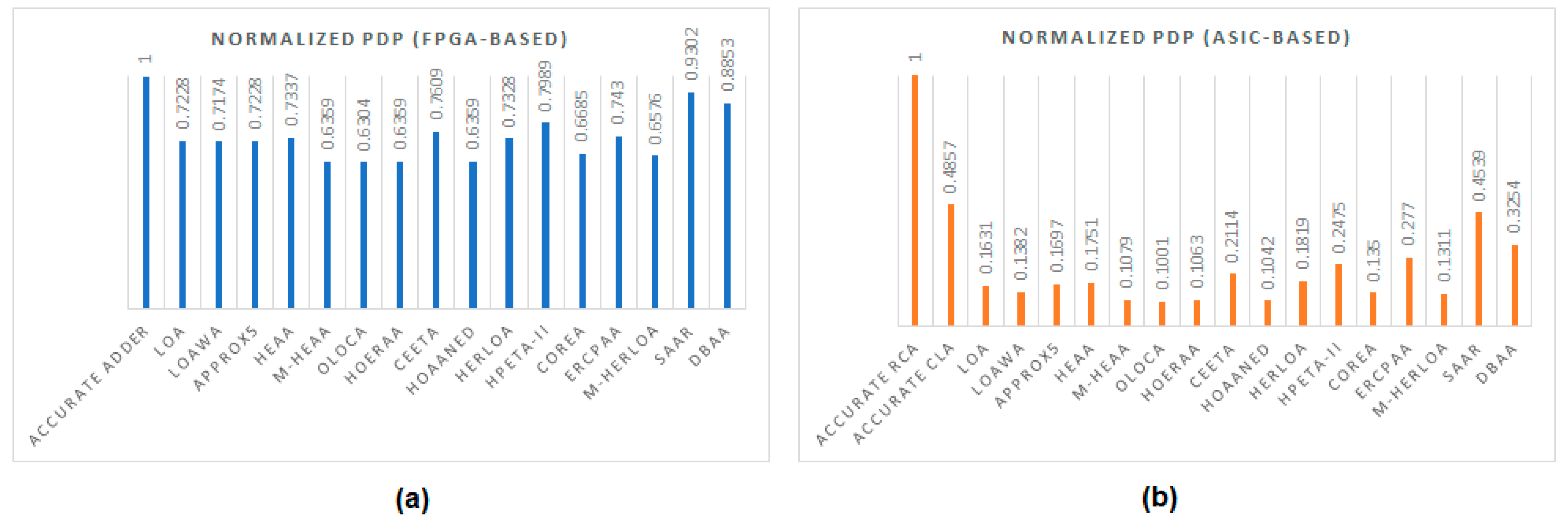
6. Design Metrics of Accurate and Inaccurate Adders
6.1. FPGA-Based Implementation
6.2. ASIC-Type (Standard Cell-Based) Implementation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, J.; Orshansky, M. Approximate computing: An emerging paradigm for energy-efficient design. In Proceedings of the 18th IEEE European Test Symposium, Avignon, France, 27–30 May 2013; pp. 1–6. [Google Scholar]
- Roy, K.; Raghunathan, A. Approximate computing: An energy-efficient computing technique for error resilient applications. In Proceedings of the IEEE Computer Society Annual Symposium on VLSI, Montpellier, France, 8–10 July 2015; pp. 473–475. [Google Scholar]
- Zhu, N.; Goh, W.L.; Zhang, W.; Yeo, K.S.; Kong, Z.H. Design of low-power high-speed truncation-error-tolerant adder and its application in digital signal processing. IEEE Trans. VLSI Syst. 2010, 18, 1225–1229. [Google Scholar]
- Zhu, N.; Goh, W.L.; Wang, G.; Yeo, K.S. Enhanced low-power high-speed adder for error-tolerant application. In Proceedings of the International SoC Design Conference, Incheon, Korea, 22–23 November 2010; pp. 323–327. [Google Scholar]
- Raha, A.; Jayakumar, H.; Raghunathan, V. Input-based dynamic reconfiguration of approximate arithmetic units for video encoding. IEEE Trans. VLSI Syst. 2016, 24, 846–857. [Google Scholar] [CrossRef]
- Breuer, M.A. Multi-media applications and imprecise computation. In Proceedings of the 8th Euromicro Conference on Digital System Design, Porto, Portugal, 30 August–3 September 2005; pp. 1–6. [Google Scholar]
- Nair, R. Big data needs approximate computing: Technical perspective. Commun. ACM 2015, 58, 104. [Google Scholar] [CrossRef]
- Panda, P.; Sengupta, A.; Sarwar, S.S.; Srinivasan, G.; Venkataramani, S.; Raghunathan, A.; Roy, K. Cross-layer approximations for neuromorphic computing: From devices to circuits and systems. In Proceedings of the 53rd Annual Design Automation Conference, Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar]
- Sarwar, S.S.; Srinivasan, G.; Han, B.; Wijesinghe, P.; Jaiswal, A.; Panda, P.; Raghunathan, A.; Roy, K. Energy efficient neural computing: A study of cross-layer approximations. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 796–809. [Google Scholar] [CrossRef]
- Sampson, A.; Deitl, W.; Fortuna, E.; Gnanapragasam, D.; Ceze, L.; Grossman, D. EnerJ: Approximate data types for safe and general low-power computation. In Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, San Jose, CA, USA, 4–8 June 2011; pp. 164–174. [Google Scholar]
- Sampson, A.; Nelson, J.; Strauss, K.; Ceze, L. Approximate storage in solid-state memories. ACM Trans. Comput. Syst. 2014, 32, 9. [Google Scholar] [CrossRef]
- Shoushtari, M.; Rahmani, A.M.; Dutt, N. Quality-configurable memory hierarchy through approximation. In Proceedings of the International Conference on Compilers, Architectures and Synthesis for Embedded Systems, Seoul, Korea, 15–20 October 2017; pp. 1–2. [Google Scholar]
- Zhang, H.; Putic, M.; Lach, J. Low power GPGPU computation with imprecise hardware. In Proceedings of the 51st Design Automation Conference, San Francisco, CA, USA, 1–5 June 2014; pp. 1–6. [Google Scholar]
- Kahng, A.B.; Kang, S. Accuracy-configurable adder for approximate arithmetic designs. In Proceedings of the Design Automation Conference, San Francisco, CA, USA, 1–5 June 2012; pp. 820–825. [Google Scholar]
- Kumar, V.; Singh, A.; Upadhyay, S.; Kumar, B. Power-delay-error-efficient approximate adder for error-resilient applications. J. Circuits Syst. Comput. 2019, 28, 1950171. [Google Scholar] [CrossRef]
- Mirzaei, M.; Mohammadi, S. Low-power and variation-aware approximate arithmetic units for image processing applications. AEU-Int. J. Electron. Commun. 2021, 138, 153825. [Google Scholar] [CrossRef]
- Fatemieh, S.E.; Farahani, S.S.; Reshadinezhad, M.R. LAHAF: Low-power, area-efficient, and high-performance approximate full adder based on static CMOS. Sustain. Comput. Inform. Syst. 2021, 30, 100529. [Google Scholar] [CrossRef]
- Prabakaran, B.S.; Rehman, S.; Hanif, M.A.; Ullah, S.; Mazaheri, G.; Kumar, A.; Shafique, M. DeMAS: An efficient design methodology for building approximate adders for FPGA-based systems. In Proceedings of the Design, Automation and Test in Europe Conference and Exhibition, Dresden, Germany, 19–23 March 2018; pp. 917–920. [Google Scholar]
- Perri, S.; Spagnolo, F.; Frustaci, F.; Corsonello, P. Efficient approximate adders for FPGA-based data-paths. Electronics 2020, 9, 1529. [Google Scholar] [CrossRef]
- Ahmad, W.; Ayrancioglu, B.; Hamzaoglu, I. Low error efficient approximate adders for FPGAs. IEEE Access 2021, 9, 117232–117243. [Google Scholar] [CrossRef]
- Mahdiani, H.R.; Ahmadi, A.; Fakhraie, S.M.; Lucas, C. Bio-inspired imprecise computational blocks for efficient VLSI implementation of soft-computing applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 850–862. [Google Scholar] [CrossRef]
- Albicocco, P.; Cardarilli, G.C.; Nannarelli, A.; Petricca, M.; Re, M. Imprecise arithmetic for low power image processing. In Proceedings of the 46th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 2012; pp. 983–987. [Google Scholar]
- Gupta, V.; Mohapatra, D.; Raghunathan, A.; Roy, K. Low-power digital signal processing using approximate adders. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 124–137. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Maskell, D. Hardware efficient approximate adder design. In Proceedings of the IEEE Region 10 Conference, Jeju, Korea, 28–31 October 2018; pp. 806–810. [Google Scholar]
- Balasubramanian, P.; Maskell, D.L.; Prasad, K. Approximate adder with reduced error. In Proceedings of the IEEE 31st International Conference on Microelectronics, Nis, Serbia, 16–18 September 2019; pp. 293–296. [Google Scholar]
- Dalloo, A.; Najafi, A.; Garcia-Ortiz, A. Systematic design of an approximate adder: The optimized lower part constant-OR adder. IEEE Trans. VLSI Syst. 2018, 26, 1595–1599. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Maskell, D.L. Hardware optimized and error reduced approximate adder. Electronics 2019, 8, 1212. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Nayar, R.; Maskell, D.L.; Mastorakis, N.E. An approximate adder with a near-normal error distribution: Design, error analysis and practical application. IEEE Access 2021, 9, 4518–4530. [Google Scholar] [CrossRef]
- Seo, H.; Yang, Y.S.; Kim, Y. Design and analysis of an approximate adder with hybrid error reduction. Electronics 2020, 9, 471. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Nayar, R.; Maskell, D.L. An approximate adder with reduced error and optimized design metrics. In Proceedings of the 17th IEEE Asia Pacific Conference on Circuits and Systems, Penang, Malaysia, 22–26 November 2021; pp. 21–24. [Google Scholar]
- Lee, J.; Seo, H.; Seok, H.; Kim, Y. A novel approximate adder design using error reduced carry prediction and constant truncation. IEEE Access 2021, 9, 119939–119953. [Google Scholar] [CrossRef]
- Seok, H.; Seo, H.; Lee, J.; Kim, Y. COREA: Delay- and energy-efficient approximate adder using effective carry speculation. Electronics 2021, 10, 2234. [Google Scholar] [CrossRef]
- Jothin, R.; Mohamed, M.P.; Vasanthanayaki, C. High performance compact energy efficient error tolerant adders and multipliers for 16-bit image processing applications. Microprocess. Microsyst. 2020, 78, 103237. [Google Scholar] [CrossRef]
- Jothin, R.; Vasanthanayaki, C. High performance error tolerant adders for image processing applications. IETE J. Res. 2021, 67, 205–216. [Google Scholar] [CrossRef]
- Maroof, N.; Al-Zahrani, A.Y. A double bit approximate adder providing a new design perspective for gate-level design. J. Circuits Syst. Comput. 2022, 31, 2250065. [Google Scholar] [CrossRef]
- Kumar, U.A.; Sahith, G.; Chatterjee, S.K.; Ahmed, S.E. A high-speed and power-efficient approximate adder for image processing applications. J. Circuits Syst. Comput. 2022, 31, 2250049. [Google Scholar] [CrossRef]
- Bovik, A. Handbook of Image and Video Processing, 2nd ed.; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar]
- Available online: https://www.eso.org/public/images/lasilla-2019-doyen-CC/ (accessed on 26 August 2021).
- Available online: https://www.eso.org/public/images/eso1907a/ (accessed on 8 August 2021).
- Chan, W.-T.J.; Kahng, A.B.; Kang, S.; Kumar, R.; Sartori, J. Statistical analysis and modeling for error composition in approximate computation circuits. In Proceedings of the IEEE 31st International Conference on Computer Design, Asheville, NC, USA, 6–9 October 2013; pp. 47–53. [Google Scholar]
- Synopsys SAED_EDK32/28_CORE Databook. Revision 1.0.0. January 2012. Available online: https://www.synopsys.com/academic-research/university.html (accessed on 12 June 2022).
- Balasubramanian, P.; Mastorakis, N.E. High-speed and energy-efficient carry look-ahead adder. J. Low Power Electron. Appl. 2022, 12, 46. [Google Scholar] [CrossRef]


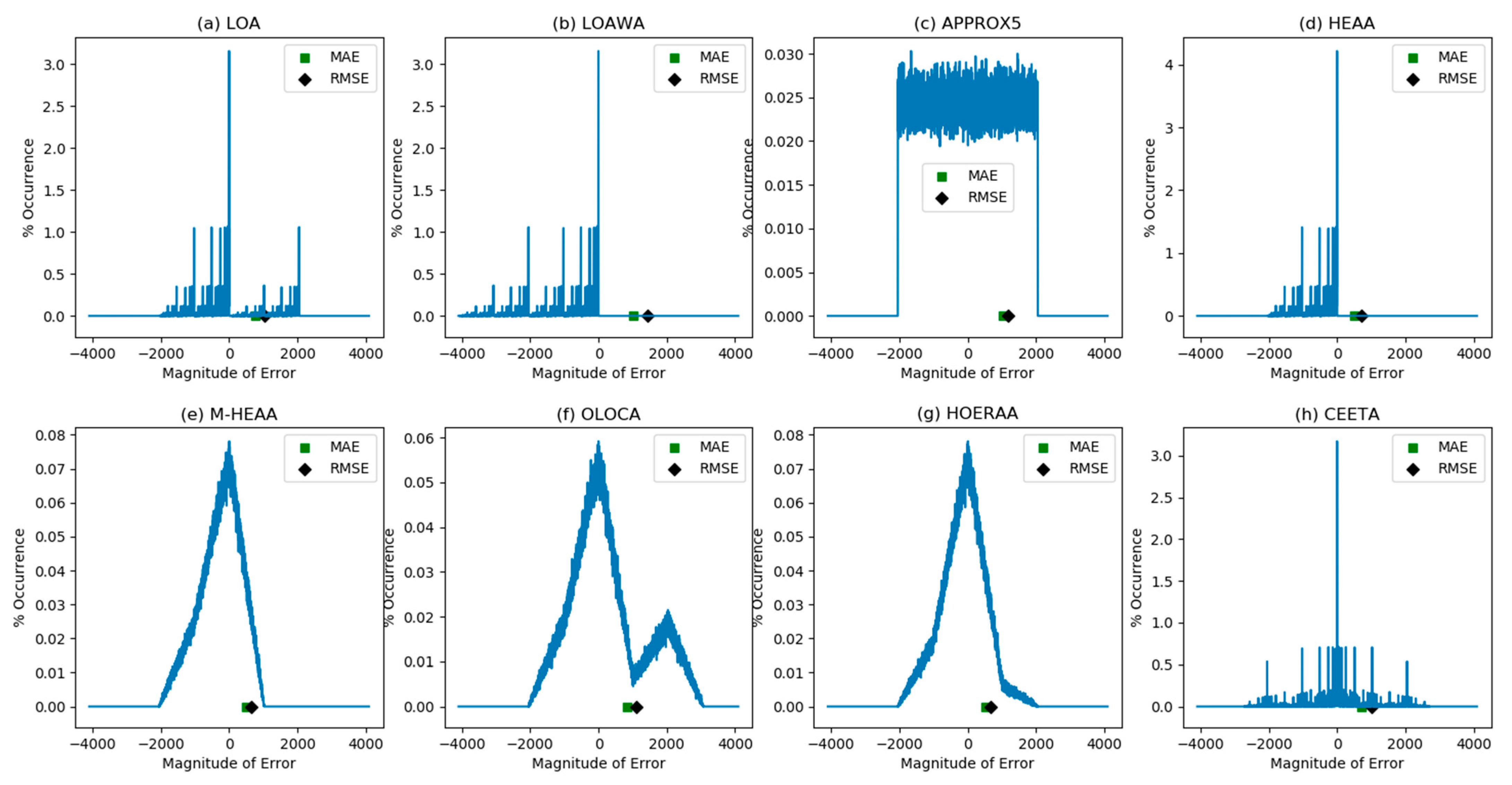
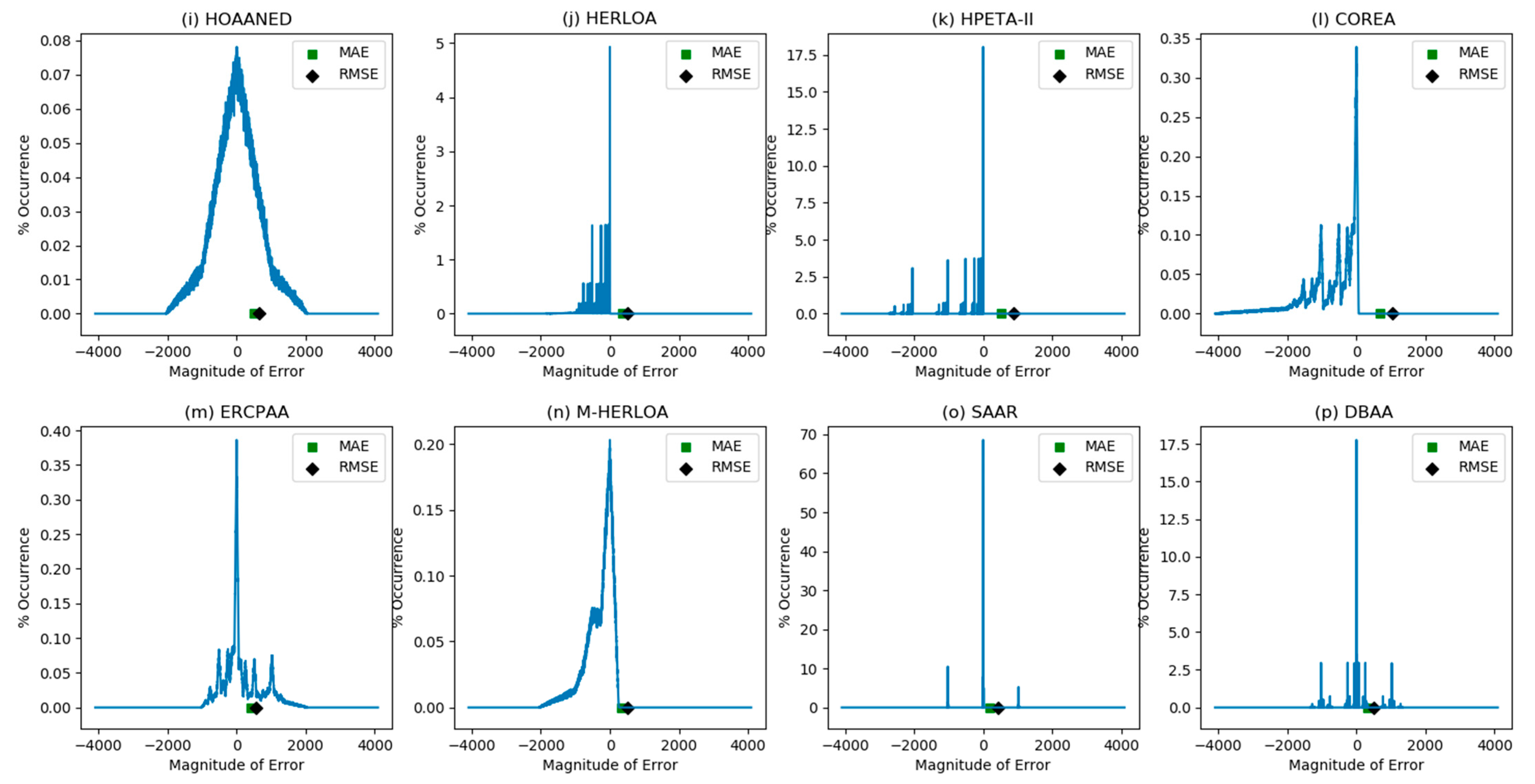
| Inaccurate Adder | Mean Absolute Error | Root Mean Square Error |
|---|---|---|
| LOA | 767.82 | 1023.93 |
| LOAWA | 1023.81 | 1448.09 |
| APPROX5 | 1024.18 | 1182.33 |
| HEAA | 511.80 | 723.93 |
| M-HEAA | 511.75 | 660.73 |
| OLOCA | 831.75 | 1105.77 |
| HOERAA | 512.13 | 661.32 |
| CEETA | 716.16 | 1023.25 |
| HOAANED | 512.19 | 661.40 |
| HERLOA | 351.65 | 517.07 |
| HPETA-II | 337.99 | 885.88 |
| COREA | 693.85 | 1026.80 |
| ERCPAA | 396.70 | 570.162 |
| M-HERLOA | 337.99 | 498.41 |
| SAAR | 193.23 | 442.52 |
| DBAA | 305.14 | 511.97 |
| Adder | Look-Up Tables | Registers | Delay (ns) | Power (W) |
|---|---|---|---|---|
| Accurate (FPGA) adder | 16 | 49 | 1.84 | 0.160 |
| Inaccurate Adders | ||||
| LOA | 16 | 49 | 1.60 | 0.133 |
| LOAWA | 16 | 49 | 1.60 | 0.132 |
| APPROX5 | 5 | 38 | 1.60 | 0.133 |
| HEAA | 16 | 49 | 1.60 | 0.135 |
| M-HEAA | 6 | 19 | 1.60 | 0.117 |
| OLOCA | 6 | 19 | 1.60 | 0.116 |
| HOERAA | 6 | 19 | 1.60 | 0.117 |
| CEETA | 12 | 49 | 1.60 | 0.140 |
| HOAANED | 6 | 19 | 1.60 | 0.117 |
| HERLOA | 12 | 49 | 1.61 | 0.134 |
| HPETA-II | 16 | 49 | 1.60 | 0.147 |
| COREA | 10 | 31 | 1.60 | 0.123 |
| ERCPAA | 12 | 36 | 1.75 | 0.125 |
| M-HERLOA | 8 | 25 | 1.60 | 0.121 |
| SAAR | 16 | 49 | 1.68 | 0.163 |
| DBAA | 13 | 49 | 1.81 | 0.144 |
| Adder | Area (µm2) | Delay (ns) | Power (µW) |
|---|---|---|---|
| Accurate Adders | |||
| RCA | 83.45 | 1.75 | 42.93 |
| CLA | 250.22 | 0.77 | 47.39 |
| Inaccurate Adders | |||
| LOA | 50.34 | 0.58 | 21.12 |
| LOAWA | 48.91 | 0.51 | 20.36 |
| APPROX5 | 47.11 | 0.54 | 23.61 |
| HEAA | 51.79 | 0.62 | 21.22 |
| M-HEAA | 42.51 | 0.62 | 13.07 |
| OLOCA | 41.06 | 0.58 | 12.97 |
| HOERAA | 47.32 | 0.58 | 13.77 |
| CEETA | 82.90 | 0.54 | 29.41 |
| HOAANED | 45.45 | 0.58 | 13.50 |
| HERLOA | 62.62 | 0.62 | 22.04 |
| HPETA-II | 99.99 | 0.58 | 32.06 |
| COREA | 53.89 | 0.51 | 19.88 |
| ERCPAA | 76.07 | 0.92 | 22.62 |
| M-HERLOA | 47.55 | 0.62 | 15.88 |
| SAAR | 97.14 | 0.81 | 42.10 |
| DBAA | 81.91 | 0.65 | 37.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasubramanian, P.; Nayar, R.; Maskell, D.L. Digital Image Blending Using Inaccurate Addition. Electronics 2022, 11, 3095. https://doi.org/10.3390/electronics11193095
Balasubramanian P, Nayar R, Maskell DL. Digital Image Blending Using Inaccurate Addition. Electronics. 2022; 11(19):3095. https://doi.org/10.3390/electronics11193095
Chicago/Turabian StyleBalasubramanian, Padmanabhan, Raunaq Nayar, and Douglas L. Maskell. 2022. "Digital Image Blending Using Inaccurate Addition" Electronics 11, no. 19: 3095. https://doi.org/10.3390/electronics11193095
APA StyleBalasubramanian, P., Nayar, R., & Maskell, D. L. (2022). Digital Image Blending Using Inaccurate Addition. Electronics, 11(19), 3095. https://doi.org/10.3390/electronics11193095







