UCAV Air Combat Maneuver Decisions Based on a Proximal Policy Optimization Algorithm with Situation Reward Shaping
Abstract
:1. Introduction
2. Air Combat Confrontation Framework
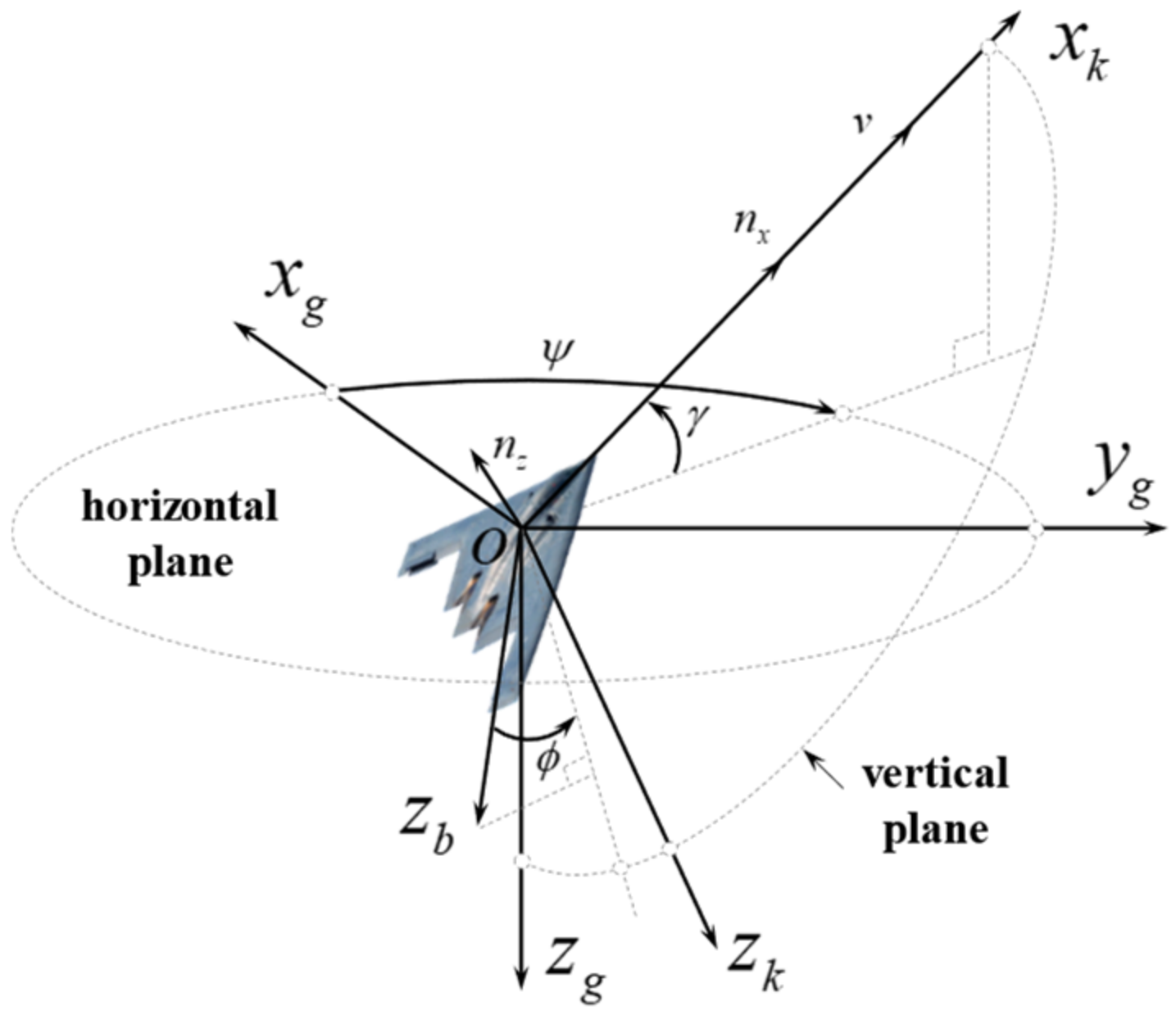
2.1. Unmanned Combat Air Vehicle Motion Model
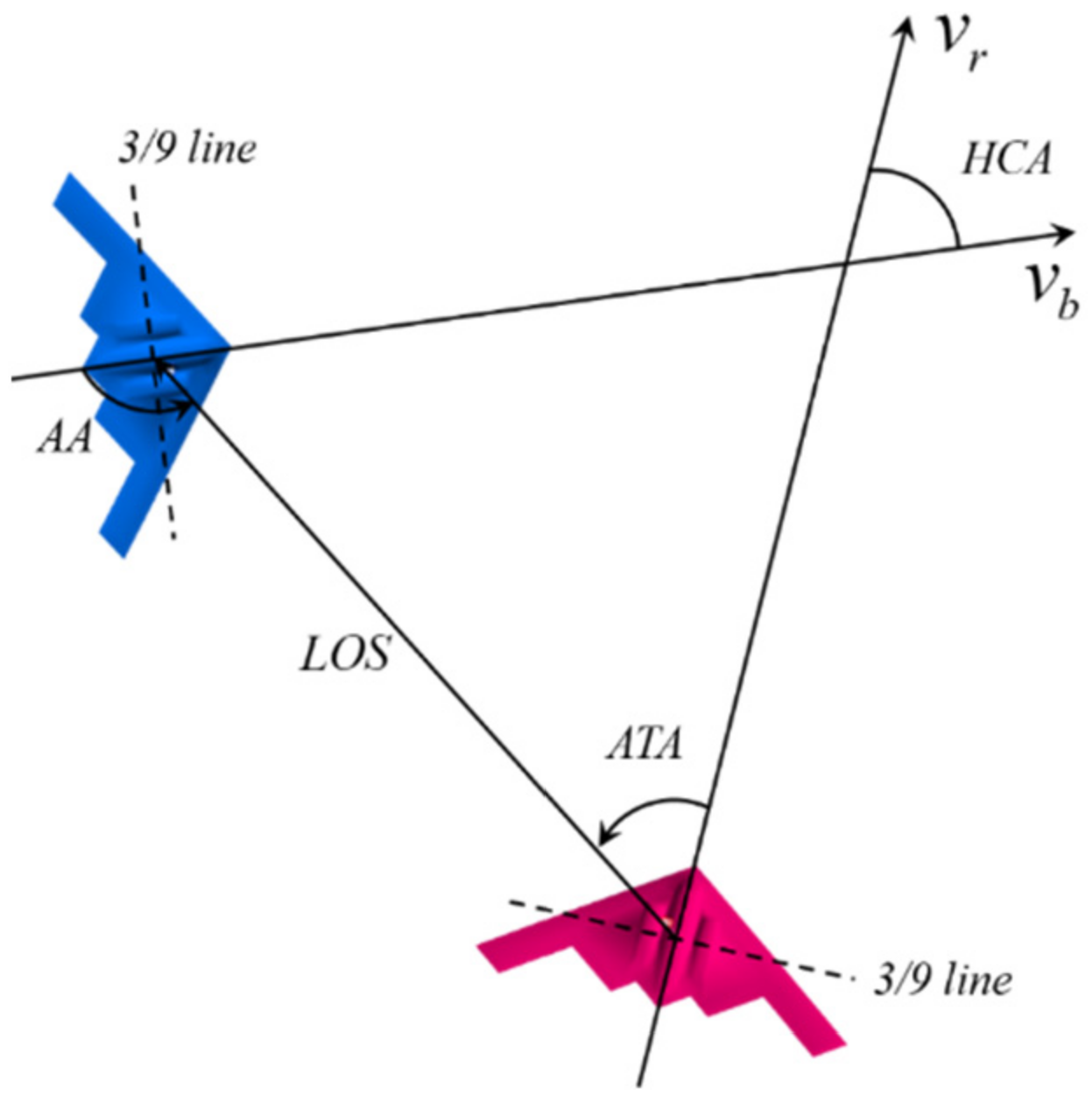
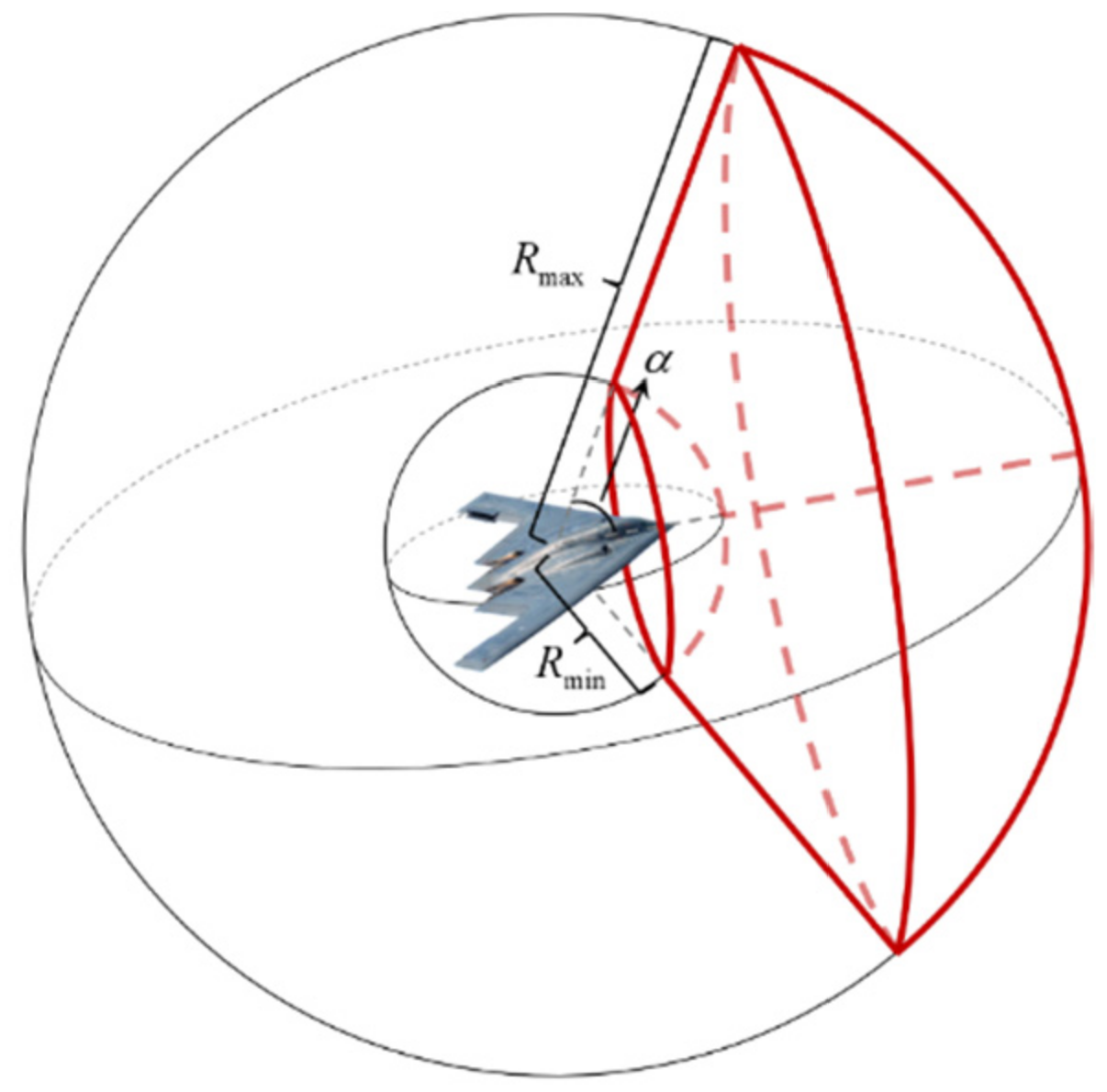
2.2. Air Combat Situation Assessment Model
2.2.1. Conditions for the End of Air Combat
- Shooting down the enemy or being shot down;
- Stalling or crashing.
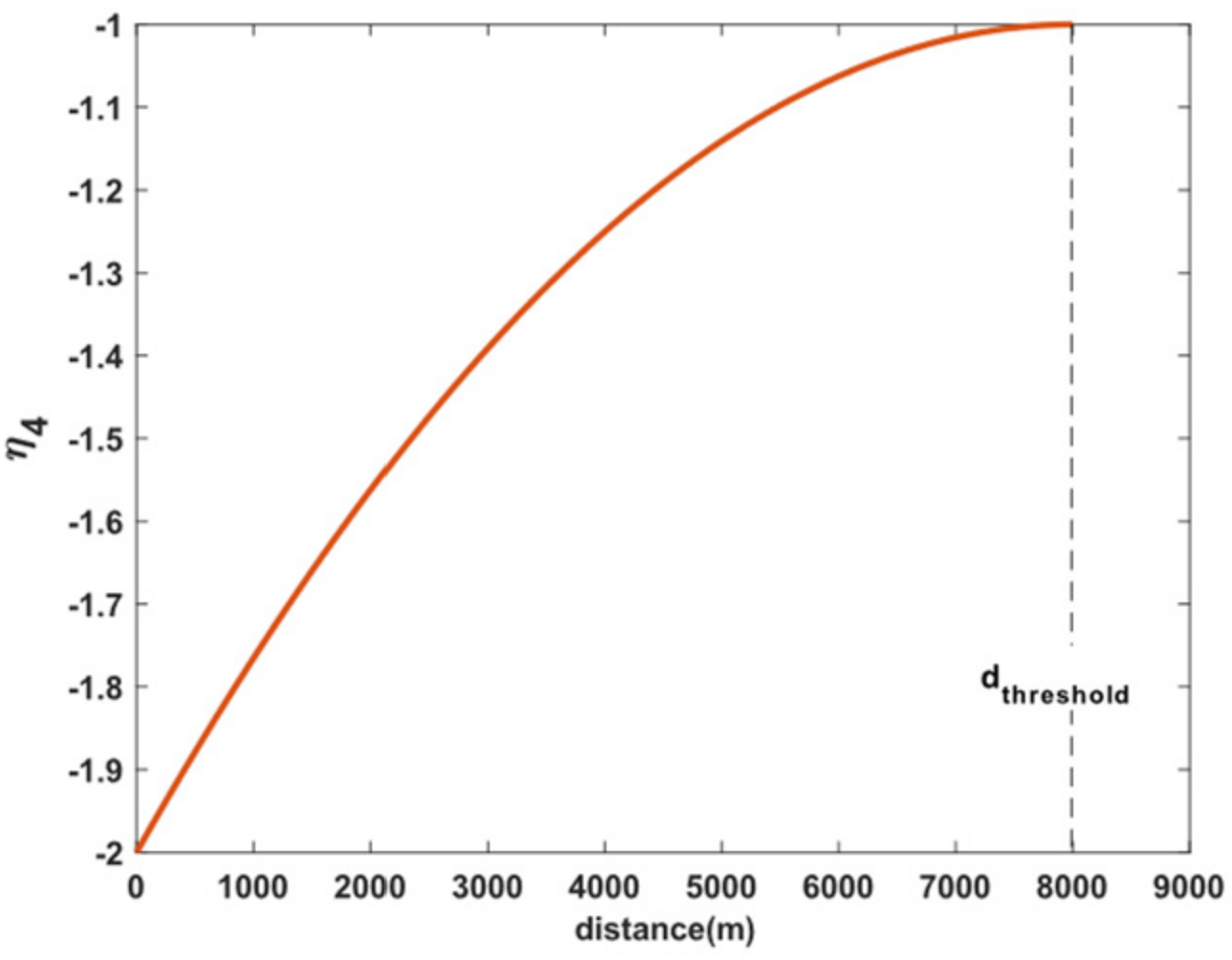
2.2.2. Situation Assessment in the Process of Air Combat
| Algorithm 1 Switching Process of an Air Combat Situation |
| If or are less than the threshold Else if Else if distance is greater than the threshold |
| Else |
2.3. Enemy Maneuver Policy
3. Maneuver Decision Method Based on a Proximal Policy Optimization Algorithm
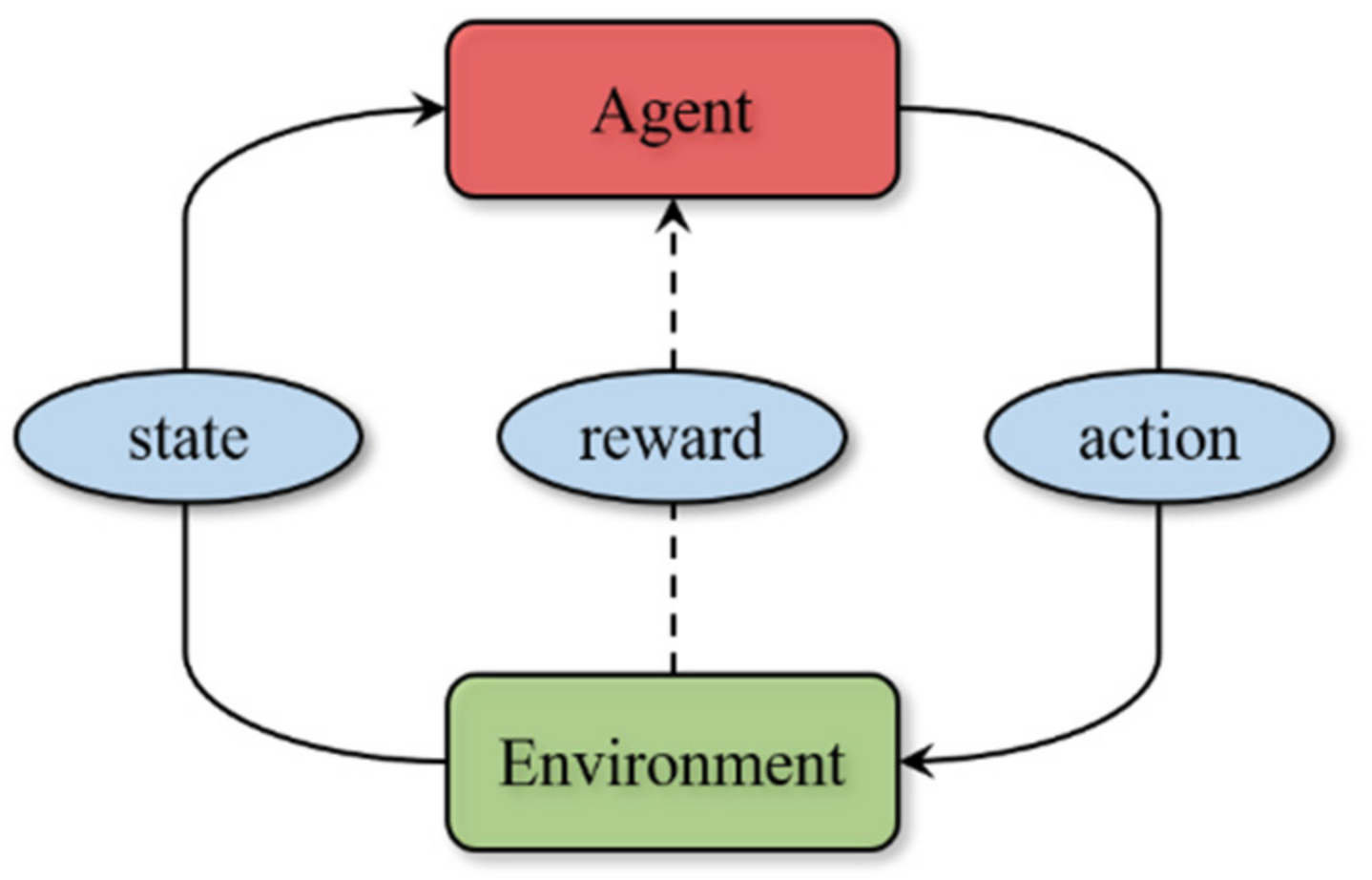
3.1. Proximal Policy Optimization Algorithm
3.2. Action Space
3.3. State Observation Space
3.4. Reward Function with Situation Reward Shaping
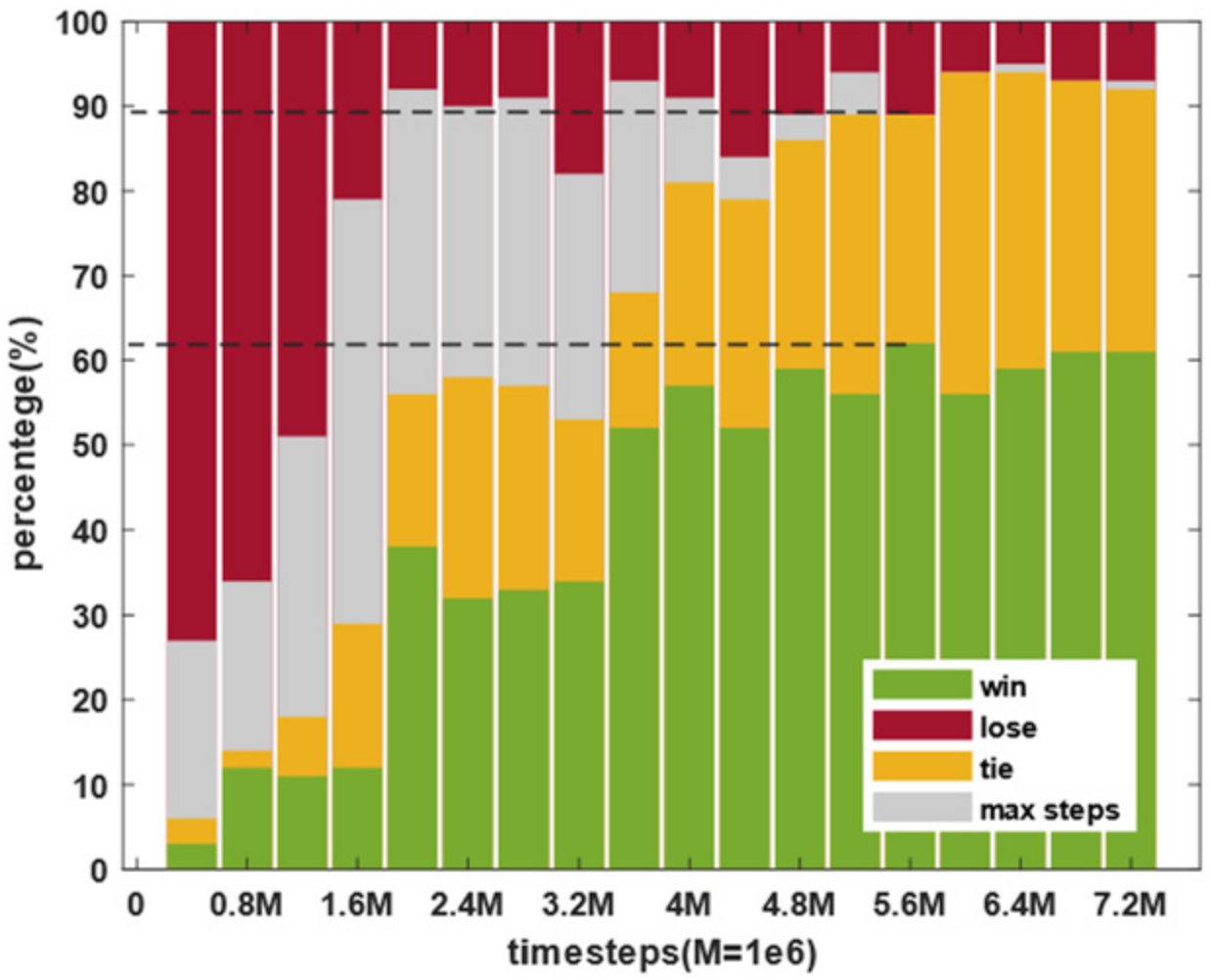
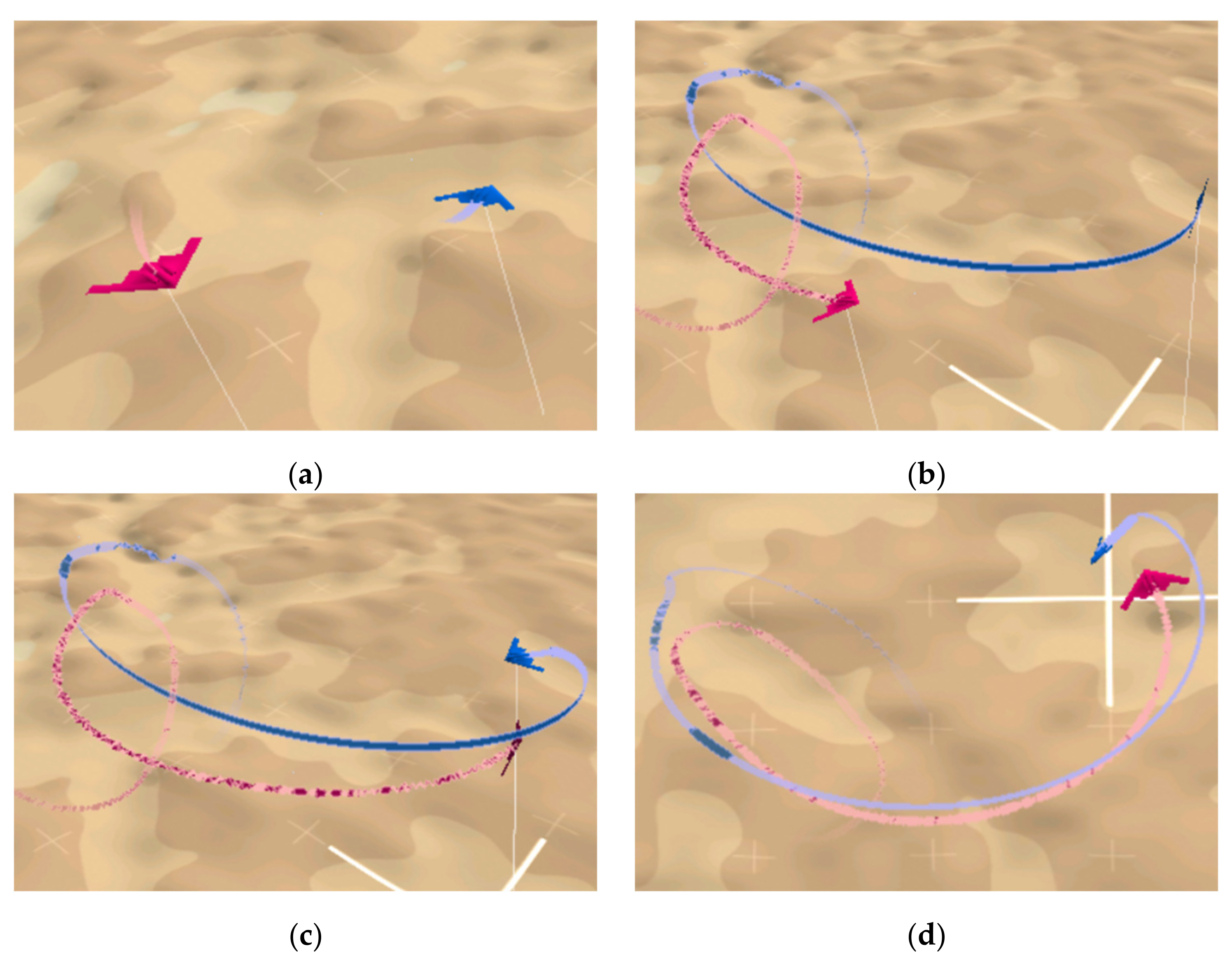
4. Simulation Results
4.1. Simulation Platform
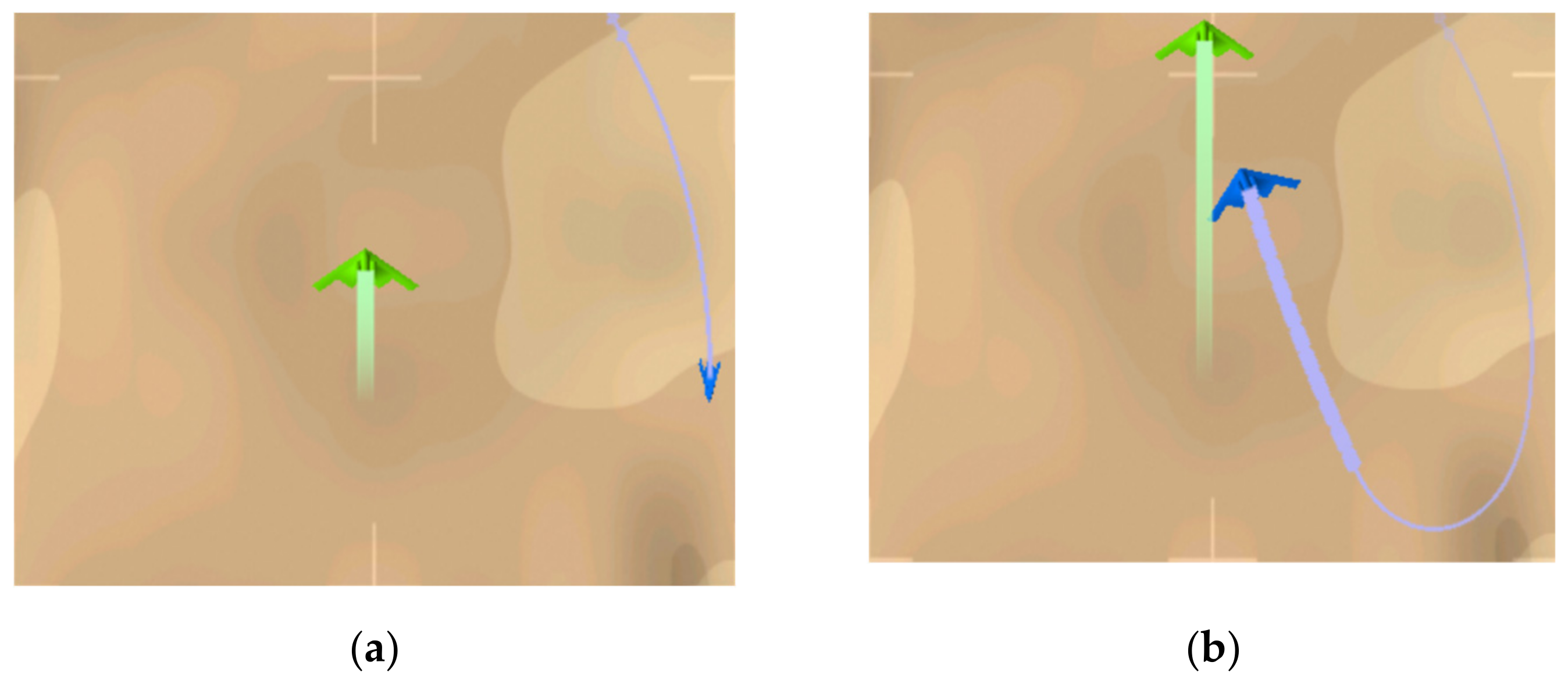
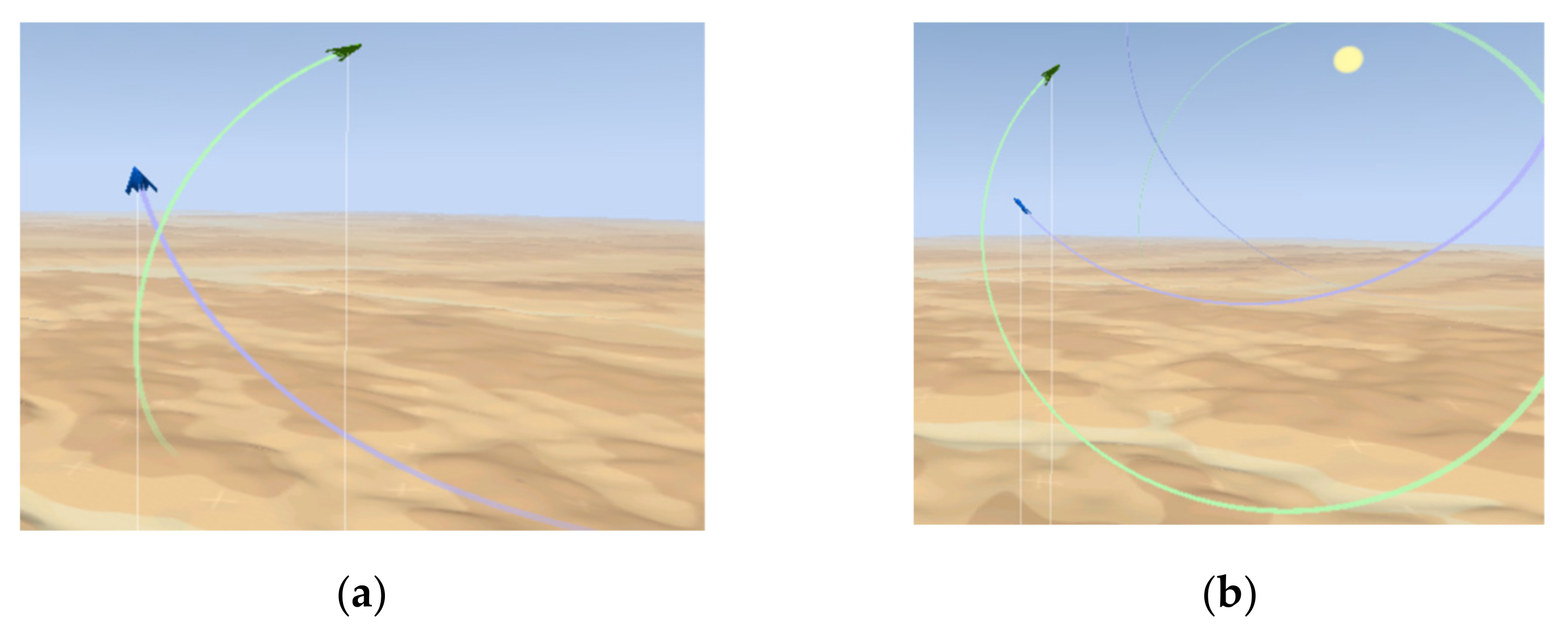
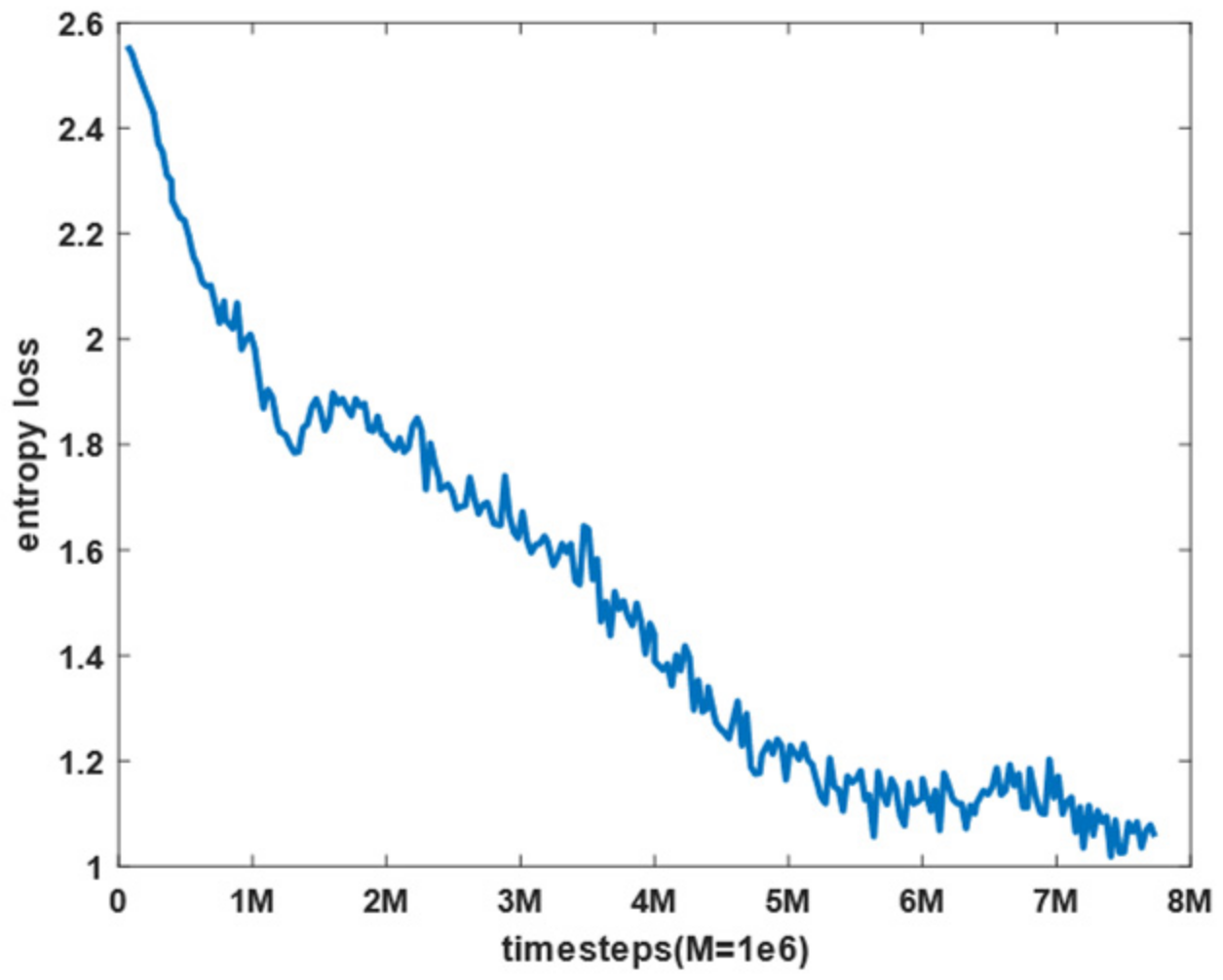
4.2. Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| position vector of a UCAV | |
| longitudinal overload my | |
| normal overload | |
| control input | |
| line of sight | |
| antenna train angle | |
| aspect angle | |
| heading crossing angle | |
| maximum attack angle of a UCAV | |
| attack range of a UCAV | |
| air combat situation | |
| maneuver policy of a UCAV | |
| Action vector of a UCAV | |
| value function of reinforcement learning | |
| loss function of a neural network | |
| probability ratio of a policy update | |
| action space of reinforcement learning | |
| state observation space of reinforcement learning | |
| discount factor of reinforcement learning | |
| value function squared-error loss coefficient | |
| entropy bonus coefficient | |
| clip range of the PPO | |
| generalized advantage estimation factor |
References
- McManus, J.W.; Chappell, A.R.; Arbuckle, P.D. Situation Assessment in the Paladin Tactical Decision Generation System. In AGARD Conference AGARD-CP-504: Air Vehicle Mission Control and Management; NATO: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Burgin, G.H. Improvements to the Adaptive Maneuvering Logic Program; NASA CR-3985; NASA: Washington, DC, USA, 1986. [Google Scholar]
- Ernest, N.; Carroll, D.; Schumacher, C.; Clark, M.; Cohen, K.; Lee, G. Genetic Fuzzy based Artificial Intelligence for Unmanned Combat Aerial Vehicle Control in Simulated Air Combat Missions. J. Def. Manag. 2016, 6, 1–7. [Google Scholar] [CrossRef]
- DARPA. Air Combat Evolution. Available online: https://www.darpa.mil/program/air-combat-evolution (accessed on 24 June 2022).
- Vajda, S. Differential Games. A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization. By Rufus Isaacs. Pp. xxii, 384. 113s. 1965. (Wiley). Math. Gaz. 1967, 51, 80–81. [Google Scholar] [CrossRef]
- Mendoza, L. Qualitative Differential Equations. Dict. Bioinform. Comput. Biol. 2004, 68, 421–430. [Google Scholar] [CrossRef]
- Park, H.; Lee, B.-Y.; Tahk, M.-J.; Yoo, D.-W. Differential Game Based Air Combat Maneuver Generation Using Scoring Function Matrix. Int. J. Aeronaut. Space Sci. 2016, 17, 204–213. [Google Scholar] [CrossRef]
- Bullock, H.E. ACE: The Airborne Combat Expert Systems: An Exposition in Two Parts. Master’s Thesis, Defense Technical Information Center, Fort Belvoir, VA, USA, 1986. [Google Scholar]
- Chin, H.H. Knowledge-based system of supermaneuver selection for pilot aiding. J. Aircr. 1989, 26, 1111–1117. [Google Scholar] [CrossRef]
- Wang, R.; Gao, Z. Research on Decision System in Air Combat Simulation Using Maneuver Library. Flight Dyn. 2009, 27, 72–75. [Google Scholar]
- Xuan, W.; Weijia, W.; Kepu, S.; Minwen, W. UAV Air Combat Decision Based on Evolutionary Expert System Tree. Ordnance Ind. Autom. 2019, 38, 42–47. [Google Scholar]
- Huang, C.; Dong, K.; Huang, H.; Tang, S.; Zhang, Z. Autonomous air combat maneuver decision using Bayesian inference and moving horizon optimization. J. Syst. Eng. Electron. 2018, 29, 86–97. [Google Scholar] [CrossRef]
- Cao, Y.; Kou, Y.-X.; Xu, A.; Xi, Z.-F. Target Threat Assessment in Air Combat Based on Improved Glowworm Swarm Optimization and ELM Neural Network. Int. J. Aerosp. Eng. 2021, 2021, 4687167. [Google Scholar] [CrossRef]
- Kaneshige, J.; Krishnakumar, K. Artificial immune system approach for air combat maneuvering. In Proceedings of the SPIE 6560, Intelligent Computing: Theory and Applications V, Orlando, FL, USA, 9–13 April 2007; Volume 6560, p. 656009. [Google Scholar] [CrossRef]
- Başpinar, B.; Koyuncu, E. Assessment of Aerial Combat Game via Optimization-Based Receding Horizon Control. IEEE Access 2020, 8, 35853–35863. [Google Scholar] [CrossRef]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- McGrew, J.S.; How, J.; Williams, B.C.; Roy, N. Air-Combat Strategy Using Approximate Dynamic Programming. J. Guid. Control Dyn. 2010, 33, 1641–1654. [Google Scholar] [CrossRef]
- Liu, P.; Ma, Y. A Deep Reinforcement Learning Based Intelligent Decision Method for UCAV Air Combat. In Modeling, Design and Simulation of Systems, Proceedings of the 17th Asia Simulation Conference, AsiaSim 2017, Malacca, Malaysia, 27–29 August 2017; Communications in Computer and Information Science; Springer: Singapore, 2017; pp. 274–286. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, G.; Yang, C.; Wu, J. Research on Air Confrontation Maneuver Decision-Making Method Based on Reinforcement Learning. Electronics 2018, 7, 279. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, J.; Shi, G.; Hu, J.; Wu, Y. Maneuver Decision of UAV in Short-Range Air Combat Based on Deep Reinforcement Learning. IEEE Access 2019, 8, 363–378. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.; Yang, Z.; Zhao, Y.; Zhang, K. UAV Autonomous Aerial Combat Maneuver Strategy Generation with Observation Error Based on State-Adversarial Deep Deterministic Policy Gradient and Inverse Reinforcement Learning. Electronics 2020, 9, 1121. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Hu, J.; Wang, L.; Hu, T.; Guo, C.; Wang, Y. Autonomous Maneuver Decision Making of Dual-UAV Cooperative Air Combat Based on Deep Reinforcement Learning. Electronics 2022, 11, 467. [Google Scholar] [CrossRef]
- Austin, F.; Carbone, G.; Falco, M.; Hinz, H.; Lewis, M. Automated maneuvering decisions for air-to-air combat. In Proceedings of the Guidance, Navigation and Control Conference, Monterey, CA, USA, 17–19 August 1987. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Paczkowski, M. Low-Friction Composite Creping Blades Improve Tissue Properties. In Proceedings of the Pulp and Paper, Stockholm, Sweden, 9 October 1996; Volume 70. [Google Scholar]
- Williams, R.J. Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, L.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning, ICML 2016, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1928–1937. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016–Conference Track Proceedings, San Juan, Puerto Rico, 2–4 May 2016; pp. 1–14. [Google Scholar]
- Riedmiller, M.; Hafner, R.; Lampe, T.; Neunert, M.; Degrave, J.; Van De Wiele, T.; Mnih, V.; Heess, N.; Springenberg, J.T. Learning by Playing Solving Sparse Reward Tasks from Scratch. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 4344–4353. [Google Scholar]
- Mukhamediev, R.I.; Symagulov, A.; Kuchin, Y.; Zaitseva, E.; Bekbotayeva, A.; Yakunin, K.; Assanov, I.; Levashenko, V.; Popova, Y.; Akzhalova, A.; et al. Review of Some Applications of Unmanned Aerial Vehicles Technology in the Resource-Rich Country. Appl. Sci. 2021, 11, 10171. [Google Scholar] [CrossRef]
- Agarwal, A.; Kumar, S.; Singh, D. Development of Neural Network Based Adaptive Change Detection Technique for Land Terrain Monitoring with Satellite and Drone Images. Def. Sci. J. 2019, 69, 474–480. [Google Scholar] [CrossRef]
- Smith, M.L.; Smith, L.N.; Hansen, M.F. The quiet revolution in machine vision–A state-of-the-art survey paper, including historical review, perspectives, and future directions. Comput. Ind. 2021, 130, 103472. [Google Scholar] [CrossRef]









| Action | |||
|---|---|---|---|
| 5 | 1 | 0 | |
| 0 | 1 | 0 | |
| −5 | 1 | 0 | |
| 5 | 5 | 0 | |
| 0 | 5 | 0 | |
| −5 | 5 | 0 | |
| 5 | 5 | ||
| 0 | 5 | ||
| −5 | 5 | ||
| 0 | 5 | arccos(1/5) | |
| −5 | 5 | arccos(1/5) | |
| 0 | 5 | −arccos(1/5) | |
| −5 | 5 | −arccos(1/5) |
| State | Value | State | Value |
|---|---|---|---|
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 3 × 103 | |||
| 500 | 20 | ||
| 2 × 103 | 500 | ||
| 100 | 2 × 103 | ||
| 2 × 103 | 8 × 103 |
| State | Value | State | Value |
|---|---|---|---|
| [−10, 10] km | [100, 600] m/s | ||
| [−10, 10] km | [−/2, /2] rad | ||
| [−12, −8] km | [−,] rad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Dong, W.; Cai, M.; Jia, S.; Liu, R. UCAV Air Combat Maneuver Decisions Based on a Proximal Policy Optimization Algorithm with Situation Reward Shaping. Electronics 2022, 11, 2602. https://doi.org/10.3390/electronics11162602
Yang K, Dong W, Cai M, Jia S, Liu R. UCAV Air Combat Maneuver Decisions Based on a Proximal Policy Optimization Algorithm with Situation Reward Shaping. Electronics. 2022; 11(16):2602. https://doi.org/10.3390/electronics11162602
Chicago/Turabian StyleYang, Kaibiao, Wenhan Dong, Ming Cai, Shengde Jia, and Ri Liu. 2022. "UCAV Air Combat Maneuver Decisions Based on a Proximal Policy Optimization Algorithm with Situation Reward Shaping" Electronics 11, no. 16: 2602. https://doi.org/10.3390/electronics11162602
APA StyleYang, K., Dong, W., Cai, M., Jia, S., & Liu, R. (2022). UCAV Air Combat Maneuver Decisions Based on a Proximal Policy Optimization Algorithm with Situation Reward Shaping. Electronics, 11(16), 2602. https://doi.org/10.3390/electronics11162602






