Adaptive Fuzzy Control for Flexible Robotic Manipulator with a Fixed Sampled Period
Abstract
:1. Introduction
- (1)
- This paper is the first work concerning adaptive fuzzy backstepping sampled-data control for a flexible robotic manipulator system. In the control process, the designed controller only needs the sampled information of states rather the continuous case.
- (2)
- By using the property of the fuzzy basic function, the algebraic loop issue caused by the non-strict feedback system is avoided. Furthermore, the designed adaptive laws also consider the sampled data, which is a great difference from previous works.
2. Preliminaries and Problem Formulation
3. Adaptive Fuzzy Controller Design and Stability Analysis
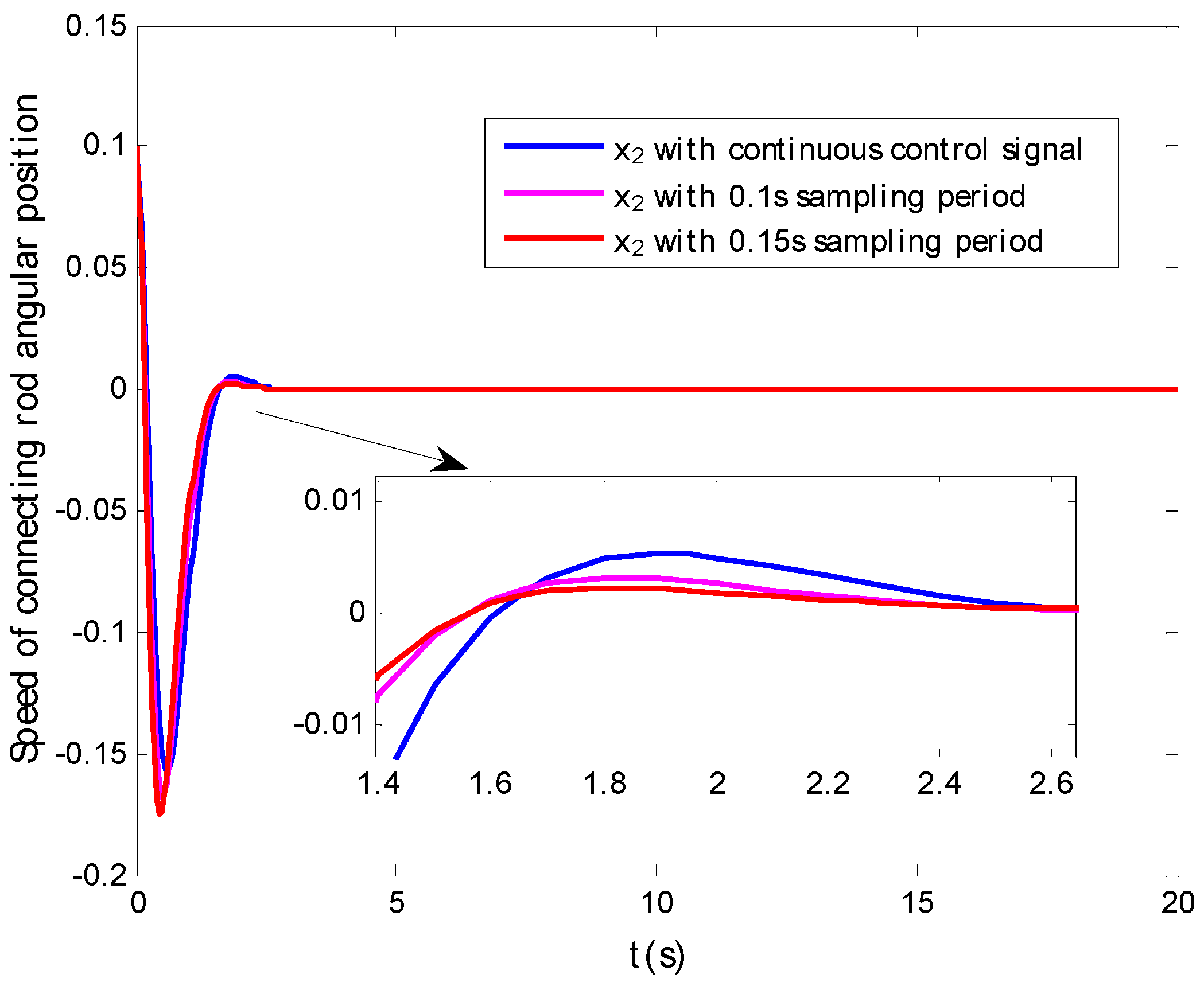
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bazzi, B.; Chalhoub, N. Fuzzy sliding mode controller for a flexible single-link robotic manipulator. J. Vib. Control 2005, 11, 295–314. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, G. Dual terminal sliding mode control design for rigid robotic manipulator. J. Frankl. Inst. 2018, 355, 9127–9149. [Google Scholar] [CrossRef]
- Alam, W.; Ahmad, S.; Mehmood, A.; Iqbal, J. Robust sliding mode control for flexible joint robotic manipulator via disturbance observer. Interdiscip. Descr. Complex Syst. INDECS 2019, 17, 85–97. [Google Scholar] [CrossRef]
- Oliveira, J.; Oliveira, P.; Boaventura, J.; Pinho, T. Chaos-based grey wolf optimizer for higher order sliding mode position control of a robotic manipulator. Nonlinear Dyn. 2017, 90, 1353–1362. [Google Scholar] [CrossRef]
- Ahmed, S.; Ahmed, A.; Mansoor, I.; Junejo, F.; Saeed, A. Output feedback adaptive fractional-order super-twisting sliding mode control of robotic manipulator. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 335–347. [Google Scholar] [CrossRef]
- Bagheri, M.; Naseradinmousavi, P.; Krstić, M. Feedback linearization based predictor for time delay control of a high-DOF robot manipulator. Automatica 2019, 108, 108485–108492. [Google Scholar] [CrossRef]
- Korayem, M.; Nekoo, S.; Kazemi, S. Finite-time feedback linearization (FTFL) controller considering optimal gains on mobile mechanical manipulators. J. Intell. Robot. Syst. 2019, 94, 727–744. [Google Scholar] [CrossRef]
- Belherazem, A.; Chenafa, M. Passivity based adaptive control of a single-link flexible manipulator. Autom. Control Comput. Sci. 2021, 55, 1–14. [Google Scholar] [CrossRef]
- Feliu, D.; Feliu, V. Passivity-based control of a single-link flexible manipulator using fractional controllers. Nonlinear Dyn. 2019, 95, 2415–2441. [Google Scholar] [CrossRef]
- Keighobadi, J.; Fateh, M.; Xu, B. Adaptive fuzzy voltage-based backstepping tracking control for uncertain robotic manipulators subject to partial state constraints and input delay. Nonlinear Dyn. 2020, 100, 2609–2634. [Google Scholar] [CrossRef]
- Sun, W.; Su, S.; Xia, J.; Nguyen, V. Adaptive fuzzy tracking control of flexible-joint robots with full-state constraints. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2201–2209. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, T.; Sun, N.; Fang, Y. An adaptive fuzzy control method of single-link flexible manipulators with input dead-zones. Int. J. Fuzzy Syst. 2020, 22, 2521–2533. [Google Scholar] [CrossRef]
- Ling, S.; Wang, H.; Liu, P. Adaptive fuzzy dynamic surface control of flexible-joint robot systems with input saturation. IEEE/CAA J. Autom. Sin. 2019, 6, 97–107. [Google Scholar] [CrossRef]
- Fateh, S.; Fateh, M. Adaptive fuzzy control of robot manipulators with asymptotic tracking performance. J. Control Autom. Electr. Syst. 2020, 31, 52–61. [Google Scholar] [CrossRef]
- Wang, Z.; Zou, L.; Su, X.; Luo, G.; Li, R.; Huang, Y. Hybrid force/position control in workspace of robotic manipulator in uncertain environments based on adaptive fuzzy control. Robot. Auton. Syst. 2021, 145, 103870–103881. [Google Scholar] [CrossRef]
- Diao, S.; Sun, W.; Yuan, W. Adaptive fuzzy practical tracking control for flexible-joint robots via command filter design. Meas. Control. 2020, 53, 814–823. [Google Scholar] [CrossRef]
- Datouo, R.; Ahanda, J.; Melingui, A.; Biya-Motto, F.; Zobo, B. Adaptive fuzzy finite-time command-filtered backstepping control of flexible-joint robots. Robotica 2021, 39, 1081–1100. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S.; Li, T. Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via backstepping. Nonlinear Anal. Real World Appl. 2013, 14, 483–494. [Google Scholar] [CrossRef]
- Chang, W.; Li, Y.; Tong, S. Adaptive fuzzy backstepping tracking control for flexible robotic manipulator. IEEE/CAA J. Autom. Sin. 2021, 8, 1923–1930. [Google Scholar] [CrossRef] [Green Version]
- Khorashadizadeh, S.; Sadeghijaleh, M. Adaptive fuzzy tracking control of robot manipulators actuated by permanent magnet synchronous motors. Comput. Electr. Eng. 2018, 72, 100–111. [Google Scholar] [CrossRef]
- Li, S.; Ahn, C.; Guo, J.; Xiang, Z. Neural network-based sampled-data control for switched uncertain nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 5437–5445. [Google Scholar] [CrossRef]
- Li, S.; Ahn, C.; Xiang, Z. Sampled-data adaptive output feedback fuzzy stabilization for switched nonlinear systems with asynchronous switching. IEEE Trans. Fuzzy Syst. 2018, 27, 200–205. [Google Scholar] [CrossRef]
- Davó, M.; Bresch-Pietri, D.; Prieur, C.; Meglio, F. Stability analysis of a 2 × 2 linear hyperbolic system with a sampled-data controller via backstepping method and looped-functionals. IEEE Trans. Autom. Control. 2018, 64, 1718–1725. [Google Scholar] [CrossRef]
- He, W.; Ahn, C.; Xiang, Z. Global fault-tolerant sampled-data control for large-scale switched time-delay nonlinear systems. IEEE Syst. J. 2019, 14, 1549–1557. [Google Scholar] [CrossRef]
- Mao, J.; Guo, J.; Xiang, Z. Sampled-data control of a class of uncertain switched nonlinear systems in nonstrict-feedback form. Int. J. Robust Nonlinear Control 2018, 28, 918–939. [Google Scholar] [CrossRef]
- Li, Y.; Yu, K. Adaptive fuzzy decentralized sampled-data control for large-scale nonlinear systems. IEEE Trans. Fuzzy Syst. 2021, 30, 1809–1822. [Google Scholar] [CrossRef]
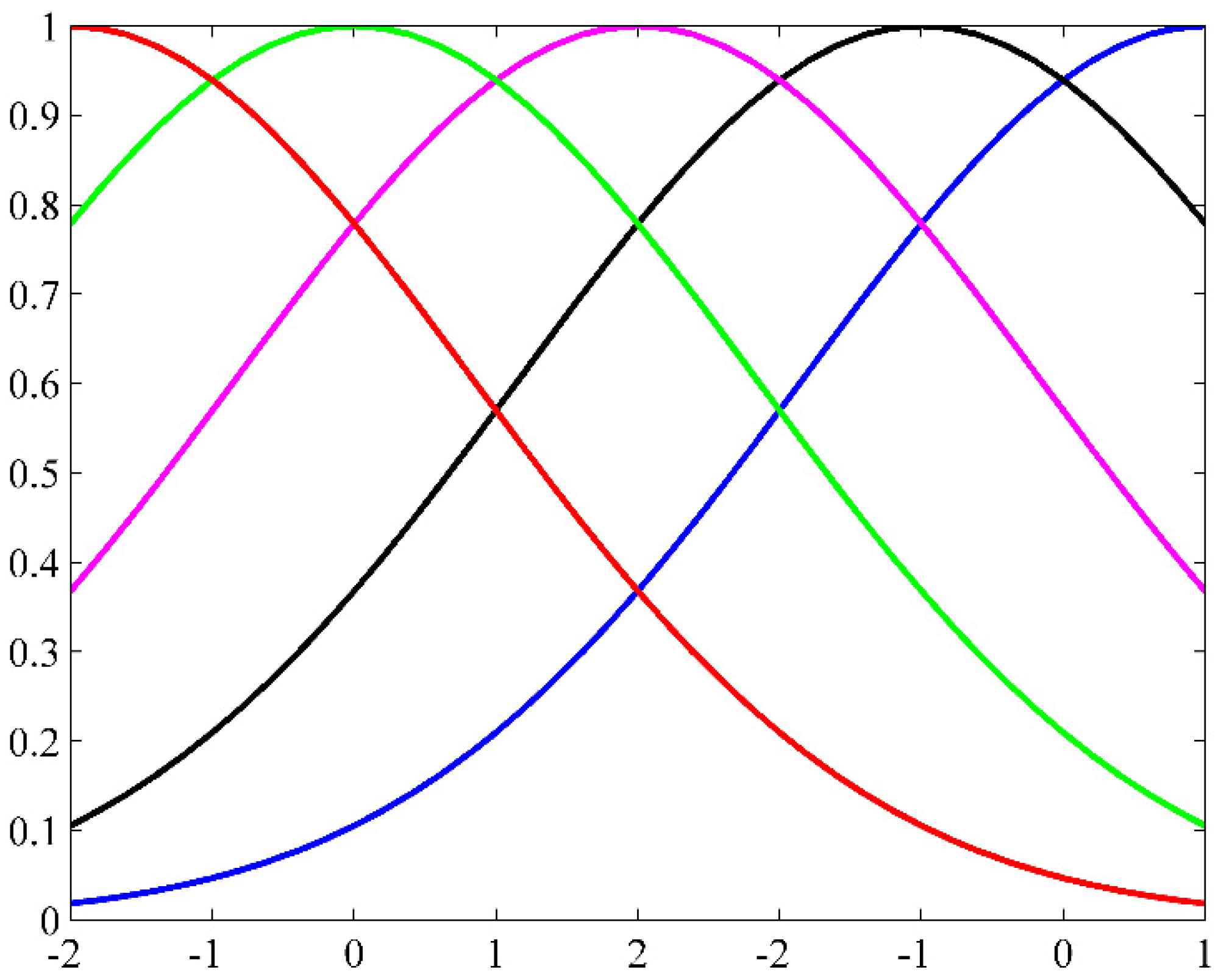






| Symbol | Value | Unit | Symbol | Value | Unit |
|---|---|---|---|---|---|
| 3 | Nms/rad | 3 | Nms/rad | ||
| 30 | kg·m2 | 30 | kgm2 | ||
| 10 | 3 | Nm/A | |||
| 6 | H | 0.976 | Nm/A | ||
| 0.4 | m | 0.102 | kg | ||
| 9.8 | N/kg | 20 | \ | ||
| 1 | \ | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Dai, X. Adaptive Fuzzy Control for Flexible Robotic Manipulator with a Fixed Sampled Period. Electronics 2022, 11, 2270. https://doi.org/10.3390/electronics11142270
Zhang J, Dai X. Adaptive Fuzzy Control for Flexible Robotic Manipulator with a Fixed Sampled Period. Electronics. 2022; 11(14):2270. https://doi.org/10.3390/electronics11142270
Chicago/Turabian StyleZhang, Jiaming, and Xisheng Dai. 2022. "Adaptive Fuzzy Control for Flexible Robotic Manipulator with a Fixed Sampled Period" Electronics 11, no. 14: 2270. https://doi.org/10.3390/electronics11142270
APA StyleZhang, J., & Dai, X. (2022). Adaptive Fuzzy Control for Flexible Robotic Manipulator with a Fixed Sampled Period. Electronics, 11(14), 2270. https://doi.org/10.3390/electronics11142270





