Abstract
Over the past few years, the computation capability of field-programmable gate arrays (FPGAs) has increased tremendously. This has led to the increase in the complexity of the designs implemented on FPGAs and to the time taken by the FPGA back-end flow. The FPGA back-end flow comprises of many steps, and routing is one of the most critical steps among them. Routing normally constitutes more than 50% of the total time taken by the back-end flow and an optimization at this step can lead to overall optimization of the back-end flow. In this work, we propose enhancements to the routing step by incorporating a reinforcement learning (RL)-based framework. In the proposed RL-based framework, we use the -greedy approach and customized reward functions to speed up the routing step while maintaining similar or better quality of results (QoR) as compared to the conventional negotiation-based congestion-driven routing solution. For experimentation, we use two sets of widely deployed, large heterogeneous benchmarks. Our results show that, for the RL-based framework, the -greedy greedy approach combined with a modified reward function gives better results as compared to purely greedy or exploratory approaches. Moreover, the incorporation of the proposed reward function in the RL-based framework and its comparison with a conventional routing algorithm shows that the proposed enhancement requires less routing time while giving similar or better QoR. On average, a speedup of 35% is recorded for the proposed routing enhancement as compared to negotiation-based congestion-driven routing solutions. Finally, the speedup of the routing step leads to an overall reduction in the execution time of the back-end flow of 25%.
1. Introduction
With the advancement of processing technology and ever-improving design techniques, field-programmable gate arrays (FPGAs) have grown immensely over the past few years, both in terms of their logical complexity and computational capability. Xilinx, in its latest release, has announced an FPGA with close to 10 million logic cells, counting over 35 billion transistors [1]. Similarly, Intel has released its latest Stratix 10 FPGA, with logic cells exceeding the 10 million mark and transistors beyond 40 billion count [2]. Previously, FPGAs were used as glue logic only, but now they are used to implement some of the most complex circuits [3]. Today, FPGAs have their applications in many important fields, such as system on chip (SoC) prototyping, call centers, and multi-media and high-performance computing applications. Over the last few years, the market of FPGA applications has grown immensely, and it is poised to become only bigger in future [4]. The generalized and reconfigurable nature of FPGAs makes them an ideal candidate for the implementation of almost any circuit. This is further aided by the ability to perform in-circuit debugging and verification [5]. However, the increasing complexity of target applications and the huge computation resources of FPGAs have greatly increased the back-end flow time of FPGAs [6]. For good-quality results, the back-end flow of FPGAs can require a high amount of human resources and effort, even leading to less-than-satisfactory or inconclusive results [7]. On the other hand, if the run time is shortened, it compromises the quality of results (QoR) of the final design. Therefore, designing a back-end flow for FPGAs that can give good QoR in a short time is a key research area, and a lot of work is being conducted in this domain.
The back-end flow in modern day FPGAs involves many complex steps. Among them, the most important include the logic optimization of design through synthesis, the placement of logic resources on the target architecture, and the routing of the mapped resources to ensure connectivity. The steps of the back-end flow are usually performed manually. Most of these steps are based on heuristic algorithms, and they require manual tuning of different parameters with a lot of iterations. To achieve the desired results, the designers rely on their know-how and expertise of the target architecture. A big part is also played by their intuition and experience with tuning different parameters, accumulated over the years. For example, for placement in FPGAs, traditionally, three techniques have been used, namely, partitioning, analytic placement, and simulated annealing-based placement. The partitioning-based placement technique [8] recursively divides the design and produces the results in minimal time. On the other hand, analytic placement techniques [9,10,11,12] achieve the placement goals through continuous and differential expressions. Analytic placers usually give good results in a short time, but they are often coupled with simulated annealing-based detailed placers for further refinement and improvement of the results [13]. Apart from being used for additional refinement, simulated annealing-based placers are also used stand-alone for placement in FPGA back-end flows [14]. Now, the results produced by a placement technique are largely dependent upon the type of the circuit under consideration. For example, the partitioning-based placement technique gives better results for hierarchical designs. However, this technique is less suitable for the designs having non-hierarchical interconnects, where the simulated annealing-based placement technique is reported to give better results [6]. Moreover, for a particular technique, parameters such as the number of iterations, the cost function, and the value of the annealing temperature play a huge role in the quality of the final design. The values of the parameters of the placement step are really important, as they can have a huge impact on the quality of the final design. As per [15], the values of the back-end flow parameters can change the final area and timing results significantly, even without changing the circuit description and the target architecture.
Routing is another critical and time-consuming step in FPGA back-end flow [16]. Routing can take up to 50% of the time of the entire back-end flow, and as the designs are becoming larger and more complex, this share is projected to rise even further [17]. For FPGAs, routing is severely constrained in the sense that the block numbers, types, locations, and the surrounding routing resources are pre-fabricated. Furthermore, the design is already mapped and placed on the target FPGA architecture. So, the designers can not modify the target architecture by inserting buffers and resizing the gates to make the circuit more efficient. In this step, using the available routing resources, a detailed routing is performed for the nets connecting different blocks. The simplest routing problem that involves one net and only two pins is considered to be an NP-complete problem. Usually, the routing of even a moderate design involves thousands of nets, where each net may consist of many interconnecting pins, and the net count can increase up to millions for more complex designs. So, this makes the routing problem extremely critical. For FPGA back-end flow, different routing approaches have been used in the past, namely, obstacle avoidance, congestion avoidance, and the negotiation-based routing approach. In the obstacle avoidance routing approach [18], integer linear programming (ILP) is used, which gives good and quick results for simple routing problems. Compared to the conventional approach, this routing approach gives 26.4% better performance results. However, for moderate to complex routing problems, this approach gives very poor or no results at all. In the congestion avoidance routing approach [19], for a conflict-free solution, already-used resources are made unavailable; hence, this approach gives a quick solution in a short time. This approach renders quick results for small benchmarks. However, this approach, does not involve any negotiation-based approach, and it does not have the ability to address/solve the congestion problems of a routing network. This approach has the tendency to fall in the local minima and report an infeasible solution even if a solution to a problem exists. The negotiation-based, congestion-driven routing approach is another technique that is widely employed in the academy and in industry. This is a time-consuming approach, although it gives good solutions to routing problems. This approach uses the Pathfinder [20] algorithm. It strives to find the solution to a routing problem in an iterative manner. The design is routed successfully over multiple iterations and the congestion in the resources is resolved through a negotiation-based approach. A detailed discussion of this approach is presented in Section 3.3 of this paper.
With the increasing complexity of designs, the challenges faced by the back-end flow of FPGAs are only going to become worse. The challenge for the placement and routing steps is even higher, as both rely on heuristic techniques, and optimal solutions to these problems do not exist. The time required by heuristic algorithms to find a feasible solution increases exponentially with the complexity of the design under consideration, sometimes even rendering infeasible solutions as the complexity of the design grows beyond the capability of the algorithm. The time taken and the quality of the solution produced by placement and routing techniques is also affected by various input parameters such as the cost function, the number of iterations, the annealing temperature calculation, etc. The quality of solution and speedup in these algorithms can be achieved through either auto parameter tuning of the flow or efficient implementation of relevant cost functions. In this regard, machine learning (ML)-based frameworks can be used that can automatically tune the flow parameters and speed up the whole process. Recently, researchers have used ML-based techniques to automate the whole design process, which gives good results in a short time. Some of the existing work focuses on the entire back-end flow and tunes the parameters through extensive training. There exist other examples also, where researchers focus on the optimization and speedup of individual back-end flow steps, such as placement [4,21]. However, to the best of our knowledge, there is little or no work that targets the speedup and optimization of the routing step of the FPGA back-end flow through ML-based techniques.
This work employs reinforcement learning (RL) to speed up the routing step of the FPGA back-end flow. We modify the routing algorithm and adapt it to implement the RL-based framework efficiently. For experimentation, we use two sets of large benchmarks. The results obtained through the proposed approach are compared with the results of the conventional, negotiation-based, congestion-driven routing approach. The comparison results show that the proposed technique gives, on average, 35% better speedup routing while giving similar or better QoR. The results further suggest that the gain of the proposed technique increases with the increase in the complexity and the size of the target design. The contributions of this paper are summarized as follows:
- Enhancement proposed to speed up the detailed routing of FPGA back-end flow through an RL-based framework;
- Extensive experimentation, exploration, and analysis of the proposed enhancement by using two sets of open-source large heterogeneous benchmarks;
- Evaluation of the proposed enhancement through comparison with the conventional negotiation-based congestion-driven routing approach.
In the remainder of the paper, Section 2 gives a comprehensive overview of the state of the art related to this work. Section 3 then highlights the important steps of the FPGA back-end flow. Section 4 presents the details of the enhancements proposed in the routing step. Section 5 provides detailed discussion on the experimentation and also presents a comparison of the existing and proposed techniques. Section 6 presents comprehensive concluding remarks and also sheds light on the proposed future work.
2. Related Work
As discussed in Section 1, for optimal results, the parameter tuning of FPGA back-end flow requires a lot of time, effort, and experience. For this purpose, machine learning algorithms can help the designers in making decisions about the back-end flow parameters and can save a lot of human time and effort without compromising the final results. In this regard, a lot of work has been conducted recently. For example, the authors in [22] describe various data mining techniques that can be used in electronic design automation (EDA). Moreover, this paper also discusses different statistical learning techniques and their usage in various learning algorithms. Next, the authors in [23] present an ML-based framework to tune the FPGA design parameters. This paper uses a sample space reduction approach to find the optimal set of parameters that can render the best possible FPGA design. Then, the authors in [24] present ML- and cloud-based techniques to help accelerate the timing closure for FPGA designs, and the authors in [25] present a different ML-based framework that generates routing-driven power distribution networks (PDNs) for FPGAs. It is important to mention here that the aforementioned state-of-the-art work mostly uses ML or artificial intelligence to optimize the auto tuning of the parameters for FPGA back-end flow. These frameworks obtain the desired results through extensive training of underlying ML algorithms, such as Support Vector Machine (SVM) [26], Bayesian Learning (BL) and Knowledge-Based Neural Networks (KBNN) [27].
Apart from the auto tuning of the parameters that are aimed at the entire FPGA back-end flow, there is research work that uses ML algorithms for the optimization of individual steps of FPGA back-end flow. For example, in the FPGA back-end flow, logic synthesis is the first critical step (further details are given in Section 3). This is a quite complex step, and optimizations performed at this step can have a lasting impact on the quality of the final design. The authors in [28] make use of a deep neural network (DNN) to automatically choose between an and-inverter graph (AIG) and a majority-inverter graph (MIG) to logically optimize the circuit under consideration. ABC [29] is an open-source logic synthesis tool that comes with many logic optimization techniques, and it is largely used by the research community. The authors in [30] use convolutional neural networks (CNN) to autonomously use this tool and produce high-quality logically synthesized designs without any prior knowledge of the design and without human intervention.
As discussed before, placement is another critical step of the FPGA back-end flow. Regarding the parameter tuning and automatic optimization, a significant amount of work has been performed on placement. Historically, the placement step of FPGA CAD flow has been critical, as it is very time-consuming. The speedup of placement in FPGA flow has traditionally been achieved either through parallel move generation [31,32] or a directed search of the solution space [33]. As far as the solutions based on ML are concerned, the authors in [4,21] present a framework that considers four different placement objectives. This framework relies on extensive training and chooses the best placement solution among seven state-of-the-art placement tools. The authors then extend their work and use a convolutional neural network (CNN) to improve upon the routing predictability of the design under consideration [34]. However, they do not use machine learning or artificial intelligence techniques to perform detailed routing. Recently, RL techniques have seen a lot of popularity because of their superior performance in electronic design automation [35,36,37]. In this regard, the authors in [38] present an RL-based framework to optimize the efficiency of the placement step. In this study, the authors report that an RL-based framework produces similar-quality results while being two times faster than conventional placement algorithms.
For routing in FPGAs, the authors in [39] present an ML-based high-level synthesis framework that predicts the routing congestion in FPGAs. However, this work does not address the detailed routing of the design under consideration. Then, the authors in [40] present another ML-based framework to manage congestion and predict the routability of a design under consideration in the FPGA back-end flow. The work in [41] presents regression-based learning methods that accurately present the congestion in routing after the placement of the design on FPGAs.
It is clear from the work cited in this section that almost all the above-cited work addresses either the parameter tuning for the entire FPGA back-end flow by using ML-based techniques, or optimizes the individual back-end flow steps, such as logic synthesis and placement. Although there is some work on the optimization of the routing step, such work mainly uses machine learning for prediction and congestion estimation. To the best of our knowledge, the speedup of detailed routing using reinforcement learning has not been investigated in detail so far, and this is the main contribution of our work. A preliminary version of our work [42] uses an RL-based framework to speed up the routing process. In the current work, we refine and extend our previous work. The main enhancements of the current work are summarized as follows:
- To make the FPGA CAD flow more efficient, we apply an RL technique to a negotiation-based routing approach;
- We further refine the reward function and explore its effect on the routing result through an enhanced exploration technique;
- We use two sets of comprehensive benchmarks for experimentation, perform extensive analysis of the results, comparing them with existing routing techniques.
To the best of our knowledge, there is no prior work that uses an RL-based framework on the detailed routing and that considers its effect on the speedup of an entire FPGA back-end flow.
In the next section, a comprehensive overview of the FPGA back-end flow is presented; then, in the subsequent section, we discuss our proposed enhancements regarding the routing step of the FPGA back-end flow.
3. FPGA Back-End Flow
3.1. Synthesis, Mapping, and Packing
A typical FPGA back-end flow is shown in Figure 1. It can be seen from the figure that FPGA CAD flow comprises many steps. The flow starts with the hardware description of the circuit under consideration, and first of all, its logic synthesis is performed. Logic synthesis tools logically optimize the design and make predictions about the final resource requirements and timing information of the design. For this step, the time consumed is not an issue, but the predictions made about the design at this level are inaccurate in nature. This is a complex process that cannot be solved optimally. Moreover, with ever-decreasing transistor sizes and increasing design complexity, the accuracy of existing synthesis algorithms is decreasing [37]. However, various ML-based techniques exist that rectify the errors and make faster predictions that are closer to the actual hardware implementation [43,44]. After the synthesis of the design, it is mapped and packed as per the resources of the target FPGA architecture, and finally, its placement and routing is performed.
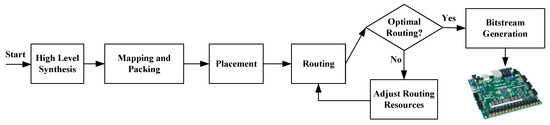
Figure 1.
An overview of the FPGA back-end Flow.
3.2. Placement
FPGAs are pre-fabricated reconfigurable devices that have a fixed number of resources. These resources can be reconfigurable logic that provides the computation power to the FPGA, or they can be reconfigurable routing resources that provide the interconnects among the logic resources of the FPGA architecture. Logic resources in FPGAs comprise of a combination of generic configurable logic blocks and some fixed purpose blocks. The fixed purpose blocks can be adders, multipliers, memory blocks, graphic processing units and, in some cases, even general-purpose processors. The grid of a typical modern heterogeneous FPGA is shown in Figure 2. The simulated annealing [45]-based approach has long been used to solve the placement problem for FPGAs. The simulated annealing approach uses a heuristic that mimics the gradual cooling of alloys. It starts with a random initial state, and then multiple iterations are made with an objective to minimize the overall wire length of the design under consideration. At the beginning, to avoid the local minima, the mode of the placement algorithm is exploratory in nature, becoming greedy over time and finishing when further improvement to the wire length is not possible. The simulated annealing approach gives good placement results but requires a lot of moves and time before it reaches a feasible solution. The number of moves and amount of time required by this approach are directly linked with the size and the complexity of the design under consideration. For modern designs, the algorithm needs a lot of time and iterations and becomes prohibitively expensive in scenarios where good QoR is required in a short time. Once the placement of the design under consideration is finished, the routing of the design is performed, which is explained next.
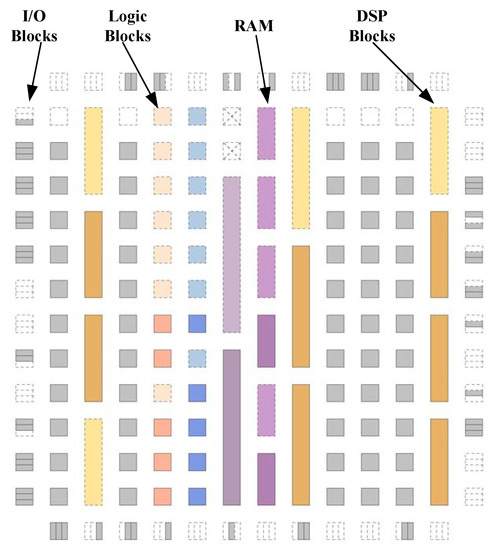
Figure 2.
Sample diagram of logic and routing architectures of a modern heterogeneous FPGA.
3.3. Routing
After placement, the routing is performed between different source and destination blocks using the existing routing resources of the FPGAs. The objective of the routing algorithm is to find conflict-free paths from the source to destination for all the blocks while using the least-possible routing resources. Pathfinder [20] is an extensively used routing algorithm that uses a negotiation-based, congestion-driven routing approach to achieve the routing objectives. In order to use Pathfinder, the routing resources of the FPGA are first represented as a directed graph. The graph has a set of vertices V and edges E. The vertices in the directed graph represent I/Os of various blocks in the FPGA, while vertices represent the potential connections between those I/Os. A sample representation of the FPGA resources as the directed graph is shown in Figure 3.
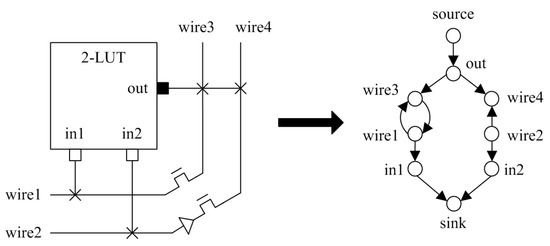
Figure 3.
FPGA logic and routing resources modeled as a directed graph.
Pathfinder uses the directed graph to find a conflict-free solution. As with simulated annealing, this is also an iterative procedure. Initially, more than one net might be using the same path, resulting in a conflict. These conflicts are later resolved through successively increasing the cost of the congested nodes. This is a very time-consuming process, as the modern designs have hundreds of thousands of nodes in their graphs and calculating and updating the congestion of each node in every iteration takes a lot of time. The routing process continues over multiple iterations until a conflict-free solution is found for the design. After finding the conflict-free solution, the binary search algorithm checks for the optimal usage of the routing resources. If further optimization is possible, the routing process starts again. This iterative procedure continues until all the routing resources are completely optimized, and finally, the bitstream of the design is generated. The bitstream is ultimately loaded onto the target FPGA for in-circuit debugging and cycle-accurate execution of the circuit, culminating the FPGA back-end flow process.
4. Proposed Enhancements
Routing constitutes a major part of FPGA back-end flow and it consumes a lot of time. In this section, a detailed discussion of reinforcement learning and how it is used to speed up the routing step of FPGA flow is presented.
4.1. Reinforcement Learning
Reinforcement learning is a machine learning-based technique that has seen huge popularity in different electronic design automation problems recently [37]. Normally, an RL-based framework finds the solution to a problem at hand by frequently taking actions and then learning from the consequences of its previously taken actions. A typical scenario based on reinforcement learning is shown in Figure 4. As can be seen from the figure, a typical RL-based framework comprises an agent that takes an action at a given time t. As a result of the action, the environment generates a reward and moves from a given state to the next state . This way, multiple actions are taken over time and a log of those actions and resulting rewards is built. Each time a new action is taken, the rewards generated after previously taken actions are also considered. The action values of the actions taken are calculated using the following function: . In this function, S corresponds to previous states and A is the action values of those states.
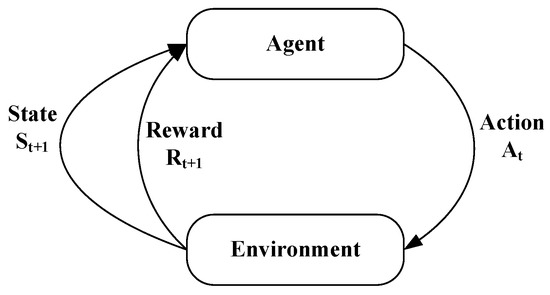
Figure 4.
A sample reinforcement learning problem.
For any RL technique, the two main considerations are action value estimation and action calculation. The action values are typically calculated using Equation (1). In this Equation, is the error between the actual and estimated award, whereas corresponds to the size of the step taken to correct that error. The value of is calculated using Equation (2), where corresponds to the memory length and M corresponds to the number of moves in each iteration. Through empirical experimentation, it is found that the small value of gives good results in a short time. In this work, we keep the value of equal to 0.1, meaning the highest weightage is given to the most recent 10% of moves during the routing process.
In RL, after a number of actions at each action point, the agent has a database of action values. To make the next move, the agent has to choose one action value among the available values. In order to save time and effort, the agent has to usually find a trade-off between exploration and optimization. In RL, this is referred as a scenario of exploration vs. exploitation [46]. A purely exploratory approach may lead to good results, but it may add a lot of delay to the final result. There is also a possibility of adding too much delay without even significantly improving the results. On the other hand, a purely exploitative approach may give results in a quick time, but this approach has the tendency of falling in local minima and producing poor results or, in some cases, even rendering infeasible results because of an insufficient exploration of the solution space. In this work, we use the -greedy approach to find the best trade-off between exploration and exploitation. In the -greedy approach, the values of and 1 correspond to purely greedy and purely exploratory approaches, respectively. To find the value of that gives the best results, we perform extensive experimentation. Further discussion on the values used in this work for the RL-based framework is given in Section 5.
4.2. Routing Enhancement
As mentioned before, the negotiation-based, congestion-driven routing algorithm is usually used in FPGAs to resolve the routing problem. The pseudo-code of the routing algorithm is shown in Algorithm 1. It can be seen that it is an iterative procedure where the routing algorithm performs routing over multiple iterations. In each iteration, all the nets of the design are routed one by one. For each net, the shortest path from the source to all its destinations is found. While routing each net, the routing algorithm updates the congestion costs of the used nodes regularly by employing the congestion cost function of Equation (3). In this equation, , and represent the base cost, historical congestion cost, and the current congestion cost of the node, respectively. Through this function, the history of the congested nodes is maintained and kept high. This way, the routing algorithm is made to avoid the congested nodes in future iterations to find alternative, low-cost, and conflict-free solutions. The iterative process continues until all the conflicts for every net of the design are resolved.
As discussed before, three different costs are maintained for each node. These costs are updated during the routing of individual nets, as well as at the end of each iteration. This is a process that is performed multiple times in every iteration and over multiple iterations; hence, it consumes a lot of time. In this work, we use an RL-based framework to find a conflict-free solution to the routing problem.
As discussed in Section 4.1, the state action value is determined in this work using the tabular method. We treat the routing problem as single-state K-arm bandit problem. In this problem, an agent chooses an action . The action is then evaluated as a result of which move is made and the change in the cost is calculated. The algorithm then decides whether to accept or reject the move. Finally, the reward value is calculated to update the Q value based on the change in the cost value, thereby influencing the future actions. In order to learn from the actions taken previously, we need to define a reward function that must satisfy our desired objectives. Our objective is to have a high-quality routing solution in the shortest possible time. To meet this objective, we initially define a reward function, which is given in Equation (4):
| Algorithm 1: Pseudo-code of the FPGA routing algorithm [20]. |
 |
The function in Equation (4) is basic reward function that calculates the change in cost resulting from a move using the change in the conflicts. Although this function satisfies our objective, it has the tendency to fall in local minima as it penalizes the moves that result in an increase in conflicts. Hence, we modify the reward function to Equation (5). This reward function favors the moves that reduce the conflict count; however, it does not penalize the moves that cause an increase in the conflicts. Hence, it favors a more exploratory approach and avoids the local minima. By using this approach, instead of maintaining three different costs for each node, a single record of node congestion is maintained. By building the table of node actions, the frequent and time-consuming step of the cost update is no longer needed. This approach gives a conflict-free solution for the routing problem in a much shorter time and with a smaller number of iterations as well. In this work, we explore the effect of both reward functions on the routing of the design under consideration. Further discussion of this exploration is presented in Section 5 of the paper.
5. Experimentation, Results, and Analysis
5.1. Benchmarks
For experimental purposes, in this work, we have used two sets of heterogeneous benchmarks. The details of the benchmarks are shown in Table 1 and Table 2, respectively. These tables specify the names of the benchmarks, the number of I/Os, the number of generic configurable logic blocks, i.e., lookup tables (LUTs), and the types and numbers of fixed purpose hard blocks. It can be seen from these tables that the first set of benchmarks uses multipliers and adders as hard blocks, whereas the second set of benchmarks uses only multipliers. The last columns of both tables briefly describe the functions of the benchmarks as well. The benchmarks used in this work are open-source and are widely available for the usage of academia and researchers. These benchmarks are passed through the FPGA back-end flow described in Section 3. The routing step of the back-end flow is modified in such a way that it can be either used to perform routing in a conventional way or to perform routing using the enhancements discussed in Section 4.

Table 1.
Heterogeneous benchmarks—set I.

Table 2.
Heterogeneous benchmarks—set II.
5.2. Proposed Enhancements—Exploration and Discussion
In this work, we perform the QoR comparison between the proposed RL-based enhancement in routing against the conventional congestion-driven routing approach. However, before performing the comparison, first of all, we determine the appropriate paramater values that give us the best results for the proposed enhancements. Among the parameters, we first determine the value of that gives the best routing results in the shortest possible time for our -greedy approach. We determine this value through exploration, where RL-based routing is performed for all the benchmarks under consideration. While varying the value of , our experimentation shows that both the purely greedy approach (i.e., ) and the purely exploratory approach (i.e., ) give poor results in terms of conflict count, which is a measure of the quality of the routing solution. On one hand, the purely greedy approach gives quick results, but they are poor in quality. On the other hand, the purely exploratory approach is unable to find a feasible solution in a suitable time. The average normalized routing results for two sets of benchmarks for varying values of are shown in Figure 5. It can be seen from this figure that the purely greedy approach gives poor results. However, as the value of is increased, relatively more importance is given to exploration. This results in a better hill climbing approach, which eventually results in better routing results. However, increasing does not necessarily increase the QoR beyond a certain limit. Rather, for short run times, it causes a degradation in the results. This trend is shown in Figure 5. Our experimentation shows that the best routing results are obtained with , and we use this value for further exploration and comparison as well.
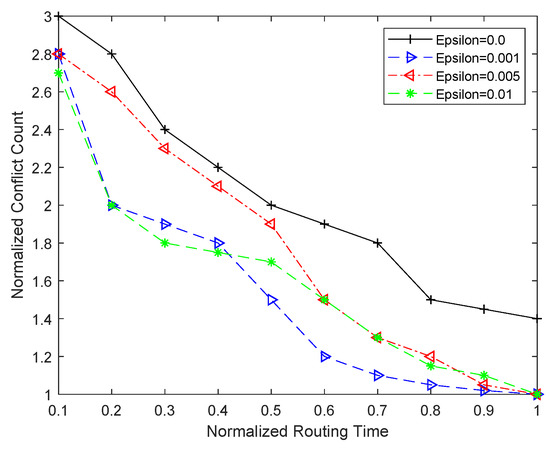
Figure 5.
Comparison of conflict count and routing time for different values of epsilon.
Once the best value of is determined, the second parameter that we determine is the reward function. As discussed in Section 4.2, in this work, we explore two reward functions for RL-based routing. In order to determine the best reward function for the proposed routing, we perform a comparison between the two. For both reward functions, the value of , as determined by Figure 5. The results of the comparison of the reward functions are shown in Figure 6. It can be seen from this figure that the basic reward function of Equation (4) performs poorly, as compared to the enhanced reward function of Equation (5). This is because of the ability and better adaptability of the enhanced reward function to avoid the local minima. We use the the epsilon value of Figure 5 and the reward function of Equation (5) for teh proposed RL-based routing and for its further comparison with the congestion-driven approach.
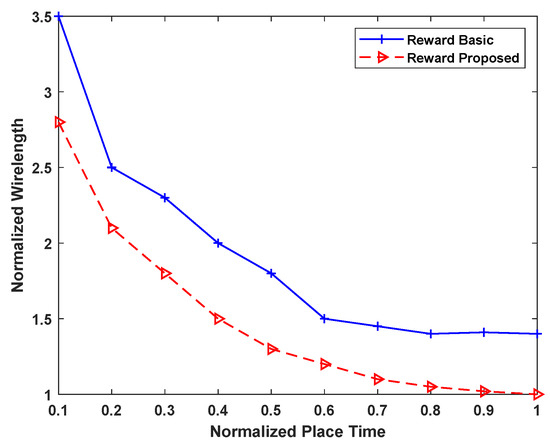
Figure 6.
Reward function comparison.
5.3. Comparison Results and Analysis
To perform the comparison between the RL-based routing approach and the conventional negotiation-based congestion-driven (NC) routing approach, we use the FPGA back-end flow described in Section 3. For comparison, each benchmark is passed through the FPGA back-end flow once using the NC routing approach and then using the RL-based approach. Furthermore, for the RL-based approach, we use the -greedy approach with two values of : one is where -greedy has no memory and a value of , and the other is where -greedy has memory and a value of . The comparison results of these approaches for critical path switches are shown in Figure 7. In this figure, the results of the RL-based approach with and without memory are indicated as “RL” and “Random”, respectively, whereas the results of the conventional routing approach are indicated as “NC”. The results shown in Figure 7 are normalized against the RL-based approach that has memory, as it gives the best results in the shortest time. The comparison results show that the RL-based approach using memory crosses the smallest number of critical path switches in the least iteration count. It can be seen from this figure that, for same number of critical path switches, the “RL” approach requires 33% less iteration counts as compared to the NC approach. Further comparison with the random approach shows that the random approach gives the worst results among the three approaches. This is because of the fact that this approach has no memory and does not learn from previously taken actions. This highlights the importance of not only taking actions, but also learning from previously taken actions.
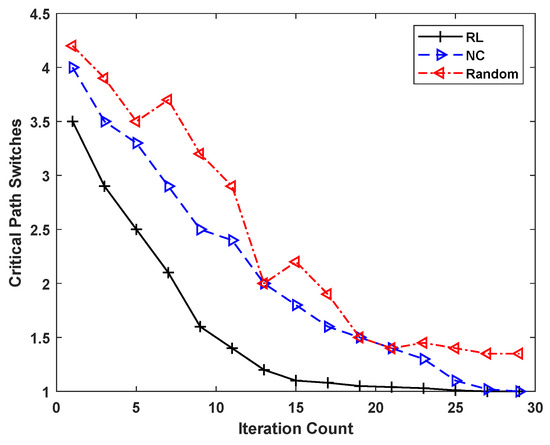
Figure 7.
Normalized routing switches vs, the number of iteration counts for different approaches.
To further consolidate our results, we perform a comparison between the iteration count and iteration time taken per iteration. These results are shown in Figure 8. It can be seen from this figure that the iteration time increases linearly for all three approaches under consideration. However, almost after a dozen iterations, the iteration time for the random and RL-based routing approaches stabilizes, while the iteration time for NC keeps increasing and rises exponentially beyond 25 iterations. The comparison shows that the beyond 20 iterations, the NC routing approach takes, on average, 50% and 30% more time per iteration than the random and RL approaches, respectively. This is because of the fact that for the NC routing approach, it becomes harder to find a conflict-free solution with the increase in the number of iterations. The NC routing approach then has to conduct more explorations and look for less-congested nodes. The RL routing approach, on the other hand, is able to contain the routing time because of its enhanced reward function and -greedy approach. It can be seen from Figure 8 that, from the perspective of iteration time, the “Random” approach gives the best results, the reason being that this approach does not possess any memory. However, this does not necessarily mean that the smaller iteration time advantage is reflected in the critical path switches and conflict count results as well, which are the ultimate measure of the quality of a routing algorithm.
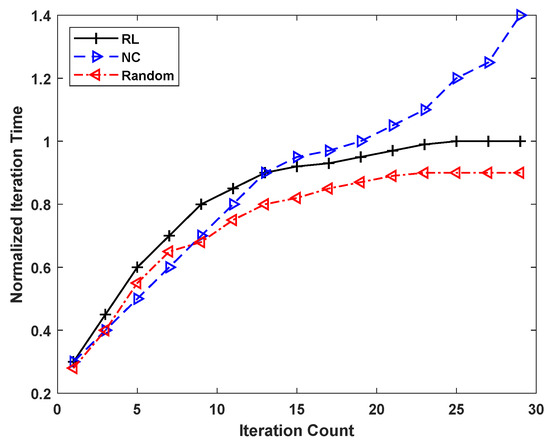
Figure 8.
Comparison of iteration time and number of iterations for the different approaches under consideration.
More time taken by increasing number of iterations reflects in the total time required by the routing algorithm to find a conflict-free solution. This trend is reflected in Figure 9. This figure shows that RL-based routing, on average, requires 35% less time to resolve the conflicts as compared to the NC-based routing approach. It is further evident from this figure that, although the random routing approach requires less time per iteration, it is unable to find a conflict-free solution in a reasonable time, as it does not learn from previous actions. The results shown in Figure 7, Figure 8 and Figure 9 clearly indicate that the proposed RL-based routing approach gives the same or better QoR as compared to the conventional NC routing approach, while requiring 35% less routing time. This is definitely significant, as routing is among the most time-consuming steps of FPGA back-end flow, and this improvement leads to overall shorter and more efficient design flow times. Finally, the individual routing time taken by the benchmarks of two sets is also given in Table 3 and Table 4. It can be seen from these tables that, compared to the NC routing approach, the speedup of the RL-based approach for individual benchmarks is not always the same; it ranges from 27% to 43.6%, and results in an average speedup of 35% for all the benchmarks under consideration. The results of the random routing approach are not included in these tables, as this routing approach is not able to find a conflict-free routing solution for the number of benchmarks shown in the two tables.
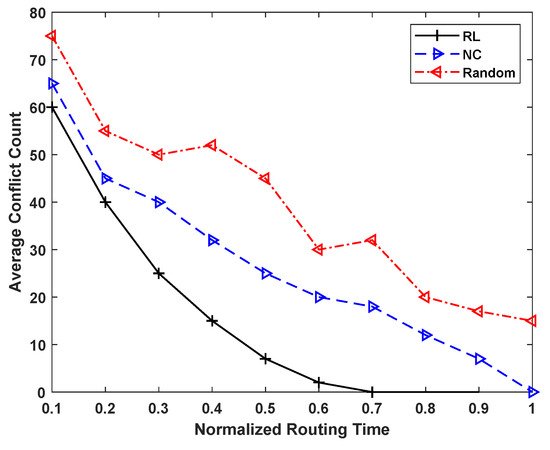
Figure 9.
Comparison of conflict count and normalized routing time for the different approaches under consideration.

Table 3.
Individual routing time comparison between the NC and RL-based routing approaches for the set I benchmarks.

Table 4.
Individual routing time comparison between the NC and RL-based routing approaches for the set II benchmarks.
6. Conclusions and Future Work
Routing is one of the most critical and time-consuming steps of FPGA back-end flow. We have used an RL-based framework in this paper to speed up the routing step of FPGA CAD flow. For this purpose, we have used the -greedy approach and modified the reward function. Compared to the conventional cost function of the negotiation-based congestion-driven routing approach, the proposed reward function navigates the solution space in more efficient way. Through an RL-based framework, we expedite the FPGA back-end flow and achieve similar or better quality of results more quickly, as compared to the conventional, negotiation-based, congestion-driven routing algorithm. For experimentation, we use two sets of open-source heterogeneous benchmarks, and our experimental results show that the RL-based framework requires 35% less execution time as compared to the conventional routing solution. Finally, the speedup gain of the routing step leads to an overall back-end flow speedup of 25%, as compared to the flow using the conventional routing approach only.
In this work, we have focused on investigating the impact of reinforcement learning on the detailed FPGA routing. In the future, we further aim to integrate machine learning techniques in other important steps of FPGA back-end flow and to investigate their impact on the overall speed of FPGA back-end flow and the quality of the final prototyped design. We also aim to extend our benchmark suite and mimic the real-life applications as closely as possible.
Author Contributions
Conceptualization, U.F. and I.B.; methodology, U.F.; software, U.F.; validation, U.F. and I.B.; formal analysis, I.B.; investigation, U.F. and I.B.; resources, U.F. and I.B.; data curation, U.F. and I.B.; writing—original draft preparation, U.F. and I.B.; writing—review and editing, U.F. and I.B.; visualization, U.F. and I.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xilinx. Virtex UltraScale+ VU19P FPGA Product Brief. 2021. Available online: https://www.xilinx.com/products/silicon-devices/fpga/virtex-ultrascale-plus.html (accessed on 25 May 2022).
- Intel. Intel Stratix10 GX 10M FPGA Product Description. 2021. Available online: https://www.intel.com/content/www/us/en/products/details/fpga/stratix/10.html (accessed on 25 May 2022).
- Farooq, U.; Mehrez, H. Pre-Silicon Verification Using Multi-FPGA Platforms: A Review. J. Electron. Test. 2021, 37, 7–24. [Google Scholar] [CrossRef]
- Al-hyari, A.; Abuowaimer, Z.; Maarouf, D.; Areibi, S.; Gréwal, G. An Effective FPGA Placement Flow Selection Framework using Machine Learning. In Proceedings of the 2018 30th International Conference on Microelectronics (ICM), Sousse, Tunisia, 16–19 December 2018; pp. 164–167. [Google Scholar]
- Farooq, U.; Alzahrani, B.A. Exploring and optimizing partitioning of large designs for multi-FPGA based prototyping platforms. Computing 2020, 102, 2361–2383. [Google Scholar] [CrossRef]
- Farooq, U.; Parvez, H.; Mehrez, H.; Marrakchi, Z. Exploration of Heterogeneous FPGA Architectures. Int. J. Reconfig. Comput. 2011, 2011, 121404. [Google Scholar] [CrossRef][Green Version]
- Chen, S.C.; Chang, Y.W. FPGA placement and routing. In Proceedings of the 2017 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Irvine, CA, USA, 13–16 November 2017; pp. 914–921. [Google Scholar]
- Kim, C.; Shin, H. A performance-driven logic emulation system: FPGA network design and performance-driven partitioning. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1996, 15, 560–568. [Google Scholar] [CrossRef]
- Abuowaimer, Z.; Maarouf, D.; Martin, T.; Foxcroft, J.; Gréwal, G.; Areibi, S.; Vannelli, A. GPlace3.0: Routability-driven analytic placer for UltraScale FPGA architectures. ACM Trans. Des. Autom. Electron. Syst. 2018, 23, 1–33. [Google Scholar] [CrossRef]
- Li, W.; Lin, Y.; Pan, D.Z. elfPlace: Electrostatics-based placement for large-scale heterogeneous fpgas. In Proceedings of the 2019 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Westminster, CO, USA, 4–7 November 2019; pp. 1–8. [Google Scholar]
- Vercruyce, D.; Vansteenkiste, E.; Stroobandt, D. Liquid: High quality scalable placement for large heterogeneous FPGAs. In Proceedings of the 2017 International Conference on Field Programmable Technology (ICFPT), Melbourne, Australia, 11–13 December 2017; pp. 17–24. [Google Scholar]
- Altan, A.; Hacıoğlu, R. Model predictive control of three-axis gimbal system mounted on UAV for real-time target tracking under external disturbances. Mech. Syst. Signal Process. 2020, 138, 106548. [Google Scholar] [CrossRef]
- Chen, G.; Pui, C.W.; Chow, W.K.; Lam, K.C.; Kuang, J.; Young, E.F.; Yu, B. RippleFPGA: Routability-driven simultaneous packing and placement for modern FPGAs. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 37, 2022–2035. [Google Scholar] [CrossRef]
- Luu, J.; Kuon, I.; Jamieson, P.; Campbell, T.; Ye, A.; Fang, W.M.; Kent, K.; Rose, J. VPR 5.0: FPGA CAD and architecture exploration tools with single-driver routing, heterogeneity and process scaling. ACM Trans. Reconfig. Technol. Syst. 2011, 4, 1–23. [Google Scholar] [CrossRef]
- Kapre, N.; Ng, H.; Teo, K.; Naude, J. Intime: A machine learning approach for efficient selection of fpga cad tool parameters. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 23–26. [Google Scholar]
- Liao, H.; Zhang, W.; Dong, X.; Poczos, B.; Shimada, K.; Burak Kara, L. A deep reinforcement learning approach for global routing. J. Mech. Des. 2020, 142, 061701. [Google Scholar] [CrossRef]
- Murray, K.E.; Whitty, S.; Liu, S.; Luu, J.; Betz, V. Titan: Enabling large and complex benchmarks in academic CAD. In Proceedings of the 2013 23rd International Conference on Field programmable Logic and Applications, Porto, Portugal, 2–4 September 2013; pp. 1–8. [Google Scholar]
- Inagi, M.; Takashima, Y.; Nakamura, Y. Globally optimal time-multiplexing in inter-FPGA connections for accelerating multi-FPGA systems. In Proceedings of the 2009 International Conference on Field Programmable Logic and Applications, Prague, Czech Republic, 31 August–2 September 2009; pp. 212–217. [Google Scholar] [CrossRef]
- Hauck, S.; DeHon, A. Reconfigurable Computing: The Theory and Practice of FPGA-Based Computation; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2007. [Google Scholar]
- McMurchie, L.; Ebeling, C. Pathfinder: A Negotiation-Based Performance-Driven Router for FPGAs. In Proceedings of the ACM International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 12–14 February 1995; ACM Press: New York, NY, USA; pp. 111–117. [Google Scholar]
- Gréwal, G.; Areibi, S.; Westrik, M.; Abuowaimer, Z.; Zhao, B. Automatic flow selection and quality-of-result estimation for FPGA placement. In Proceedings of the 2017 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Lake Buena Vista, FL, USA, 29 May–2 June 2017; pp. 115–123. [Google Scholar]
- Wang, L.C.; Abadir, M.S. Data mining in EDA-basic principles, promises, and constraints. In Proceedings of the 2014 51st ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 1–5 June 2014; pp. 1–6. [Google Scholar]
- Mametjanov, A.; Balaprakash, P.; Choudary, C.; Hovland, P.D.; Wild, S.M.; Sabin, G. Autotuning FPGA design parameters for performance and power. In Proceedings of the 2015 IEEE 23rd Annual International Symposium on Field-Programmable Custom Computing Machines, Vancouver, BC, Canada, 2–6 May 2015; pp. 84–91. [Google Scholar]
- Kapre, N.; Chandrashekaran, B.; Ng, H.; Teo, K. Driving timing convergence of FPGA designs through machine learning and cloud computing. In Proceedings of the 2015 IEEE 23rd Annual International Symposium on Field-Programmable Custom Computing Machines, Vancouver, BC, Canada, 2–6 May 2015; pp. 119–126. [Google Scholar]
- Chang, W.H.; Lin, C.H.; Mu, S.P.; Chen, L.D.; Tsai, C.H.; Chiu, Y.C.; Chao, M.C.T. Generating routing-driven power distribution networks with machine-learning technique. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2017, 36, 1237–1250. [Google Scholar] [CrossRef]
- Manimegalai, R.; Soumya, E.S.; Muralidharan, V.; Ravindran, B.; Kamakoti, V.; Bhatia, D. Placement and routing for 3D-FPGAs using reinforcement learning and support vector machines. In Proceedings of the 18th International Conference on VLSI Design Held Jointly with 4th International Conference on Embedded Systems Design, Kolkata, India, 3–7 January 2005; pp. 451–456. [Google Scholar]
- Liu, Q.; Gao, M.; Zhang, Q. Knowledge-based neural network model for FPGA logical architecture development. IEEE Trans. Very Large Scale Integr. Syst. 2015, 24, 664–677. [Google Scholar] [CrossRef]
- Neto, W.L.; Austin, M.; Temple, S.; Amaru, L.; Tang, X.; Gaillardon, P.E. LSOracle: A logic synthesis framework driven by artificial intelligence. In Proceedings of the 2019 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Westminster, CO, USA, 4–7 November 2019; pp. 1–6. [Google Scholar]
- Brayton, R.; Mishchenko, A. ABC: An academic industrial-strength verification tool. In Proceedings of the International Conference on Computer Aided Verification, Edinburgh, UK, 15–19 July 2010; pp. 24–40. [Google Scholar]
- Yu, C.; Xiao, H.; De Micheli, G. Developing synthesis flows without human knowledge. In Proceedings of the 55th Annual Design Automation Conference, San Francisco, CA, USA, 24–29 June 2018; pp. 1–6. [Google Scholar]
- An, M.; Steffan, J.G.; Betz, V. Speeding up FPGA placement: Parallel algorithms and methods. In Proceedings of the 2014 IEEE 22nd Annual International Symposium on Field-Programmable Custom Computing Machines, Boston, MA, USA, 11–13 May 2014; pp. 178–185. [Google Scholar]
- Fobel, C.; Grewal, G.; Stacey, D. A scalable, serially-equivalent, high-quality parallel placement methodology suitable for modern multicore and GPU architectures. In Proceedings of the 2014 24th International Conference on Field Programmable Logic and Applications (FPL), Munich, Germany, 2–4 September 2014; pp. 1–8. [Google Scholar]
- Vorwerk, K.; Kennings, A.; Greene, J.W. Improving simulated annealing-based FPGA placement with directed moves. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2009, 28, 179–192. [Google Scholar] [CrossRef]
- Alhyari, A.; Shamli, A.; Abuwaimer, Z.; Areibi, S.; Grewal, G. A Deep Learning Framework to Predict Routability for FPGA Circuit Placement. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 8–12 September 2019; pp. 334–341. [Google Scholar]
- He, Z.; Ma, Y.; Zhang, L.; Liao, P.; Wong, N.; Yu, B.; Wong, M.D. Learn to floorplan through acquisition of effective local search heuristics. In Proceedings of the 2020 IEEE 38th International Conference on Computer Design (ICCD), Hartford, CT, USA, 18–21 October 2020; pp. 324–331. [Google Scholar]
- Mirhoseini, A.; Goldie, A.; Yazgan, M.; Jiang, J.; Songhori, E.; Wang, S.; Lee, Y.J.; Johnson, E.; Pathak, O.; Bae, S.; et al. Chip placement with deep reinforcement learning. arXiv 2020, arXiv:2004.10746. [Google Scholar]
- He, Z.; Zhang, L.; Liao, P.; Ma, Y.; Yu, B. Reinforcement learning driven physical synthesis. In Proceedings of the 2020 IEEE 15th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Kunming, China, 3–6 November 2020; pp. 1–4. [Google Scholar]
- Murray, K.E.; Betz, V. Adaptive FPGA placement optimization via reinforcement learning. In Proceedings of the ACM/IEE Workshop on Machine Learning for CAD (MLCAD19), Canmore, AB, Canada, 3–4 September 2019; pp. 1–6. [Google Scholar]
- Zhao, J.; Liang, T.; Sinha, S.; Zhang, W. Machine learning based routing congestion prediction in FPGA high-level synthesis. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019; pp. 1130–1135. [Google Scholar]
- Szentimrey, H.; Al-Hyari, A.; Foxcroft, J.; Martin, T.; Noel, D.; Grewal, G.; Areibi, S. Machine learning for congestion management and routability prediction within FPGA placement. ACM Trans. Des. Autom. Electron. Syst. 2020, 25, 1–25. [Google Scholar] [CrossRef]
- Goswami, P.; Bhatia, D. Congestion Prediction in FPGA Using Regression Based Learning Methods. Electronics 2021, 10, 1995. [Google Scholar] [CrossRef]
- Farooq, U.; Ul Hasan, N.; Baig, I.; Zghaibeh, M. Efficient FPGA Routing using Reinforcement Learning. In Proceedings of the 2021 12th International Conference on Information and Communication Systems (ICICS), Valencia, Spain, 24–26 May 2021; pp. 106–111. [Google Scholar] [CrossRef]
- Dai, S.; Zhou, Y.; Zhang, H.; Ustun, E.; Young, E.F.; Zhang, Z. Fast and accurate estimation of quality of results in high-level synthesis with machine learning. In Proceedings of the 2018 IEEE 26th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Boulder, CO, USA, 29 April–1 May 2018; pp. 129–132. [Google Scholar]
- Ferianc, M.; Fan, H.; Chu, R.S.; Stano, J.; Luk, W. Improving performance estimation for fpga-based accelerators for convolutional neural networks. In Proceedings of the International Symposium on Applied Reconfigurable Computing, Toledo, Spain, 1–3 April 2020; pp. 3–13. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).