WeaveNet: Solution for Variable Input Sparsity Depth Completion
Abstract
:1. Introduction
2. Related Work
2.1. Methods Based on Sparsity Invariant Convolutions
2.2. Methods Not Based on Sparsity Invariant Convolutions
3. Our Method
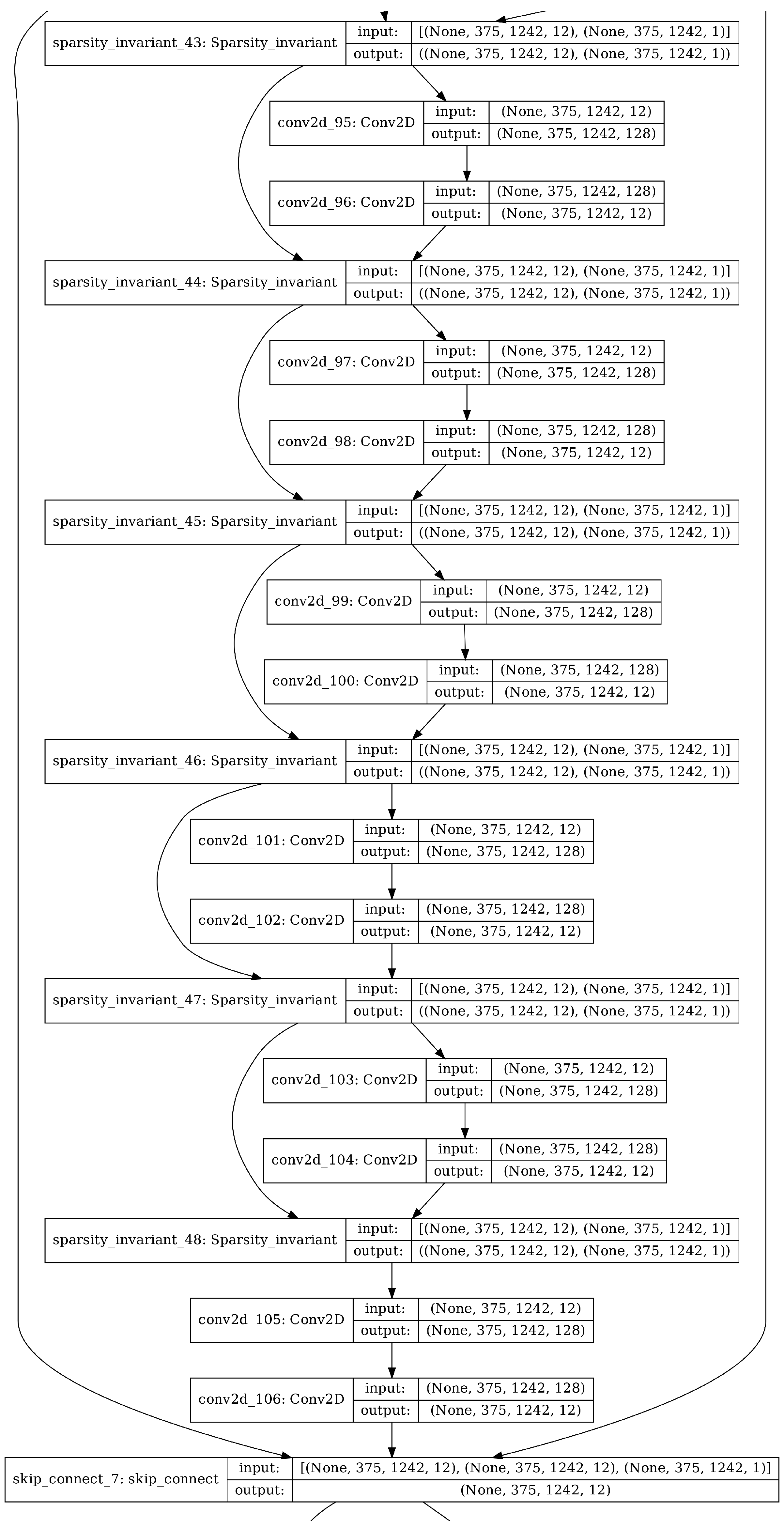
3.1. WeaveBlock
- A pointwise convolution with a small number of channels;
- A sparsity invariant convolution with a long and narrow vertical kernel and a small number of channels;
- A pointwise convolution with a large number of channels;
- A pointwise convolution with a small number of channels;
- A sparsity invariant convolution with a long and narrow horizontal kernel and a small number of channels;
- A pointwise convolution with a large number of channels.
3.2. Unguided WeaveNet Architecture
3.3. Guided WeaveNet Architecture
- A pointwise convolution with a small number of channels;
- A 3 × 3 convolution with a small number of channels;
- A pointwise convolution with a large number of channels.
3.4. Notes on the Input and Output Modality
- We found that using batch normalization in the LIDAR processing stream leads to greatly inferior results.
- We performed experiments using the same network architecture and activation functions other than ReLU. We found that using activation functions whose output may be negative such as Swish [20] and exponential linear unit (ELU) [21] leads to worse performance in the depth completion task than simple ReLU.
3.5. Training Process
- The first version was trained in a standard way (utilizing two training phases: pretraining and standard input density training).
- The second version was trained using universal sparsity training, which consisted of three training phases: pretraining, standard input density training and a variable input sparsity training.
- The third version was trained in a four phase specific sparsity training (pretraining, standard input density training, variable input sparsity training and a final phase of retraining the network at a specific input sparsity).
- A pretraining phase, during which instead of using LIDAR pointcloud as the input of the network, the network was fed with semi-dense depth labels. To be exact, the network was fed with KITTI Depth Completion labels with 50% of pixels masked with zeros. The pretraining phase was relatively short—only one epoch, utilizing approximately 20% of training set frames. This phase was performed using 10−3 learning rate. We found that this short pretraining phase greatly increases the speed of convergence in the future phases;
- The main training phase, during which the network was fed standard sparse input. This phase lasted 30 epochs. The optimizer learning rate was decreased from 10−3 to 10−4, then to 10−5, and finally to 10−6 during this phase. We found it beneficial to apply additive, normally distributed noise to the network weights during this phase of training (approach closer examined in [22]);
- The variable sparsity training phase. During this phase, the network was fed with input for which between 0% and 99.2% of the standard sparse input was masked with zeros. For a particular frame, the input density (i.e., the number of pixels that were not masked with zeros) was randomly sampled according to a formula:where and are the lowest (0.008) and highest (1.0) possible density levels, respectively, and is a random variable sampled uniformly between and .Such a sampling method achieves the goal that the probability of sampling a number from the interval and the probability of sampling a number from the interval is equal if and only if . This phase lasted 10 epochs and was performed with a 10−6 learning rate;
- The fixed sparsity training phase. The goal of the last training phase was to train the network at the target data sparsity (50% masked pixels, 75% masked pixels, 90% masked pixels, 95% masked pixels and 99% masked pixels). This phase lasted 2 epochs for each version of the network for a particular sparsity and was performed with a 10−6 learning rate.
- The RGB-encoder training phase. During this phase the weights of the LIDAR encoder were frozen. This phase lasted 10 epochs. The optimizer learning rate was decreased from 10−4 to 10−5 and finally to 10−6 during this phase;
- The joint training phase. During this phase the whole network was trained (no weights were frozen). This phase lasted 10 epochs and was performed with a 10−6 learning rate.
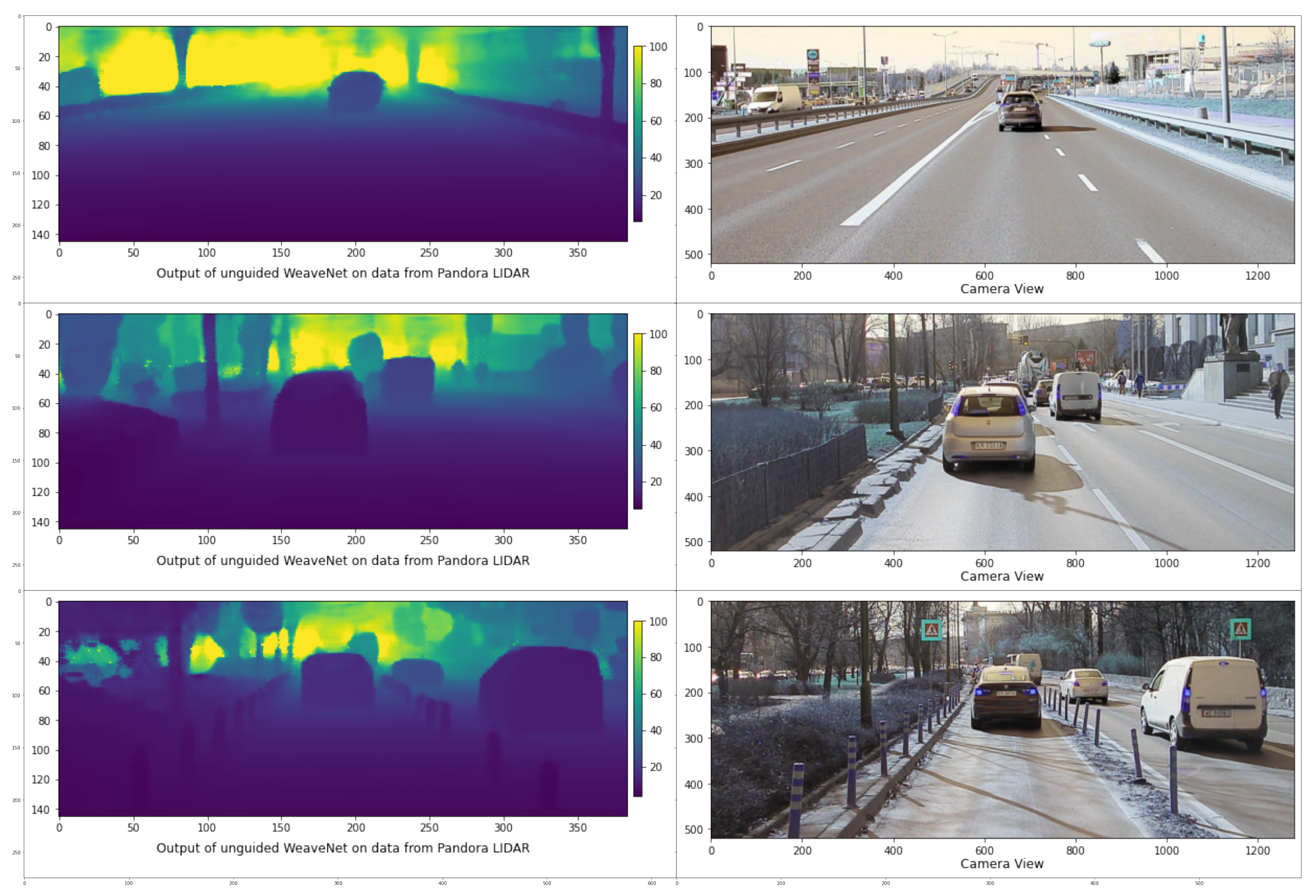
4. Experiments
4.1. Results on Standard Input Density
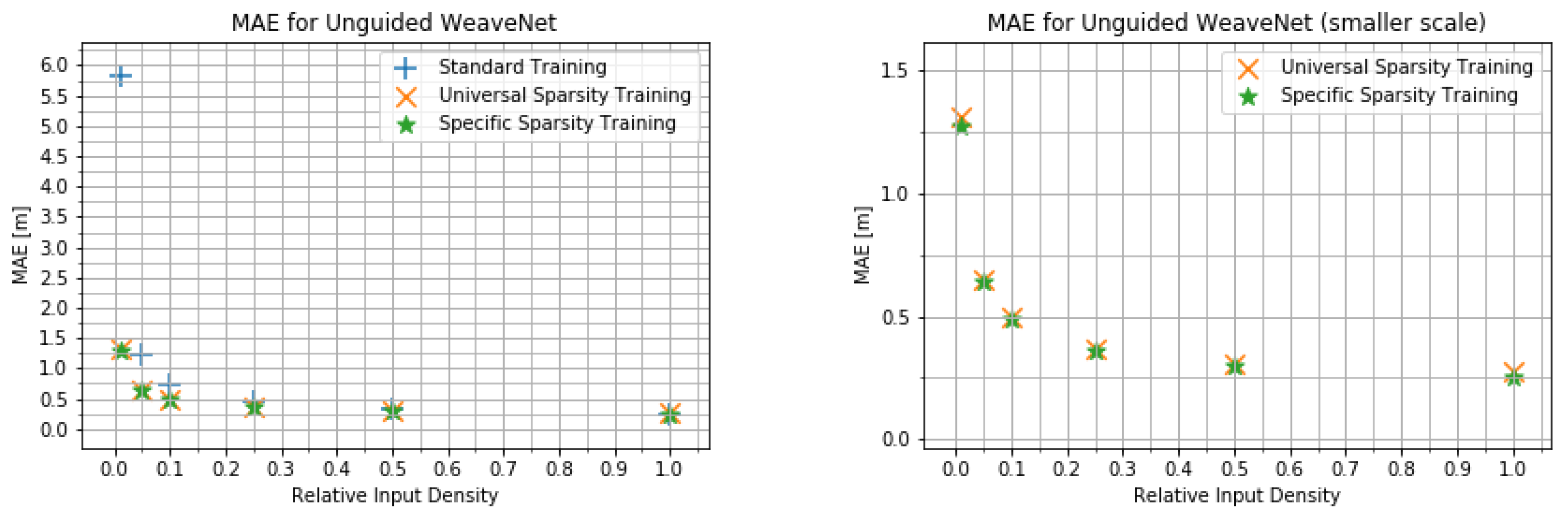
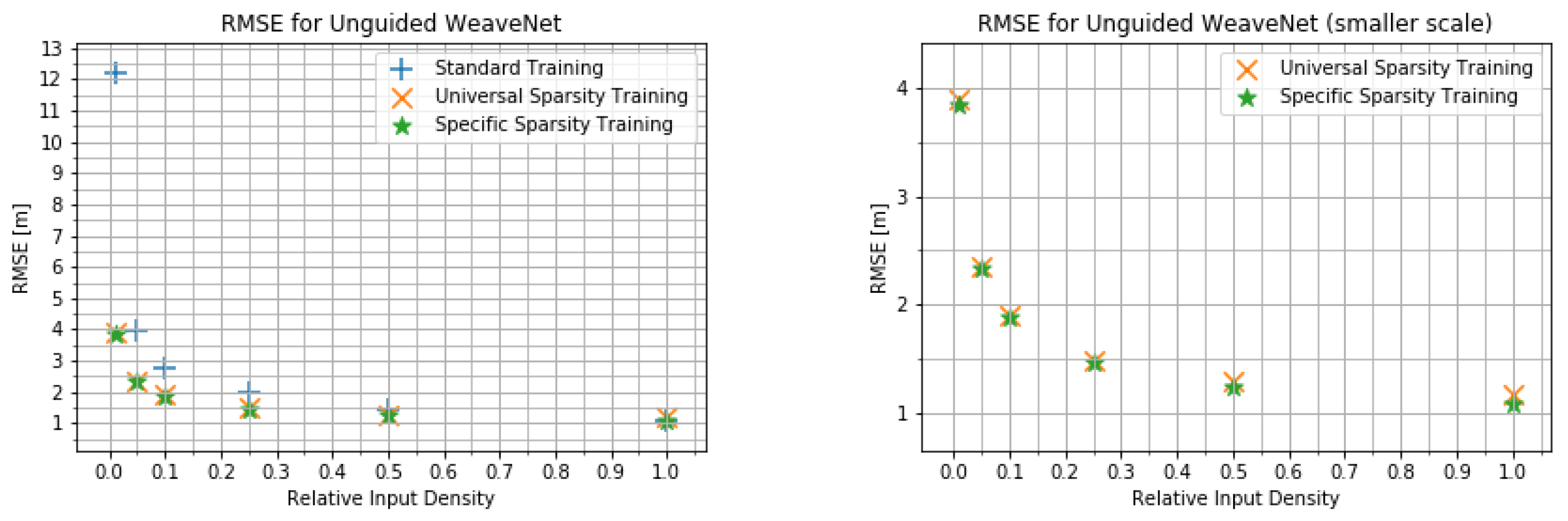
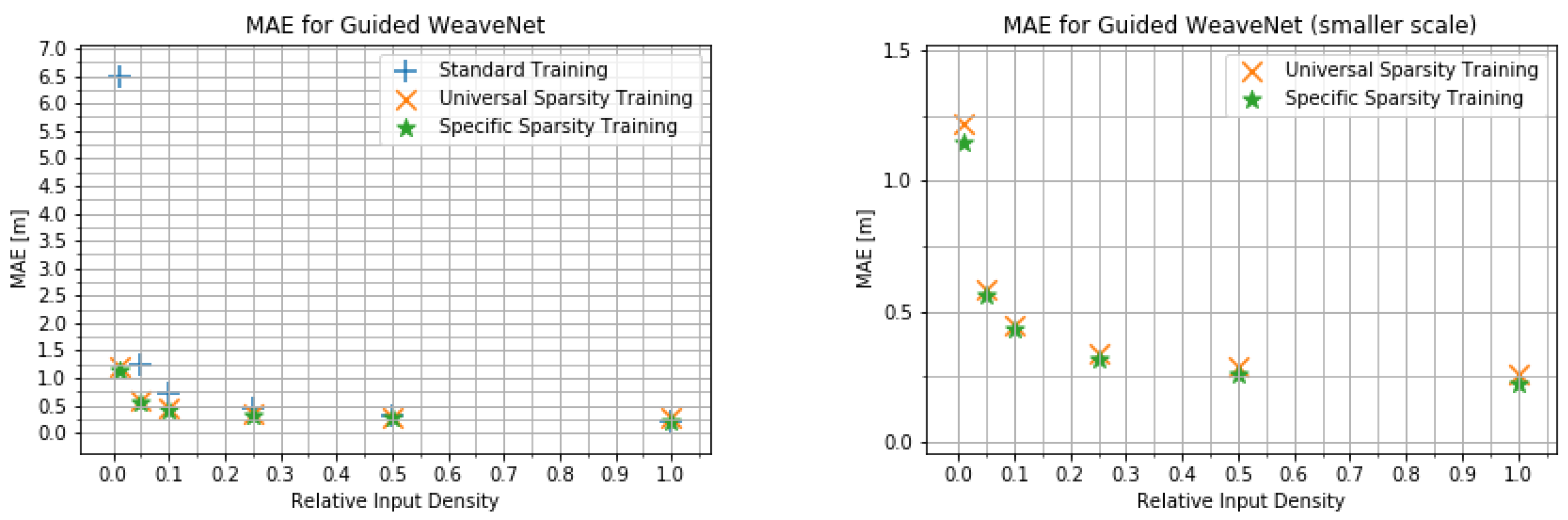
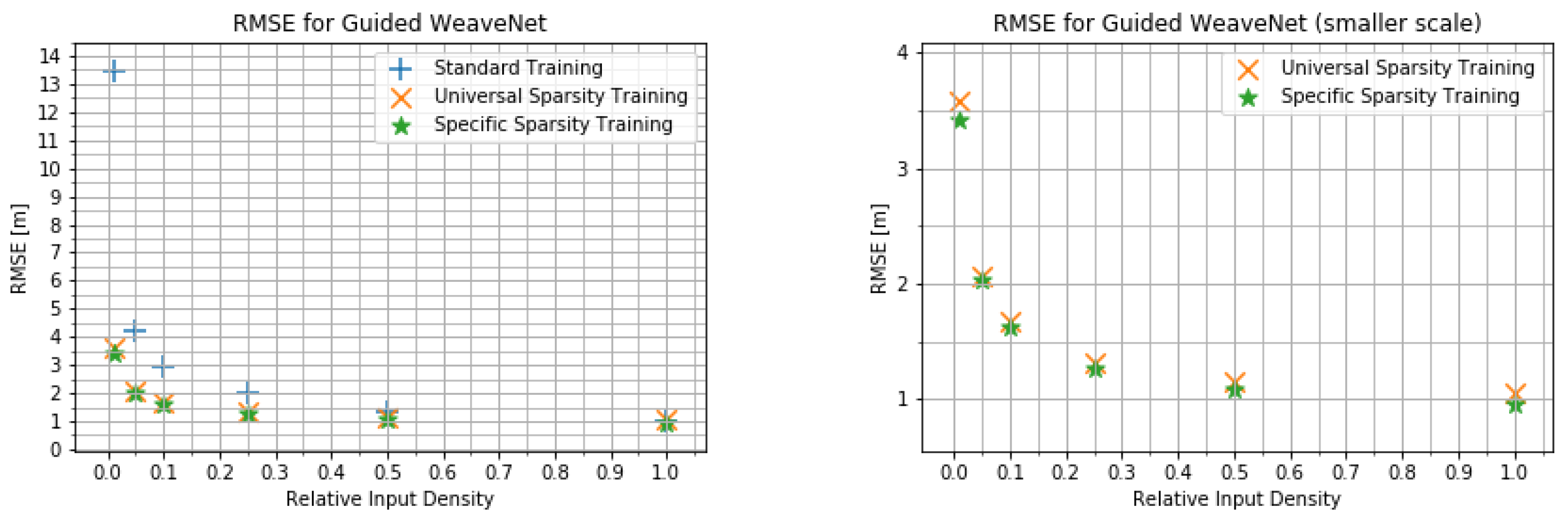
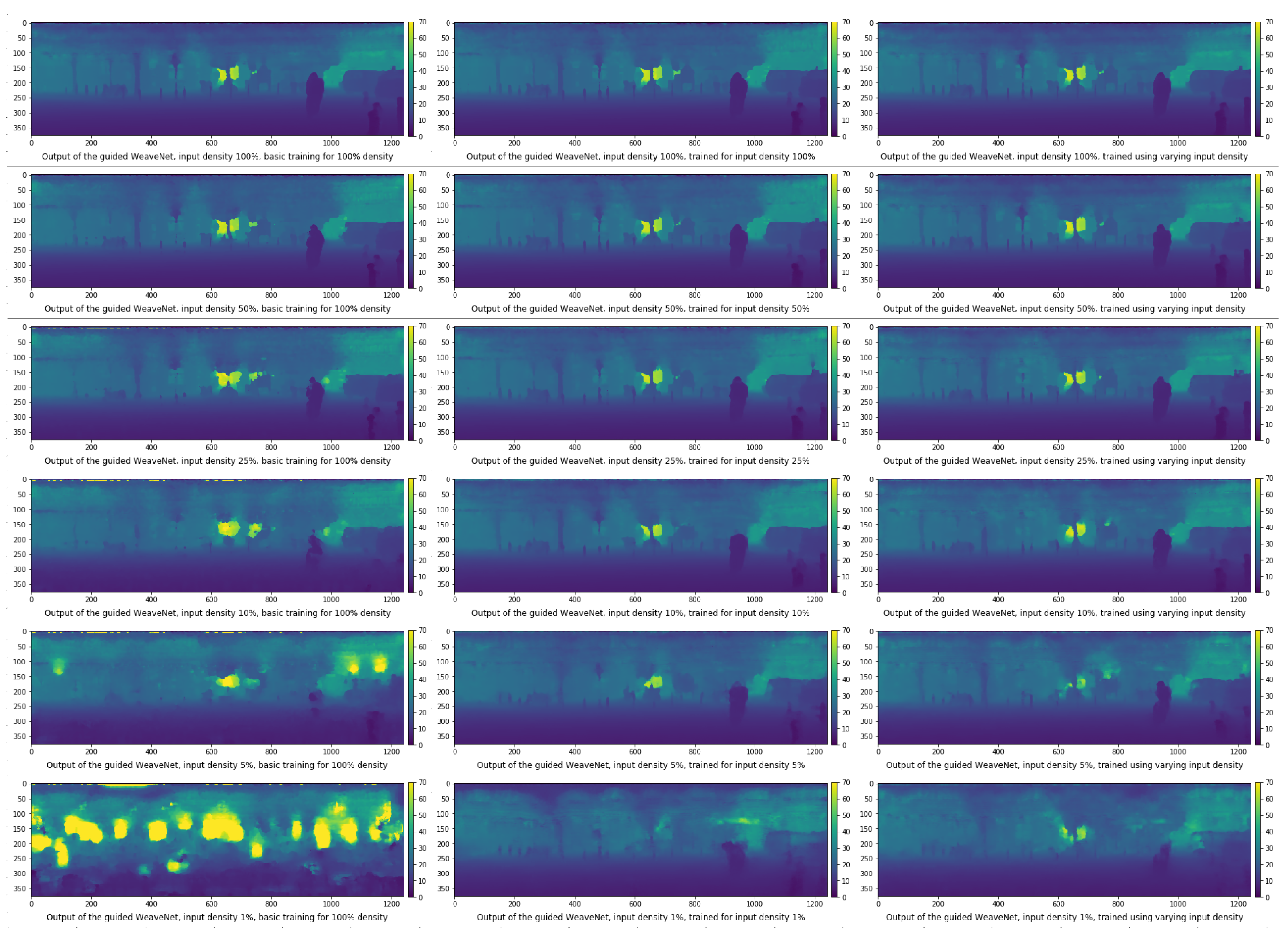
4.2. Input Density Ablation Study
- The network trained on the default KITTI data;
- The network trained with variable input sparsity;
- The network trained with the input at the specific sparsity level.
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uhrig, J.; Schneider, N.; Schneider, L.; Franke, U.; Brox, T.; Geiger, A. Sparsity Invariant CNNs. In Proceedings of the International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets Robotics: The KITTI Dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. arXiv 2017, arXiv:1612.00593. [Google Scholar]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. arXiv 2017, arXiv:1711.06396. [Google Scholar]
- Huang, Z.; Fan, J.; Cheng, S.; Yi, S.; Wang, X.; Li, H. Hms-net: Hierarchical multi-scale sparsity-invariant network for sparse depth completion. IEEE Trans. Image Process. 2019, 29, 3429–3441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eldesokey, A.; Felsberg, M.; Khan, F.S. Propagating Confidences through CNNs for Sparse Data Regression. arXiv 2018, arXiv:1805.11913. [Google Scholar]
- Chen, Y.; Yang, B.; Liang, M.; Urtasun, R. Learning joint 2d–3d representations for depth completion. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 10023–10032. [Google Scholar]
- Park, J.; Joo, K.; Hu, Z.; Liu, C.K.; Kweon, I.S. Non-Local Spatial Propagation Network for Depth Completion. arXiv 2020, arXiv:2007.10042. [Google Scholar]
- Tang, J.; Tian, F.P.; Feng, W.; Li, J.; Tan, P. Learning Guided Convolutional Network for Depth Completion. arXiv 2019, arXiv:1908.01238. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Cui, Z.; Zhang, Y.; Zhang, X.; Liu, S.; Zeng, B.; Pollefeys, M. DeepLiDAR: Deep Surface Normal Guided Depth Prediction for Outdoor Scene from Sparse LiDAR Data and Single Color Image. arXiv 2019, arXiv:1812.00488. [Google Scholar]
- Cheng, X.; Wang, P.; Guan, C.; Yang, R. CSPN++: Learning Context and Resource Aware Convolutional Spatial Propagation Networks for Depth Completion. arXiv 2019, arXiv:1911.05377. [Google Scholar] [CrossRef]
- Ma, F.; Cavalheiro, G.V.; Karaman, S. Self-supervised Sparse-to-Dense: Self-supervised Depth Completion from LiDAR and Monocular Camera. arXiv 2018, arXiv:1807.00275. [Google Scholar]
- Yan, L.; Liu, K.; Belyaev, E. Revisiting Sparsity Invariant Convolution: A Network for Image Guided Depth Completion. IEEE Access 2020, 8, 126323–126332. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, P.; Yang, R. Learning Depth with Convolutional Spatial Propagation Network. arXiv 2019, arXiv:1810.02695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, S.; Mello, S.D.; Gu, J.; Zhong, G.; Yang, M.H.; Kautz, J. Learning Affinity via Spatial Propagation Networks. arXiv 2017, arXiv:1710.01020. [Google Scholar]
- Wang, S.; Suo, S.; Ma, W.C.; Pokrovsky, A.; Urtasun, R. Deep parametric continuous convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2589–2597. [Google Scholar]
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An Open Urban Driving Simulator. In Proceedings of the 1st Annual Conference on Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv 2016, arXiv:1511.07289. [Google Scholar]
- Nowak, M.K.; Lelowicz, K. Weight Perturbation as a Method for Improving Performance of Deep Neural Networks. In Proceedings of the 2021 25th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 23–26 August 2021; pp. 127–132. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
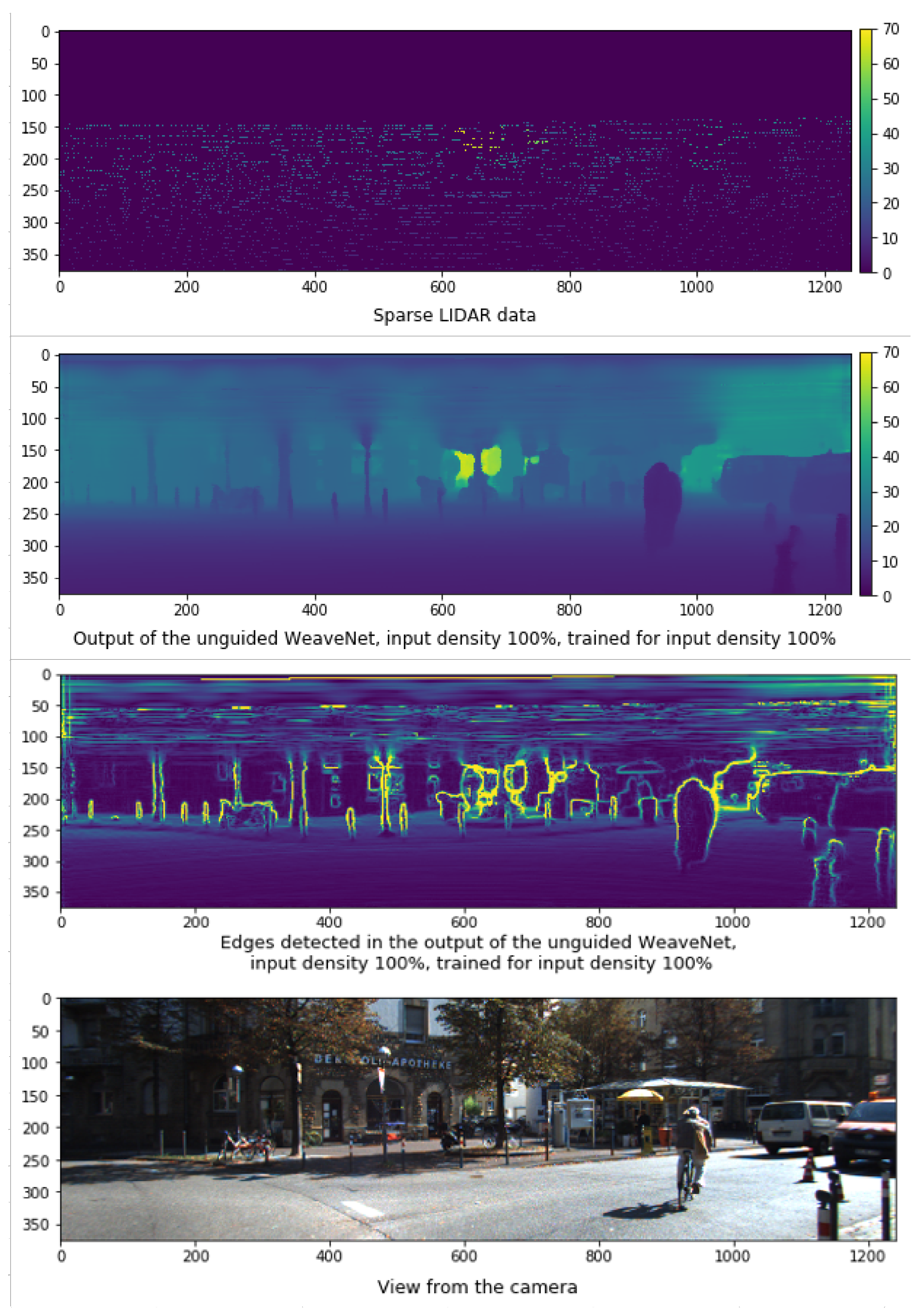
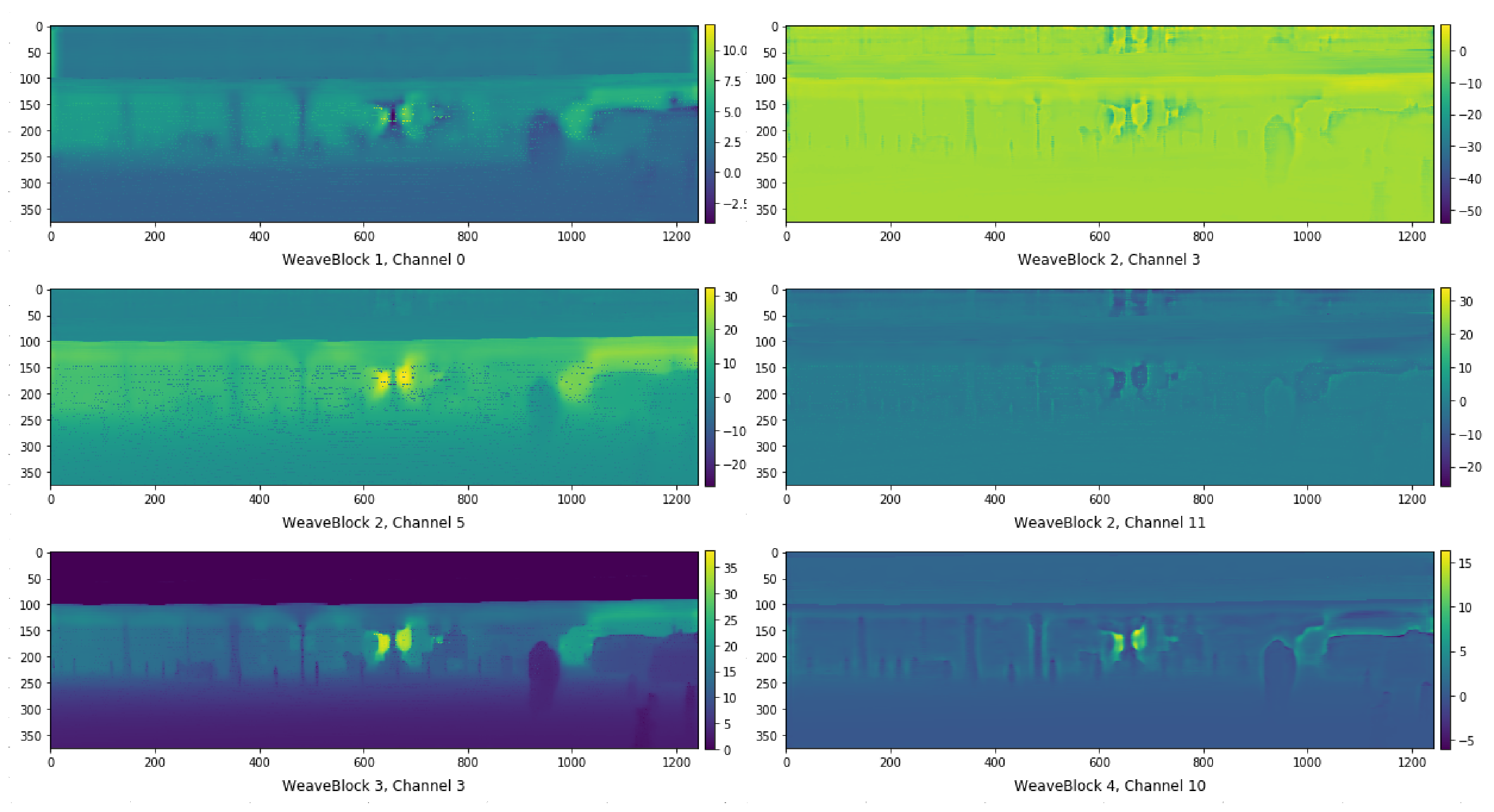

| Model | RMSE [m] | MAE [m] |
|---|---|---|
| Eldesokey et al. [6] | 1.37 | 0.38 |
| Tang et al. [9] | 0.77778 | 0.22159 |
| Park et al. [8] | 0.88410 | not provided |
| Cheng et al. [11] | 0.72543 | 0.20788 |
| Chen et al. [7] | 0.75288 | 0.22119 |
| Qiu et al. [10] | 0.68700 | 0.21538 |
| Yan et al. [13] | 0.79280 | 0.22581 |
| Ma et al. [12] | 0.856754 | not provided |
| Huang et al. [5] | 0.88374 | 0.25711 |
| Ours (standard training) | 0.97175 | 0.22060 |
| Ours (universal sparsity training) | 1.05978 | 0.26249 |
| Ours (specific sparsity training) | 0.94849 | 0.22623 |
| Model | RMSE [m] | MAE [m] |
|---|---|---|
| Uhrig et al. [1] | 2.01 | 0.68 |
| Ma et al. [12] | 0.99135 | not provided |
| Huang et al. [5] | 0.99414 | 0.26241 |
| Ours (standard training) | 1.09596 | 0.24512 |
| Ours universal sparsity training) | 1.17372 | 0.27323 |
| Ours (specific sparsity training) | 1.08774 | 0.25310 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowak, M.K. WeaveNet: Solution for Variable Input Sparsity Depth Completion. Electronics 2022, 11, 2222. https://doi.org/10.3390/electronics11142222
Nowak MK. WeaveNet: Solution for Variable Input Sparsity Depth Completion. Electronics. 2022; 11(14):2222. https://doi.org/10.3390/electronics11142222
Chicago/Turabian StyleNowak, Mariusz Karol. 2022. "WeaveNet: Solution for Variable Input Sparsity Depth Completion" Electronics 11, no. 14: 2222. https://doi.org/10.3390/electronics11142222
APA StyleNowak, M. K. (2022). WeaveNet: Solution for Variable Input Sparsity Depth Completion. Electronics, 11(14), 2222. https://doi.org/10.3390/electronics11142222






