Optimum Extrapolation Techniques for Two-Dimensional Antenna Array Tapered Beamforming
Abstract
1. Introduction
1.1. Background and Motivations
1.2. Paper Contributions
1.3. Paper Organization
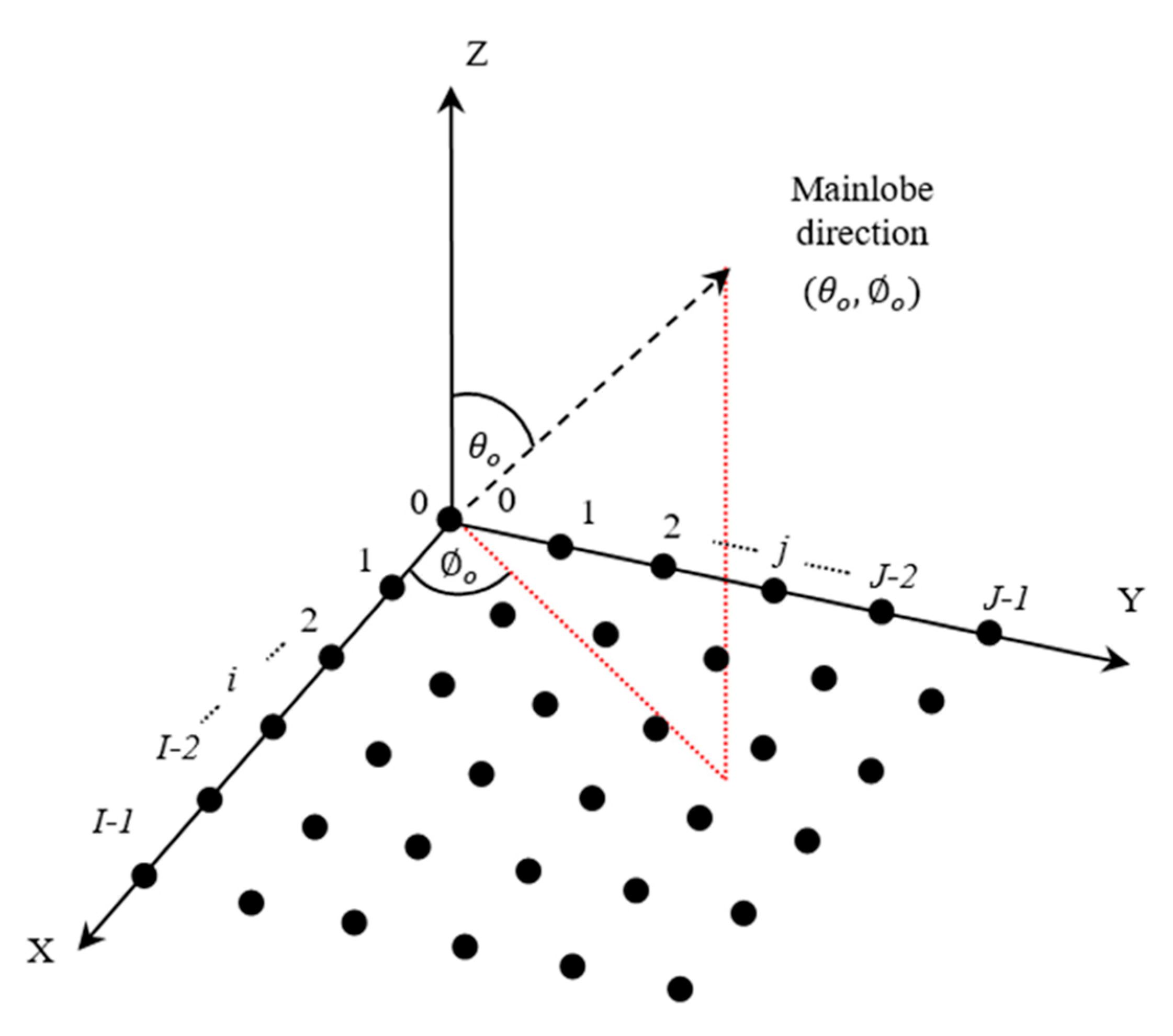
2. 2D Tapered Windows Modelling and Extrapolation Techniques
2.1. Cross-Linear 2D Tapered Window Extrapolation Technique
2.2. Adaptive Radial Tapering for 2D Tapered Window Extrapolation
3. Results and Performance of the Proposed Techniques
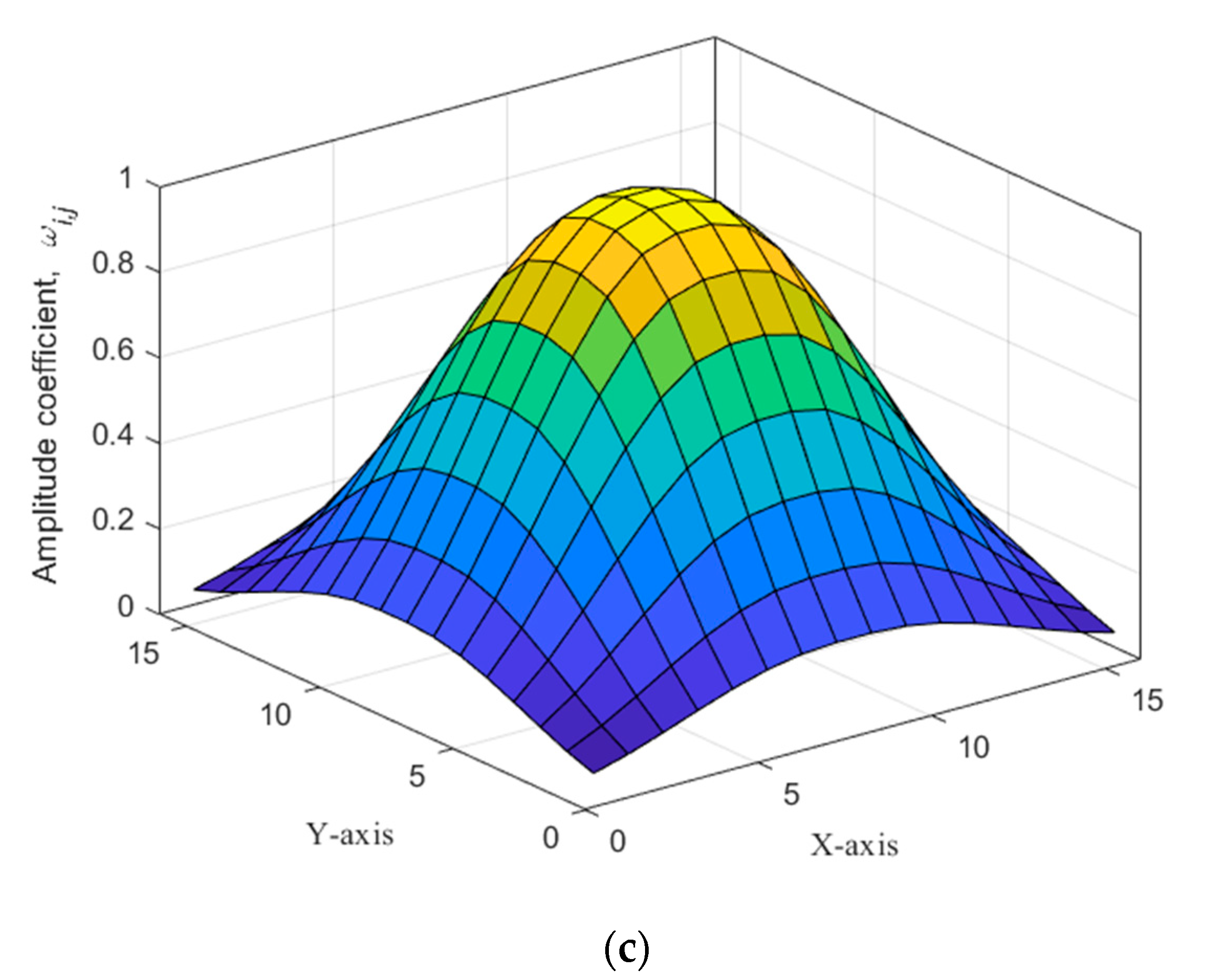
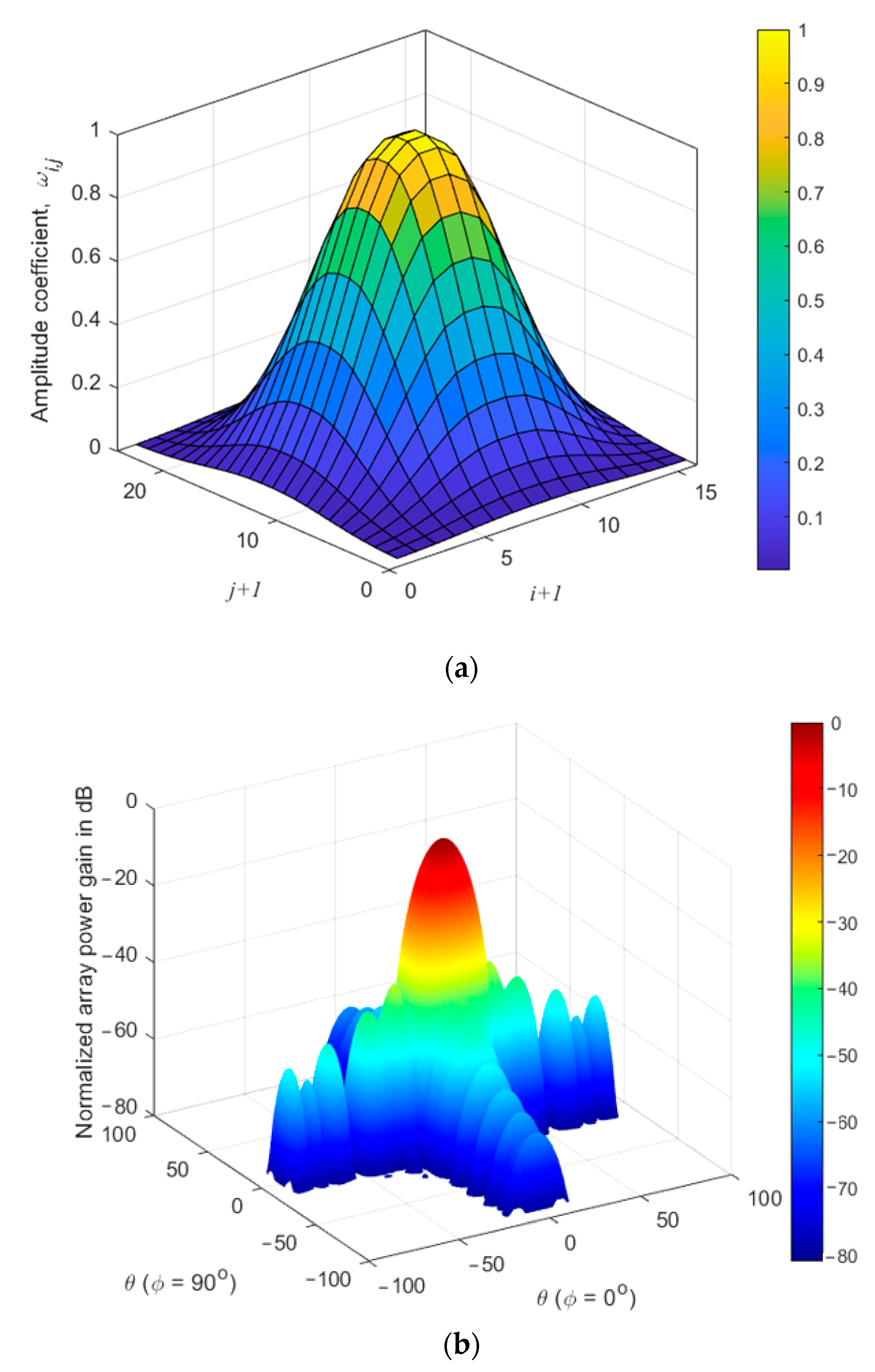
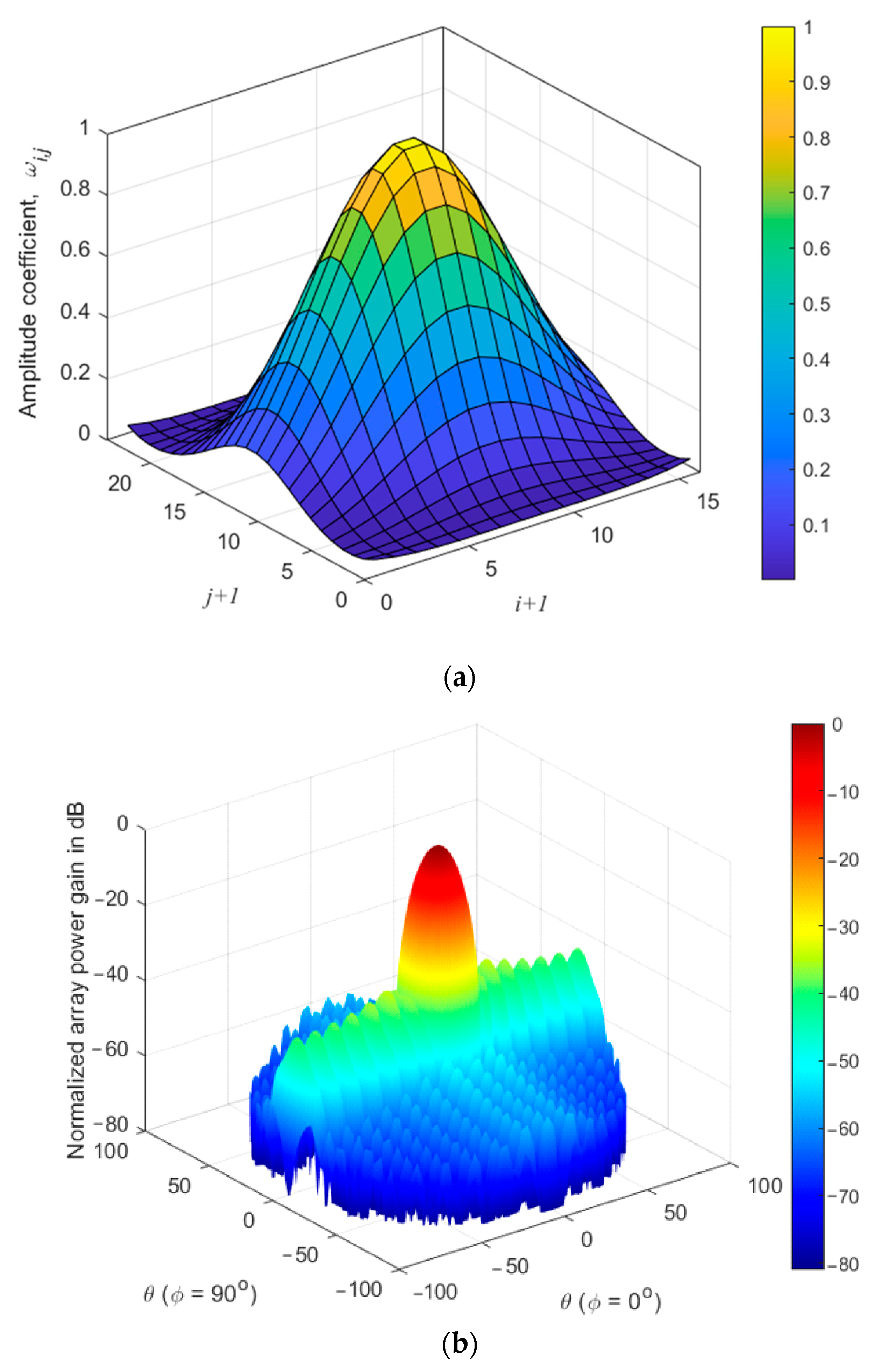
3.1. Cross-Linear Tapering Extrapolation Performance
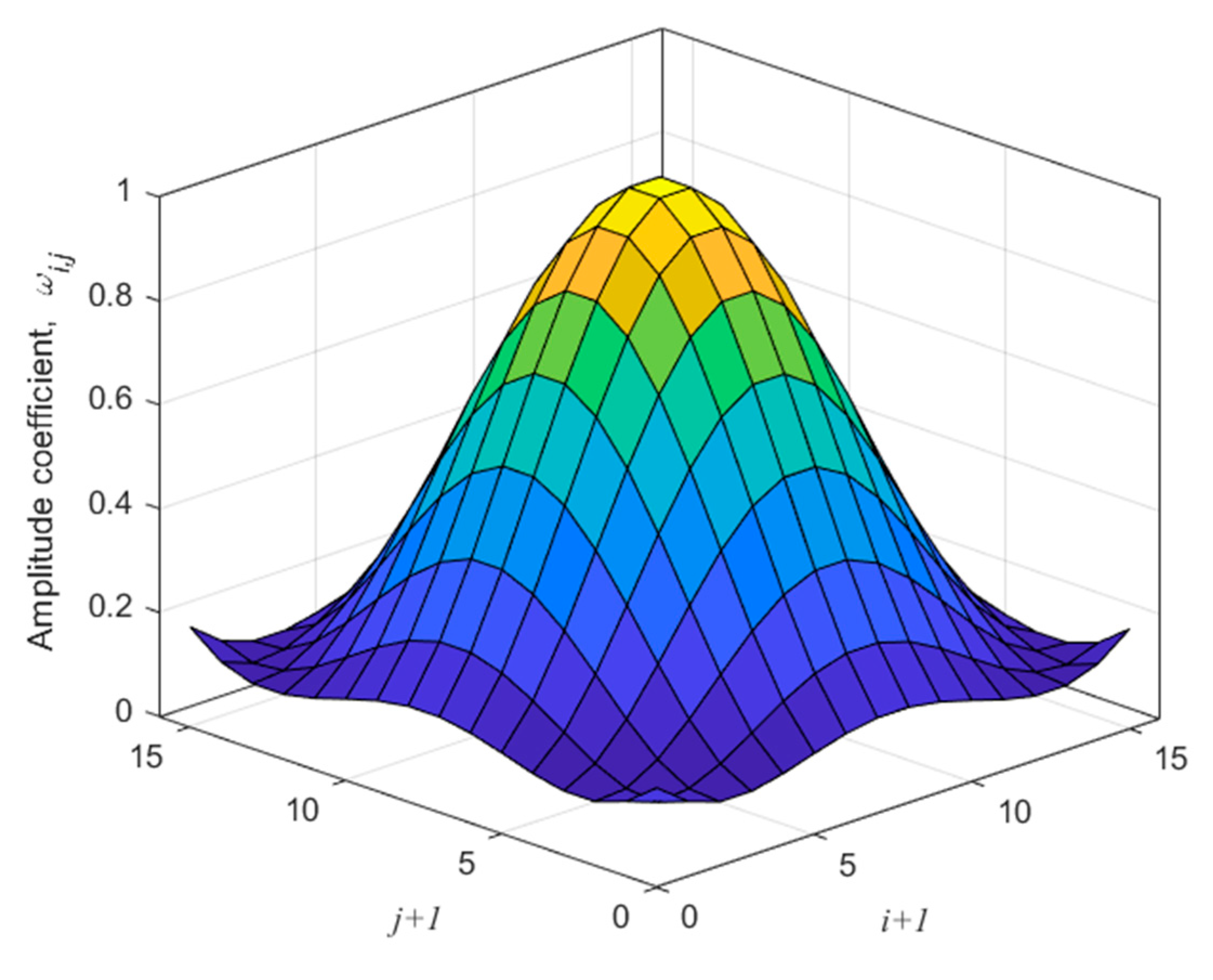
3.2. Performance of Adaptive Radial Tapering
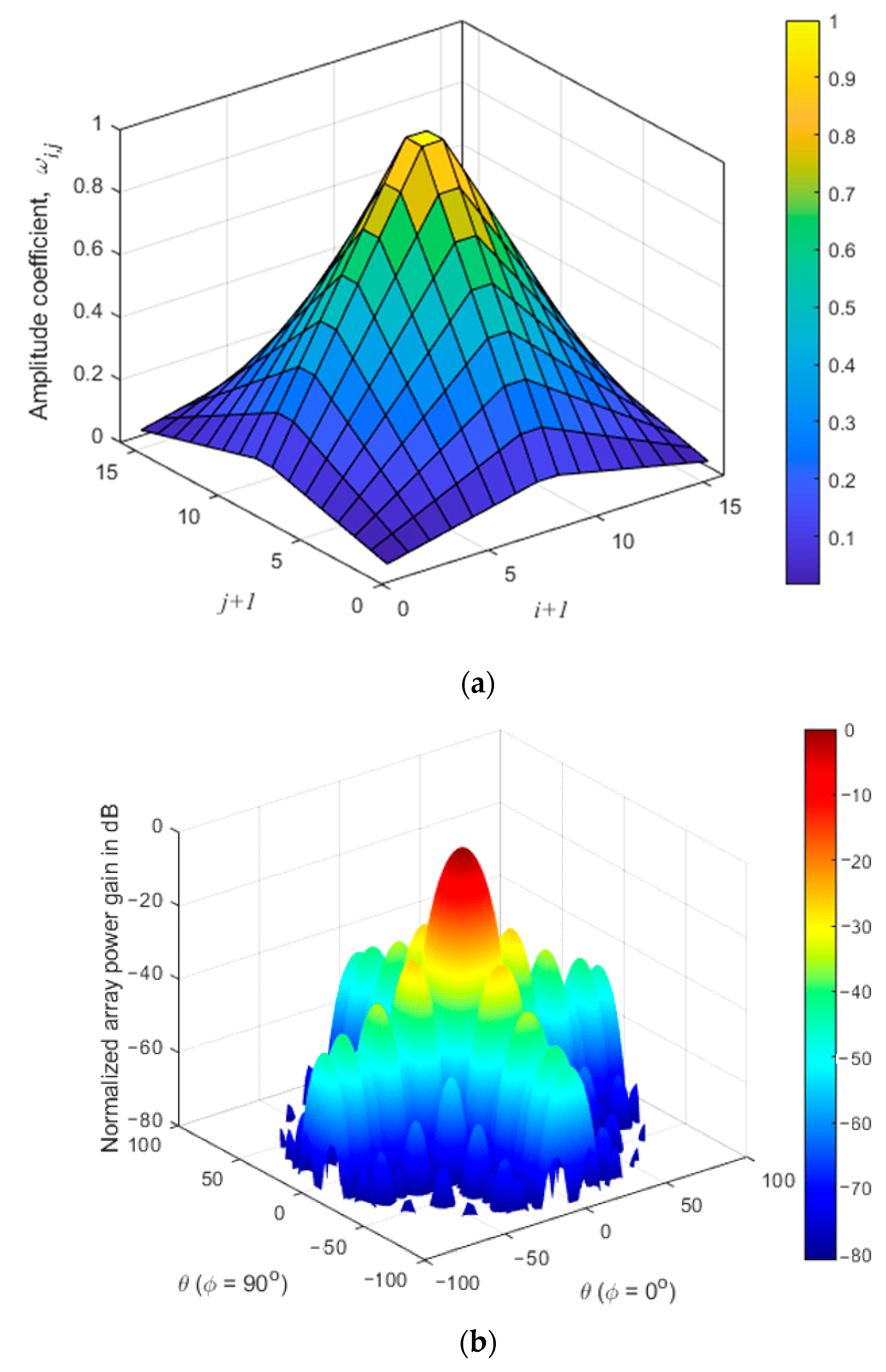
3.3. Performance of the Proposed Techniques for Rectangular Arrays
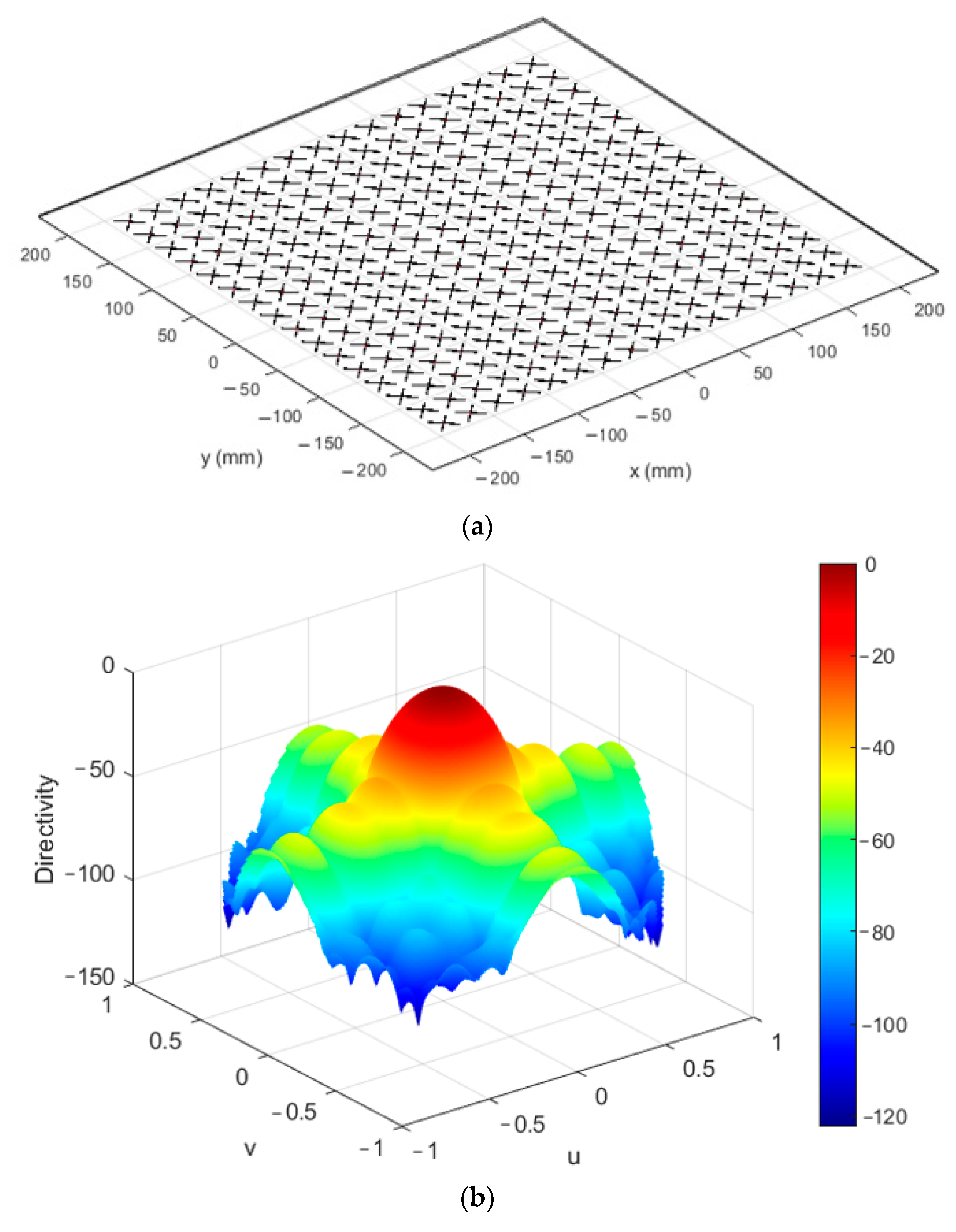
3.4. Simulation Results of the Proposed Techniques for Crossed-dipole 2D Arrays
- -
- Operating frequency: 5 GHz;
- -
- Dipole length: 0.476 ;
- -
- Antenna inter-separation distance: ;
- -
- Dipole width: .
4. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pałczyński, K.; Śmigiel, S.; Gackowska, M.; Ledziński, D.; Bujnowski, S.; Lutowski, Z. IoT Application of Transfer Learning in Hybrid Artificial Intelligence Systems for Acute Lymphoblastic Leukemia Classification. Sensors 2021, 21, 8025. [Google Scholar] [CrossRef] [PubMed]
- Cray, B.A.; Kirsteins, I. A Comparison of Optimal SONAR Array Amplitude Shading Coefficients. Acoustics 2019, 1, 808–815. [Google Scholar] [CrossRef]
- Said, O.; Albagory, Y.; Nofal, M.; Al Raddady, F. IoT-RTP and IoT-RTCP: Adaptive Protocols for Multimedia Transmission Over Internet Of Things Environments. IEEE Access 2017, 5, 16757–16773. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Al-Rizzo, H. Beamforming Optimization in Internet of Things Applications Using Robust Swarm Algorithm in Conjunction with Connectable and Collaborative Sensors. Sensors 2020, 20, 2048. [Google Scholar] [CrossRef]
- Sabban, A. Active compact wearable body area networks for wireless communication, medical and IoT applications. Appl. Syst. Innov. 2018, 1, 46. [Google Scholar] [CrossRef]
- Ruiz-de-Azua, J.A.; Garzaniti, N.; Golkar, A.; Calveras, A.; Camps, A. Towards Federated Satellite Systems and Internet of Satellites: The Federation Deployment Control Protocol. Remote Sens. 2021, 13, 982. [Google Scholar] [CrossRef]
- Mujkic, S.; Kasapovic, S.; Abuibaid, M. Energy-efficient resource optimization for massive mimo networks considering network load. Comput. Mater. Contin. 2022, 71, 871–888. [Google Scholar]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Bogale, T.E.; Le, L.B. Massive MIMO and mmwave for 5G wireless HetNet: Potential benefits and challenges. IEEE Veh. Technol. Mag. 2016, 11, 64–75. [Google Scholar] [CrossRef]
- Mohammed, S.L.; Alsharif, M.H.; Gharghan, S.K.; Khan, I.; Albreem, M. Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry 2019, 11, 1424. [Google Scholar] [CrossRef]
- Riviello, D.G.; Di Stasio, F.; Tuninato, R. Performance Analysis of Multi-User MIMO Schemes under Realistic 3GPP 3-D Channel Model for 5G mmWave Cellular Networks. Electronics 2022, 11, 330. [Google Scholar] [CrossRef]
- Artiga, X.; Perruisseau-Carrier, J.; Pérez-Neira, A.I. Antenna array configurations for massive MIMO outdoor base stations. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM 2014), A Coruna, Spain, 22–25 June 2014; pp. 281–284. [Google Scholar]
- Nofal, M.; Aljahdali, S.; Albagory, Y. Tapered beamforming for concentric ring arrays. AEU-Int. J. Electron. Commun. 2012, 67, 58–63. [Google Scholar] [CrossRef]
- Rohit, H.R.; Sachin, B.S.; Aditya, P.; Bhishm, T.; Premananda, B.S. Performance evaluation of various beamforming techniques for phased array antennas. In Proceedings of the 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 1–3 July 2020; pp. 1–6. [Google Scholar]
- Deepshikha, A.R.; Raut, A.; Bazil Raj, A.A. Signal Processing for Digital Beamforming on Transmit in MIMO Radar. In Proceedings of the Second International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 15–17 July 2020; pp. 1106–1111. [Google Scholar]
- Prabhu, K.M.M. Window Functions and Their Applications in Signal Processing; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Aljahdali, S.; Nofal, M.; Albagory, Y. A modified array processing technique based on Kaiser window for concentric circular arrays. In Proceedings of the 2012 International Conference on Multimedia Computing and Systems, ICMCS 2012, Tangiers, Morocco, 10–12 May 2012. [Google Scholar]
- Albagory, Y. Sectorized hamming concentric circular arrays for stratospheric platforms cellular design. Int. J. Comput. Netw. Inf. Secur. 2013, 5, 21–27. [Google Scholar] [CrossRef][Green Version]
- Albagory, Y.; Said, O. Concentric Circular Arrays for Stratospheric High-Altitude Platforms Wireless Sensor Networks. Wirel. Pers. Commun. 2015, 81, 593–605. [Google Scholar] [CrossRef]
- Alsharif, S.; Saeed, R.A.; Albagory, Y. An efficient haps cross-layer design to mitigate covid-19 consequences. Intell. Autom. Soft Comput. 2022, 31, 43–59. [Google Scholar] [CrossRef]
- Available online: https://www.mathworks.com/products/matlab.html (accessed on 6 May 2022).


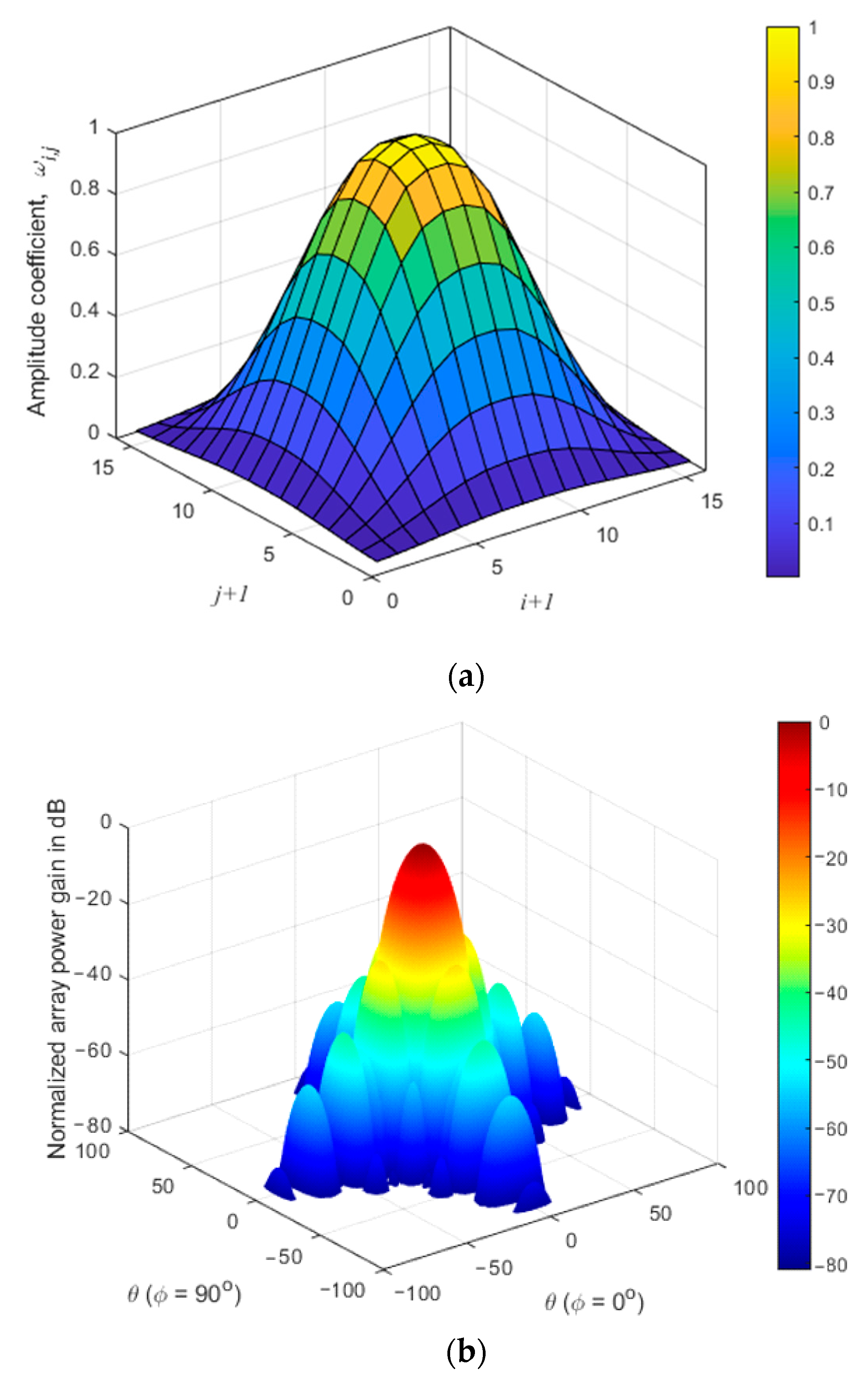
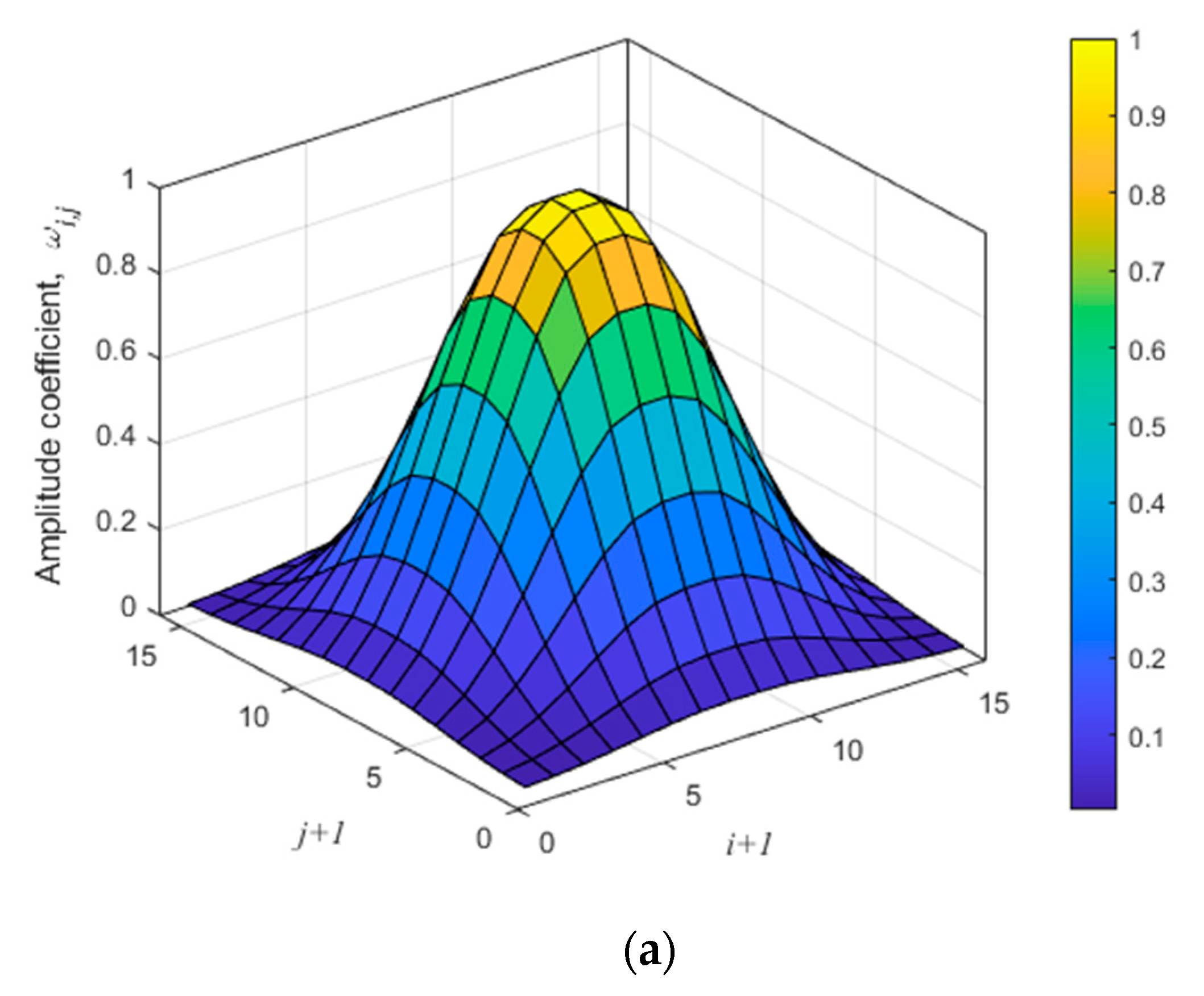



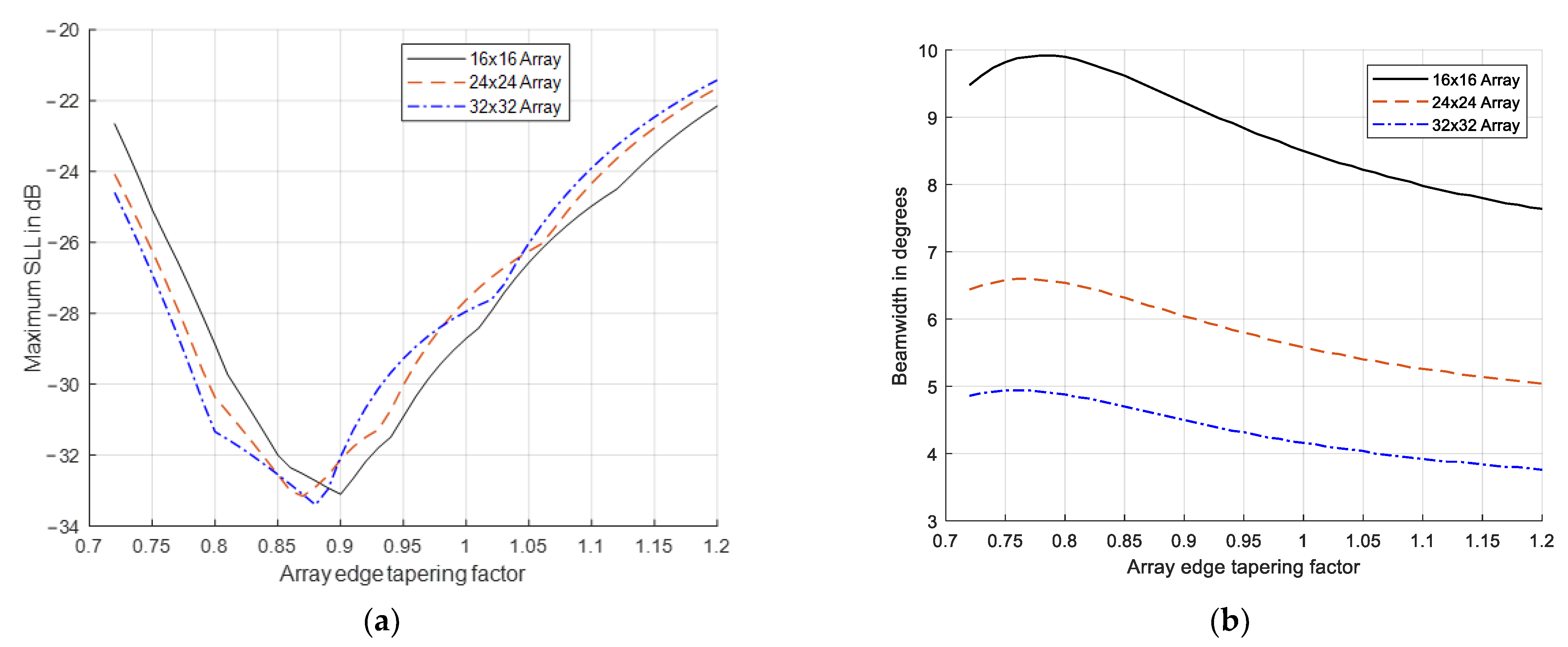
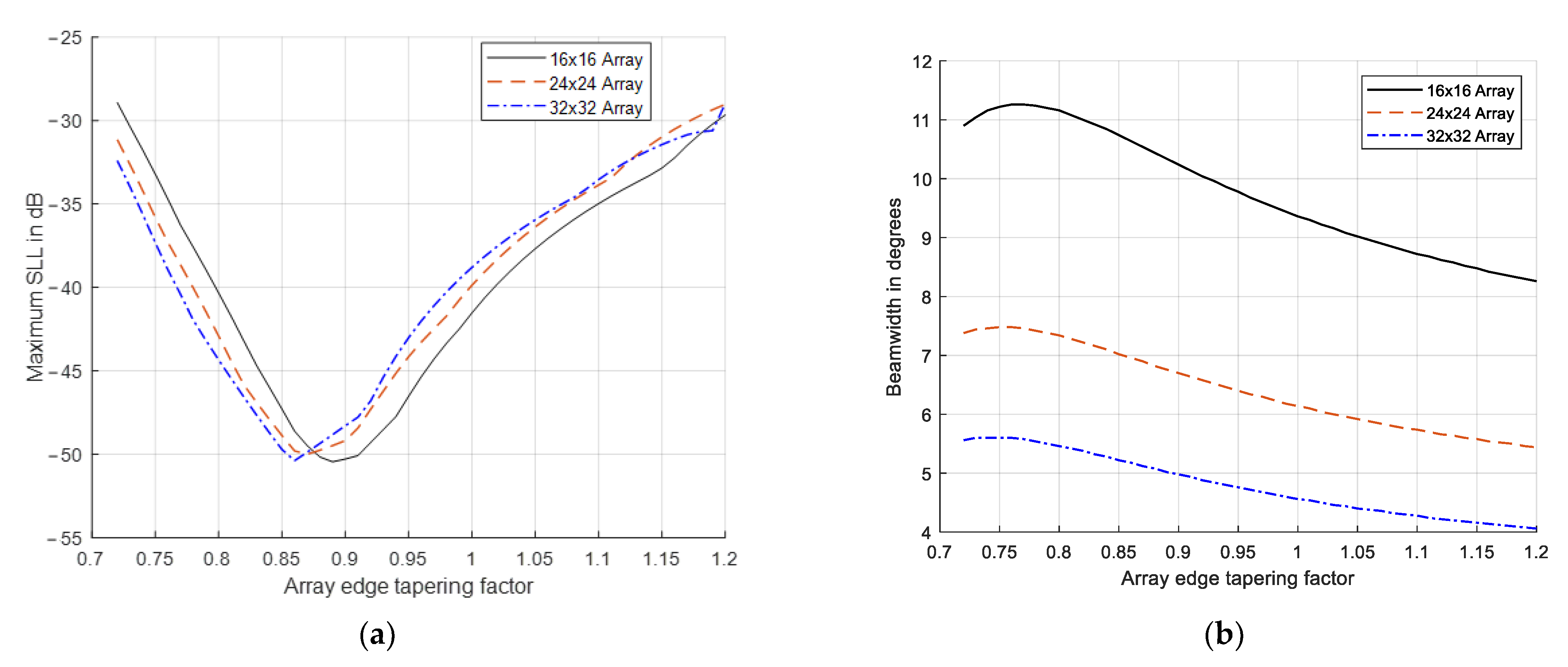


| Maximum SLL in dB | Beamwidth in Degrees | |||||
|---|---|---|---|---|---|---|
| Array Size | 16 × 16 | 24 × 24 | 32 × 32 | 16 × 16 | 24 × 24 | 32 × 32 |
| Triangular window(Figure 4) | −26.34 | −26.5 | −26.47 | 8.66 | 5.88 | 4.44 |
| Hamming window (Figure 5) | −26.2 | −29.4 | −31.37 | 8.26 | 5.72 | 4.38 |
| Cosine-square window (Figure 6) | −27.3 | −28.6 | −29.21 | 9.54 | 6.54 | 4.96 |
| Blackman window (Figure 7) | −35 | −38.66 | −41.62 | 9.78 | 6.9 | 5.34 |
| Maximum SLL in dB | Beamwidth in Degrees | |||||
|---|---|---|---|---|---|---|
| Array Size | 16 × 16 | 24 × 24 | 32 × 32 | 16 × 16 | 24 × 24 | 32 × 32 |
| Triangular window (Figure 8) | −27.56 dB | −27.63 dB | −27.8 dB | 8.46 | 6 | 4.12 |
| 0.89 | 0.83 | 0.89 | 0.89 | 0.83 | 0.89 | |
| Hamming window (Figure 9) | −32.18 dB | −33.33 dB | −33.6 dB | 8.46 | 5.6 | 4.24 |
| 0.87 | 0.87 | 0.84 | 0.87 | 0.87 | 0.84 | |
| Cosine-square window (Figure 10) | −33.1 dB | −33.11 dB | −33.4 dB | 9.22 | 6.2 | 4.58 |
| 0.9 | 0.87 | 0.88 | 0.81 | 0.87 | 0.88 | |
| Blackman window (Figure 11) | −50.45 dB | −50 dB | −50.38 dB | 10.34 | 6.9 | 5.18 |
| 0.89 | 0.87 | 0.86 | 0.89 | 0.87 | 0.86 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albagory, Y.; Alraddady, F. Optimum Extrapolation Techniques for Two-Dimensional Antenna Array Tapered Beamforming. Electronics 2022, 11, 1995. https://doi.org/10.3390/electronics11131995
Albagory Y, Alraddady F. Optimum Extrapolation Techniques for Two-Dimensional Antenna Array Tapered Beamforming. Electronics. 2022; 11(13):1995. https://doi.org/10.3390/electronics11131995
Chicago/Turabian StyleAlbagory, Yasser, and Fahad Alraddady. 2022. "Optimum Extrapolation Techniques for Two-Dimensional Antenna Array Tapered Beamforming" Electronics 11, no. 13: 1995. https://doi.org/10.3390/electronics11131995
APA StyleAlbagory, Y., & Alraddady, F. (2022). Optimum Extrapolation Techniques for Two-Dimensional Antenna Array Tapered Beamforming. Electronics, 11(13), 1995. https://doi.org/10.3390/electronics11131995







